Aerodynamic Characteristics of a Square Cylinder with Vertical-Axis Wind Turbines at Corners
Abstract
:1. Introduction
2. Numerical Simulation Configurations
2.1. Numerical Method
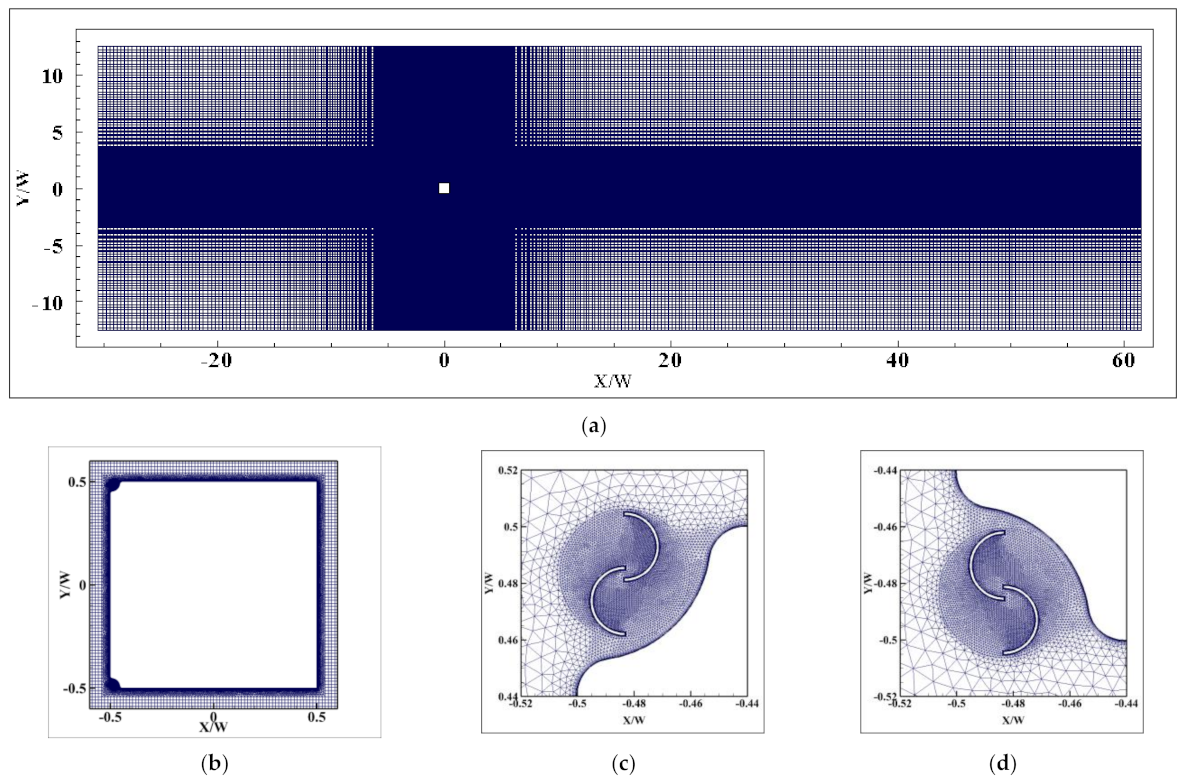
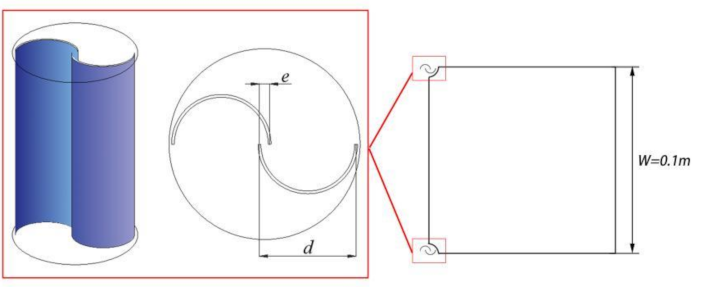
2.2. Computational Configuration and Mesh Arrangement
2.3. Grid Size and Time Step Configuration
2.4. Simulation Cases
3. Results and Discussions
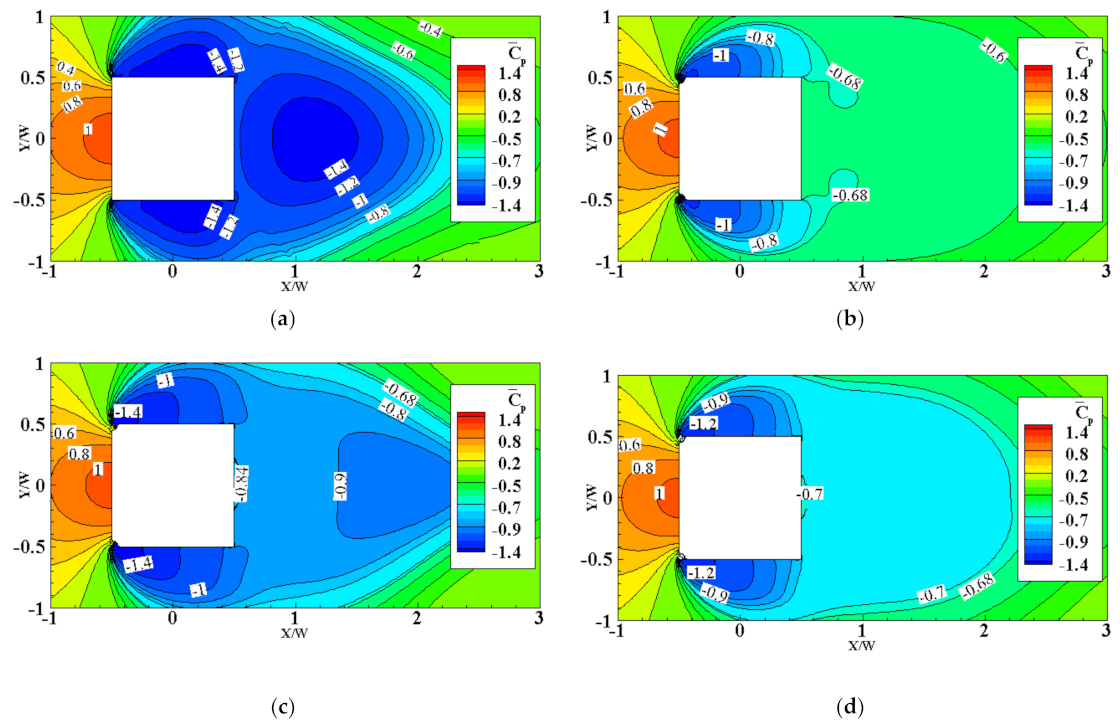
3.1. Mean Pressure Coefficients
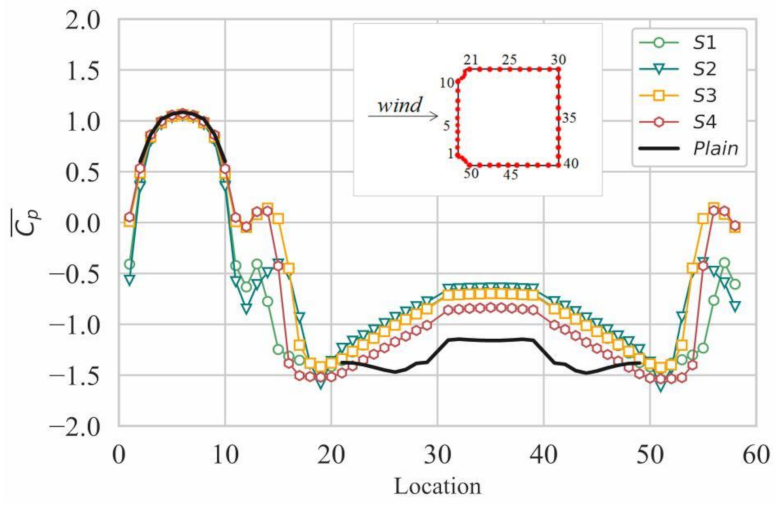
3.1.1. Stationary Wind Turbines at Cylinder Corners
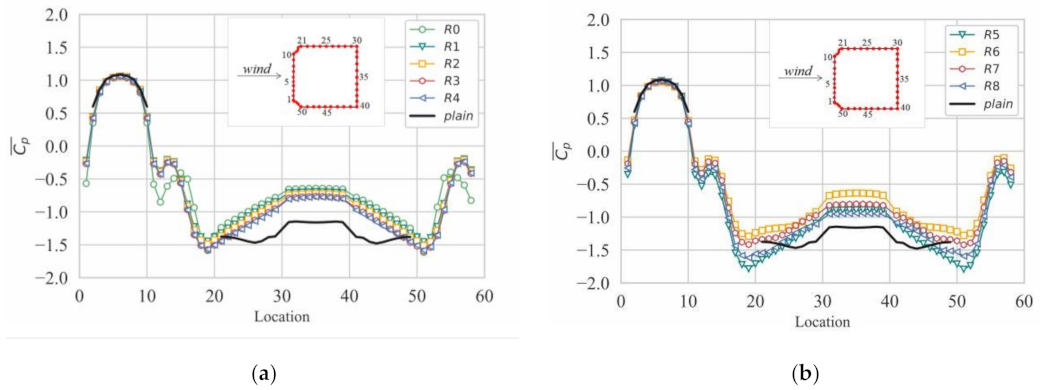
3.1.2. Rotating Wind Turbines at Cylinder Corners
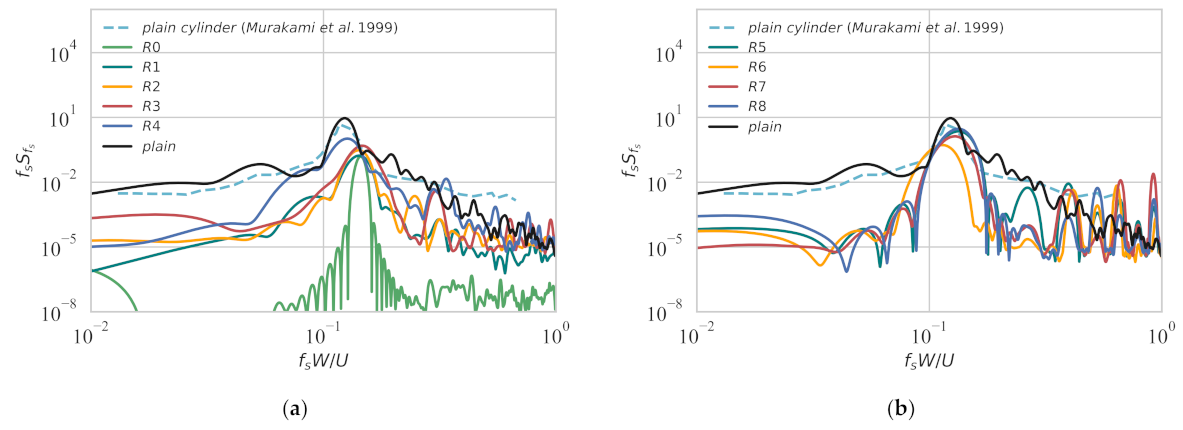
3.2. Force Coefficients and Vortex Shedding Characteristics
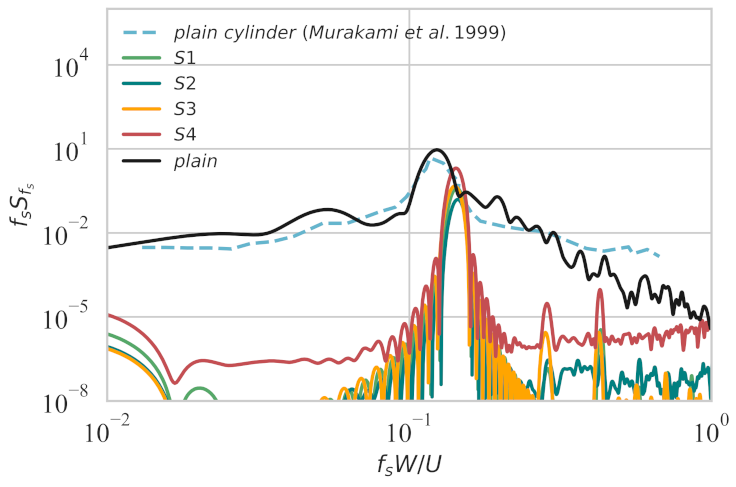
3.2.1. Stationary Wind Turbines at Cylinder Corners
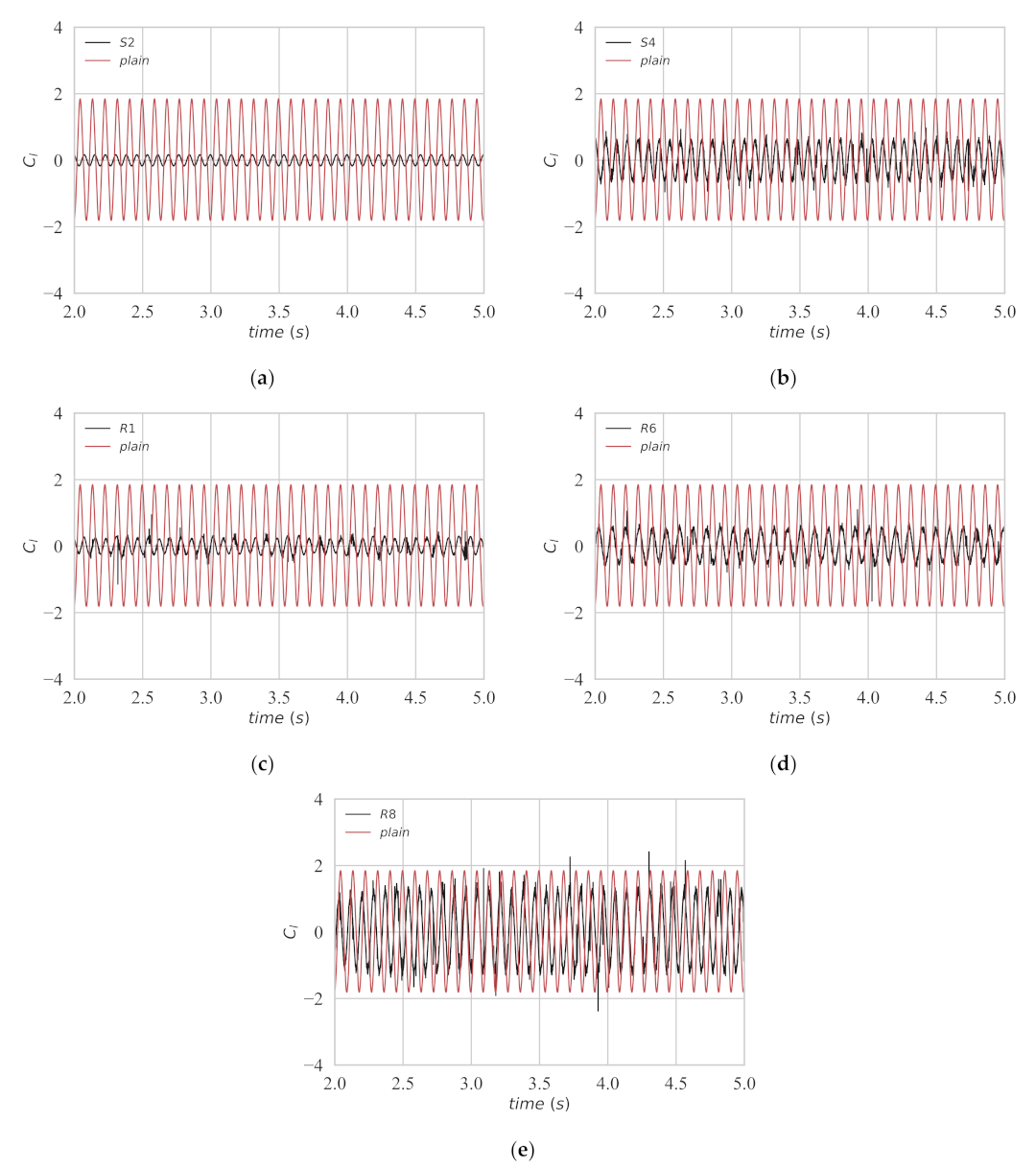
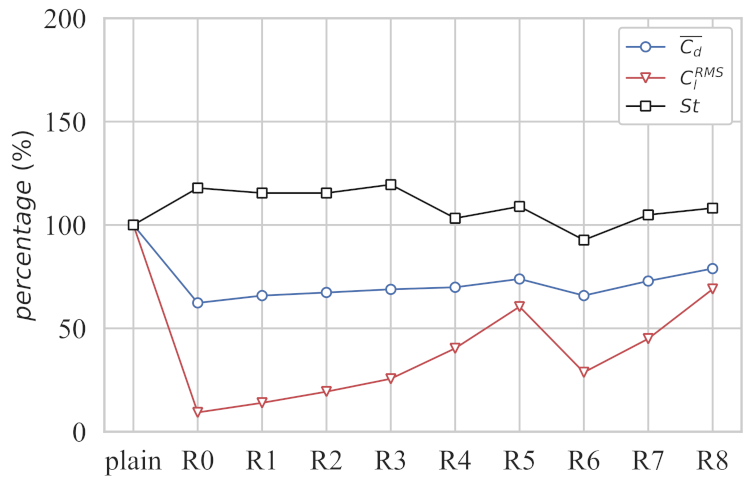
3.2.2. Rotating Wind Turbines at Cylinder Corners
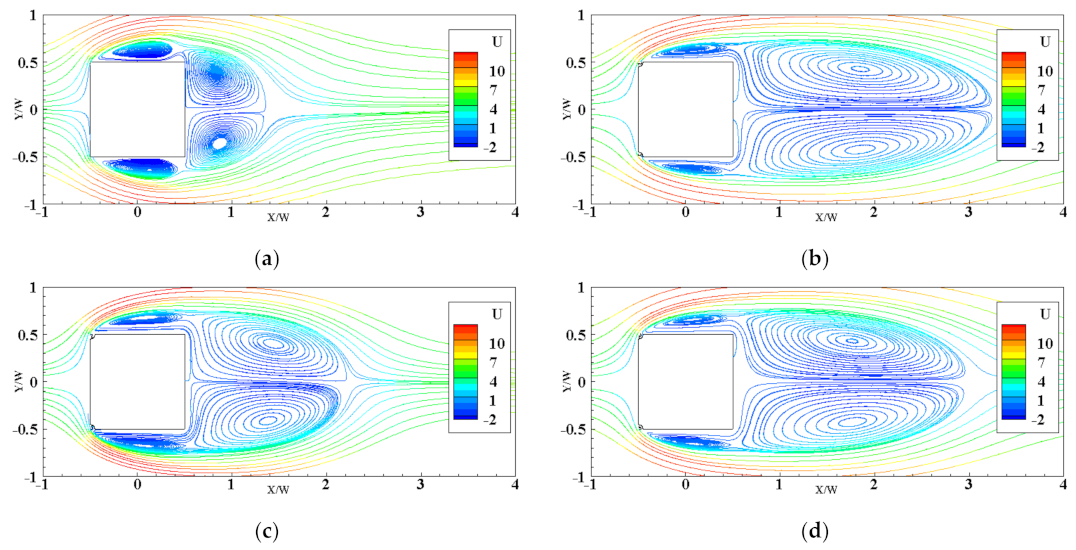
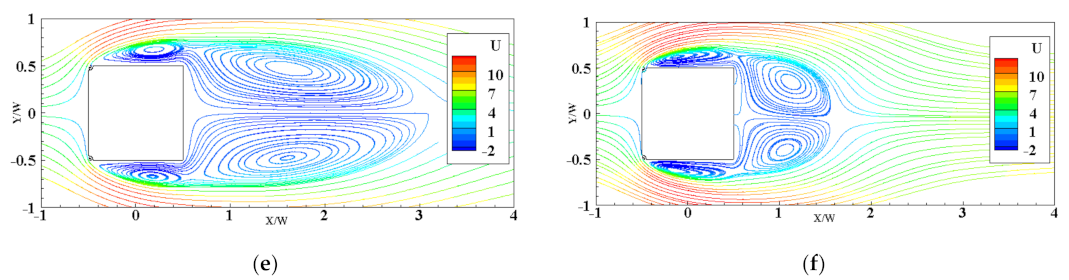
3.3. Flow Pattern around the Cylinders
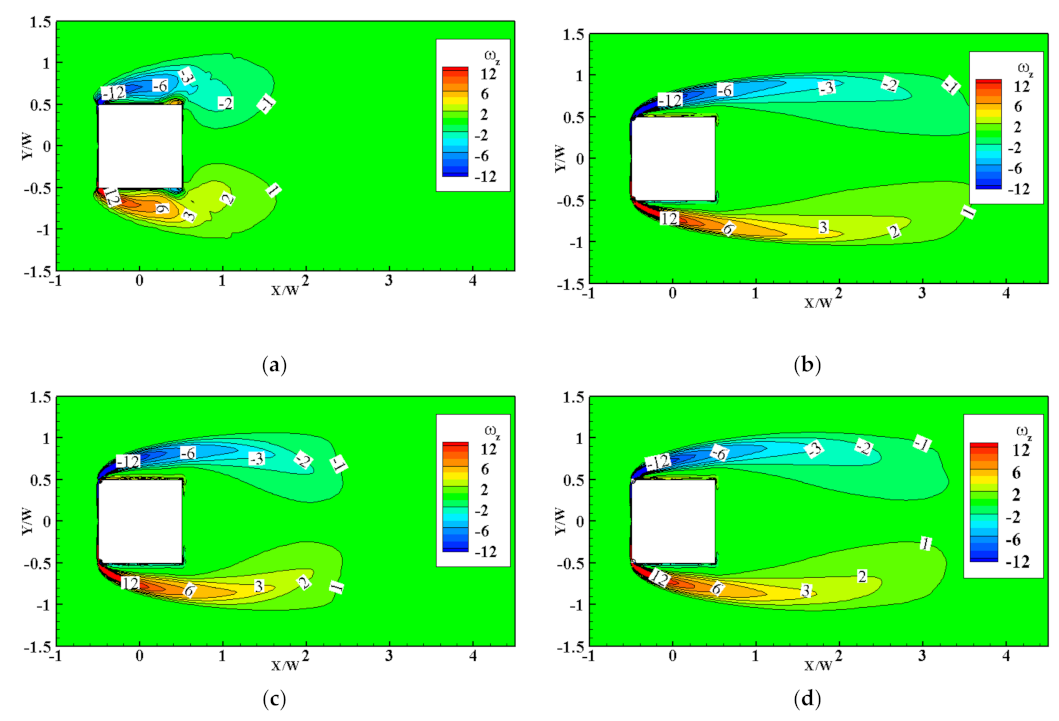
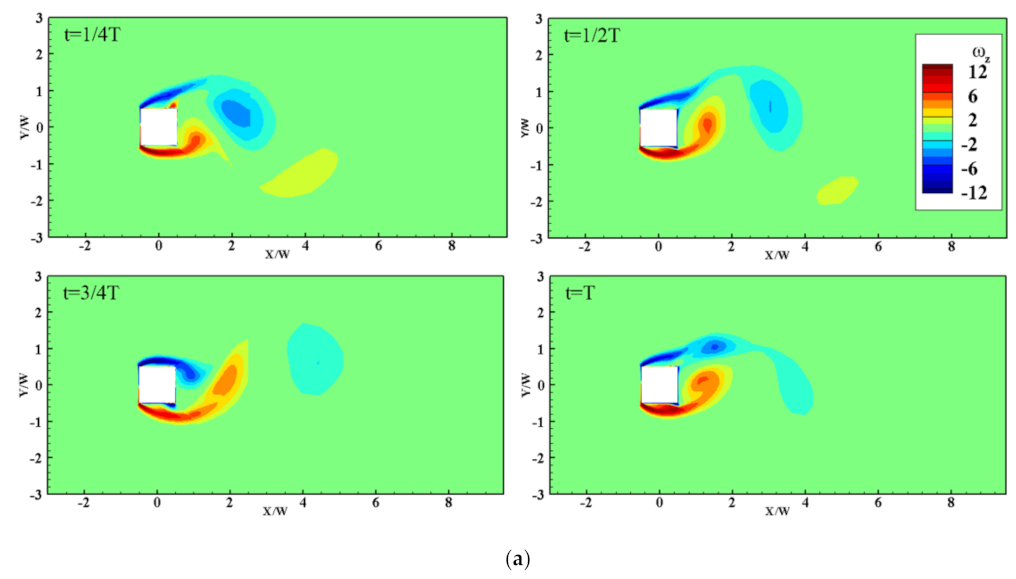
3.3.1. Stationary Wind Turbines at Cylinder Corners
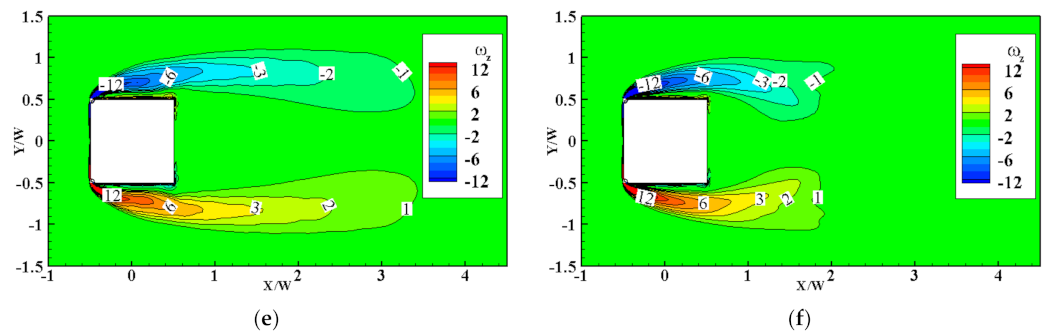
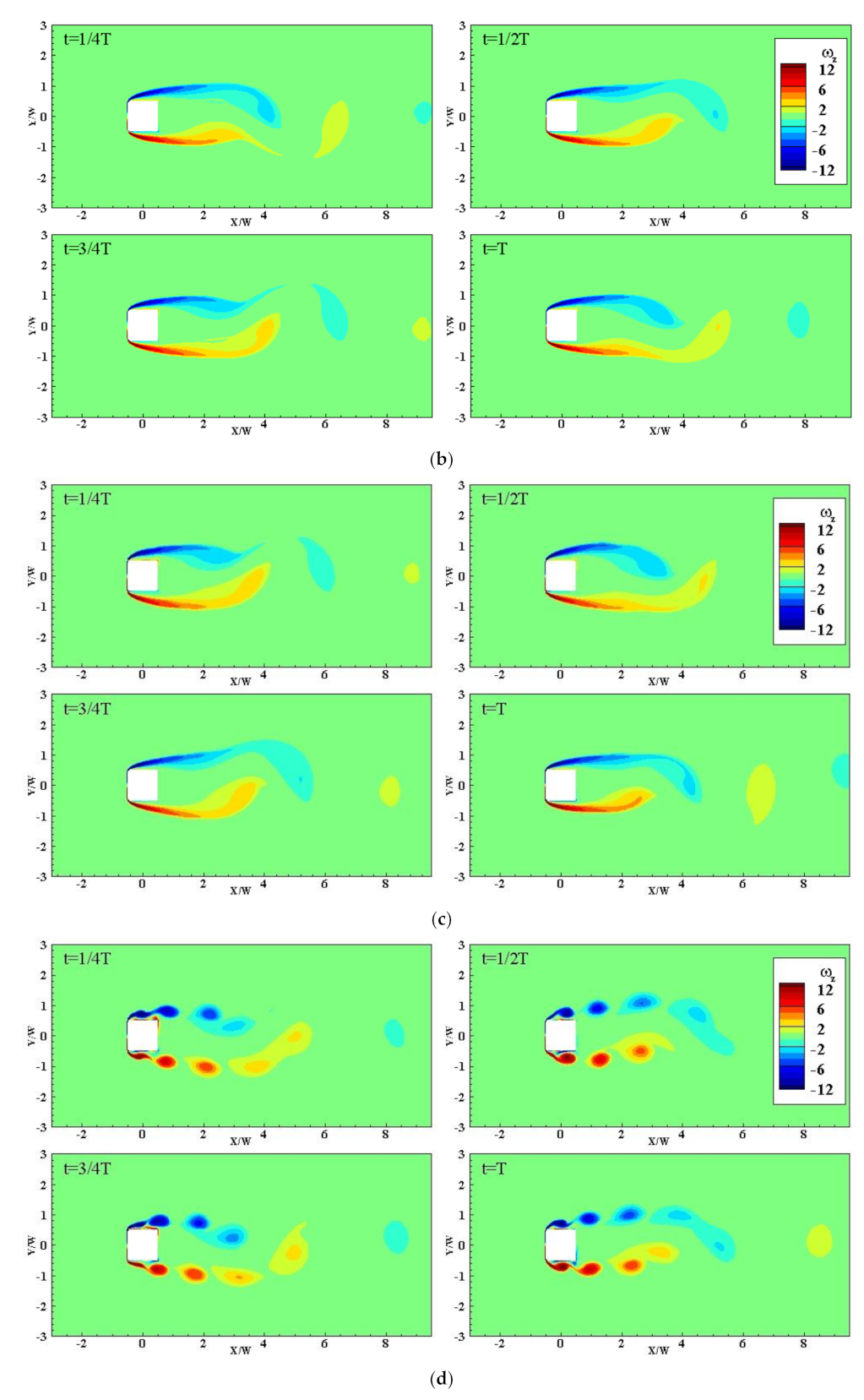
3.3.2. Rotating Wind Turbines at Cylinder Corner
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Carassale, L.; Freda, A.; Marre-Brunenghi, M. Experimental investigation on the aerodynamic behavior of square cylinders with rounded corners. J. Fluids Struct. 2014, 44, 195–204. [Google Scholar] [CrossRef]
- Tamura, T.; Miyagi, T. The effect of turbulence on aerodynamic forces on a square cylinder with various corner shapes. J. Wind. Eng. Ind. Aerodyn. 1999, 83, 135–145. [Google Scholar] [CrossRef]
- Tamura, T.; Miyagi, T.; Kitagishi, T. Numerical prediction of unsteady pressures on a square cylinder with various corner shapes. J. Wind. Eng. Ind. Aerodyn. 1998, 74, 531–542. [Google Scholar] [CrossRef]
- He, G.S.; Li, N.; Wang, J.J. Drag reduction of square cylinders with cut-corners at the front edges. Exp. Fluids 2014, 55, 1745. [Google Scholar] [CrossRef]
- Kurata, M.; Ueda, Y.; Kida, T.; Iguchi, M. Drag reduction due to cut-corners at the front-edge of a rectangular cylinder with the length-to-breadth ratio being less than or equal to unity. J. Fluids Eng. 2009, 131, 064501. [Google Scholar] [CrossRef]
- Tse, K.; Hitchcock, P.A.; Kwok, K.C.; Thepmongkorn, S.; Chan, C.M. Economic perspectives of aerodynamic treatments of square tall buildings. J. Wind. Eng. Ind. Aerodyn. 2009, 97, 455–467. [Google Scholar] [CrossRef]
- Kwok, K.; Wilhelm, P.A.; Wilkie, B.G. Effect of edge configuration on wind-induced response of tall buildings. Eng. Struct. 1988, 10, 135–140. [Google Scholar] [CrossRef]
- Kwok, K.C.; Bailey, P.A. Aerodynamic devices for tall buildings and structures. J. Eng. Mech. 1987, 113, 349–365. [Google Scholar] [CrossRef]
- Bearman, P.W.; Trueman, D.M. An investigation of the flow around rectangular cylinders. Aeronaut. Q. 1972, 23, 229–237. [Google Scholar] [CrossRef]
- Modi, V.J.; Deshpande, V.S. Fluid dynamics of a cubic structure as affected by momentum injection and height. J. Wind. Eng. Ind. Aerodyn. 2001, 89, 445–470. [Google Scholar] [CrossRef]
- Munshi, S.R.; Modi, V.J.; Yokomizo, T. Aerodynamics and dynamics of rectangular prisms with momentum injection. J. Fluids Struct. 1997, 11, 873–892. [Google Scholar] [CrossRef]
- Hu, G.; Tse, K.T.; Wei, M.; Naseer, R.; Abdelkefi, A.; Kwok, K. Experimental investigation on the efficiency of circular cylinder-based wind energy harvester with different rod-shaped attachments. Appl. Energy 2018, 226, 682–689. [Google Scholar] [CrossRef]
- Li, Q.S.; Chen, F.B.; Li, Y.G.; Lee, Y.Y. Implementing wind turbines in a tall building for power generation: A study of wind loads and wind speed amplifications. J. Wind. Eng. Ind. Aerodyn. 2013, 116, 70–82. [Google Scholar] [CrossRef]
- Jafari, S.; Kwok, K.C.; Hassanli, S. Integration of wind turbines in tall buildings for wind power generation. In Proceedings of the 8th International Colloquium on Bluff Body Aerodynamics and Applications, Boston, MA, USA, 7–11 June 2016. [Google Scholar]
- Cochran, B.C.; Damiani, R.R. Harvesting wind power from tall buildings. In Wind Power; CPP, Inc.: Mountain View, CA, USA, 2008. [Google Scholar]
- Li, T.; Qin, D.; Zhang, J. Effect of RANS turbulence model on aerodynamic behavior of trains in crosswind. Chin. J. Mech. Eng. 2019, 32, 85. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Yang, M.; Qian, B. The influence of reduced cross-section on pressure transients from high-speed trains intersecting in a tunnel. J. Wind. Eng. Ind. Aerodyn. 2020, 201, 104–161. [Google Scholar] [CrossRef]
- Deng, E.; Yang, W.; He, X.; Zhu, Z.; Wang, H.; Wang, Y. Aerodynamic response of high-speed trains under crosswind in a bridge-tunnel section with or without a wind barrier. J. Wind. Eng. Ind. Aerodyn. 2021, 210, 104–502. [Google Scholar] [CrossRef]
- Wang, T.; Wu, F.; Yang, M.; Ji, P.; Qian, B. Reduction of pressure transients of high-speed train passing through a tunnel by cross-section increase. J. Wind. Eng. Ind. Aerodyn. 2018, 183, 235–242. [Google Scholar] [CrossRef]
- Rodi, W.; Ferziger, J.H.; Breuer, M.; Pourquie, M. Status of large eddy simulation: Results of a workshop. Trans.-Am. Soc. Mech. Eng. J. Fluids Eng. 1997, 119, 248–262. [Google Scholar] [CrossRef]
- Voke, P.R. Flow past a square cylinder: Test case LES2. In Direct and Large-Eddy Simulation II; Kleiser, L., Ed.; Springer: Dordrecht, The Netherlands, 1997; Volume 5, pp. 355–373. [Google Scholar]
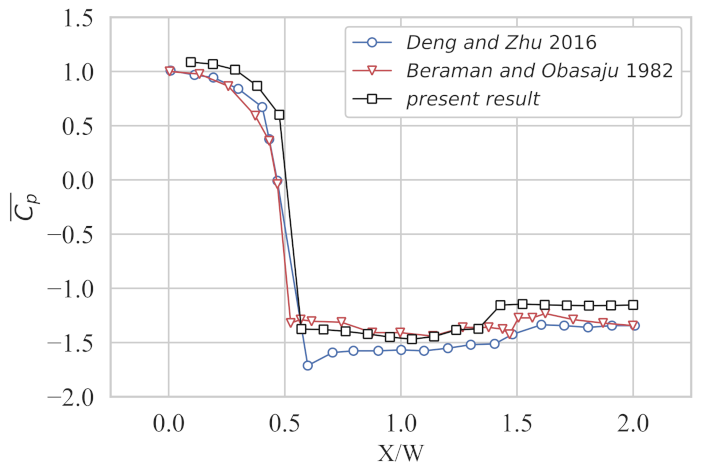
- Deng, Y.; Zhu, Z. Numerical simulation of two dimensional flow around square column at full wind Angle. J. Railw. Sci. Eng. 2016, 13, 1796–1802. [Google Scholar]
- Bearman, P.W.; Obasaju, E.D. An experimental study of pressure fluctuations on fixed and oscillating square-section cylinders. J. Fluid Mech. 1982, 119, 297–321. [Google Scholar] [CrossRef]
- Lee, B.E. The effect of turbulence on the surface pressure field of a square prism. J. Fluid Mech. 1975, 69, 263–282. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, Q.; Hu, G.; Chen, X.; Li, C.; Xiao, Y. Aerodynamic characteristics of a square cylinder with corner fins. Adv. Bridge Eng. 2021, 2, 20. [Google Scholar] [CrossRef]
- Lyn, D.A.; Einav, S.; Rodi, W.; Park, J.H. A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder. J. Fluid Mech. 1995, 304, 285–319. [Google Scholar] [CrossRef]
- Lyn, D.A.; Rodi, W. The flapping shear layer formed by flow separation from the forward corner of a square cylinder. J. Fluid Mech. 1994, 267, 353–376. [Google Scholar] [CrossRef]
- Hangan, H.M. Wake Aerodynamics for 2D Bluff Bodies. Ph.D. Thesis, The University of Western Ontario, London, ON, Cnada, 1997. [Google Scholar]
- Xu, J. Effects of Vertical Clearance on Aerodynamic Characteristics of Long-Span Bridge Girders; Hunan University: Changsha, China, 2014. [Google Scholar]
- Wenehenubun, F.; Saputra, A.; Sutanto, H. An experimental study on the performance of Savonius wind turbines related with the number of blades. Energy Procedia 2015, 68, 297–304. [Google Scholar] [CrossRef] [Green Version]
- Murakami, S.; Iizuka, S.; Ooka, R. CFD analysis of turbulent flow past square cylinder using dynamic LES. J. Fluids Struct. 1999, 13, 1097–1112. [Google Scholar] [CrossRef]
- Gao, D.; Chen, G.; Chen, W.; Huang, Y.; Li, H. Active control of circular cylinder flow with windward suction and leeward blowing. Exp. Fluids 2019, 2, 60. [Google Scholar] [CrossRef]
- Konstantinidis, E.; Balabani, S.; Yianneskis, M. The effect of flow perturbations on the near wake characteristics of a circular cylinder. J. Fluids Struct. 2003, 18, 367–386. [Google Scholar] [CrossRef]
- Gao, D.; Chen, G.; Huang, Y.; Chen, W.; Li, H. Flow characteristics of a fixed circular cylinder with an upstream splitter plate: On the plate-length sensitivity. Exp. Therm. Fluid Sci. 2020, 117, 110135. [Google Scholar] [CrossRef]
- Gao, D.; Huang, Y.; Chen, W.; Chen, G.; Li, H. Control of circular cylinder flow via bilateral splitter plates. Phys. Fluids 2019, 31, 057105. [Google Scholar] [CrossRef]
- Bearman, P.W. Investigation of the flow behind a two-dimensional model with a blunt trailing edge and fitted with splitter plates. J. Fluid Mech. 1965, 21, 241–255. [Google Scholar] [CrossRef]
- Chen, W.; Xin, D.; Xu, F.; Li, H.; Ou, J.; Hu, H. Suppression of vortex-induced vibration of a circular cylinder using suction-based flow control. J. Fluids Struct. 2013, 42, 25–39. [Google Scholar] [CrossRef]
- Gao, D.; Meng, H.; Huang, Y.; Chen, G.; Chen, W. Active flow control of the dynamic wake behind a square cylinder using combined jets at the front and rear stagnation points. Phys. Fluids 2021, 33, 047–101. [Google Scholar] [CrossRef]
- Lam, K.; Lin, Y.F. Large eddy simulation of flow around wavy cylinders at a subcritical Reynolds number. Int. J. Heat Fluid Flow 2008, 29, 1071–1088. [Google Scholar] [CrossRef]
- Gao, D.; Chen, W.; Li, H.; Hu, H. Flow around a circular cylinder with slit. Exp. Therm. Fluid Sci. 2017, 82, 287–301. [Google Scholar] [CrossRef]
- Chen, W.; Gao, D.; Yuan, W.; Li, H.; Hu, H. Passive jet control of flow around a circular cylinder. Exp. Fluids 2015, 11, 56. [Google Scholar] [CrossRef]
- Gao, D.; Chen, W.; Chen, G.; Li, H. Effects of steady wake-jets on subcritical cylinder flow. Exp. Therm. Fluid Sci. 2019, 102, 575–588. [Google Scholar] [CrossRef]
- Gao, D.; Deng, Z.; Yang, W.; Chen, W. Review of the excitation mechanism and aerodynamic flow control of vortex-induced vibration of the main girder for long-span bridges: A vortex-dynamics approach. J. Fluids Struct. 2021, 105, 103348. [Google Scholar] [CrossRef]



| Grid Schemes | Cell Numbers | |||||
|---|---|---|---|---|---|---|
| G1 | 1.1 × 105 | 0.66 | 4 × 10−5 | 1.43 | 0.69 | 0.136 |
| G2 | 1.3 × 105 | 0.52 | 4 × 10−5 | 1.41 | 0.63 | 0.136 |
| G3 | 1.7 × 105 | 0.55 | 4 × 10−5 | 1.42 | 0.61 | 0.136 |
| G4 | 2.4 × 105 | 0.57 | 4 × 10−5 | 1.47 | 0.78 | 0.134 |
| G5 | 3.0 × 105 | 0.61 | 4 × 10−5 | 1.48 | 0.78 | 0.134 |
| Data from Previous Studies | Re | δcd | |||
|---|---|---|---|---|---|
| Experimental results: | |||||
| [24] | 1.76 × 105 | 2.05 | - | 0.122 | 2.93% |
| [26,27] | 2.14 × 104 | 2.1 | - | 0.132 | 5.24% |
| [28] | 2.20 × 104 | 2.09 | 0.95 | 0.123 | 4.78% |
| Simulation results: | |||||
| [22] | 6.0 × 104 | 2.26 | 1.52 | 0.132 | 11.9% |
| [25] | 1.9 × 104 | 2.37 | 1.37 | 0.122 | 16.0% |
| [29] | 2.2 × 104 | 2.26 | 1.60 | 0.136 | 11.9% |
| Present simulation results: | 6.0 × 104 | 1.99 | 1.29 | 0.123 | - |
| Cases | Plain | R0 | R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 |
|---|---|---|---|---|---|---|---|---|---|---|
| Vt/fs | - | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 | 2 | 3 | 4 |
| Vt (r/s) | - | 0 | 2.38 | 4.75 | 7.13 | 9.50 | 11.88 | 23.76 | 35.64 | 47.52 |
| Cases | Plain | S1 | S2 | S3 | S4 |
|---|---|---|---|---|---|
| - |
| Case | Cell Numbers | |||||
|---|---|---|---|---|---|---|
| Plain cylinder | 2.0 × 104 | 1.4 | 2 × 10−4 | 1.99 | 1.29 | 0.123 |
| S1 | 2.4 × 105 | 0.41 | 4 × 10−5 | 1.26 | 0.19 | 0.144 |
| S2 | 2.4 × 105 | 0.43 | 4 × 10−5 | 1.24 | 0.12 | 0.145 |
| S3 | 2.4 × 105 | 0.44 | 4 × 10−5 | 1.35 | 0.21 | 0.141 |
| S4 | 2.4 × 105 | 0.59 | 4 × 10−5 | 1.48 | 0.43 | 0.143 |
| Case | Cell Numbers | |||||
|---|---|---|---|---|---|---|
| Plain cylinder | 2.0 × 104 | 1.4 | 2 × 10−4 | 1.99 | 1.29 | 0.123 |
| R0 (S2) | 2.4 × 105 | 0.43 | 4 × 10−5 | 1.24 | 0.12 | 0.145 |
| R1 | 2.4 × 105 | 0.46 | 4 × 10−5 | 1.31 | 0.18 | 0.142 |
| R2 | 2.4 × 105 | 0.49 | 4 × 10−5 | 1.34 | 0.25 | 0.142 |
| R3 | 2.4 × 105 | 0.53 | 4 × 10−5 | 1.37 | 0.33 | 0.147 |
| R4 | 2.4 × 105 | 0.50 | 4 × 10−5 | 1.39 | 0.52 | 0.127 |
| R5 | 2.4 × 105 | 0.57 | 4 × 10−5 | 1.47 | 0.78 | 0.134 |
| R6 | 2.4 × 105 | 0.46 | 4 × 10−5 | 1.31 | 0.37 | 0.114 |
| R7 | 2.4 × 105 | 0.51 | 4 × 10−5 | 1.45 | 0.58 | 0.129 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Hu, G.; Zhang, D.; Kim, B.; Xu, F.; Xiao, Y. Aerodynamic Characteristics of a Square Cylinder with Vertical-Axis Wind Turbines at Corners. Appl. Sci. 2022, 12, 3515. https://doi.org/10.3390/app12073515
Wang Z, Hu G, Zhang D, Kim B, Xu F, Xiao Y. Aerodynamic Characteristics of a Square Cylinder with Vertical-Axis Wind Turbines at Corners. Applied Sciences. 2022; 12(7):3515. https://doi.org/10.3390/app12073515
Chicago/Turabian StyleWang, Zhuoran, Gang Hu, Dongqin Zhang, Bubryur Kim, Feng Xu, and Yiqing Xiao. 2022. "Aerodynamic Characteristics of a Square Cylinder with Vertical-Axis Wind Turbines at Corners" Applied Sciences 12, no. 7: 3515. https://doi.org/10.3390/app12073515
APA StyleWang, Z., Hu, G., Zhang, D., Kim, B., Xu, F., & Xiao, Y. (2022). Aerodynamic Characteristics of a Square Cylinder with Vertical-Axis Wind Turbines at Corners. Applied Sciences, 12(7), 3515. https://doi.org/10.3390/app12073515







