Numerical Modeling of Individual Plasma Dynamic Characteristics of a Light-Erosion MPC Discharge in Gases

Abstract

A mathematical model is formulated, and a numerical study of magneto-plasma compressor (MPC) discharges in gases for a wide range of changes in the main electrical parameters and the characteristics of the surrounding gas environment is carried out. The performed calculations showed, depending on the role of one or another heating mode (Ohmic, transient, and plasma dynamic), three different types of quasi-stationary spatial distributions of plasma parameters, which can be used to judge the features of the emerging structures and the dynamics of plasma propagation, and, therefore, to speak about the modes of discharge. The features of the radiation plasma dynamic structures and the change in the main parameters of the plasma of an MPC discharge in the transient regime are considered.

1. Introduction

The problems considered in the paper relate to the interdisciplinary field of physics (radiation plasma dynamics), which studies the physical and physicochemical processes of the generation of strong shock waves, explosive and cumulative phenomena, thermal broadband radiation in media of finite pressure and vacuum, as well as a complex of the phenomena accompanying the interaction of powerful electromagnetic radiation of different spectral compositions and strong shock waves with matter.

Based on the study of these tasks, radiative plasma dynamic systems (RPDS) are developed to solve various problems of engineering, technology, and scientific research, among which the following can be distinguished:

-

electric discharge sources of ultraviolet (UV) radiation and shock waves;

-

development of a new generation of compact, controllable electrophysical neutron sources;

-

optical pumping of powerful gas lasers in the visible and UV spectral ranges;

-

work related to plasma dynamics in coaxial plasma accelerators with an azimuthal magnetic field;

-

solution of the problem of controlled thermonuclear fusion;

-

solution of a number of environmental problems, such as the purification of natural and industrial (exhaust) gases from harmful impurities (hydrogen sulfide, nitrogen oxides, sulfur dioxide, hydrocarbons, etc.);

-

solution of a wide range of scientific problems (geophysical research, the creation of brightness standards, the study of the processes of interaction of powerful radiation fluxes and intense shock waves with matter, etc.).

A great contribution to the study of radiative plasma dynamics was made by the studies carried out in the 1970s [1,2,3,4,5]. The completed series of theoretical and numerical studies was mainly related to plasma dynamics in coaxial plasma accelerators with an azimuthal magnetic field, which, in particular, led to the creation of a powerful quasi-stationary plasma accelerator. (A plasma flow velocity of more than 400 km/s was achieved.)

Carrying out real physical experiments in the considered area of RPDS is characterized by high costs and is associated with many technological and technical difficulties. Therefore, one of the main directions in the development of RPDS at the present stage is the search for effective nonlinear computational models and using them to perform studies of radiation–plasma processes in technical devices, which is of great practical and scientific interest. Thus, it is expedient to determine the radiation and shock-wave characteristics of RPDS by calculation-theoretical methods.

At the same time, from the point of view of numerical implementation, mathematical models of RPDS (electric discharge sources) have a number of specific features that must be taken into account when choosing and developing effective methods for their numerical analysis. Let us briefly discuss the most important of them.

First, the plasma of the discharges under study consists, as a rule, of several regions with different chemical and physical properties, and the boundaries of these regions undergo strong deformation over time. At the same time, due to the processes of radiative heat transfer and the evaporation of the condensed medium, new portions of matter can enter the computational zone through the indicated boundaries, i.e., there are characteristic difficulties associated with the variability of the gas mass involved in the calculation. For these reasons, the use of Lagrangian coordinates seems inconvenient. When using Euler coordinates, certain problems also arise, the removal of which imposes corresponding requirements on the applied solution methods. In particular, since during the calculation the contact boundary separating plasma regions with different properties can move noticeable distances, the computational scheme of the gasdynamic stage must have a small countable diffusion in order not to “smear” the contact boundary zone. When using Euler coordinates, in situations where most of the plasma is concentrated in a relatively narrow spatial region (e.g., at the beginning of the calculation), the number of computational grid cells that this zone falls into may turn out to be small, which leads to the need to use monotonic hybrid schemes, having the highest order of accuracy in the “smooth” part of the solution.

Second, the need to calculate discontinuous solutions to the equations of gasdynamics, due to the presence of shock waves and contact discontinuities in the flows under study, leads to the need to search for and numerically solve the equations of continuum mechanics using difference schemes of increased resolution, which allow one to find both exact and monotonic solutions. Standard TVD schemes, which have a second order of accuracy far from discontinuities and solution extrema, are well suited for calculating supersonic flows with a small number of isolated shock waves. However, radiation–plasma dynamic systems require the solution of much more complex problems of continuum mechanics. Therefore, we use a variant of a nonlinear, quasi-monotone compact-polynomial difference scheme of an increased order of accuracy, which has an increased (above the second) order of accuracy and allows the use of both structured and hybrid (including unstructured) computational grids and makes it possible to calculate complex supersonic flows in pulsed radiation–magneto gasdynamic systems.

Third, carrying out numerical calculations of the electromagnetic field, including in spatial regions with low conductivity of the medium, requires the construction of a homogeneous difference scheme (based on splitting schemes in directions), which makes it possible to carry out the calculation for any values of the electrical conductivity of the medium without explicit selection of the boundaries of nonconductive and conductive regions. (It is necessary to use the flow sweep when solving the equations of the electromagnetic field.)

The fourth feature of the problem being solved is related to the fact that the coefficients of the differential, elliptic radiative transfer equation change very strongly (by orders of magnitude) in the computational zone, which leads to a strong change in the boundaries of the spectrum of the differential operator. Hence, it becomes necessary to use an economical, three-layer, modified, alternating-triangular method with conjugate gradients when solving the radiative transfer equation, the convergence rate of which weakly depends on the magnitude of the change in the spectral boundaries.

And finally, the nonlinearity of the initial equations with a strong mutual influence of various processes (here the problem is related to the different characteristic times of the processes taken into account) leads to the need to use economical and efficient numerical methods, which include the method of splitting the equations of a mathematical model into physical and spatial directions, in order to obtain numerical results for reasonable time. The requirement for the efficiency of the numerical scheme leads to the need to use so-called conditionally stable schemes since the system of equations of radiative magnetic gasdynamics considered here belongs to the class of mixed hyperbolic–parabolic equations. In this case, the “hyperbolic” terms of the equations of plasma dynamics can be calculated explicitly. Therefore, the corresponding stability condition has a rather “weak” form of the Courant–Friedrichs–Lewy stability criterion, and the “parabolic” terms, in order to ensure the efficiency of the method, should be determined implicitly.

A review of literature sources showed that computational problems similar to the one under consideration (for example: the calculation of coaxial plasma accelerators) have already been repeatedly solved by a number of authors, including using commercial software packages. Here, we note that such commercial software packages, as a rule, do not allow the user to interfere (including operationally) in the software and physical and mathematical part of the package in the event of abnormal situations (such nonstandard situations include RPDS tasks) when performing complex computational and theoretical research.

2. MPC and Plasma Discharge

Improving the physical and technical characteristics of compact radiation sources and pulsed plasma jets has been the object of research for scientists around the world over the past decade. The study of such a plasma is of interest for various areas of technical physics: physics of nonequilibrium high-density plasma; expanding recombination plasma physics; atomic and molecular spectroscopy; physics of scattering, large-scale, long-lived radiating plasma formations (taking into account the presence of an external magnetic field) interacting with the background environment; and physics of chemically and laser-active media [6,7,8,9,10].

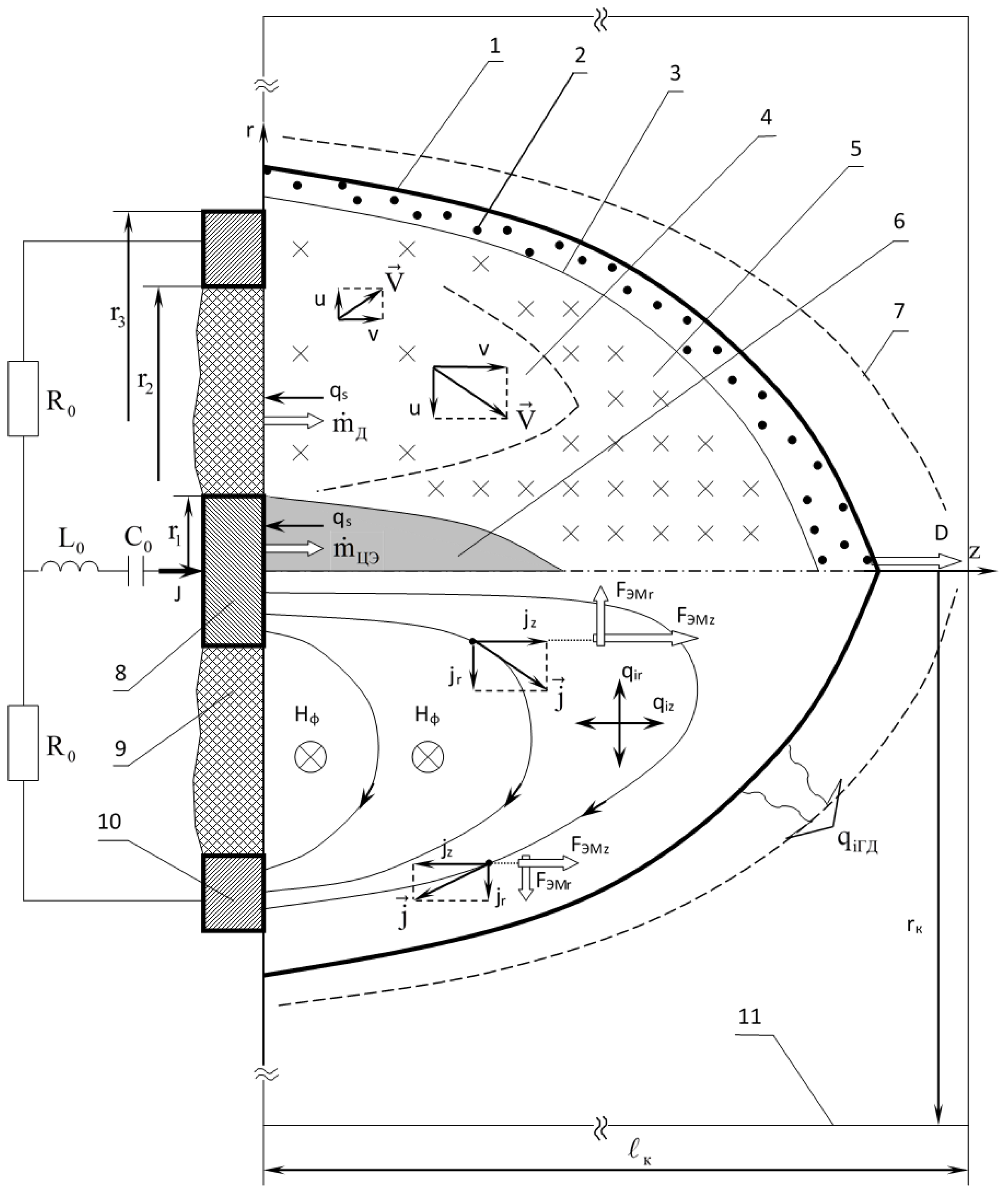
One of the promising methods for thermalizing the kinetic energy of the plasma flow (created by a special, pulsed plasma accelerator of the erosion type—a magneto plasma compressor (MPC)) is the use of a gas that acts as a deformable barrier [11,12,13]. In this case, the main configuration of the electrode assembly is a coaxial electrode system (Figure 1) with a short channel length < 1 cm (end-type MPC discharge) with a central electrode diameter of 0.8–1.5 cm and an outer electrode of $2r_2=3÷10$ cm. Energy storage is low-inductive (less than 100 nH) capacitor banks with a capacity C of 30 to 900 μF with stored energy W₀ = 0.3–500 kJ. In this case, variations in the duration of the current pulse of the discharge can be 5–100 μs for the range of the current amplitude $J_m\approx 100÷2000$ kA. With the model MPC configuration chosen as the base, the diagram of the equivalent electric-discharge circuit with a capacitive energy storage and the qualitative structure of the formed plasma is shown in Figure 1. The end-type MPC electrode assembly is a system of coaxial electrodes separated by an interelectrode dielectric insert (IDI). The origin of the cylindrical coordinate system R0Z is located in the center of the central electrode, the 0Z axis is the axis of symmetry; the axis 0r runs along the plane of the end face of the electric discharge system.

The formation of an MPC-discharge plasma in a gas is three-dimensional in nature, determined by azimuthal fluctuations of the thermal gas dynamic parameters of the plasma and gas in the formed shock wave (SW)-structures and contact boundaries. These fluctuations are caused both by the spatiotemporal inhomogeneity of the plasma parameters at the initial (breakdown) stage and by the subsequent development of magneto gasdynamic instabilities [14].

The initial stage of the discharge development—the stage of breakdown of the interelectrode gap with a duration of ≤1 μs—is characterized by a pronounced inhomogeneity of the distribution of plasma parameters in the interelectrode gap in azimuth. This stage ends with the formation of a narrow (~1 mm) layer of weakly ionized, vapor–gas plasma adjacent to the surface of the end face of the W~W₀ electrode system, short-circuiting the interelectrode gap. The energy spent at the breakdown stage and the initial stage of the discharge, from the energetic point of view, does not have a significant effect on the further plasma dynamics of the MPC discharge.

After that, the capacitive storage begins to discharge into the interelectrode gap, and the main high-current stage of the discharge begins. From this moment in time, the composition of the electric-discharge plasma is determined by the erosion products of the IDI and the accelerator electrodes, which are formed mainly under the action of radiation fluxes from the plasma on them. The light erosion plasma accelerated by magneto gasdynamic forces is decelerated by the surrounding gas. In a radially inhomogeneous plasma flow incident on a gas barrier, a flow with a complex structure with a system of shock-wave discontinuities and contact boundaries arises (Figure 1). In this case, in the unperturbed gas surrounding the plasma jet, a SW arises with a characteristic conical shape.

The topology of currents $\overrightarrow{j}$ and an intrinsic magnetic field, which in the ideal axis symmetric case has only a component H_φ, is characterized by a high degree of spatial nonuniformity in the distribution of electromagnetic forces acting on the plasma, both in magnitude and direction (Figure 1). The interaction of the r-th component of the current density j_r with H_φ is responsible for the appearance of the axial component of the force F_EM~j_r H_φ/c, which is always directed away from the surface of the MPC discharge end face. Due to the spatial weakening of the current density j_r~1/r and magnetic field H_φ~1/r, the electromagnetic force F_EM~1/r² accelerating the flow significantly weakens in the regions adjacent to the external electrode of the system.

The multi-directionality of the vectors of the axial component of the current density j_z in different regions of the discharge leads to the appearance of the multidirectional radial components of the acting pondermotor forces. In the area adjacent to the central electrode, F_EMr, it is directed towards the axis of the system, and in the area of the outer electrode, on the contrary, it acts in the positive direction of the r axis. The noted fact of the existence of spatial inhomogeneity $\overrightarrow{j},\overrightarrow{\mathrm{H}}$ and $\overrightarrow{E}=(E_{\mathrm{r}},E_z,0)$ is evidence of the fundamentally two-dimensional nature of the plasma dynamics of the formed plasma.

For MPC discharges in a gas with electrical power supplied to the plasma discharge P_el > 10⁷ W, the erosive evaporation begins immediately after the end of the breakdown. At the main stage of the discharge, i.e., energy release of the power storage, a high-current discharge is organized between the electrodes, and the discharge current flows and is distributed over the plasma of the erosion products of the IDI materials and the electrodes of the system. The continuous flow of the plasma-forming substance into the discharge zone occurs under the action of powerful $q_s\le {10}^6$ W/cm² radiation fluxes from the discharge zone. The same radiation fluxes, together with the Joule energy, provide effective ionization of vapors. Note that all structural elements of the electrode system are subject to light erosion evaporation, i.e., IDI and electrodes. Plasma in MPC discharges consists of a number of regions with different chemical (elemental) compositions. With a noticeable difference in the thermal physical and optical properties, such an inhomogeneity of the composition can strongly affect the discharge parameters, and, therefore, it must be taken into account both in the interpretation of experiments and in the construction of mathematical models.

3. Mathematical Modeling

It follows from what has been said that the mathematical model of the MPC discharge can be constructed on the basis of a two-dimensional (axis-symmetric), unsteady system of equations of viscous, one-temperature radiation, plasma dynamics.

Electromagnetic processes are described by the system of Maxwell and Ohm equations in a plasma with finite conductivity. Radiation transfer is calculated within the multigroup diffusion approximation. The system is supplemented by equations, which describe the heating and evaporation (within the framework of the model with a Knudsen layer) of the surfaces of the structural elements of the electrode assembly. The system is closed by the equations of the electric circuit of the discharge. This system of equations takes into account the methods for calculating the equations of the state of matter, the absorption coefficients of the intrinsic radiation of the plasma, and is written in a curvilinear coordinate system (obtained by passing from $\left(z,\mathrm{r}\right)$ to $\left(\mathsf{\xi },\mathsf{\eta }\right)$):

$$\begin{gathered} \frac{\partial \mathsf{\rho }}{\partial t}+\frac{1}{J}\frac{\partial \left(J\mathsf{\rho }{V}_{\mathsf{\xi }}\right)}{\partial \mathsf{\xi }}+\frac{1}{J}\frac{\partial \left(J\mathsf{\rho }{V}_{\mathsf{\eta }}\right)}{\partial \mathsf{\eta }}=-\mathsf{\alpha }\frac{\mathsf{\rho }u}{r} \\ \frac{\partial \mathsf{\rho }u}{\partial t}+\frac{1}{J}\frac{\partial \left(J\mathsf{\rho }u{V}_{\mathsf{\xi }}\right)}{\partial \mathsf{\xi }}+\frac{1}{J}\frac{\partial \left(J\mathsf{\rho }u{V}_{\mathsf{\eta }}\right)}{\partial \mathsf{\eta }}=-{\mathsf{\xi }}_r\frac{\partial P}{\partial \mathsf{\xi }}-{\mathsf{\eta }}_r\frac{\partial P}{\partial \mathsf{\eta }}-\mathsf{\alpha }\frac{\mathsf{\rho }{u}^2}{r}+\frac{S_r}{\mathrm{Re}}+\frac{1}{c}{\left[\overrightarrow{j}\overrightarrow{H}\right]}_r \\ \frac{\partial \mathsf{\rho }\mathrm{v}}{\partial t}+\frac{1}{J}\frac{\partial \left(J\mathsf{\rho }\mathrm{v}{V}_{\mathsf{\xi }}\right)}{\partial \mathsf{\xi }}+\frac{1}{J}\frac{\partial \left(J\mathsf{\rho }\mathrm{v}{V}_{\mathsf{\eta }}\right)}{\partial \mathsf{\eta }}=-{\mathsf{\xi }}_z\frac{\partial P}{\partial \mathsf{\xi }}-{\mathsf{\eta }}_z\frac{\partial P}{\partial \mathsf{\eta }}-\mathsf{\alpha }\frac{\mathsf{\rho }u\mathrm{v}}{r}+\frac{S_z}{\mathrm{Re}}+\frac{1}{c}{\left[\overrightarrow{j}\overrightarrow{H}\right]}_z, \\ \frac{\partial \mathsf{\rho }e}{\partial t}+\frac{1}{J}\frac{\partial \left(J\mathsf{\rho }e{V}_{\mathsf{\xi }}+J{\displaystyle \sum q_{i\mathsf{\xi }}}\right)}{\partial \mathsf{\xi }}+\frac{1}{J}\frac{\partial \left(J\mathsf{\rho }e{V}_{\mathsf{\eta }}+J{\displaystyle \sum q_{i\mathsf{\eta }}}\right)}{\partial \mathsf{\eta }}=-\frac{P}{J}\left\{\frac{\partial \left(J{V}_{\mathsf{\xi }}\right)}{\partial \mathsf{\xi }}+\frac{\partial \left(J{V}_{\mathsf{\eta }}\right)}{\partial \mathsf{\eta }}\right\}-\mathsf{\alpha }\frac{Pu}{r}-\mathsf{\alpha }\frac{\mathsf{\rho }eu}{r}+\frac{S_e}{\mathrm{Re}}+\overrightarrow{j}\overrightarrow{E}, \\ D=2\left[{\left(e_{rr}\right)}^2+{\left(e_{zz}\right)}^2+{\left(e_{\mathsf{\phi }\mathsf{\phi }}\right)}^2\right]+{\left(e_{rz}\right)}^2-\frac{2}{3}{\left(div\overrightarrow{V}\right)}^2,di\mathrm{v}\overrightarrow{V}=\frac{1}{J}\left[\frac{\partial \left(J{V}_{\mathsf{\xi }}\right)}{\partial \mathsf{\xi }}+\frac{\partial \left(J{V}_{\mathsf{\eta }}\right)}{\partial \mathsf{\eta }}\right]+\mathsf{\alpha }\frac{u}{r}, \\ {S}_e={\mathsf{\mu }}_{\sum }D+\frac{\mathsf{\gamma }}{\mathrm{Pr}}di\mathrm{v}\left({\mathsf{\lambda }}_{\sum }gradT\right). \end{gathered}$$

(1)

The quantities $S_r,S_z$ describe mathematically the forces arising in the gas flow due to the presence of viscous friction forces in it. The variable S_e is the sum of the work of the forces of viscous friction ${\mathsf{\mu }}_{\sum }D$, and the heat transfer by the heat conduction mechanism $di\mathrm{v}\left({\mathsf{\lambda }}_{\sum }gradT\right)$. $\mathrm{Re}=\frac{L_{\ast }{\mathsf{\rho }}_{\ast }{V}_{\ast }}{{\mathsf{\mu }}_{\ast }}$ is the Reynolds number; $\mathrm{Pr}={\mathsf{\mu }}_{\ast }{C}_{p\ast }/{\mathsf{\lambda }}_{\ast }$ is the Prandtl number.

All quantities included in this equation are determined using additional relations:

$$e_{rr}={\mathsf{\xi }}_r\frac{\partial u}{\partial \mathsf{\xi }}+{\mathsf{\eta }}_r\frac{\partial u}{\partial \mathsf{\eta }},e_{zz}={\mathsf{\xi }}_z\frac{\partial \mathrm{v}}{\partial \mathsf{\xi }}+{\mathsf{\eta }}_z\frac{\partial \mathrm{v}}{\partial \mathsf{\eta }},e_{\mathsf{\phi }\mathsf{\phi }}=\mathsf{\alpha }\frac{u}{r},$$

$$e_{rz}=\left({\mathsf{\xi }}_z\frac{\partial u}{\partial \mathsf{\xi }}+{\mathsf{\eta }}_z\frac{\partial u}{\partial \mathsf{\eta }}\right)+\left({\mathsf{\xi }}_r\frac{\partial \mathrm{v}}{\partial \mathsf{\xi }}+{\mathsf{\eta }}_r\frac{\partial \mathrm{v}}{\partial \mathsf{\eta }}\right),$$

$${\mathsf{\sigma }}_{rz}={\mathsf{\mu }}_{\sum }\left[\left({\mathsf{\xi }}_z\frac{\partial u}{\partial \mathsf{\xi }}+{\mathsf{\eta }}_z\frac{\partial u}{\partial \mathsf{\eta }}\right)+\left({\mathsf{\xi }}_r\frac{\partial \mathrm{v}}{\partial \mathsf{\xi }}+{\mathsf{\eta }}_r\frac{\partial \mathrm{v}}{\partial \mathsf{\eta }}\right)\right],$$

$${\mathsf{\sigma }}_{rr}={\mathsf{\mu }}_{\sum }\left[\frac{4}{3}\left({\mathsf{\xi }}_r\frac{\partial u}{\partial \mathsf{\xi }}+{\mathsf{\eta }}_r\frac{\partial u}{\partial \mathsf{\eta }}\right)-\frac{2}{3}\left({\mathsf{\xi }}_z\frac{\partial \mathrm{v}}{\partial \mathsf{\xi }}+{\mathsf{\eta }}_z\frac{\partial \mathrm{v}}{\partial \mathsf{\eta }}\right)-\mathsf{\alpha }\frac{2u}{3r}\right],$$

$${\mathsf{\sigma }}_{zz}={\mathsf{\mu }}_{\sum }\left[\frac{4}{3}\left({\mathsf{\xi }}_z\frac{\partial \mathrm{v}}{\partial \mathsf{\xi }}+{\mathsf{\eta }}_z\frac{\partial \mathrm{v}}{\partial \mathsf{\eta }}\right)-\frac{2}{3}\left({\mathsf{\xi }}_r\frac{\partial u}{\partial \mathsf{\xi }}+{\mathsf{\eta }}_r\frac{\partial u}{\partial \mathsf{\eta }}\right)-\mathsf{\alpha }\frac{2u}{3r}\right],$$

$$\begin{gathered} S_r=\frac{1}{J}\frac{\partial \left(J\left\{{\mathsf{\xi }}_r{\mathsf{\sigma }}_{rr}+{\mathsf{\xi }}_z{\mathsf{\sigma }}_{rz}\right\}\right)}{\partial \mathsf{\xi }}+\frac{1}{J}\frac{\partial \left(J\left\{{\mathsf{\eta }}_r{\mathsf{\sigma }}_{rr}+{\mathsf{\eta }}_z{\mathsf{\sigma }}_{rz}\right\}\right)}{\partial \mathsf{\eta }}+ \\ \mathsf{\alpha }\frac{2{\mathsf{\mu }}_{\sum }\left[{\mathsf{\xi }}_r\frac{\partial u}{\partial \mathsf{\xi }}+{\mathsf{\eta }}_r\frac{\partial u}{\partial \mathsf{\eta }}\right]-2\mathsf{\alpha }{\mathsf{\mu }}_{\sum }\frac{u}{r}}{r}, \end{gathered}$$

$$S_z=\frac{1}{J}\frac{\partial \left(J\left\{{\mathsf{\xi }}_r{\mathsf{\sigma }}_{zr}+{\mathsf{\xi }}_z{\mathsf{\sigma }}_{zz}\right\}\right)}{\partial \mathsf{\xi }}+\frac{1}{J}\frac{\partial \left(J\left\{{\mathsf{\eta }}_r{\mathsf{\sigma }}_{zr}+{\mathsf{\eta }}_z{\mathsf{\sigma }}_{zz}\right\}\right)}{\partial \mathsf{\eta }}+\mathsf{\alpha }\frac{{\mathsf{\sigma }}_{rz}}{r},$$

$$\begin{gathered} div\left({\mathsf{\lambda }}_{\sum }gradT\right)=\frac{1}{J}\frac{\partial \left\{{\mathsf{\lambda }}_{\sum }J\left({\mathsf{\xi }}_r^2+{\mathsf{\xi }}_z^2\right)T_{\mathsf{\xi }}+{\mathsf{\lambda }}_{\sum }J\left({\mathsf{\xi }}_r{\mathsf{\eta }}_r+{\mathsf{\xi }}_z{\mathsf{\eta }}_z\right)T_{\mathsf{\eta }}\right\}}{\partial \mathsf{\xi }}+ \\ \frac{1}{J}\frac{\partial \left\{{\mathsf{\lambda }}_{\sum }J\left({\mathsf{\eta }}_r{\mathsf{\xi }}_r+{\mathsf{\eta }}_z{\mathsf{\xi }}_z\right)T_{\mathsf{\xi }}+{\mathsf{\lambda }}_{\sum }J\left({\mathsf{\eta }}_r^2+{\mathsf{\eta }}_z^2\right)T_{\mathsf{\eta }}\right\}}{\partial \mathsf{\eta }}+\mathsf{\alpha }\frac{{\mathsf{\lambda }}_{\sum }}{r}\left\{{\mathsf{\xi }}_r\frac{\partial T}{\partial \mathsf{\xi }}+{\mathsf{\eta }}_r\frac{\partial T}{\partial \mathsf{\eta }}\right\}, \end{gathered}$$

where $u(\mathsf{\xi },\mathsf{\eta },t),\mathrm{v}(\mathsf{\xi },\mathsf{\eta },t)$ are the projections of the velocity vector $\overrightarrow{V}(\mathsf{\xi },\mathsf{\eta },t)$ on the 0r and 0z axes, is the specific internal plasma energy, $\overrightarrow{j}$ is the electric current density, $J=\partial \left(r,z\right)/\partial \left(\mathsf{\xi },\mathsf{\eta }\right)$ is the Jacobian of the transition from a cylindrical coordinate system ($r,z$) to a curvilinear coordinate system ($\mathsf{\xi },\mathsf{\eta }$), $V_{\mathsf{\xi }}={\mathsf{\xi }}_{r}u+{\mathsf{\xi }}_z\mathrm{v}$, $V_{\mathsf{\eta }}={\mathsf{\eta }}_{r}u+{\mathsf{\eta }}_z\mathrm{v}$ are the contravariant components of the velocity vector $\overrightarrow{V}$ in a curvilinear coordinate system ($\mathsf{\xi },\mathsf{\eta }$), $\mathsf{\rho },P$ are the plasma density and pressure, ${\displaystyle \sum _i{q}_{i\mathsf{\xi }}},{\displaystyle \sum _i{q}_{i\mathsf{\eta }}}$ are the projections of the radiant energy flux density vector $\overrightarrow{q}$ on the axis of the curvilinear coordinate system, and $\mathsf{\alpha }=0$, $\mathsf{\alpha }=1$ are plane and axis symmetric flow cases, respectively.

To obtain the dimensionless form of the equations under consideration, we refer all the gasdynamic variables included in the system of equations to their characteristic values, and the spatial $\overline{\mathsf{\xi }},\overline{\mathsf{\eta }}$ and temporal $\overline{t}$ variables, respectively, to the characteristic size $\overline{t}$ and characteristic time $t_{\ast }$. We introduce the following notation for the dimensionless variables:

$$\begin{gathered} t=U_{\ast }\overline{t}/L_{\ast },\mathsf{\xi }=\overline{\mathsf{\xi }}/L_{\ast },\mathsf{\eta }=\overline{\mathsf{\eta }}/L_{\ast },V_{\mathsf{\xi }}=\overline{V}/V_{\ast },V_{\mathsf{\eta }}={\overline{V}}_{\mathsf{\eta }}/V_{\ast },u=\overline{u}/V_{\ast },\mathrm{v}=\overline{\mathrm{v}}/V_{\ast }, \\ T=\overline{T}/T_{\ast },e=\overline{e}/e_{\ast },\mathsf{\rho }=\overline{\mathsf{\rho }}/{\mathsf{\rho }}_{\ast },P=\overline{P}/P_{\ast },{\mathsf{\mu }}_{\sum }={\overline{\mathsf{\mu }}}_{\sum }/{\mathsf{\mu }}_{\ast },{\mathsf{\lambda }}_{\sum }={\overline{\mathsf{\lambda }}}_{\sum }/{\mathsf{\lambda }}_{\ast }, \\ \mathsf{\gamma }=C_{p\ast }/C_{\mathrm{v}\ast },q=\overline{q}/q_{\ast },\mathsf{\omega }=\overline{\mathsf{\omega }}/{\mathsf{\omega }}_{\ast }. \end{gathered}$$

To determine the spatial–temporal position of the contact boundary separating the plasma of the ablating material of the obstacle from the plasma of the environment, the method of fictitious impurity is used. For this, an additional equation is introduced into the system of the above equations $\left({\mathsf{\rho }}_g\in \left[0,1\right]\right)$: $\partial {\mathsf{\rho }}_g/\partial t+\overrightarrow{V}\nabla {\mathsf{\rho }}_g=0$. If ${\mathsf{\rho }}_g$ is known, one can determine the interface Г(t) = {($\mathsf{\xi },\mathsf{\eta }$): ${\mathsf{\rho }}_g\left(\mathsf{\xi },\mathsf{\eta },t\right)=0$}, which divides the entire computational domain into two areas, each of which corresponds to the ablating material of the obstacle or the plasma of the environment, depending on the sign of the function. A complete description of the method for calculating the contact boundary and gasdynamic parameters near it is given in [15].

The research assumes a coaxial character of the MPC-discharge electrode system. In this case, in the axially symmetric discharge plasma formed above the surface of the end of the system, an electric field with an intensity $\overrightarrow{E}\left(\mathsf{\xi },\mathsf{\eta },\mathrm{t}\right)=(E_{\mathrm{r}},E_z,0)$ is created and a current flows with a density $\overrightarrow{\mathrm{j}}\left(\mathsf{\xi },\mathsf{\eta },\mathrm{t}\right)=({\mathrm{j}}_{\mathrm{r}},j_z,0)$, providing energy release in the plasma with a specific (per unit volume) power $\overrightarrow{j}\overrightarrow{E}$. The current flowing through the plasma is a source of its own magnetic field with an intensity $\overrightarrow{B}$ having only an azimuthal component $B_{\mathsf{\phi }}\left(\mathsf{\xi },\mathsf{\eta },\mathrm{t}\right)$. Plasma dynamics processes occurring in the capillary discharge plume are considered under the assumption that the electromagnetic field has axial symmetry and one component $B_{\mathsf{\phi }}$.

$$\begin{gathered} \frac{\partial B_{\mathsf{\phi }}}{\partial t}=-{\left({\mathsf{\xi }}_r\frac{\partial u{B}_{\mathsf{\phi }}}{\partial \mathsf{\xi }}+{\mathsf{\eta }}_r\frac{\partial u{B}_{\mathsf{\phi }}}{\partial \mathsf{\eta }}\right)}_z-{\left({\mathsf{\xi }}_z\frac{\partial \mathrm{v}{B}_{\mathsf{\phi }}}{\partial \mathsf{\xi }}+{\mathsf{\eta }}_z\frac{\partial \mathrm{v}{B}_{\mathsf{\phi }}}{\partial \mathsf{\eta }}\right)}_r+ \\ \frac{c^2}{4\mathsf{\pi }}\frac{t_{\ast }}{L_{\ast }^2}{\mathsf{\xi }}_z\frac{\partial }{\partial \mathsf{\xi }}\left(\frac{1}{\mathsf{\sigma }}{\left({\mathsf{\xi }}_z\frac{\partial B_{\mathsf{\phi }}}{\partial \mathsf{\xi }}+{\mathsf{\eta }}_z\frac{\partial B_{\mathsf{\phi }}}{\partial \mathsf{\eta }}\right)}_r\right)+ \\ +\frac{c^2}{4\mathsf{\pi }}\frac{t_{\ast }}{L_{\ast }^2}{\mathsf{\xi }}_r\frac{\partial }{\partial \mathsf{\xi }}\left(\frac{1}{\mathsf{\sigma }}\left[{\left({\mathsf{\xi }}_r\frac{\partial B_{\mathsf{\phi }}}{\partial \mathsf{\xi }}+{\mathsf{\eta }}_r\frac{\partial B_{\mathsf{\phi }}}{\partial \mathsf{\eta }}\right)}_z+\frac{B_{\mathsf{\phi }}}{r}\right]\right)+ \\ \frac{c^2}{4\mathsf{\pi }}\frac{t_{\ast }}{L_{\ast }^2}{\mathsf{\eta }}_r\frac{\partial }{\partial \mathsf{\eta }}\left(\frac{1}{\mathsf{\sigma }}\left[{\left({\mathsf{\xi }}_r\frac{\partial B_{\mathsf{\phi }}}{\partial \mathsf{\xi }}+{\mathsf{\eta }}_r\frac{\partial B_{\mathsf{\phi }}}{\partial \mathsf{\eta }}\right)}_z+\frac{B_{\mathsf{\phi }}}{r}\right]\right). \end{gathered}$$

(2)

Electrical conductivity $\mathsf{\sigma }$ takes into account plasma magnetization [16].

Coefficients of turbulent viscosity ${\mathsf{\mu }}_{\sum }$ and thermal conductivity ${\mathsf{\lambda }}_{\sum }$ are calculated using the Boussinesq hypothesis, according to which the effective viscosity of a gas flow is determined by the formula:

$${\mathsf{\mu }}_{\sum }={\mathsf{\mu }}_m+{\mathsf{\mu }}_t,$$

where ${\mathsf{\mu }}_m$ is the dynamic viscosity coefficient, which takes into account atomic–molecular collisional processes, ${\mathsf{\mu }}_t$ is the coefficient of turbulent viscosity, which is determined using the $q-\mathsf{\omega }$ Coakley model. We use the assumption that the molecular Prandtl number Pr = 0.72 and the turbulent Prandtl number Pr = 0.9.

Then, the corresponding thermal conductivity coefficient can be found: ${\mathsf{\lambda }}_t=c_P\left(\frac{{\mathsf{\mu }}_m}{\mathrm{Pr}}+\frac{{\mathsf{\mu }}_t}{{\mathrm{Pr}}_t}\right)$. The equations of the Coakley model in a curvilinear coordinate system ($\mathsf{\xi },\mathsf{\eta }$) can be written in the following form:

$$\begin{gathered} \frac{\partial \mathsf{\rho }q}{\partial t}+\frac{1}{J}\frac{\partial \left(J\mathsf{\rho }{V}_{\mathsf{\xi }}q\right)}{\partial \mathsf{\xi }}+\frac{1}{J}\frac{\partial \left(J\mathsf{\rho }{V}_{\mathsf{\eta }}q\right)}{\partial \mathsf{\eta }}+\mathsf{\alpha }\frac{\mathsf{\rho }qu}{r}=S_q+\frac{\mathsf{\rho }q}{2\mathsf{\omega }}\left(C_{\mathsf{\mu }}fD-\frac{2}{3}\mathsf{\omega }div\overrightarrow{V}-{\mathsf{\omega }}^2\right), \\ \frac{\partial \mathsf{\rho }\mathsf{\omega }}{\partial t}+\frac{1}{J}\frac{\partial \left(J\mathsf{\rho }{V}_{\mathsf{\xi }}\mathsf{\omega }\right)}{\partial \mathsf{\xi }}+\frac{1}{J}\frac{\partial \left(J\mathsf{\rho }{V}_{\mathsf{\eta }}\mathsf{\omega }\right)}{\partial \mathsf{\eta }}+\mathsf{\alpha }\frac{\mathsf{\rho }\mathsf{\omega }u}{r}=S_{\mathsf{\omega }}+\mathsf{\rho }\left(C_1\left(C_{\mathsf{\mu }}D-\frac{2}{3}\mathsf{\omega }div\overrightarrow{V}\right)-C_2{\mathsf{\omega }}^2\right), \\ {S}_q=\frac{1}{J}\frac{\partial \left\{{\mathsf{\mu }}_{\sum q}J\left({\mathsf{\xi }}_r^2+{\mathsf{\xi }}_z^2\right)q_{\mathsf{\xi }}+{\mathsf{\mu }}_{\sum q}J\left({\mathsf{\xi }}_r{\mathsf{\eta }}_r+{\mathsf{\xi }}_z{\mathsf{\eta }}_z\right)q_{\mathsf{\eta }}\right\}}{\partial \mathsf{\xi }}+ \\ \frac{1}{J}\frac{\partial \left\{{\mathsf{\mu }}_{\sum q}J\left({\mathsf{\eta }}_r{\mathsf{\xi }}_r+{\mathsf{\eta }}_z{\mathsf{\xi }}_z\right)q_{\mathsf{\xi }}+{\mathsf{\mu }}_{\sum q}J\left({\mathsf{\eta }}_r^2+{\mathsf{\eta }}_z^2\right)q_{\mathsf{\eta }}\right\}}{\partial \mathsf{\eta }}+\mathsf{\alpha }\frac{{\mathsf{\mu }}_{\sum q}}{r}\left\{{\mathsf{\xi }}_r\frac{\partial q}{\partial \mathsf{\xi }}+{\mathsf{\eta }}_r\frac{\partial q}{\partial \mathsf{\eta }}\right\} \\ {S}_{\mathsf{\omega }}=\frac{1}{J}\frac{\partial \left\{{\mathsf{\mu }}_{\sum \mathsf{\omega }}J\left({\mathsf{\xi }}_r^2+{\mathsf{\xi }}_z^2\right){\mathsf{\omega }}_{\mathsf{\xi }}+{\mathsf{\mu }}_{\sum \mathsf{\omega }}J\left({\mathsf{\xi }}_r{\mathsf{\eta }}_r+{\mathsf{\xi }}_z{\mathsf{\eta }}_z\right){\mathsf{\omega }}_{\mathsf{\eta }}\right\}}{\partial \mathsf{\xi }}+ \\ +\frac{1}{J}\frac{\partial \left\{{\mathsf{\mu }}_{\sum \mathsf{\omega }}J\left({\mathsf{\eta }}_r{\mathsf{\xi }}_r+{\mathsf{\eta }}_z{\mathsf{\xi }}_z\right){\mathsf{\omega }}_{\mathsf{\xi }}+{\mathsf{\mu }}_{\sum \mathsf{\omega }}J\left({\mathsf{\eta }}_r^2+{\mathsf{\eta }}_z^2\right){\mathsf{\omega }}_{\mathsf{\eta }}\right\}}{\partial \mathsf{\eta }}+\mathsf{\alpha }\frac{{\mathsf{\mu }}_{\sum \mathsf{\omega }}}{r}\left\{{\mathsf{\xi }}_r\frac{\partial \mathsf{\omega }}{\partial \mathsf{\xi }}+{\mathsf{\eta }}_r\frac{\partial \mathsf{\omega }}{\partial \mathsf{\eta }}\right\}, \\ {\mathsf{\mu }}_{\sum q}={\mathsf{\mu }}_m+{\mathsf{\mu }}_t,{\mathsf{\mu }}_{\sum \mathsf{\omega }}={\mathsf{\mu }}_m+1,3{\mathsf{\mu }}_t,{\mathsf{\mu }}_t=C_{\mathsf{\mu }}f\left(n\right)\mathsf{\rho }\frac{q^2}{\mathsf{\omega }}, \end{gathered}$$

(3)

$$C_1=0.045+0.405f(n),C_2=0.92,C_{\mathsf{\mu }}=0.09,f\left(n\right)=1-\exp \left(-0,0065\frac{\mathsf{\rho }qn}{{\mathsf{\mu }}_m}\right),$$

where q is the pseudo-velocity, $\mathsf{\omega }$ is the pseudo-vorticity, $f\left(n\right)$ is the wall function introduced in order for the model to correctly describe the flow parameters in a laminar sublayer formed on solid streamlined surfaces, and n is the normal distance from the point under consideration to the nearest surface.

To calculate the radiation fields, the radiation transfer equation was used, presented in the form of a system of equations for the multigroup diffusion approximation:

$$\frac{1}{J}\frac{\partial \left(J{q}_{i\mathsf{\xi }}\right)}{\partial \mathsf{\xi }}+\frac{1}{J}\frac{\partial \left(J{q}_{i\mathsf{\eta }}\right)}{\partial \mathsf{\eta }}+{\chi }_{i}c{U}_i=4{\chi }_i{\mathsf{\sigma }}_i{T}^4,\frac{c}{3}\frac{\partial U_i}{\partial \mathsf{\xi }}+{\chi }_i{q}_{i\mathsf{\xi }}=0,\frac{c}{3}\frac{\partial U_i}{\partial \mathsf{\eta }}+{\chi }_i{q}_{i\mathsf{\eta }}=0,$$

(4)

where $U_i(y,z,t)$ is the density of radiant energy in the i-th spectral group, ${\chi }_i$ is the spectral absorption coefficient. Instead of the diffusion approximation ($D_I=c/3{\chi }_i$) of the radiation transfer equation, the performed calculations use the functions of flux limiters [17]: $\mathsf{\lambda }\left(\mathsf{\alpha }\right)=1/\sqrt[m]{1+{\mathsf{\alpha }}^m}$. Then the diffusion coefficient can be represented as follows: $D_I=c\mathsf{\lambda }/3{\chi }_i$, where $\mathsf{\alpha }=\left|\nabla U_i\right|/\left(3{\chi }_i{U}_i\right)$. At $\mathsf{\alpha }\to \infty$, the radiation flux is $q_i=-D\nabla U_i\to c{U}_i$, and at $\mathsf{\alpha }\to 0$ the radiation flux is equal to the flux $q_i=-D\nabla U_i\to -c\nabla U_i/3{\chi }_i$ of the diffusion approximation:

The value ${\mathsf{\sigma }}_i$ is calculated by the formula [18]:

$${\mathsf{\sigma }}_i=2k^2\mathsf{\pi }\left[f\left({\mathsf{\alpha }}_{i+1}\right)-f\left({\mathsf{\alpha }}_i\right)\right]\left(c^2{h}^3\right),{\mathsf{\alpha }}_{\mathrm{i}}=h{\mathsf{\nu }}_i/kT,$$

f(α) = α³(1/3 − α/8 + α²/62.4) for α < 2,

f(α) = 6.4939 − e^−α (α³ + 3α² + 6α + 7.28) for α ≥ 2.

The numerical calculation method is detailed in [15,19,20]. The system of equations describing the heating and evaporation of the IDI surface material and the discharge electrodes under the action of an incident and completely absorbed thermal radiation flux with density $q_z$, without taking into account hydrodynamic processes in a condensed medium, consists of a quasi-one-dimensional heat conduction equation in a moving (associated with the evaporation wave front) coordinate system with an 0z axis perpendicular to the surface and an 0r axis parallel to the surface:

$$\frac{\partial T_s}{\partial t}=a_M\frac{{\partial }^2{T}_s}{\partial z^2}+V_0\frac{\partial T_s}{\partial z},$$

(5)

with boundary and initial conditions:

$$k_m\frac{\partial T_s}{\partial z}\left(0,\mathrm{r},\mathrm{t}\right)=q_z\left(0,\mathrm{r},\mathrm{t}\right)-L_v\mathsf{\rho }\left(0,\mathrm{r},\mathrm{t}\right)\mathrm{v}\left(0,\mathrm{r},\mathrm{t}\right),$$

and systems of equations that determine the kinetics of evaporation of the surface of condensed matter in the framework of the model with a Knudsen layer [21]:

$$\frac{T\left(0,\mathrm{t}\right)}{T_s\left(0,\mathrm{t}\right)}={\left[\sqrt{1+\mathsf{\pi }{\left(\frac{\left(\mathsf{\gamma }-1\right)m}{\left(\mathsf{\gamma }+1\right)2}\right)}^2}-\sqrt{\mathsf{\pi }}\frac{\mathsf{\gamma }-1}{\mathsf{\gamma }+1}\frac{m}{2}\right]}^2,$$

$$\frac{\mathsf{\rho }\left(0,\mathrm{t}\right)}{{\mathsf{\rho }}_s\left(0,\mathrm{t}\right)}=\sqrt{\frac{T_s\left(0,\mathrm{t}\right)}{T\left(0,\mathrm{t}\right)}}\left[\left(m^2+\frac{1}{2}\right)e^{m^2}erfc\left(m\right)-\frac{m}{\sqrt{\mathsf{\pi }}}\right]+\frac{1}{2}\frac{T_s\left(0,\mathrm{t}\right)}{T\left(0,\mathrm{t}\right)}\left[1-\sqrt{\mathsf{\pi }}m{e}^{m^2}erfc\left(m\right)\right],$$

$$p_s\left(t\right)=p_1\exp \left[\frac{\Im L_v}{R{T}_1}\left(1-\frac{T_1}{T_s\left(0,\mathrm{t}\right)}\right)\right],m=\frac{V\left(0,\mathrm{t}\right)}{\sqrt{2RT\left(0,\mathrm{t}\right)/\Im }},\mathsf{\rho }\left(0,\mathrm{r},\mathrm{t}\right)\mathrm{v}\left(0,\mathrm{r},\mathrm{t}\right)={\mathsf{\rho }}_m{V}_0,$$

where $T_s$ is the temperature of the condensed medium at the moment of time $t,{\mathrm{a}}_{\mathrm{M}},{\mathrm{k}}_{\mathrm{M}},{\mathsf{\rho }}_{\mathrm{m}}$ are the coefficients of thermal diffusivity, thermal conductivity and density of the material, respectively, $V_0$ is the speed of the evaporation wave, $p_s,{\mathsf{\rho }}_{\mathrm{s}}$ are the pressure and density of the saturated vapor of condensed matter at surface temperature $T_s$, R is the universal gas constant, $T_1$ is the value of the surface temperature of the condensed medium, corresponding to the pressure of saturated vapor $p_1$, $L_v$ is the latent heat of vaporization, $\Im$ is the molar mass of vapor, $T\left(0,\mathrm{t}\right),\mathsf{\rho }\left(0,\mathrm{t}\right),\mathrm{v}\left(0,\mathrm{t}\right)$ are the temperature, density, and velocity of the plasma at the outer boundary of the Knudsen layer, and $\mathsf{\gamma }$ is the adiabatic exponent of condensed matter vapors.

The condition for applying the quasi-one-dimensional approximation is determined by the possibility of neglecting the term ${\partial }^2{\mathrm{T}}_{\mathrm{s}}/\partial {\mathrm{r}}^2$ in the two-dimensional heat equation, which is justified by its smallness with respect to the derivative with respect to the normal component, i.e., $\left({\partial }^2{\mathrm{T}}_{\mathrm{s}}/\partial {\mathrm{r}}^2\right)/\left({\partial }^2{\mathrm{T}}_{\mathrm{s}}/\partial {\mathrm{z}}^2\right)\approx {10}^{-3}÷{10}^{-4}$.

The electrical equation of the equivalent discharge circuit for the case when a capacitor bank with a capacitance C is used as a power energy storage device has the form [22]:

$$\frac{1}{c^2}\frac{d{L}_{C}J}{dt}+R_{C}J=U_{к},\frac{d{U}_{к}}{dt}=-\frac{J}{C},$$

and initial conditions

$$t=0,J=0,U_{к}\left(t=0\right)=U_0,$$

(6)

where J is the full discharge current; $R_C=R_0+R_{pl}-\frac{1}{2c^2}\frac{d{L}_{pl}}{dt},L_C=L_0+L_{pl}$, $L_0,R_0$ are the resistance and inductance of the external circuit, $U_0,U_{к}\left(t\right)$ are the initial and current voltage across the capacitor bank (“к” indicates the number of the frequency band), $L_{pl}=\frac{c^2}{4\mathsf{\pi }{J}^2}{\displaystyle \underset{V}{\int }{H}^{2}dV,R_{pl}=\frac{1}{J^2}{\displaystyle \underset{V}{\int }\frac{j^2}{\mathsf{\sigma }}dV}}$ are the inductance and Ohmic resistance of the discharge plasma, in the calculation of which the integration is carried out over the volume of the computational domain, at the boundaries of which the value of the magnetic field strength tends to zero.

4. Initial and Boundary Conditions

At the moment of time t = 0, the computational space is uniformly filled with a stationary gas medium with known properties and initial thermal dynamic parameters (temperature T₀ = 300 K and pressure $p_0={10}^3÷{10}^5$ Pa). The electrical breakdown of the gas gap between the electrodes is modeled as the instantaneous appearance at the moment of time adjacent to the surface of the end face of the MPC layer (2 counting cells thick) of ionized gas with parameters T ≈ 15 kK and pressure $p_0$. At t = 0, the discharge current $J(0)=0$, the voltage across the capacitor $U_{к}(0)=U_0$, and the magnetic field is zero, there is no radiation.

The formulation of the boundary conditions requires setting the values of the gas dynamic, radiative, and electromagnetic parameters at the boundaries Г of the computational domain G. The rectangular boundary Г in the rz plane (Figure 1) consists of the surface of the dielectric insert and end electrodes with coordinates ($z=0,\mathrm{r}\in \left[{0,\mathrm{r}}_{\mathrm{к}}\right]$), the 0z axis of symmetry for $z\in \left[0,{𝓁}_{\mathrm{к}}\right]$, and lines ($r=r_{к},\mathrm{z}\in \left[0,{𝓁}_{\mathrm{к}}\right]$), ($z=𝓁,\mathrm{r}\in \left[0,r_{к}\right]$).

Gasdynamic parameters: velocity $\overrightarrow{V}\left(0,\mathrm{r},\mathrm{t}\right)$, density $\mathsf{\rho }\left(0,\mathrm{r},\mathrm{t}\right)$, pressure $p\left(0,\mathrm{r},\mathrm{t}\right)$, internal energy $e\left(0,\mathrm{r},\mathrm{t}\right)$, from the IDI and electrodes ($z=0,\mathrm{r}\le {\mathrm{r}}_3$) are determined by the no-flow conditions in the absence of evaporation, i.e., when the saturated vapor pressure $p_s\left(0,\mathrm{r},\mathrm{t}\right)<p\left(0,\mathrm{r},\mathrm{t}\right)$ or, according to Equation (4), in the case when the dielectric insert and the electrodes evaporate. On all other boundaries of the computational domain, the impermeability conditions were set, and on the $0Z$ symmetry axis—the symmetry conditions.

When solving the equations of radiation transfer at the boundaries of the computational domain, the conditions were set for the absence of radiation incident from the outside, and on the symmetry axis—the condition for the symmetry of the radiation fluxes.

To determine the magnetic field strength $B_{\mathsf{\phi }}\left(r,\mathrm{z},\mathrm{t}\right)$ on the left ($z=0$) boundary of the computational domain, we used the relations:

$$\begin{array}{l}{B}_{\mathsf{\phi }}=\frac{2Jr}{c{r}_1^2}\mathrm{for}\mathrm{r}\le {\mathrm{r}}_1;{\mathrm{B}}_{\mathsf{\phi }}=\frac{2J}{cr}\mathrm{for}\mathrm{r}\in \left[{\mathrm{r}}_1,{\mathrm{r}}_2\right];\\ B_{\mathsf{\phi }}=\frac{2J}{cr}\frac{r_3^2-r^2}{r_3^2-r_2^2}\mathrm{for}\mathrm{r}\in \left[{\mathrm{r}}_2,{\mathrm{r}}_3\right];{\mathrm{B}}_{\mathsf{\phi }}=0\mathrm{for}\mathrm{r}\in \left[{\mathrm{r}}_3,{\mathrm{r}}_{\mathrm{к}}\right].\end{array}$$

$B_{\mathsf{\phi }}\equiv 0$ on all other boundaries of the computational domain.

5. Computational Algorithm

The numerical solution of the nonstationary, two-dimensional, radiation–gasdynamic model developed in the work is based on the method of splitting into physical processes and spatial directions. The developed computational codes use a multiblock, multigrid technology for calculations on nonorthogonal, structured grids. To solve the gasdynamic part of the system of equations, a nonlinear, quasi-monotone, compact-polynomial difference scheme of increased order of accuracy [23] is used, as well as the spatial splitting of the Reynolds equations [15], written in an arbitrary curvilinear coordinate system ($\mathsf{\xi },\mathsf{\eta }$). When calculating the flux vectors at the boundaries of the computational cell, the procedure for calculating the decay of the discontinuity developed in [24] was used. Other details of the nonlinear, quasi-monotone, compact-polynomial difference scheme are given in [24,25]. The rigid part of the system of equations of the $q-\mathsf{\omega }$ Coakley model was solved using the implicit Rosenbrock method.

The method for calculating the transfer of broadband radiation is considered on the basis of the multigroup diffusion approximation [17,18]. To find a numerical solution to the diffusion approximation of the radiation transfer equation, a modified, alternating triangular method was applied using a three-layer iterative scheme, in which the iterative timestep is found using the method of conjugate directions [26]. The timestep Δt necessary for the integration of the above difference scheme is selected from the condition of the Courant–Friedrichs–Levy stability criterion.

The hyperbolic (convective) part of the computer model was tested on a one-dimensional version of the Riemann problem (Soda problem) on the decay of an unstable discontinuity of a given configuration. A comparison of the exact and approximate solutions showed that the difference is no more than a percent [23,27]. Verification calculations (in order to assess the degree of attenuation of the system of reflected shock waves) were carried out for experimental conditions. The calculations performed in [28] showed that the calculation error is within the experimental accuracy of the results and can reach a level of 10%. These results are also in good agreement [23] with the indicated calculations. (The relative error is 0.4%.)

The parabolic (thermal) part of the model was tested on some problems that admit exact analytical solutions: heating of a continuous medium [27,29] filling a flat semi-bounded space $r>0$ by a heat flux through the left fixed boundary $r=0$. (The relative error is less 1%.)

6. Numerical Calculation Results

Calculations were carried out for MPC in argon and air in the range of pressure $p_0={10}^3÷{10}^5$ Pa at temperature $T_0=300$ K. Basic geometric dimensions of MPC: r₁ = 0.8 cm, r₂ = 5 cm, r₃ = 6 cm. Separate calculations were performed for MPC discharges with a variation in r₁ = 0.4–1 cm, r₂ = 2–5 cm. PTFE-4 was selected as the IDI material. The electrodes were made of copper.

The capacity of the power storage took the values C = 28.6 μF (with variation of the initial voltage $U_0=10÷200$ kV, W₀ = 1.43–570 kJ) and $C=750$ μF ($U_0=2÷20$ kV, W₀ = 1.5–150 kJ). The value of the external active resistance of the discharge was $R_0={10}^{-4}$ Ohm, and the external inductance of the discharge circuit was $L_0\approx 70$ nH.

Let us introduce the value ${\mathsf{\lambda }}_R$ for the analysis of the obtained results:

λ_R = R_Ohm/R_pl,

where R_Ohm is the Ohmic resistance of the MPC-discharge and R_pl is the plasma resistance.

The value ${\mathsf{\lambda }}_R$ is proportional to the ratio of the Joule heating power to the total power supplied to the plasma load. It reflects the contribution of Ohmic and plasma dynamic mechanisms of plasma heating.

In addition, we introduce a dimensionless criterion $A_m$, which can be used to characterize the entire sum of modes in an MPC discharge. This dimensionless criterion is the ratio of the mean integral (along the midsection of the MPC) magnetic pressure ${\overline{p}}_m\left(z=0,{\mathrm{t}}_{\mathrm{m}}\right)$ to the total velocity head ${\mathsf{\rho }}_0{D}^2$ of the gas flow “incident” to SW. This parameter can be used to estimate the contribution of the plasma dynamic and Ohmic mechanisms of energy dissipation to the discharge plasma:

$$A_m={\left(\frac{{\overline{p}}_m\left(z=0,{\mathrm{t}}_{\mathrm{m}}\right)}{{\mathsf{\rho }}_0{D}^2}\right)}^{1/2}.$$

In structure, this parameter is the square root of the Alfven number. Physically, it can be interpreted as the ratio of the pondermotor forces acting on the plasma, which characterize the work of electromagnetic forces (and, consequently, the role of the plasma dynamic mechanism of energy dissipation) to the characteristic value of all forces actually acting on the plasma, including gasdynamic forces (reflecting the influence of the Joule dissipation mechanism energy), causing the movement of the SW head in gas at an average speed D. At values $A_m\to 1$, the influence of pondermotor forces and the work performed by them becomes decisive both in power and in energy terms—the fraction of the Ohmic resistance of the plasma load should tend to the minimum value (${\mathsf{\lambda }}_R\to {\mathsf{\lambda }}_{R\min }$), and, therefore, the plasma dynamic mechanism of energy dissipation becomes the main one. At $A_m\to 0$, on the contrary, the plasma is heated only as a result of Ohmic heating, and acceleration—under the action of gasdynamic forces.

The calculations showed that, depending on the value $A_m$, i.e., depending on the role of one or another heating mode (Ohmic, transient, and plasma dynamic), there are three different types of quasi-stationary spatial distributions of plasma parameters which can be used to judge the features of the emerging structures and the dynamics of plasma propagation, and, consequently, to discuss the modes of discharge. At A_m < 0.4, the Ohmic heating mode (λ_R ≥ 0.8) is realized with an insignificant fraction of kinetic energy in the total plasma energy (λ_E ≤ 0.1). In the range A_m ≈ 0.4–0.8, a transitional mode (λ_R ≈ 0.4–0.8) is realized, in which the role of the Ohmic and plasma dynamic heating mechanisms are approximately the same.

In what follows, we will consider only the features of radiation plasma dynamics (RPD) structures and the behavior of the main parameters of the MPC discharge plasma in the transition regime, which is most interesting from the physical point of view.

In the first half-period of the discharge current (when the main part of the energy is supplied to the discharge plasma, and the plasma parameters reach their extreme values), a time interval can be distinguished (starting from a certain moment of time t_in and practically until the end of the first half-period $t_1$) during which the spatial distributions of the main RPD parameters of the plasma acquire the property of quasi-stationarity, i.e., remain qualitatively similar in time.

At the initial stage, a nonstationary transition occurs from the initial one (which simulates the “breakdown” phase of the interelectrode gap) to a quasi-stationary state. From the moment t = 0, the power capacitor starts to discharge through the gas plasma layer adjacent to the surface of the electrode system, providing the release of Joule energy in it and its heating.

After reaching temperatures of 25 kK, the gas plasma begins to emit light streams with a density of 0.1–1 MW/cm², causing the IDI material to heat up and vaporize. Here, we note that the initial phase of a quasi-stationary plasma formation is characterized by the absence of plasma of the erosion products of the central electrode. This is due to the time delay in the evaporation of the central electrode. The duration of the delay time can vary in the range 0.1–0.4 t_m and depends on the thermal physical properties of the electrode material, the density of the environment, and the power–power mode of the MPC-discharge.

It can be seen in Figure 2 and Figure 3 that the light erosion vapor entering the discharge zone is ionized and heated as a result of the combined action of radiation fluxes, plasma dynamic, and Joule heating. Under the action of gas dynamic and pondermotor forces, collapse on the MPC axis occurs, the light-erosion plasma of the dielectric is accelerated, and the gas is forced out of the regions adjacent to the surface of the electrode system.

$$p={10}^{-2}\mathrm{MPa}(A_m=0.6).$$

The discharge current begins to flow mainly through the higher-temperature regions filled with light-erosion plasma, providing its further heating, acceleration, and the formation of characteristic quasi-stationary RPD structures. The initial stage ends at the moment of the formation of the characteristic structure of the outer region of the discharge plasma (Figure 1): a shock wave propagates through the undisturbed gas in the gas (GSW, pos. 1), a shock wave appears in the plasma of light-erosion vapors (PSW, pos. 11) and a contact boundary (pos. 3) separating the regions of shock-compressed gas (pos. 2) and plasma of light-erosion vapors (pos. 12). The duration of the initial stage t_in does not exceed 2 μs (depending on the rate of energy input into the plasma load).

At large values of the amplitude of the discharge current J_m and (or) with a decrease in the density of the surrounding gas ${\mathsf{\rho }}_0$, the operating mode of the MPC discharge changes from Ohmic to transient. This regime is characterized by an increase in plasma dynamic effects associated with an increase in the role of ponderomotive forces. In this case, in the first half-period of the discharge current, the structure and parameters of the MPC-discharge plasma have a number of characteristic distinctive features. The main elements of the structure of the plasma formation typical for this mode are shown in Figure 2a.

The outer boundary of the discharge plasma is a strong gasdynamic shock wave (GSW) with a pronounced conical shape. Behind the GSW front, there are shock-compressed regions of the surrounding gas (SCG) and light erosion plasma (SCP) separated by a contact boundary (CB). The distribution of the thermal gasdynamic parameters of plasma and gas in the indicated regions along the front of the outer boundary of the discharge is characterized by a high degree of inhomogeneity. The propagation velocity of GSW in the paraxial region is two or more times higher than the GSW velocity in the peripheral regions of the discharge. An important distinguishing feature (from the Ohmic mode) of the transient mode is the significantly large value of the axial coordinate of the position of the GSW front in the paraxial region, the value of which, at the time of the maximum discharge current, is of the order of the size of the MPC midsection, i.e., $z_m\approx D{t}_m\ge 2r_2$.

The region of the plasma of light-erosion vapors of structural materials of the MPC electrode assembly elements is directly adjacent to the region of the shock-compressed gas. In contrast to the explosive distribution of all the main thermal gasdynamic parameters of light-erosion plasma, it is characterized by significant spatial inhomogeneity, the presence of regions with different intensities, and the nature of the processes occurring in them. The analysis of the results obtained revealed three main characteristic regions in the quasi-stationary structure of the light-erosion plasma, schematically shown in Figure 2a.

In the area of the MPC axis, a cumulation zone is formed—region I (Figure 2a) of a high-speed, high-temperature, and dense plasma flow, limited by the surfaces of the magneto gasdynamic SW-discontinuity (AΦ line, Figure 2a), tangential discontinuity (ΦC line, Figure 2a), and SW-discontinuity, which is a shock wave (PSW) formed during the plasma dynamic deceleration of a high-speed plasma flow when interacting with the surrounding gaseous medium.

The rest of the light-erosion plasma, separated from the dense and “hot” axial zone of cumulation by the rupture surface (AΦC line, Figure 2a), is filled with a rarefied (ρ_p0/ρ₀ ≤ 0.1) and much less heated (10–30 kK) plasma of IDI light-erosion vapors. This region is divided by a conical magneto-gasdynamic discontinuity (ΦB line) into region II (with the AΦB boundary, Figure 2a), within which the electromagnetic acceleration of the dielectric plasma occurs, and zone III (with the CΦB boundary, Figure 2a), filled with the plasma of dielectric vapors, passes through the gap (line ΦB, Figure 2a).

The spatial position of the boundaries and the values of the plasma parameters of the selected structural zones of the MPC discharge change with time but remain geometrically and physically similar. The composition and thermal gasdynamic parameters of the cumulation region are subject to the most significant changes in time. Calculations have shown that, in the time interval t_in < t < 0.2 t₁ during which there is a delay in the light-erosion evaporation of the central electrode material, the cumulation region is formed only from the plasma of the vapors of the dielectric insert. The high-temperature-emitting plasma of the dielectric formed at the surface of the central electrode intensifies the heating of the MPC-discharge electrodes.

At the moment of time ~0.2 t₁, surface evaporation of the central electrode begins, and the plasma jet of its light-erosion vapors flows into the dielectric plasma of the cumulation zone. In this case, the radial expansion of the metal plasma jet is restrained by the action of the forces of the dynamic pressure converging to the axis of the dielectric plasma flow and magnetic pressure. As a result, a narrow (with a radius smaller than the cathode radius) jet is formed, the axial continuous acceleration of which to supersonic speeds is carried out mainly by gasdynamic forces. The flow is accelerated up to the sonic velocity near the electrode on a narrowing section under the conditions of Joule heat release up to supersonic speeds—in the expansion zone under conditions of heat release by radiation and interaction with a high-speed dielectric plasma flow. Shockless acceleration of the axial jet of metal plasma occurs up to contact with the shock-compressed plasma region in the axial part of the outer boundary of the discharge. By the moment of time 0.3–0.4 t₁, the area of cumulation I takes the form shown in Figure 2a and consists of the axial zone Ia of the metal vapor plasma of the central electrode and the surrounding zone Ib of the dielectric vapor plasma.

Typical for a given transient regime, the distribution patterns in space of the main thermal gasdynamic parameters at the time 15.3 μs of the maximum discharge current (285 kA) for an MPC discharge in Ar with an initial pressure 0.1 atm at $C=750$ μF and $U_0=5$ kV (A_m = 0.6) are shown in Figure 2 and Figure 3.

The outer boundary of the discharge is a strong gasdynamic SW. At the speed of movement of the GSW axial part D ≈ 6.5 km/s, the density ratio ρ_SW/ρ₀ ≈ 8 reaches its limiting gasdynamic value. The value of the axial coordinate $z_m$ of the position of the bow shock wave at the time of the current maximum reaches values $z_m\approx 85$ mm. The radial expansion of SW along the surface of the electrode system is much lower (D_r ≈ 1.5 km/s, ρ_SW/ρ₀ ≈ 3). With a general conical shape of the SW, characteristic (for modes with manifestation of plasma dynamic effects) kinks of the GSW front are observed at the point with coordinates $r\approx 36$ mm, $\mathrm{z}\approx 36$ mm (at a given time), arising from the intersection of GSW with different intensities.

Radiation-magneto plasma dynamics processes occurring with the light erosion plasma of dielectric vapors in zone II determine the further dynamics of plasma formation, its structure, and parameters. The near-surface plasma of a dielectric is accelerated by electromagnetic forces in the z-th direction up to velocities of 5 $÷$ 10 km/s in a narrow (0.5 cm), radially limited ($r\le 3$cm) layer. In the IDI zone, adjacent to the outer surface of the central electrode, the flowing currents have commensurate components j_z ≈ j_r, which lead to the appearance of the movement of the dielectric plasma in the radial direction (to the axis of the system) in the region of point A.

The pattern of the further movement of the formed flows of the erosional plasma of the dielectric is determined by the space–time distribution of the current density. Calculations have shown that, for transient regimes with A_m~0.4–0.8, the region of current flow is limited by zone II and the initial ($0<z<z_{\Phi }$) cumulation region. At the same time, in the axial region, the current density has mainly only the j_z-th component, the value of which monotonically decreases with distance from the MPC end face, and at $z\approx z_{\Phi }$, $j_z\approx 0$.

In zone II, filled with dielectric plasma, the direction of the current density vector $\overrightarrow{j}$ is characterized by the presence of two radial j_r and axial j_z components approximately equivalent in magnitude, the interaction of which with the azimuthal magnetic field $H_{\mathsf{\phi }}\left(r,\mathrm{z}\right)$ provides continuous electromagnetic plasma acceleration both in the axial and radial directions up to velocities equal to the local values of the Alfven velocities $V_A$, upon reaching which, magneto-gasdynamic discontinuities AΦ and ΦB are formed.

The calculated position of these discontinuities, which are the boundary of region II of the effective pondermotor acceleration of the dielectric plasma at time ~15 μs, is illustrated by the spatial distributions of the Alfven velocity (Figure 3a) and the modulus of the plasma flow velocity (Figure 3b). A distinctive (from the explosive mode) feature of V_A ≈ (p_M/p)^1/2 behavior is its monotonic SW increase with distance from the surface of the electrode system and the achievement of maximum values at the point Φ of intersection of shock-wave discontinuities (lines AΦ and BΦ, Figure 2a). A characteristic feature of the transient regime is the relative smallness $V_A$ in zones I (in the $z>z_{\Phi }$) and III, which indicates that the movement of plasma flows in these areas occurs mainly under the action of gasdynamic forces.

The absolute velocity of dielectric plasma in zone II increases, approaching the boundaries of the discontinuities (lines AΦ and ΦB, Figure 2a), reaching the maximum values 30 km/s at the point of their intersection (Φ). The characteristic level of the velocities achieved in this regime is much higher than the values of the plasma flow velocities in the Ohmic regime. The plasma density in zone II decreases monotonically with distance from the IDI surface, changing along the AΦ discontinuity from values $\mathsf{\rho }\approx 0.03$ kg/m³ (in the area of point A) to a value of $\mathsf{\rho }\approx 0.01$ kg/m³ in the area of point Φ. An increase in the modulus of the dielectric plasma velocity along the discontinuities (lines AΦ and ΦB, Figure 2a) indicates an increase in the intensity of these discontinuities when approaching the point Φ.

The appearance of significant values of the radial components of the plasma flow velocity IDI (10–30 km/s) in zone II before the AΦ discontinuity and its interaction with the dense paraxial plasma of metal vapors leads to shock-wave deceleration and, accordingly, the formation of a shock-compressed and heated region of dielectric plasma (zone Ib), which is the peripheral part of the cumulation zone I. The intensity of the strong magneto-gasdynamic SW, which is the outer boundary of this region, increases with distance from the surface of the MPC end, reaching a maximum in the region of the point Φ. However, despite an increase in the intensity of the rupture (AΦ line, Figure 2a), the density of the shock-compressed dielectric plasma in the cumulation zone ρ_c ≈ ρ_p0(γ + 1)/(γ − 1) decreases with increasing z due to a decrease in the incident flow density ρ_p0. Here, it is important to pay attention to the fact that the temperature of the shock-compressed plasma immediately behind the discontinuity along the AΦ shock wave is practically constant and reaches values of 50–60 kK. This is because the plasma near the surface of the central electrode, where the current density is maximum flowing through it, is subject to maximum Joule heating, while the plasma temperature in the cumulation zone in the region of the Φ point is determined only by the effect of plasma dynamic heating on SW.

It is important to pay attention to the fact that, in this mode, the dynamics of the formation of the initial cumulation zone are such that the dielectric plasma does not collapse directly on the axis of the system, and SW deceleration occurs on a dense paraxial metal vapor plasma. In such a physical situation, the work of electromagnetic forces (that is, forces that accelerate the dielectric plasma in zone II and the magnetic pressure forces of currents flowing in the cumulation zone) are converted into internal energy of both the “inhibited” dielectric plasma (zone Ib) and plasma metal (zone Ia). Consequently, the appearance of a dense and relatively cold metallic plasma in the initial cumulation region reduces the efficiency of plasma-dynamic heating of the plasma, i.e., limiting the level of maximum plasma temperatures in this part of the cumulation region. Since metal plasma enters the cumulation zone at a low (7 ÷ 10 kK) temperature, its heating requires a large amount of energy. As a result, nonuniformity of the temperature distribution in the radial direction arises: the temperature of the peripheral shock-compressed dielectric plasma is higher than the temperature of the narrow ($r\le 2÷3$ mm) paraxial region of the metal plasma (Figure 2b).

The front (AΦ line, Figure 2a) of the magneto-gasdynamic SW at the moment of the maximum discharge current has the shape of an expanding cone, the radius of the base of which in the region of the central electrode is equal to mm, and the radius in the region of the point Φ is ~15 mm. The maximum values of plasma temperature (60–80 kK) and density (ρ ≈ 0.1–0.4 kg/m³) are reached in this cumulation zone. Inside the cumulation region, there is a radial motion of the shock-compressed plasma, which leads to the expansion of this region, which indicates the absence of force equilibrium in the radial direction. The axial component of the cumulative jet velocity has a minimum on the axis and a maximum in the peripheral part.

This character of the distribution of the axial velocity component clearly shows the difference in the mechanisms of longitudinal (along 0z) plasma acceleration in the initial area of the cumulation region. The axial region (with $r\le 2÷3$ mm) of the erosional plasma of the metal is accelerated as a result of the action of gasdynamic forces and viscous interaction with the plasma jet of the dielectric. Dielectric plasma in the peripheral region of the cumulation zone (shock-compressed dielectric plasma) moves under the action of electromagnetic forces.

The formation of the flow cumulation area and its parameters are determined by electromagnetic effects (Ohmic heating, pinch compression, and plasma dynamic deceleration). Next comes the gasdynamic jet flow area ($z>z_{\Phi }$), limited by a tangential discontinuity (ΦC line, Figure 2a), and in which electromagnetic processes are of little importance. The parameters of the cumulative flow in this region depend both on the parameters of the flow in its initial section $z\approx z_{\Phi }$ and on the nature of its interaction with the dielectric plasma flow in the zone III. The velocity of the plasma flow electromagnetically accelerated in zone II at the discontinuity (line ΦB, Figure 2a) decreases its normal (with respect to the ΦB line) component, while maintaining the tangential component, i.e., the flow turns towards the MPC axis. Plasma density in zone III is 2–3 times higher than in electromagnetic acceleration zone II. The flow temperature after rupture changes insignificantly and is approximately equal to 20–30 kK. Forming beyond the boundary [30,31,32] of the conical magneto-gasdynamic discontinuity, a dielectric plasma flow with a velocity directed almost parallel to the discontinuity surface interacts with a high-speed plasma jet of the cumulative region, resulting in a tangential discontinuity (line ΦC, Figure 2a).

In this case, the flow of the incident plasma itself in zone III turns and moves along the tangential discontinuity (ΦC line, Figure 2a) at a speed parallel to the velocity of the dielectric plasma in the peripheral zones of the axial region (see Figure 2b and Figure 3). The practical disappearance in this zone of cumulation of the compressive action of the flow by the magnetic pressure of the axial current and a significant weakening of the dynamic pressure from the radially moving flow of dielectric plasma in zone III leads to a more significant expansion (the opening angle of the conical discontinuity of the AΦ is approximately 2 times less than that of the tangential discontinuity of the ΦC), an axial plasma jet and, accordingly, to its acceleration (supersonic jet in an expanding “nozzle”) [33,34,35]. In this case, the irregularity of the radial distributions of the velocity and flux density in this area is significantly weakened.

In the axial direction, the velocity of both metallic and dielectric plasma of the cumulative flow increases monotonically to supersonic speeds, reaching the maximum values ahead of the PSW 20 ÷ 24 km/s ($M\ge 4$).

7. Conclusions

In the presented work, the radiation-magneto plasma dynamic processes of powerful electric-discharge sources, in particular, a magneto-plasma compressor (MPC), are modeled and analyzed. Such MPCs and accelerators are used in plasma technologies, plasma dynamics, nuclear fusion, space propulsion, etc. The paper presents the results of the numerical simulation of the plasma dynamic characteristics of an MPC discharge in gases and electric discharge sources.

The features of the radiation dynamics of plasma and the behavior of the main parameters of the plasma of an MPC, the most interesting from the physical point of view of a transient regime, are considered. It is found that there are three different types of quasi-stationary spatial distributions of plasma parameters. These distributions indicate the features of the formed structures and the dynamics of plasma propagation and the discharge regimes.

The nonlinearity of the initial equations with a strong mutual influence of various processes (here the problem is related to the different characteristic times of the processes taken into account) leads to the need to use economical and efficient numerical methods, which include the method of splitting the equations of a mathematical model into physical and spatial directions, in order to obtain numerical results in a reasonable amount of time. The requirement for the efficiency of the numerical scheme leads to the need to use the so-called conditionally stable schemes since the system of equations of radiative magnetic gasdynamics considered here belongs to the class of mixed hyperbolic–parabolic equations.

The paper presents a mathematical model of MPC discharges in gases for a wide range of changes in the main parameters and the surrounding gas environment. This model is based on a nonstationary, axisymmetric, two-dimensional system of equations for viscous, one-temperature, radiation plasma dynamics. The numerical solution of the nonstationary, two-dimensional, radiation-gasdynamic model developed in the work is based on the method of splitting into physical processes and spatial directions. The developed computational code uses a multiblock, multigrid technology for calculations on nonorthogonal, structured grids. On the basis of the performed computational studies, quantitative data were obtained on the modes, structures, and plasma dynamics of the end-type MPC for the transient power–power mode of the MPC—a discharge in gas.