A Numerical Simulation of an Experimental Melting Process of a Phase-Change Material without Convective Flows
Abstract
:Featured Application
Abstract
1. Introduction
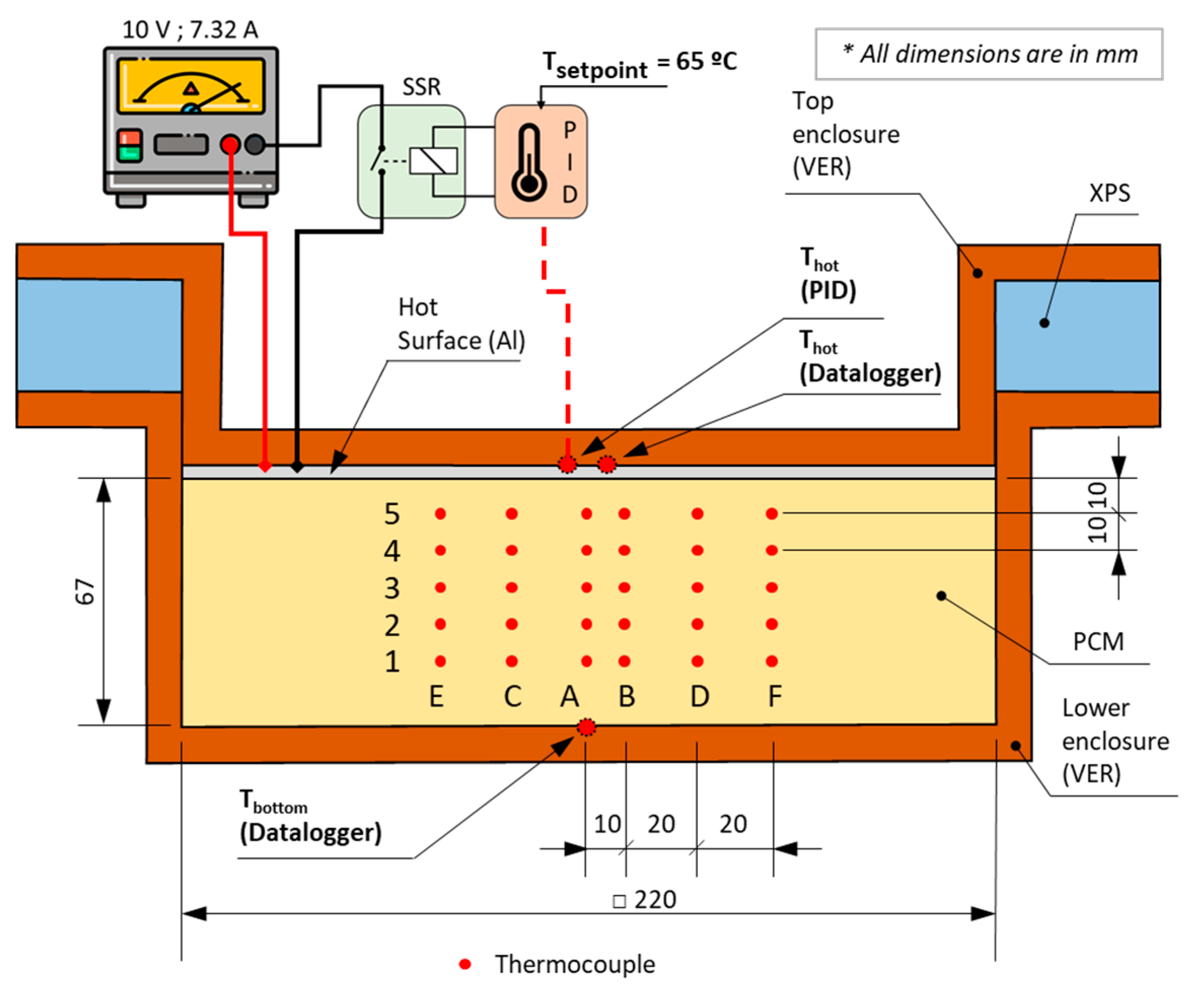
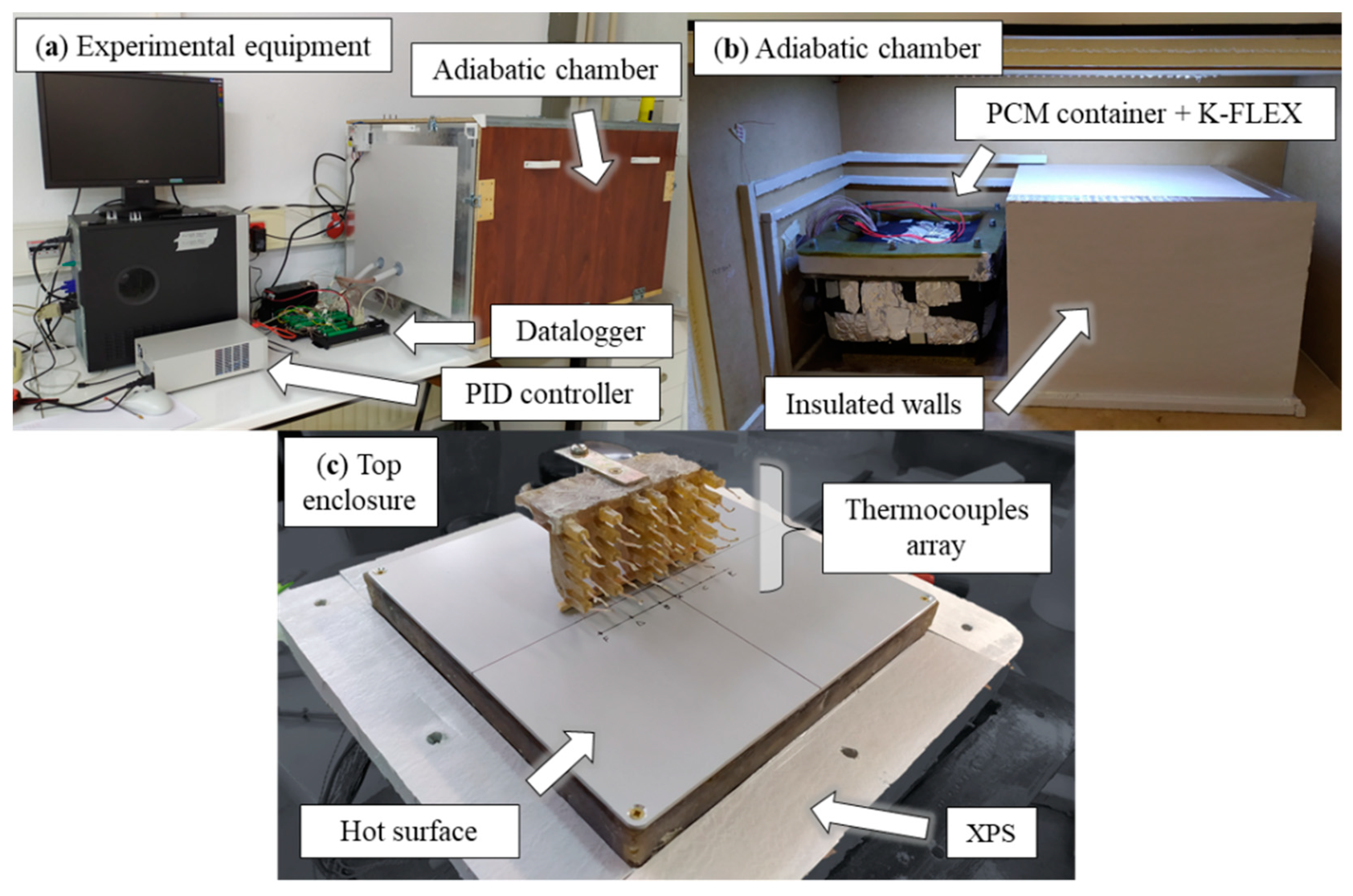
2. Experimental Section
2.1. Experimental Procedure
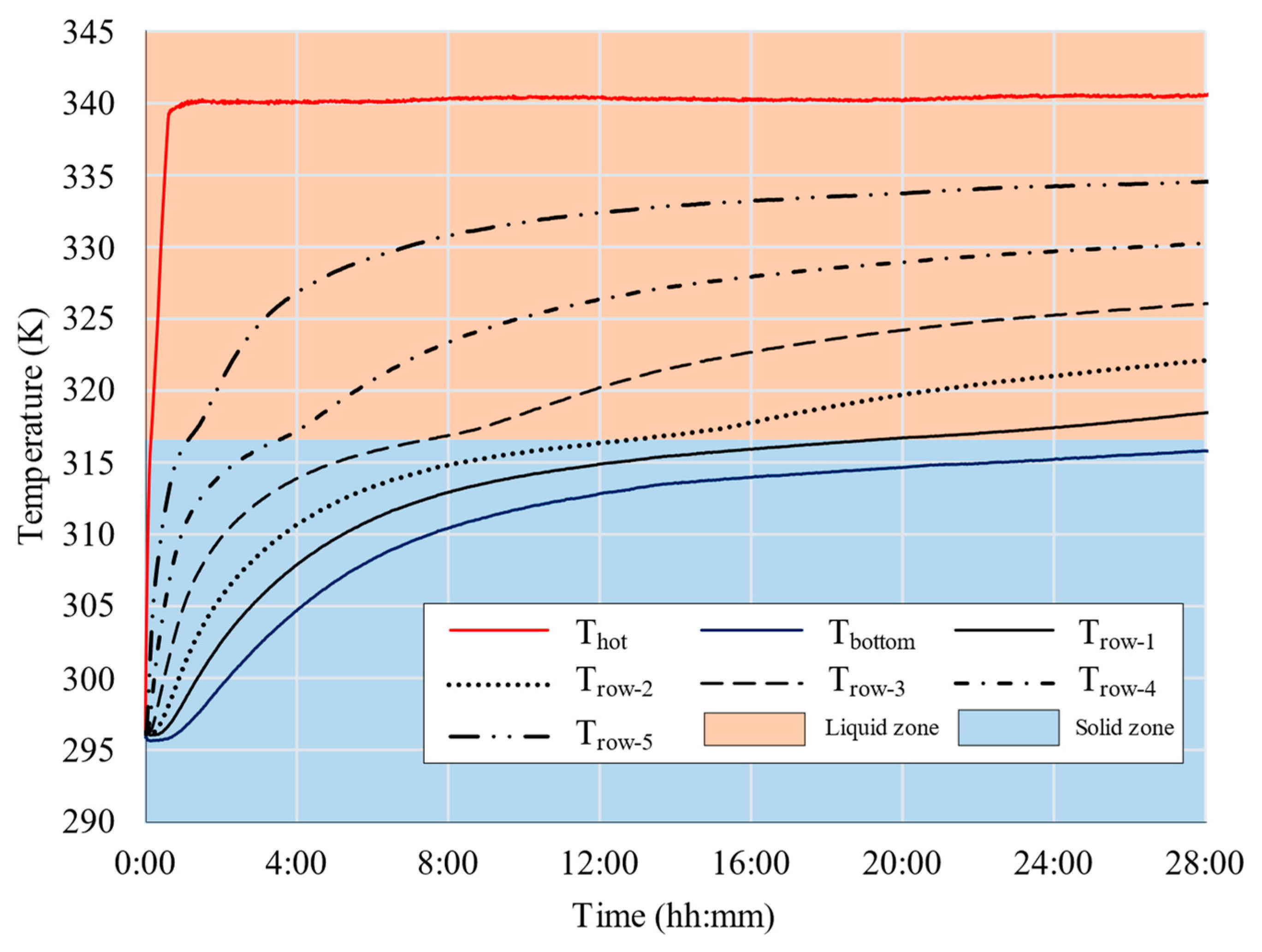
2.2. Experimental Results
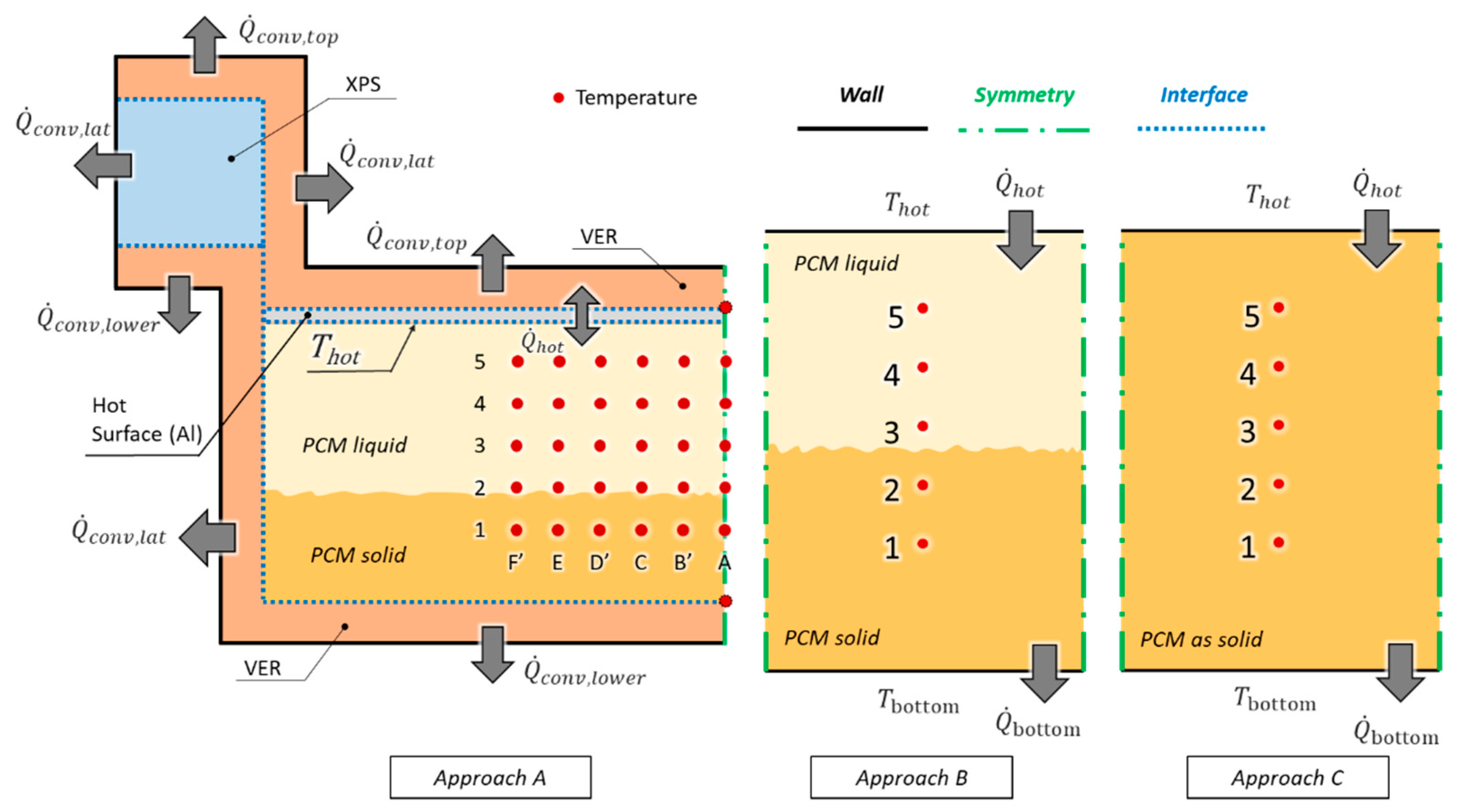
3. Numerical Model
3.1. Approach A—Complete
3.2. Approach B—Simple
3.3. Approach C—Solid
4. Computational Approach
4.1. Enthalpy—Porosity Method (EP)
4.2. Effective Heat Capacity Method (EHC)
4.3. Computational Procedure
4.4. Mesh Studies
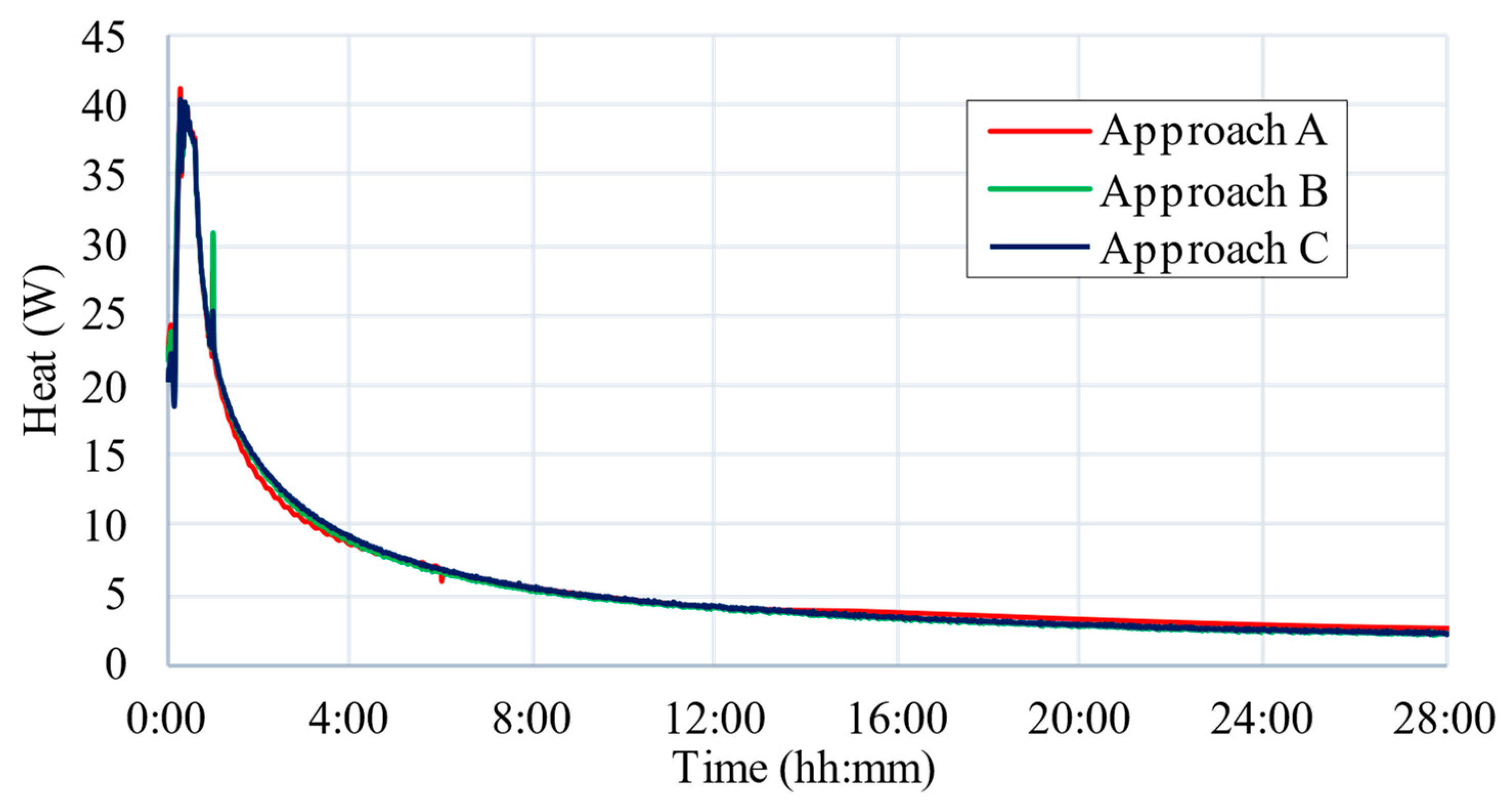
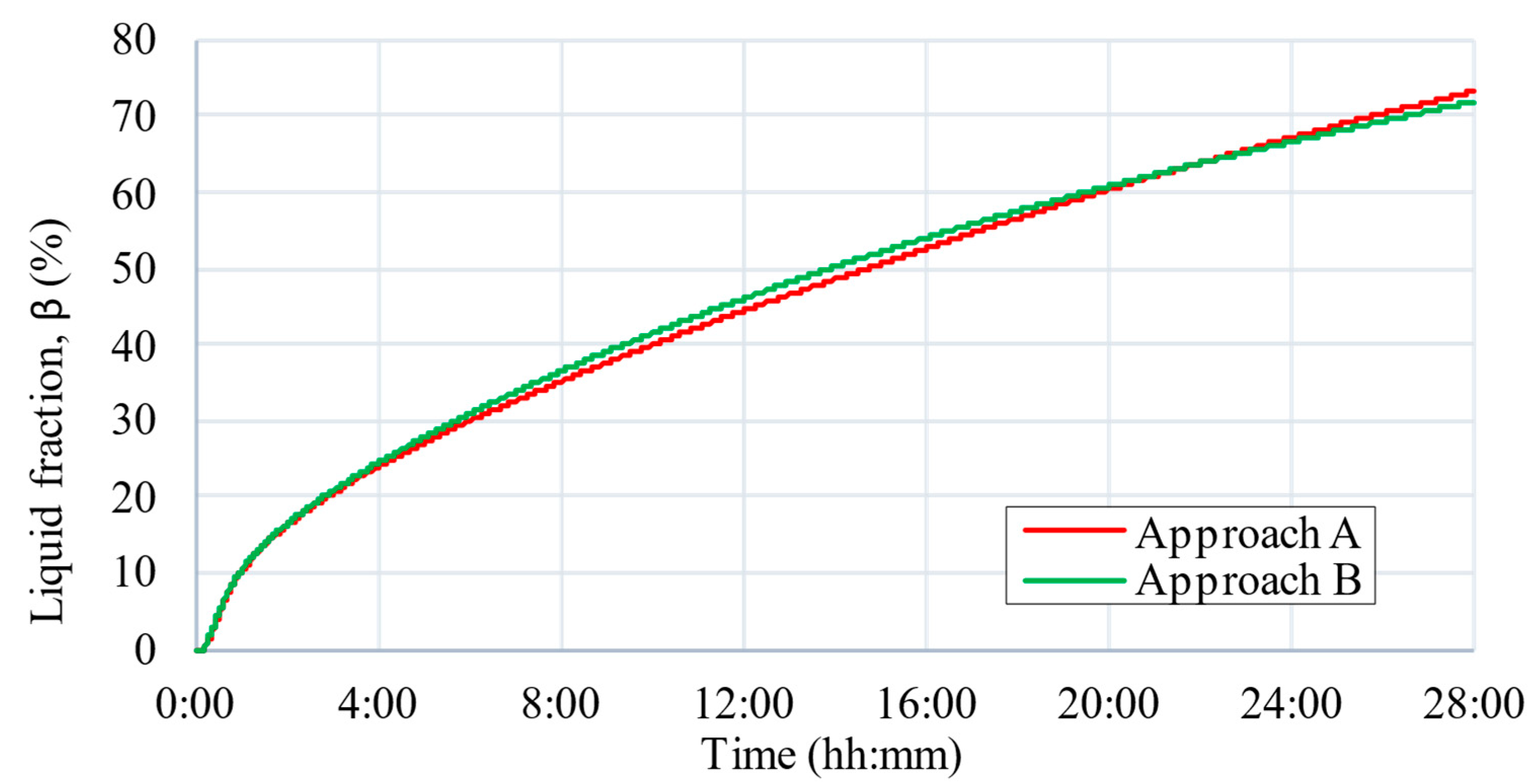
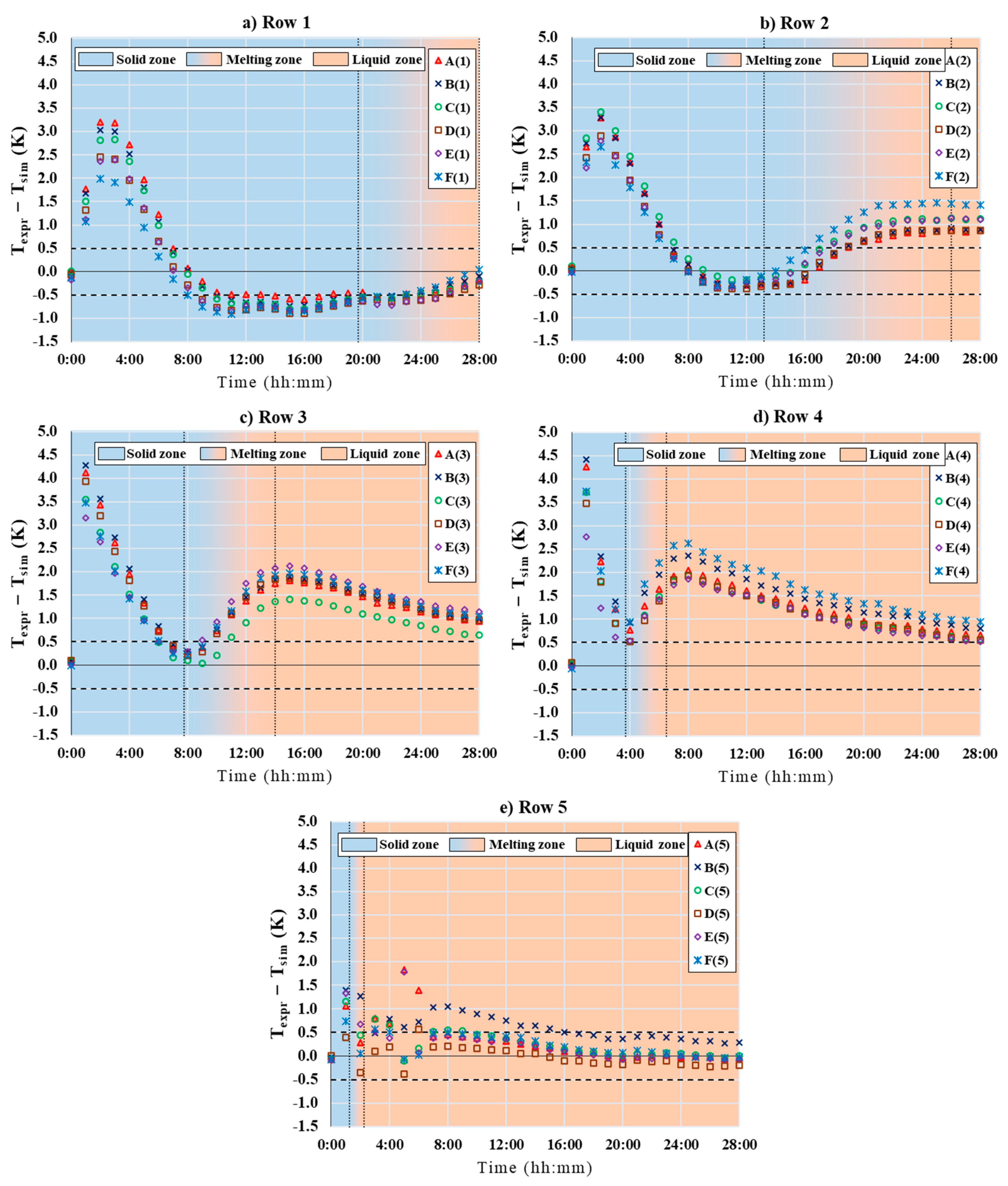
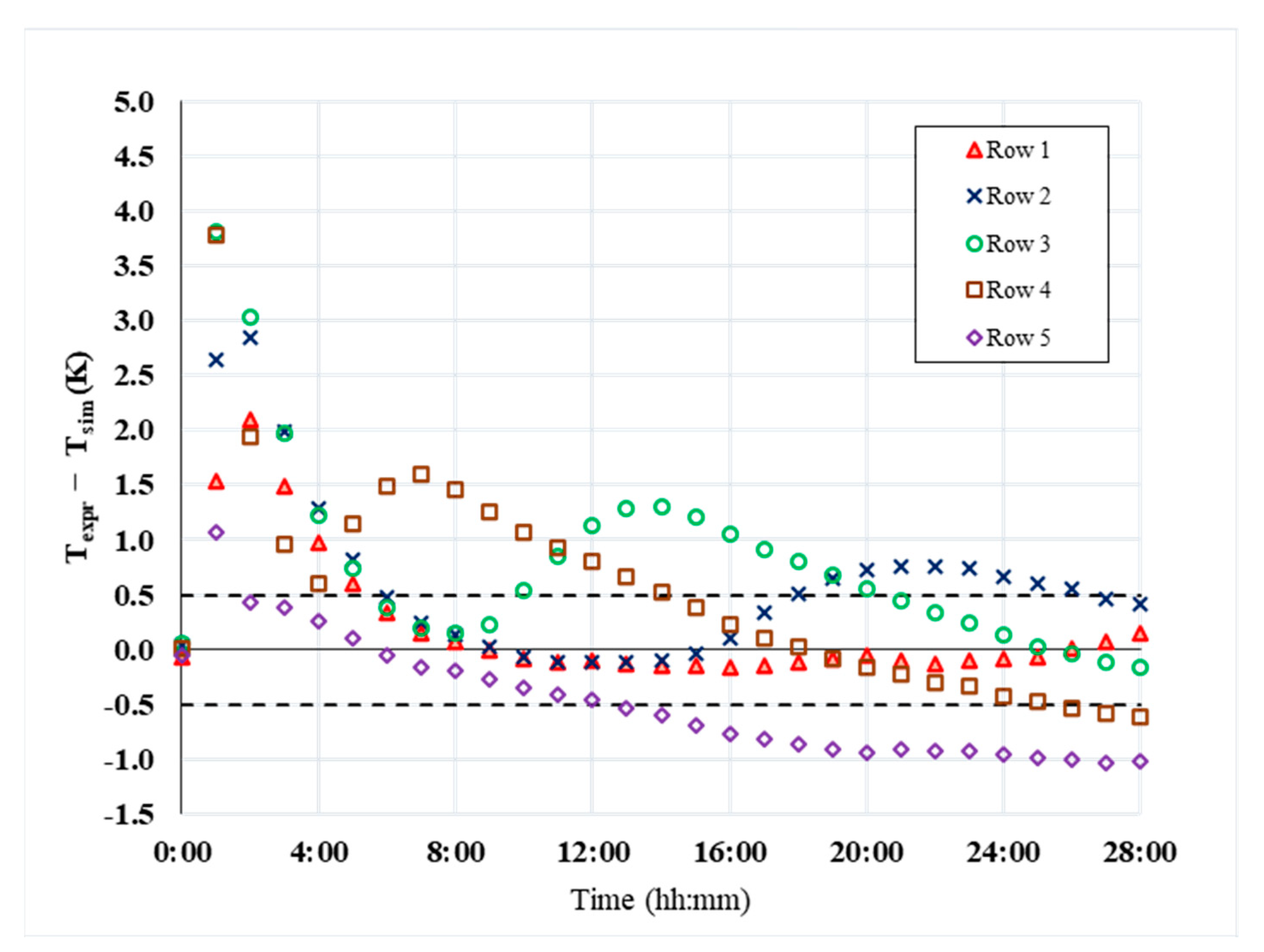
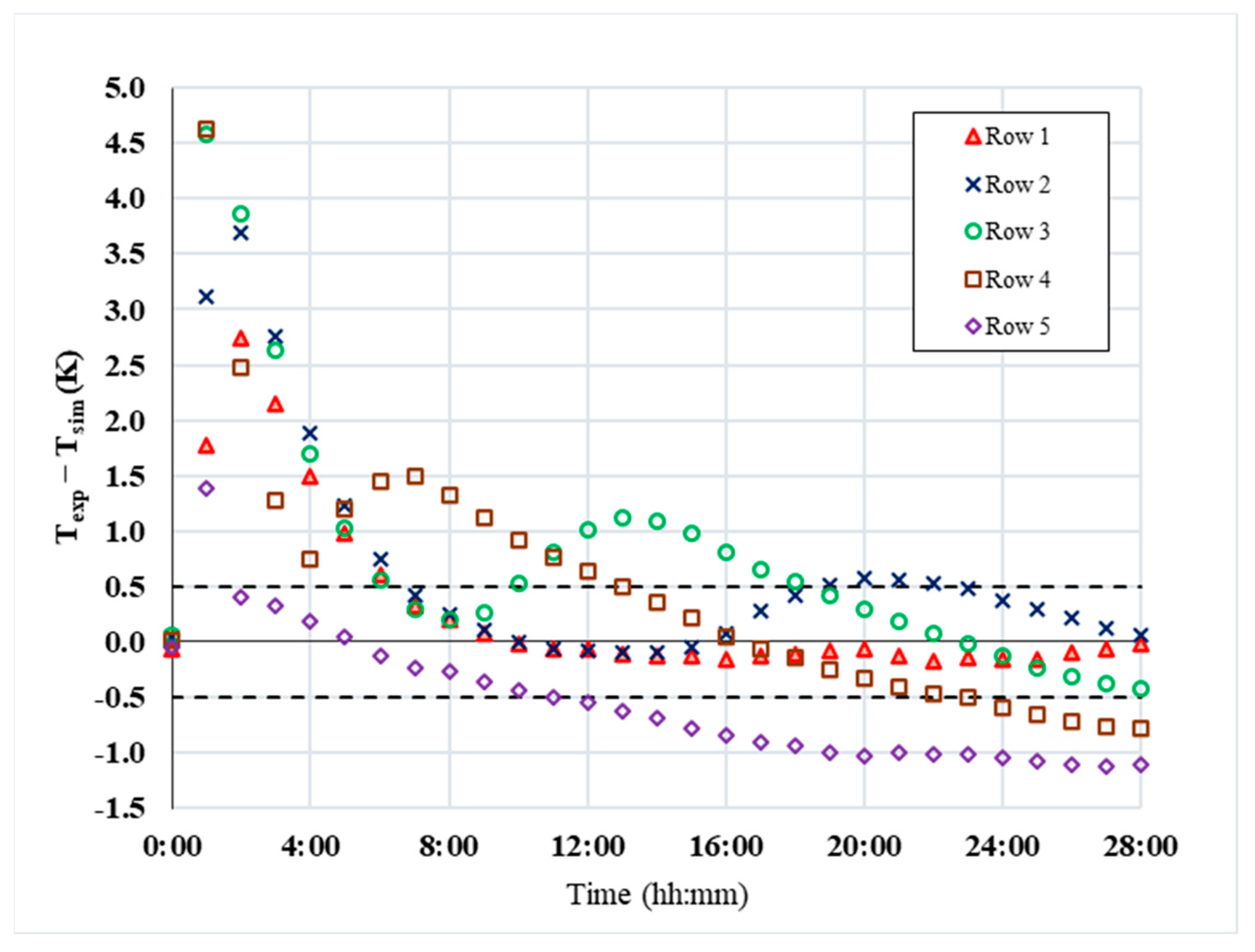
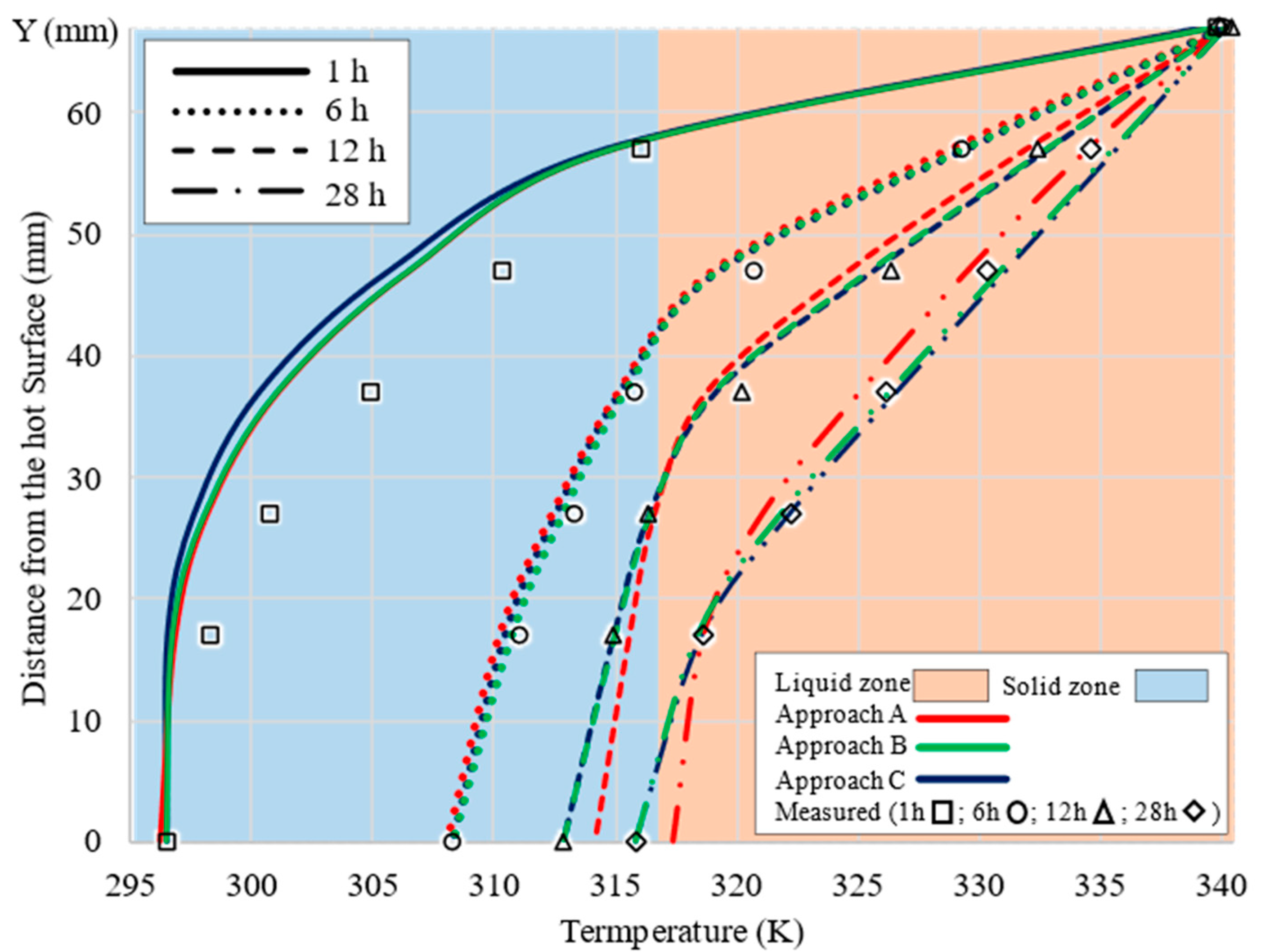
5. CFD Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| Mushy zone constant (kg/s·m3) | |
| Area of the horizontal plate (m2) | |
| Specific heat (J/kg·K) | |
| Gravity (9.81 m/s2) | |
| Convection coefficient (W/m2·K) | |
| Enthalpy (J) − (J/kg) | |
| Thermal conductivity (W/m·K) | |
| Latent heat of fusion (J/kg) | |
| Length of the vertical plate (m) | |
| Characteristic length (m) | |
| Total number of measurements | |
| Nusselt number | |
| Perimeter of the horizontal plate (m) | |
| Prandtl number | |
| Heat flux (W) | |
| Rayleigh number | |
| Coefficient of determination | |
| Root mean square error (K) | |
| Source term (from the Carman–Koseny equation) (W/m3) | |
| Temperature (K) | |
| Fluid velocity (m/s) | |
| Temperature value from the experimental measures (K) | |
| Temperature value from the simulate case (K) | |
| Average of the temperature values from the experimental measures (K) | |
| Greek symbols | |
| Volumetric liquid fraction of PCM | |
| Thermal expansion (K−1) | |
| Constant from the Carman–Koseny equation | |
| Dynamic viscosity (kg/m·s) | |
| Kinematic viscosity (m2/s) | |
| Density (kg/m3) | |
| Subscripts | |
| Air | |
| Bottom surface of the container | |
| Effective value | |
| Hot surface of the container | |
| Liquid | |
| Reference value | |
| Solid; surface | |
| ∞ | Free flow conditions (outside the thermal boundary layer) |
References
- Pielichowska, K.; Pielichowski, K. Phase Change Materials for Thermal Energy Storage. Prog. Mater. Sci. 2014, 65, 67–123. [Google Scholar] [CrossRef]
- Agyenim, F.; Hewitt, N.; Eames, P.; Smyth, M. A Review of Materials, Heat Transfer and Phase Change Problem Formulation for Latent Heat Thermal Energy Storage Systems (LHTESS). Renew. Sustain. Energy Rev. 2010, 14, 615–628. [Google Scholar] [CrossRef]
- Tao, M.; Zhenpeng, L.; Jiaxin, Z. Photovoltaic Panel Integrated with Phase Change Materials (PV-PCM): Technology Overview and Materials Selection. Renew. Sustain. Energy Rev. 2019, 116, 109406. [Google Scholar] [CrossRef]
- Sharif, M.K.A.; Al-Abidi, A.A.; Mat, S.; Sopian, K.; Ruslan, M.H.; Sulaiman, M.Y.; Rosli, M.A.M. Review of the Application of Phase Change Material for Heating and Domestic Hot Water Systems. Renew. Sustain. Energy Rev. 2015, 42, 557–568. [Google Scholar] [CrossRef]
- Douvi, E.; Pagkalos, C.; Dogkas, G.; Koukou, M.K.; Stathopoulos, V.N.; Caouris, Y.; Vrachopoulos, M.G. Phase Change Materials in Solar Domestic Hot Water Systems: A Review. Int. J. 2021, 10, 100075. [Google Scholar] [CrossRef]
- Iten, M.; Liu, S.; Shukla, A. A Review on the Air-PCM-TES Application for Free Cooling and Heating in the Buildings. Renew. Sustain. Energy Rev. 2016, 61, 175–186. [Google Scholar] [CrossRef]
- Dardir, M.; Panchabikesan, K.; Haghighat, F.; El Mankibi, M.; Yuan, Y. Opportunities and Challenges of PCM-to-Air Heat Exchangers (PAHXs) for Building Free Cooling Applications—A Comprehensive Review. J. Energy Storage 2019, 22, 157–175. [Google Scholar] [CrossRef]
- Zhou, D.; Zhao, C.Y.; Tian, Y. Review on Thermal Energy Storage with Phase Change Materials (PCMs) in Building Applications. Appl. Energy 2012, 92, 593–605. [Google Scholar] [CrossRef] [Green Version]
- Al-Yasiri, Q.; Szabó, M. Incorporation of Phase Change Materials into Building Envelope for Thermal Comfort and Energy Saving: A Comprehensive Analysis. J. Build. Eng. 2021, 36, 102122. [Google Scholar] [CrossRef]
- Bayram, U.; Aksöz, S.; Maraşll, N. Temperature Dependency of Thermal Conductivity of Solid Phases for Fatty Acids. J. Therm. Anal. Calorim. 2014, 118, 311–321. [Google Scholar] [CrossRef]
- Jmal, I.; Baccar, M. Numerical Study of PCM Solidification in a Finned Tube Thermal Storage Including Natural Convection. Appl. Therm. Eng. 2015, 84, 320–330. [Google Scholar] [CrossRef]
- Kean, T.H.; Sidik, N.A.C.; Asako, Y.; Ken, T.L.; Aid, S.R. Numerical Study on Heat Transfer Performance Enhancement of Phase Change Material by Nanoparticles: A Review. J. Adv. Res. Fluid Mech. Therm. Sci. 2018, 45, 55–63. [Google Scholar]
- Shokouhmand, H.; Kamkari, B. Experimental Investigation on Melting Heat Transfer Characteristics of Lauric Acid in a Rectangular Thermal Storage Unit. Exp. Therm. Fluid Sci. 2013, 50, 201–212. [Google Scholar] [CrossRef]
- Kamkari, B.; Shokouhmand, H. Experimental Investigation of Phase Change Material Melting in Rectangular Enclosures with Horizontal Partial Fins. Int. J. Heat Mass Transf. 2014, 78, 839–851. [Google Scholar] [CrossRef]
- Voller, V.R.; Prakash, C. A Fixed Grid Numerical Modelling Methodology for Convection-Diffusion Mushy Region Phase-Change Problems. Int. J. Heat Mass Transf. 1987, 30, 1709–1719. [Google Scholar] [CrossRef]
- Poirier, D.; Salcudean, M. On Numerical Methods Used in Mathematical Modeling of Phase Change in Liquid Metals. J. Heat Transf. 1988, 110, 562–570. [Google Scholar] [CrossRef]
- Al-Saadi, S.N.; Zhai, Z. Modeling Phase Change Materials Embedded in Building Enclosure: A Review. Renew. Sustain. Energy Rev. 2013, 21, 659–673. [Google Scholar] [CrossRef]
- Hu, Z.; Li, A.; Gao, R.; Yin, H. A Comparison Study on Melting inside the Rectangular and Curved Unit with a Vertical Heating Wall. J. Therm. Anal. Calorim. 2015, 122, 831–842. [Google Scholar] [CrossRef]
- Wang, Y.; Dai, J.; An, D. Numerical Investigations on Melting Behavior of Phase Change Material in a Rectangular Cavity at Different Inclination Angles. Appl. Sci. 2018, 8, 1627. [Google Scholar] [CrossRef] [Green Version]
- Libeer, W.; Ramos, F.; Newton, C.; Alipanahrostami, M.; Depcik, C.; Li, X. Two-Phase Heat and Mass Transfer of Phase Change Materials in Thermal Management Systems. Int. J. Heat Mass Transf. 2016. [Google Scholar] [CrossRef]
- Lee, D.; Kim, H.; Kang, C. Single Phase-Change Analysis of Two Different PCMs Filled in a Heat Transfer Module. J. Mech. Sci. Technol. 2014. [Google Scholar] [CrossRef]
- Diarce, G.; Campos-Celador, Á.; Martin, K.; Urresti, A.; García-Romero, A.; Sala, J.M. A Comparative Study of the CFD Modeling of a Ventilated Active Façade Including Phase Change Materials. Appl. Energy 2014, 126, 307–317. [Google Scholar] [CrossRef]
- Iten, M.; Liu, S.; Shukla, A. Experimental Validation of an Air-PCM Storage Unit Comparing the Effective Heat Capacity and Enthalpy Methods through CFD Simulations. Energy 2018, 155, 495–503. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, N.; Tao, W.; Cao, X.; He, Y. Fatty Acids as Phase Change Materials: A Review. Renew. Sustain. Energy Rev. 2014, 29, 482–498. [Google Scholar] [CrossRef]
- Desgrosseilliers, L.; Whitman, C.A.; Groulx, D.; White, M.A. Dodecanoic Acid as a Promising Phase-Change Material for Thermal Energy Storage. Appl. Therm. Eng. 2013, 53, 37–41. [Google Scholar] [CrossRef]
- Hasan, A.; Sayigh, A.A. Some Fatty Acids as PCM Energy Storage Materials. Renew. Energy 1994, 4, 69–76. [Google Scholar] [CrossRef]
- Sharma, A.; Shukla, A.; Chen, C.R.; Wu, T.N. Development of Phase Change Materials (PCMs) for Low Temperature Energy Storage Applications. Sustain. Energy Technol. Assess. 2014, 7, 17–21. [Google Scholar] [CrossRef]
- Mahfuz, M.H.; Anisur, M.R.; Kibria, M.A.; Saidur, R.; Metselaar, I.H.S.C. Performance Investigation of Thermal Energy Storage System with Phase Change Material (PCM) for Solar Water Heating Application. Int. Commun. Heat Mass Transf. 2014, 57, 132–139. [Google Scholar] [CrossRef]
- Desgrosseilliers, L.; Murray, R.; Safatli, A.; Marin, G.; Stewart, J.; Osbourne, N.; White, M.A.; Groulx, D. Phase Change Material Selection in the Design of a Latent Heat Energy Storage System Coupled with a Domestic Hot Water Solar Thermal System. In Proceedings of the ASHRAE Transactions; ASHRAE: Atlanta, GA, USA, 2011; Volume 117, pp. 183–190. [Google Scholar]
- Sari, A. Thermal Reliability Test of Some Fatty Acids as PCMs Used for Solar Thermal Latent Heat Storage Applications. Energy Convers. Manag. 2003, 44, 2277–2287. [Google Scholar] [CrossRef]
- König-Haagen, A.; Franquet, E.; Faden, M.; Brüggemann, D. Influence of the Convective Energy Formulation for Melting Problems with Enthalpy Methods. Int. J. Therm. Sci. 2020, 158, 106477. [Google Scholar] [CrossRef]
- Malvi, C.S.; Dixon-Hardy, D.W.; Crook, R. Energy Balance Model of Combined Photovoltaic Solar-Thermal System Incorporating Phase Change Material. Sol. Energy 2011, 85, 1440–1446. [Google Scholar] [CrossRef]
- K-FLEX ST|K-Flex Catalog. Available online: https://kflex.com/index.php/products/fef/k-flex-st (accessed on 1 September 2021).
- Lauric Acid >= 98 %, FCC, FG|143-07-7|Sigma-Aldrich. Available online: https://www.sigmaaldrich.com/catalog/product/aldrich/w261408?lang=es®ion=ES (accessed on 3 February 2021).
- Kahwaji, S.; Johnson, M.B.; Kheirabadi, A.C.; Groulx, D.; White, M.A. Fatty Acids and Related Phase Change Materials for Reliable Thermal Energy Storage at Moderate Temperatures. Sol. Energy Mater. Sol. Cells 2017, 167, 109–120. [Google Scholar] [CrossRef]
- Resinas Castro, S.L. Vinyl Ester Resin ACT. Available online: https://www.castrocompositesshop.com/en/resins/1082-resina-de-vinilester-act.html (accessed on 19 October 2021).
- Ministerio de Fomento Catálogo de Elementos Constructivos Del CTE. Available online: https://itec.cat/cec/Pages/BusquedaSC.aspx (accessed on 19 October 2021).
- Oktay, H.; Argunhan, Z.; Yumrutas, R. An Investigation of the Influence of Thermophysical Properties of Multilayer Walls and Roofs on the Dynamic Thermal Characteristics. Mugla J. Sci. Technol. 2016, 2, 48–54. [Google Scholar] [CrossRef] [Green Version]
- ChovA ChovAFOAM 300 M—INVERTED ROOF. Available online: https://chova.com/en/products/chovafoam-300-m/ (accessed on 19 October 2021).
- Maragkos, G.; Beji, T. Review of Convective Heat Transfer Modelling in CFD Simulations of Fire-Driven Flows. Appl. Sci. 2021, 11, 5240. [Google Scholar] [CrossRef]
- Lloyd, J.R.; Moran, W.R. Natural Convection Adjacent to Horizontal Surfaces of Various Planforms. Am. Soc. Mech. Eng. 1974, 96, 443–447. [Google Scholar] [CrossRef]
- McAdams, W.H. Heat Transmission; McGraw-Hill Book Company: New York, NY, USA, 1957. [Google Scholar]
- Fluent, A. Ansys Fluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Kozak, Y.; Ziskind, G. Novel Enthalpy Method for Modeling of PCM Melting Accompanied by Sinking of the Solid Phase. Int. J. Heat Mass Transf. 2017, 112, 568–586. [Google Scholar] [CrossRef]
- Budak, B.M.; Sobol’eva, E.N.; Uspenskii, A.B. A Difference Method with Coefficient Smoothing for the Solution of Stefan Problems. USSR Comput. Math. Math. Phys. 1965, 5, 59–76. [Google Scholar] [CrossRef]
- Hashemi, H.; Sliepcevich, C.M. A Numerical Method for Heat Conduction with Change of Phase. Chem. Eng. Prog. Symp. Ser. 1967, 63, 34–41. [Google Scholar]
- Iten, M.; Liu, S.; Shukla, A.; Silva, P.D. Investigating the Impact of Cp-T Values Determined by DSC on the PCM-CFD Model. Appl. Therm. Eng. 2017, 117, 65–75. [Google Scholar] [CrossRef]
- Antony Aroul Raj, V.; Velraj, R. Heat Transfer and Pressure Drop Studies on a PCM-Heat Exchanger Module for Free Cooling Applications. Int. J. Therm. Sci. 2011, 50, 1573–1582. [Google Scholar] [CrossRef]
- König-Haagen, A.; Franquet, E.; Pernot, E.; Brüggemann, D. A Comprehensive Benchmark of Fixed-Grid Methods for the Modeling of Melting. Int. J. Therm. Sci. 2017, 118, 69–103. [Google Scholar] [CrossRef]
- Lamberg, P.; Lehtiniemi, R.; Henell, A.M. Numerical and Experimental Investigation of Melting and Freezing Processes in Phase Change Material Storage. Int. J. Therm. Sci. 2004, 43, 277–287. [Google Scholar] [CrossRef]
- Hed, G.; Bellander, R. Mathematical Modelling of PCM Air Heat Exchanger. Energy Build. 2006, 38, 82–89. [Google Scholar] [CrossRef]
- Fadl, M.; Eames, P.C. Numerical Investigation of the Influence of Mushy Zone Parameter Amush on Heat Transfer Characteristics in Vertically and Horizontally Oriented Thermal Energy Storage Systems. Appl. Therm. Eng. 2019, 151, 90–99. [Google Scholar] [CrossRef]
- Kheirabadi, A.C.; Groulx, D. The Effect Of The Mushy-Zone Constant On Simulated Phase Change Heat Transfer. In Proceedings of the CHT-15, New Brunswick, NJ, USA, 27 October 2015; p. 22. [Google Scholar]
- Kabbara, M.; Kheirabadi, A.C.; Groulx, D. Numerical Modelling of Natural Convection Driven Melting for an Inclined/Finned Rectangular Enclosure. In Proceedings of the ASME 2016 Heat Transfer Summer Conference Collocated, Washington, DC, USA, 10–14 July 2016; pp. 1–10. [Google Scholar]
| Properties | Solid | Liquid |
|---|---|---|
| (K) | 316.65 | 321.35 |
| (kg/m3) | 940 | 885 |
| (J/kg K) | 2180 | 2390 |
| (W/m·K) | 0.16 | 0.14 |
| (kg/m·s) | 0.08 | 0.008 |
| (K−1) | 0.0008 | |
| (J/kg) | 187210 | |
| Material | (Kg/m3) | (J/kg·K) | (W/m·K) | Ref. |
|---|---|---|---|---|
| Vinyl ester resin (VER) | 1110 | 1400 | 0.21 | [36,37] |
| Aluminum (Al) | 2719 | 871 | 202.4 | ANSYS Fluent defaults |
| Extruded polystyrene (XPS) | 30 | 1280 | 0.031 | [38,39] |
| Arrangement | Characteristic Length, | Limits | Ref. | |
|---|---|---|---|---|
| Vertical plate | 104–109 109–1013 | [40] | ||
| Horizontal plate; top surface of a hot plate | 104–107 107–1011 | [41] | ||
| Horizontal plate; bottom surface of a hot plate | 105–1011 | [42] |
| Mesh | Fine | Medium | Coarse |
|---|---|---|---|
| Approach A | 185,163 (0.2 × 0.2 mm) | 30,393 (0.5 × 0.5 mm) | 8283 (1 × 1 mm) |
| Approach B | 81,070 (0.2 × 0.2 mm) | 12,998 (0.5 × 0.5 mm) | 3216 (1 × 1 mm) |
| Approach C | 12,998 (0.5 × 0.5 mm) | 3216 (1 × 1 mm) | 816 (2 × 2 mm) |
| CFD Model | RMSD (K) | R2 |
|---|---|---|
| Approach A | 1.24 | 0.9882 |
| Approach B | 0.78 | 0.9965 |
| Approach C | 0.92 | 0.9951 |
| Thermocouple’s Row | Model | Phase-Change Start (hh: mm) | Phase-Change End (hh: mm) | Duration |
|---|---|---|---|---|
| Row 1 | EP | 19:16 | - | Not completed |
| EHC | 19:15 | - | Not completed | |
| Row 2 | EP | 12:39 | 26:57 | 14 h 18 min |
| EHC | 12:44 | 25:58 | 12 h 14 min | |
| Row 3 | EP | 7:50 | 15:35 | 7 h 45 min |
| EHC | 7:57 | 15:12 | 7 h 16 min | |
| Row 4 | EP | 4:03 | 7:35 | 3 h 32 min |
| EHC | 4:09 | 7:29 | 3 h 22 min | |
| Row 5 | EP | 1:18 | 2:14 | 56 min |
| EHC | 1:20 | 2:14 | 54 min |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Fuente, M.; González-Peña, D.; Alonso-Tristán, C. A Numerical Simulation of an Experimental Melting Process of a Phase-Change Material without Convective Flows. Appl. Sci. 2022, 12, 3640. https://doi.org/10.3390/app12073640
García-Fuente M, González-Peña D, Alonso-Tristán C. A Numerical Simulation of an Experimental Melting Process of a Phase-Change Material without Convective Flows. Applied Sciences. 2022; 12(7):3640. https://doi.org/10.3390/app12073640
Chicago/Turabian StyleGarcía-Fuente, Manuel, David González-Peña, and Cristina Alonso-Tristán. 2022. "A Numerical Simulation of an Experimental Melting Process of a Phase-Change Material without Convective Flows" Applied Sciences 12, no. 7: 3640. https://doi.org/10.3390/app12073640







