Research on Equivalent Static Load of High-Rise/Towering Structures Based on Wind-Induced Responses
Abstract
:1. Introduction
2. Refinement of Structural Wind-Induced Response Assessment Method
2.1. The Full Three-Component Expressions in the Frequency Domain
2.2. The Full Three-Component Expressions in Time Domain
2.3. Comparison of Time–Frequency Domain Results for the Full Three Components
3. The Assessment Method for the Equivalent Static Wind Load of Arbitrary Structural Response
Theoretical Analysis
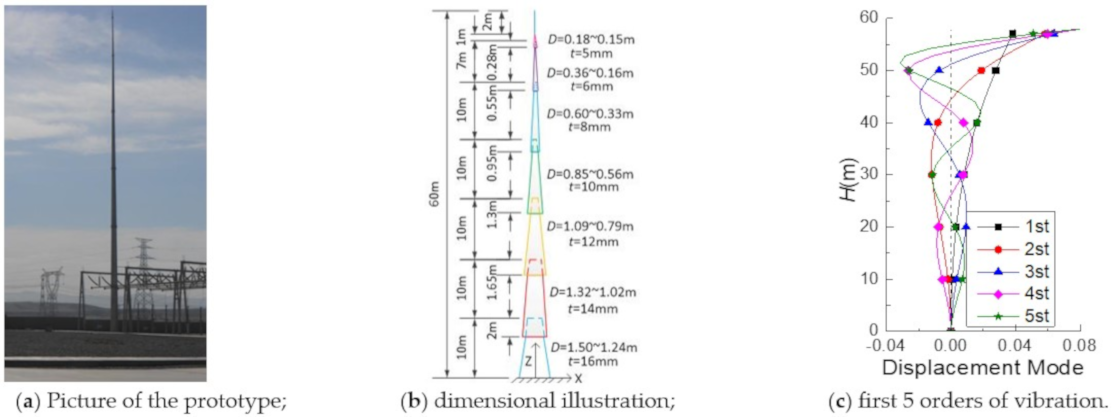
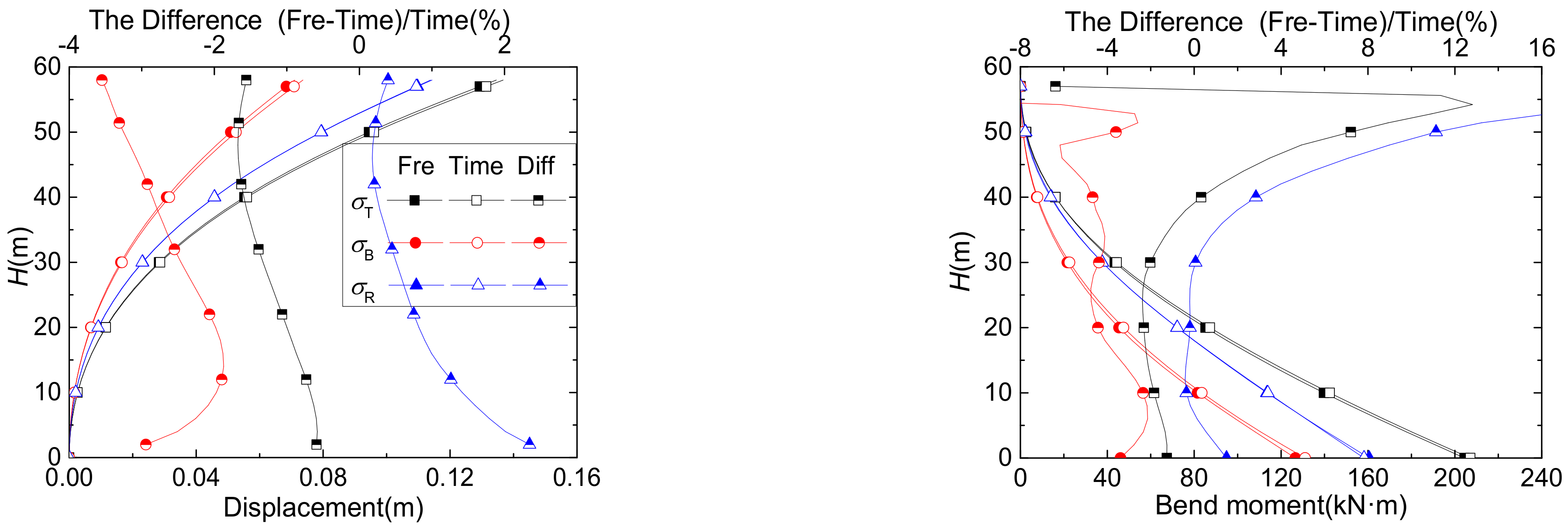
4. Example and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Longarini, N.; Cabras, L.; Zucca, M.; Chapain, S.; Aly, A.M. Structural Improvements for Tall Buildings under Wind Loads: Comparative Study. Shock Vib. 2017, 2017, 2031248. [Google Scholar] [CrossRef] [Green Version]
- Chapain, S.; Aly, A.M. Vibration attenuation in high-rise buildings to achieve system-level performance under multiple hazards. Eng. Struct. 2019, 197, 109352. [Google Scholar] [CrossRef]
- Scanlan, R. The action of flexible bridges under wind, II: Buffeting theory. J. Sound Vib. 1978, 60, 201–211. [Google Scholar] [CrossRef]
- Su, Y.; Di, J.; Li, S.; Jian, B.; Liu, J. Buffeting Response Prediction of Long-Span Bridges Based on Different Wind Tunnel Test Techniques. Appl. Sci. 2022, 12, 3171. [Google Scholar] [CrossRef]
- Brownjohn, J.; Carden, E.; Goddard, C.; Oudin, G. Real-time performance monitoring of tuned mass damper system for a 183m reinforced concrete chimney. J. Wind Eng. Ind. Aerodyn. 2010, 98, 169–179. [Google Scholar] [CrossRef]
- Gao, D.; Chen, G.; Chen, W.; Huang, Y.; Li, H. Active control of circular cylinder flow with windward suction and leeward blowing. Exp. Fluids 2019, 60, 26. [Google Scholar] [CrossRef]
- Bernuzzi, C.; Crespi, P.; Montuori, R.; Nastri, E.; Simoncelli, M.; Stochino, F.; Zucca, M. Resonance of steel wind turbines: Problems and solutions. Structures 2021, 32, 65–75. [Google Scholar] [CrossRef]
- Rahman, M.; Ong, Z.C.; Chong, W.T.; Julai, S.; Khoo, S.Y. Performance enhancement of wind turbine systems with vibration control: A review. Renew. Sustain. Energy Rev. 2015, 51, 43–54. [Google Scholar] [CrossRef]
- Sari, D.P.; Cho, K.-P. Performance Comparison of Different Building Shapes Using a Wind Tunnel and a Computational Model. Buildings 2022, 12, 144. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, M.; Øiseth, O.; Rønnquist, A. Wind deflection analysis of railway catenary under crosswind based on nonlinear finite element model and wind tunnel test. Mech. Mach. Theory 2021, 168, 104608. [Google Scholar] [CrossRef]
- Gao, D.; Chen, W.; Zhang, R.; Huang, Y.; Li, H. Multi-modal vortex- and rain–wind- induced vibrations of an inclined flexible cable. Mech. Syst. Signal Process. 2019, 11, 8245–8258. [Google Scholar] [CrossRef]
- Chen, W.-L.; Zhang, Q.-Q.; Li, H.; Hui, L. An experimental investigation on vortex induced vibration of a flexible inclined cable under a shear flow. J. Fluids Struct. 2015, 54, 297–311. [Google Scholar] [CrossRef]
- Zhong, Y.; Li, S.; Jin, W.; Yan, Z.; Liu, X.; Li, Y. Frequency Domain Analysis of Alongwind Response and Study of Wind Loads for Transmission Tower Subjected to Downbursts. Buildings 2022, 12, 148. [Google Scholar] [CrossRef]
- Davenport, A.G. The Application of Statistical Concepts to the Wind Loading of Structures. Proc. Inst. Civ. Eng. 1961, 19, 449–472. [Google Scholar] [CrossRef]
- Davenport, A.G. Gust Loading Factors. J. Struct. Div. 1967, 93, 11–34. [Google Scholar] [CrossRef]
- Zhang, X. Wind Load Theory and Wind-Resistance Design Manual for Engineering Structures; Tongji University Press: Shanghai, China, 1990; pp. 92–98. [Google Scholar]
- Kasperski, M.; Niemann, H.-J. The L.R.C. (load-response-correlation)-method a general method of estimating unfavourable wind load distributions for linear and non-linear structural behaviour. J. Wind Eng. Ind. Aerodyn. 1992, 43, 1753–1763. [Google Scholar] [CrossRef]
- Kasperski, M. Design wind loads for low-rise buildings: A critical review of wind load specifications for industrial buildings. J. Wind Eng. Ind. Aerodyn. 1996, 61, 169–179. [Google Scholar] [CrossRef]
- Zhou, Y. Theoretical and Experimental Study of High-Rise Building Static Equivalent Wind Loads and Response; Tongji University: Shanghai, China, 2001. [Google Scholar]
- Zhou, Y.; Kareen, A. Gust loading factor: A new model. ASCE J. Struct. Eng. 2001, 127, 168–175. [Google Scholar] [CrossRef]
- Holmes, J. Effective static load distributions in wind engineering. J. Wind Eng. Ind. Aerodyn. 2002, 90, 91–109. [Google Scholar] [CrossRef]
- Holmes, J.D. Wind Loading of Structure; Spon Press: London, UK, 2001. [Google Scholar]
- Gu, M.; Ye, F. Characteristics of wind induced responses and equivalent static wind loads of tall building. Eng. Mech. 2006, 23, 93–98. [Google Scholar] [CrossRef]
- Ye, F.; Gu, M. Along-wind background response and background equivalent wind loads of tall buildings. J. Build. Struct. 2002, 23, 58–60. [Google Scholar] [CrossRef]
- Xie, Z.N.; Fang, X.D.; Ni, Z.H. Equivalent static wind liads on tall building the extended load response correlation (ELRC) approach. J. Vib. Eng. 2008, 21, 398–403. [Google Scholar] [CrossRef]
- Lin, Y.; Lin, C.; Lin, X.; Zhang, J.; Song, J. Research on equivalent static load of high- rise buildings based on wind-induced responses. J. Southwest Jiaotong Univ. 2019, 54, 137–144. [Google Scholar]
- Ke, S.; Ge, Y. Refined research on wind-induced response of roof structure of a large museum based on consistent coupled method. J. Build. Struct. 2012, 33, 111–117. [Google Scholar]
- Cao, S.; Ke, S.; Zhang, W.; Zhao, L.; Ge, Y.; Cheng, X. Load–response correlation-based equivalent static wind loads for large cooling towers. Adv. Struct. Eng. 2019, 22, 2464–2475. [Google Scholar] [CrossRef]
- Zhang, J.-F.; Ge, Y.-J.; Zhao, L.; Zhu, B. Wind induced dynamic responses on hyperbolic cooling tower shells and the equivalent static wind load. J. Wind Eng. Ind. Aerodyn. 2017, 169, 280–289. [Google Scholar] [CrossRef]
- Solari, G. Wind Loading of Structures: Framework, Phenomena, Tools and Codification. Structures 2017, 12, 265–285. [Google Scholar] [CrossRef]
- Gu, M.; Zhou, X.; Huang, P. A study on wind-induced buffeting responses of large-span roof structures. China Civ. Eng. J. 2006, 39, 37–42. [Google Scholar] [CrossRef]
- Li, S.K.; Li, S.Y.; Fang, X.L.; Sun, H.X.; Li, H.L. Refined study on wind-induced response of structure by stochastic wind load. Eng. Mech. 2015, 32, 111–115. [Google Scholar] [CrossRef]
- Zou, L.; Shi, T.; Liang, S.; Song, J.; Li, F. Simplified calculation of along-wind dynamic responses of high-rise buildings considering second mode. J. Build. Struct. 2018, 39, 18–25. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Q.; Yang, J.; Tu, B. A method of separating the background and resonant components of wind dynamic effects in time domain. J. Disaster Prev. Mitig. Eng. 2020, 40, 365–371. [Google Scholar]
- Zeng, J.; Li, M.; Li, S. Spatial correlation of downwind pulsating wind loads in rectangular high-rise buildings. J. Harbin Inst. Technol. 2017, 49, 150–155. [Google Scholar]
- Yu, P. Research on Wind Vibration Response of Substation Lightning Rod Structure Downwind; Zhengzhou University: Zhengzhou, China, 2018. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. GB 50009-2012. Code for Structural Loading of Buildings; China Construction Industry Press: Beijing, China, 2012.
- Gu, M.; Ye, F. Along-wind equivalent wind loads and responses on tall buildings. J. Wind. Eng. 2001, 89, 609–612. [Google Scholar]


| Condition | Vibration Index β | Mass Discount Factor λ |
|---|---|---|
| 1 | 1.0 | 0.0 |
| 2 | 1.6 | 0.0 |
| 3 | 1.0 | 0.2 |
| 4 | 1.6 | 0.2 |
| Top Displacement | Basal Bend Moment | Basal Shear Force | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Condition | GYB | GYR | DGLF | GMB | GMR | MGLF | GQB | GQR | QGLF |
| 1 | 0.6520 (1.000) | 0.9761 (0.998) | 2.1738 (0.999) | 0.6520 (1.000) | 0.9761 (1.000) | 2.1738 (1.000) | 0.6560 (0.994) | 0.8275 (1.002) | 2.0560 (1.000) |
| 2 | 0.6591 | 1.0302 | 2.2230 | 0.6520 (1.000) | 0.9532 (1.000) | 2.1549 (1.000) | 0.6560 (0.994) | 0.7460 (1.003) | 1.9934 (0.999) |
| 3 | 0.6520 | 0.9761 | 2.1738 | 0.6520 (1.000) | 0.9761 (1.000) | 2.1738 (1.000) | 0.6560 (0.994) | 0.8438 (1.001) | 2.0688 (0.999) |
| 4 | 0.6591 | 1.0302 | 2.2230 | 0.6520 (1.000) | 0.9589 (1.000) | 2.1596 (1.000) | 0.6560 (0.994) | 0.7612 (1.002) | 2.0049 (1.000) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Zhang, J.; Li, C. Research on Equivalent Static Load of High-Rise/Towering Structures Based on Wind-Induced Responses. Appl. Sci. 2022, 12, 3729. https://doi.org/10.3390/app12083729
Yang J, Zhang J, Li C. Research on Equivalent Static Load of High-Rise/Towering Structures Based on Wind-Induced Responses. Applied Sciences. 2022; 12(8):3729. https://doi.org/10.3390/app12083729
Chicago/Turabian StyleYang, Junhui, Junfeng Zhang, and Chao Li. 2022. "Research on Equivalent Static Load of High-Rise/Towering Structures Based on Wind-Induced Responses" Applied Sciences 12, no. 8: 3729. https://doi.org/10.3390/app12083729
APA StyleYang, J., Zhang, J., & Li, C. (2022). Research on Equivalent Static Load of High-Rise/Towering Structures Based on Wind-Induced Responses. Applied Sciences, 12(8), 3729. https://doi.org/10.3390/app12083729







