Effect of Dimensional Variables on the Behavior of Trees for Biomechanical Studies
Abstract
:1. Introduction
2. Materials and Methods
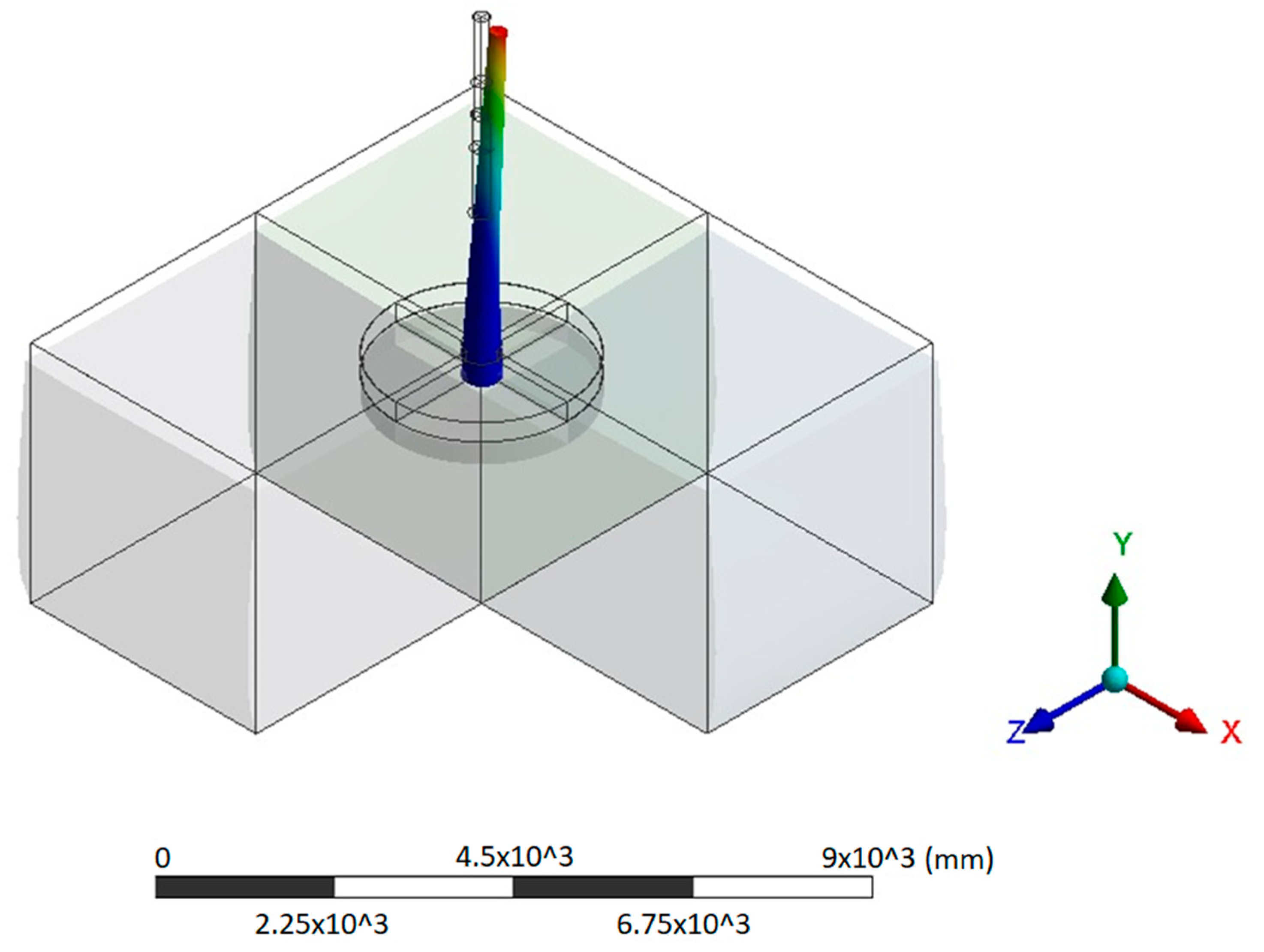
2.1. Finite-Element Model
2.2. Horizontal Load
2.3. Material Properties
2.4. FEM Simulation
2.5. Safety Factors
3. Results and Discussion
3.1. Deflection
3.1.1. Comparison with Literature
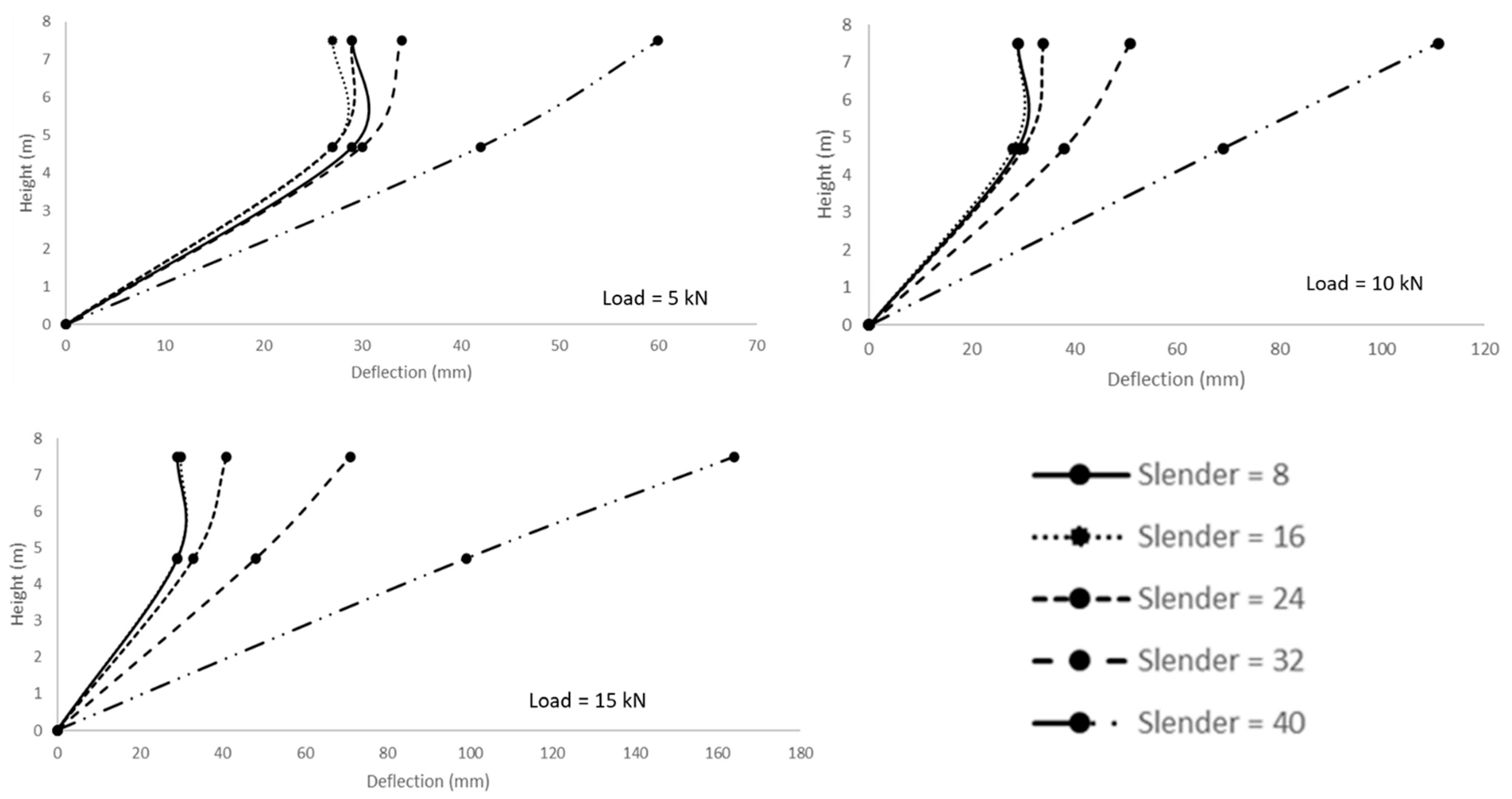
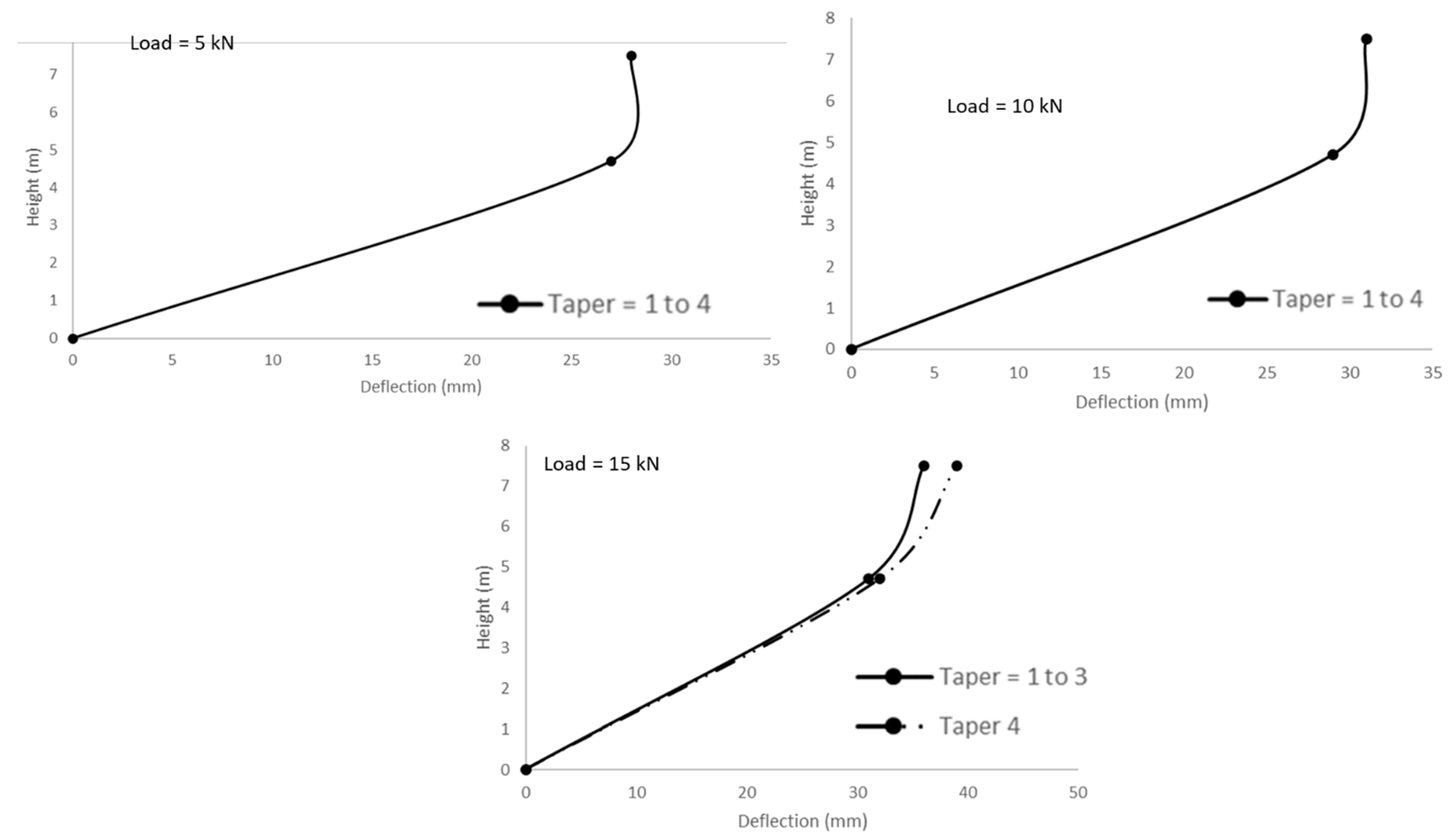
3.1.2. Behavior of Trunk Deflection with Tree Height
3.2. Normal Stresses
3.3. Shear Stresses
3.4. General Behavior of the Stresses along the Trunk
3.5. Safety Factors
4. Conclusions
- -
- The deflections’ behavior showed that the linearity with height is valid up to the point of application of the horizontal load, but from that point onwards, it depends on the diameter and, in some cases, also on the loading level.
- -
- Since the model considers the geometric variations of the section (deflections and diameter variations), the stresses show smooth variations along the trunk. However, the maximum values positive and negative, in module, are not equal and can undergo sudden variations in position along the trunk when local maximum stresses become global maximums.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dahle, G.A.; James, K.R.; Kane, B.; Grabosky, J.C.; Detter, A. A Review of Factors That Affect the Static Load-Bearing Capacity of Urban Trees. Arboric. Urban For. 2017, 43, 89–106. [Google Scholar] [CrossRef]
- James, K.R.; Dahle, G.A.; Grabosky, J.; Kane, B.; Detter, A. Tree Biomechanics Literature Review: Dynamics. Arboric. Urban For. 2014, 40, 1–15. [Google Scholar] [CrossRef]
- Gonçalves, R.; Linhares, C.; Yojo, T. Drag coefficient in urban trees. Trees 2020. [Google Scholar] [CrossRef]
- Timoshenko, S.P. Theory of Elastic Stability; McGraw-Hill: New York, NY, USA, 1956. [Google Scholar]
- Tateno, M.; Bae, K. Comparison of lodging safety factor of untreated and succinic acid 2,2-dimethylhydrazide-treated shoots of mulberry tree. Plant Physiol. 1990, 92, 12–16. [Google Scholar] [CrossRef] [Green Version]
- Tateno, M. Increase in lodging safety factor of thigmomorphometrically dwarfed shoots of mulberry tree. Physiol. Plant 1991, 81, 239–243. [Google Scholar] [CrossRef]
- Mattheck, C.; Bethge, K.; Schäfer, J. Safety factors in trees. J. Theor. Biol. 1993, 165, 185–189. [Google Scholar] [CrossRef]
- Niklas, K.J. Interspecific allometries of critical buckling height and actual plan height. Am. J. Bot. 1994, 81, 1275–1279. [Google Scholar] [CrossRef]
- Niklas, K.J. Computing factors of safety against wind-induced tree stem damage. J. Exp. Bot. 2000, 51, 797–806. [Google Scholar] [CrossRef] [PubMed]
- Niklas, K.J.; Spatz, H.-C. Wind-induced stresses in cherry trees: Evidence against the hypothesis of constant stress levels. Trees 2000, 14, 230–237. [Google Scholar] [CrossRef]
- Detter, A.; Brudi, E.; Bischoff, F. Statics Integrated Methods: Results from pulling tests in the past decades. In Proceedings of the Conference Actas del 9º Congreso de Arboricultura, Barcelona, La Visión del Árbol, Spain, 1–3 September 2005; pp. 103–112. [Google Scholar]
- Detter, A.; Rust, S.; Rust, C.; Maybaum, G. Determining strength limits for standing tree stems from bending tests. In Proceedings of the 18th International Nondestructive Testing of Wood Symposium, Madison, WI, USA, 24–27 September 2013. [Google Scholar]
- Ruel, J.; Lachance, G. Mathematical modeling and experimental testing of three bioreactor configurations based on windkessel models. Heart Int. 2010, 5, e1. [Google Scholar] [CrossRef] [PubMed]
- Spatz, H.-C.; Bruechert, F. Basic biomechanics of self-supporting plants: Wind loads and gravitational loads on a Norway spruce tree. For. Ecol. Manag. 2000, 135, 33–44. [Google Scholar] [CrossRef]
- Marchi, L.; Mologni, O.; Trutalli, D.; Scotta, R.; Cavalli, R.; Montecchio, L.; Grigolato, S. Safety assessment of trees used as anchors in cable-supported tree harvesting based on experimental observations. Biosyst. Eng. 2019, 186, 71–82. [Google Scholar] [CrossRef]
- James, K.R.; Hallam, C.; Spencer, C. Measuring tilt of tree structural root zones under static and wind loading. Agric. For. Meteorol. 2013, 168, 160–167. [Google Scholar] [CrossRef]
- Sani, L.; Lisci, R.; Moschi, M.; Sarri, D.; Rimediotti, M.; Vieri, M.; Tofanelli, S. Preliminary experiments and verification of controlled pulling tests for tree stability assessments in Mediterranean urban areas. Biosyst. Eng. 2012, 112, 218–226. [Google Scholar] [CrossRef]
- James, K.R.; Moore, K.R.; Slater, D.; Dahle, G.A. Tree Biomechanics. CAB Rev. Perspect. Agric. Vet. Sci. Nutr. Nat. Resour 2017, 12, 1–15. [Google Scholar] [CrossRef]
- Beezleyet, K.E.; Dahle, G.A.; Miesbauer, J.; DeVallance, D. Strain Patterns across the Root-Stem Transition Zone in Urban Trees. Arboric. Urban For. 2020, 46, 321–332. [Google Scholar] [CrossRef]
- Sebera, V.; Praus LTippner, J.; Kunecký, J.; Cepela, J.; Wimmer, R. Using optical full-field measurement based on digital image. Trees 2014, 28, 1173–1184. [Google Scholar] [CrossRef]
- Sebera, V.; Kunecký, J.; Praus, L.; Tippner, J.; Horácek, P. Strain transfer from xylem to bark surface analyzed by digital image correlation. Wood Sci. Technol. 2016, 50, 773–787. [Google Scholar] [CrossRef]
- Ciftci, C.; Brena, S.F.; Kane, B.; Arwade, S.R. The effect of crown architecture on dynamic amplification factor of an open-grown sugar maple (Acer saccharum L.). Trees 2013, 27, 1175–1189. [Google Scholar] [CrossRef]
- Gaffrey, D.; Kniemayer, O. The elasto-mechanical behaviour of Douglas fir, its sensitivity to tree-specific properties, wind and snow loads, and implications for stability—A simulation study. J. For. Sci. 2002, 48, 49–69. [Google Scholar] [CrossRef]
- Vojácková, B.; Tippner, J.; Horácek, P.; Sebera, V.; Praus, L.; Marík, R.; Brabec, M. The effect of stem and root-plate defects on the tree response during static loading—Numerical analysis. Urban For. Urban Green. 2021, 59, 127002. [Google Scholar] [CrossRef]
- Tesari, I.; Mattheck, C. The maximum shear stress at the base of the stem and the influence of root architecture and soil properties. In Proceedings of the 9th VTA- VTA Special Seminar “Measurement and Assessment on the Tree”, Research Center Karlsruhe, Karlsruhe, Germany, 1–2 April 2003. [Google Scholar]
- Rahardjo, H.; Harnas, F.R.; Indrawan, I.G.B.; Leong, E.C.; Tan, P.Y.; Fong, Y.K.; Ow, L.F. Understanding thestabilityof Samanea saman trees throughtree pulling, analytical calculations and numerical models. Urban For. Urban Green. 2014, 13, 355–364. [Google Scholar] [CrossRef]
- Lang, R.; Kaliske, M. Description of inhomogeneities in wooden structures:modelling of branches. Wood Sci. Technol. 2013, 47, 1051–1070. [Google Scholar] [CrossRef]
- Moore, J.R.; Maguire, D.A. Simulating the dynamic behavior of Douglas-fir trees under applied loads by the finite element method. Tree Physiol. 2008, 28, 75–83. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Défossez, P.; Danjon, F.; Fourcaud, T. Tree stability under wind: Simulating uprooting with root breakage using a finite element method. Ann. Bot. 2014, 114, 695–709. [Google Scholar] [CrossRef]
- Sellier, D.; Fourcaud, T. Crown structure and wood properties: Influence on tree sway and response to high winds. Am. J. Bot. 2009, 96, 885–896. [Google Scholar] [CrossRef]
- Ancelin, P.; Courbaud, B.; Fourcaud, T. Development of an individual tree-based mechanical model to predict wind damage within forest stands. For. Ecol. Manag. 2004, 203, 101–121. [Google Scholar] [CrossRef]
- Brüchert, F.; Gardiner, B. The effect of wind exposure on the tree aerial architecture and biomechanics of Sitka spruce (Picea sitchensis, Pinaceae). Am. J. Bot. 2006, 93, 1512–1521. [Google Scholar] [CrossRef] [PubMed]
- Milne, R.; Blackburn, P. The elasticity and vertical distribution of stress within stems of Picea sitchensis. Tree Physiol. 1989, 5, 195–205. [Google Scholar] [CrossRef] [PubMed]
- Rahardjo, H.; Harnas, F.R.; Leong, E.C.; Tan, P.Y.; Fong, Y.K.; Sim, E.K. Tree stability in an improved soil to withstand wind loading. Urban For. Urban Green. 2009, 8, 355–364. [Google Scholar] [CrossRef]
- Ruy, M. Modelagem do Comportamento Biomecânico de Árvores. Ph.D. Thesis, Faculdade de Engenharia Agrícola/Unicamp, Campinas, Brazil, 2020. [Google Scholar]
- Souza, A.L.; de Soares, C.P.B. Florestas Nativas; UFV: Viçosa, Brazil, 2013. [Google Scholar]
- ABNT NBR 6123; Forças Devidas ao Vento em Edificações. Brazilian Association of Technical Standards: Rio de Janeiro, Brazil, 1988.
- Vázquez, C.; Gonçalves, R.; Bertoldo, C.; Baño, V.; Vega, A.; Crespo, J.; Guaita, M. Determination of the mechanical properties of Castanea sativa Mill. using ultrasonic wave propagation and comparison with static compression and bending methods. Wood Sci. Technol. 2015, 49, 607–622. [Google Scholar] [CrossRef]
- Gonçalves, R.; Trinca, A.J.; Pellis, B.P. Elastic constants of wood determined by ultrasound using three geometries of specimens. Wood Sci. Technol. 2014, 48, 269–287. [Google Scholar] [CrossRef]
- EN 338; Structural Timber. Strength Classes. European Committee of Standardization (CEN): Brussels, Belgium, 2016.
- EN 384: 2016+A1; Structural Timber. Determination of Characteristic Values of Mechanical Properties and Density. European Committee of Standardization (CEN): Brussels, Belgium, 2018.
- EN 14081-1:2016+A1; Timber Structures—Strength Graded Structural Timber with Rectangular cross Section—Part 1: General Requirements. European Committee of Standardization (CEN): Brussels, Belgium, 2019.
- Nirbito, W.; Ardianto, A.; Ramadham, M.; Dhelika, R. Validation of strength and flexibility of sengon (Paraserianthes falcataria) by experimental tree-pulling test and numerical simulation. J. Appl. Eng. Sci. 2019, 17, 443–448. [Google Scholar] [CrossRef] [Green Version]
- EN 1995-1-1; Eurocode 5: Design of Timber Structures—Part 1-1: General–Common Rules and Rules for Buildings. European Committee of Standardization (CEN): Brussels, Belgium, 2016.
- Neild, S.A.; Wood, C.J. Estimating stem and root-anchorage flexibility in trees. Tree Physiol. 1999, 19, 141–151. [Google Scholar] [CrossRef] [PubMed]
- Mamada, S.; Kawamura, Y.; Yashiro, M.; Taniguchi, T. The strength of plantation sugi trees. J. Jpn. Wood Res. Soc. 1984, 30, 443–466. [Google Scholar]
- Petty, J.A.; Swain, C. Factors Influencing Stem Breakage of Conifers in High Winds. J. For. 1985, 58, 75–101. [Google Scholar] [CrossRef]





| Scenario | H m | λ | T | DBH m | Db m | Dt m | YM1 m | YM2 m | YM3 m | YFH m |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 22 | 0.030 | 0.23 | 0.27 | 0.116 | 2.00 | 3.00 | 4.00 | 3.50 |
| 10 | 22 | 0.030 | 0.45 | 0.49 | 0.194 | 2.00 | 4.67 | 7.33 | 6.0 | |
| 15 | 22 | 0.030 | 0.68 | 0.72 | 0.271 | 2.00 | 6.33 | 10.67 | 8.50 | |
| 20 | 22 | 0.030 | 0.91 | 0.95 | 0.348 | 2.00 | 8.00 | 14.00 | 11.00 | |
| 25 | 22 | 0.030 | 1.14 | 1.18 | 0.425 | 2.00 | 9.67 | 17.33 | 13.5 | |
| 2 | 7.5 | 8 | 0.030 | 0.94 | 0.98 | 0.752 | 2.00 | 3.83 | 5.67 | 4.75 |
| 7.5 | 16 | 0.030 | 0.47 | 0.51 | 0.283 | 2.00 | 3.83 | 5.67 | 4.75 | |
| 7.5 | 24 | 0.030 | 0.31 | 0.35 | 0.127 | 2.00 | 3.83 | 5.67 | 4.75 | |
| 7.5 | 32 | 0.030 | 0.23 | 0.27 | 0.048 | 2.00 | 3.83 | 5.67 | 4.75 | |
| 7.5 | 40 | 0.030 | 0.19 | 0.23 | 0.002 | 2.00 | 3.83 | 5.67 | 4.75 | |
| 3 | 7.5 | 22 | 0.010 | 0.34 | 0.35 | 0.279 | 2.00 | 3.83 | 5.67 | 4.75 |
| 7.5 | 22 | 0.020 | 0.34 | 0.37 | 0.217 | 2.00 | 3.83 | 5.67 | 4.75 | |
| 7.5 | 22 | 0.030 | 0.34 | 0.38 | 0.155 | 2.00 | 3.83 | 5.67 | 4.75 | |
| 7.5 | 22 | 0.050 | 0.34 | 0.41 | 0.031 | 2.00 | 3.83 | 5.67 | 4.75 | |
| Validation | 9.4 | 39 | na | 0.24 | 0.32 | na | 3.00 | 5.13 | 7.23 | 6.20 |
| 5 kN | 10 kN | 15 kN | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenario | H m | Dc m | Ac m2 | q N/m2 | V m/s | q N/m2 | V m/s | q N/m2 | V m/s |
| 1 | 5 | 3 | 7.1 | 707 | 34.0 | 1415 | 48.0 | 2122 | 58.8 |
| 10 | 8 | 50.3 | 99 | 12.7 | 199 | 18.0 | 298 | 22.1 | |
| 15 | 13 | 132.7 | 38 | 7.8 | 75 | 11.1 | 113 | 13.6 | |
| 20 | 18 | 254.5 | 20 | 5.7 | 39 | 8.0 | 59 | 9.8 | |
| 25 | 23 | 415.5 | 12 | 4.4 | 24 | 6.3 | 36 | 7.7 | |
| 2 and 3 | 7.5 | 5.5 | 23.8 | 210 | 18.5 | 421 | 26.2 | 631 | 32.1 |
| Validation | 9.4 | 6.4 | 32.2 | 155 | 15.9 | 311 | 22.5 | 466 | 27.6 |
| Elastic Parameters | Directions or Planes | ||
|---|---|---|---|
| Longitudinal modulus of elasticity | Longitudinal | [MPa] | 10387 |
| Radial | [MPa] | 1908 | |
| Tangential | [MPa] | 1290 | |
| Shear module | Radial/Tangential | [MPa] | 515 |
| Longitudinal/Tangential | [MPa] | 1173 | |
| Longitudinal/Radial | [MPa] | 1573 | |
| Poisson’s ratio | Radial/Longitudinal | 0.09 | |
| Tangential/Longitudinal | 0.08 | ||
| Longitudinal/Radial | 0.49 | ||
| Tangential/Radial | 0.46 | ||
| Longitudinal/Tangential | 0.64 | ||
| Radial/Tangential | 0.78 |
| H | λ | T | δM | Y | δL | Y | σ− | Y | σ+ | Y | τ− | Y | τ+ | Y |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 22 | 3 | 13 | 100 | 10 | 70.0 | 2.70 | 40 | 2.72 | 40 | 0.54 | 40 | 0.47 | 40 |
| 10 | 22 | 3 | 58 | 100 | 57 | 60.0 | 0.85 | 19 | 0.70 | 19 | 0.50 | 46 | 0.33 | 19 |
| 15 | 22 | 3 | 152 | 100 | 152 | 56.7 | 1.68 | 0 | 0.74 | 70 | 0.78 | 0 | 1.02 | 0 |
| 20 | 22 | 3 | 293 | 100 | 293 | 55.0 | 2.51 | 0 | 2.00 | 0 | 1.99 | 0 | 1.52 | 0 |
| 25 | 22 | 3 | 440 | 100 | 440 | 54.0 | 3.45 | 0 | 2.51 | 0 | 2.19 | 0 | 2.14 | 0 |
| 7.5 | 8 | 3 | 29 | 100 | 29 | 63.3 | 0.74 | 0 | 0.17 | 75 | 0.29 | 0 | 0.27 | 0 |
| 7.5 | 16 | 3 | 27 | 100 | 27 | 63.3 | 0.66 | 63 | 0.37 | 26 | 0.29 | 26 | 0.27 | 75 |
| 7.5 | 24 | 3 | 29 | 100 | 27 | 63.3 | 2.20 | 26 | 1.79 | 26 | 0.56 | 26 | 0.58 | 51 |
| 7.5 | 32 | 3 | 34 | 100 | 30 | 63.3 | 4.40 | 26 | 4.70 | 26 | 1.01 | 26 | 0.88 | 26 |
| 7.5 | 40 | 3 | 60 | 100 | 42 | 63.3 | 9.32 | 26 | 10.38 | 26 | 2.50 | 26 | 2.94 | 26 |
| 7.5 | 22 | 1 | 28 | 100 | 27 | 63.3 | 0.98 | 26 | 0.60 | 26 | 0.32 | 26 | 0.30 | 26 |
| 7.5 | 22 | 2 | 28 | 100 | 27 | 63.3 | 1.03 | 26 | 1.30 | 26 | 0.29 | 26 | 0.25 | 26 |
| 7.5 | 22 | 3 | 28 | 100 | 27 | 63.3 | 1.13 | 26 | 1.12 | 26 | 0.38 | 26 | 0.32 | 26 |
| 7.5 | 22 | 4 | 28 | 100 | 27 | 63.3 | 1.51 | 63 | 2.18 | 26 | 0.51 | 26 | 0.49 | 51 |
| H | λ | T | δM | Y | δL | Y | σ− | Y | σ+ | Y | τ− | Y | τ+ | Y |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 22 | 3 | 22 | 100 | 16 | 70.0 | 5.35 | 40 | 5.48 | 40 | 1.08 | 40 | 0.93 | 40 |
| 10 | 22 | 3 | 59 | 100 | 58 | 60.0 | 1.58 | 19 | 1.53 | 19 | 0.50 | 46 | 0.33 | 19 |
| 15 | 22 | 3 | 153 | 100 | 153 | 56.7 | 1.69 | 0 | 0.74 | 12 | 0.78 | 0 | 1.02 | 0 |
| 20 | 22 | 3 | 294 | 100 | 294 | 55.0 | 2.51 | 0 | 2.00 | 0 | 1.99 | 0 | 1.52 | 0 |
| 25 | 22 | 3 | 440 | 100 | 440 | 54.0 | 3.46 | 0 | 2.51 | 0 | 2.19 | 0 | 2.14 | 0 |
| 7.5 | 8 | 3 | 29 | 100 | 29 | 63.3 | 0.89 | 63 | 0.20 | 63 | 0.29 | 0 | 0.27 | 0 |
| 7.5 | 16 | 3 | 29 | 100 | 28 | 63.3 | 1.30 | 63 | 0.80 | 26 | 0.29 | 26 | 0.27 | 75 |
| 7.5 | 24 | 3 | 34 | 100 | 30 | 63.3 | 4.49 | 26 | 3.51 | 26 | 1.08 | 26 | 1.12 | 51 |
| 7.5 | 32 | 3 | 51 | 100 | 38 | 63.3 | 8.74 | 26 | 9.45 | 26 | 2.02 | 26 | 1.77 | 26 |
| 7.5 | 40 | 3 | 111 | 100 | 69 | 63.3 | 18.72 | 26 | 20.74 | 26 | 5.02 | 26 | 5.80 | 26 |
| 7.5 | 22 | 1 | 31 | 100 | 29 | 63.3 | 1.81 | 26 | 1.37 | 26 | 0.44 | 0 | 0.47 | 0 |
| 7.5 | 22 | 2 | 31 | 100 | 29 | 63.3 | 2.03 | 26 | 2.54 | 26 | 0.50 | 26 | 0.51 | 26 |
| 7.5 | 22 | 3 | 31 | 100 | 29 | 63.3 | 2.22 | 26 | 2.30 | 26 | 0.77 | 26 | 0.67 | 26 |
| 7.5 | 22 | 4 | 33 | 100 | 29 | 63.3 | 3.03 | 63 | 4.32 | 26 | 1.03 | 26 | 0.95 | 26 |
| H | λ | T | δM | Y | δL | Y | σ− | Y | σ+ | Y | τ− | Y | τ+ | Y |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 22 | 3 | 31 | 100 | 21 | 70.0 | 8.00 | 40 | 8.24 | 40 | 1.62 | 40 | 1.38 | 40 |
| 10 | 22 | 3 | 62 | 100 | 59 | 60.0 | 2.31 | 46 | 2.35 | 19 | 0.50 | 19 | 0.44 | 19 |
| 15 | 22 | 3 | 155 | 100 | 153 | 56.7 | 2.03 | 0 | 0.77 | 0 | 0.78 | 0 | 1.02 | 0 |
| 20 | 22 | 3 | 295 | 100 | 294 | 55.0 | 2.64 | 0 | 2.00 | 0 | 1.99 | 0 | 1.52 | 0 |
| 25 | 22 | 3 | 441 | 100 | 441 | 54.0 | 3.53 | 0 | 2.51 | 0 | 2.19 | 0 | 2.14 | 0 |
| 7.5 | 8 | 3 | 29 | 100 | 29 | 63.3 | 1.15 | 0 | 0.31 | 0 | 0.28 | 0 | 0.29 | 0 |
| 7.5 | 16 | 3 | 30 | 100 | 29 | 63.3 | 1.95 | 26 | 1.23 | 26 | 0.41 | 26 | 0.30 | 26 |
| 7.5 | 24 | 3 | 41 | 100 | 33 | 63.3 | 6.78 | 26 | 5.23 | 51 | 1.59 | 26 | 1.65 | 51 |
| 7.5 | 32 | 3 | 71 | 100 | 48 | 63.3 | 13.08 | 26 | 14.20 | 26 | 3.03 | 26 | 2.66 | 26 |
| 7.5 | 40 | 3 | 164 | 100 | 99 | 63.3 | 28.12 | 26 | 31.09 | 26 | 7.55 | 26 | 8.67 | 26 |
| 7.5 | 22 | 1 | 36 | 100 | 31 | 63.3 | 2.68 | 26 | 2.14 | 26 | 0.66 | 26 | 0.71 | 26 |
| 7.5 | 22 | 2 | 36 | 100 | 31 | 63.3 | 3.03 | 26 | 3.78 | 26 | 0.76 | 26 | 0.78 | 26 |
| 7.5 | 22 | 3 | 36 | 100 | 31 | 63.3 | 3.32 | 26 | 3.48 | 26 | 1.16 | 51 | 1.02 | 26 |
| 7.5 | 22 | 4 | 39 | 100 | 32 | 63.3 | 4.56 | 26 | 6.46 | 51 | 1.55 | 26 | 1.43 | 51 |
| Variables | Regression Model | Load Level kN | p-Value | R2 (%) |
|---|---|---|---|---|
| Negative Normal Stresses (σ−) | ||||
| σ− × H | - | 5 | 0.2498 * | - |
| - | 10 | 0.2121 * | - | |
| - | 15 | 0.0634 * | - | |
| σ− × λ | σ−= 0.54 − 0.006 λ2 | 5 | 0.0047 | 95.1 |
| σ−= 0.54 − 0.006 λ2 | 10 | 0.0034 | 96.1 | |
| σ−= 0.54 − 0.006 λ2 | 15 | 0.0032 | 96.2 | |
| σ− × T | σ−= 0.54 − 0.006 T2 | 5 | 0.0014 | 99.7 |
| σ−= 0.54 − 0.006 T2 | 10 | 0.0017 | 99.7 | |
| σ−= 0.54 − 0.006 T2 | 15 | 0.0020 | 99.6 | |
| Positive Normal Stresses (σ+) | ||||
| σ+ × H | - | 5 | 0.5016 * | - |
| σ+ = sqrt (−6.4 + 65/H) | 10 | 0.0474 | 77.9 | |
| σ+ = sqrt (−20.7 + 411/H) | 15 | 0.0209 | 86.9 | |
| σ+ × λ | σ+ = −1.25 + 0.07 λ2 | 5 | 0.0042 | 95.4 |
| σ+ = −2.56 + 0.013 λ2 | 10 | 0.0039 | 95.6 | |
| σ+ = −3.83 + 0.020 λ2 | 15 | 0.0039 | 95.6 | |
| σ+ × T | σ+ = sqrt (0.35 + 0.0017 T2) | 5 | 0.0409 | 92.0 |
| σ+ = sqrt (1.61 + 0.0066 T2) | 10 | 0.0329 | 93.5 | |
| σ+ = sqrt (3.81 + 0.015 T2) | 15 | 0.0303 | 94.0 | |
| Variables | Regression Model | Load Level kN | p-Value | R2 (%) |
|---|---|---|---|---|
| Negative Normal Stresses (σ−) | ||||
| τ− × H | τ− = −0.31 − 0.0032 H2 | 5 | 0.0142 | 89.8 |
| - | 10 | 0.0631 * | - | |
| - | 15 | 0.2136 * | - | |
| τ− × λ | τ− = 0.07 − 0.0014 λ2 | 5 | 0.0135 | 90.2 |
| τ− = 0.42 − 0.0031 λ2 | 10 | 0.0084 | 92.8 | |
| τ− = 0.72 − 0.0046 λ2 | 15 | 0.0072 | 93.5 | |
| τ− × T | τ− = −0.29 − 0.00009 T2 | 5 | 0.0321 | 93.7 |
| τ− = −0.44 − 0.00024 T2 | 10 | 0.0332 | 93.5 | |
| τ− = −0.67 − 0.00037 T2 | 15 | 0.0330 | 93.5 | |
| Positive Normal Stresses (σ+) | ||||
| τ+ × H | τ+ = sqrt (−0.42 + 0.008 H2) | 5 | 0.0027 | 96.6 |
| τ+ = sqrt (−0.11 + 0.007 H2) | 10 | 0.0148 | 89.6 | |
| - | 15 | 0.0810 * | - | |
| τ+ × λ | τ+ = sqrt (−1.55 + 0.0016 λ2) | 5 | 0.0418 | 97.4 |
| τ+ = sqrt (−1.49 + 0.0021 λ2) | 10 | 0.0024 | 95.6 | |
| τ+ = sqrt (−1.38 + 0.0023 λ2) | 15 | 0.0022 | 94.2 | |
| τ+ × T | τ+ = sqrt (0.054 + 0.00007 T2) | 5 | 0.0409 | 92.0 |
| τ+ = sqrt (0.17 + 0.00029 T2) | 10 | 0.0329 | 99.5 | |
| τ+ = sqrt (0.41 + 0.00065 T2) | 15 | 0.0303 | 99.6 | |
| Scenario | C | Force of 5 kN | Force of 10 kN | Force of 15 kN | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| σ− | σ+ | τ− | τ+ | σ− | σ+ | τ− | τ+ | σ− | σ+ | τ− | τ+ | ||
| 1 | 1 | 7.8 | 7.7 | 3.9 | 3.8 | 2.6 | 2.5 | 3.7 | 4.3 | 1.9 | 2.2 | 1.2 | 1.4 |
| 2 | 24.8 | 29.9 | 13.3 | 13.7 | 9.1 | 8.9 | 4.0 | 6.1 | 4.0 | 6.1 | 4.0 | 4.6 | |
| 3 | 12.5 | 28.2 | 12.4 | 28.2 | 10.3 | 27.1 | 2.6 | 2.0 | 2.6 | 2.0 | 2.6 | 2.0 | |
| 4 | 8.4 | 10.5 | 8.4 | 10.5 | 7.9 | 10.5 | 1.0 | 1.3 | 1.0 | 1.3 | 1.0 | 1.3 | |
| 5 | 6.1 | 8.4 | 6.1 | 8.4 | 5.9 | 8.4 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | |
| 2 | 1 | 28.4 | 120 | 23.6 | 104 | 18.2 | 66.9 | 7.0 | 7.5 | 7.0 | 7.5 | 7.0 | 7.0 |
| 2 | 31.8 | 56.6 | 16.1 | 26.2 | 10.8 | 17.1 | 7.0 | 7.5 | 7.0 | 7.5 | 4.9 | 6.7 | |
| 3 | 9.5 | 11.8 | 4.7 | 6.0 | 3.1 | 4.0 | 3.6 | 3.4 | 1.9 | 1.8 | 1.3 | 1.2 | |
| 4 | 4.8 | 4.5 | 2.4 | 2.2 | 1.6 | 1.5 | 2.0 | 2.3 | 1.0 | 1.1 | 0.7 | 0.8 | |
| 5 | 2.3 | 2.0 | 1.1 | 1.0 | 0.7 | 0.7 | 0.8 | 0.7 | 0.4 | 0.3 | 0.3 | 0.2 | |
| 3 | 1 | 21.5 | 35.3 | 11.6 | 15.3 | 7.8 | 9.8 | 6.3 | 6.6 | 4.6 | 4.2 | 3.0 | 2.8 |
| 2 | 20..4 | 16..1 | 10..4 | 8..3 | 6..9 | 5..6 | 7.0 | 8.0 | 4.0 | 3.9 | 2.6 | 2.6 | |
| 3 | 18.6 | 18.8 | 9.4 | 9.1 | 6.3 | 6.0 | 5.2 | 6.2 | 2.6 | 3.0 | 1.7 | 2.0 | |
| 4 | 14.0 | 9.7 | 6.9 | 4.9 | 4.6 | 3.2 | 4.0 | 4.1 | 1.9 | 2.1 | 1.3 | 1.4 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruy, M.; Gonçalves, R.; Vicente, W. Effect of Dimensional Variables on the Behavior of Trees for Biomechanical Studies. Appl. Sci. 2022, 12, 3815. https://doi.org/10.3390/app12083815
Ruy M, Gonçalves R, Vicente W. Effect of Dimensional Variables on the Behavior of Trees for Biomechanical Studies. Applied Sciences. 2022; 12(8):3815. https://doi.org/10.3390/app12083815
Chicago/Turabian StyleRuy, Monica, Raquel Gonçalves, and William Vicente. 2022. "Effect of Dimensional Variables on the Behavior of Trees for Biomechanical Studies" Applied Sciences 12, no. 8: 3815. https://doi.org/10.3390/app12083815






