A Novel Hybrid Model for the Prediction and Classification of Rolling Bearing Condition
Abstract
:1. Introduction
2. Theoretical Foundation
2.1. Variational Model Decomposition
2.2. Prediction Model
2.2.1. Autoregressive Moving Average Model
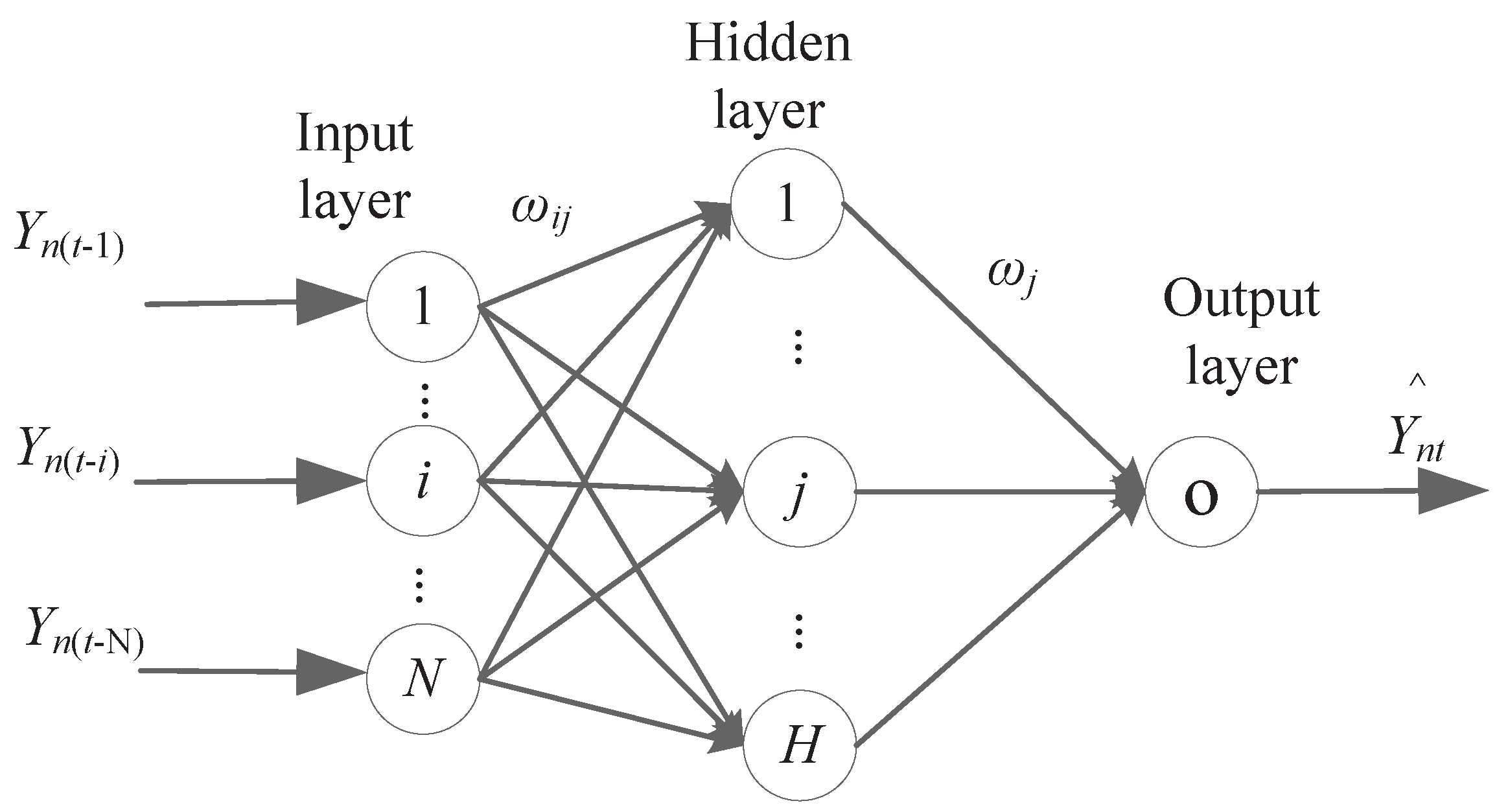
2.2.2. Artificial Neural Network Model
2.2.3. Hybrid Prediction Model
2.3. Feature Extraction
2.4. Support Vector Machine
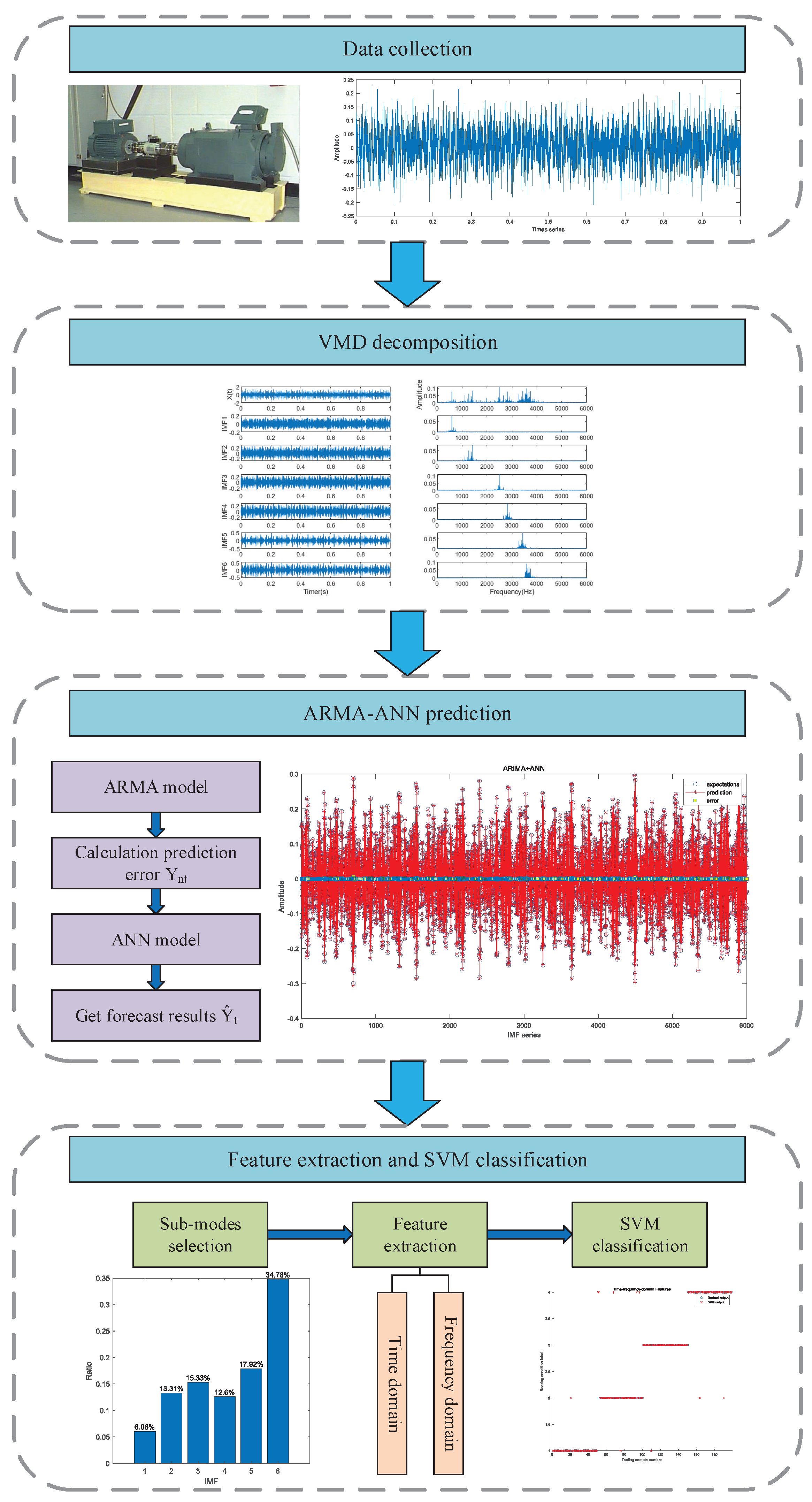
3. Proposed Architecture
- (1)
- The VMD algorithm decomposes the multi-component vibration signal of rolling bearing into several IMFs. The descriptions of the VMD algorithm are presented in Section 2.1;
- (2)
- Based on the established ARMA-ANN prediction model, the prediction of each IMF is conducted, and the sensitive IMFs are selected;
- (3)
- The multi-domain features set, i.e., T-F features set including time domain and frequency domain, are extracted as characteristic parameters from the sensitive IMFs. The specific features are presented in Section 2.3;
- (4)
- The classification of the condition is performed by a SVM classifier based on T-F features.
4. Experimental Analysis
4.1. Data Description
4.2. Experimental Results and Analysis
4.2.1. Decomposing the Vibration Signal Using VMD
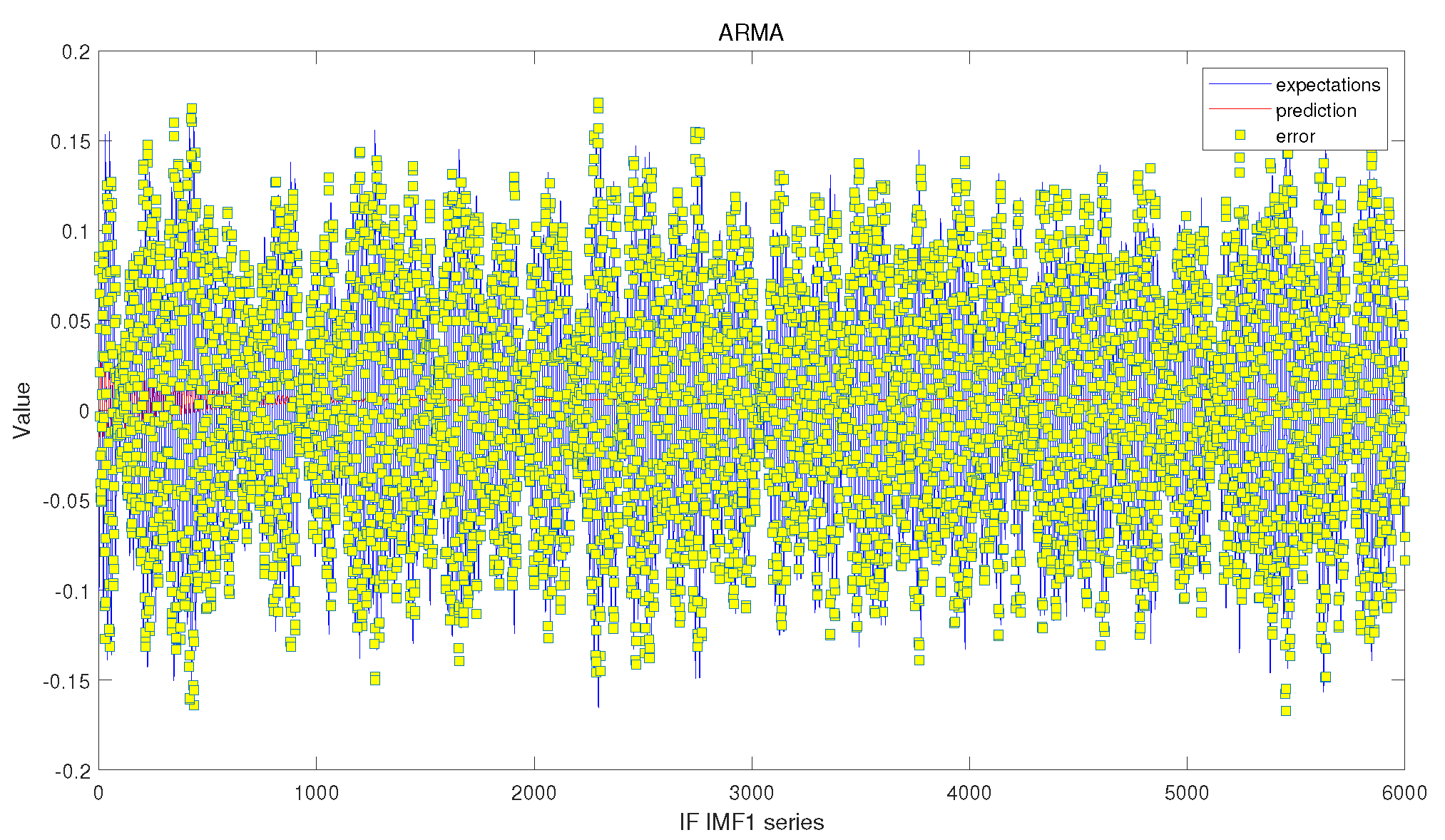
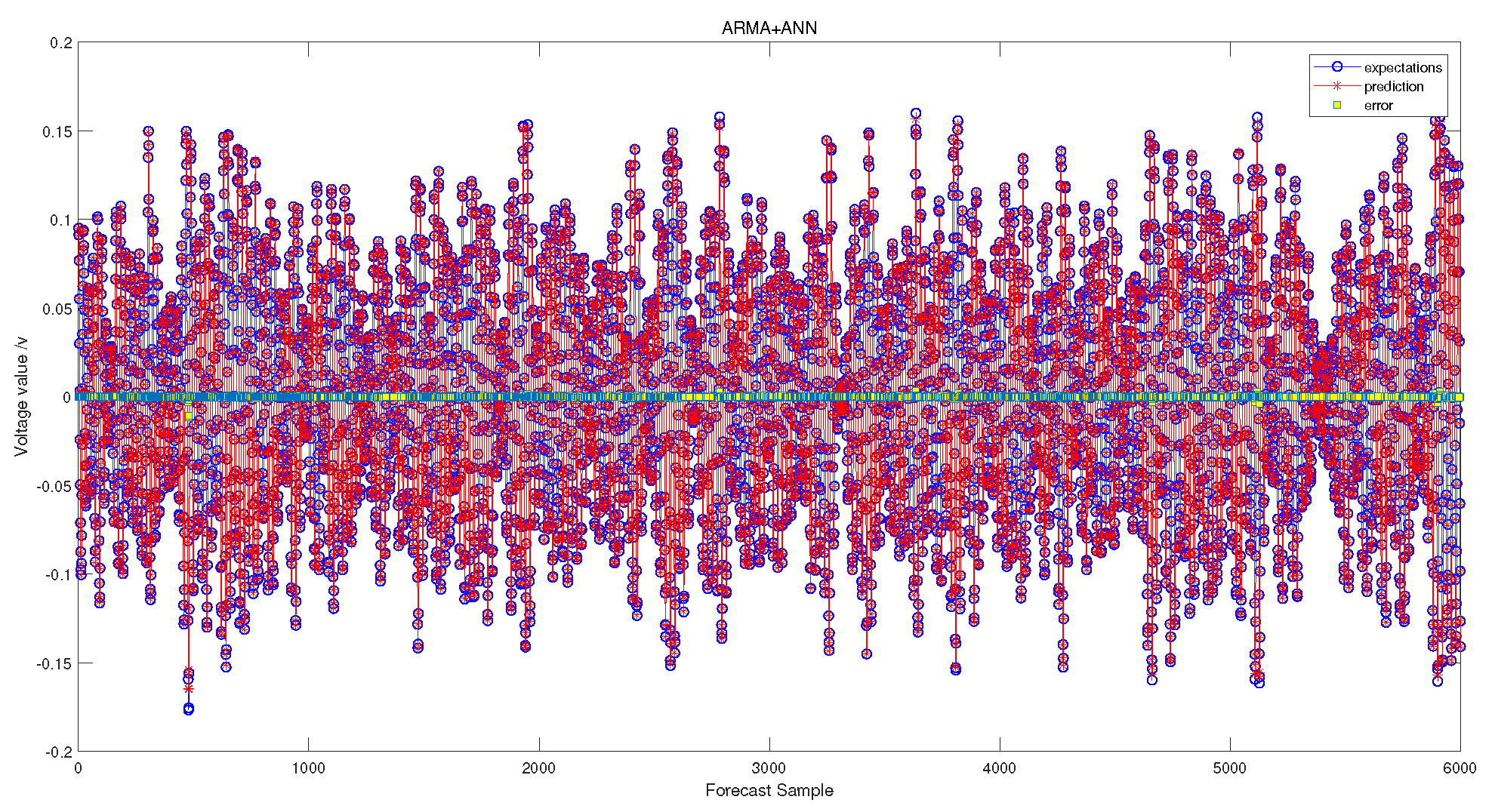
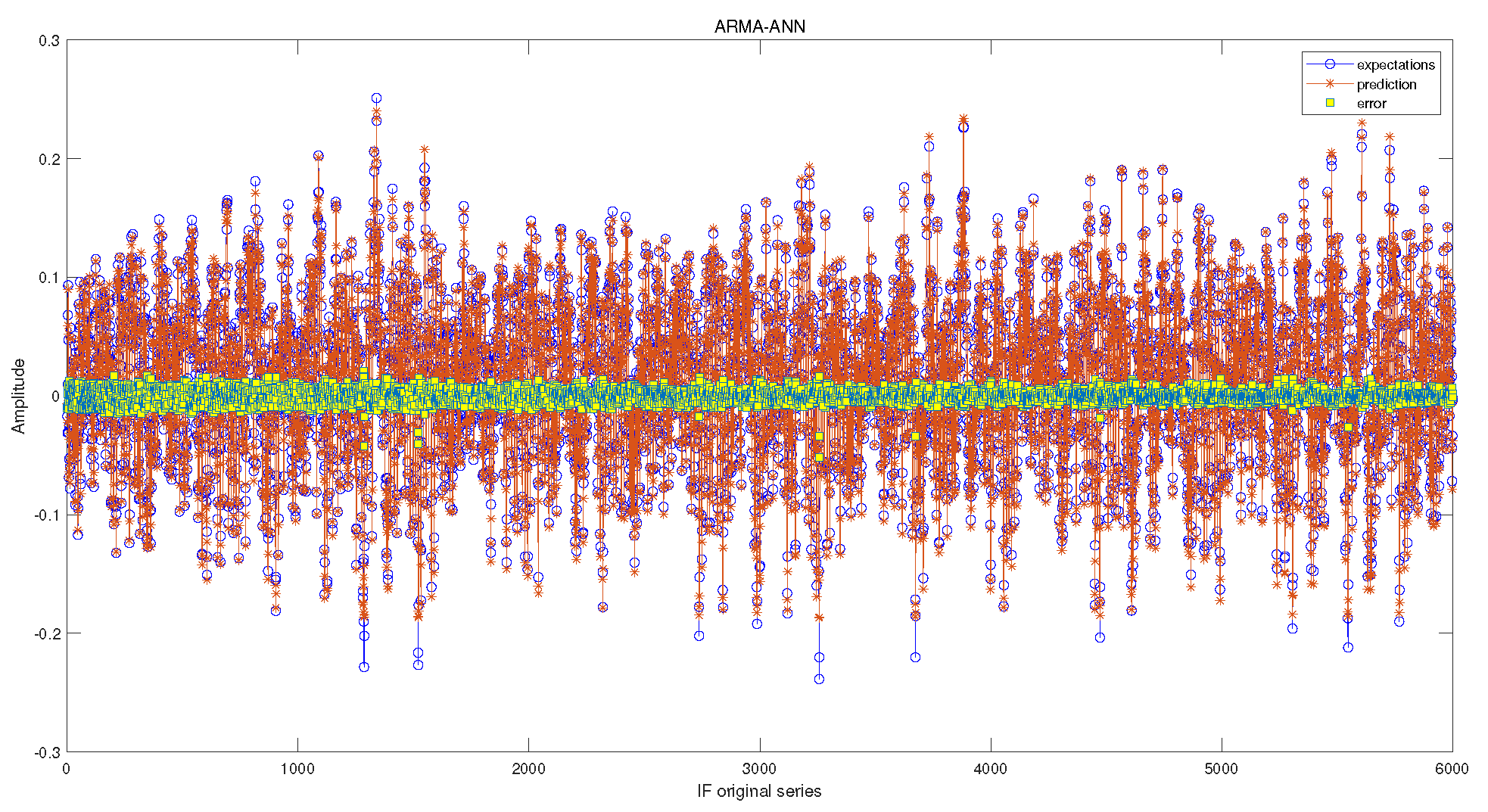
4.2.2. Prediction Based on Hybrid Prediction Model
4.2.3. Feature Extraction
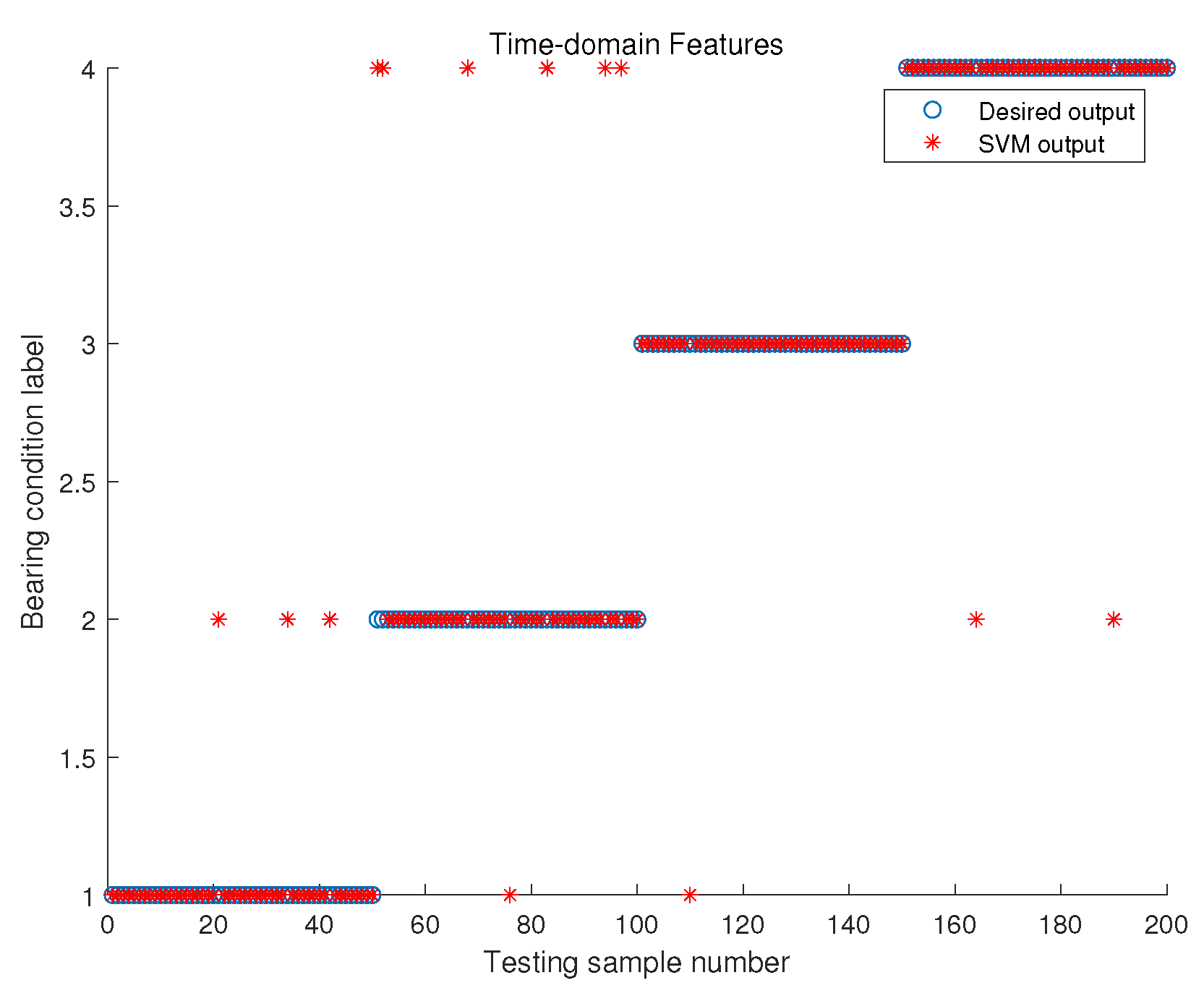
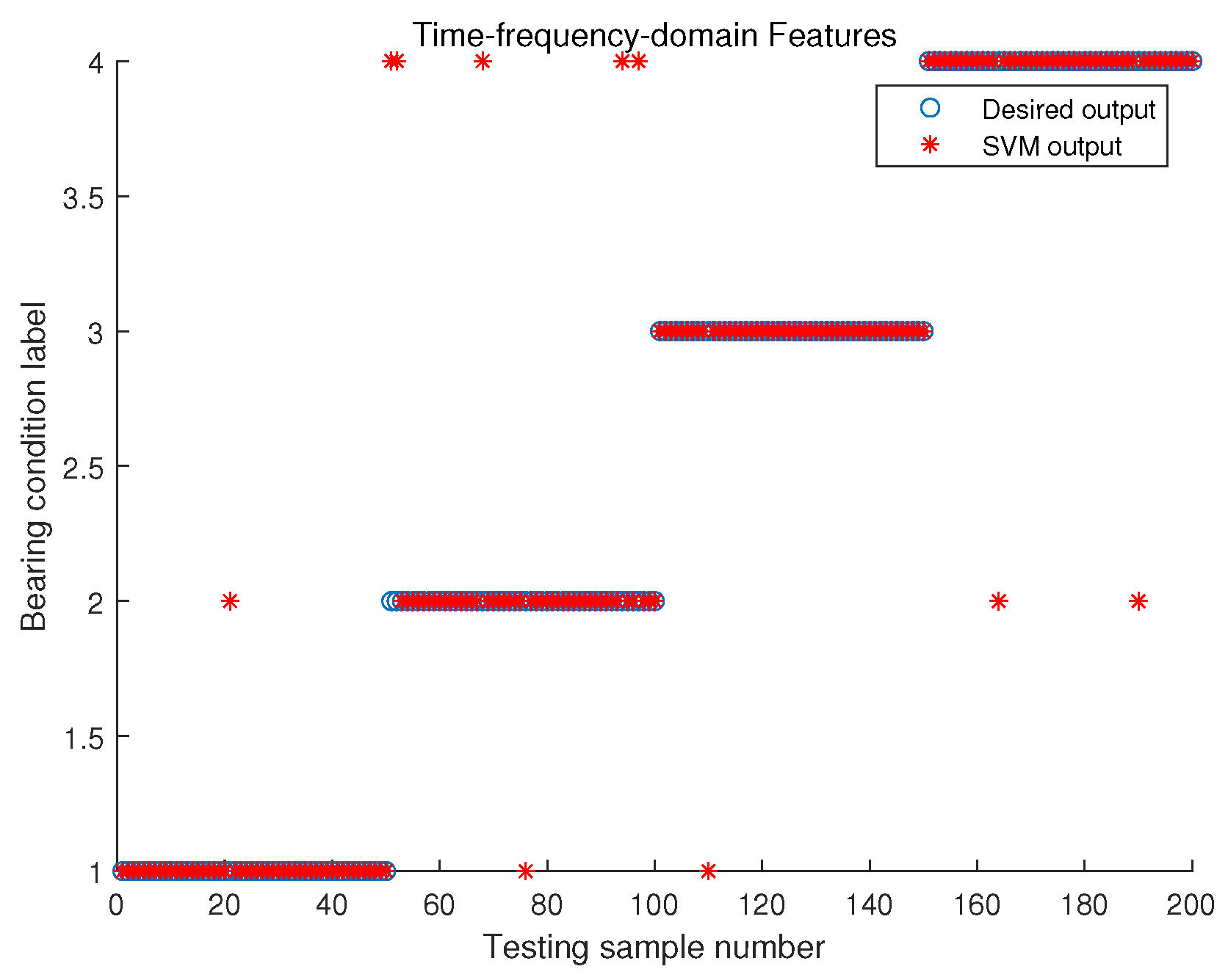
4.2.4. Classification Based on SVM
4.2.5. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| VMD | Variational mode decomposition |
| IMFs | Intrinsic mode functions |
| ARMA | Autoregressive moving average |
| ANN | Artificial neural network |
| ARMA-ANN | Autoregressive moving average-Artificial neural network |
| SVM | Support vector machine |
| CWRU | Case Western Reserve University |
| WT | Wavelet decomposition |
| EEMD | Ensemble empirical mode decomposition |
| EMD | Empirical mode decomposition |
| ADMM | Alternate direction method of multipliers |
| RBF | Radial basis function |
| AR | Auto-regression |
| MA | Moving average |
| T-F | Time-frequency |
| IF | Inner race fault |
| OF | Outer race fault |
| BF | Ball fault |
| PSD | Power spectral density |
| RMSE | Root-mean-square error |
| MAPE | Mean average percentage error |
| MAE | Mean absolute error |
References
- Shen, X.; Wu, Y.; Shen, T. Logical control scheme with real-time statistical learning for residual gas fraction in IC engines. Sci. China Inf. Sci. 2018, 61, 010203. [Google Scholar] [CrossRef]
- Wu, Y.; Shen, T. Policy iteration approach to control residual gas fraction in IC engines under the framework of stochastic logical dynamics. IEEE Trans. Control. Syst. Technol. 2016, 25, 1100–1107. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, X.; Wu, Y.; Shen, T. On-board knock probability map learning–based spark advance control for combustion engines. Int. J. Engine Res. 2019, 20, 1073–1088. [Google Scholar] [CrossRef]
- Wu, Y.; Guo, Y.; Toyoda, M. Policy iteration approach to the infinite horizon average optimal control of probabilistic Boolean networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 2910–2924. [Google Scholar] [CrossRef] [PubMed]
- Brito, L.C.; Susto, G.A.; Brito, J.N.; Duarte, M.A. An explainable artificial intelligence approach for unsupervised fault detection and diagnosis in rotating machinery. Mech. Syst. Signal Process. 2022, 163, 108105. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Randall, R.B. Vibration-Based Condition Monitoring: Industrial, Automotive and Aerospace Applications; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Vishwakarma, M.; Purohit, R.; Harshlata, V.; Rajput, P. Vibration analysis & condition monitoring for rotating machines: A review. Mater. Today Proc. 2017, 4, 2659–2664. [Google Scholar]
- Wang, D.; Miao, Q.; Fan, X.; Huang, H.Z. Rolling element bearing fault detection using an improved combination of Hilbert and wavelet transforms. J. Mech. Sci. Technol. 2009, 23, 3292–3301. [Google Scholar] [CrossRef]
- Li, Z.; Feng, Z.; Chu, F. A load identification method based on wavelet multi-resolution analysis. J. Sound Vib. 2014, 333, 381–391. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z. A review on Hilbert-Huang transform: Method and its applications to geophysical studies. Rev. Geophys. 2008, 46. [Google Scholar] [CrossRef] [Green Version]
- Huang, N.E. Introduction to the Hilbert–Huang transform and its related mathematical problems. In Hilbert–Huang Transform and Its Applications; World Scientific: Singapore, 2014; pp. 1–26. [Google Scholar]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y. Application of the EEMD method to rotor fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2009, 23, 1327–1338. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, M.; Yu, Q.; Zhang, H. Comparing the applications of EMD and EEMD on time–frequency analysis of seismic signal. J. Appl. Geophys. 2012, 83, 29–34. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, T.; Wang, Y.; Wang, K.; Shen, Y. A parameter optimized variational mode decomposition method for rail crack detection based on acoustic emission technique. Nondestruct. Test. Eval. 2021, 36, 411–439. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Lei, Z.; Wen, G.; Dong, S.; Huang, X.; Zhou, H.; Zhang, Z.; Chen, X. An intelligent fault diagnosis method based on domain adaptation and its application for bearings under polytropic working conditions. IEEE Trans. Instrum. Meas. 2020, 70, 3505914. [Google Scholar] [CrossRef]
- Wang, Y.; Markert, R.; Xiang, J.; Zheng, W. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system. Mech. Syst. Signal Process. 2015, 60, 243–251. [Google Scholar] [CrossRef]
- Wang, X.B.; Yang, Z.X.; Yan, X.A. Novel particle swarm optimization-based variational mode decomposition method for the fault diagnosis of complex rotating machinery. IEEE/ASME Trans. Mechatron. 2017, 23, 68–79. [Google Scholar] [CrossRef]
- Lian, J.; Liu, Z.; Wang, H.; Dong, X. Adaptive variational mode decomposition method for signal processing based on mode characteristic. Mech. Syst. Signal Process. 2018, 107, 53–77. [Google Scholar] [CrossRef]
- Chen, Y.; Liang, X.; Zuo, M.J. Sparse time series modeling of the baseline vibration from a gearbox under time-varying speed condition. Mech. Syst. Signal Process. 2019, 134, 106342. [Google Scholar] [CrossRef]
- Doroudyan, M.H.; Niaki, S.T.A. Pattern recognition in financial surveillance with the ARMA-GARCH time series model using support vector machine. Expert Syst. Appl. 2021, 182, 115334. [Google Scholar] [CrossRef]
- Zaw, T.; Kyaw, S.S.; Oo, A.N. ARMA Model for Revenue Prediction. In Proceedings of the 11th International Conference on Advances in Information Technology, Bangkok, Thailand, 1–3 July 2020; pp. 1–6. [Google Scholar]
- Zhang, Y.; Zhao, Y.; Kong, C.; Chen, B. A new prediction method based on VMD-PRBF-ARMA-E model considering wind speed characteristic. Energy Convers. Manag. 2020, 203, 112254. [Google Scholar] [CrossRef]
- Bang, S.; Bishnoi, R.; Chauhan, A.S.; Dixit, A.K.; Chawla, I. Fuzzy Logic based Crop Yield Prediction using Temperature and Rainfall parameters predicted through ARMA, SARIMA, and ARMAX models. In Proceedings of the 2019 Twelfth International Conference on Contemporary Computing (IC3), Noida, India, 8–10 August 2019; pp. 1–6. [Google Scholar]
- Ji, W.; Chee, K.C. Prediction of hourly solar radiation using a novel hybrid model of ARMA and TDNN. Sol. Energy 2011, 85, 808–817. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. Statistical and Machine Learning forecasting methods: Concerns and ways forward. PLoS ONE 2018, 13, e0194889. [Google Scholar] [CrossRef] [Green Version]
- Moon, J.; Hossain, M.B.; Chon, K.H. AR and ARMA model order selection for time-series modeling with ImageNet classification. Signal Process. 2021, 183, 108026. [Google Scholar] [CrossRef]
- Aras, S.; Kocakoç, İ.D. A new model selection strategy in time series forecasting with artificial neural networks: IHTS. Neurocomputing 2016, 174, 974–987. [Google Scholar] [CrossRef]
- Chandran, V.; K Patil, C.; Karthick, A.; Ganeshaperumal, D.; Rahim, R.; Ghosh, A. State of charge estimation of lithium-ion battery for electric vehicles using machine learning algorithms. World Electr. Veh. J. 2021, 12, 38. [Google Scholar] [CrossRef]
- Anushka, P.; Upaka, R. Comparison of different artificial neural network (ANN) training algorithms to predict the atmospheric temperature in Tabuk, Saudi Arabia. Mausam 2020, 71, 233–244. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Brusa, E.; Bruzzone, F.; Delprete, C.; Di Maggio, L.G.; Rosso, C. Health indicators construction for damage level assessment in bearing diagnostics: A proposal of an energetic approach based on envelope analysis. Appl. Sci. 2020, 10, 8131. [Google Scholar] [CrossRef]
- Alessandro Paolo, D.; Luigi, G.; Alessandro, F.; Stefano, M. Performance of Envelope Demodulation for Bearing Damage Detection on CWRU Accelerometric Data: Kurtogram and Traditional Indicators vs. Targeted a Posteriori Band Indicators. Appl. Sci. 2021, 11, 6262. [Google Scholar] [CrossRef]
- Zhang, X.; Miao, Q.; Zhang, H.; Wang, L. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery. Mech. Syst. Signal Process. 2018, 108, 58–72. [Google Scholar] [CrossRef]
- Gao, Y.; Mosalam, K.M.; Chen, Y.; Wang, W.; Chen, Y. Auto-Regressive Integrated Moving-Average Machine Learning for Damage Identification of Steel Frames. Appl. Sci. 2021, 11, 6084. [Google Scholar] [CrossRef]
- Yan, X.; Jia, M. A novel optimized SVM classification algorithm with multi-domain feature and its application to fault diagnosis of rolling bearing. Neurocomputing 2018, 313, 47–64. [Google Scholar] [CrossRef]
- Cervantes, J.; Garcia-Lamont, F.; Rodríguez-Mazahua, L.; Lopez, A. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Pang, H.; Wang, S.; Dou, X.; Liu, H.; Chen, X.; Yang, S.; Wang, T.; Wang, S. A Feature Extraction Method Using Auditory Nerve Response for Collapsing Coal-Gangue Recognition. Appl. Sci. 2020, 10, 7471. [Google Scholar] [CrossRef]
- Xiang, J.; Zhong, Y. A novel personalized diagnosis methodology using numerical simulation and an intelligent method to detect faults in a shaft. Appl. Sci. 2016, 6, 414. [Google Scholar] [CrossRef] [Green Version]
- Paolanti, M.; Romeo, L.; Felicetti, A.; Mancini, A.; Frontoni, E.; Loncarski, J. Machine learning approach for predictive maintenance in industry 4.0. In Proceedings of the 2018 14th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Oulu, Finland, 2–4 July 2018; pp. 1–6. [Google Scholar]
- Mamuya, Y.D.; Lee, Y.D.; Shen, J.W.; Shafiullah, M.; Kuo, C.C. Application of machine learning for fault classification and location in a radial distribution grid. Appl. Sci. 2020, 10, 4965. [Google Scholar] [CrossRef]
- Long, B.; Wu, K.; Li, P.; Li, M. A Novel Remaining Useful Life Prediction Method for Hydrogen Fuel Cells Based on the Gated Recurrent Unit Neural Network. Appl. Sci. 2022, 12, 432. [Google Scholar] [CrossRef]
- Ren, Y.; Suganthan, P.; Srikanth, N. A comparative study of empirical mode decomposition-based short-term wind speed forecasting methods. IEEE Trans. Sustain. Energy 2014, 6, 236–244. [Google Scholar] [CrossRef]
- Bi, F.; Li, X.; Liu, C.; Tian, C.; Ma, T.; Yang, X. Knock detection based on the optimized variational mode decomposition. Measurement 2019, 140, 1–13. [Google Scholar] [CrossRef]
- Maldonado, S.; López, J. Dealing with high-dimensional class-imbalanced datasets: Embedded feature selection for SVM classification. Appl. Soft Comput. 2018, 67, 94–105. [Google Scholar] [CrossRef]
- Gu, R.; Chen, J.; Hong, R.; Wang, H.; Wu, W. Incipient fault diagnosis of rolling bearings based on adaptive variational mode decomposition and Teager energy operator. Measurement 2020, 149, 106941. [Google Scholar] [CrossRef]
- Burges, C.J. A tutorial on support vector machines for pattern recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Razzak, I.; Zafar, K.; Imran, M.; Xu, G. Randomized nonlinear one-class support vector machines with bounded loss function to detect of outliers for large scale IoT data. Future Gener. Comput. Syst. 2020, 112, 715–723. [Google Scholar] [CrossRef]
- Shao, X.; Pu, C.; Zhang, Y.; Kim, C.S. Domain fusion CNN-LSTM for short-term power consumption forecasting. IEEE Access 2020, 8, 188352–188362. [Google Scholar] [CrossRef]
- Shao, X.; Kim, C.S.; Kim, D.G. Accurate multi-scale feature fusion CNN for time series classification in smart factory. Comput. Mater. Contin. 2020, 65, 543–561. [Google Scholar] [CrossRef]







| Time-Domain Parameter | Feature Expression | Frequency-Domain Parameter | Feature Expression |
|---|---|---|---|
| F1 | F6 | ||
| F2 | F7 | ||
| F3 | F8 | ||
| F4 | F9 | ||
| F5 | F10 |
| Algorithm | Parameter | Setting |
|---|---|---|
| VMD | K | 6 |
| 2891 | ||
| DC | 0 | |
| tau | 0 | |
| init | 1 | |
| tol |
| Condition | Model | RMSE | MAPE | MAE |
|---|---|---|---|---|
| IF | ARMA | 1.0279 × | 1.1276 × | 8.2175 × |
| ANN | 9.6119 × | 2.9847 × | 7.5156 × | |
| ARMA-ANN | 3.6904 × | 2.2367 × | 2.6025 × | |
| NS | ARMA | 1.4100 × | 1.8500 × | 1.1707 × |
| ANN | 1.1744 × | 1.8433 × | 9.4530 × | |
| ARMA-ANN | 4.6082 × | 3.0578 × | 2.9941 × | |
| BF | ARMA | 4.2184 × | 1.3759 × | 3.4340 × |
| ANN | 3.9973 × | 4.0775 × | 3.2100 × | |
| ARMA-ANN | 8.1888 × | 4.3402 × | 2.6100 × | |
| OF | ARMA | 1.2997 × | 1.0736 × | 1.0533 × |
| ANN | 1.2400 × | 2.1900 × | 9.9000 × | |
| ARMA-ANN | 2.4100 × | 2.9969 × | 1.5100 × |
| Condition | Series | RMSE | MAPE | MAE |
|---|---|---|---|---|
| IF | Original | 5.2744 × | 3.0023 × | 4.1815 × |
| Subseries | 3.6904 × | 2.2367 × | 2.6025 × | |
| NS | Original | 5.3683 × | 3.1319 × | 4.2680 × |
| Subseries | 4.6082 × | 3.0578 × | 2.9941 × | |
| BF | Original | 5.2354 × | 3.0846 × | 4.1308 × |
| Subseries | 8.1888 × | 4.3402 × | 2.6100 × | |
| OF | Original | 5.1080 × | 3.0283 × | 4.0719 × |
| Subseries | 2.4100 × | 2.9969 × | 1.5100 × |
| Domain | Classification Accuracy | Average Accuracy | |||
|---|---|---|---|---|---|
| IF | BF | OF | Normal | ||
| Time domain | 94% | 86% | 98% | 96% | 93.5% |
| Frequency domain | 78% | 68% | 88% | 98% | 83% |
| Time-frequency domain | 98% | 88% | 98% | 96% | 95% |
| Operating Condition | Method | RMSE | MAPE | MAE |
|---|---|---|---|---|
| Inner Race | LSTM | 5.5412 × | 7.0271 × | 4.1816 × |
| ARMA-ANN | 5.2744 × | 3.0023 × | 4.1815 × | |
| Normal | LSTM | 1.2815 × | 4.5444 × | 9.6361 × |
| ARMA-ANN | 5.3683 × | 3.1319 × | 4.2680 × | |
| Ball | LSTM | 2.8762 × | 4.0346 × | 2.1655 × |
| ARMA-ANN | 5.2354 × | 3.0846 × | 4.1308 × | |
| Outer Race | LSTM | 1.0495 × | 1.3158 × | 7.7409 × |
| ARMA-ANN | 5.1080 × | 3.0283 × | 4.0719 × |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, A.; Li, Y.; Yao, Z.; Zhong, C.; Xue, B.; Guo, Z. A Novel Hybrid Model for the Prediction and Classification of Rolling Bearing Condition. Appl. Sci. 2022, 12, 3854. https://doi.org/10.3390/app12083854
Wang A, Li Y, Yao Z, Zhong C, Xue B, Guo Z. A Novel Hybrid Model for the Prediction and Classification of Rolling Bearing Condition. Applied Sciences. 2022; 12(8):3854. https://doi.org/10.3390/app12083854
Chicago/Turabian StyleWang, Aina, Yingshun Li, Zhao Yao, Chongquan Zhong, Bin Xue, and Zhannan Guo. 2022. "A Novel Hybrid Model for the Prediction and Classification of Rolling Bearing Condition" Applied Sciences 12, no. 8: 3854. https://doi.org/10.3390/app12083854
APA StyleWang, A., Li, Y., Yao, Z., Zhong, C., Xue, B., & Guo, Z. (2022). A Novel Hybrid Model for the Prediction and Classification of Rolling Bearing Condition. Applied Sciences, 12(8), 3854. https://doi.org/10.3390/app12083854





