The New Physics in LILITA_N21: An Improved Description of the Reaction 190 MeV 40Ar + 27Al
Abstract
1. Introduction
2. Materials and Methods
The Model
3. Results
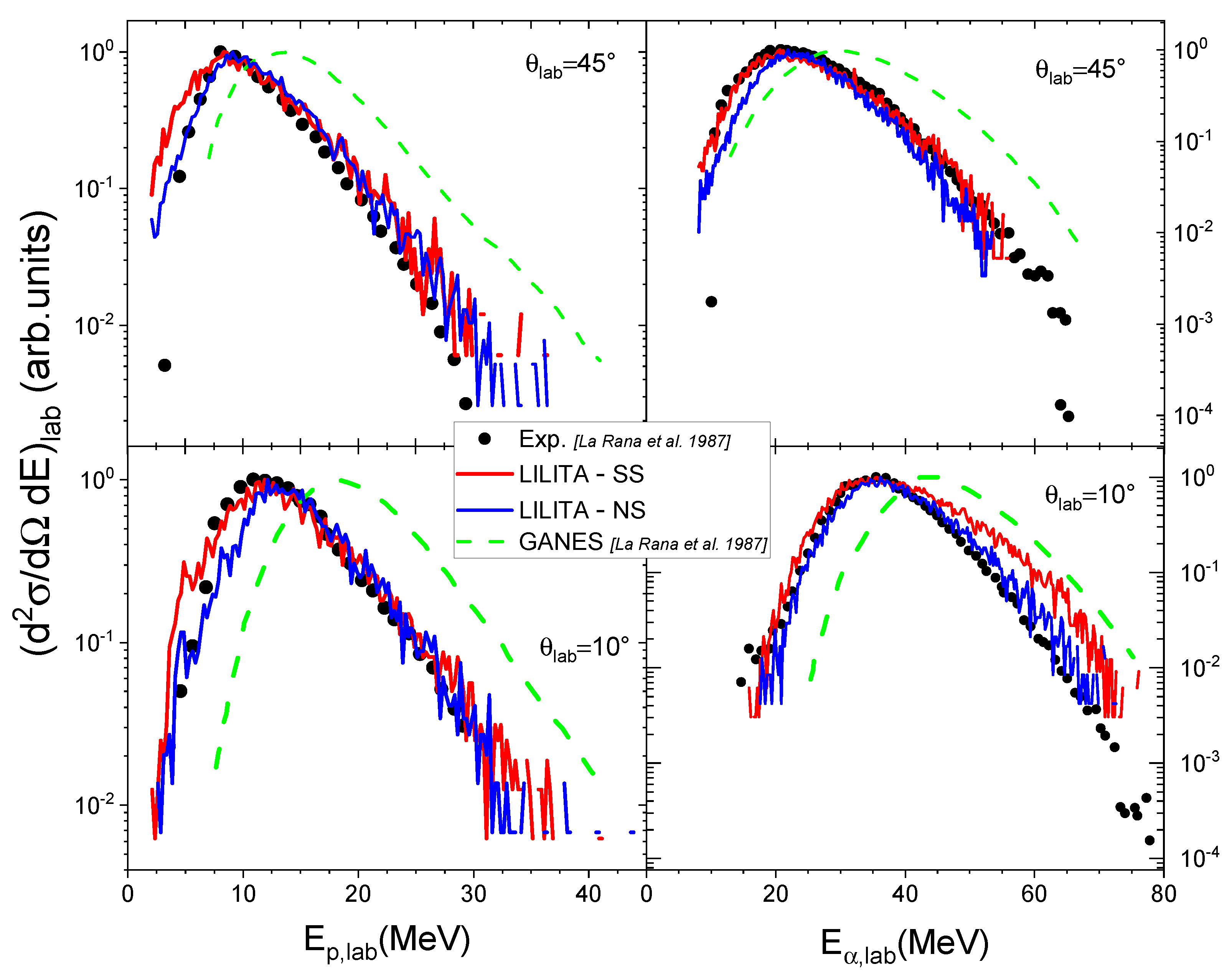
3.1. Light Charged Particle Spectra
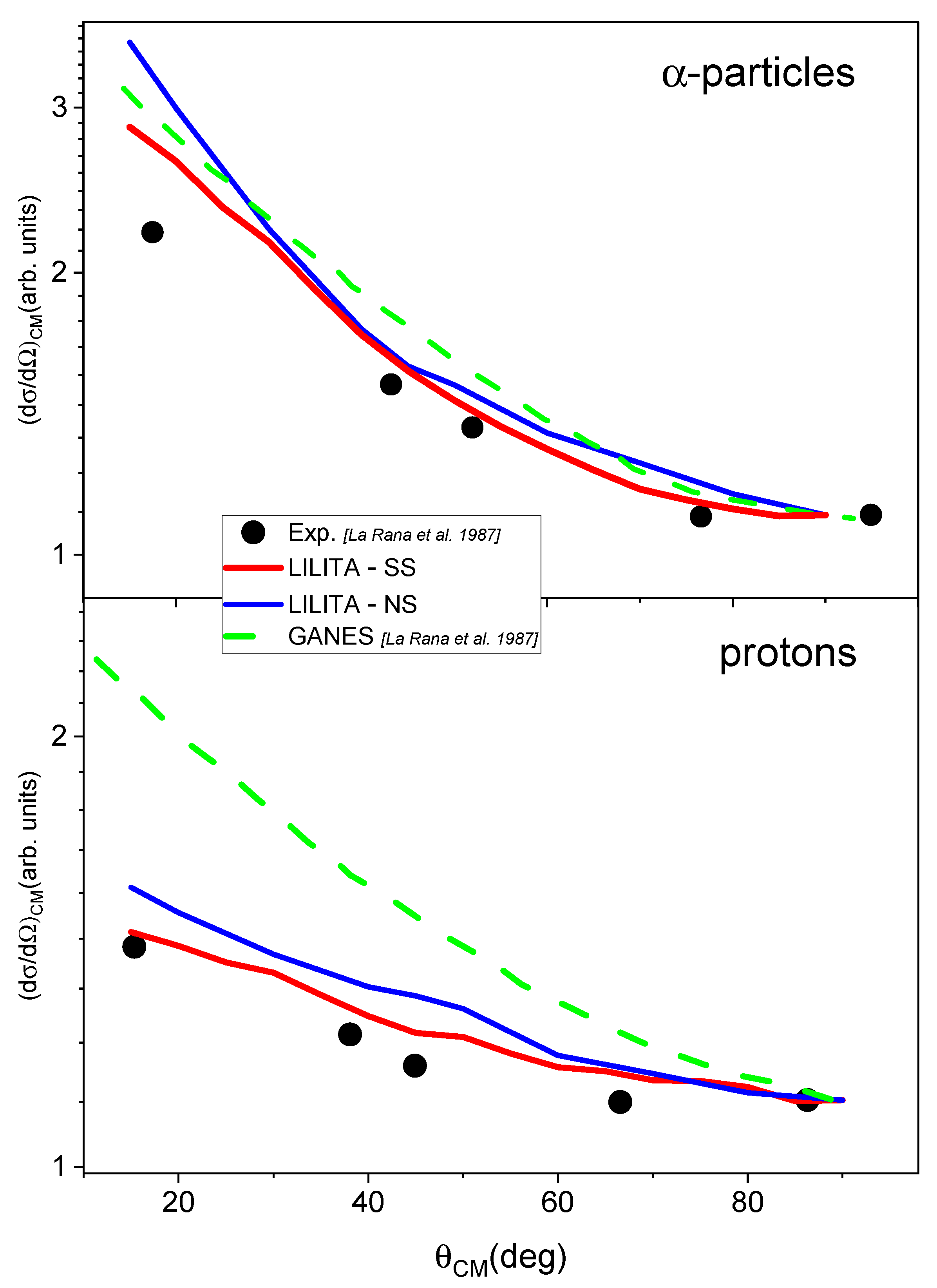
3.2. Angular Distributions
3.3. Differential Multiplicities
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Weisskopf, V. Statistics and nuclear reactions. Phys. Rev. 1937, 52, 295–303. [Google Scholar] [CrossRef]
- Weisskopf, V.F.; Ewing, D.H. On the yield of nuclear reactions with heavy elements. Phys. Rev. 1940, 57, 472–485. [Google Scholar] [CrossRef]
- Feshbach, H. Nuclear Spectroscopy, Part B; Academic Press: New York, NY, USA, 1960; p. 625. [Google Scholar]
- Vardaci, E.; Di Nitto, A.; Nadtochy, P.N.; La Rana, G. Fission dynamics in systems of intermediate fissility. J. Phys. G Nucl. Part. Phys. 2019, 46, 115111. [Google Scholar] [CrossRef]
- Moro, R.; Brondi, A.; Gelli, N.; Barbui, M.; Boiano, A.; Cinausero, M.; Di Nitto, A.; Fabris, D.; Fioretto, E.; La Rana, G.; et al. Compound nucleus evaporative decay as a probe for the isospin dependence of the level density. Eur. Phys. J. A 2012, 48, 159. [Google Scholar] [CrossRef]
- Di Nitto, A.; Vardaci, E.; Brondi, A.; La Rana, G.; Cinausero, M.; Gelli, N.; Moro, R.; Nadtochy, P.N.; Prete, G.; Vanzanella, A. Clustering effects in 48Cr composite nuclei produced via the 24Mg + 24Mg reaction. Phys. Rev. C 2016, 93, 044602. [Google Scholar] [CrossRef]
- Di Nitto, A.; Vardaci, E.; La Rana, G.; Nadtochy, P.N.; Boiano, A.; Cinausero, M.; Prete, G.; Gelli, N.; Kozulin, E.M.; Knyazheva, G.N.; et al. Evaporation and fission decay of 158Er composite nuclei within the statistical model. Phys. Rev. C 2020, 102, 024624. [Google Scholar] [CrossRef]
- Gonin, M.; Cooke, L.; Hagel, K.; Lou, Y.; Natowitz, J.B.; Schmitt, R.P.; Shlomo, S.; Srivastava, B.; Turmel, W.; Utsunomiya, H.; et al. Dynamical effects on the de-excitation of hot nuclei with A ≃ 160. Phys. Rev. C 1990, 42, 2125–2142. [Google Scholar] [CrossRef]
- Charity, R.J.; Sobotka, L.G.; Cibor, J.; Hagel, K.; Murray, M.; Natowitz, J.B.; Wada, R.; El Masri, Y.; Fabris, D.; Nebbia, G.; et al. Emission of unstable clusters from hot Yb compound nuclei. Phys. Rev. C 2001, 63, 024611. [Google Scholar] [CrossRef]
- Vardaci, E.; Di Nitto, A.; Brondi, A.; La Rana, G.; Moro, R.; Nadotchy, P.N.; Trotta, M.; Ordine, A.; Boiano, A.; Cinausero, M.; et al. Inadequacy of the statistical model: Some evidence for compound nuclei in the A ≈ 150 and Ex≈ 100–200 MeV region. Eur. Phys. J. A 2010, 43, 127. [Google Scholar] [CrossRef][Green Version]
- La Rana, G.; Moro, R.; Brondi, A.; Cuzzocrea, P.; D’Onofrio, A.; Perillo, E.; Romano, M.; Terrasi, F.; Vardaci, E.; Dumont, H. Unexpected large deformations in 60Ni nuclei produced in the reaction 120 MeV 30Si + 30Si. Phys. Rev. C 1988, 37, 1920. [Google Scholar] [CrossRef]
- La Rana, G.; Moses, D.J.; Parker, W.E.; Kaplan, M.; Logan, D.; Lacey, R.; Alexander, J.M.; Welberry, R.J. Need for new physics in statistical models of nuclear de-excitation. Phys. Rev. C 1987, 35, 373. [Google Scholar] [CrossRef]
- Batko, G.; Civitarese, O. Nuclear stratosphere formation and its effects upon statistical particle emission processes. Phys. Rev. C 1988, 37, 2647–2650. [Google Scholar] [CrossRef]
- Davide, F.; Di Nitto, A.; Vardaci, E.; La Rana, G. LILITA_N21: Updated version of the Monte Carlo fusion–evaporation code. Nucl. Instrum. Meth. Phys. Res. A 2022, 1025, 166178. [Google Scholar] [CrossRef]
- Hodgson, P.E. Nuclear Heavy-Ion Reactions; Clarendon Press: Oxford, UK, 1978; p. 588. [Google Scholar]
- Pühlhofer, F. Computer code CASCADE. Nucl. Phys. A 1977, 280, 267. [Google Scholar] [CrossRef]
- Reisdorf, W. Analysis of fissionability data at high excitation energies. Z. Phys. A 1981, 300, 227–238. [Google Scholar] [CrossRef]
- Gavron, A. Statistical model calculations in heavy ion reactions. Phys. Rev. C 1980, 21, 230. [Google Scholar] [CrossRef]
- Tarasov, O.; Bazin, D. LISE++: Radioactive beam production with in-flight separators. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2008, 266, 4657–4664. [Google Scholar] [CrossRef]
- Gomez del Campo, J.; Stockstad, R.G. Description and Use of the Monte Carlo Code LILITA [Modeling of Equilibrium Decay of Heavy Ion Reaction Products]; Oak Ridge National Laboratory Report No. TM7295; Oak Ridge National Lab.: Oak Ridge, TN, USA, 1981. [Google Scholar]
- Bohr, A.; Mottelson, B.R. Nuclear Structure; W. A. Benjamin: New York, NY, USA, 1969; Volume I, p. 152. [Google Scholar]
- Fornal, B.; Gramegna, F.; Prete, G.; Burch, R.; D’Erasmo, G.; Fiore, E.M.; Fiore, L.; Pantaleo, A.; Paticchio, V.; Viesti, G.; et al. Level density of hot nuclei with A ⩽ 40. Phys. Rev. C 1991, 44, 2588–2597. [Google Scholar] [CrossRef]
- Di Nitto, A.; Vardaci, E.; La Rana, G.; Nadtochy, P.N.; Prete, G. Evaporation channel as a tool to study fission dynamics. Nucl. Phys. A 2018, 971, 21–34. [Google Scholar] [CrossRef]
- Huizenga, J.; Igo, G. Theoretical reaction cross sections for alpha particles with an optical model. Nucl. Phys. 1962, 29, 462–473. [Google Scholar] [CrossRef]
- Perey, F.G. Optical-model analysis of proton elastic scattering in the range of 9 to 22 MeV. Phys. Rev. 1963, 131, 745–763. [Google Scholar] [CrossRef]
- Wilmore, D.; Hodgson, P. The calculation of neutron cross-sections from optical potentials. Nucl. Phys. 1964, 55, 673–694. [Google Scholar] [CrossRef]
- Köning, A.; Delaroche, J. Local and global nucleon optical models from 1 keV to 200 MeV. Nucl. Phys. A 2003, 713, 231–310. [Google Scholar] [CrossRef]
- Su, X.W.; Han, Y.L. Global optical model potential for alpha projectile. Int. J. Mod. Phys. E 2015, 24, 1550092. [Google Scholar] [CrossRef]
- Beck, C.; Papka, P.; Zafra, A.S.i.; Thummerer, S.; Azaiez, F.; Bednarczyk, P.; Courtin, S.; Curien, D.; Dorvaux, O.; Lebhertz, D.; et al. Binary reaction decays from 24Mg + 12C. Phys. Rev. C 2009, 80, 034604. [Google Scholar] [CrossRef]
- Mahboub, D.; Beck, C.; Djerroud, B.; Freeman, R.M.; Haas, F.; Nouicer, R.; Rousseau, M.; Papka, P.; Sànchez iZafra, A.; Cavallaro, S.; et al. Light particle emission in 35Cl + 24Mg fusion reactions at high excitation energy and angular momentum. Phys. Rev. C 2004, 69, 034616. [Google Scholar] [CrossRef]
- Rousseau, M.; Beck, C.; Bhattacharya, C.; Rauch, V.; Dorvaux, O.; Eddahbi, K.; Enaux, C.; Freeman, R.M.; Haas, F.; Mahboub, D.; et al. Highly deformed 40Ca configurations in 28Si + 12C. Phys. Rev. C 2002, 66, 034612. [Google Scholar] [CrossRef]
- Sierk, A.J. Macroscopic model of rotating nuclei. Phys. Rev. C 1986, 33, 2039. [Google Scholar] [CrossRef]
- Cohen, S.; Plasil, F.; Swiatecki, W.J. Equilibrium configurations of rotating charged or gravitating liquid masses with surface tension. II. Ann. Phys. 1974, 82, 557–596. [Google Scholar] [CrossRef]
- Vaz, L.C.; Alexander, J.M. Empirical and theoretical fusion barriers for1H and4He: Connections to evaporation from hot nuclei. Z. Phys. A 1984, 318, 231–237. [Google Scholar] [CrossRef]
- Prajapati, G.K.; Gupta, Y.K.; John, B.V.; Joshi, B.N.; Kaur, H.; Kumar, N.; Danu, L.S.; Mukhopadhyay, S.; Dubey, S.; Jain, S.R.; et al. Temperature and isospin dependence of the level-density parameter in the A≈110 mass region. Phys. Rev. C 2020, 102, 054605. [Google Scholar] [CrossRef]
- Roy, P.; Banerjee, K.; Rana, T.K.; Kundu, S.; Manna, S.; Sen, A.; Mondal, D.; Sadhukhan, J.; Senthil Kannan, M.T.; Ghosh, T.K.; et al. Evidence for the reduction of nuclear level density away from the β-stability line. Phys. Rev. C 2020, 102, 061601. [Google Scholar] [CrossRef]
- Hüyük, T.; Di Nitto, A.; Jaworski, G.; Gadea, A.; Javier Valiente-Dobón, J.; Nyberg, J.; Palacz, M.; Söderström, P.A.; Jose Aliaga-Varea, R.; de Angelis, G.; et al. Conceptual design of the early implementation of the NEutron Detector Array (NEDA) with AGATA. Eur. Phys. J. A 2016, 52, 55. [Google Scholar] [CrossRef]
- Di Nitto, A.; Brondi, A.; La Rana, G.; Moro, R.; Nadtochy, P.; Vardaci, E.; Gelli, N.; Cinausero, M.; Prete, G. The role of isospin in fusion evaporation reactions. J. Phys. Conf. Ser. 2011, 267, 012053. [Google Scholar] [CrossRef]
- Modamio, V.; Valiente-Dobón, J.; Jaworski, G.; Hüyük, T.; Triossi, A.; Egea, J.; Di Nitto, A.; Söderström, P.A.; Agramunt Ros, J.; de Angelis, G.; et al. Digital pulse-timing technique for the neutron detector array NEDA. Nucl. Instrum. Methods Phys. Res. Sect. A 2015, 775, 71–76. [Google Scholar] [CrossRef]
- Valiente-Dobón, J.; Jaworski, G.; Goasduff, A.; Egea, F.; Modamio, V.; Hüyük, T.; Triossi, A.; Jastrzab, M.; Söderström, P.; Di Nitto, A.; et al. NEDA—NEutron Detector Array. Nucl. Instrum. Meth. Phys. Res. A 2019, 927, 81–86. [Google Scholar] [CrossRef]
- Vardaci, E.; Pulcini, A.; Kozulin, E.M.; Matea, I.; Verney, D.; Maj, A.; Schmitt, C.; Itkis, I.M.; Knyazheva, G.N.; Novikov, K.; et al. Using γ rays to disentangle fusion-fission and quasifission near the Coulomb barrier: A test of principle in the fusion-fission and quasielastic channels. Phys. Rev. C 2020, 101, 064612. [Google Scholar] [CrossRef]
| NLD “a” | Nuclear Shape Parameters | TC | |
|---|---|---|---|
| SS | A/8 | = 1.2 fm | OM [27,28] |
| NS | A/8 | () = (0.079, 0.7) | OM [27,28] |
| Exp. [12] | LILITA-SS | LILITA-NS | |
|---|---|---|---|
| 1.56 | 2.04 | 1.62 | |
| 0.55 | 1.12 | 0.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Nitto, A.; Davide, F.; Vardaci, E.; Bianco, D.; La Rana, G.; Mercogliano, D. The New Physics in LILITA_N21: An Improved Description of the Reaction 190 MeV 40Ar + 27Al. Appl. Sci. 2022, 12, 4107. https://doi.org/10.3390/app12094107
Di Nitto A, Davide F, Vardaci E, Bianco D, La Rana G, Mercogliano D. The New Physics in LILITA_N21: An Improved Description of the Reaction 190 MeV 40Ar + 27Al. Applied Sciences. 2022; 12(9):4107. https://doi.org/10.3390/app12094107
Chicago/Turabian StyleDi Nitto, Antonio, Federico Davide, Emanuele Vardaci, Davide Bianco, Giovanni La Rana, and Daniela Mercogliano. 2022. "The New Physics in LILITA_N21: An Improved Description of the Reaction 190 MeV 40Ar + 27Al" Applied Sciences 12, no. 9: 4107. https://doi.org/10.3390/app12094107
APA StyleDi Nitto, A., Davide, F., Vardaci, E., Bianco, D., La Rana, G., & Mercogliano, D. (2022). The New Physics in LILITA_N21: An Improved Description of the Reaction 190 MeV 40Ar + 27Al. Applied Sciences, 12(9), 4107. https://doi.org/10.3390/app12094107







