Influence of Twist-Angle and Concentration Disorder on the Density of Electronic States of Twisted Graphene
Abstract
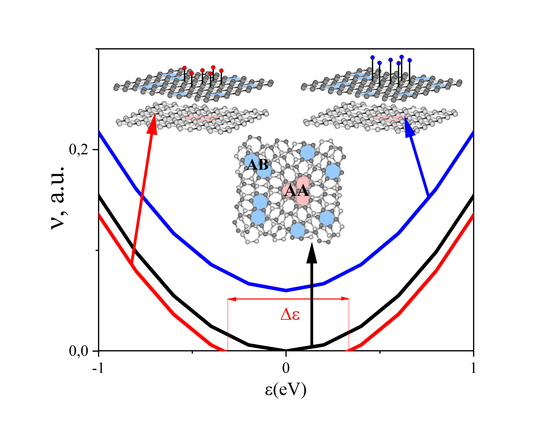
:1. Introduction
2. Calculation of the Density of Electronic States of Disordered tBLG in an External Field
3. Regularities of Variation in the DOS of Perfect and Disordered tBLG
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [Green Version]
- Garlow, J.A.; Barrett, L.K.; Wu, L.; Kisslinger, K.; Zhu, Y.; Pulecio, J.F. Large-Area Growth of Turbostratic Graphene on Ni(111) via Physical Vapor Deposition. Sci. Rep. 2016, 6, 19804. [Google Scholar] [CrossRef] [Green Version]
- Wollbrink, A.; Volgmann, K.; Koch, J.; Kanthasamy, K.; Tegenkamp, C.; Li, Y.; Richter, H.; Kamnitz, S.; Steinbach, F.; Feldhoff, A.; et al. Amorphous, turbostratic and crystalline carbon membranes with hydrogen selectivity. Carbon 2016, 106, 93–105. [Google Scholar] [CrossRef]
- Zhou, Z.; Bouwman, W.G.; Schut, H.; Pappas, C. Interpretation of X-ray diffraction patterns of (nuclear) graphite. Carbon 2014, 69, 17–24. [Google Scholar] [CrossRef]
- Kim, K.; Yankowitz, M.; Fallahazad, B.; Kang, S.; Movva, H.C.P.; Huang, S.; Larentis, S.; Corbet, C.M.; Taniguchi, T.; Watanabe, K.; et al. van der Waals Heterostructures with High Accuracy Rotational Alignment. Nano Lett. 2016, 16, 1989–1995. [Google Scholar] [CrossRef]
- Chen, X.-D.; Xin, W.; Jiang, W.-S.; Liu, Z.-B.; Chen, Y.; Tian, J.-G. High-Precision Twist-Controlled Bilayer and Trilayer Graphene. Adv. Mater. 2016, 28, 2563–2570. [Google Scholar] [CrossRef]
- Tan, Z.; Yin, J.; Chen, C.; Wang, H.; Lin, L.; Sun, L.; Wu, J.; Sun, X.; Yang, H.; Chen, Y.; et al. Building Large-Domain Twisted Bilayer Graphene with van Hove Singularity. ACS Nano 2016, 10, 6725–6730. [Google Scholar] [CrossRef]
- Kim, K.; DaSilva, A.; Huang, S.; Fallahazad, B.; Larentis, S.; Taniguchi, T.; Watanabe, K.; LeRoy, B.J.; MacDonald, A.H.; Tutuc, E. Tunable moiré bands and strong correlations in small-twist-angle bilayer graphene. Proc. Natl. Acad. Sci. USA 2017, 114, 3364–3369. [Google Scholar] [CrossRef] [Green Version]
- Brihuega, I.; Mallet, P.; Gonzalez-Herrero, H.; Trambly de Laissardiere, G.; Ugeda, M.M.; Magaud, L.; Gomez-Rodríguez, J.M.; Yndurain, F.; Veuillen, J.Y. Unraveling the Intrinsic and Robust Nature of van Hove Singularities in Twisted Bilayer Graphene by Scanning Tunneling Microscopy and Theoretical Analysis. Phys. Rev. Lett. 2012, 109, 196802. [Google Scholar] [CrossRef] [Green Version]
- Bistritzer, R.; MacDonald, A.H. Transport between twisted graphene layers. Phys. Rev. B 2010, 81, 245412. [Google Scholar] [CrossRef] [Green Version]
- Bistritzer, R.; MacDonald, A.H. Moiré bands in twisted double-layer graphene. Proc. Natl. Acad. Sci. USA 2011, 108, 12233–12237. [Google Scholar] [CrossRef] [Green Version]
- Trambly de Laissardiere, G.; Mayou, D.; Magaud, L. Numerical studies of confined states in rotated bilayers of graphene. Phys. Rev. B 2012, 86, 125413. [Google Scholar] [CrossRef] [Green Version]
- Luican, A.; Li, G.; Reina, A.; Kong, J.; Nair, R.R.; Novoselov, K.S.; Geim, A.K.; Andrei, E.Y. Single-Layer Behavior and Its Breakdown in Twisted Graphene Layers. Phys. Rev. Lett. 2011, 106, 126802. [Google Scholar] [CrossRef]
- Cao, Y.; Fatemi, V.; Demir, A.; Fang, S.; Tomarken, S.L.; Luo, J.Y.; Sanchez-Yamagishi, J.D.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 2018, 556, 80–84. [Google Scholar] [CrossRef]
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43–50. [Google Scholar] [CrossRef]
- Mogera, U.; Kulkarni, G.U. A new twist in graphene research: Twisted graphene. Carbon 2020, 156, 470–487. [Google Scholar] [CrossRef]
- Nimbalkar, A.; Kim, H. Opportunities and Challenges in Twisted Bilayer Graphene: A Review. Nano-Micro Lett. 2020, 12, 126. [Google Scholar] [CrossRef]
- Cress, C.D.; Schmucker, S.W.; Friedman, A.L.; Dev, P.; Culbertson, J.C.; Lyding, J.W.; Robinson, J.T. Nitrogen-Doped Graphene and Twisted Bilayer Graphene via Hyperthermal Ion Implantation with Depth Control. ACS Nano 2016, 10, 3714–3722. [Google Scholar] [CrossRef] [PubMed]
- Hong, S.J.; Park, M.; Kang, H.; Lee, M.; Soler-Delgado, D.; Jeong, D.H.; Park, Y.W.; Kim, B.H. Manipulation of electrical properties in CVD-grown twisted bilayer graphene induced by dissociative hydrogen adsorption. Curr. Appl. Phys. 2016, 16, 1637–1641. [Google Scholar] [CrossRef]
- Mahapatra, P.S.; Ghawri, B.; Garg, M.; Mandal, S.; Watanabe, K.; Taniguchi, T.; Jain, M.; Mukerjee, S.; Ghosh, A. Misorientation-Controlled Cross-Plane Thermoelectricity in Twisted Bilayer Graphene. Phys. Rev. Lett. 2020, 125, 226802. [Google Scholar] [CrossRef]
- Muniz, A.R.; Maroudas, D. Superlattices of Fluorinated Interlayer-Bonded Domains in Twisted Bilayer Graphene. J. Phys. Chem. C 2013, 117, 7315–7325. [Google Scholar] [CrossRef]
- Uchida, K.; Furuya, S.H.; Iwata, J.-I.; Oshiyama, A. Atomic corrugation and electron localization due to Moiré patterns in twisted bilayer graphenes. Phys. Rev. B 2014, 90, 155451. [Google Scholar] [CrossRef]
- Kulothungan, J.; Muruganathana, M.; Mizuta, H. Modulation of twisted bilayer CVD graphene interlayer resistivity by an order of magnitude based on in-situ annealing. Carbon 2019, 153, 355–363. [Google Scholar] [CrossRef] [Green Version]
- Schmucker, S.W.; Cress, C.D.; Culbertson, J.C.; Beeman, J.W.; Dubon, O.D.; Robinson, J.T. Raman signature of defected twisted bilayer graphene. Carbon 2015, 93, 250–257. [Google Scholar] [CrossRef] [Green Version]
- Dahal, H.P.; Balatsky, V.; Zhu, J.-X. Tuning impurity states in bilayer graphene. Phys. Rev. B 2008, 77, 115114. [Google Scholar] [CrossRef] [Green Version]
- Sahu, S.; Parashar, S.K.S.; Rout, G.C. Theoretical Study of Band Gap opening in AB- stacked Bi-layer Graphene by Impurity and Electric Field Effects. Mater. Today Proc. 2016, 3, 39–44. [Google Scholar] [CrossRef]
- Gupta, S.K.; Soni, H.R.; Jha, P.K. Electronic and phonon bandstructures of pristine few layer and metal doped graphene using first principles calculations. AIP Adv. 2013, 3, 032117. [Google Scholar] [CrossRef]
- Belosludtseva, A.; Barkalov, L.; Bobenko, N.; Melnikova, N. Concentration and configurational dependence of the short-range order parameter in two-layer graphene. AIP Conf. Proc. 2019, 2167, 020033. [Google Scholar] [CrossRef]
- Iveronova, V.I.; Katsnelson, A.A. Modern Problems of Short-Range Order. In Order-Disorder Transformations in Alloys; Warlimont, H., Ed.; Springer: Berlin, Germany, 1973; Volume 197, pp. 306–331. [Google Scholar]
- Bobenko, N.G.; Egorushkin, V.E.; Melnikova, N.V.; Ponomarev, A.N. Are carbon nanotubes with impurities and structure disorder metals or semiconductors? Phys. E 2014, 60, 11–16. [Google Scholar] [CrossRef]
- Rozhkov, A.V.; Sboychakov, A.O.; Rakhmanov, A.L.; Nori, F. Electronic properties of graphene-based bilayer systems. Phys. Rep. 2016, 648, 1–104. [Google Scholar] [CrossRef] [Green Version]
- Ulman, K.; Narasimhan, S. Point defects in twisted bilayer graphene: A density functional theory study. Phys. Rev. B 2014, 89, 245429. [Google Scholar] [CrossRef] [Green Version]
- Namarvar, O.F.; Missaoui, A.; Magaud, L.; Mayou, D.; Trambly de Laissardiere, G. Electronic structure and quantum transport in twisted bilayer graphene with resonant scatterers. Phys. Rev. B 2020, 101, 245407. [Google Scholar] [CrossRef]
- Yin, L.-J.; Qiao, J.-B.; Wang, W.-X.; Zuo, W.-J.; Yan, W.; Xu, R.; Dou, R.-F.; Nie, J.-C.; He, L. Landau quantization and Fermi velocity renormalization in twisted graphene bilayers. Phys. Rev. B 2015, 92, 201408(R). [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Liu, M.; Qiu, X. Scanning Probe Microscopy of Topological Structure Induced Electronic States of Graphene. Small Methods 2020, 4, 1900683. [Google Scholar] [CrossRef]
- Lu, C.-P.; Rodriguez-Vega, M.; Li, G.; Luican-Mayer, A.; Watanabe, K.; Taniguchi, T.; Rossi, E.; Andrei, E.Y. Local, global, and nonlinear screening in twisted double-layer graphene. Proc. Natl. Acad. Sci. USA 2016, 113, 6623–6628. [Google Scholar] [CrossRef] [Green Version]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bobenko, N.; Chumakov, Y.; Belosludtseva, A. Influence of Twist-Angle and Concentration Disorder on the Density of Electronic States of Twisted Graphene. Appl. Sci. 2022, 12, 4109. https://doi.org/10.3390/app12094109
Bobenko N, Chumakov Y, Belosludtseva A. Influence of Twist-Angle and Concentration Disorder on the Density of Electronic States of Twisted Graphene. Applied Sciences. 2022; 12(9):4109. https://doi.org/10.3390/app12094109
Chicago/Turabian StyleBobenko, Nadezhda, Yurii Chumakov, and Anna Belosludtseva. 2022. "Influence of Twist-Angle and Concentration Disorder on the Density of Electronic States of Twisted Graphene" Applied Sciences 12, no. 9: 4109. https://doi.org/10.3390/app12094109
APA StyleBobenko, N., Chumakov, Y., & Belosludtseva, A. (2022). Influence of Twist-Angle and Concentration Disorder on the Density of Electronic States of Twisted Graphene. Applied Sciences, 12(9), 4109. https://doi.org/10.3390/app12094109