Analysis of Negative Skin Friction on a Single Pile Based on the Effective Stress Method and the Finite Element Method
Abstract
:1. Introduction
2. Methods
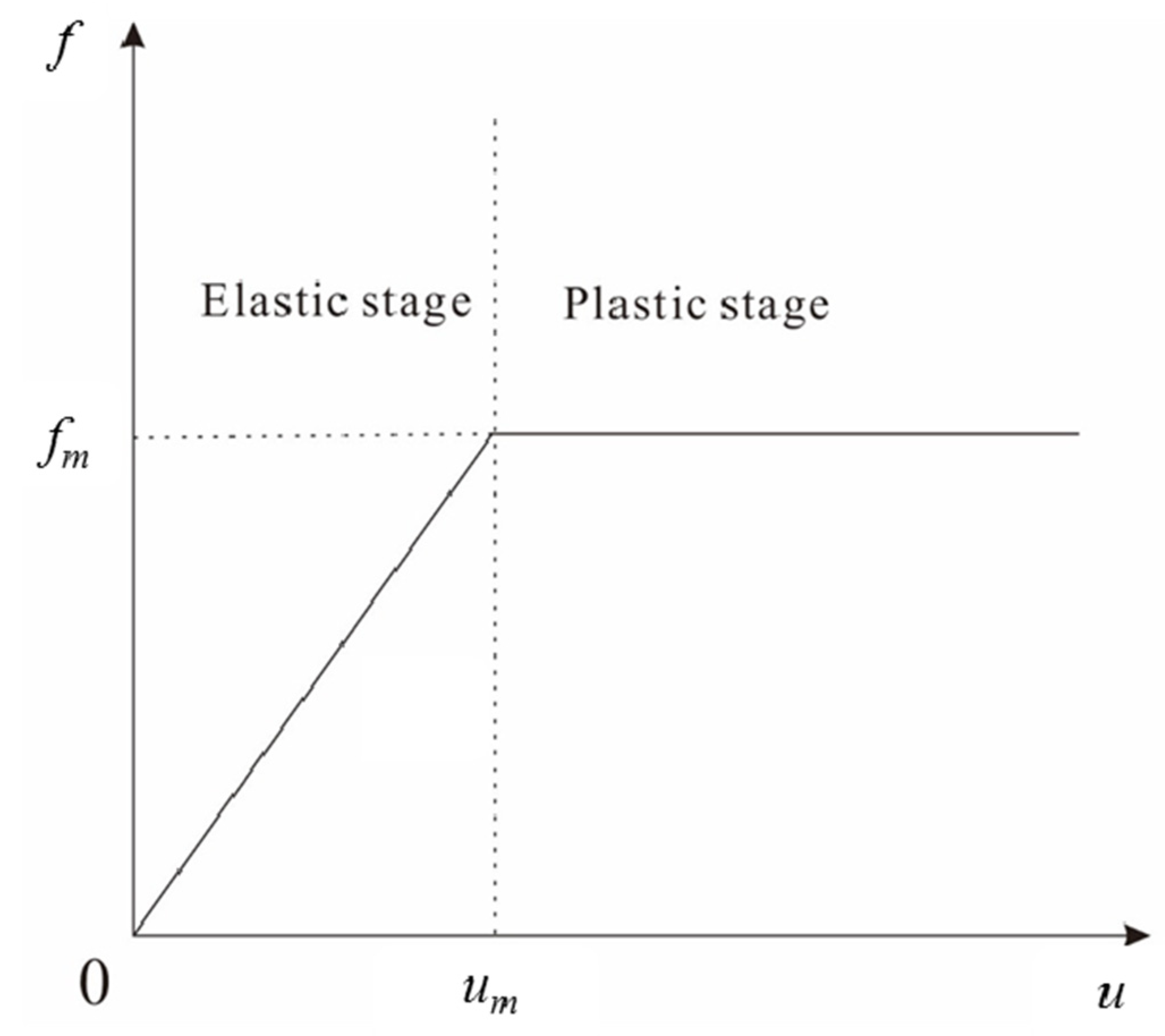
2.1. Effective Stress Method (ESM)
2.2. Parametric Analyses of NSF
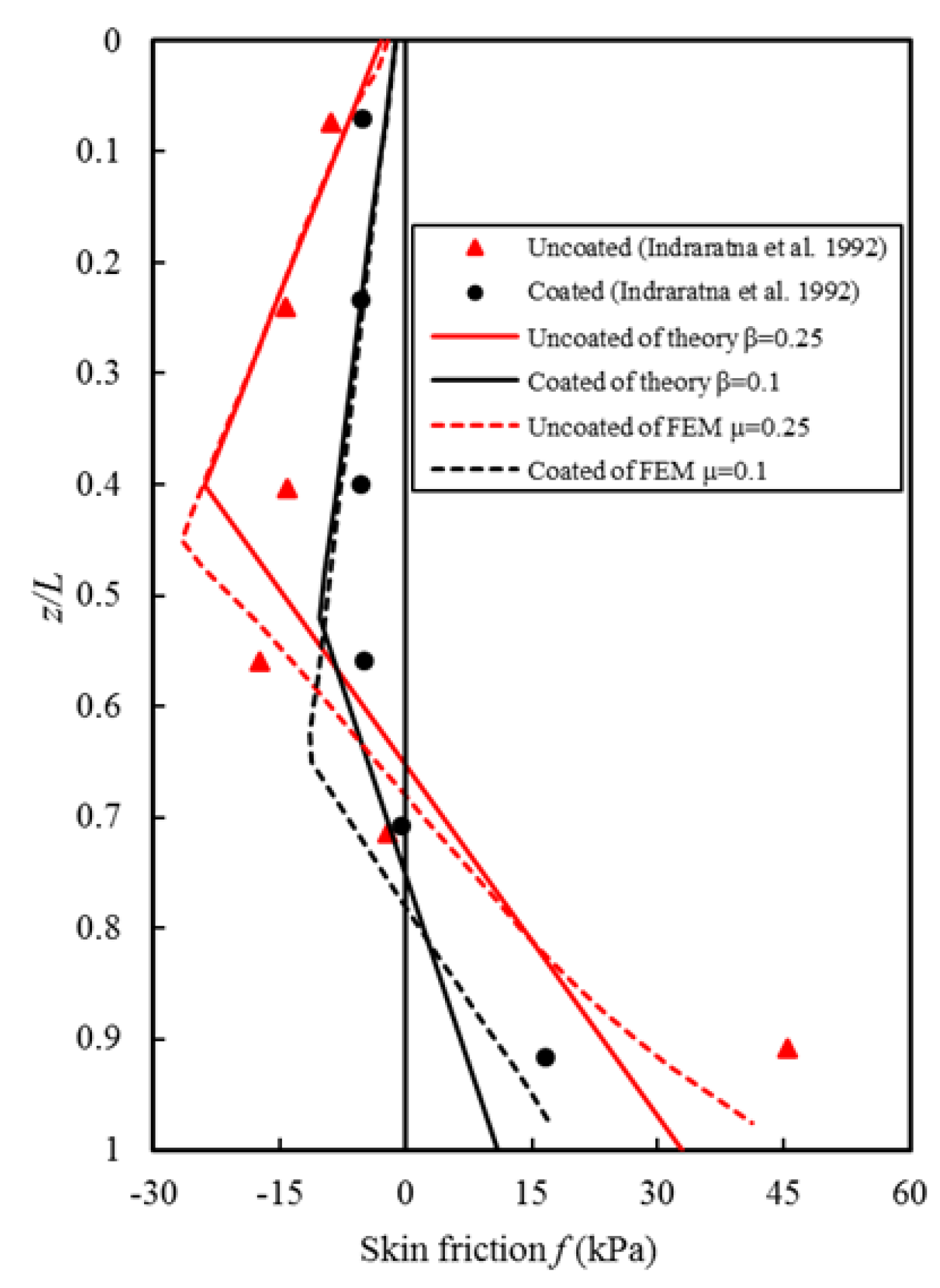
3. Results and Discussion
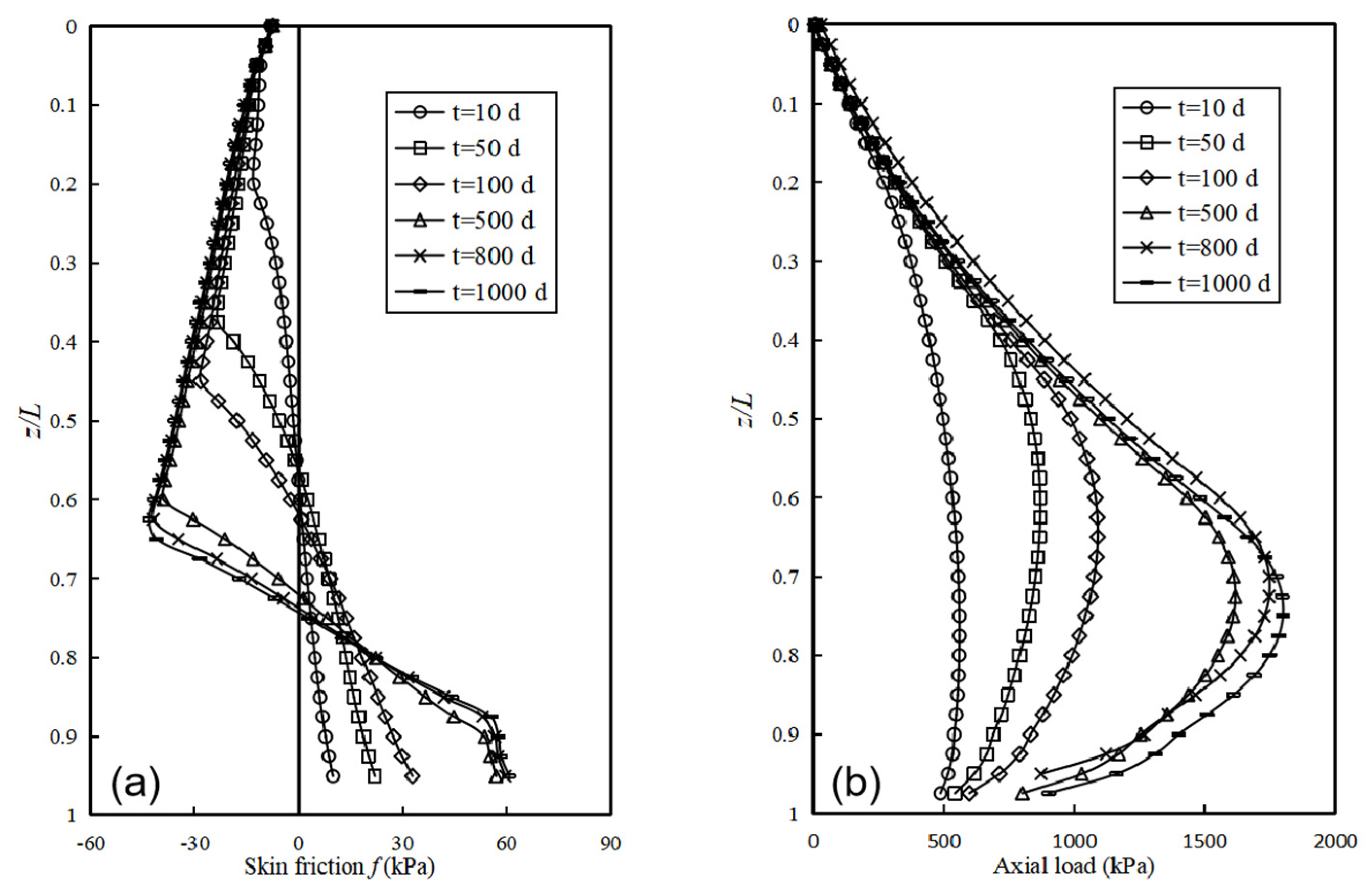
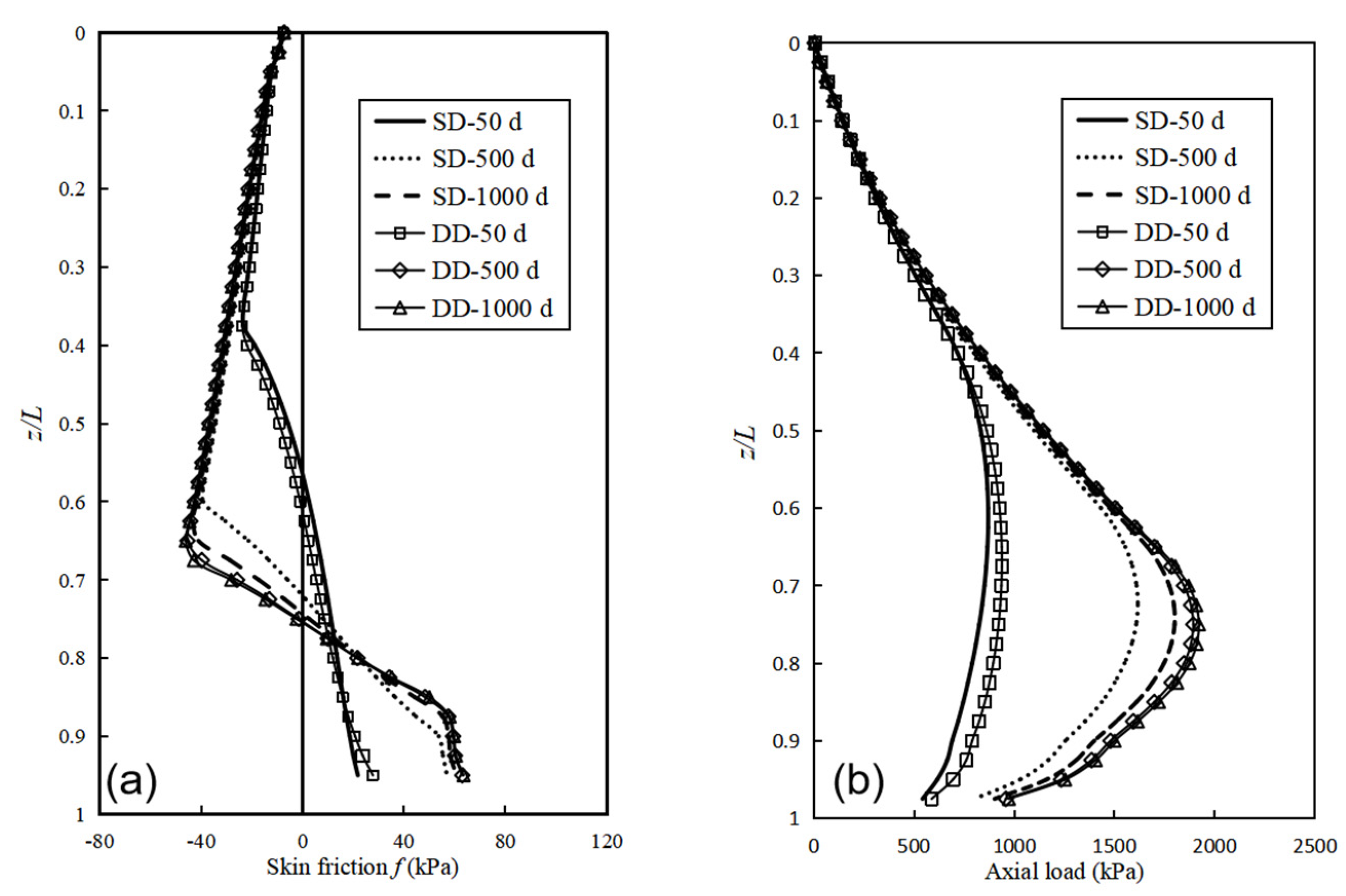
3.1. Effect of Consolidation Time
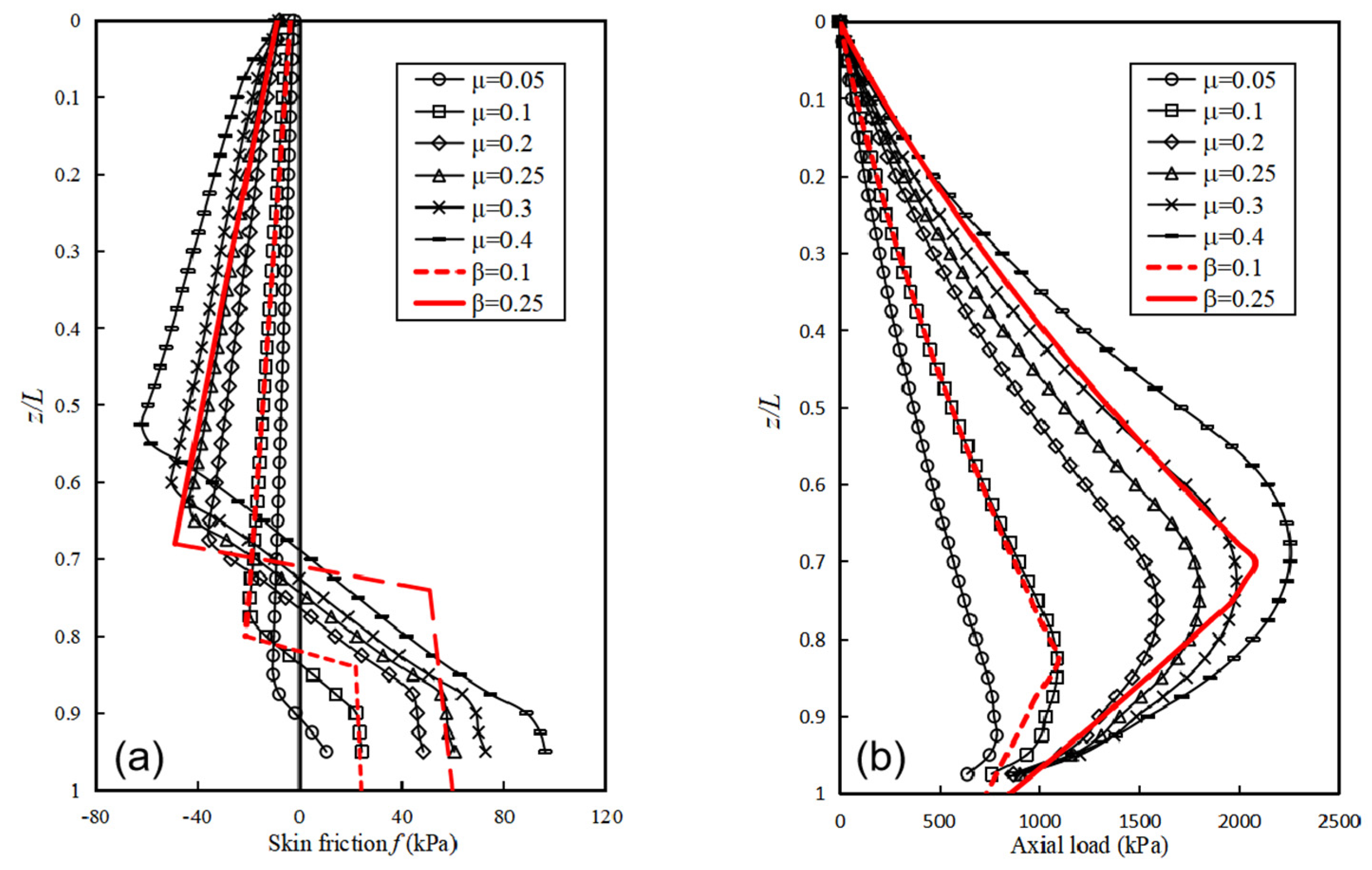
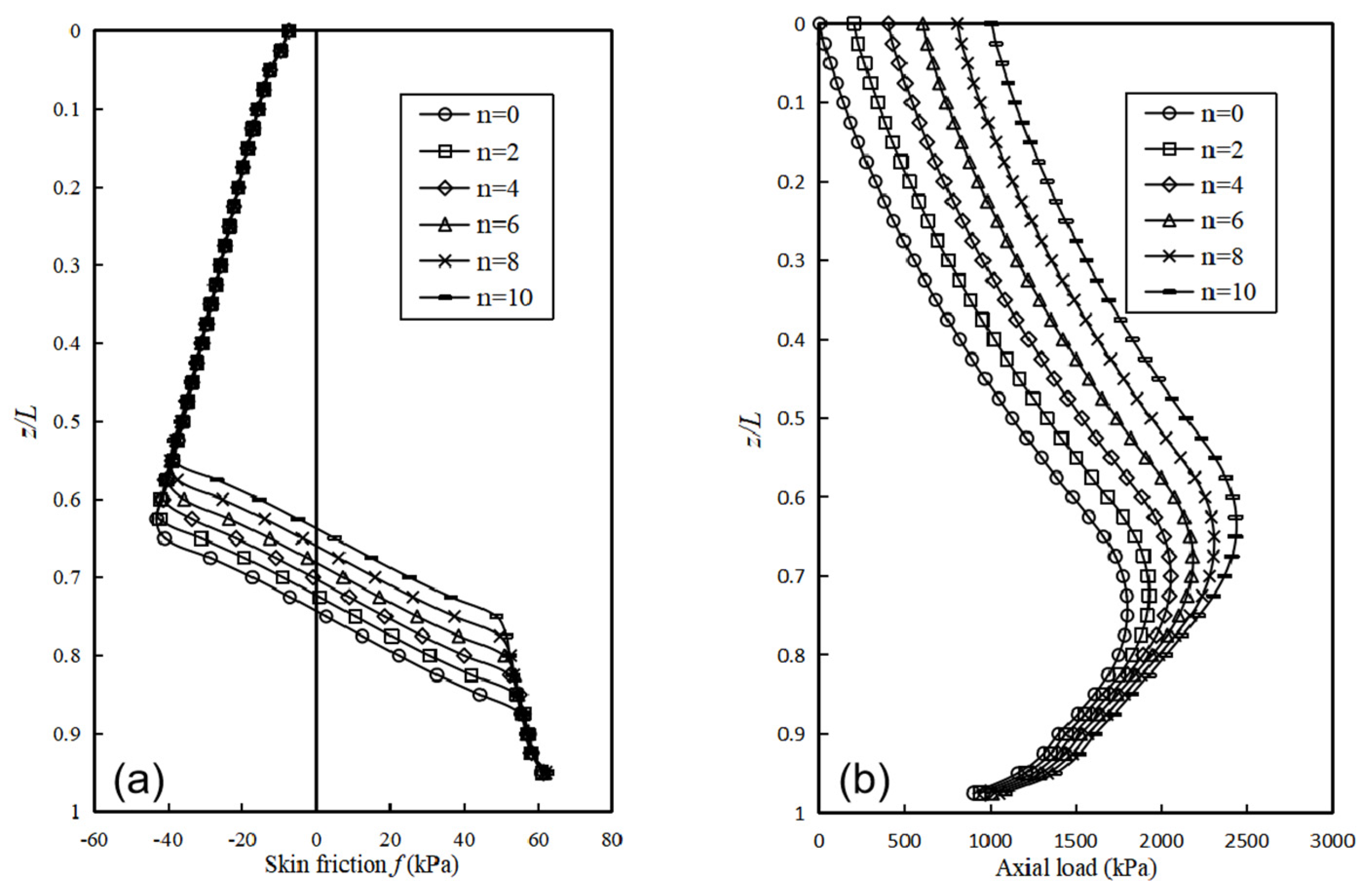
3.2. Effect of Friction Coefficient
3.3. Effect of Drainage Condition
3.4. Effect of Consolidation Pressure
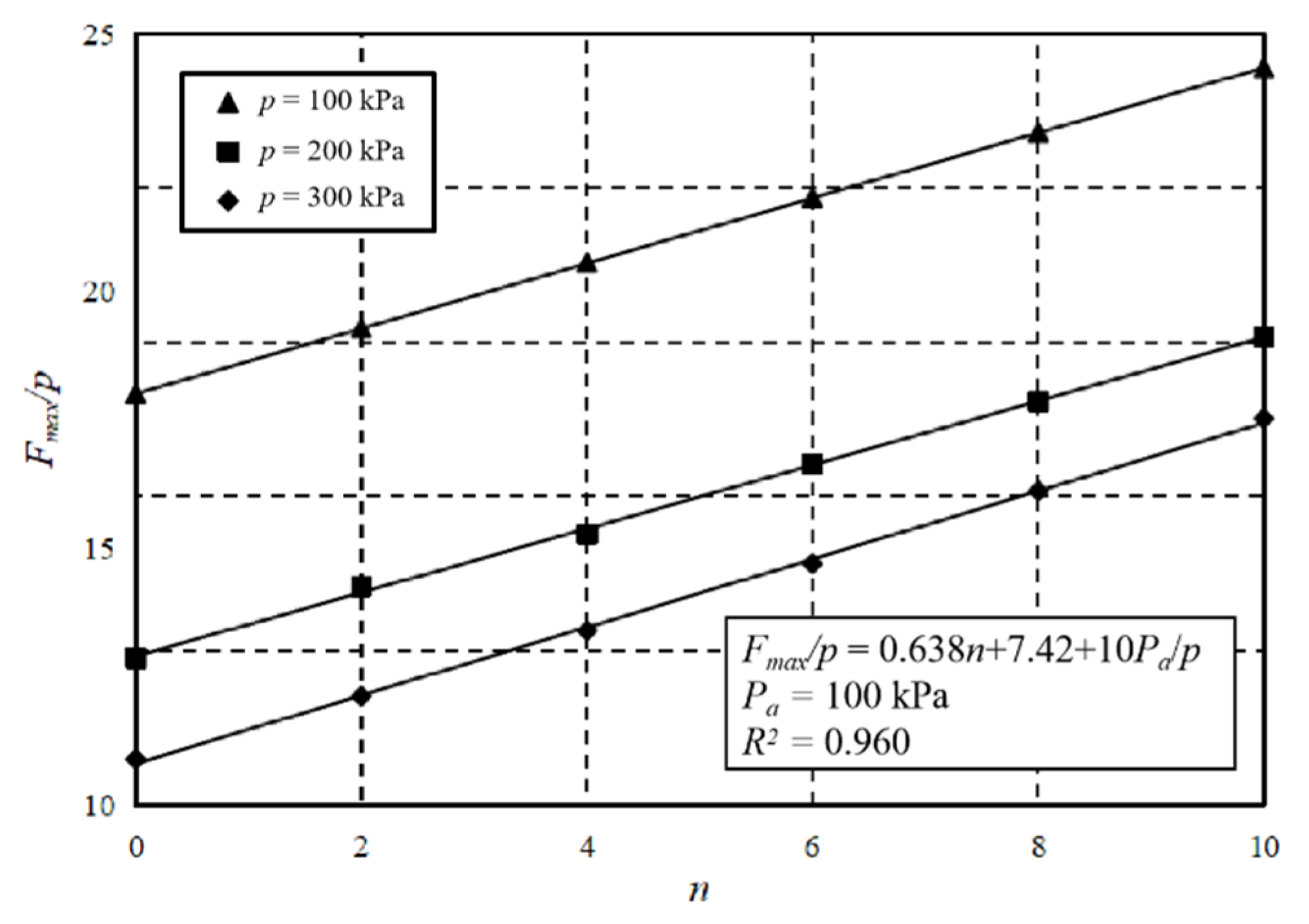
3.5. Effect of Pressure Ratio
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Madhav, M.R.; Sharma, J.; Sivakumar, V. Settlement of and load distribution in a granular piled raft. Gé;oméch. Eng. 2009, 1, 97–112. [Google Scholar] [CrossRef]
- Wu, Y.D.; Liu, J.; Chen, R. An analytical analysis of a single axially-loaded pile using a nonlinear softening model. Géoméch. Eng. 2015, 8, 769–781. [Google Scholar] [CrossRef]
- Ko, J.; Cho, J.; Jeong, S. Nonlinear 3D interactive analysis of superstructure and piled raft foundation. Eng. Struct. 2017, 143, 204–218. [Google Scholar] [CrossRef]
- Bakholdin, B.V.; Berman, V.I. Investigations of negative skin friction on piles and suggestions on its calculation. Soil Mech. Found. Eng. 1974, 11, 238–244. [Google Scholar] [CrossRef]
- Kim, K.D.; Plodpradit, P.; Kim, B.J.; Sinsabvarodom, C.; Kim, S. Interface behavior of grouted connection on monopile wind turbine offshore structure. Int. J. Steel Struct. 2014, 14, 439–446. [Google Scholar] [CrossRef]
- Zhao, M.H.; He, W.; Cao, W.G. Study on calculation of negative skin friction resistance on piles. Rock Soil Mech. 2004, 25, 1442–1446. [Google Scholar] [CrossRef]
- Chen, R.; Zhou, W.; Chen, Y. Influences of soil consolidation and pile load on the development of negative skin friction of a pile. Comput. Geotech. 2009, 36, 1265–1271. [Google Scholar] [CrossRef]
- Kim, H.J.; Mission, J.L.C. Negative skin friction on piles based on finite strain consolidation theory and the nonlinear load transfer method. KSCE J. Civ. Eng. 2009, 13, 107–115. [Google Scholar] [CrossRef]
- Wong, K.S.; Teh, C.I. Negative Skin Friction on Piles in Layered Soil Deposits. J. Geotech. Eng. 1995, 121, 457–465. [Google Scholar] [CrossRef]
- Chow, Y.K.; Chin, J.T.; Lee, S.L. Negative skin friction on pile groups. Int. J. Numer. Anal. Methods Géoméch. 1990, 14, 75–91. [Google Scholar] [CrossRef]
- Li, X.Y.; Bai, X.Y.; Zhang, M.Y. Study on bearing capacity characteristics of rock socketed short pile in weathered rock site. J. Eng. Res. 2019, 7, 76–89. [Google Scholar]
- Rajan, P.M.; Krishnamurthy, P. Termination Criteria of Bored Pile Subjected to Axial Loading. Indian Geotech. J. 2019, 49, 566–579. [Google Scholar] [CrossRef]
- Ai, Z.Y.; Chen, Y.F. FEM-BEM coupling analysis of vertically loaded rock-socketed pile in multilayered transversely isotropic saturated media. Comput. Geotech. 2020, 120, 103437. [Google Scholar] [CrossRef]
- Liu, J.; Gao, H.; Liu, H. Finite element analyses of negative skin friction on a single pile. Acta Geotech. 2012, 7, 239–252. [Google Scholar] [CrossRef]
- Indraratna, B.; Balasubramaniam, A.S.; Phamvan, P.; Wong, Y.K. Development of negative skin friction on driven piles in soft Bangkok clay. Can. Geotech. J. 1992, 29, 393–404. [Google Scholar] [CrossRef]
- Xing, H.; Liu, L. Field Tests on Influencing Factors of Negative Skin Friction for Pile Foundations in Collapsible Loess Regions. Int. J. Civ. Eng. 2018, 16, 1413–1422. [Google Scholar] [CrossRef]
- Lv, Y.; Liu, H.; Ding, X.; Kong, G. Field Tests on Bearing Characteristics of X-Section Pile Composite Foundation. J. Perform. Constr. Facil. 2012, 26, 180–189. [Google Scholar] [CrossRef]
- Yan, W.M.; Sun, T.K.; Tham, L.G. Coupled-Consolidation Modeling of a Pile in Consolidating Ground. J. Geotech. Geoenvironmental Eng. 2012, 138, 789–798. [Google Scholar] [CrossRef]
- Yao, W.; Liu, Y.; Chen, J. Characteristics of Negative Skin Friction for Superlong Piles under Surcharge Loading. Int. J. Géoméch. 2012, 12, 90–97. [Google Scholar] [CrossRef]
- Lam, S.Y.; Ng, C.W.W.; Poulos, H.G. Shielding Piles from Downdrag in Consolidating Ground. J. Geotech. Geoenviron. Eng. 2013, 139, 956–968. [Google Scholar] [CrossRef]
- Cao, W.; Chen, Y.; Wolfe, W.E. New Load Transfer Hyperbolic Model for Pile-Soil Interface and Negative Skin Friction on Single Piles Embedded in Soft Soils. Int. J. Géoméch. 2014, 14, 92–100. [Google Scholar] [CrossRef]
- Ma, L.; Wang, Y.K. Calculation and analysis of negative skin of monopile applied for offshore wind turbine. Mar. Georesources Geotechnol. 2015, 35, 275–280. [Google Scholar] [CrossRef]
- Haigh, S.K.; Madabhushi, S.G. Centrifuge modelling of pile-soil interaction in liquefiable slopes. Géoméch. Eng. 2011, 3, 1–16. [Google Scholar] [CrossRef]
- Muhammed, R.D.; Canou, J.; Dupla, J.-C.; Tabbagh, A. Laboratory Study of Local Clay-Pile Friction Evolution for Large Numbers of Cycles. In Lecture Notes in Civil Engineering; Springer: Singapore, 2018; Volume 8, pp. 746–755. [Google Scholar] [CrossRef]
- Johannessen, I.J.; Bjerrum, L. Measurements of the compression of a steel pile to rock due to settlement of the surrounding clay. In Proceedings of the 6th International Conference on Soil Mechanics and Foundation Engineering, Montreal, QC, Canada, 8–15 September 1965; pp. 261–264. [Google Scholar] [CrossRef] [Green Version]
- Hanna, A.M.; Sharif, A. Drag Force on Single Piles in Clay Subjected to Surcharge Loading. Int. J. Géoméch. 2006, 6, 89–96. [Google Scholar] [CrossRef]
- Comodromos, E.; Bareka, S.V. Evaluation of negative skin friction effects in pile foundations using 3D nonlinear analysis. Comput. Geotech. 2005, 32, 210–221. [Google Scholar] [CrossRef]





| Soil | β |
|---|---|
| Clay | 0.2–0.25 |
| Silty soil | 0.25–0.35 |
| Sand | 0.35–0.5 |
| Depth (m) | Weight (kN/m3) | Elastic Modulus (MPa) | Poisson’s Ratio | Cohesion (kPa) | Friction Angle (°) | Coefficient of Permeability (×10−10 m/s) |
|---|---|---|---|---|---|---|
| 0–4 | 18 | 5 | 0.2 | 3 | 26 | 78.2 |
| 4–10 | 18 | 5 | 0.2 | 6 | 25 | 6.37 |
| 10–20 | 18 | 5 | 0.2 | 15 | 25 | 3.04 |
| 20– | 18 | 6.5 | 0.2 | 6 | 23 | 4.31 |
| Length (m) | Diameter (m) | Weight (kN/m3) | Elastic Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|---|
| 25 | 0.4 | 20 | 30,000 | 0.33 |
| Component | Properties | Value |
|---|---|---|
| Pile | Length (m) | 20 |
| Diameter (m) | 1 | |
| Weight (kN/m3) | 18 | |
| Elastic modulus (MPa) | 30,000 | |
| Poisson’s ratio | 0.15 | |
| Consolidating layer | Weight (kN/m3) | 18 |
| Poisson’s ratio | 0.3 | |
| Elastic modulus (MPa) | 5 | |
| Cohesion (kPa) | 5 | |
| Friction angle (°) | 20 | |
| Void ratio | 1 | |
| Coefficient of permeability (×10−4 m/d) | 6.8 | |
| Bearing layer | Weight (kN/m3) | 18 |
| Poisson’s ratio | 0.3 | |
| Elastic modulus (MPa) | 30 | |
| Cohesion (kPa) | 5 | |
| Friction angle (°) | 30 | |
| Void ratio | 1 | |
| Coefficient of permeability (×10−4 m/d) | 6.8 | |
| Interface | Elastic critical value of relative settlement of pile soil (mm) | 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Ren, Y.; Liu, J.; Ma, L. Analysis of Negative Skin Friction on a Single Pile Based on the Effective Stress Method and the Finite Element Method. Appl. Sci. 2022, 12, 4125. https://doi.org/10.3390/app12094125
Wu Y, Ren Y, Liu J, Ma L. Analysis of Negative Skin Friction on a Single Pile Based on the Effective Stress Method and the Finite Element Method. Applied Sciences. 2022; 12(9):4125. https://doi.org/10.3390/app12094125
Chicago/Turabian StyleWu, Yuedong, Yuzhe Ren, Jian Liu, and Lu Ma. 2022. "Analysis of Negative Skin Friction on a Single Pile Based on the Effective Stress Method and the Finite Element Method" Applied Sciences 12, no. 9: 4125. https://doi.org/10.3390/app12094125
APA StyleWu, Y., Ren, Y., Liu, J., & Ma, L. (2022). Analysis of Negative Skin Friction on a Single Pile Based on the Effective Stress Method and the Finite Element Method. Applied Sciences, 12(9), 4125. https://doi.org/10.3390/app12094125







