Hierarchy Establishment from Nonlinear Social Interactions and Metabolic Costs: An Application to Harpegnathos saltator
Abstract
:1. Introduction
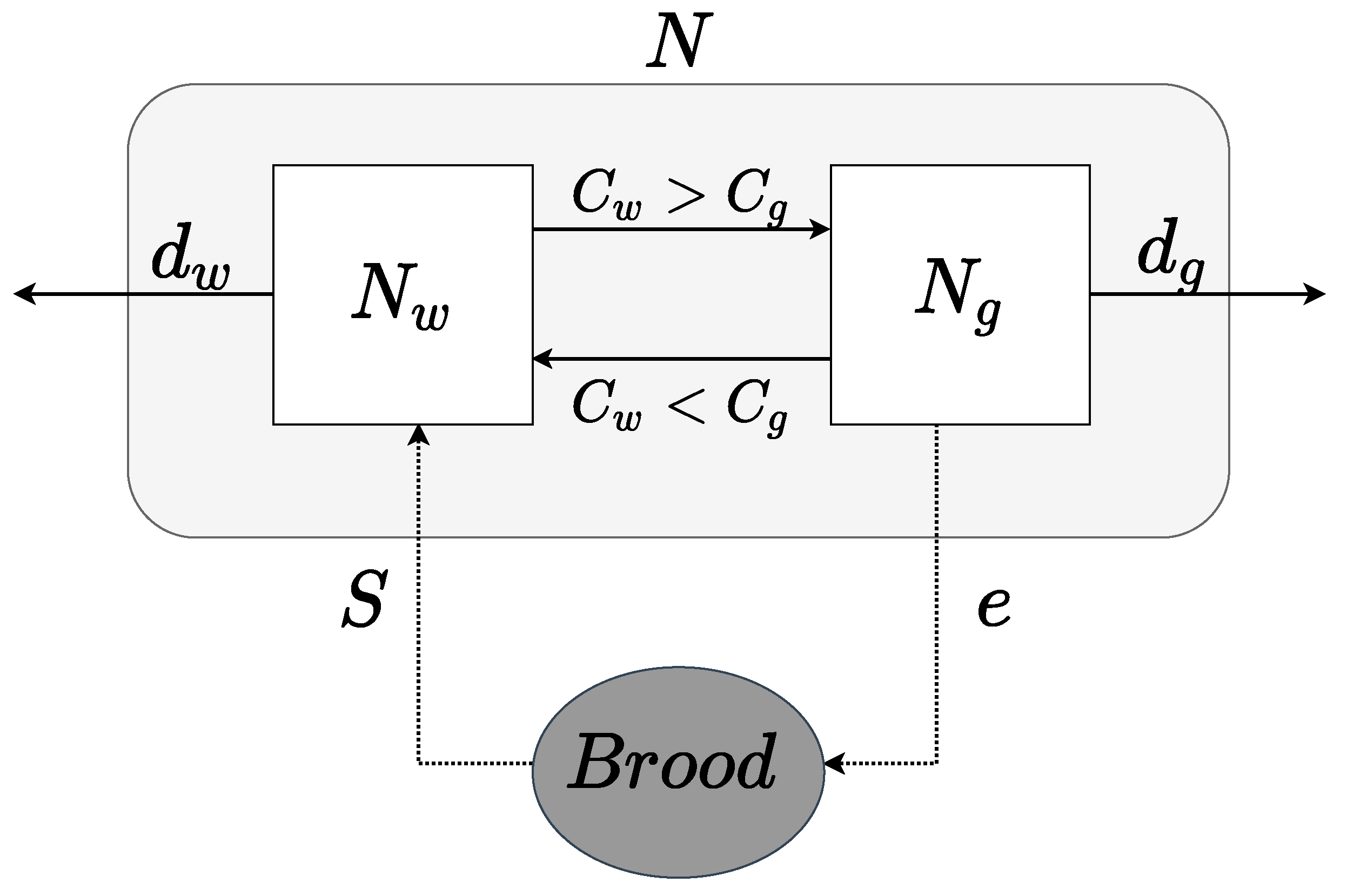
2. Model Formulation
- (a)
- Modeling Relative Cost: Assuming that gamergates are the only members of the colony who actively reproduce, the cost for all gamergates of remaining in their status in the colony is measured by (Kcal) which consists of the energy cost of laying eggs as well as the energy to perform behaviors that maintain the social hierarchy such as antennal dueling and dominance behaviors. According to the ecological metabolism theory, the formulation of is modeled bywhere is a normalization constant (measured in microwatts per gram μW/gr). This coefficient corresponds to the variation in metabolic rates across gamergates in the group. Then, is a scaling exponent, which describes how fast the cost/metabolic rate changes with respect to the biomass of the group of gamergates [34]. If , then the metabolic rate of the group grows slower than the biomass. Instead, if the metabolic rate of the group grows faster than the biomass. From the literature, the values of for social insects (e.g., ants) should be in the range 0–1.75 [20,35]. Adopting a similar modeling approach for the non-reproductive worker population, the cost of all non-reproductive workers to maintain their status in the colony is , given bywhich includes the energy cost of providing resources for the whole colony, such as brood care, foraging, etc. We assume that is proportional to the total colony size N as the non-reproductive workers take care of the whole colony (and not just themselves, unlike gamergates). Based on their faster relative speed [32], non-reproductive workers most likely have a higher metabolic cost compared to gamergates [27], i.e., . Therefore, the relative cost for gamergates is defined byApplying the similar arguments to non-reproductive workers , their relative cost is defined asNote that
- (b)
- Colony Size N: Let e be the average number of eggs produced per gamergate, then the total number of eggs produced at time t would be . The survival of eggs is directly linked to the care provided by the number of non-reproductive workers [32]. Thus, we assume that the survival rate of eggs is proportional to the relative cost of the worker class . Therefore, the input of new members is obtained as followsWe assume that the colony has a density-dependent mortality rate due to limited resources, given bywhere and represent the mortality rate of workers and gamergates, respectively. Therefore, the colony size is modeled as follows
- (c)
- Gamergates and Workers : We adopt the concept of [15] to model that a non-reproductive worker would leave its worker status and enter into the gamergate phase when the worker’s relative cost is higher than the gamergate’s relative cost , and vice versa [15,32]. Since it has been shown that gamergates can revert to worker status [31] and non-reproductive workers can become gamergates [33], we assume that an ant can interchange between a gamergate and non-reproductive worker status based on the relative cost of remaining in a particular group. This relative cost derives from metabolic costs and is also related to its contribution to colony function. Thus, the population dynamics of gamergates is modeled as followsTo model the non-reproductive workers’ population dynamics, we assume that all newborns are in the non-reproductive worker status first, with the possibility of transitioning into the status of gamergates. We apply a similar approach as above so that the population dynamics of non-reproductive workers is given by
- What are the key life-history parameters that determine the dynamics of the different classes in the colony ?
- How do the metabolic parameters, such as , and the exponent parameters affect the colony size, N, and the size of the reproductive class ?
- How do the colony size, N, and the number of established gamergates, , regulate each other?
3. Mathematical Analysis
- 1.
- If , then there exists such that and has a unique solution in and no solution in .
- 2.
- If , has a unique solution in and no solution in .
- 3.
- If , then there exists such that and has no solution in . In , we have the following statements:
- (a)
- If , has at least one positive solution.
- (b)
- If , has no positive solution provided that is small enough.
- (c)
- If , has at least one positive solution provided that , while no positive solution provided that is small enough.
- The values of and are determined by the average reproduction ability of gamergate e and the average mortality of gamergates and workers, which provide an upper bound for the reproductive ratio.
- Note that can be rewritten asprovided that . Due tois increasing as increases. If , we also have that is increasing as increases. One potential biological meaning of this result is that when the mortality of the non-reproductive workers is sufficiently close but larger than that of the gamergates, increasing the mortality of the non-reproductive workers would cause a higher proportion of gamergates in the colony since they would reproduce more to make up for the loss of non-reproductive workers.
- Note that can be rewritten aswhich suggests that the value of the upper bound decreases when the value of increases. Thus, this provides a potential smaller value of due toOne potential biological meaning of this result is that when the mortality of non-reproductive workers is much larger than that of the gamergates, decreasing the mortality of gamergates would result in a smaller proportion of gamergates as they would reproduce more during its life time.
4. Model Validations and Simulations
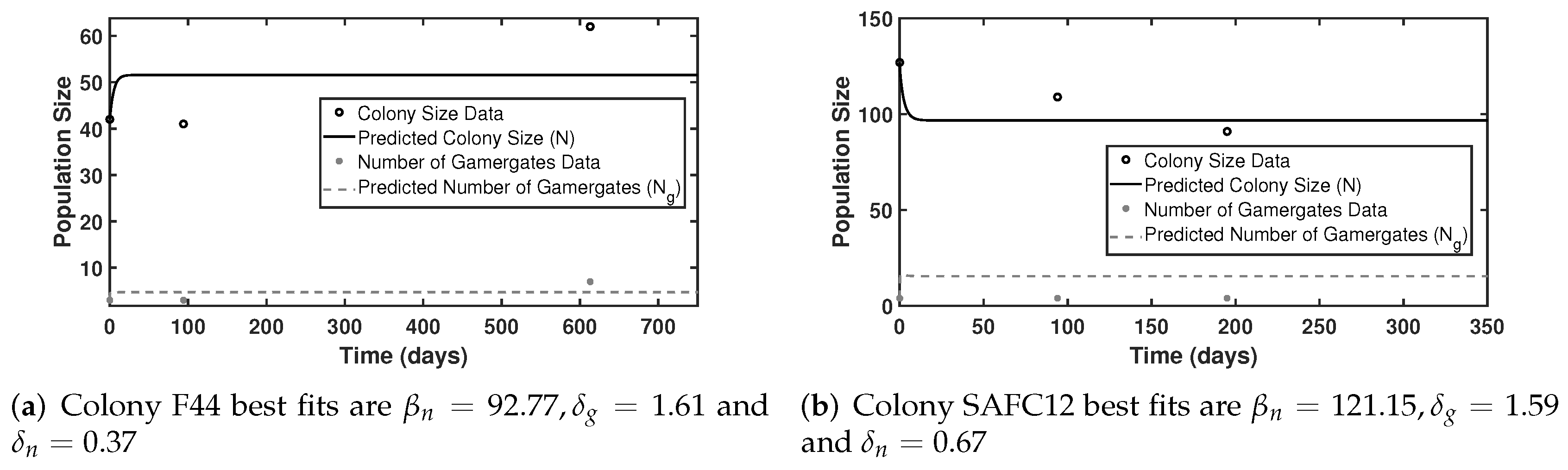
4.1. Data and Parameter Estimations
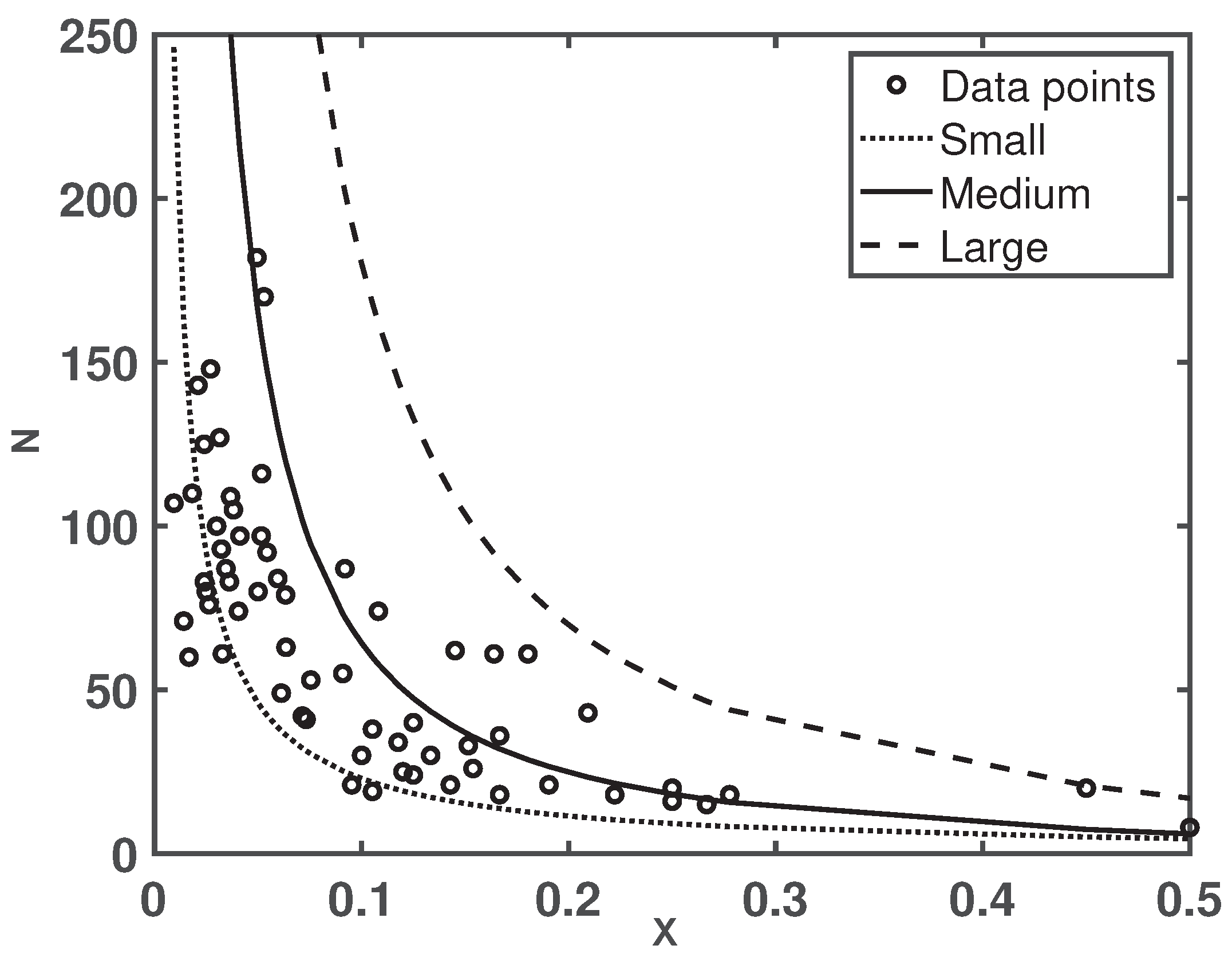
4.2. Simulations and Bifurcations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Mathematical Proofs
Appendix A.1. Proof of Theorem 1
- . Let , thenSolving the above differential equation gives
- , thenSolving the above differential equation gives
- . Let , thenSolving the above differential equation gives
Appendix A.2. Proof of Theorem 2
- , is increasing in the both intervals of and , and for and for ;
- .
- , , is increasing in the both intervals of and , and for and for ;
- .
- When , we can get , and henceNotice that , and is increasing from zero to infinity in , we can conclude that has at least one positive solution in .
- When , we can get . Due toand is increasing in , there exists such thatLetThen, if is large such that , we haveNotice that . Thus, if is small enough, then , and hence has no solution in .
- When , we have . Since is increasing in from zero to infinity while is increasing in from zero to infinity, we can get that has at least one positive solution in if , i.e., . If , then similar to the arguments for case , we can prove that has no solution in if is small enough.
References
- Fewell, J.H.; Harrison, J.F. Scaling of work and energy use in social insect colonies. Behav. Ecol. Sociobiol. 2016, 70, 1047–1061. [Google Scholar] [CrossRef]
- Sidanius, J.; Pratto, F. Social Dominance: An Intergroup Theory of Social Hierarchy and Oppression; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar] [CrossRef]
- Chase, I.D.; Tovey, C.; Spangler-Martin, D.; Manfredonia, M. Individual differences versus social dynamics in the formation of animal dominance hierarchies. Proc. Natl. Acad. Sci. USA 2002, 99, 5744–5749. [Google Scholar] [CrossRef] [Green Version]
- Broom, M. A unified model of dominance hierarchy formation and maintenance. J. Theor. Biol. 2002, 219, 63–72. [Google Scholar] [CrossRef]
- Hickey, J.; Davidsen, J. Self-organization and time-stability of social hierarchies. PLoS ONE 2019, 14, e0211403. [Google Scholar] [CrossRef] [Green Version]
- Chase, I.D.; Seitz, K. Self-Structuring Properties of Dominance Hierarchies: A New Perspective. Adv. Genet. 2011, 75, 51. [Google Scholar]
- Sasaki, T.; Penick, C.A.; Shaffer, Z.; Haight, K.L.; Pratt, S.C.; Liebig, J.; van Doorn, G.S.; Bronstein, J.L. A Simple Behavioral Model Predicts the Emergence of Complex Animal Hierarchies. Am. Nat. 2016, 187, 765–775. [Google Scholar] [CrossRef] [Green Version]
- Uhrich, J. The social hierarchy in albino mice. J. Comp. Psychol. 1938, 25, 373–413. [Google Scholar] [CrossRef]
- Kinsey, K.P. Social behaviour in confined populations of the Allegheny woodrat, Neotoma floridana magister. Anim. Behav. 1976, 24, 181–187. [Google Scholar] [CrossRef]
- Deslippe, R.J.; M’Closkey, R.T.; Dajczak, S.P.; Szpak, C.P. A quantitative study of the social behavior of tree lizards, Urosaurus ornatus. J. Herpetol. 1990, 24, 337–341. [Google Scholar] [CrossRef]
- Harcourt, A.H.; De Waal, F.B.M. (Eds.) Coalitions and Alliances in Humans and Other Animals; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Reeve, H.K.; Keller, L. Tests of reproductive-skew models in social insects. Annu. Rev. Entomol. 2001, 46, 347–385. [Google Scholar] [CrossRef] [Green Version]
- Peeters, C.; Hölldobler, B. Reproductive cooperation between queens and their mated workers: The complex life history of an ant with a valuable nest. Proc. Natl. Acad. Sci. USA 1995, 92, 10977–10979. [Google Scholar] [CrossRef] [Green Version]
- Peelers, C.; Crozier, R.H. Caste and reproduction in ants: Not all mated egg-layers are “queens”. Psyche 1988, 95, 283–288. [Google Scholar] [CrossRef] [Green Version]
- Monnin, T.; Ratnieks, F.L. Reproduction versus work in queenless ants: When to join a hierarchy of hopeful reproductives? Behav. Ecol. Sociobiol. 1999, 46, 413–422. [Google Scholar] [CrossRef]
- Cant, M.A.; Field, J. Helping effort in a dominance hierarchy. Behav. Ecol. 2005, 16, 708–715. [Google Scholar] [CrossRef]
- Broom, M.; Cannings, C. Modelling dominance hierarchy formation as a multi-player game. J. Theor. Biol. 2002, 219, 397–413. [Google Scholar] [CrossRef]
- Beaugrand, J.P. Relative importance of initial individual differences, agonistic experience, and assessment accuracy during hierarchy formation: A simulation study. Behav. Process. 1997, 41, 177–192. [Google Scholar] [CrossRef]
- Jaffe, K. Quantifying social synergy in insect and human societies. Behav. Ecol. Sociobiol. 2010, 64, 1721–1724. [Google Scholar] [CrossRef]
- Waters, J.S.; Holbrook, C.T.; Fewell, J.H.; Harrison, J.F. Allometric scaling of metabolism, growth, and activity in whole colonies of the seed-harvester ant Pogonomyrmex californicus. Am. Nat. 2010, 176, 501–510. [Google Scholar] [CrossRef]
- Shik, J.Z.; Hou, C.; Kay, A.; Kaspari, M.; Gillooly, J.F. Towards a general life-history model of the superorganism: Predicting the survival, growth and reproduction of ant societies. Biol. Lett. 2012, 8, 1059–1062. [Google Scholar] [CrossRef]
- Dial, K.P.; Greene, E.; Irschick, D.J. Allometry of behavior. Trends Ecol. Evol. 2008, 23, 394–401. [Google Scholar] [CrossRef]
- Shik, J. Ant colony size and the scaling of reproductive effort. Funct. Ecol. 2008, 22, 674–681. [Google Scholar] [CrossRef]
- Cao, T.; Dornhaus, A. Larger laboratory colonies consume proportionally less energy and have lower per capita brood production in Temnothorax ants. Insectes Sociaux 2013, 60, 1–5. [Google Scholar] [CrossRef]
- Cole, B.; Wiernasz, D. Colony size and reproduction in the western harvester ant, Pogonomyrmex occidentalis. Insectes Sociaux 2000, 47, 249–255. [Google Scholar] [CrossRef]
- Penick, C.A.; Prager, S.S.; Liebig, J. Juvenile hormone induces queen development in late-stage larvae of the ant Harpegnathos saltator. J. Insect Physiol. 2012, 58, 1643–1649. [Google Scholar] [CrossRef]
- Ghaninia, M.; Haight, K.; Berger, S.L.; Reinberg, D.; Zwiebel, L.J.; Ray, A.; Liebig, J. Chemosensory sensitivity reflects reproductive status in the ant Harpegnathos saltator. Sci. Rep. 2017, 7, 3732. [Google Scholar] [CrossRef]
- Peeters, C.; Liebig, J.; Hölldobler, B. Sexual reproduction by both queens and workers in the ponerine ant Harpegnathos saltator. Insectes Sociaux 2000, 47, 325–332. [Google Scholar] [CrossRef]
- Liebig, J.; Poethke, H.J. Queen lifespan and colony longevity in the ant Harpegnathos saltator. Ecol. Entomol. 2004, 29, 203–207. [Google Scholar] [CrossRef]
- Mayoral, A. Analysis of Egg-Laying Rates of Harpegnathos saltator through Different Methods of Observation. Ph.D. Thesis, Arizona State University, Tempe, AZ, USA, 2017. [Google Scholar]
- Penick, C.A.; Ghaninia, M.; Haight, K.L.; Opachaloemphan, C.; Yan, H.; Reinberg, D.; Liebig, J. Reversible plasticity in brain size, behaviour and physiology characterizes caste transitions in a socially flexible ant (Harpegnathos saltator). Proc. R. Soc. B 2021, 288, 20210141. [Google Scholar] [CrossRef]
- Liebig, J. Eusociality, Female Caste Specialization, and Regulation of Reproduction in the Ponerine ant Harpegnathos Saltator Jerdon; Wiss.-und-Technik: Berlin, Germany, 1998. [Google Scholar]
- Liebig, J.; Hölldobler, B.; Peeters, C. Are ant workers capable of colony foundation? Naturwissenschaften 1998, 85, 133–135. [Google Scholar] [CrossRef]
- Waters, J.S.; Ochs, A.; Fewell, J.H.; Harrison, J.F. Differentiating causality and correlation in allometric scaling: Ant colony size drives metabolic hypometry. Proc. Biol. Sci. 2017, 284, 20162582. [Google Scholar] [CrossRef] [Green Version]
- Chown, S.; Marais, E.; Terblanche, J.; Klok, C.; Lighton, J.; Blackburn, T. Scaling of insect metabolic rate is inconsistent with the nutrient supply network model. Funct. Ecol. 2007, 21, 282–290. [Google Scholar] [CrossRef]
- Bourke, A.F. Worker reproduction in the higher eusocial Hymenoptera. Q. Rev. Biol. 1988, 63, 291–311. [Google Scholar]
- Franks, N.R.; Ireland, B.; Bourke, A.F. Conflicts, social economics and life history strategies in ants. Behav. Ecol. Sociobiol. 1990, 27, 175–181. [Google Scholar] [CrossRef]
- Stephens, D.W.; Krebs, J.R. Foraging Theory; Princeton University Press: Princeton, NJ, USA, 1986. [Google Scholar]
- Poethke, H.J.; Liebig, J. Risk-sensitive foraging and the evolution of cooperative breeding and reproductive skew. BMC Ecol. 2008, 8, 2. [Google Scholar] [CrossRef] [Green Version]
- Liebig, J.; Peeters, C.; Hölldobler, B. Worker policing limits the number of reproductives in a ponerine ant. Proc. R. Soc. Lond. Biol. Sci. 1999, 266, 1865–1870. [Google Scholar] [CrossRef]
- Hölldobler, B.; Wilson, E.O. The Superorganism: The Beauty, Elegance, and Strangeness of Insect Societies; WW Norton & Company: New York, NY, USA, 2009. [Google Scholar]


| Parameter | Description | Best Estimation | Range | Units | Reference |
|---|---|---|---|---|---|
| e | Egg-laying rate | 2.42 | eggs/day | Estimated | |
| Natural death rate of gamergates | 0.00028 | [27] | |||
| Natural death rate of workers | 0.0025 | [27] | |||
| Normalized metabolic rates for gamergates | 33.00 | Assumed | |||
| Normalized metabolic rates for workers | 74.60 | Assumed | |||
| Hypometric relation factor of gamergates | 0.99 | 1 | Assumed | ||
| Hypometric relation factor of workers | 0.261 | 1 | Assumed |
| Colony | Day | Colony Size (N) | Number of Gamergates () | Reproductive Ratio (X) |
|---|---|---|---|---|
| F44 | 0 | 42 | 3 | 0.0714 |
| 94 | 41 | 3 | 0.0732 | |
| 613 | 62 | 7 | 0.1129 | |
| SAFC12 | 0 | 127 | 4 | 0.0315 |
| 94 | 109 | 4 | 0.0360 | |
| 125 | 91 | 4 | 0.0440 |
| Colony | ||||||
|---|---|---|---|---|---|---|
| F44 | 92.77 | 1.61 | 0.37 | 51 | 5 | 0.098 |
| SAFC12 | 121.15 | 1.59 | 0.67 | 97 | 15 | 0.155 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bustamante-Orellana, C.; Bai, D.; Cevallos-Chavez, J.; Kang, Y.; Pyenson, B.; Xie, C. Hierarchy Establishment from Nonlinear Social Interactions and Metabolic Costs: An Application to Harpegnathos saltator. Appl. Sci. 2022, 12, 4239. https://doi.org/10.3390/app12094239
Bustamante-Orellana C, Bai D, Cevallos-Chavez J, Kang Y, Pyenson B, Xie C. Hierarchy Establishment from Nonlinear Social Interactions and Metabolic Costs: An Application to Harpegnathos saltator. Applied Sciences. 2022; 12(9):4239. https://doi.org/10.3390/app12094239
Chicago/Turabian StyleBustamante-Orellana, Carlos, Dingyong Bai, Jordy Cevallos-Chavez, Yun Kang, Benjamin Pyenson, and Congbo Xie. 2022. "Hierarchy Establishment from Nonlinear Social Interactions and Metabolic Costs: An Application to Harpegnathos saltator" Applied Sciences 12, no. 9: 4239. https://doi.org/10.3390/app12094239







