Reliability Prediction Method for Low-Cycle Fatigue Life of Compressor Disks Based on the Fusion of Simulation and Zero-Failure Data

Abstract

Targeting reliability assessment problems with a small sample size and large amount of zero-failure data which appear in the life assessment tests of aero-engine compressor disks, a reliability assessment method and simulation test method were developed by fusing numerical simulation and zero-failure data based on the life reliability assessment method for zero-failure data. The developed method was verified by numerical examples, and further applied in the reliability analysis of compressor disks by combining the test and simulation results. The results indicated that fusing the test data with the simulation data increased the amount of information, improved the life prediction accuracy, and increased the lower confidence limit of the reliable life by 6.02% compared with the case where the test data alone were used.

1. Introduction

Compressor disk is one of the life limit parts in aero-engine, the reliability of which is directly related to the safety of aero-engine. Reliability analysis of fatigue life is a way to quantify risk and improve performance of structures, in which the reliability results with its confidence limits can generally be estimated based on the observations of life tests. In the life tests of compressor disk, the tests are generally terminated at censored time, which is generally 3 times the safe life. If the compressor disk does not fail, it is considered to pass the test, and the fatigue life of the compressor is defined as the safety life [1]. In this kind of test, the test data is zero-failure data, and the amount of data available is few. On the other hand, the reliability evaluation of the compressor disk can also be evaluated through reliability simulation by quantifying the uncertainties of materials, geometry, loads and so on. In this process, a large amount of life data can be obtained. In order to improve the accuracy of reliability analysis, simulation data and test data can be fused to utilize full use of the life information contained in both types of data fully. However, since the data from different sources differ significantly, if they are directly analyzed as a whole sample data, the valuable test information is easily lost. Thus, it is necessary to develop a reliability assessment method based on the fusion of the test data and simulation results.

In the fusion of simulation data and test data, the accuracy of simulation calculation process should be guaranteed. Verification, Validation, and Accreditation (VV&A) [2] is the main approach to evaluate whether the simulation result is realistic and credible. There are mainly inspection methods for product life simulation as following [3]: (1) nonparametric test, (2) parametric test. Nonparametric tests are used when the distribution of simulation objects is not considered, or the distribution is unknown. A non-parametric test of the simulation results is performed through a sign test, rank sum test, χ² goodness-of-fit test, and Kolmogorov–Smirnov (K-S) test. This method needs to be supported by a large number of real experimental data and is not suitable for the case of less experimental data. Parametric test introduces the distribution function. The form of the distribution of the two matrices is assumed, and statistical theories, e.g., hypothesis testing or significance testing, are used to consider the consistency of the distribution function of the simulation results and the reference data. At this point, the problem is transformed into determining whether the parameters of the two distributions are equal, parametric methods such as the F-test, the t-test, confidence interval estimation, and the Cramér–von Mises test can be used to evaluate the simulation results. However, this method does not have enough reason to accept the null hypothesis when it cannot reject it. Therefore, Fu [4] proposed the concept of confidence distribution of matrix eigenvalues based on “small probability principle” and established the confidence test theory, which can well meet the requirements of engineering test.

In order to improve the accuracy of reliability, the multi-source information fusion technology has been introduced into the reliability analysis, which can be divided into three categories as [5]: (1) the weighted-average method, (2) the neural-network method, and (3) the Bayes method. The weighted-average method estimates the reliability parameter by using certain weights to combine the data from different sources. In this method, it is crucial to determine the weights of the data from different sources. Numerous researchers have adopted the multi-source data fusion method, which is a type of weighted-average method, for reliability assessment of aircraft clutches, aero-engine rotors, turbofan engines, etc., [6,7,8,9]. However, the weighted average method has high requirements on the amount of data and has the disadvantages of strong subjectivity under small samples, so its application is limited. The neural network method [10,11,12,13] directly establishes the connection between the raw data and the output results by using multi-layer perceptron. The neurons in the multi-layer perceptron can be nonlinear functions, which can simulate simple nonlinear data. To ensure the accuracy of the output results, numerous samples must be used for training in the early stage. Thus, the amount of data required for the neural-network method is large, making the method unsuitable for small-sample size situations. The Bayes method uses the reliability data from other sources as a priori information, and the posterior distribution of the reliability parameters is obtained by using the Bayes formula together with the current source data to achieve the fusion of multi-source reliability information [14]. Many researchers have proposed the data fusion process of the Bayes method to combine expert experience, test data, and performance degradation data for product life and reliability assessment [15,16,17,18,19,20,21,22]. The Bayes criterion has become the mainstream method for multi-source reliability information fusion [16]. However, this method needs to obtain prior distribution by combining multi-source historical data and then fuse it according to the current data. In the case of small sample size, it is difficult to obtain prior distribution. The data fusion method based on fuzzy set theory and Dempster-Shafer evidence theory [23] adopts probability interval and uncertainty interval to inference without prior information, which can solve the problem of insufficient prior information.

In this paper, we propose a method to solve the reliability evaluation problem in the case of less compression disk test data and mostly trouble-free data. In Section 2, the first part reviews the bayes estimation method for failure probability under zero-failure data, then we can give reliability distribution parameter estimation by the least square method. The second part introduces the reliability simulation test method based on confidence test theory of matrix eigenvalue confidence distribution, and the interval fusion method is introduced. The confidence lower limit of life under reliability can be determined according to the fusion prediction of simulation and test data. In Section 3, a numerical example is presented to verify the data fusion method. In Section 4, we give an example of reliability evaluation of compressor disk with the data fusion method.

2. Reliability Assessment Method Based on Fusion of Simulation and Test Data

2.1. Life Reliability Assessment Method for Zero-Failure Data

2.1.1. Bayes Estimation Method for Failure Probability

Assume that the distribution function of the product lifetime satisfies $T~F_{\theta }\left(t\right),t>0,\theta \in \mathsf{\Theta }$. There are S test pieces divided into m batches for a fixed time truncated test before the life test, and the truncated time $t_i\left(i=1,\cdots ,m\right)$ satisfies $t_1<t_2<\cdots <t_m$. None of the $n_i$ specimens in each batch have failed; i.e., the life of all $n_i$ specimens in the $i$th batch is >$t_i$. The above zero-failure test data is denoted as $\left(t_i,n_i\right),i=1,\cdots ,m$. Introduce $s_i$ to represent the total number of specimens without failure at $t_i$ time, and $s_i={\displaystyle \sum }_{j=i}^m{n}_j$. The failure probability is $p_i=F_{\theta }\left(t_i\right)=P\left(T\le t_i\right),i=1,\cdots ,m$.

Step 1: Construct the uninformative prior distribution of failure probability $p_i$.

Since the product lifetime test data are zero-failure data, for high-reliability products, when $n_m$ is relatively large, it can be assumed that the probability that the product lifetime is <$t_m$ is low. We assume that the probability of failure does not exceed q. Using the a priori information [24]:

$$p_m=P\{t<t_m\}<q\le 0.5$$

(1)

when $F_{\theta }\left(t\right)$ is a concave function on $t$, take $t_0=0$; then, we have $p_0\simeq 0$, and,

$$0<\frac{p_1}{t_1}<\frac{p_2}{t_2}<...<\frac{p_m}{t_m}<\frac{q}{t_m}$$

(2)

From Equation (2), we know that for any $2\le i\le m$, $p_i\le q·\frac{t_i}{t_m}$ when we can take the uniform distribution on $\left[{\widehat{p}}_{i-1},q·\frac{t_i}{t_m}\right]$ as the prior distribution of $p_i$, that is,

$$\pi (p_i)=\{\begin{array}{cc}\frac{t_m}{q{t}_i-t_m{\widehat{p}}_{i-1}},& {\widehat{p}}_{i-1}<p_i<\frac{q{t}_i}{t_m}\\ 0,& \mathrm{other}\end{array}$$

(3)

where the value of $p_1$ needs to be estimated in advance. First, we consider a fixed timed truncated test with n specimens. The test truncated time is ${\tau }_r$. Suppose that there are r specimen failures before the truncated time $\tau$, and ${\tau }_r$ and ${\tau }_{r+1}$ represent the $r\mathrm{th}$ and $\left(r+1\right)\mathrm{th}$ failure moments, respectively. Then, we have ${\tau }_r\le \tau \le {\tau }_{r+1}$ and $F_{\theta }\left({\tau }_r\right)\le F_{\theta }\left(\tau \right)\le F_{\theta }\left({\tau }_{r+1}\right)$, and,

$$E[F_{\theta }({\tau }_r)]=\frac{r}{n+1},E[F_{\theta }({\tau }_{r+1})]=\frac{r+1}{n+1}$$

(4)

Take the estimate of $F_{\theta }\left(\tau \right)$ as ${\widehat{F}}_{\theta }\left(\tau \right)=\frac{r+0.5}{n+1}$, at which time ${\widehat{F}}_{\theta }\left(\tau \right)$ is the summation estimate of $F_{\theta }\left(\tau \right)$, i.e., $\underset{n\to \infty }{\lim }{\widehat{F}}_{\theta }\left(\tau \right)=F_{\theta }\left(\tau \right)$. Thus, at the moment of $t_1$, the estimate of $p_1$ can be taken as ${\widehat{p}}_1=\frac{0.5}{s_1+1}$ in the case where none of the $s_1$ specimens fails.

Step 2: Calculate the likelihood function of failure probability $p_i$.

There are $s_i$ specimens that have zero-failure at time $t_i$, and the corresponding likelihood is $L_A\left(p_i|s_i\right)={\left(1-p_i\right)}^{s_i}$. In addition, the test data before $t_i$ are $\left(t_j,n_j\right),1\le j\le i-1$. For each j, there are $n_j$ specimens without failure at time $t_j$; thus, each of these $n_j$ specimens will fail with probability $P_j=\frac{p_i-p_j}{1-p_j}$ before $t_i$ and with probability $1-P_j=\frac{1-p_i}{1-p_j}$ after $t_i$. Therefore, the likelihood of $p_i$ corresponding to the data $\left(t_j,n_j\right)$ is,

$$L_j(p_i|(t_j,n_j))=p_i^{n_j{p}_j}\cdot {(1-p_i)}^{n_j(1-p_j)}$$

(5)

Considering the entire previous test data of $t_i$, i.e., $\left(t_j,n_j\right),1\le j\le i-1$, the corresponding likelihood is,

$$L_B(p_i)={\displaystyle {\prod }_{j=1}^{i-1}{p}_i^{n_j{p}_j}\cdot {(1-p_i)}^{n_j(1-p_j)}}=p_i^{{\displaystyle {\sum }_{j=1}^{i-1}{n}_j{p}_j}}\cdot {(1-p_i)}^{{\displaystyle {\sum }_{j=1}^{i-1}{n}_j(1-p_j)}}$$

(6)

The likelihood function corresponding to the full test data at this point is,

$$L(p_i)=L_A(p_i|s_i)\cdot L_B(p_i)$$

(7)

when $i=1$, $L_B\left(p_1\right)=1$.

Step 3: Predict the estimated failure probability $p_i$.

After $p_1,\cdots ,p_{i-1}$ in Equation (7) is replaced with its estimator ${\widehat{p}}_1,\cdots ,{\widehat{p}}_{i-1}$, the approximate likelihood function $\tilde{L}\left(p_i\right)={\tilde{L}}_A\left(p_i\mid s_i\right)\cdot {\tilde{L}}_B\left(p_i\right)$ of $p_i$ can be obtained, and the Bayes estimation formula for $p_i\left(i=2,\cdots ,m\right)$ under the squared loss can be obtained by combining the prior distribution $\pi \left(p_i\right)$ of $p_i$ and applying the Bayes formula.

$${\widehat{p}}_i=\frac{{\displaystyle {\int }_{{\widehat{p}}_{i-1}}^{q\frac{t_i}{t_m}}{p}_i\cdot L(p_i)d{p}_i}}{{\displaystyle {\int }_{{\widehat{p}}_{i-1}}^{q\frac{t_i}{t_m}}L(p_i)d{p}_i}},i=2,...,m$$

(8)

2.1.2. Calculation of Life Confidence Limits

In this study, the partition distribution curve method [25] was used to obtain the parameter estimation of the distribution function. This method is based on the estimation results for $p_1,\cdots ,p_m$. The life distribution function was converted into a linear regression model, and the estimated value $\widehat{\theta }$ of the design life distribution parameter $\theta$ was obtained using the least-squares method or the minimal ${\mathsf{\chi }}^2$ estimation method [26]. The calculation methods for the commonly used distributions in engineering are as follows.

1.

Normal distribution

For a normal distribution $F_{\theta }\left(t\right)=\mathsf{\Phi }\left(\frac{t-\mu }{\eta }\right),t>0,\mu \in R,{\sigma }^2>0,\theta =(\mu ,{\sigma }^2)$, the following linear regression model can be developed:

$$t_i=\mu +\sigma \cdot {\mathsf{\Phi }}^{-1}({\widehat{p}}_i),i=1,...,m$$

(9)

where ${\mathsf{\Phi }}^{-1}$ is the inverse function of the standard normal distribution function, taking,

$$y=\left[\begin{array}{l}{t}_1\\ t_2\\ ⋮\\ t_m\end{array}\right],A=\left[\begin{array}{cc}1& {\mathsf{\Phi }}^{-1}({\widehat{p}}_1)\\ 1& {\mathsf{\Phi }}^{-1}({\widehat{p}}_2)\\ ⋮& ⋮\\ 1& {\mathsf{\Phi }}^{-1}({\widehat{p}}_m)\end{array}\right],\beta =\left[\begin{array}{l}\mu \\ \sigma \end{array}\right]$$

(10)

The least-squares estimate of the parameter β is,

$$\widehat{\beta }=\left[\begin{array}{l}\widehat{\mu }\\ \widehat{\sigma }\end{array}\right]={(A^{T}A)}^{-1}{A}^{T}y$$

(11)

According to the given reliability $R$, the one-sided confidence lower bound formula [27] of the Q-percentile life $t_R$ with a confidence coefficient of $\gamma$ is,

$$t_{RL}=\overline{t}-(t_R-t_{R_0})\sigma$$

(12)

where $\overline{t}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{t}_i$, $t_R={\mathsf{\Phi }}^{-1}\left(R\right)$, $t_{R0}={\mathsf{\Phi }}^{-1}\left(R_0\right)$ and $R_0={\left(1-\gamma \right)}^{1/n}$, and the standard deviation $\sigma$ is typically determined by engineering experience, but in this case it can be replaced with the fitted result $\widehat{\sigma }$ instead.

2.

Weibull distribution

For the Weibull distribution $F_{\theta }\left(t\right)=1-\exp \left\{-{\left(\frac{t}{\eta }\right)}^k\right\}$, where $\theta =\left(\mu ,\sigma \right)$, it is known that $\ln \frac{1}{1-F_{\theta }\left(t\right)}={\left(\frac{t}{\eta }\right)}^k$; thus, the following linear regression equation is obtained:

$$\ln t_i=a+b\cdot \ln \ln \frac{1}{1-{\widehat{p}}_i}+{\epsilon }_i,i=1,...,m$$

(13)

where $a=\ln \eta$ and $b=\frac{1}{k}$. Note that,

$$y=\left[\begin{array}{l}\ln t_1\\ \ln t_2\\ ⋮\\ \ln t_m\end{array}\right],A=\left[\begin{array}{cc}1& \ln \ln \frac{1}{1-{\widehat{p}}_1}\\ 1& \ln \ln \frac{1}{1-{\widehat{p}}_2}\\ ⋮& ⋮\\ 1& \ln \ln \frac{1}{1-{\widehat{p}}_m}\end{array}\right],\beta =\left[\begin{array}{l}a\\ b\end{array}\right]$$

(14)

Then, the least-squares estimate of the parameter β is,

$$\widehat{\beta }=\left[\begin{array}{c}\widehat{a}\\ \widehat{b}\end{array}\right]={(A^{T}A)}^{-1}{A}^{T}y$$

(15)

When,

$$R\ge \exp \left\{\ln (1-\gamma )\exp \left\{\frac{{\displaystyle {\sum }_{i=1}^n{t}_i^{{\alpha }_0}\ln t_i^{{\alpha }_0}}}{{\displaystyle {\sum }_{i=1}^n{t}_i^{{\alpha }_0}}}-\ln {\displaystyle {\sum }_{i=1}^n{t}_i^{{\alpha }_0}}\right\}\right\}$$

(16)

In which the reliability $R$ being given, the one-sided confidence lower bound formula [27] of the Q-percentile life $t_R$ with a confidence coefficient of γ is,

$$t_{RL}={[\frac{\ln R}{\ln (1-\gamma )}{\displaystyle {\sum }_{i=1}^n{t}_i^k}]}^{1/k}$$

(17)

The shape parameter k, which is usually determined by engineering experience, can be replaced with the fitting results $\widehat{k}$.

2.2. Reliability Assessment Method for Fusion of Simulation and Test Data

2.2.1. Lifetime Reliability Simulation Test Method

The correctness of the simulation results must be judged before they are used. If the simulation is incorrect, the use of simulation data will exacerbate the deviation of the evaluation results from the true results. In this study, according to the concept of the confidence distribution of parent eigenvalues and confidence test theory [4,28], we established a reliability simulation test method that can evaluate whether the product reliability life is correct at a high confidence level.

Let the random variable T be the product life and $t_R$ be the life percentile value for a given reliability $R \left(R\ge 50\%\right)$. The reliable life $t_{S,R}$ of the product with reliability $R$ is obtained through simulation, and because $t_R$ is unknown, it is not yet possible to directly determine whether $t_{S,R}$ and $t_R$ are equal.

Let $t_{N,RU}$ and $t_{N,RL}$ be the upper and lower one-sided confidence limits, respectively, for the confidence level of $\gamma \left(\gamma \ge 50\%\right)$ for the reliable life $t_R$ obtained via the test. The confidence limits of $t_R$ can be obtained using the test results. Reliable-life simulation tests were performed using statistical methods, as shown in

Table 1. Life reliability simulation test criteria.

Conditions	Conclusions
$t_{S,R}>t_{N,RU}$	The simulation was found to be incorrect at confidence level γ The simulation is more adventurous than the real situation and is dangerous for engineering applications.
$t_{S,R}<t_{N,RL}$	The simulation was found to be incorrect at confidence level γ However, because the simulation is more conservative and safer than the real situation, it can be applied in engineering.
$t_{N,RL}<t_{S,R}<t_{N,RU}$	When $t_{N,RU}-t_{N,RL}\le \delta$, the confidence level 2γ − 1 determines that the simulation is correct, i.e., $t_{S,R}=t_R$, at the given accuracy δ.
$t_{N,RL}<t_{S,R}<t_{N,RU}$	When $t_{N,RU}-t_{N,RL}>\delta$, additional testing with additional specimens is needed to determine the reliability.

.

Here, the precision δ is manually determined. In the case where $t_{N,RL}\le t_{S,R}\le t_{N,RU}$, our test method is equivalent to the hypothesis test where the simulated reliable life $t_{S,R}$ is not rejected at the significance level of $\alpha =2\left(1-\gamma \right)$ as equal to the actual reliable product life $t_R$, i.e., the hypothesis that $t_{S,R}=t_R$.

2.2.2. Lifetime Reliability Prediction Method Based on Data Fusion

The zero-failure data with sample sizes of $n_N$, $n_S$, and $n_{O,i}$($i=1,2,\cdots ,m$) were obtained from the test, the simulation, and m groups of previous test results, respectively. By applying the calculation method for the lower confidence limit described in Section 2.1, we obtained the lower confidence limits $t_{N,RL}$, $t_{S,RL}$, and $t_{O,RLi}$($i=1,2,\cdots ,m$) of the logarithmic reliable life with a confidence level of γ and reliability of R. The shape parameters corresponding to different $t_{O,RLi}$ values can be different. The predicted life fusion equations for the commonly used distributions in engineering are as follows.

1.

Normal distribution

$$t_{T,RL}=\frac{n_N}{n_T}{t}_{N,RL}+\frac{n_S}{n_T}{t}_{S,RL}+{\displaystyle \sum _{i=1}^m\frac{n_{O,i}}{n_T}{t}_{O,RLi}+(t_{T,R_0}-\frac{n_N}{n_T}{t}_{N,R_0}-\frac{n_S}{n_T}{t}_{S,R_0}-{\displaystyle \sum _{i=1}^m\frac{n_{O,i}}{n_T}{t}_{O,R_{0}i}})}\widehat{\sigma }$$

(18)

Here, $n_T=n_N+n_S+{\sum }_{i=1}^m n_{o,i}$, $t_{T,R_0}={\mathsf{\Phi }}^{-1}\left[{(1-\gamma )}^{1/n_T}\right]$, ${\mathsf{\Phi }}^{-1}\left[{(1-\gamma )}^{1/n_N}\right]$, $t_{S,R_0}={\mathsf{\Phi }}^{-1}\left[{(1-\gamma )}^{1/n_s}\right]$, and $t_{O,R_{0}i}={\mathsf{\Phi }}^{-1}\left[{(1-\gamma )}^{1/n_{o,i}}\right]$.

As indicated by Equation (12), $t_{T,RL}$ is a one-sided lower confidence limit for the logarithmically reliable life $t_R$ with a confidence level of γ, i.e., $P \left(t_R\ge t_{T,RL}\right)\ge \gamma$.

2.

Weibull distribution

$$t_{T,RL}={(t_{N,RL}^{\widehat{k}}+t_{S,RL}^{\widehat{k}}+{\displaystyle {\sum }_{i=1}^m{t}_{O,RLi}^{\widehat{k}}})}^{1/\widehat{k}}$$

(19)

According to Equation (17), $t_{T,RL}$ is a one-sided lower confidence limit for the logarithmically reliable life $t_R$ with a confidence level of γ, i.e., $P \left(t_R\ge t_{T,RL}\right)\ge \gamma$.

3. Numerical Example

In this section, the simulation and test data fusion method is validated through a numerical example. Assume that we have the following function: $T\left(x_1,x_2\right)=e^{x_1}+\frac{x_2}{e^{x_1}}$, where $x_1$ and $x_2$ are mutually independent random variables satisfying the lognormal and normal distributions, respectively, $\ln x_1~ N\left(5, 0.2\right), x_2 ~ N\left(34500, 100\right)$. Let $G\left(x_1,x_2\right)=e^{x_1}+\frac{x_2}{e^{x_1}}-6050$; when G > 0, the data are considered as failure data, and when G < 0, the data are considered as zero failure data.

First, 300 individual points were sampled, and the sample set D was obtained using the function T. The criterion function $G\left(x_1,x_2\right)$ was used to determine whether the data were zero-failure data. The sample set D was used to construct the proxy model $\tilde{T}\left(x_1,x_2\right)$, which described the simulation computation process. A radial basis function neural network (RBFNN) was used to construct the proxy model. The $\tilde{T}$ and $T$ are different here, indicating differences in the distributions of the simulation data and the test data.

Second, sampling was performed 10⁶ times based on Monte Carlo simulation (MCS), and with the help of the function $T\left(x_1,x_2\right)$ and the proxy model $\tilde{T}\left(x_1,x_2\right)$, stable distributions of the random variables $T$ and $T$ were obtained, as shown Figure 1.

Last, we determined that the reliability was R = 0.95, the true value was 6385, and the simulation prediction was 5994.

The zero-failure data in sample set D were used as the truncated test data. The distribution of the random variable $\tilde{T}$ approximately followed the normal distribution, and the probability of failure at 6050 did not exceed 0.1; thus, q was 0.1. The truncated test data and the probability of failure estimated using the Bayes method are shown in

Table 2. Zero-failure data.

Number	Zero-Failure Value	${\mathit{n}}_{\mathit{i}}$	${\mathit{s}}_{\mathit{i}}$	${\widehat{\mathit{p}}}_{\mathit{i}}$
1	5995	15	42	0.0116
2	6015	12	27	0.0332
3	6030	9	15	0.0528
4	6050	6	6	0.0681

.

According to the reliability parameter estimation method presented in Section 2.1, the point $\widehat{k}$ was estimated as 281.6698 using Equation (15). Additionally, using Equation (12), we obtained the confidence level γ = 0.95, and the life one-sided lower confidence limit $t_{N,RL}$ with reliability R = 0.95 was obtained as 6192.

Since $t_{S,R}<t_{N,RL}$, it was concluded that the predicted value obtained from the simulation at the confidence level γ = 0.95 was smaller than the true value; i.e., the simulation results were conservative, and the simulation data could be used for fusion. The fusion of $t_{N,RL}$ and $t_{S,RL}$ was performed in accordance with Equation (19). The confidence level was γ = 0.95, and the life one-sided lower confidence limit $t_{T,RL}$ with reliability R = 0.98 was 6042 after the fusion.

4. Reliability Analysis of Compressor Disks

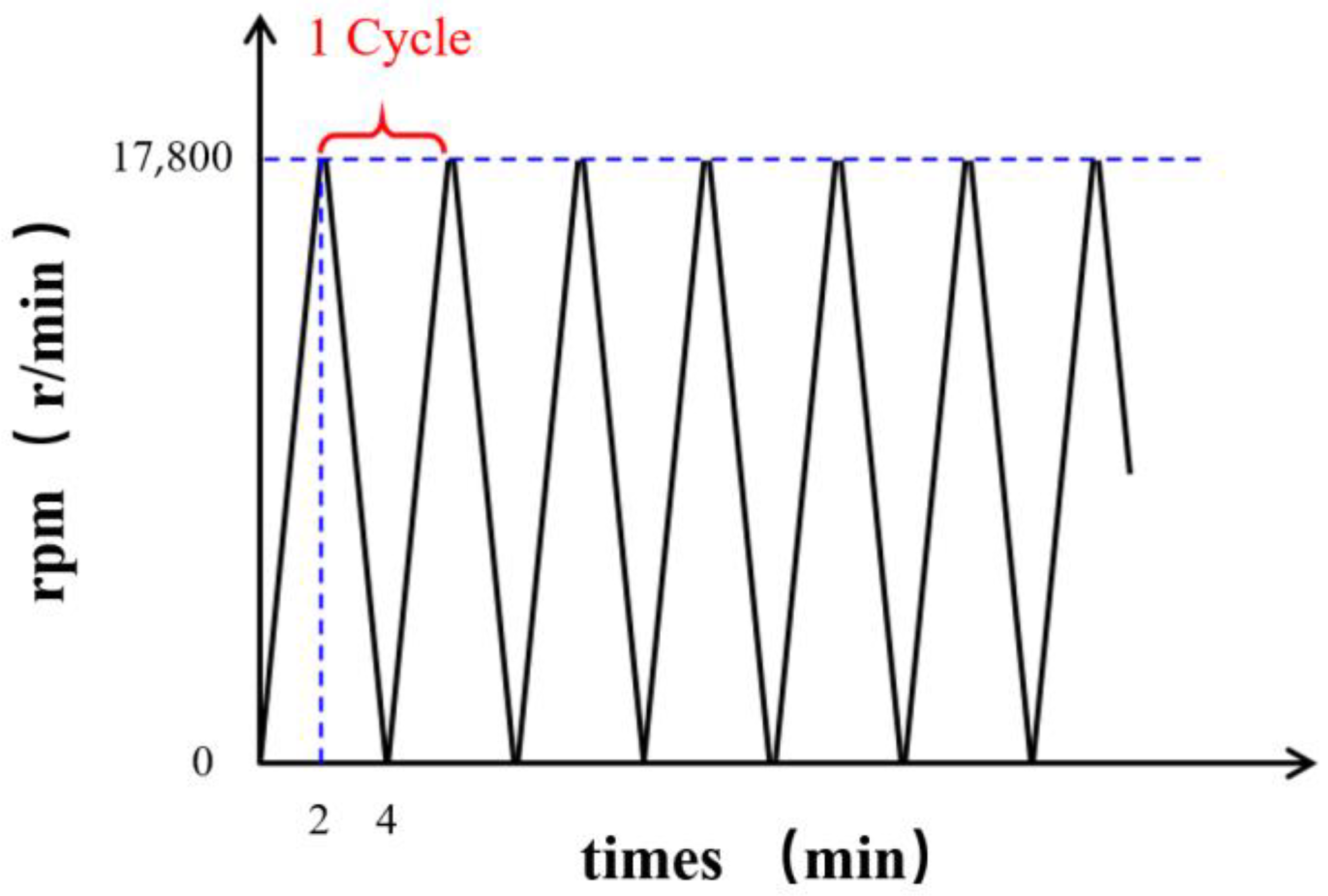
4.1. Low-Cycle Fatigue Test of Compressor Disks

The compressor disk is shown in Figure 2. The wheel spokes were evenly spaced with 36 bolt holes, through which they were connected to the rest of the structure.

As indicated by

Table 3. Life reliability prediction results.

	Bayes Method Prediction Results	Simulation Prediction Results	Fusion Method Predicted Results	True Results
Value	6000	5994	6042	6385
Error	385	391	343	0

, after the current test data were fused with the simulation data, the predicted life error was reduced by 10.9% compared with the error obtained by using only the current test data. It is worth noting that the life reliability prediction using the data fusion method with a reasonable simulation process will not exceed the true life distribution and can ensure the safety of the predicted life.

The compressor disk was designed for a life of 36,265 cycles, and a low-cycle fatigue (LCF) test was performed using a rotor tester with an LCF load spectrum of 0 r/min–17,800 r/min–0 r/min, a test temperature of 500 °C, a triangular load waveform, and a loading rate of 3 Hz, as shown in Figure 3.

All 13 test disks passed the test experiment. According to engineering experience, the safety coefficient is generally set as 2.4; therefore, the life of the disk was set as 15,110.

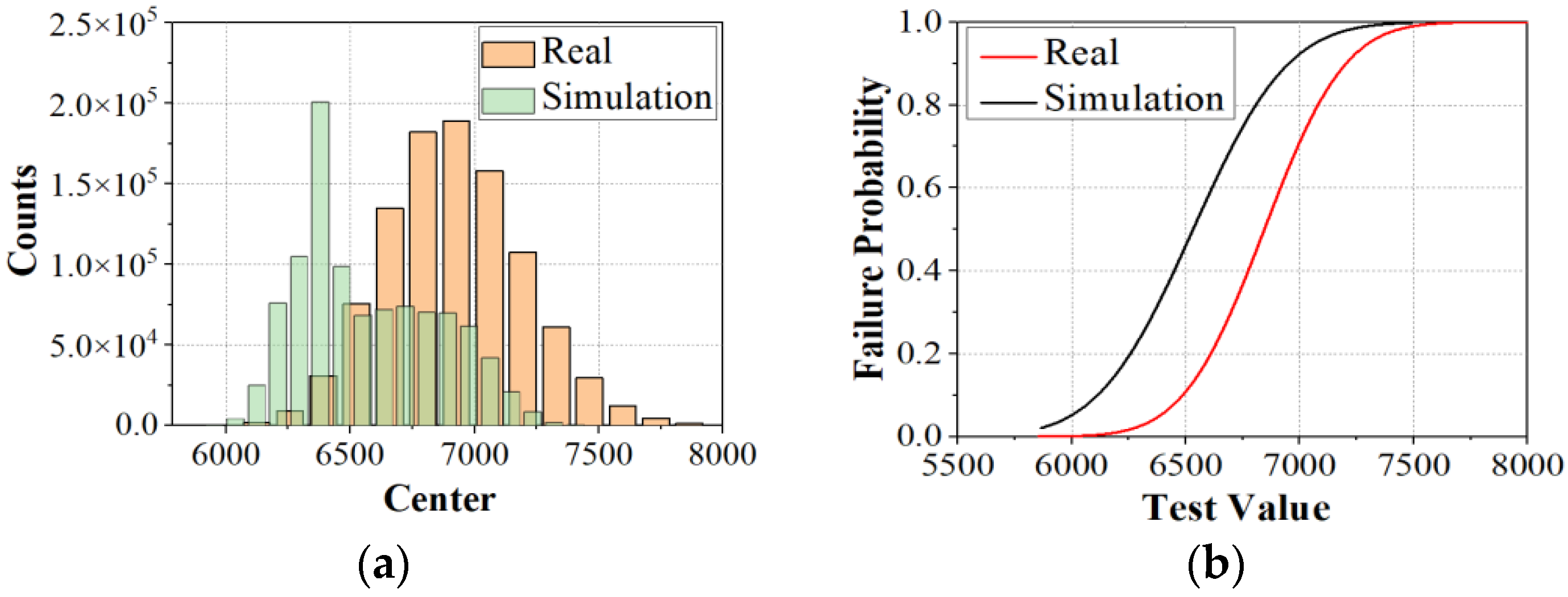
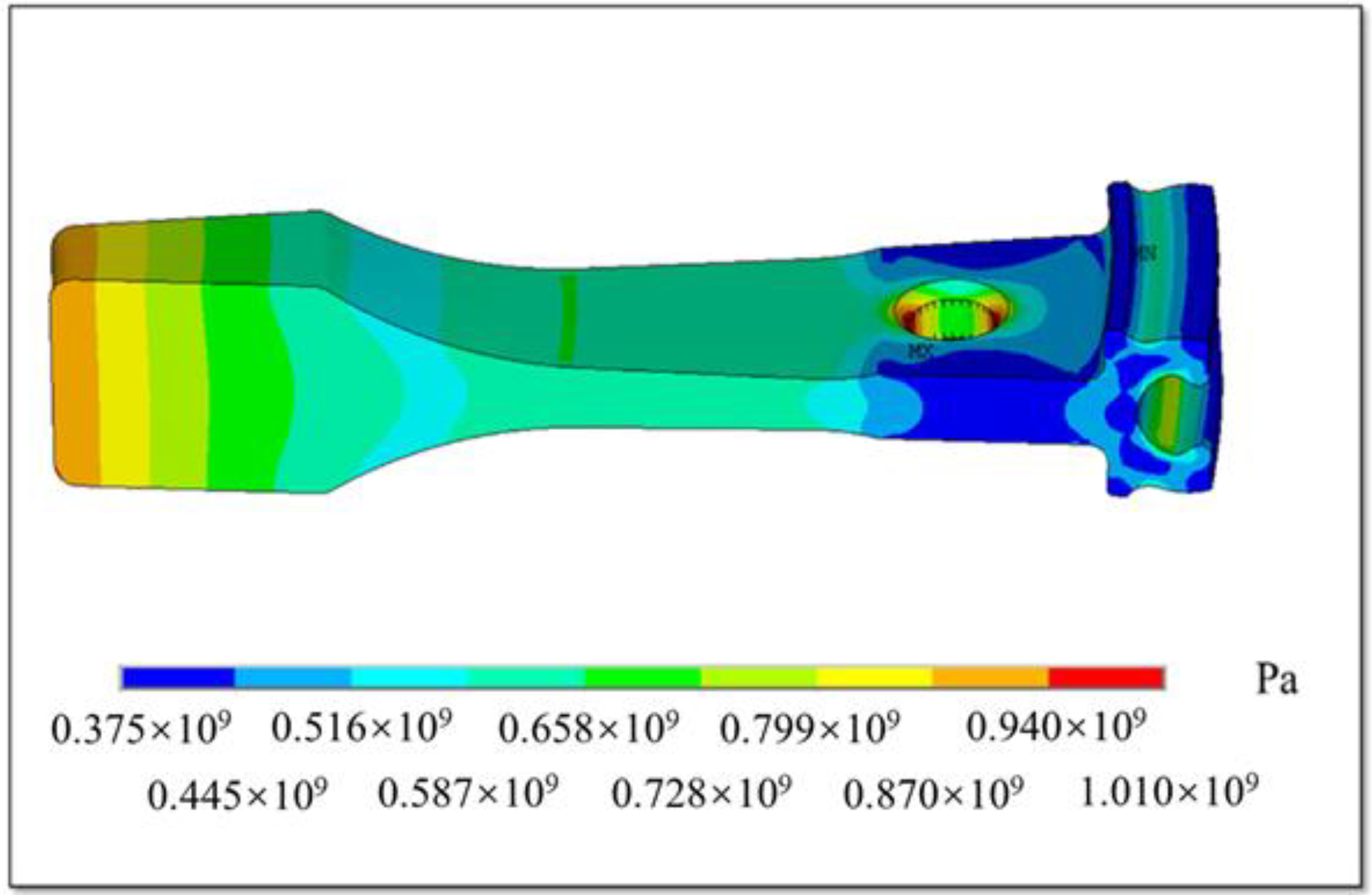
4.2. Simulation-Based Uncertainty Analysis of Compressor Disks

Considering the periodic symmetry of the structure, 1/36th of the wheel sector was selected for analysis, and a 20-node hexahedral mesh was established, with the wheel material as GH4169 and a density of 8240 kg/m³. The blade material was DD6, and the equivalent pressure on the contact surface of the tongue and groove was 426.91 MPa during rotation. The deterministic results of the finite-element analysis are shown in Figure 4.

The uncertainty of the load and geometric input variables and the uncertainty of the life model were considered in the reliability analysis. Probability distributions were used to characterize the uncertainties of the speed and temperature in the load, and r₁ (inner diameter of the wheel disk), r₂ (outer diameter of the wheel disk), w₁ (width of the wheel disk), w₇ (width of the tenon slot), and ra₇ (thickness of the tenon slot) were selected as geometric uncertainty parameters via a sensitivity analysis [29], as shown in Figure 5. To obtain the distributions, measurements of 10 actual compressor disks were performed, followed by a K-S test [30].

The Ramberg–Osgood equation was used to describe the stress–strain relationship [31], and a modified Smith–Watson–Topper model based on the theory of critical distance [32] was used for life prediction. They are expressed as follows:

$$\frac{\Delta {\epsilon }_t}{2}=\frac{\Delta {\epsilon }_e}{2}+\frac{\Delta {\epsilon }_p}{2}=\frac{\Delta \sigma }{2E}+{\left(\frac{\Delta \sigma }{2K^{\prime }}\right)}^{1/n^{\prime }}$$

(20)

$${\left({\sigma }_{max}\frac{\Delta {\epsilon }_t}{2}\right)|}_{r=L}=\frac{{\left({{\sigma }^{\prime }}_f\right)}^2}{E}{\left(2N_f\right)}^{2b}+{{\sigma }^{\prime }}_f{{\epsilon }^{\prime }}_f{\left(2N_f\right)}^{b+c}$$

(21)

where Δε_t represents the total strain range; Δε_e and Δε_p represent the elastic and plastic strain ranges, respectively; Δσ represents the stress range; σ_max represents the maximum stress; N_f represents the LCF life; and E represents elastic modulus of the material. The parameters ${\sigma }_f^{\prime }$, $b$, ${\epsilon }_f^{\prime }$, and c are the fatigue strength coefficient, fatigue strength index, fatigue ductility coefficient, and fatigue ductility index, respectively, which can be obtained from material fatigue tests.

The r represents the distance from the edge of the notch to a position on the maximum stress gradient line, and L represents the critical distance. These two variables have a power-function relationship with the life:

$$L=A{N}_f^B$$

(22)

To evaluate the uncertainty of the model parameters, 42 test specimens of the actual compressor disk were used for fatigue tests, as shown in Figure 6. According to Bayes’ theorem, the distribution type and distribution parameters of the model parameters were obtained using the Markov chain Monte Carlo method [29]. The Detailed distribution of model parameters including the geometry, loading, and model uncertainty, are presented in

Table 4. Uncertainty of model parameters.

Parameter	Unit	Distribution Type	Mean Value	Lower Bound of the Mean Value	Upper Bound of the Mean Value	Coefficient of Variation
r1	mm	normal distribution	67.15	67.13	67.18	4.77 × 10−4
r2	mm	normal distribution	209.32	209.25	209.39	4.26 × 10−4
w1	mm	normal distribution	29.00	28.99	29.01	2.76 × 10−4
w7	mm	normal distribution	23.00	22.99	23.01	4.35 × 10−4
ra7	mm	normal distribution	10.00	9.99	10.00	3.00 × 10−4
${\sigma }_f^{\prime }$	MPa	lognormal distribution	7.0712			0.0242
b	-	normal distribution	−0.0197			−0.628
${\epsilon }_f^{\prime }$	-	normal distribution	1.8230			0.445
c	-	normal distribution	−3.5230			−0.106
A	mm	normal distribution	6.4013			0.195
B	-	normal distribution	−3.5146			−0.0818
Angular velocity	r/min	normal distribution	17,800			0.020
Temperature	°C	normal distribution	600			0.020

.

The RBFNN was used to build the proxy model G between the input random variables and the output LCF life for sampling to predict the LCF life [29], and life was obtained to take the distribution with the bottom logarithm of 10 to approximately follow a normal distribution, as shown in Figure 7. According to the results of the obtained life distribution, the lower life limit $x_{S,RL}$ with reliability R = 0.9987 was predicted to be 16,251.

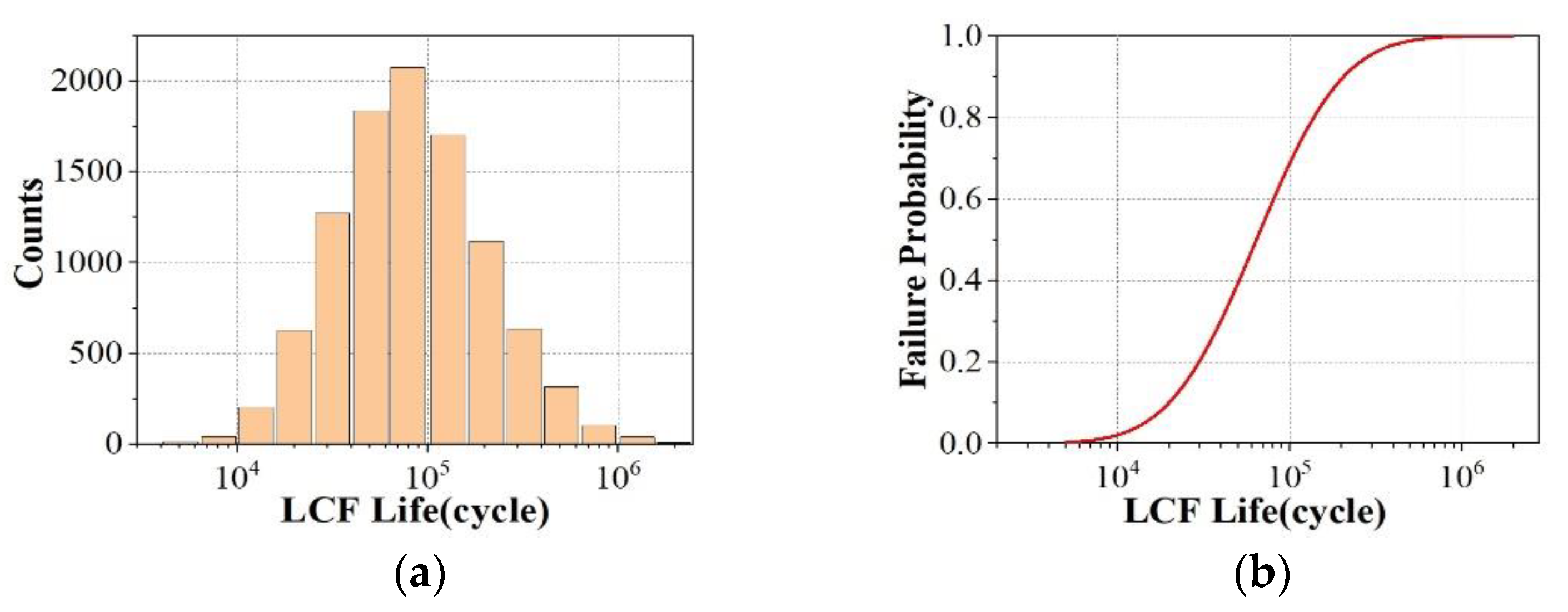
4.3. Life Reliability Assessment

The compressor disk had zero-failure before the designed life of 36,265 cycles. Assuming that the life follows a normal distribution, according to the prediction of the simulation analysis method, the probability of failure for a cycle life of <36,265 is ≤0.05, that is, q ≤ 0.078. The cycles were equally divided into four classes according to the batch, and taking q = 0.078, the probability of failure was estimated using the Bayes method, as shown in

Table 5. Zero-failure data.

Number	Zero-Failure Value	${\mathit{n}}_{\mathit{i}}$	${\mathit{s}}_{\mathit{i}}$	${\widehat{\mathit{p}}}_{\mathit{i}}$
1	33,012	5	13	0.0357
2	33,997	3	8	0.0536
3	34,415	3	5	0.0639
4	36,265	2	2	0.0712

.

Similarly, the point $\widehat{\sigma }$ was estimated as 8255.3; then, according to Equation (12), the one-sided lower confidence limit $x_{N,RL}$ of the life with confidence level γ = 0.95 and reliability R = 0.9987 was obtained as 16,340. According to the obtained life distribution results, the lower confidence limit $x_{S,RL}$. of the life with reliability R = 0.9987 was predicted as 16,251.

According to the reliability simulation test method proposed in Section 4.2, because $x_{S,R}<x_{N,RL}$, it could be concluded that the reliability life obtained from the simulation was shorter than the actual reliability life of the disk at the confidence level γ = 0.95; i.e., the simulation results were conservative. Since the compressor disk is the off-weight part of the aero-engine, conservative results are beneficial for ensuring safety, and the disk can be used in engineering. Following Equation (18), $x_{N,RL}$ and $x_{S,RL}$ were fused, and the life one-sided lower confidence limit $x_{T,RL}$ with confidence level γ = 0.95 and reliability R = 0.9987 was obtained as 17,324 after the fusion.

The analysis results are presented in

Table 6. Reliable life prediction results obtained by fusing current test data with simulation data (Unit: cycles).

Test Prediction Results	Simulation Prediction Results	Fusion Predicted Results	Percentage Increase of Lower Confidence Limit for Reliable Life
16,340	16,251	17,324	6.02%

. Although the simulation prediction results were small compared with the test prediction results, they can be used as a valid source of reliability information.

The simulation data and test data were fused through the proposed data fusion method. The fusion of test data and simulation data increased the amount of information and improved the accuracy of life prediction. The lower confidence limit of the reliable life of the compressor disk was increased by 6.02% compared with the original prediction using only test data.

Compressor disk is the important part of aero engine, once failure will cause serious consequences. Thus, the life confidence lower limit is usually used as the safety life of the disks in engineering. By combining simulation data with test data, the life of compressor disk is evaluated more accurately, and the design life of compressor disks is improved. On the other hand, extended maintenance cycle can reduce the waste of life due to conservative estimation.

5. Conclusions

The main contributions of the present study are summarized as follows:

• A reliability assessment method involving the fusion of simulation and test data, as well as a simulation evaluation method, was proposed. On the basis of the Bayesian method for zero-failure data, a reliability life prediction method based on data fusion theory was proposed that involves the fusion of test and simulation data. According to the principle of “high probability”, we developed a method for stimulating the life and reliability testing through confidence limits. This method can solve problems of non-normal distributions such as the Weibull distribution, which is commonly used in engineering.
• The proposed simulation and test data fusion method was validated by a numerical example. The results indicated that the error of the predicted life was reduced by 10.9% compared with that obtained using the original method under reasonable simulation conditions.
• An LCF life reliability assessment was conducted for an aero-engine compressor disk, taking advantage of zero-failure data from the test and the simulation reliability assessment. Multiple sources of uncertainty were fully considered and quantified, such as the geometry, model parameters, and discrete errors. The uncertainties were quantified via geometric measurements of 13 actual compressor disks and fatigue test data of 42 specimens.
• An LCF life reliability analysis of compressor disks was performed using the proposed reliability assessment method based on the fusion of test and simulation data. The results indicated that the lower confidence limit of the life predicted via the method using the fusion of test and simulation data was 6.02% higher than that of the evaluation method based on zero-failure test data at a reliability of 99.87% and a confidence level of γ = 0.95.

In summary, this paper introduces the concept of exploiting zero-failure test data and high-precision simulation results for reliability assessment of events related to aero-engine disks with a low failure probability. The proposed method can also provide guidance for the development of validation test programs for disk components and the design of life extension programs.