Study on Band Gap and Sound Insulation Characteristics of an Adjustable Helmholtz Resonator
Abstract
:1. Introduction
2. Structural Design and Band Gap Analysis
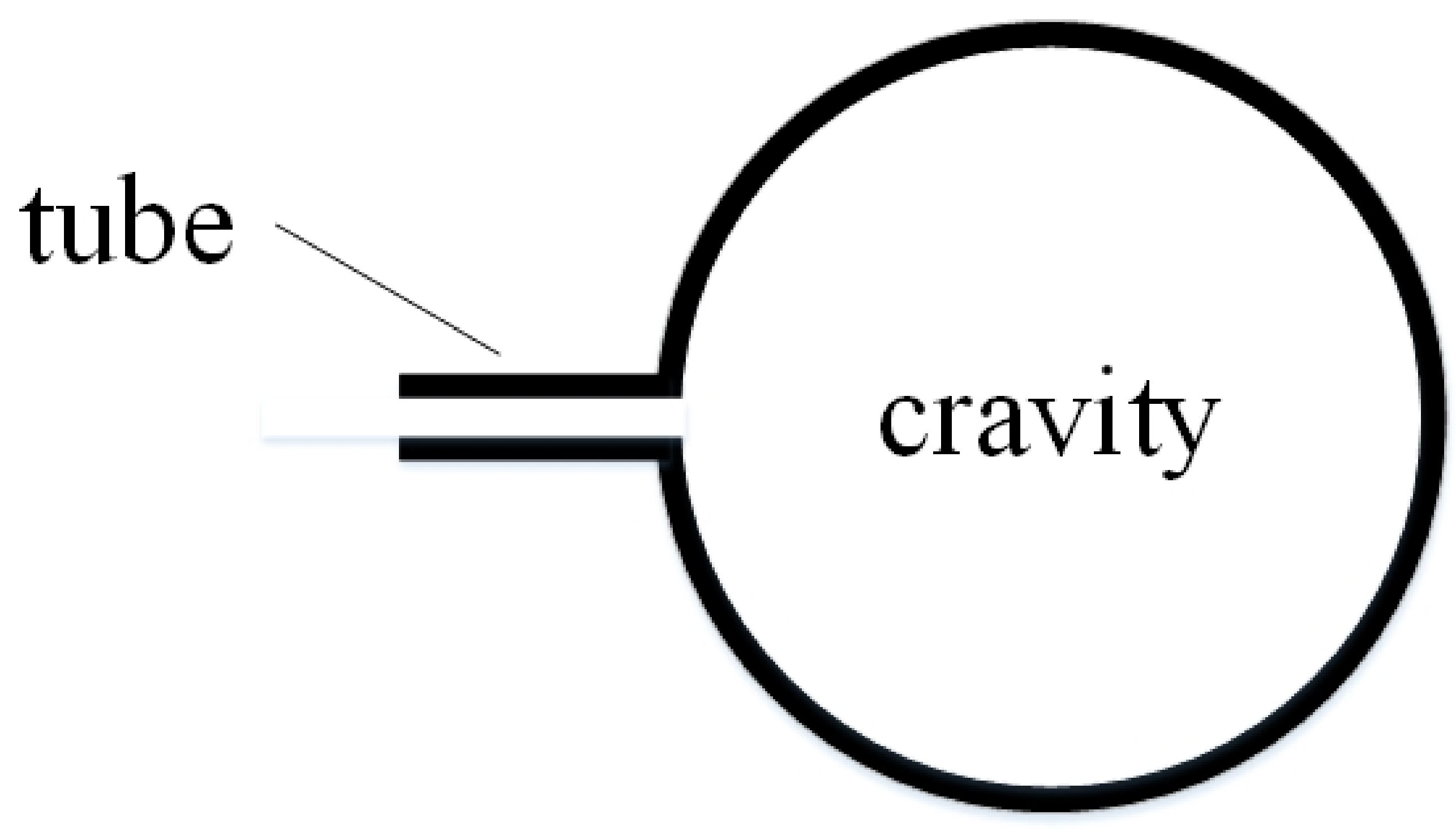
2.1. Structural Design
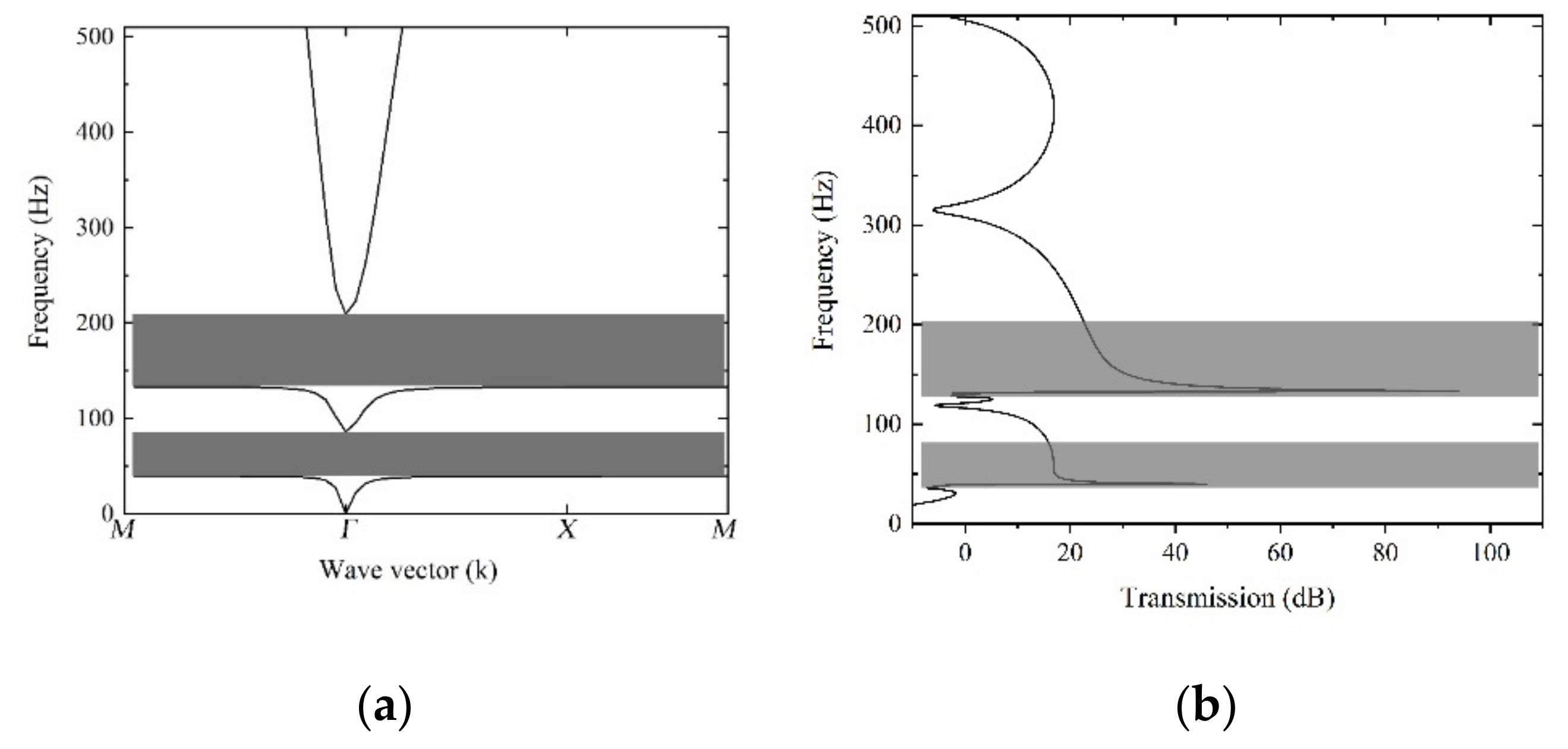
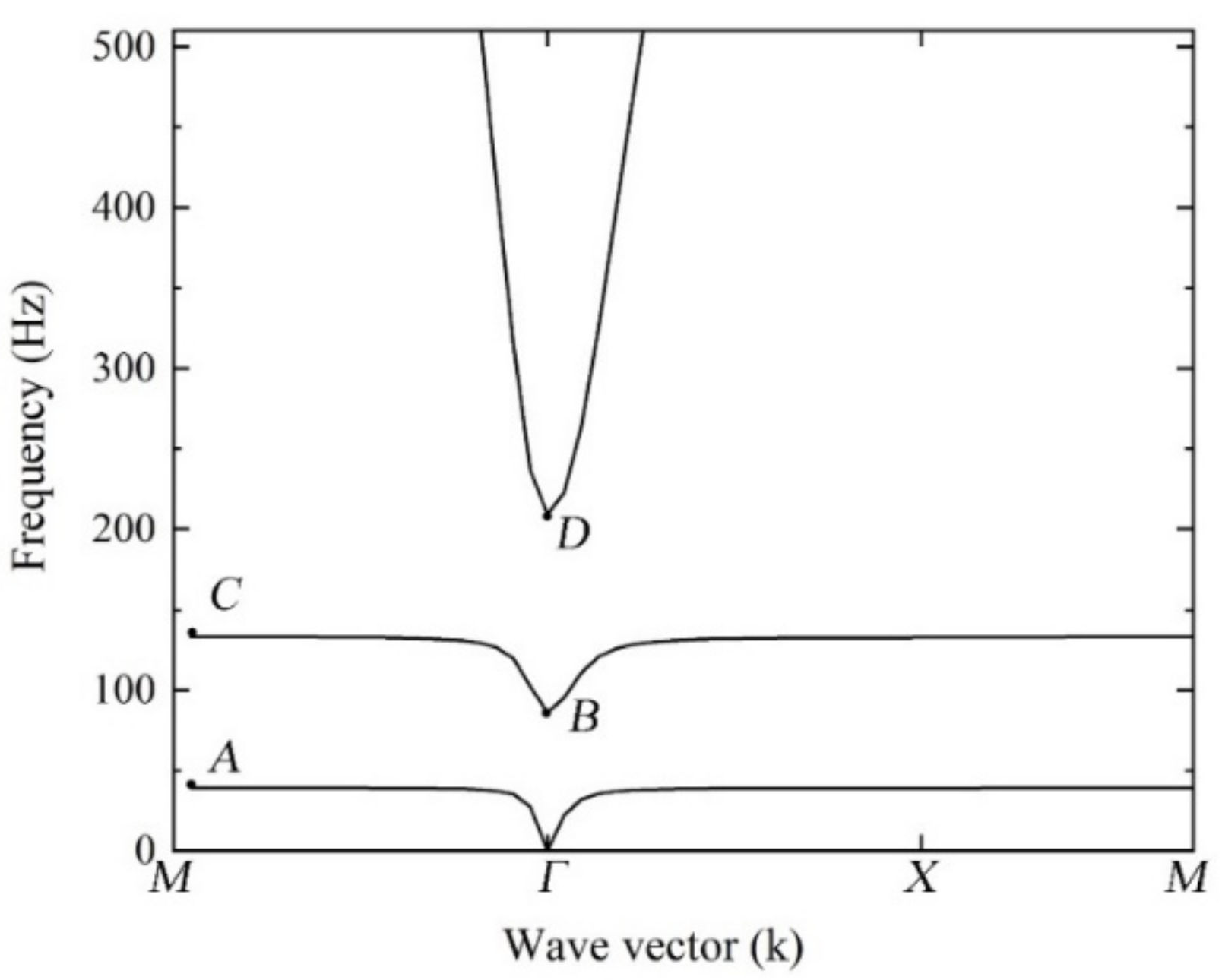
2.2. Band Structure Analysis
3. Modeling and Analysis of Low-Frequency Band Gap Formation Mechanism
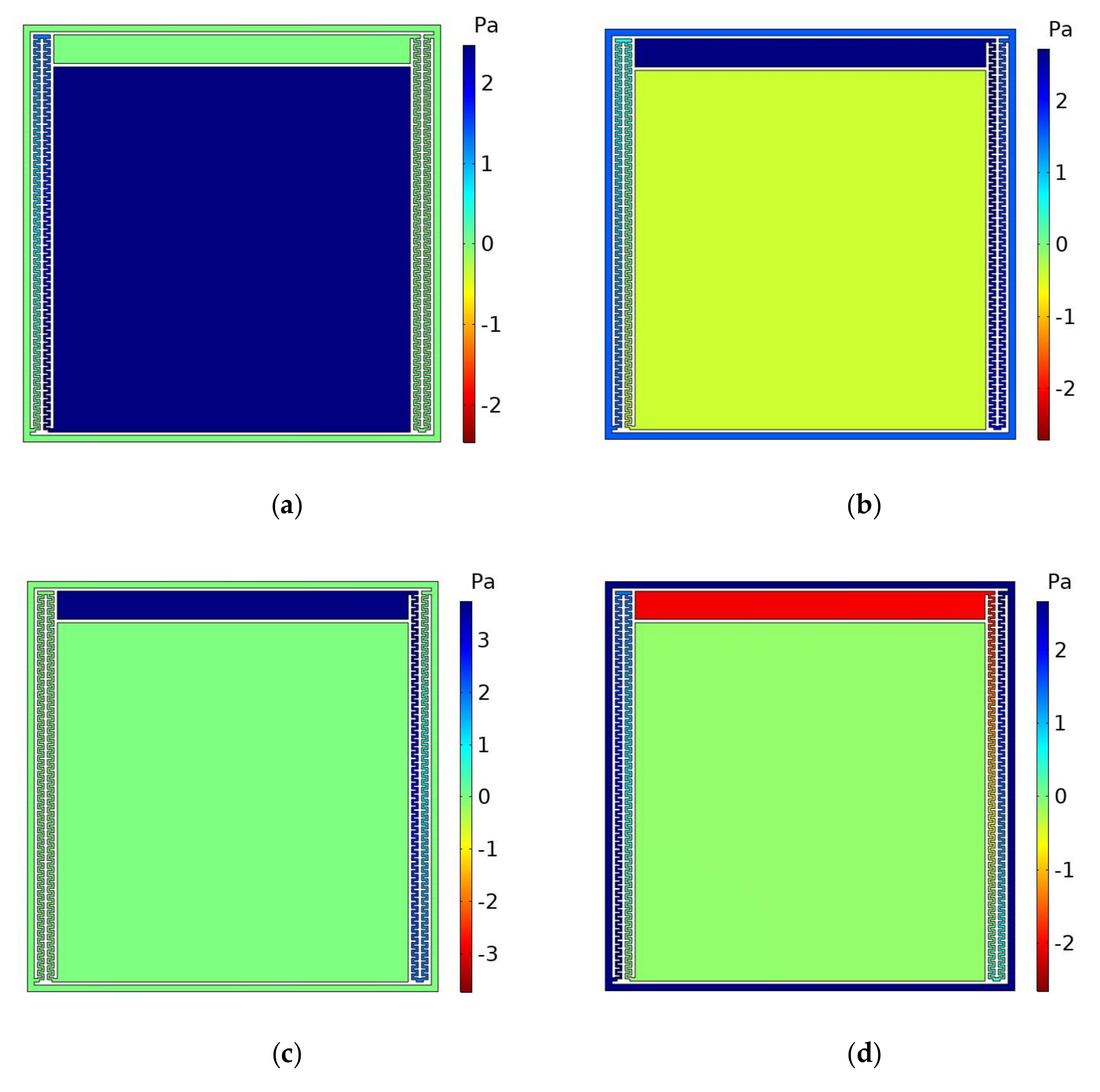
3.1. Study on Band Gap Mechanism
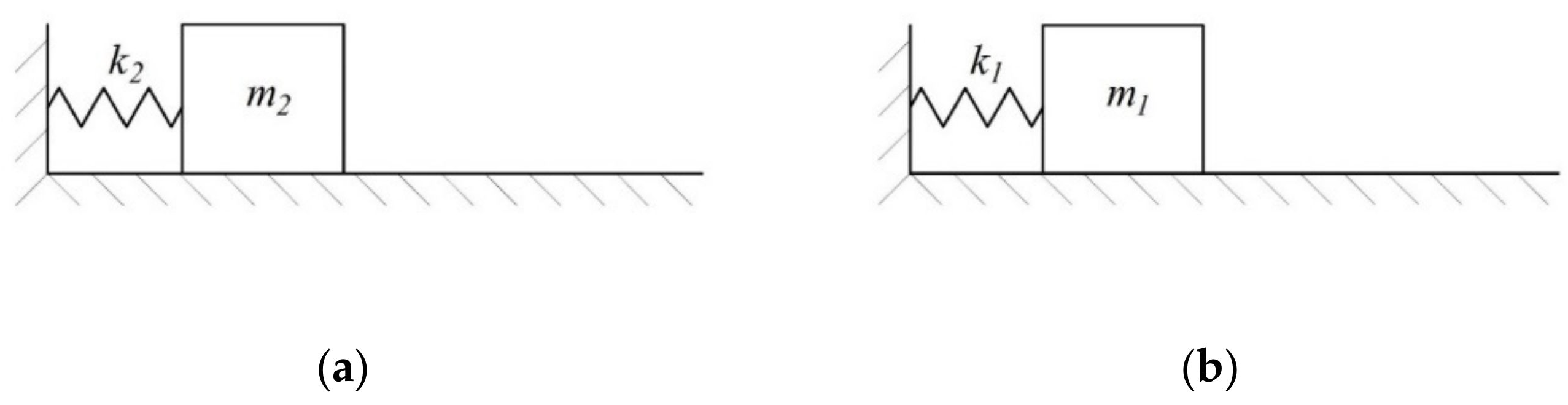
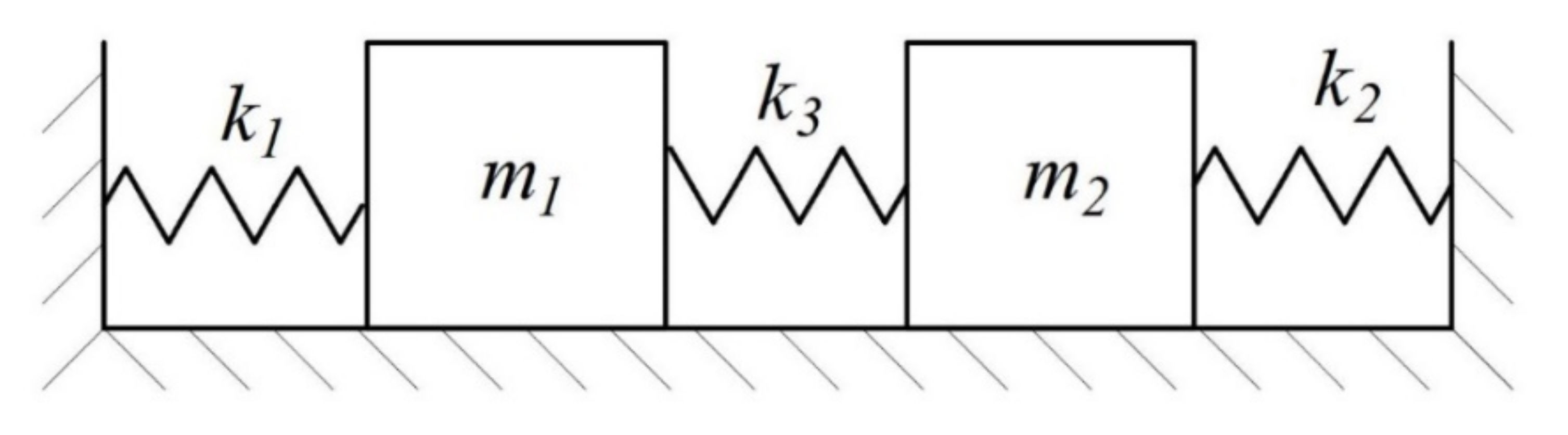
3.2. Establishment of Equivalent Model
- 1.
- The volume of tubes is much smaller than that of cavity Ⅰ and cavity Ⅱ;
- 2.
- The linearity of the cell is much smaller than the wavelength of low-frequency sound waves;
- 3.
- The wall of the cavity does not deform when the air in the inner cavity is compressed and expanded.
4. Discussion
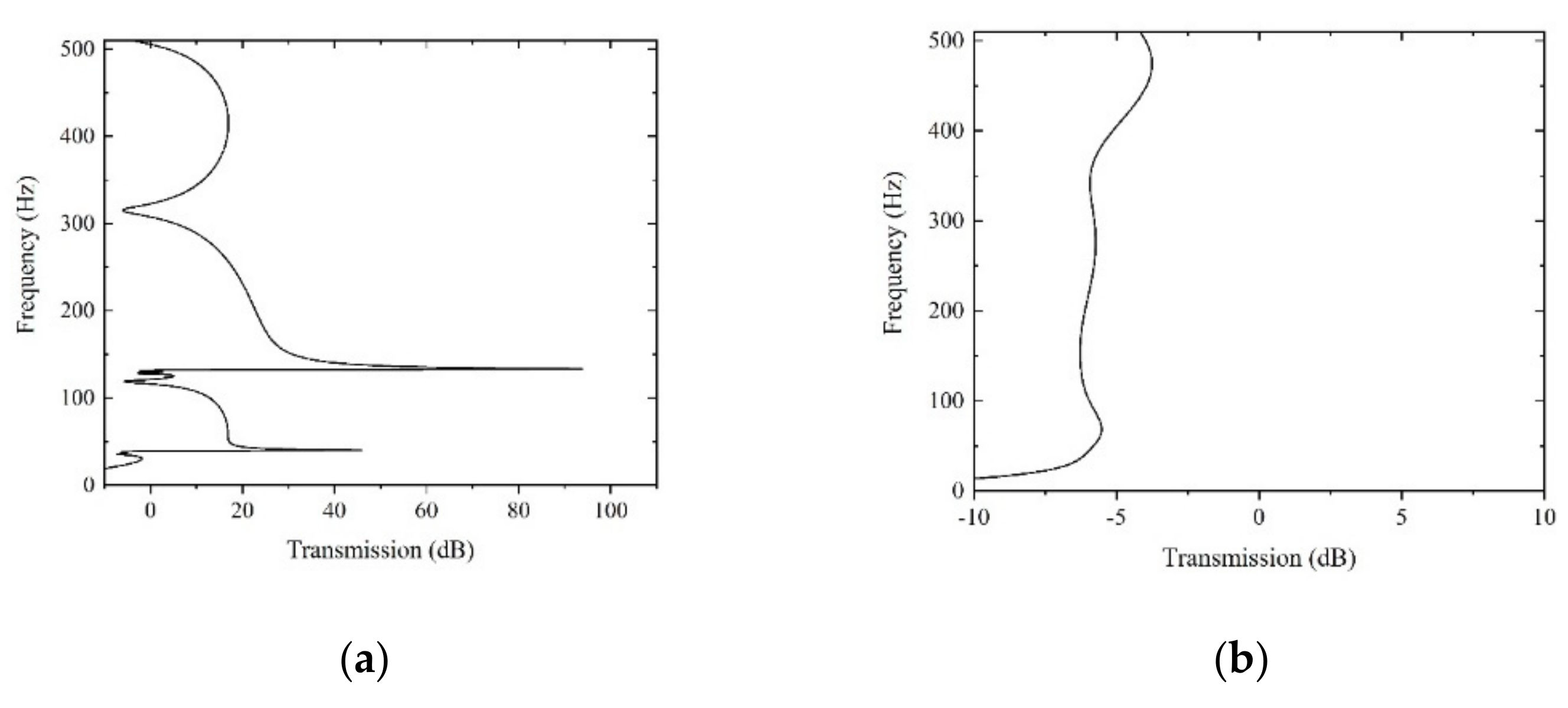
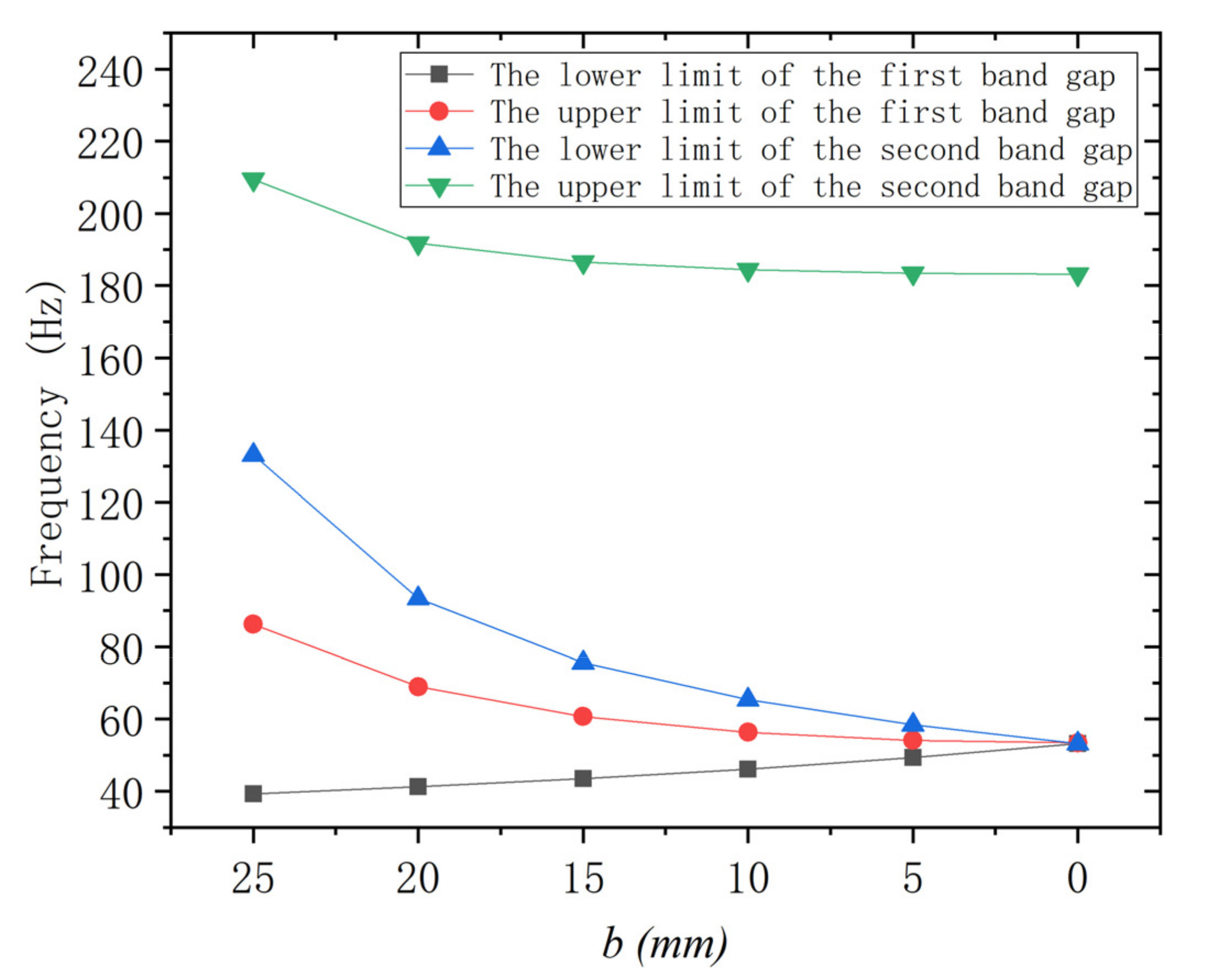
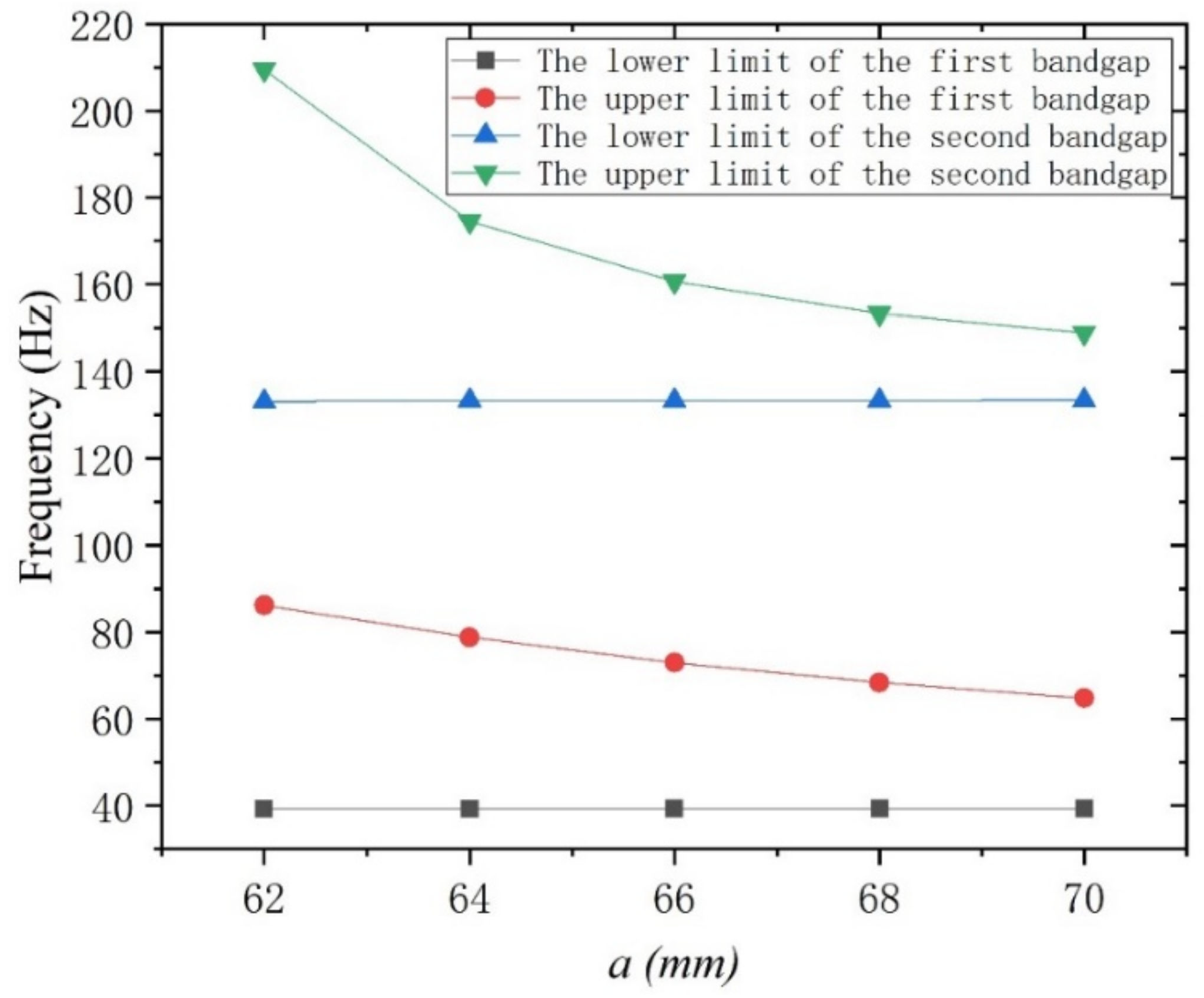
4.1. Influence of Cavity Structure on Band Gap
4.2. Influence of the Spacing of Cells on Band Gap
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ge, H.; Yang, M.; Ma, C.; Lu, M.-H.; Chen, Y.-F.; Fang, N.; Sheng, P. Breaking the barriers: Advances in acoustic functional materials. Natl. Sci. Rev. 2018, 5, 159–182. [Google Scholar] [CrossRef]
- Krushynska, A.O.; Bosia, F.; Pugno, N.M. Labyrinthine Acoustic Metamaterials with Space-Coiling Channels for Low-Frequency Sound Control. Acta Acust. United Acust. 2018, 104, 200–210. [Google Scholar] [CrossRef] [Green Version]
- Liang, Y.-J.; Chen, L.-W.; Wang, C.-C.; Chang, I.-L. An acoustic absorber implemented by graded index phononic crystals. J. Appl. Phys. 2014, 115, 244513. [Google Scholar] [CrossRef]
- Kolken, H.M.A.; Zadpoor, A.A. Auxetic mechanical metamaterials. RSC Adv. 2017, 7, 5111–5129. [Google Scholar] [CrossRef] [Green Version]
- Pedroso, M.; De Brito, J.; Silvestre, J.D. Characterization of walls with eco-efficient acoustic insulation materials (traditional and innovative). Constr. Build. Mater. 2019, 222, 892–902. [Google Scholar] [CrossRef]
- Li, J.; Chan, C.T. Double-negative acoustic metamaterial. Phys. Rev. E 2004, 70, 055602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tian, Y.; Ge, H.; Lu, M.-H.; Chen, Y.-F. Research advances in acoustic metamaterials. Acta Phys. Sin. 2019, 68, 194301. [Google Scholar] [CrossRef]
- Romero-García, V.; Jiménez, N.; Theocharis, G.; Achilleos, V.; Merkel, A.; Richoux, O.; Tournat, V.; Groby, J.-P.; Pagneux, V. Design of acoustic metamaterials made of Helmholtz resonators for perfect absorption by using the complex frequency plane. C. R. Phys. 2020, 21, 713–749. [Google Scholar] [CrossRef]
- Wen, X.S.; Wen, J.H.; Yu, D.L.; Wang, G.; Liu, Y.Z.; Han, X.Y. Phononic Crystals; National Defense Industry Press: Beijing, China, 2009; p. 170. [Google Scholar]
- Wen, J.H.; Wang, G.; Liu, Y.Z.; Wen, X.S. Lumped-mass method on calculation of elastic band gaps of one-dimensional phononic crystals. Acta Phys. Sin. 2004, 53, 3384. [Google Scholar]
- Méndez, J.F.; Reyes, A.C.P.; Jiménez, A.H.H.; Lázaro, R.C.A.; Morales-Sánchez, A.; Moreno, M.M.; Luna-López, J.A.; Carrillo, F.S.; Melo, M.A.M. Discretization Approach for the Homogenization of Three-Dimensional Solid-Solid Phononic Crystals in the Quasi-Static Limit: Density and Elastic Moduli. Appl. Sci. 2022, 12, 2987. [Google Scholar] [CrossRef]
- Fang, N.; Xi, D.; Xu, J.; Ambati, M.; Srituravanich, W.; Sun, C.; Zhang, X. Ultrasonic metamaterials with negative modulus. Nat. Mater. 2006, 5, 452–456. [Google Scholar] [CrossRef]
- Zhou, X.M.; Hu, G.K. Analytic model of elastic metamaterials with local resonances. Phys. Rev. B 2009, 79, 195109. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Lai, Y.; Zhang, Z.-Q. Elastic Metamaterials with Simultaneously Negative Effective Shear Modulus and Mass Density. Phys. Rev. Lett. 2011, 107, 105506. [Google Scholar] [CrossRef]
- Xu, C.; Guo, H.; Chen, Y.; Dong, X.; Ye, H.; Wang, Y. Study on broadband low-frequency sound insulation of multi-channel resonator acoustic metamaterials. AIP Adv. 2021, 11, 045321. [Google Scholar] [CrossRef]
- Han, D.-H.; Zhao, J.-B.; Zhang, G.-J.; Yao, H. Study on Low-Frequency Band Gap Characteristics of a New Helmholtz Type Phononic Crystal. Symmetry 2021, 13, 1379. [Google Scholar] [CrossRef]
- Guan, D.; Wu, J.H.; Jing, L.; Gao, N.; Hou, M. Application of a Helmholtz structure for low frequency noise reduction. Noise Control Eng. J. 2015, 63, 20–35. [Google Scholar] [CrossRef] [Green Version]
- Gao, D.B.; Liu, X.J.; Tian, Z.F.; Zhou, Z.M.; Zeng, X.W.; Han, K.F. A broadband low-frequency sound insulation structure based on two-dimensionally inbuilt Helmholtz resonator. Acta Phys. Sin. 2017, 66, 190. [Google Scholar]
- Luo, Y.Q.; Lou, J.J.; Zhang, Y.B. An acoustic absorbing metamaterial with multi-Helmholtz resonators at low-frequency underwater. Mod. Phys. Lett. B 2021, 35, 2150397. [Google Scholar] [CrossRef]
- Jing, L.; Wu, J.H.; Guan, D.; Gao, N. Multilayer-split-tube resonators with low-frequency band gaps in phononic crystals. J. Appl. Phys. 2014, 116, 103514. [Google Scholar] [CrossRef]
- Cheng, X.; Chen, X.; Rong, J.; Fan, B.; Nisu, A. Low-Frequency Noise Reduction of Rocket Fairings Using Horn-Shaped-Neck Helmholtz Resonators. J. Spacecr. Rocket. 2019, 56, 273–282. [Google Scholar] [CrossRef]
- Jiang, J.L.; Yao, H.; Du, J.; Zhao, J.B.; Deng, T. Low frequency band gap characteristics of double-split Helmholtz locally resonant periodic structures. Acta Phys. Sin. 2017, 66, 136–142. [Google Scholar] [CrossRef]
- He, Z.-H.; Zhao, J.-B.; Yao, H.; Chen, X. Sound insulation performance of Helmholtz cavity with thin film bottom. Acta Phys. Sin. 2019, 68, 148–159. [Google Scholar] [CrossRef]
- Chen, X.; Yao, H.; Zhao, J.-B.; Zhang, S.; He, Z.-H.; Jiang, J.-N. Low frequency band gaps of Helmholtz resonator coupled with membrane. Acta Phys. Sin. 2019, 68, 214208. [Google Scholar] [CrossRef]
- Jiang, J.L.; Yao, H.; Du, J.; Zhao, J. Multi-cavity locally resonant structure with the low frequency and broad band-gaps. AIP Adv. 2016, 6, 115024. [Google Scholar] [CrossRef] [Green Version]
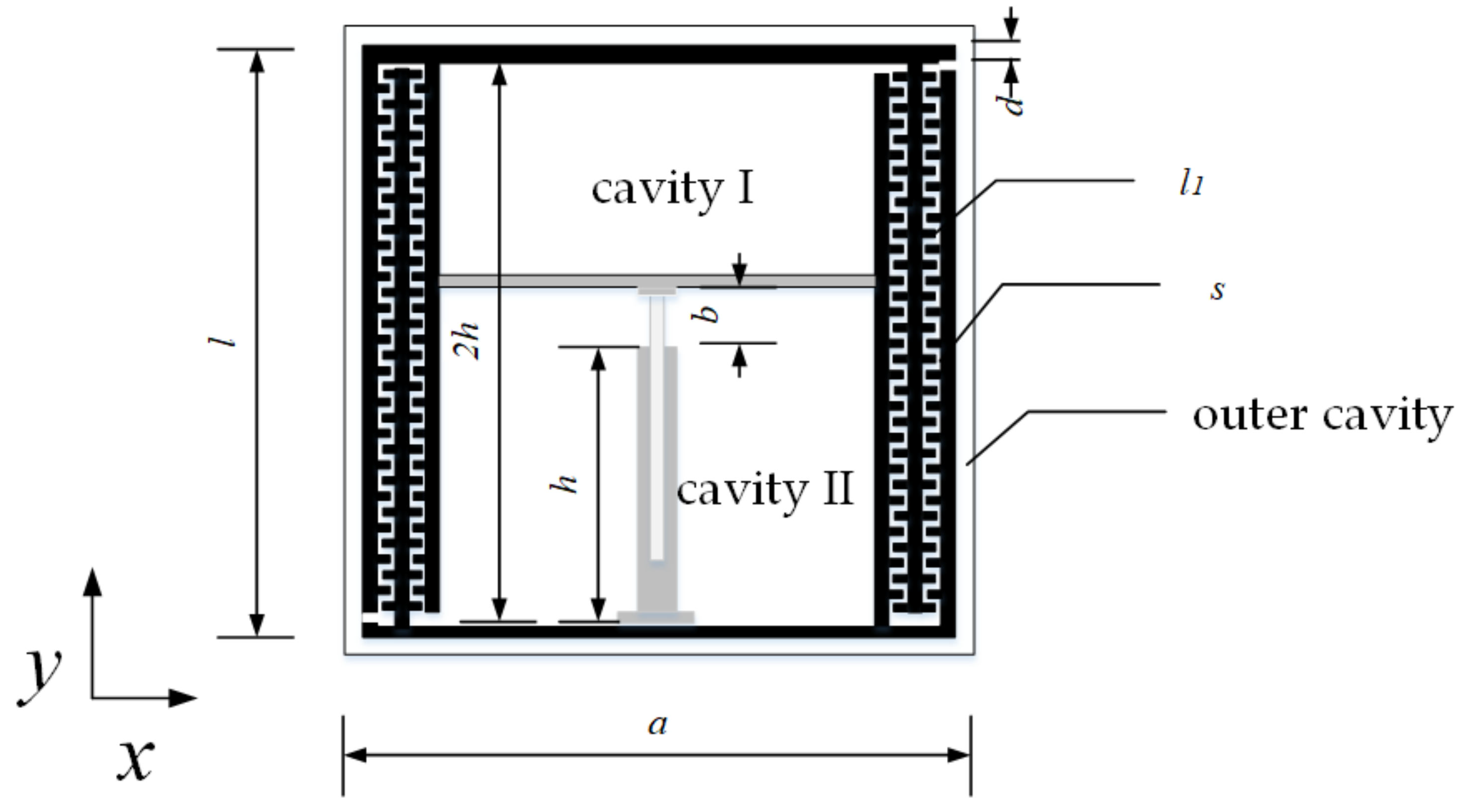


| l/mm | a/mm | s/mm | b/mm | d/mm | l1/mm | h/mm |
|---|---|---|---|---|---|---|
| 60 | 62 | 0.35 | 25 | 0.5 | 254.8 | 24.5 |
| Methods | The Lower Limit of the First Band Gap | The Upper Limit of the First Band Gap | The Lower Limit of the Second Band Gap | The Upper Limit of the Second Band Gap |
|---|---|---|---|---|
| FEM/Hz | 39.27 | 86.18 | 133.12 | 209.44 |
| Equivalent model/Hz | 37.73 | 88.45 | 134.80 | 212.89 |
| Error | −3.92% | 2.63% | 1.26% | 1.64% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, D.; Zhang, G.; Zhao, J.; Yao, H.; Liu, H. Study on Band Gap and Sound Insulation Characteristics of an Adjustable Helmholtz Resonator. Appl. Sci. 2022, 12, 4512. https://doi.org/10.3390/app12094512
Han D, Zhang G, Zhao J, Yao H, Liu H. Study on Band Gap and Sound Insulation Characteristics of an Adjustable Helmholtz Resonator. Applied Sciences. 2022; 12(9):4512. https://doi.org/10.3390/app12094512
Chicago/Turabian StyleHan, Donghai, Guangjun Zhang, Jingbo Zhao, Hong Yao, and Hong Liu. 2022. "Study on Band Gap and Sound Insulation Characteristics of an Adjustable Helmholtz Resonator" Applied Sciences 12, no. 9: 4512. https://doi.org/10.3390/app12094512
APA StyleHan, D., Zhang, G., Zhao, J., Yao, H., & Liu, H. (2022). Study on Band Gap and Sound Insulation Characteristics of an Adjustable Helmholtz Resonator. Applied Sciences, 12(9), 4512. https://doi.org/10.3390/app12094512





