Heat Transfer Analysis of the Flat Plate Solar Thermal Collectors with Elliptical and Circular Serpentine Tubes

Abstract

In this study, the heat transfer characteristics of the flat plate collectors with circular and elliptical serpentine tubes are theoretically analyzed and compared in terms of $\dot{m}$, $Re$, $Nu$, $h_{fi}$, $F_R$, $Q_u$, and ${\mu }_{Th}$ under various water flow rates and the standard test conditions. The results reveal that the maximum ${\mu }_{Th}$ correspondence to the elliptical serpentine design with 56% under turbulent flow, and the minimum ${\mu }_{Th}$ of 47% for the circular cross-section under laminar flow. In addition, it was found that the highest useful energy gain per unit time (493.8 W) through the system is possible when $F_R$, $h_{fi}$, $Nu$, and $\dot{m}$ are maximum and vice versa. It was concluded that, at the same area, the larger contact area in the elliptical cross-section compared to the circular would improve $F_R$ and $Q_u$ by an average of 2%. Overall, it is crucial to evaluate the thermal parameters of the thermal collector during the preliminary design stage to fabricate a highly efficient system and save time as well as initial cost.

1. Introduction

Today, energy resource shortages and global warming concerns are growing rapidly due to increasing worldwide energy demand by ongoing industrialization, urbanization, and population growth [1,2,3,4,5]. Hence, renewable energy sources and improving energy efficiency have attracted attention and remain a high priority globally. Over the past few decades, several different resources for sustainable power generation have been considered [6,7,8]. Solar energy is an appropriate alternative to conventional counterparts due to technological developments and its global availability [9,10,11,12]. There are a variety of technologies for harvesting solar energy, which is now cost-effective, practical, and sustainable [13,14,15]. Solar is mainly extracted by employing solar cells and thermal collectors to produce electrical and thermal energy [16,17,18]. Electricity generation is the function of the solar cells known as the Photovoltaic (PV), while thermal generation is accessible using a solar thermal collector [19,20,21].

The flat plate solar thermal collectors (FPSCs) are the conventional solar thermal collectors. The FPSCs absorb solar radiation through a highly absorptive surface (plate) and convey the extracted heat into a working medium (water, air, nanofluid), circulating inside the tubes naturally or using external force. The obtained thermal energy can be stored and utilized for hot water provision, space heating/cooling/drying, industrial energy demand, and applications demanding moderate temperature energy delivery (less than $100 °\mathrm{C}$) [22,23,24,25,26,27,28,29]. Their low-maintenance structures are regularly positioned with a set orientation tailored for a specific location, such as a rooftop or as an integral component of a wall body [22]. A standard FPSC has a glass or plastic cover (called glazing), an insulated metal box, and an absorbing metal plate. The tubes are bonded to the absorbing plate in various designs [30,31].

The FPSCs can be classified into four sub-categories (Figure 1); however, the serpentine design is the most suitable type [32]. A serpentine tube includes a one-way flow channel that provides higher fluid temperature differences through the system because the water stays more in the collector given the greater tube length, which can be implemented. The serpentine designs benefit the lower manufacturing costs and stay efficient even at low flow rates, improving thermal stratification in the water tanks [30,33]. Figure 2 indicates the FPSC with serpentine tubes [30]. Water is regarded as the most typical working fluid used through solar thermal systems that benefit from its cooling characteristics, abundance, economic viability [34]. Due to the higher thermal capacity of water, the water-based systems have higher efficiency than the air-based systems [35,36]. The solar thermal collectors can be integrated with PV panels to form a hybrid photovoltaic thermal (PV/T) system that produces both heat and electricity. Several studies have proved that due to heat dissipation from PV panels, a PV/T collector performance as a single combined system is superior to a photovoltaic system and a thermal collector being employed separately [17,18,37,38,39,40].

The heat transfer rate (the useful energy gain) is the major contributing factor to the design of any solar thermal system and is mainly affected by tube configuration and thermal properties of the working fluid. Increasing the contact surface between the absorber plate and working fluid improves the heat transfer rate, generally [41]. Mohammadi Sardouie et al. [42] numerically and experimentally studied the cross-section of the different thermal collector designs. They found that square cross-sectional tubes have a better heat transfer rate than round tube collectors due to the greater contact area, which suffers from a smaller contact surface in their design. Razi et al. [43] investigated the heat transfer characteristics of the circular and flattened tubes in an experimental study. They found that the heat transfer coefficient was enhanced notably for flattened tube collectors at the same flow conditions compared to circular tubes. Rosli et al. [23] theoretically investigated the round, square, and rectangular tubes. They argued that rectangular cross-sections had superior heat transfer performance to round and square counterparts.

Literature review revealed that only a few studies focused on developing serpentine collector designs with different and effective cross-sections (

Table 1. Literature reviews regarding serpentine designs with different cross-sections.

Authors	Year of Study	Cross-Section	Type of Study	Location
Xu et al. [44]	2020	Circular	Experimental	China
Korres and Tzivanidis [30]	2018	Circular	theoretical	Greece
Shah et al. [45]	2018	Circular	Experimental and simulation	India
Al-Waeli et al. [46]	2017	Circular	Experimental	Malaysia
Jarimi et al. [47]	2016	Circular	theoretical and experimental	Malaysia
Rosli et al. [23]	2014	Circular, rectangular, and square	Theoretical	Malaysia
Ibrahim et al. [48]	2009	Circular	Theoretical and simulation	Malaysia

), while for typical cooling applications such as solar thermal collectors, heat transfer enhancement greatly depends on the tube cross-section. Analytical studies regarding appropriate tube configurations before the manufacturing stage will lead to designing the foremost and most effective solar thermal systems.

This research aims to theoretically analyze the heat transfer characteristics of serpentine solar thermal collectors with elliptical and circular cross-sections. The solar thermal collector performance will be evaluated in terms of the mass flow rate, Reynolds number, Nusselt number, heat transfer coefficient, heat removal factor, useful energy gain, and thermal efficiency. These heat transfer controlling parameters must be calculated and determined before any manufacturing process to achieve a highly efficient and cost-effective design. This process paves the way for future research as well as encourages public investment in solar thermal collectors’ technologies.

2. Materials and Methods

Evaluation of Heat Removal Factor

The performance of a flat plate solar collector can be defined by several different operational and design factors [33]. The instantaneous thermal energy per unit time or the useful energy gain ($Q_u$) generated by an FPSC can be expressed using the Hottel and Whillier-Bliss Equation [32,49,50], as in Equation (1):

$$Q_u=A_C{F}_R\left[\left(G_T\left(\tau \alpha \right)-U_L\left(T_i-T_a\right)\right)\right]$$

(1)

According to the Hottel and Whillier-Bliss Equation, the contributing variables are the incident solar flux (G_T), the heat removal factor (F_R), the collector area (A_C), the total heat loss coefficient (U_L), and the effective transmittance-absorptance product of the cover system ($\tau \alpha$). T_a and T_i are the ambient and the fluid inlet temperature, respectively. S is equal G_T ($\tau \alpha$) and represents the absorbed solar energy per unit time per unit area of the collector and is equal to G_T ($\tau \alpha$). Thus, F_R can be expressed as in Equation (2) [32,51]:

$$F_R=\frac{\dot{m}{C}_P\left(T_o-T_i\right)}{A_C\left[S-U_L\left(T_i-T_a\right)\right]}$$

(2)

In Equation (2), the working fluid’s mass flow rate is expressed by $\dot{m}$. C_p and T_o denote the fluid specific heat and the outlet temperature, respectively. If F_R and U_L values are computed appropriately, it is possible to calculate the useful energy gain of the FPSCs (Equation (1)). F_R determines the effectiveness of a solar thermal collector design, and all factors that contribute to FPSC efficiency are combined into it [51,52]. It is explained as the ratio of actual $Q_u$ to the maximum possible $Q_u$ of a collector. The highest possible $Q_u$ (heat transfer) is achieved when the collector temperature is the same as the working fluid’s inlet temperature and the collector’s heat loss is minimum. Figure 3 shows the schematic diagram of a flat plate serpentine tube collector with inside and outside diameters of $D_i$ and $D_o$, respectively. The collector consists of an absorbing metal plate with a thickness of ${\delta }_P$ and thermal conductivity of $K_P$. The N segments of the serpentine tube with a spacing of W and length of $L_s$ are attached to the plate. The first and last segments are placed at a distance of $\frac{W}{2}$ from their respective ends of the plate. The area ($A_C$) of the collector was described as $A_C=W\times N\times L_s$ [32,49,50,51,52,53,54,55].

Due to a serpentine collector’s complicated heat transfer model, the heat removal factor cannot be simply expressed using Equation (2). Several authors [44,51,52,53,54,55] have proposed various analytical solutions and modifications to obtain the heat removal factor of a serpentine design during the last four decades. Zhang and Lavan [32,49] used matrix differential equations to modify the serpentine flow equations [44]. They pointed out that F_R can be determined through a set of non-dimensional parameters $F_1$–$F_6$ within Equation (3) as defined below. Equations (3)–(9) are proper for any number of bends if $F_3$ is greater than about 1 [32,53].

$$F_R=F_1\times F_3\times F_5\times \left[\frac{2F_4}{F_6\times exp\left(\frac{-\sqrt{1-F_2^2}}{F_3}\right)+F_5}-1\right]$$

(3)

$$F_1=\frac{Nk{L}_S}{U_L{A}_C}\frac{kR{\left(1+\gamma \right)}^2-1-\gamma -kR}{{\left[kR\left(1+\gamma \right)-1\right]}^2-{\left(kR\right)}^2}$$

(4)

$$F_2=\frac{1}{kR{\left(1+\gamma \right)}^2-1-\gamma -kR}$$

(5)

$$F_3=\frac{\dot{m}{C}_P}{F_1{U}_L{A}_C}$$

(6)

$$F_4={\left[\frac{1-F_2^2}{F_2^2}\right]}^{\frac{1}{2}}$$

(7)

$$F_5=\frac{1}{F_2}+F_4-1$$

(8)

$$F_6=1-\frac{1}{F_2}+F_4$$

(9)

where the parameters $n, k,$ and $\gamma$ are non-dimensional quantities and can be calculated as follows [39,40,41,42,43,44]:

$$n=\sqrt{\frac{U_L{\left(W-D_o\right)}^2}{K_p{\delta }_p}}$$

(10)

$$k=\frac{K_p{\delta }_{p}n}{\left(W-D_o\right)\sinh n}$$

(11)

$$\gamma =-2\cosh n-\frac{D_o{U}_L}{k}$$

(12)

The value of the total heat loss coefficient (U_L) is obtained through subsequent equation [15,42]:

$$\begin{gathered} U_L={\left(\frac{N_g }{\frac{c}{T_m}{\left[\frac{T_m-T_a}{N_g+f}\right]}^e}+\frac{1}{h_w}\right)}^{-1}+\left(\frac{\sigma \left(T_m+T_a\right)\left(T_m^2+T_a^2\right)}{\frac{1}{{\epsilon }_p+0.00591N_g{h}_w}+\frac{2N_g+f-1+0.133{\epsilon }_p}{{\epsilon }_g}-N_g}\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{k_{bin}}{{\delta }_{bin}}+\frac{\frac{K_{ein}}{{\delta }_{ein}}\times P_c\times {\delta }_c}{A_c} \end{gathered}$$

(13)

$$c=520\left(1-0.000051{\theta }^2\right) for 0<\theta <70°$$

(14)

$$e=0.430\left(1-\frac{100}{T_m}\right)$$

(15)

$$f=\left(1+0.089h_w-0.1166h_w{\epsilon }_p\right)\left(1+0.07866N_g\right)$$

(16)

The parameter R is the thermal resistance between the absorbing plate and working fluid, and is written as [29,39,40,41,42,43,44]:

$$R=\frac{1}{\pi h_{fi}{D}_i}+\frac{1}{C_b}$$

(17)

where, $h_{fi}$ is the heat transfer coefficient:

$$h_{fi}=\frac{\left(Nu\right)K_w}{D_i}$$

(18)

In Equation (18), the Nusselt number $\left(Nu\right)$ is gained by Equations (19)–(21) [55,56]:

$$Nu=1.86+{\left(\frac{RePr{D}_i}{L}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}{\left(\frac{{\mu }_b}{{\mu }_w}\right)}^{0.14}for laminar flow$$

(19)

$$Nu=0.023{\left(Re\right)}^{\frac{2}{3}}{(\mathrm{Pr})}^{0.4}{\left(\frac{{\mu }_b}{{\mu }_w}\right)}^{0.14}for transition flow$$

(20)

$$Nu=0.023{\left(Re\right)}^{0.8}{(\mathrm{Pr})}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}{\left(\frac{{\mu }_b}{{\mu }_w}\right)}^{0.14} for turbulent flow$$

(21)

while the Reynolds ($Re$) and the Prandtl ($Pr$) numbers are defined by Equations (22) and (23) [55]:

$$Re=\frac{D_{i}V\rho }{{\mu }_d}$$

(22)

$$Pr=\frac{{\mu }_d{C}_P}{K_w}$$

(23)

The thermal efficiency (${\mu }_{Th}$) of the collector is calculated by Equation (24) [30]:

$${\eta }_{Th}=\frac{Q_u}{A_{C}S}$$

(24)

where, $Q_u$, $A_C$, and $S$ denotes the useful energy gain, collector area, and absorbed solar energy, respectively.

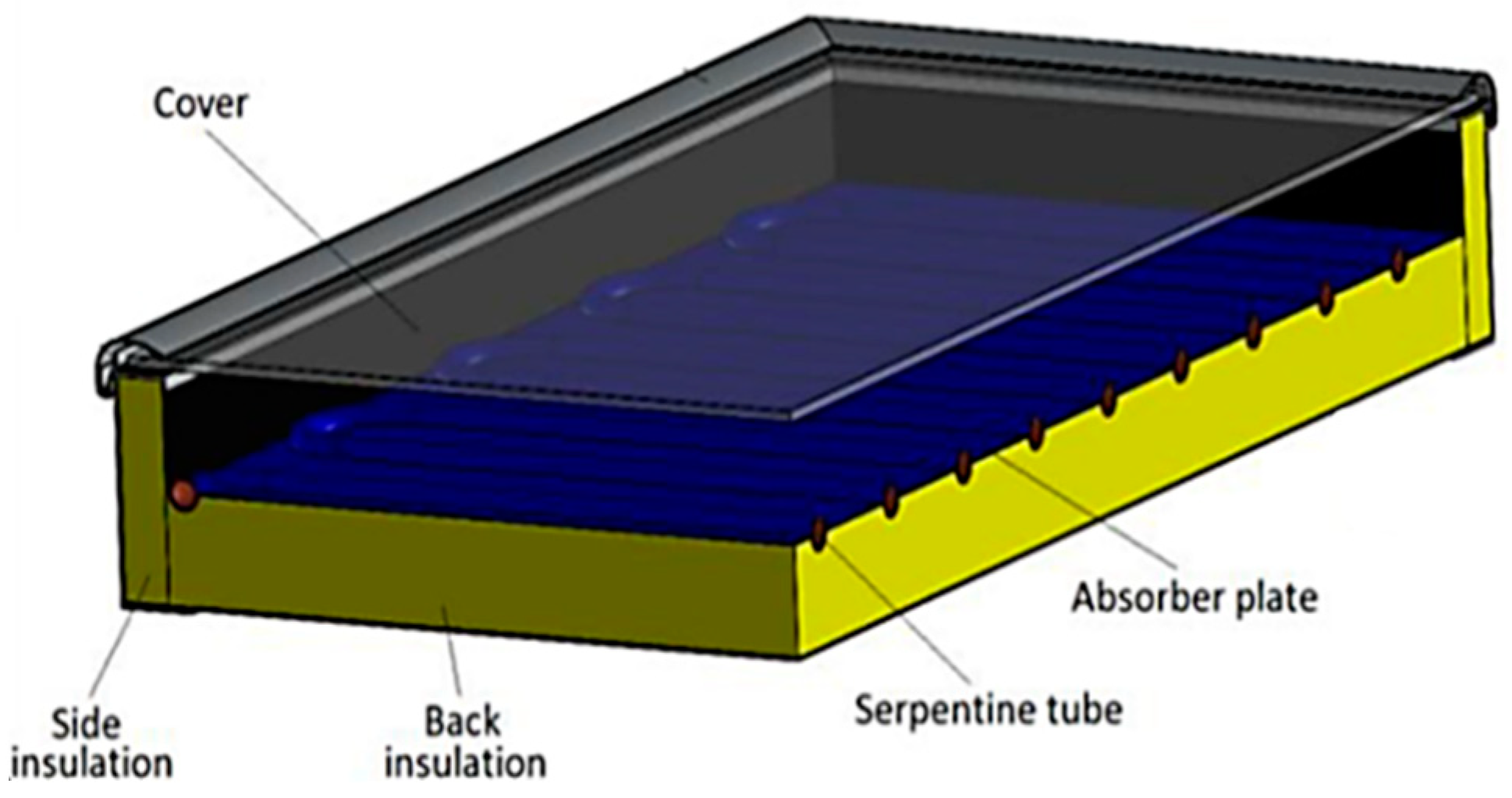
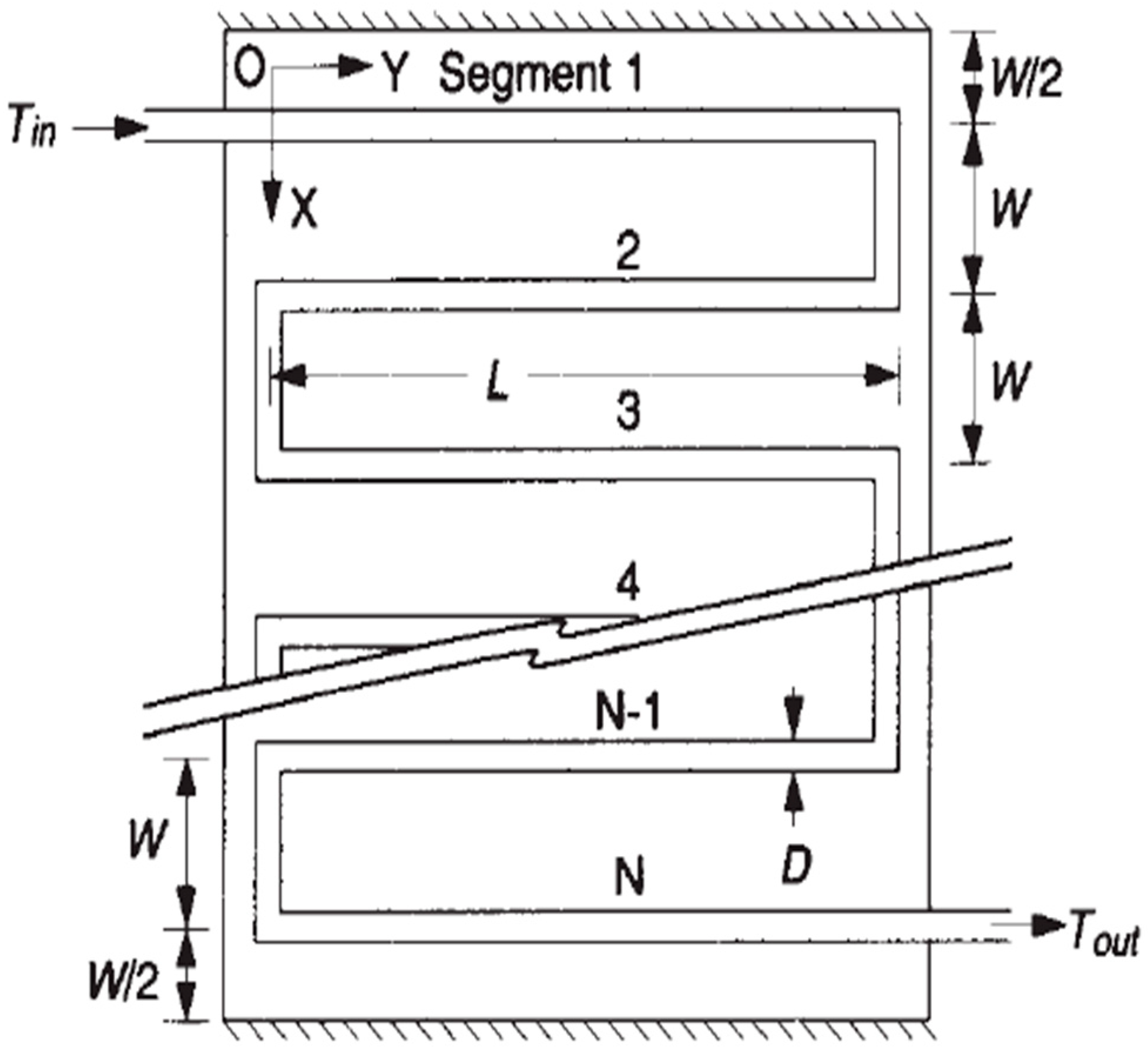
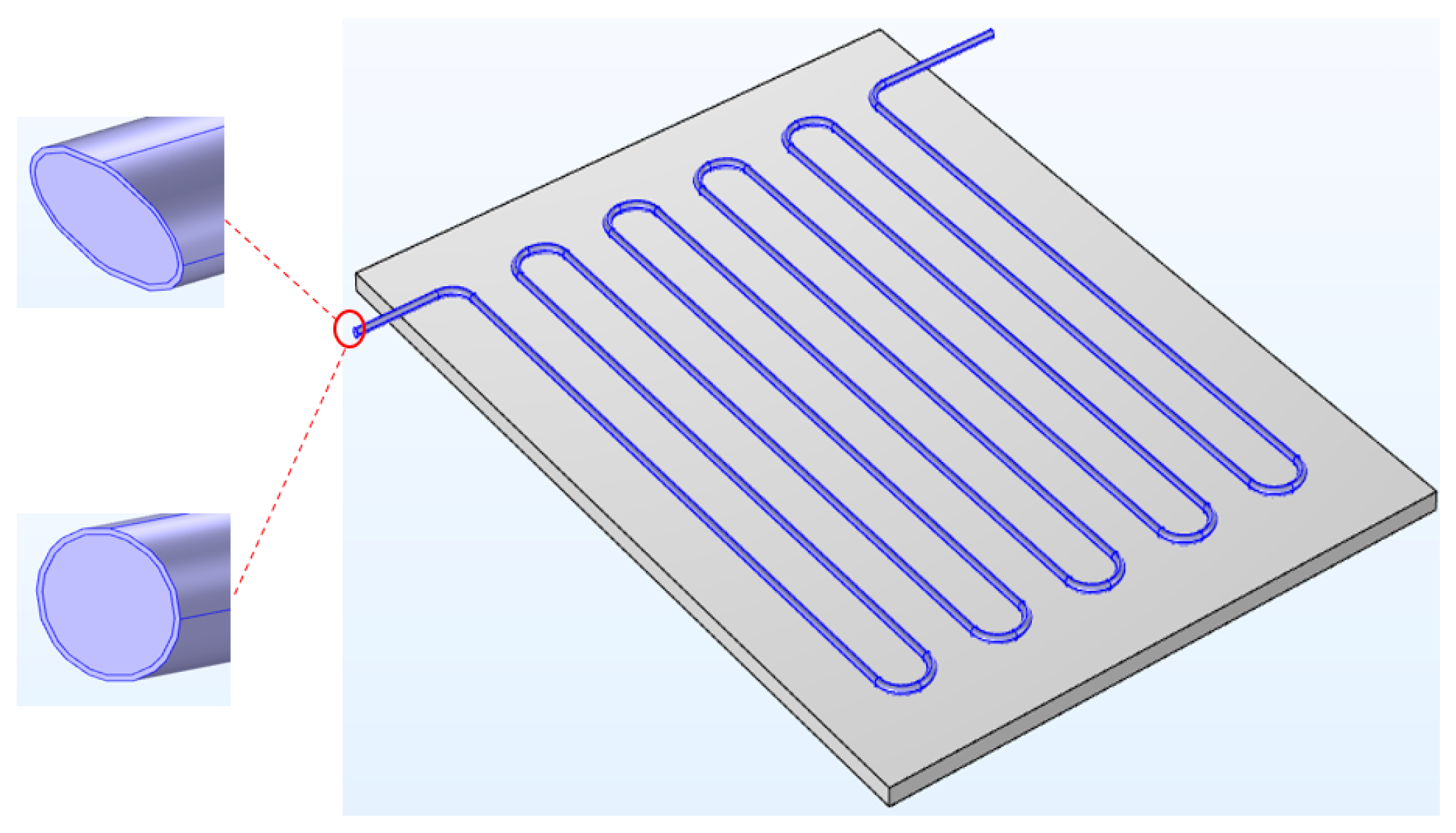
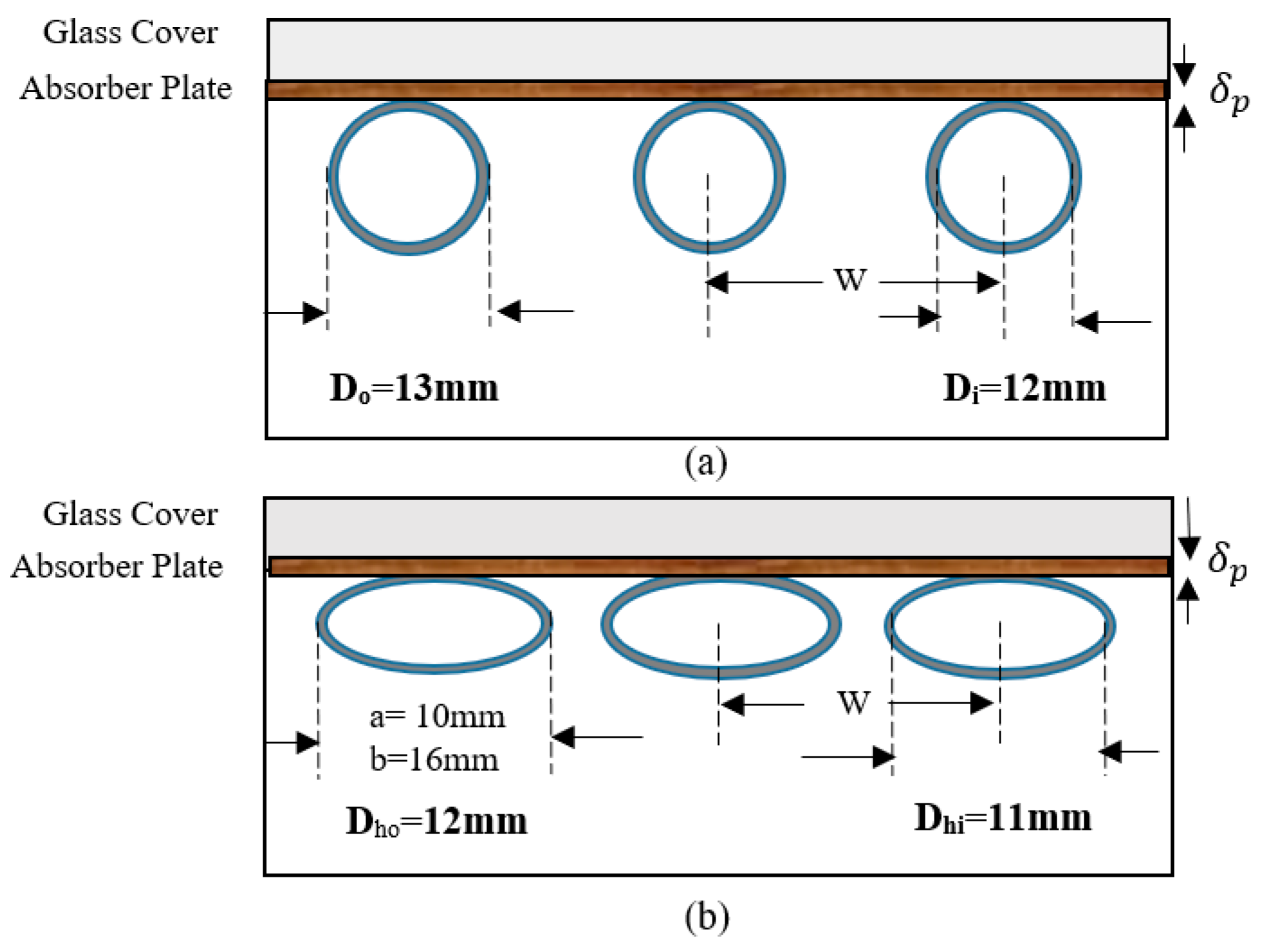
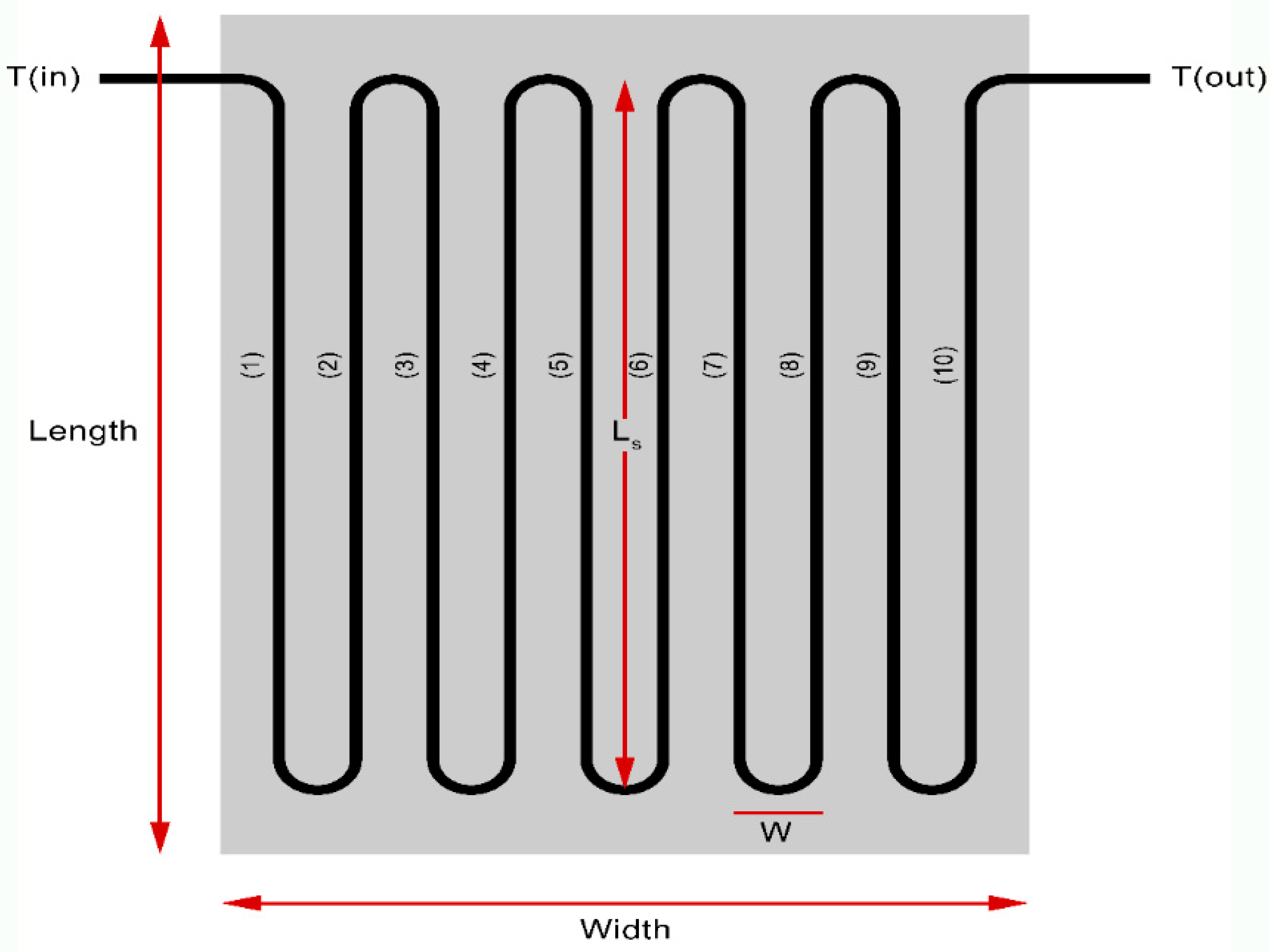
3. Design of the Flat Plate Solar Collectors with Elliptical and Circular Serpentine Tubes

Figure 4 and Figure 5 indicate the proposed elliptical and circular serpentine tubes in 3D and cross-sectional views. The technical manufacturing data and design parameters are summarized in

Table 2. Technical data on manufacturing serpentine tubes with elliptical and circular cross-sections.

Components	Material	$\mathbf{Thickness} \left(\mathit{\delta }\right)$	Optical and Thermal Properties
Metal box	Aluminum	35 mm	$K_{Aluminum}=205$$\left({\mathrm{W} \mathrm{m}}^{-1}{\mathrm{K}}^{-1}\right)$
Cover	Glass with anti-reflecting coating	5 mm	${\epsilon }_g=0.88$ $N_g=1$
Metal absorber plate	Zinc oxide	1 mm	${\epsilon }_p=0.13, K_P=60 \left({\mathrm{W} \mathrm{m}}^{-1}{\mathrm{K}}^{-1}\right)$
Serpentine tubes	copper	1 mm	$K_{Copper}=385 \left({\mathrm{W} \mathrm{m}}^{-1}{\mathrm{K}}^{-1}\right)$
Back insulation	Glass wool	20 mm	$K_{bin}=0.04 \left({\mathrm{W} \mathrm{m}}^{-1}{\mathrm{K}}^{-1}\right)$
Side insulation	Glass wool	20 mm	$K_{ein}=0.04 \left({\mathrm{W} \mathrm{m}}^{-1}{\mathrm{K}}^{-1}\right)$

and

Table 3. Values of different parameters to determine FR.

Symbols	Parameters	Values
Ls	Length of the serpentine segments	$1.1 \left(\mathrm{m}\right)$
W	Serpentine spacing	$0.08 \left(\mathrm{m}\right)$
N	Number of segments in the serpentine tube	10
Ac	Collector area	$0.88 \left({\mathrm{m}}^2\right)$
Cp	$\mathrm{Specific} \mathrm{heat} \mathrm{capacity} \mathrm{of} \mathrm{water} \mathrm{at} 25 °\mathrm{C}$	$0.6 \left({\mathrm{J} \mathrm{kg}}^{-1}{ \mathrm{K}}^{-1}\right)$
Kw	$\mathrm{Thermal} \mathrm{conductivity} \mathrm{of} \mathrm{water} \mathrm{at} 25 °\mathrm{C}$	$0.6 \left({\mathrm{W} \mathrm{m}}^{-1} {\mathrm{K}}^{-1}\right)$
Ta	Ambient temperature	$298 \left(°\mathrm{K}\right)$
Tm	Mean plate Temperature	$297.5 \left(°\mathrm{K}\right)$
Ti	Inlet fluid temperature	$295 \left(°\mathrm{K}\right)$
$\theta$	Collector tilt	$15°$
Lbl	Collector back length	$1.3 \left(\mathrm{m}\right)$
Lbw	Collector back width	$1 \left(\mathrm{m}\right)$
Pc	Collector perimeter	$4.8 \left(\mathrm{m}\right)$
hw	Wind heat transfer coefficient	$10 \left({\mathrm{W} \mathrm{m}}^{-2}{ \mathrm{K}}^{-1}\right)$
µd	$\mathrm{Dynamic} \mathrm{viscosity} \mathrm{at} 25 °\mathrm{C}$	$8.9 \times {10}^{-4} \left(\mathrm{Pa}·\mathrm{s}\right)$
µb	$\mathrm{The} \mathrm{bulk} \mathrm{viscosity} \mathrm{at} 25 °\mathrm{C}$	$2.47 \times {10}^{-3} \left(\mathrm{Pa}·\mathrm{s}\right)$
μw	$\mathrm{The} \mathrm{wall} \mathrm{viscosity} \mathrm{at} 25 °\mathrm{C}$	$1.00 \times {10}^{-3} \left(\mathrm{Pa}·\mathrm{s}\right)$
$\sigma$	Stephen Boltzmann constant	$5.67 \times {10}^{-8} \left({\mathrm{W} \mathrm{m}}^{-2}{ \mathrm{K}}^{-4}\right)$
S	Absorbed solar energy	$1000 \left({\mathrm{W} \mathrm{m}}^{-2}\right)$
$\rho$	$\mathrm{Density} \mathrm{of} \mathrm{water} \mathrm{at} 25 °\mathrm{C}$	$997 ({\mathrm{kg} \mathrm{m}}^{-3}$)

. Table 2 shows the materials’ optical and thermal properties of the collector’s components, whereas the collector’s dimension and contributing parameters to determine F_R are listed in Table 3.

An analytical investigation was conducted on each design of an elliptical and a circular serpentine solar collector. Figure 6 represents the preliminary design of an elliptical and a circular serpentine solar collector using water as the working fluid. It is worth mentioning that all numerical calculation was carried out under the standard test conditions ($S=$ 1000 W ${\mathrm{m}}^{-2}$, $T_a$ = 25$°\mathrm{C}$). To investigate non-circular cross-sections such as elliptical, the authors used the concept of hydraulic diameter ($D_h$). For an ellipse, the hydraulic diameter is defined by Equation (25) [57]:

$$D_h=\frac{a\times b}{\sqrt{\frac{a^2+b^2}{2}}}$$

(25)

where $a$ and $b$ are the minor and major axes of the ellipse, respectively. For a circle, $D_h$ is equivalent to circle diameter. To investigate the role of working fluid patterns within the tubes with different cross-section geometry, the Reynolds number ($Re$) assumed laminar ($Re<2300$), transition ($2300<Re<4000$), and turbulent ($Re>4000$). The bond conductance ($C_b$) is an important parameter in evaluating solar thermal collector performance. The experiments have proved that good contact between the absorbing plate and the tube in the thermal collectors leads to a bond conductance greater than 30 W/m $°\mathrm{C}$ and prevents significant heat loss [53]. In this study, it was supposed that the absorbing plate was bound to the tubes effectively. Thus, the term ($\frac{1}{C_b}$), in Equation (17), is negligible.

4. Results and Discussion

Figure 7 indicates that $Re$, $Nu$, and $F_R$ show an upward trend by increasing $\dot{m}$ from 0.01 to 0.05 (kg s⁻¹) for both cross-sections. The Nusselt number values for laminar flow ($Re<2300$) are less than 10, while they increase approximately two times for the Reynolds number greater than 2300 (non-laminar flow). It means that the heat transfer characteristics of the working fluid (water) will improve under non-laminar flow rates. The Nusselt number is slightly higher for the elliptical cross-section. Thus, the heat transfer will be higher compared to the circular one. The highest values of the heat removal factor correspond to the elliptical and circular cross-section under turbulent flow ($\dot{m}=$ 0.05 (kg s⁻¹)) with 0.539 and 0.538, respectively.

As shown in Figure 8, raising $\dot{m}$ from 0.01 to 0.05 (kg s⁻¹) will lead to a higher $h_{fi}$, $F_R$, $Q_u$, and ${\mu }_{Th}$ for both cross-sections. It means that the cooling effect of water will increase by mass flow rate directly. The highest values for heat removal factor, useful energy gain, and thermal efficiency are possible when the heat transfer coefficient is maximum and vice versa for both cross-sections. All heat transfer parameters increase significantly by changing $\dot{m}$ from 0.02 to 0.03 (kg s⁻¹). It is due that water flow moves from laminar to transition states at these flow rates. The largest amounts of useful energy gain (493.8 W and 493 W) and thermal efficiency (56% and 55.8%) correspond to the elliptical and circular cross-sections, respectively, with $\dot{m}=$0.05 (kg s⁻¹) (turbulent flow).

As it can be seen from Figure 9, $Re$ values directly impact the heat transfer governing factors of the system, namely $h_{fi}$, $F_R$, $Q_u$, and ${\mu }_{Th}$. $h_{fi}$ rises approximately three times by increasing $Re$ from laminar to turbulent flow for both cross-sections. All governing parameters increase sharply by changing laminar to transition flow ($Re$ > 2300). It is due that the Nusselt number (Figure 7) will increase significantly by altering laminar to transition flow; however, they raise smoothly under laminar flow ($Re<2300$) and from transition ($2300<Re<4000$) to turbulent ($Re$ > 4000) flow rates. As explained previously, however, the Reynolds numbers are higher for the circular tube, the heat transfer rate decreases due to the greater hydraulic diameter value for circular cross-section (13 mm) compared to the elliptical one (12 mm) at the same area.

Figure 10 shows the contributing factors in determining ${\mu }_{Th}$ in one diagram. $Q_u$ and ${\mu }_{Th}$ are plotted by bar charts and $h_{fi} \mathrm{is} \mathrm{shown} \mathrm{by}$ line graphs, respectively. The bar chart colour and thickness are related to $F_R$ and $\dot{m}$ values, respectively. In addition, the darkest and the lightest blue in the bar charts are related to the maximum and minimum $F_R$ values, respectively. The thickness of the line graphs represents $Nu$ amounts. As it can be seen, the maximum $Q_u$ and ${\mu }_{Th}$ (493.8 W and 56%, respectively) are accessible using the elliptical cross-section tube with ($Nu$= 16.5, $F_R$= 0.539, and $h_{fi }$= 827 $\left({\mathrm{Wm}}^{-2}{\mathrm{K}}^{-1}\right)$). It means that the larger contact area for the elliptical tube compared to the circular one will improve $F_R$ and $Q_u$ by an average of 2%.

5. Validation of Results

It has been proven that the heat transfer rate will rise by increasing the contact surface between the working fluid and the solid surface of the tube, generally. Al-Tajer et al. [58] conducted experiments on the heat transfer performance of circular and elliptical cross-sectional tubes under identical circumference and surface areas. They used Nanofluid (Al₂O₃-distilled water) as the working fluid and investigated the Nusselt number and the Reynolds number under turbulent flow conditions. The results revealed that the heat transfer coefficient and Nusselt number increased by increasing the Reynolds number and the nanoparticle volume concentration to 1.5%. Additionally, the elliptical tube showed a small enhancement in heat transfer since the obtained Nusselt number was higher compared to circular cross-sectional tube. This means that the mathematical modelling results of this paper are in good agreement with experimental findings of previous works.

6. Conclusions

The flat plate solar collector (FPSC) performance depends on contributing factors such as $\dot{m}$, $Re$, $Nu$, $h_{fi}$, $F_R$, $Q_u$, and ${\mu }_{Th}$. In this paper, the heat transfer characteristics of the flat plate solar thermal collectors with circular and elliptical serpentine designs, using water as the working fluid, were theoretically investigated in detail under the standard test conditions ($S=$1000 W${\mathrm{m}}^{-2}$, $T_a$= 25$°\mathrm{C}$). It was concluded that:

• The lower manufacturing costs and high efficiency even at low flow rates of circulating fluid are principal advantages of serpentine designs compared to their counterparts. However, they require pumping systems at higher flow rates.
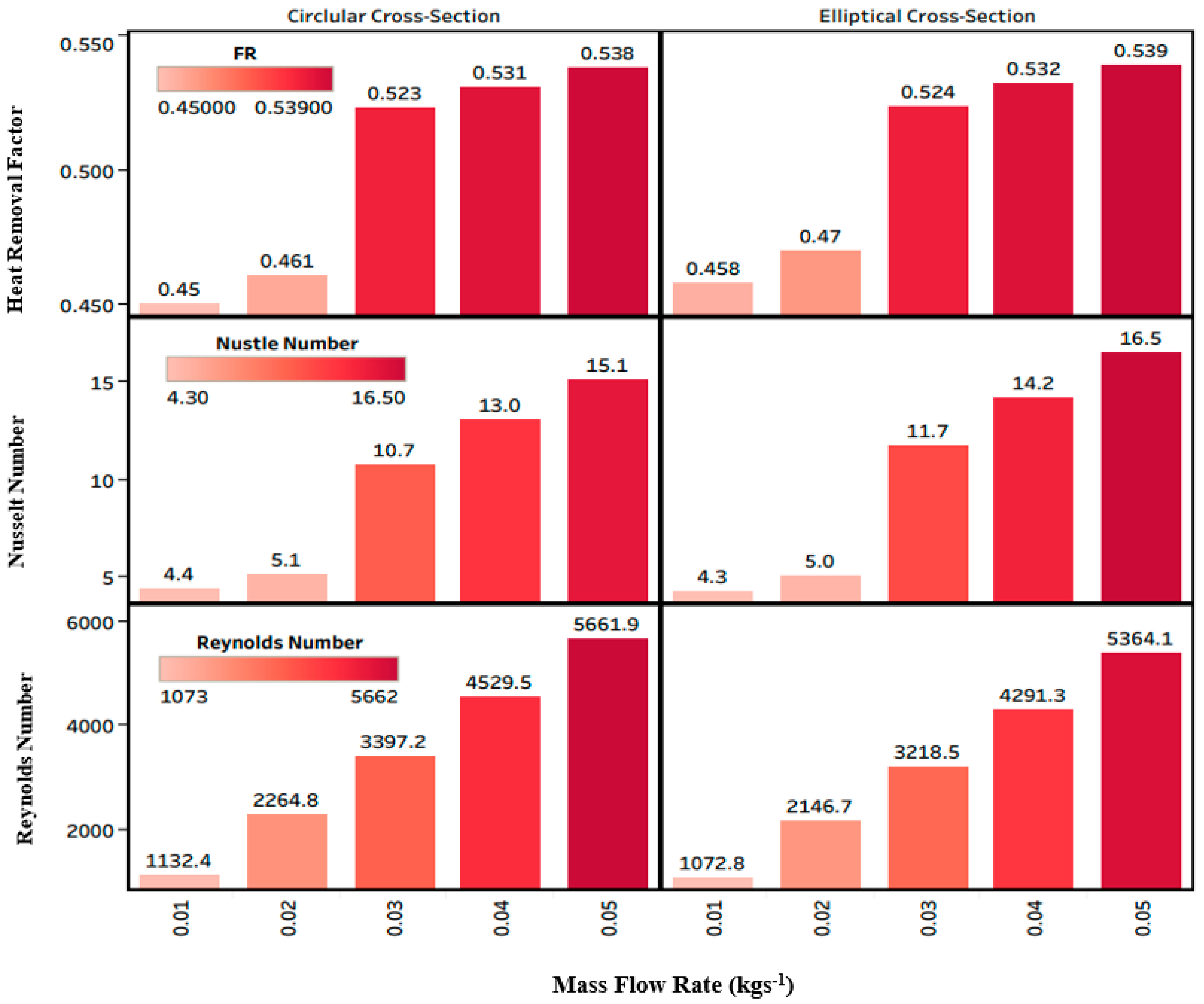
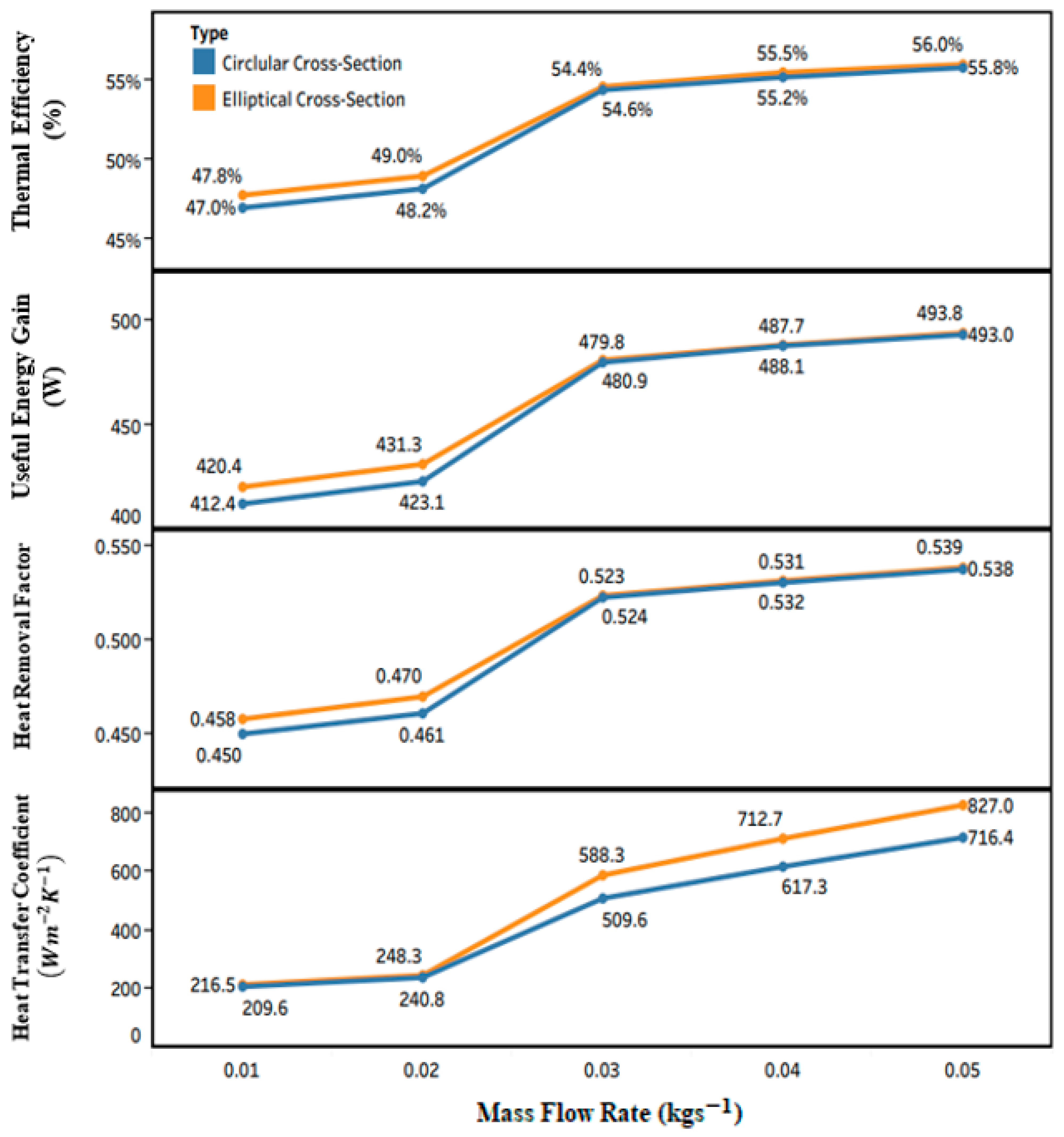
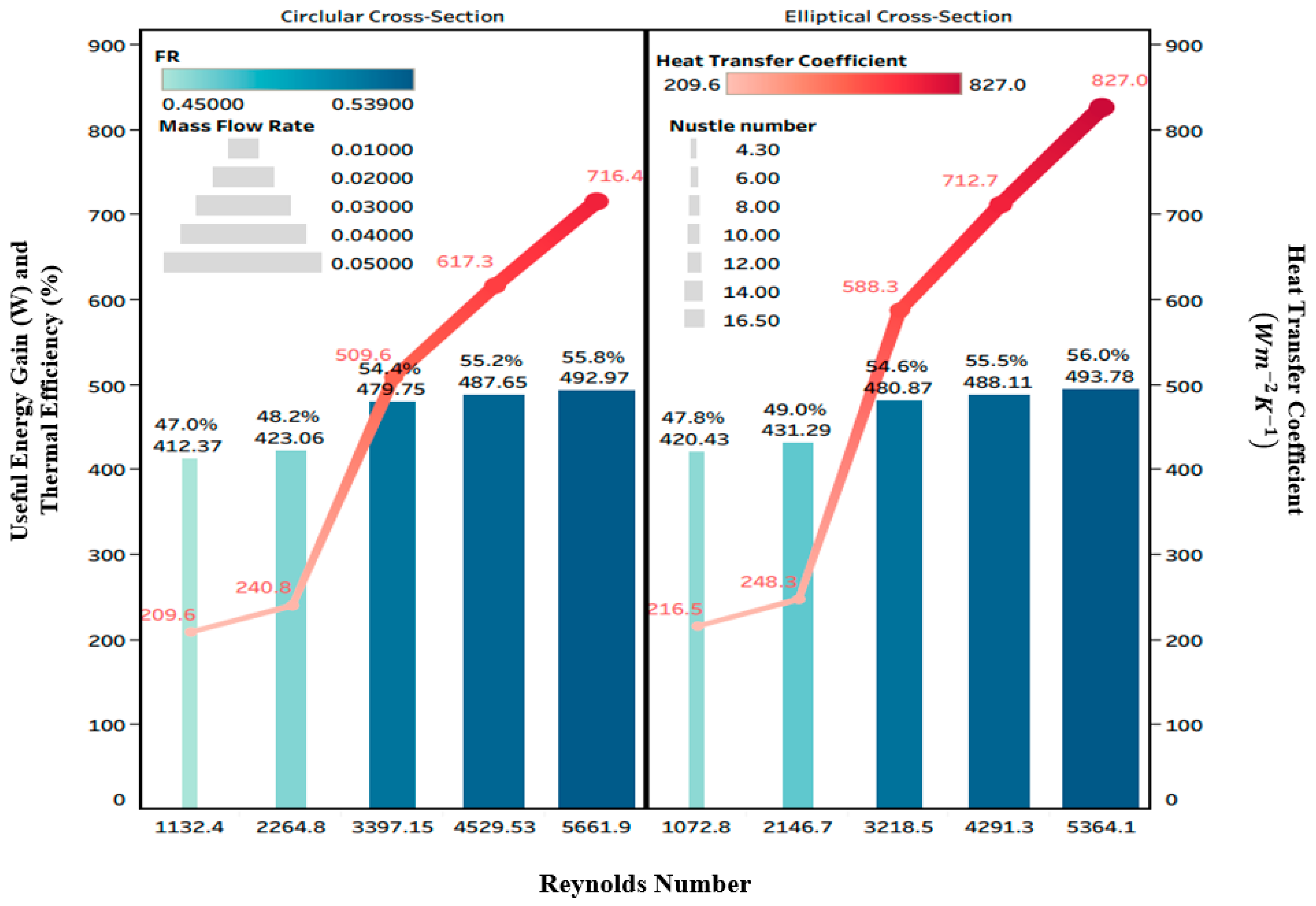
• The greatest values of $Q_u$ were obtained for elliptical and circular cross-sections (493.8 W and 493 W, respectively) under turbulent flow ($\dot{m}=$ of 0.05 kg s⁻¹), even though the lowest values were 420.4 W and 412.4 W for circular and elliptical design under laminar flow ($\dot{m}=$ 0.01 kg s⁻¹), respectively. The maximum thermal efficiency (56%) is achievable under turbulent flow for the elliptical cross-section.
• The highest values of $F_R$ corresponded to elliptical and circular design under turbulent flow with 0.538 and 0.539, respectively, and $F_R$ was the minimum for circular and elliptical designs with 0.458 and 0.450, respectively, under laminar flow.
• At various mass flow rates, the tubes with different cross-sections lead to various values for $Re$, $Nu$, $h_{fi}$, $F_R$, $Q_u$, and ${\mu }_{Th}$, while the $Pr$ remains constant as it does not depend on the geometry of the tube.
• All heat transfer governing parameters increased notably by changing laminar to non-laminar flow rates for both cross-sections. It was due to the cooling effect of water showing better performance under non-laminar flow rates.
• It was concluded that at the same area, the cross-section geometry with lower values of hydraulic diameter (12 mm for elliptical design) had higher heat transfer characteristics in comparison to a cross-section with a greater hydraulic diameter (13 mm for circular design).
• At the same area, the elliptical tube increased the heat transfer rate ($Q_u$) by approximately 2% in comparison to a circular tube due to a larger contact area between the working fluid and the solid surface of tubes.

In summary, it is essential to conduct an analytical study on the heat transfer parameters of a solar thermal collector in the primary stage of its design to fabricate a highly efficient system and save time as well as manufacturing costs. The authors suggest that employing nanofluids and phase change materials alongside effective cross-sections might significantly enhance the thermal characteristic of a solar thermal system.