Optimized Pilot Point Emplacement Based Groundwater Flow Calibration Method for Heterogeneous Small-Scale Area
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Datasets
2.3. Preprocessing
2.3.1. Geological Modeling
2.3.2. Conceptual Modeling
2.3.3. Model Parameterization
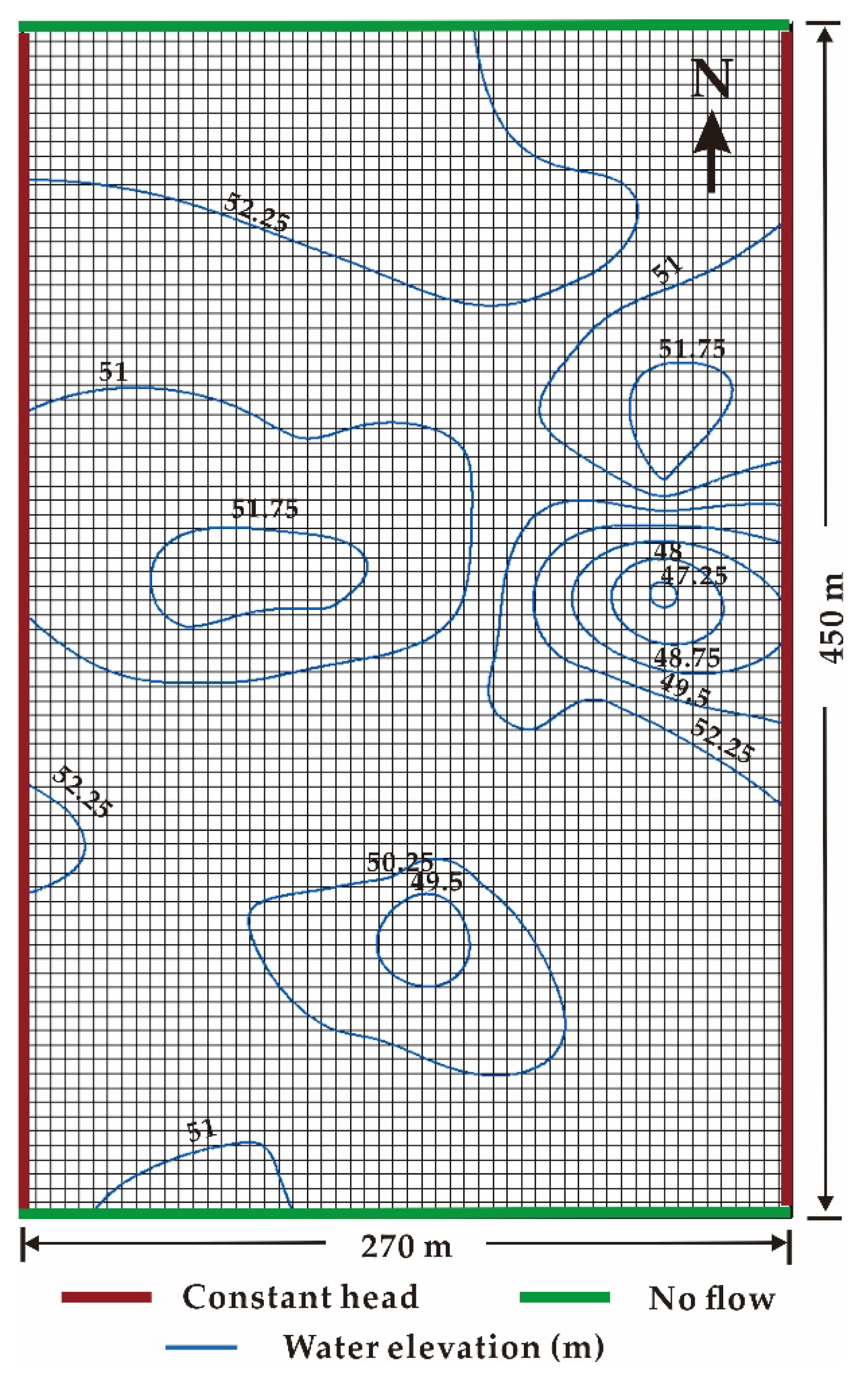
2.4. Groundwater Flow Simulation
2.5. Model Calibration
2.5.1. Pilot Point Placement Design
2.5.2. Regular Pilot Point Placement
2.5.3. Middle Head Measurement Down Gradient Pilot Points Placement
2.5.4. Pilot Point Placement Criteria
3. Results
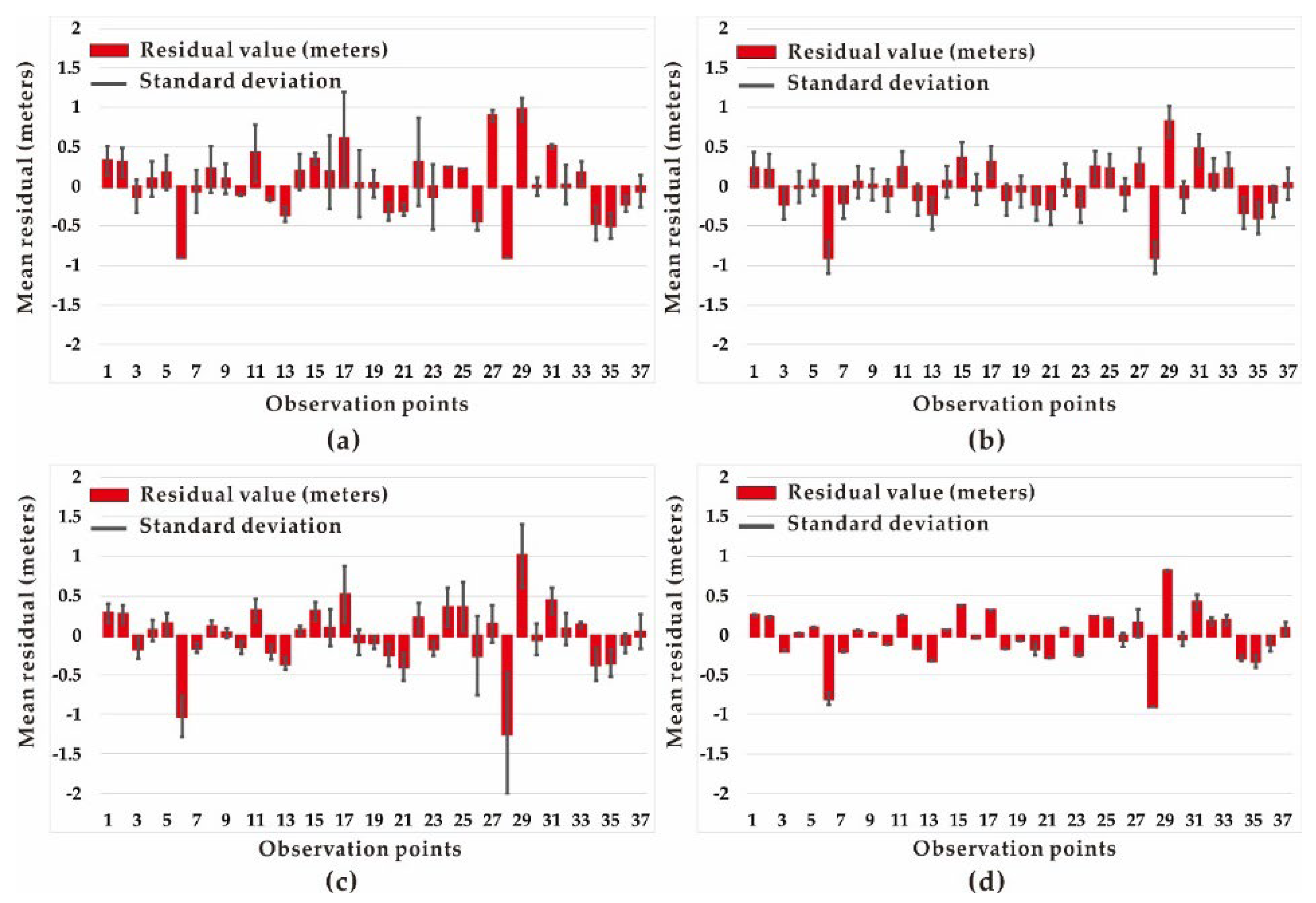
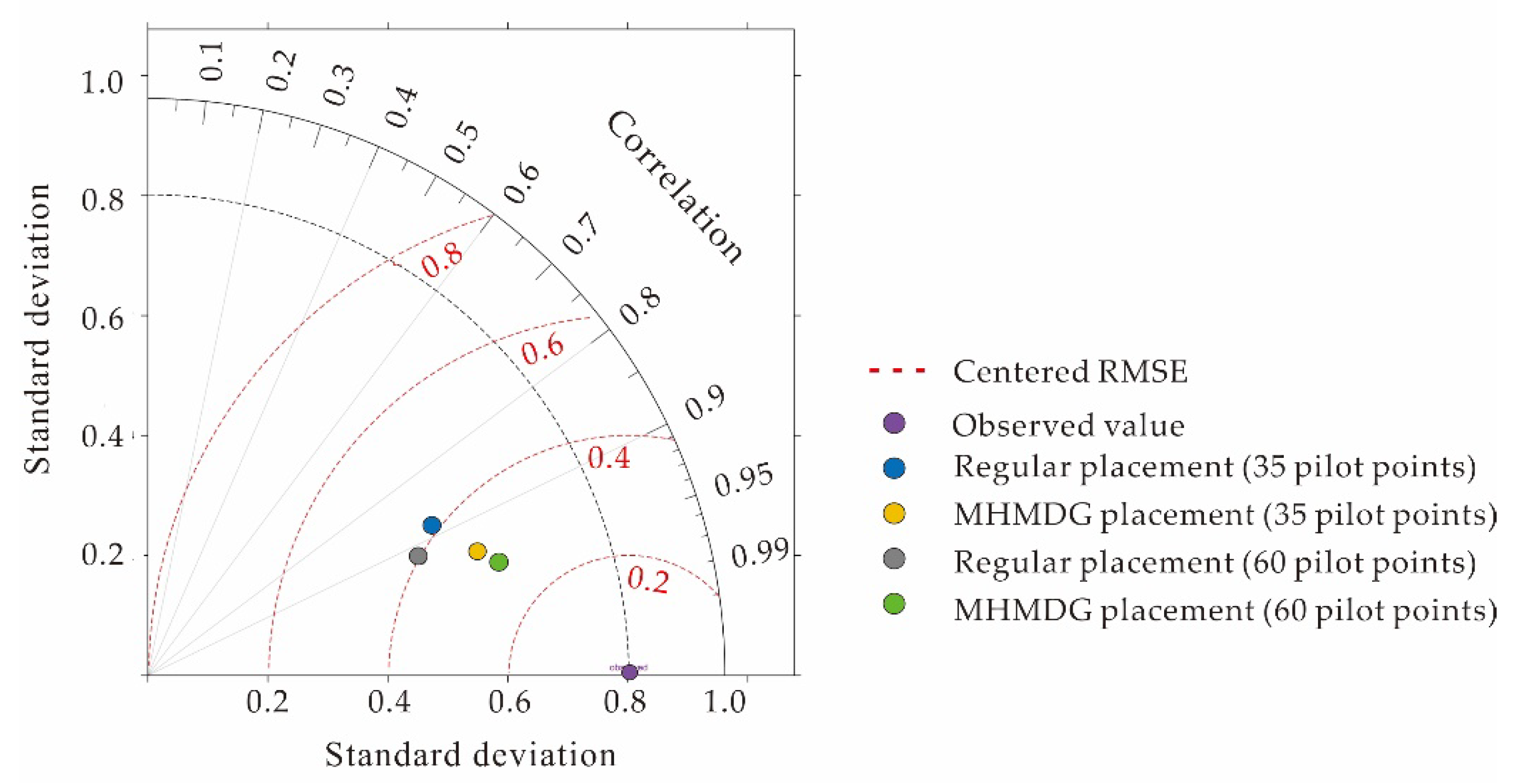
3.1. Pilot Point Placement and Frequency Effect
3.2. Mean Residual Error Analysis
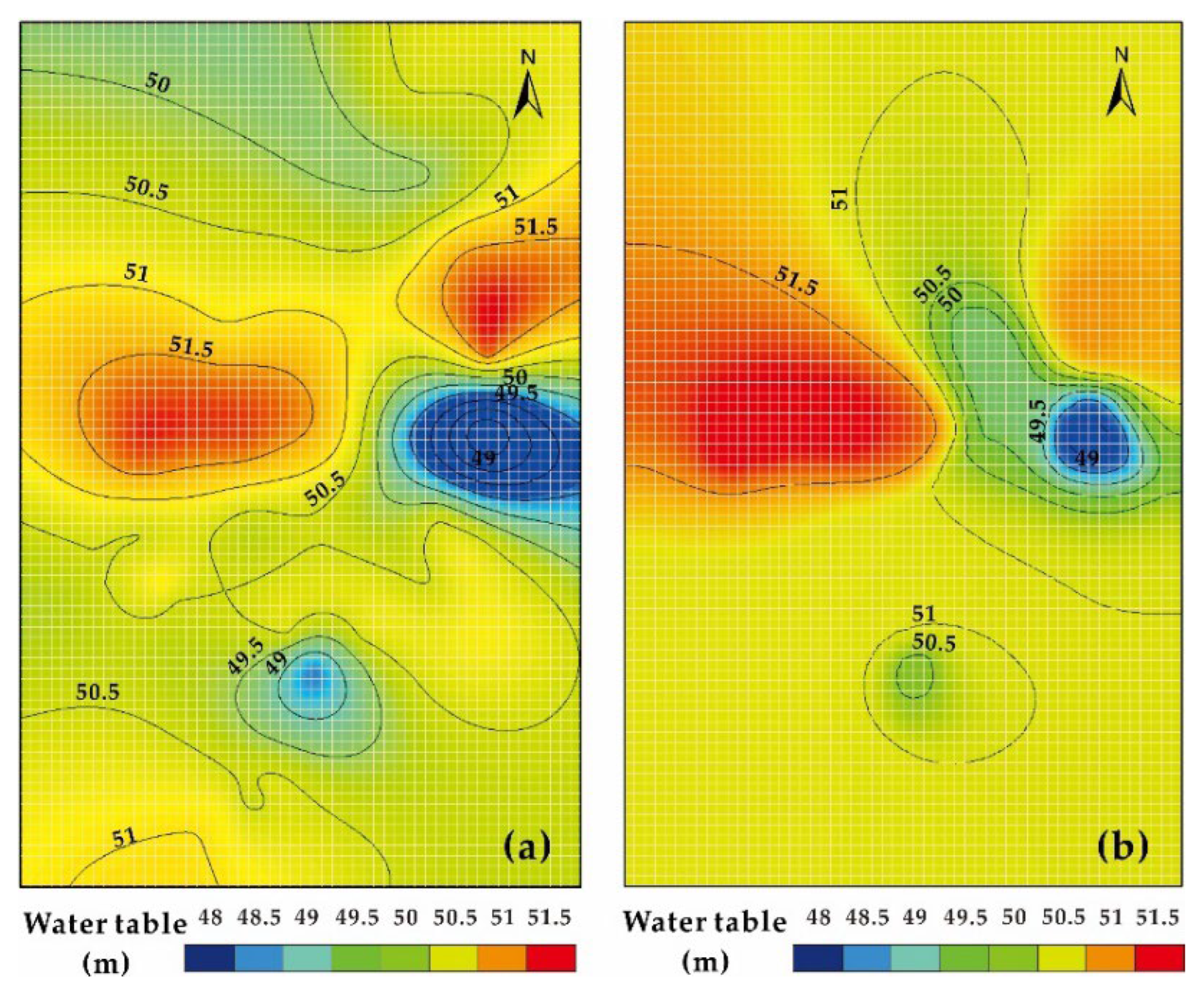
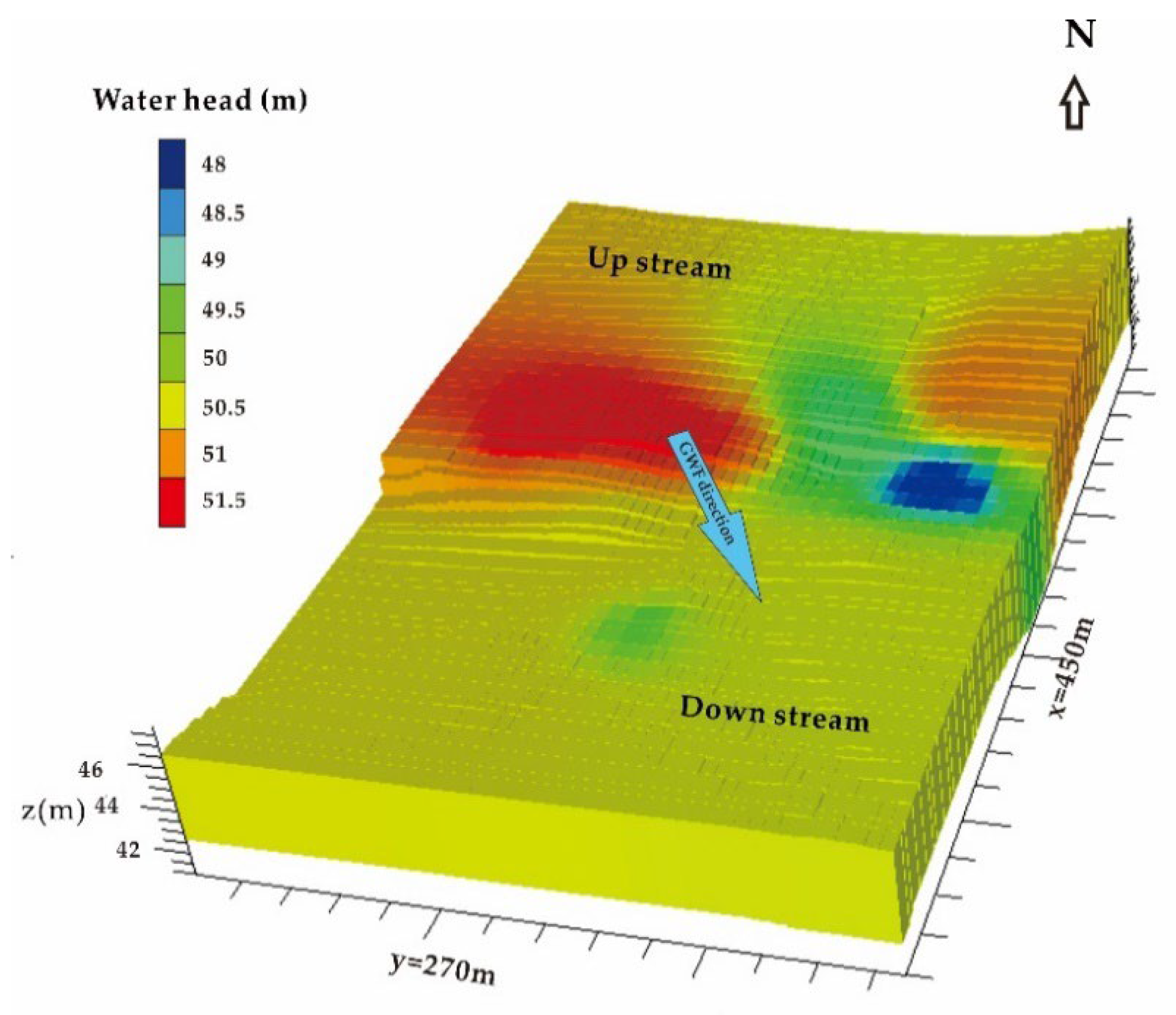
3.3. Hydraulic Head
3.4. Parameter Sensitivity Analysis
4. Discussion
4.1. Pilot Point Based Calibration Evaluation
4.2. Comparative Analysis
5. Conclusions
- (1)
- The calibration evaluation compared the simulated hydraulic head to the observed data. The conceptualization method has a significant impact on the result, especially the grid structure and elevation, which define the deformation of the grid and the relief of the surface. The geological structure could be well reflected by the surface interpolated from a SGrid model elevation point. The accuracy depends on the interpolation method, which is the primary source of uncertainty. The kriging interpolation remains the most effective and accurate for groundwater model conceptualization.
- (2)
- The calibration method based on the pilot point method is effective in the small-scale area, as proved by this experimental study; however, it massively pivots on the pilot point emplacement strategy and density. In our application case, the MHMDG placement method with a large density gives the best R-squared 0.901 compared to 0.880 for the regular placement. The kriging interpolation used in inverse modeling reflects the value of the hydraulic conductivity of every pilot point. The initial value of the pilot points impacts the accuracy of the result and the computation time. The calculation is more complicated in heterogeneous media and generates a computation burden that affects the model stability.
- (3)
- The choice of the solution model and the engines adapted to the context is critical for simulation, especially when using the MODFLOW numerical code. It might yield an excellent calculation outcome of unrealistic value. The MODFLOW 2005 and the PEST combination are perfect solutions for small-scale areas. The consideration of small-scale simulation with regularization is a future topic for another research. It helps to understand the calibration solution’s uniqueness of using the pilot point method and zonation focused on the middle head measurement on the downgradient technics.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kresic, N. Hydrogeology and Groundwater Modeling; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Arshad, A.; Zhang, Z.; Zhang, W.; Dilawar, A. Mapping favorable groundwater potential recharge zones using a GIS-based analytical hierarchical process and probability frequency ratio model: A case study from an agro-urban region of Pakistan. Geosci. Front. 2020, 11, 1805–1819. [Google Scholar] [CrossRef]
- Salam, M.; Cheema, M.J.M.; Zhang, W.; Hussain, S.; Khan, A.; Bilal, M.; Arshad, A.; Ali, S.; Zaman, M.A. Groundwater storage change estimation using grace satellite data in Indus basin. Big Data Water Resour. Eng. 2020, 1, 13–18. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, W. A review of regional groundwater flow modeling. Geosci. Front. 2011, 2, 205–214. [Google Scholar] [CrossRef] [Green Version]
- Aslam, M.; Arshad, M.; Hussain, S.; Usman, M.; Zahid, M.B.; Sattar, J.; Arshad, A.; Iqbal, M.M.; Waqas, M.S. An integrated approach for estimation of van genuchten model parameters in undisturbed and unsaturated soils. Pak. J. Agric. Sci. 2021, 58, 1887–1893. [Google Scholar] [CrossRef]
- Shoarinezhad, V.; Wieprecht, S.; Haun, S. Comparison of local and global optimization methods for calibration of a 3D morphodynamic model of a curved channel. Water 2020, 12, 1333. [Google Scholar] [CrossRef]
- Xu, T.; Valocchi, A.J. A Bayesian approach to improved calibration and prediction of groundwater models with structural error. Water Resour. Res. 2015, 51, 9290–9311. [Google Scholar] [CrossRef]
- Doherty, J. Ground water model calibration using pilot points and regularization. Ground Water 2003, 41, 170–177. [Google Scholar] [CrossRef]
- Fienen, M.N.; Muffels, C.T.; Hunt, R.J. On constraining pilot point calibration with regularization in PEST. Ground Water 2009, 47, 835–844. [Google Scholar] [CrossRef]
- Kapoor, A.; Kashyap, D. Parameterization of pilot point methodology for supplementing sparse transmissivity data. Water 2021, 13, 2082. [Google Scholar] [CrossRef]
- Zhuang, C.; Zhou, Z.; Illman, W.A.; Wang, J. Geostatistical inverse modeling for the characterization of aquitard heterogeneity using long-term multi-extensometer data. J. Hydrol. 2019, 578, 124024. [Google Scholar] [CrossRef]
- Giudici, M.; Colpo, F.; Ponzini, G.; Romano, E.; Parravicini, G. Calibration of groundwater recharge and hydraulic conductivity for the aquifer system beneath the city of Milan (Italy). In Impact of Human Activity on Groundwater Dynamics; IAHS-AISH: Maastricht, The Netherlands, 2001; pp. 43–50. [Google Scholar]
- Doherty, J. Model-Independent Parameter Estimation User Manual, 5th ed.; PEST, Watermark Numerical Computing: Brisbane, Australia, 2010; Volume 268.
- Jarray, H.; Zammouri, M.; Ouessar, M. Assessment of groundwater salinization using PEST and sensitivity analysis: Case of Zeuss-Koutine and Mio-Plio-Quaternary aquifers. Arab. J. Geosci. 2020, 13, 999. [Google Scholar] [CrossRef]
- González-Quirós, A.; Comte, J.-C. Hydrogeophysical model calibration and uncertainty analysis via full integration of PEST/PEST++ and COMSOL. Environ. Model. Softw. 2021, 145, 105183. [Google Scholar] [CrossRef]
- Baalousha, H.M.; Fahs, M.; Ramasomanana, F.; Younes, A. Effect of pilot-points location on model calibration: Application to the northern karst aquifer of Qatar. Water 2019, 11, 679. [Google Scholar] [CrossRef] [Green Version]
- Tziatzios, G.; Sidiropoulos, P.; Vasiliades, L.; Lyra, A.; Mylopoulos, N.; Loukas, A. The use of the pilot points method on groundwater modelling for a degraded aquifer with limited field data: The case of Lake Karla aquifer. Water Supply 2021, 21, 2633–2645. [Google Scholar] [CrossRef]
- Ni, X.D.; Chen, K. Study on the conversion of GOCAD models to FLAC3D models. Appl. Mech. Mater. 2014, 501–504, 2527–2531. [Google Scholar] [CrossRef]
- Harbaugh, A.W. MODFLOW-2005, the U.S. Geological Survey Modular Ground-Water Model—The Ground-Water Flow Process; U.S. Geological Survey: Reston, VA, USA, 2005.
- Zhuang, C.; Zhou, Z.; Zhan, H.; Wang, J.; Li, Y.; Dou, Z. New graphical methods for estimating aquifer hydraulic parameters using pumping tests with exponentially decreasing rates. Hydrol. Process. 2019, 33, 2314–2322. [Google Scholar] [CrossRef]
- Zhuang, C.; Li, Y.; Zhou, Z.; Illman, W.A.; Dou, Z.; Wang, J.; Yan, L. A Type-curve method for the analysis of pumping tests with piecewise-linear pumping rates. Ground Water 2020, 58, 788–798. [Google Scholar] [CrossRef]
- Yongcheng, L.; Naiqi, S.; Biao, L.; Yan, Y.; Mei, D. Research on 3D geological modeling by using GOCAD software. In Proceedings of the 2010 Second World Congress on Software Engineering, Wuhan, China, 19–20 December 2010; pp. 259–263. [Google Scholar]
- Ross, M.; Aitssi, L.; Martel, R.; Parent, M. From geological to groundwater flow models: An example of inter-operability for semi-regular grids. Geol. Surv. Can. Open File 2006, 5048, 67–70. [Google Scholar] [CrossRef]
- Watson, C.; Richardson, J.; Wood, B.; Jackson, C.; Hughes, A. Improving geological and process model integration through TIN to 3D grid conversion. Comput. Geosci. 2015, 82, 45–54. [Google Scholar] [CrossRef] [Green Version]
- Witter, J.B. GOCAD® mining suite software as a tool for improved geothermal exploration. In Proceedings of the World Geothermal Congress, Melbourne, Australia, 16–24 April 2015. [Google Scholar]
- Gao, Y.; Du, E.; Yi, S.; Han, Y.; Zheng, C. An improved numerical model for groundwater flow simulation with MPFA method on arbitrary polygon grids. J. Hydrol. 2021, 606, 127399. [Google Scholar] [CrossRef]
- Al-Hashmi, S.; Gunawardhana, L.; Sana, A.; Baawain, M. A numerical groundwater flow model of wadi SAMAIL catchment using MODFLOW software. Int. J. GEOMATE 2020, 18, 30–36. [Google Scholar] [CrossRef]
- Golden Software, Inc. Golden Software. Available online: https://www.goldensoftware.com (accessed on 15 November 2020).
- Zhou, Y.; Herath, H.M.P.S.D. Geoscience frontiers evaluation of alternative conceptual models for groundwater modelling. Geosci. Front. 2017, 8, 437–443. [Google Scholar] [CrossRef] [Green Version]
- Rojas, R.; Feyen, L.; Batelaan, O.; Dassargues, A. On the value of conditioning data to reduce conceptual model uncertainty in groundwater modeling. Water Resour. Res. 2010, 46, 1–20. [Google Scholar] [CrossRef]
- Cui, T.; Sreekanth, J.; Pickett, T.; Rassam, D.; Gilfedder, M.; Barrett, D. Impact of model parameterization on predictive uncertainty of regional groundwater models in the context of environmental impact assessment. Environ. Impact Assess. Rev. 2021, 90, 106620. [Google Scholar] [CrossRef]
- Knox, R.C. Spatial moment analysis for mass balance calculations and tracking movement of a subsurface hydrocarbon mound. Ground Water Monit. Remediat. 1993, 13, 139–147. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, S.; Kong, X.; Zheng, W.; Feng, W.; Zhang, X.; Yuan, R.; Song, X.; Sprenger, M. Interaction of surface water and groundwater influenced by groundwater over-extraction, waste water discharge and water transfer in Xiong’an New Area, China. Water 2019, 11, 539. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Hu, G.; Zhang, Z.; Lou, W.; Zou, Y.; Li, X.; Zhang, K. Experimental study and numerical simulation on the migration and transformation mechanism of Cr(Ⅵ) in contaminated site. Rock Soil Mech. 2022, 43. [Google Scholar] [CrossRef]
- Rahnama, M.B.; Zamzam, A. Quantitative and qualitative simulation of groundwater by mathematical models in Rafsanjan aquifer using MODFLOW and MT3DMS. Arab. J. Geosci. 2013, 6, 901–912. [Google Scholar] [CrossRef]
- Locatelli, L.; Binning, P.J.; Sanchez-Vila, X.; Søndergaard, G.L.; Rosenberg, L.; Bjerg, P.L. A simple contaminant fate and transport modelling tool for management and risk assessment of groundwater pollution from contaminated sites. J. Contam. Hydrol. 2019, 221, 35–49. [Google Scholar] [CrossRef]
- Sepúlveda, N.; Doherty, J. Uncertainty analysis of a groundwater flow model in east-central Florida. Ground Water 2015, 53, 464–474. [Google Scholar] [CrossRef]
- Mani, S.K.; Singh, S.K.; Pandey, S.N.; Pachauri, A.K. Numerical modelling of flow towards a well in a two layer aquifer. ISH J. Hydraul. Eng. 1999, 5, 68–76. [Google Scholar] [CrossRef]
- Khan, U.; Faheem, H.; Jiang, Z.; Wajid, M.; Younas, M.; Zhang, B. Integrating a GIS-based multi-influence factors model with hydro-geophysical exploration for groundwater potential and hydrogeological assessment: A case study in the Karak Watershed, Northern Pakistan. Water 2021, 13, 1255. [Google Scholar] [CrossRef]
- Nakagawa, S.; Schielzeth, H. A general and simple method for obtainingR2from generalized linear mixed-effects models. Methods Ecol. Evol. 2012, 4, 133–142. [Google Scholar] [CrossRef]
- RamaRao, B.S.; Lavenue, A.M.; De Marsily, G.; Marietta, M.G. Pilot point methodology for automated calibration of an ensemble of conditionally simulated transmissivity fields: 1. Theory and computational experiments. Water Resour. Res. 1995, 31, 475–493. [Google Scholar] [CrossRef]
- Doherty, J.E.; Fienen, M.N.; Hunt, R.J. Approaches to Highly Parameterized Inversion: Pilot-Point Theory, Guidelines, and Research Directions; U.S. Geological Survey Scientific Investigations Report 2010–5168; U.S. Geological Survey: Reston, VA, USA, 2010; 38p.
- Bamisaiye, O.A. Subsurface mapping: Selection of best interpolation method for borehole data analysis. Spat. Inf. Res. 2018, 26, 261–269. [Google Scholar] [CrossRef]
- Jones, J.P.; Sudicky, E.A.; McLaren, R.G. Application of a fully-integrated surface-subsurface flow model at the watershed-scale: A case study. Water Resour. Res. 2008, 44, 1–13. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Courier Corporation: Dover, DE, USA, 1988. [Google Scholar]
- Greskowiak, J.; Prommer, H.; Liu, C.; Post, V.E.A.; Ma, R.; Zheng, C.; Zachara, J.M. Comparison of parameter sensitivities between a laboratory and field-scale model of uranium transport in a dual domain, distributed rate reactive system. Water Resour. Res. 2010, 46, 1–13. [Google Scholar] [CrossRef]
- Al-Muqdadi, S.W.H.; Abo, R.; Khattab, M.O.; Abdulhussein, F.M. Groundwater flow-modeling and sensitivity analysis in a hyper arid region. Water 2020, 12, 2131. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Zeydalinejad, N. Artificial neural networks vis-à-vis MODFLOW in the simulation of groundwater: A review. Model. Earth Syst. Environ. 2022, 1–22. [Google Scholar] [CrossRef]
- Coppola, E.; Poulton, M.; Charles, E.; Dustman, J.; Szidarovszky, F. Application of artificial neural networks to complex groundwater management problems. Nonrenewable Resour. 2003, 12, 303–320. [Google Scholar] [CrossRef]
- Mustafa, S.M.T.; Nossent, J.; Ghysels, G.; Huysmans, M. Integrated bayesian multi-model approach to quantify input, parameter and conceptual model structure uncertainty in groundwater modeling. Environ. Model. Softw. 2020, 126, 104654. [Google Scholar] [CrossRef]
- Hassan, A.E.; Bekhit, H.M.; Chapman, J.B. Using Markov Chain Monte Carlo to quantify parameter uncertainty and its effect on predictions of a groundwater flow model. Environ. Model. Softw. 2009, 24, 749–763. [Google Scholar] [CrossRef]

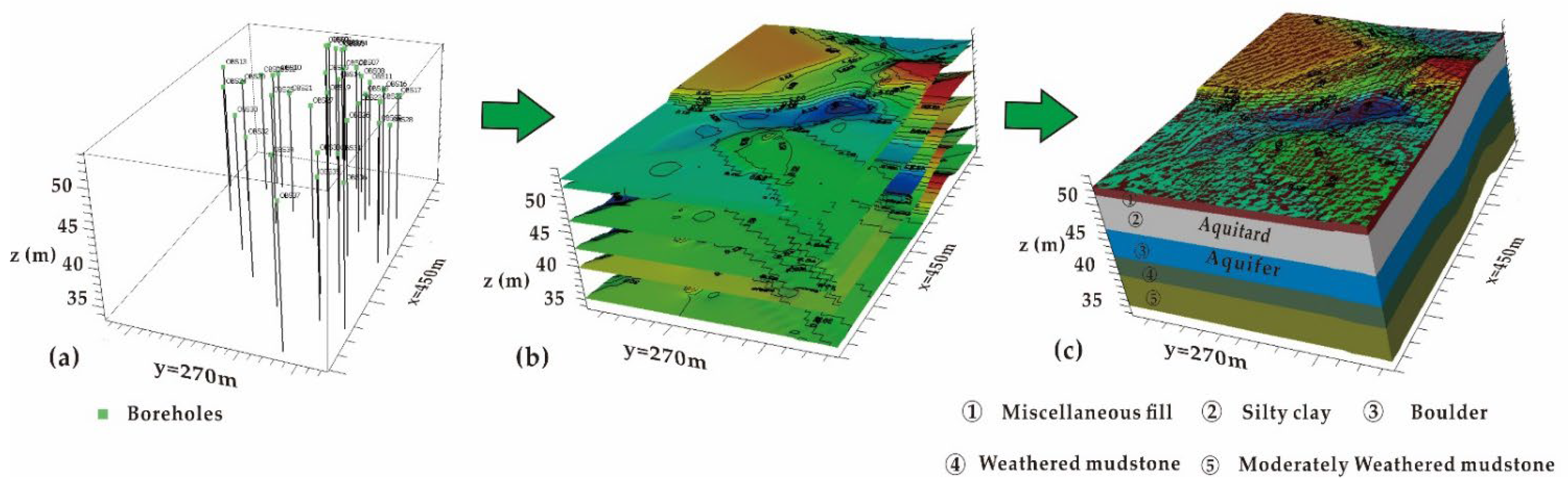


| Modeling Phases | Geological Modeling | Conceptual Modeling | Groundwater Flow Simulation |
|---|---|---|---|
| Data | 8 cross-sections, 37 borehole data | Surface data, GIS data (.shp) topographic data, borehole data | Observation wells data, laboratory experiment results, pumping test results |
| Statistics | Non Calibrated | 35 Points | 60 Points | ||
|---|---|---|---|---|---|
| Regular | MHMDG | Regular | MHMDG | ||
| Mean r squared | 0.396 | 0.695 | 0.683 | 0.886 | 0.901 |
| RMS (m) | 0.69 | 0.38 | 0.34 | 0.37 | 0.32 |
| Normalized RMS (%) | 14.65 | 8.035 | 7.2 | 7.78 | 6.78 |
| Max residual (m) | −1.6 | −0.96 | 0.9 | −1 | 0.9 |
| Min residual (m) | 0.078 | 0.0014 | −0.0033 | 0.011 | −0.0053 |
| residual Mean (m) | −0.22 | 0.0063 | 0.024 | −0.0067 | 0.015 |
| Standard error of estimation (m) | 0.11 | 0.063 | 0.056 | 0.061 | 0.053 |
| K min | 4.71 × 10−5 | 4.6 × 10−7 | 1.7643 × 10−7 | 1.7643 × 10−7 | 1.2867 × 10−7 |
| K max | 4.716 × 10−5 | 1.037081 | 2.445149 | 2.445149 | 0.2444386 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rabemaharitra, T.P.; Zou, Y.; Yi, Z.; He, Y.; Khan, U. Optimized Pilot Point Emplacement Based Groundwater Flow Calibration Method for Heterogeneous Small-Scale Area. Appl. Sci. 2022, 12, 4648. https://doi.org/10.3390/app12094648
Rabemaharitra TP, Zou Y, Yi Z, He Y, Khan U. Optimized Pilot Point Emplacement Based Groundwater Flow Calibration Method for Heterogeneous Small-Scale Area. Applied Sciences. 2022; 12(9):4648. https://doi.org/10.3390/app12094648
Chicago/Turabian StyleRabemaharitra, Tahirinandraina Prudence, Yanhong Zou, Zhuowei Yi, Yong He, and Umair Khan. 2022. "Optimized Pilot Point Emplacement Based Groundwater Flow Calibration Method for Heterogeneous Small-Scale Area" Applied Sciences 12, no. 9: 4648. https://doi.org/10.3390/app12094648
APA StyleRabemaharitra, T. P., Zou, Y., Yi, Z., He, Y., & Khan, U. (2022). Optimized Pilot Point Emplacement Based Groundwater Flow Calibration Method for Heterogeneous Small-Scale Area. Applied Sciences, 12(9), 4648. https://doi.org/10.3390/app12094648






