Influence of Surface Tilt Angle on a Chromatic Confocal Probe with a Femtosecond Laser
Abstract
:1. Introduction
2. Theoretical Equations for the Tracking Local Minimum Method of Mode-Locked Femtosecond Laser Dual-Fiber Differential Detector-Type Chromatic Confocal Probe
2.1. Principle of the Tracking Local Minimum Method
2.2. Modeling for Theoretical Equations
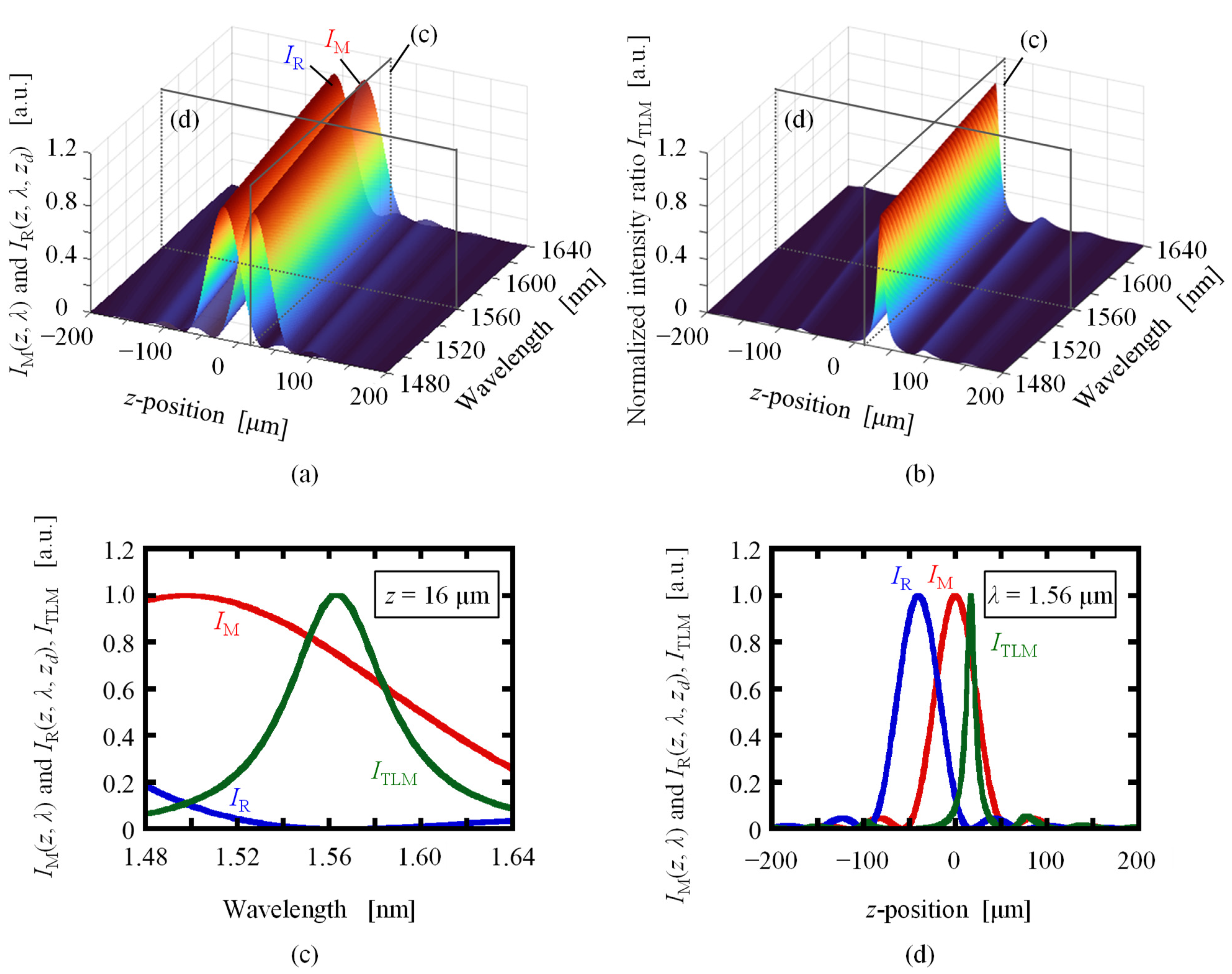
3. Numerical Calculation Results for the Tracking Local Minimum Method
4. Experimental Investigation Results for the Tracking Local Minimum Method
4.1. Experimental Configuration for the Tracking Local Minimum Method
4.2. Alignment Method of the Optical System
4.3. Experimental Analysis of the Influence of the Tilt Angle of the Measurement Object on the Tracking Local Minimum Method
4.4. Discussion about the Influence of the Tilt Angle of the Measurement Object on the Tracking Local Minimum Method
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, W.; Kim, S.W.; Bosse, H.; Haitjema, H.; Chen, Y.L.; Lu, X.D.; Knapp, W.; Weckenmann, A.; Estler, W.T.; Kunzmann, H. Measurement technologies for precision positioning. CIRP Ann. Manuf. Technol. 2015, 64, 773–796. [Google Scholar] [CrossRef]
- Gao, W.; Haitjema, H.; Fang, F.Z.; Leach, R.K.; Cheung, C.F.; Savio, E.; Linares, J.M. On-machine and in-process surface metrology for precision manufacturing. CIRP Ann. Manuf. Technol. 2019, 68, 843–866. [Google Scholar] [CrossRef] [Green Version]
- Fang, F.Z.; Zhanga, X.D.; Gao, W.; Guo, Y.B.; Byrne, G.; Hansen, H.N. Nanomanufacturing—Perspective and applications. CIRP Ann. Manuf. Technol. 2017, 66, 683–705. [Google Scholar] [CrossRef] [Green Version]
- Wilson, T. Imaging Properties and Applications of Scanning Optical Microscopes. Appl. Phys. 1980, 22, 119–128. [Google Scholar] [CrossRef]
- Wilson, T.; Sheppard, C.J.R. Theory and Practice of Scanning Optical Microscopy; Academic Press: London, UK, 1984. [Google Scholar]
- Gu, M. Principles of Three Dimensional Imaging in Confocal Microscopes; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 1996. [Google Scholar]
- Marvin, M. Microscopy Apparatus. U.S. Patent 3013467, 19 December 1961. [Google Scholar]
- Minsky, M. Memoir on inventing the confocal scanning microscope. Scanning 1988, 10, 128–134. [Google Scholar] [CrossRef]
- Wilson, T.; Masters, B.R. Confocal microscopy. Appl. Opt. 1994, 33, 565–566. [Google Scholar] [CrossRef] [PubMed]
- Mikulewitsch, M.; Auerswald, M.M.; Freyberg, A.; Fischer, A. Geometry measurement of submerged metallic micro-parts using confocal fluorescence microscopy. Nanomanuf. Metrol. 2018, 1, 171–179. [Google Scholar] [CrossRef]
- Molesini, G.; Pedrini, G.; Poggi, P.; Quercioli, F. Focus-wavelength encoded optical profilometer. Opt. Commun. 1984, 49, 229–233. [Google Scholar] [CrossRef]
- Browne, M.A.; Akinyemi, O.; Boyde, A. Confocal surface profiling utilizing chromatic aberration. Scanning 1992, 14, 145–153. [Google Scholar] [CrossRef]
- Tiziani, H.J.; Uhde, H.-M. Three-dimensional image sensing by chromatic confocal microscopy. Appl. Opt. 1994, 33, 1838–1843. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.; Shi, K.; Li, H.; Xu, Q.; Gopalan, V.; Liu, Z. Chromatic second harmonic imaging. Opt. Express 2010, 18, 23837–23843. [Google Scholar] [CrossRef] [PubMed]
- Minoni, U.; Manili, G.; Bettoni, S.; Varrenti, E.; Modotto, D.; De Angelis, C. Chromatic confocal setup for displacement measurement using a supercontinuum light source. Opt. Laser Technol. 2013, 49, 91–94. [Google Scholar] [CrossRef] [Green Version]
- Bai, J.; Li, X.; Wang, X.; Zhou, Q.; Ni, K. Chromatic confocal displacement sensor with optimized dispersion probe and modified centroid peak extraction algorithm. Sensors 2019, 19, 3592. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, W.; Tan, J.; Qiu, L. Bipolar absolute differential confocal approach to higher spatial resolution. Opt. Express 2004, 12, 5013–5021. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.-R.; Kim, Y.-D.; Gweon, D.-G.; Yoo, H. Dual-detection confocal fluorescence microscopy: Fluorescence axial imaging without axial scanning. Opt. Express 2013, 21, 17839–17848. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.C.; Nguyen, D.T.; Chang, Y.W. Precise optical surface profilometry using innovative chromatic differential confocal microscopy. Opt. Lett. 2016, 41, 5660–5663. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.; Kim, S.H.; Do, D.H.; Yoo, H.; Gweon, D. Chromatic confocal microscopy with a novel wavelength detection method using transmittance. Opt. Express 2013, 21, 6286–6294. [Google Scholar] [CrossRef]
- Tan, J.; Liu, J.; Wang, Y. Differential confocal microscopy with a wide measuring range based on polychromatic illumination. Meas. Sci. Technol. 2010, 21, 054013. [Google Scholar] [CrossRef]
- Chen, X.; Nakamura, T.; Shimizu, Y.; Chen, C.; Chen, Y.L.; Matsukuma, H.; Gao, W. A chromatic confocal probe with a mode-locked femtosecond laser source. Opt. Laser Technol. 2018, 103, 359–366. [Google Scholar] [CrossRef]
- Chen, C.; Sato, R.; Shimizu, Y.; Nakamura, T.; Matsukuma, H.; Gao, W. A Method for Expansion of Z-Directional Measurement Range in a Mode-Locked Femtosecond Laser Chromatic Confocal Probe. Appl. Sci. 2019, 9, 454. [Google Scholar] [CrossRef] [Green Version]
- Sato, R.; Shimizu, Y.; Chen, C.; Matsukuma, H.; Gao, W. Investigation and Improvement of Thermal Stability of a Chromatic Confocal Probe with a Mode-Locked Femtosecond Laser Source. Appl. Sci. 2019, 9, 4084. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Shimizu, Y.; Sato, R.; Matsukuma, H.; Gao, W. An Off-Axis Differential Method for Improvement of a Femtosecond Laser Differential Chromatic Confocal Probe. Appl. Sci. 2020, 10, 7235. [Google Scholar] [CrossRef]
- Sato, R.; Chen, C.; Matsukuma, H.; Shimizu, Y.; Gao, W. A new signal processing method for a differential chromatic confocal probe with a mode-locked femtosecond laser. Meas. Sci. Technol. 2020, 31, 094004. [Google Scholar] [CrossRef]
- Matsukuma, H.; Sato, R.; Shimizu, Y.; Gao, W. Measurement Range Expansion of Chromatic Confocal Probe with Supercontinuum Light Source. Int. J. Autom. Technol. 2021, 15, 529–536. [Google Scholar] [CrossRef]
- Sheppard, C.J.R.; Cogswell, C.J. Three-dimensional image formation in confocal microscopy. J. Microsc. 1990, 159, 179–194. [Google Scholar] [CrossRef]
- Sheppard, C.J.R. Aberrations in high aperture conventional and confocal imaging systems. Appl. Opt. 1988, 22, 4782–4786. [Google Scholar] [CrossRef]
- Aguilar, J.F.; Méndez, E.R. On the limitations of the confocal scanning optical microscope as a profilometer. J. Mod. Opt. 1995, 42, 1785–1794. [Google Scholar] [CrossRef]
- Rahlves, M.; Roth, B.; Reithmeier, E. Systematic errors on curved microstructures caused by aberrations in confocal surface metrology. Opt. Express 2015, 23, 9640–9648. [Google Scholar] [CrossRef]
- Pribošek, J.; Diaci, J.; Sinzinger, S. Aperture-coded confocal profilometry. Opt. Lett. 2016, 41, 5523. [Google Scholar] [CrossRef]
- Mauch, F.; Lyda, W.; Gronle, M.; Osten, W. Improved signal model for confocal sensors accounting for object depending artifacts. Opt. Express 2012, 20, 19936–19945. [Google Scholar] [CrossRef]
- Béguelin, J.; Scharf, T.; Noell, W.; Voelkel, R. Correction of spherical surface measurements by confocal microscopy. Meas. Sci. Technol. 2020, 31, 075002. [Google Scholar] [CrossRef]
- Sheppard, C.J.R.; Gu, M. Aberration compensation in confocal microscopy. Appl. Opt. 1991, 30, 3563–3568. [Google Scholar] [CrossRef] [PubMed]
- Sheppard, C.J.R.; Gu, M.; Brain, K.; Zhou, H. Influence of spherical aberration on axial imaging of confocal reflection microscopy. Appl. Opt. 1994, 33, 616–624. [Google Scholar] [CrossRef] [PubMed]
- Sheppard, C.J.R.; Cogswell, C.J. Effects of aberrating layers and tube length on con focal imaging properties. Optik 1991, 87, 34–38. [Google Scholar]
- Wilson, T.; Gannaway, J.N.; Sheppard, C.J.R. Optical fibre profiling using a scanning optical microscope. Opt. Quant. Electron. 1980, 12, 341–345. [Google Scholar] [CrossRef]
- Matthews, H.J.; Hamilton, D.K.; Sheppard, C.J.R. Aberration measurement by confocal interferometry. J. Mod. Opt. 1989, 36, 233–250. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics; Pergamon: New York, NY, USA, 1980. [Google Scholar]











Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sato, R.; Shimizu, Y.; Matsukuma, H.; Gao, W. Influence of Surface Tilt Angle on a Chromatic Confocal Probe with a Femtosecond Laser. Appl. Sci. 2022, 12, 4736. https://doi.org/10.3390/app12094736
Sato R, Shimizu Y, Matsukuma H, Gao W. Influence of Surface Tilt Angle on a Chromatic Confocal Probe with a Femtosecond Laser. Applied Sciences. 2022; 12(9):4736. https://doi.org/10.3390/app12094736
Chicago/Turabian StyleSato, Ryo, Yuki Shimizu, Hiraku Matsukuma, and Wei Gao. 2022. "Influence of Surface Tilt Angle on a Chromatic Confocal Probe with a Femtosecond Laser" Applied Sciences 12, no. 9: 4736. https://doi.org/10.3390/app12094736
APA StyleSato, R., Shimizu, Y., Matsukuma, H., & Gao, W. (2022). Influence of Surface Tilt Angle on a Chromatic Confocal Probe with a Femtosecond Laser. Applied Sciences, 12(9), 4736. https://doi.org/10.3390/app12094736







