Study on Mechanical Properties and Constitutive Equation of Earth Materials under Uniaxial Compression
Abstract
:1. Introduction
2. Uniaxial Compression Test on Earth Materials
2.1. Selection and Preparation of Specimens
- The sieved soil material is dried in an oven, and the optimum water content is used as the control index to add water to mix the earth material. Then, it is sealed with a cling film and left to stand for one hour so that the moisture is evenly distributed in the earth material.
- Filling the mold with wet soil, using manual compaction in multiple layers, the compaction height of each layer is approximately 38 mm, and the compaction work W is 592.2 kJ∙m−3. The number of times of compaction per layer and the number of layers of compaction are calculated according to Equation (1), and the results are shown in Table 4 to ensure that the specimen is formed under a more uniform standard and achieves the maximum dry density. After each layer of compaction, the surface of the compacted soil is roughened to ensure close contact between the surfaces.where W is the compaction work, kJ·m−3; m is the weight of the hammer, taken as 2.5 Kg; h is the drop height of the hammer, taken as 305 mm; g is the acceleration of gravity, taken as 9.8 m∙s−2; n is the number of layers of compaction; s is the number of compactions per layer; and V is the volume of the test block, cm3.
- After the specimen is created, in order to slow down the initial water loss and hardening rate of the specimen and prevent cracking, it is covered with a cling film. To ensure that the specimens could be hardened at 28 d, the conservation method was referred to in [34]. The conservation was carried out in a laboratory at a temperature of 30 °C (±5 °C) and a humidity of 55–60%. To ensure the quality of demolding, it was carried out after 3 days of curing (after the specimens had obtained some of their strength). The average water content of the specimens at 14 d, 21 d, and 28 d was 8.8%, 4.3%, and 3.5%, respectively. The densities of 70.7 mm, 100 mm, and 150 mm cubic specimens and Φ102 × 116 cylindrical specimens at 28 d were 1.69 g∙cm−3, 1.70 g∙cm−3, 1.71 g∙cm−3, and 1.70 g∙cm−3.This indicates that the specimens are basically hardened.
2.2. Test Device and Procedure
2.3. Experimental Results and Discussion
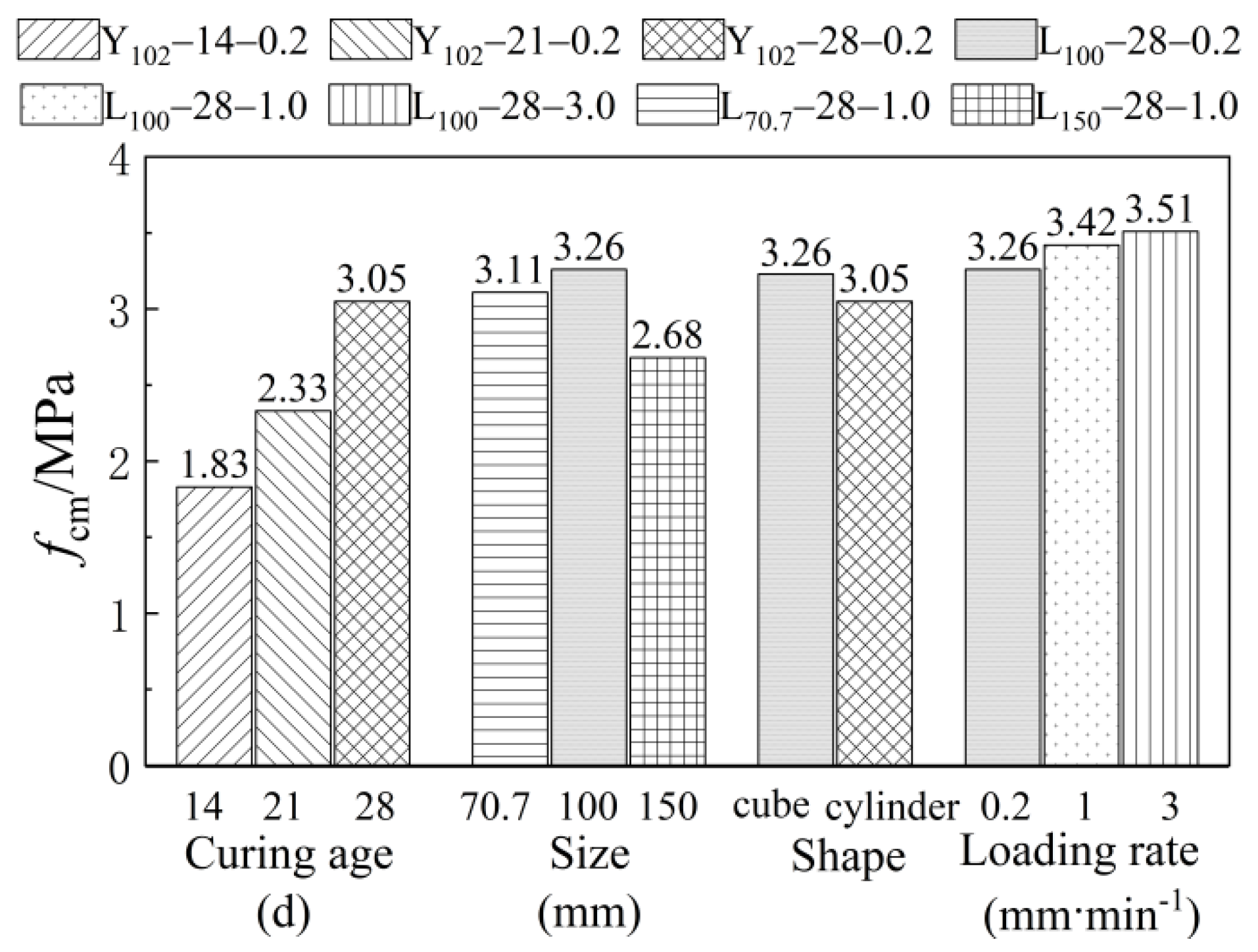
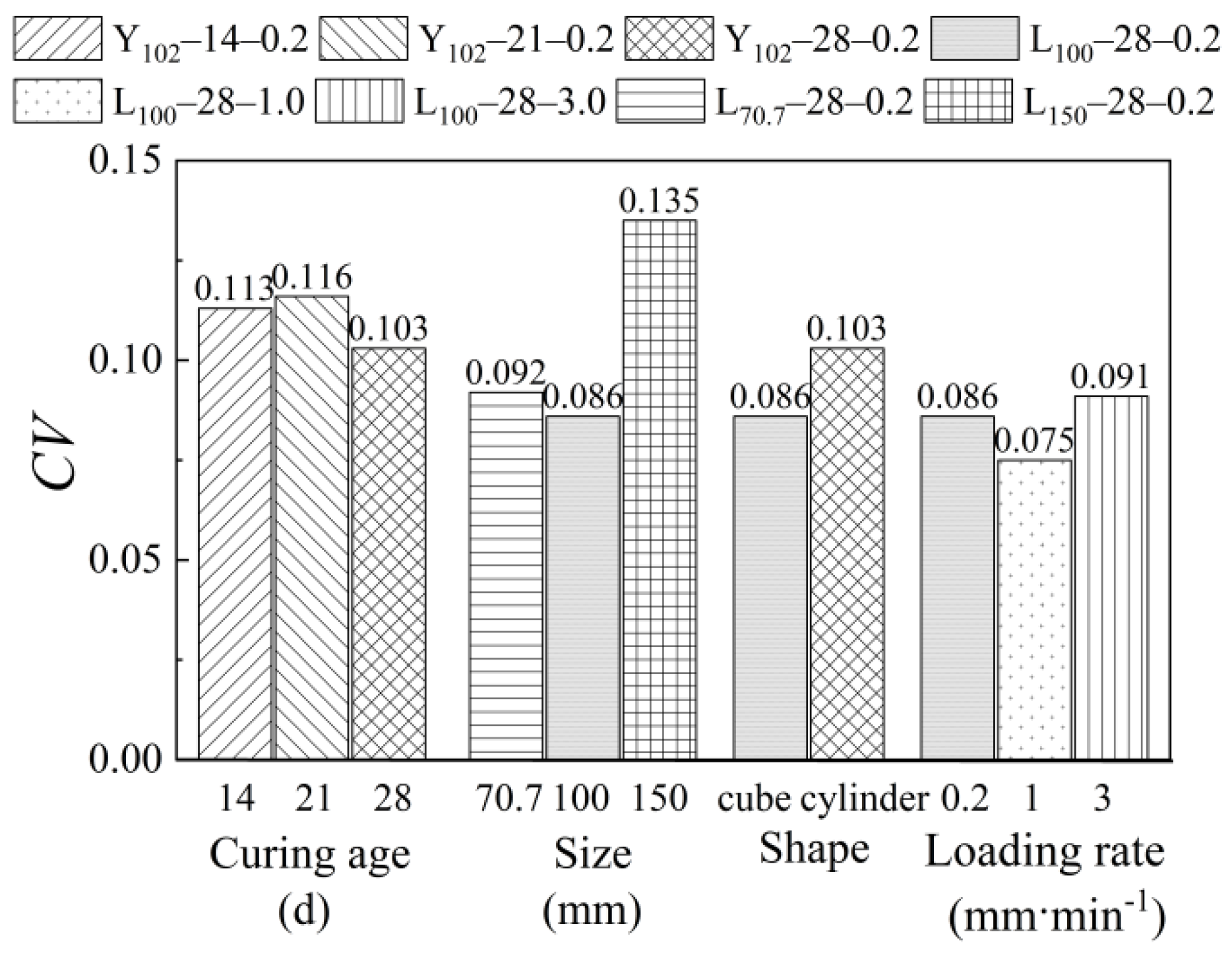
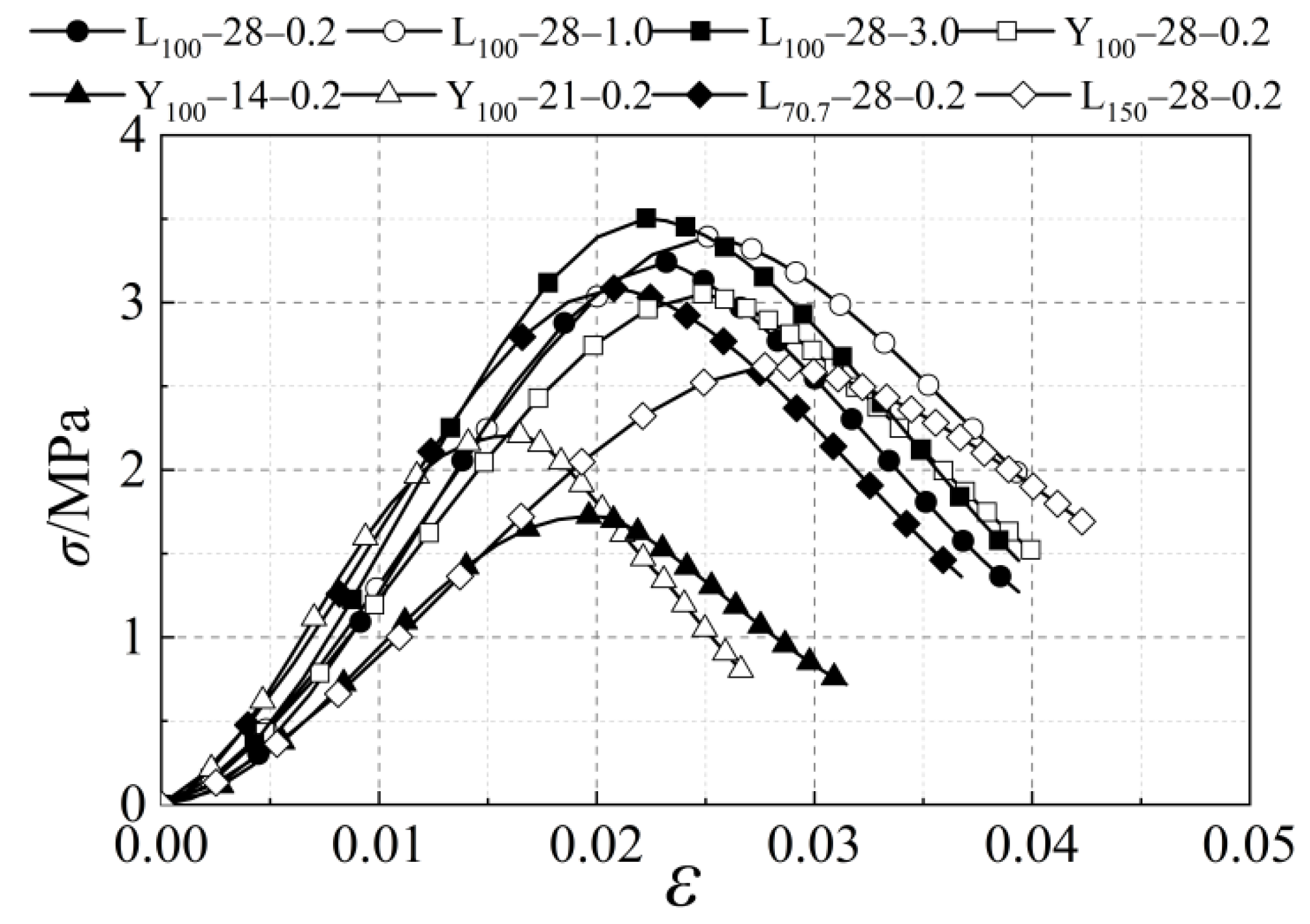
- The compressive strength of the specimens increased with the increase in curing age. The compressive strengths of specimens Y102-14-0.2, Y102-21-0.2, and Y102-28-0.2 were 59% and 76% of 28 d at 14 d and 21 d, respectively. The reason is that the longer the age, the more sufficient the water loss hardening reaction inside the specimen. The internal soil particles have higher cohesion, stronger compactness, and higher compressive strength.
- With the increase in size, the strength of the specimen first increased and then decreased. A 100-mm-cube specimen had the highest strength, and the effect of the size factor on the compressive strength was more significant. A 70.7-mm-cube had 96% of the compressive strength of a 100-mm-cube. A 150-mm-cube had only 83% of the compressive strength of a 100-mm-cube.
- The specimen shape and loading rate have a slight effect on the compressive strength. The compressive strength of cylindrical specimens was 5.6% lower than that of cubic specimens. The compressive strengths of specimens with loading rates of 0.2 mm∙min−1 and 3.0 mm∙min−1 were 95.3% and 102.6% of the compressive strengths of specimens with 1 mm∙min−1, respectively. The strength differences of the specimens were all within the range of 6%.
- It is recommended to use a 100 mm × 100 mm × 100 mm cube with a curing age of 28 d as the standard specimen. Then, 1.0 mm∙min−1 was adopted as the recommended loading rate for uniaxial compression testing of earth materials. As can be seen from Figure 9, the strength coefficient of variation of the specimens under the above test conditions is minimal, and the test results are relatively stable.
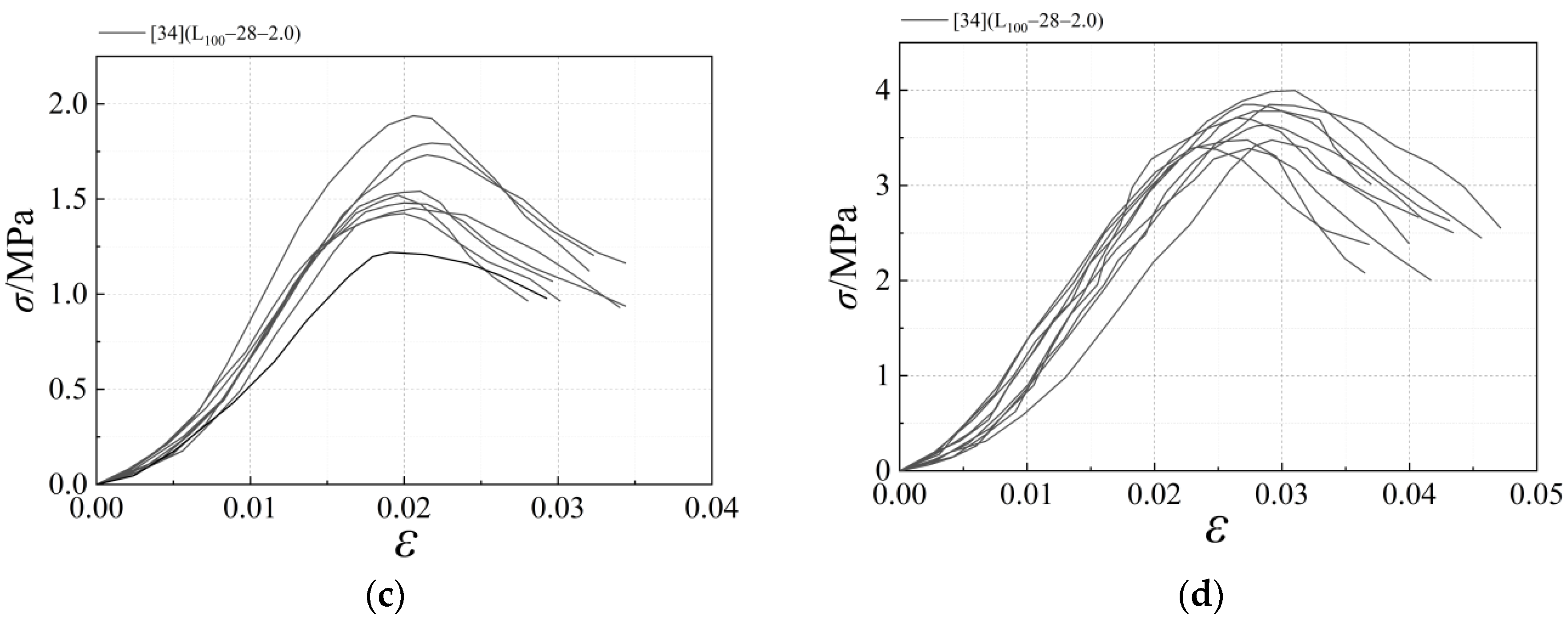
2.4. Experimental Stress-Strain Curve
3. Uniaxial Compressive Constitutive Equation Establishment
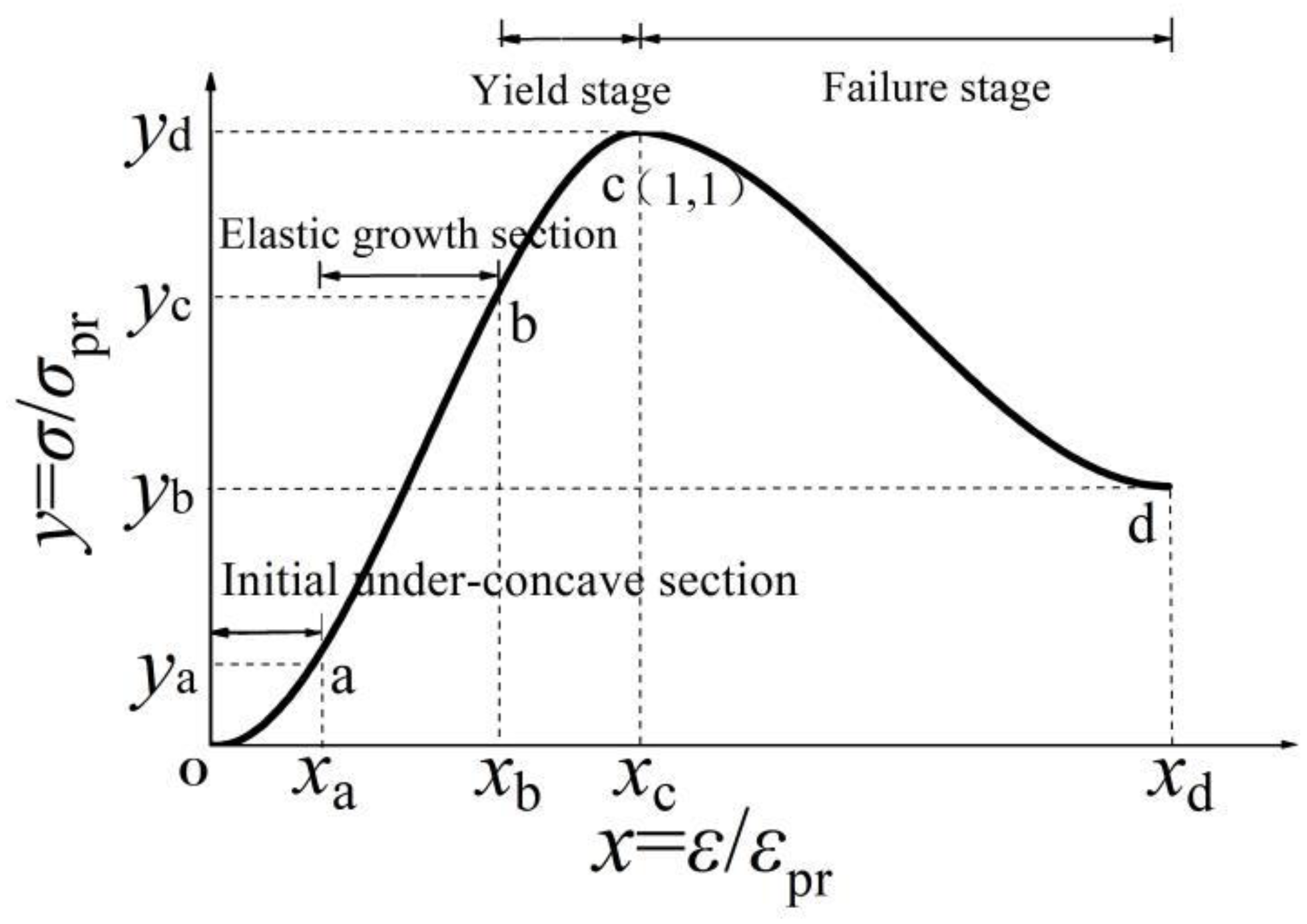
3.1. Proposition of Modified Constitutive Equation
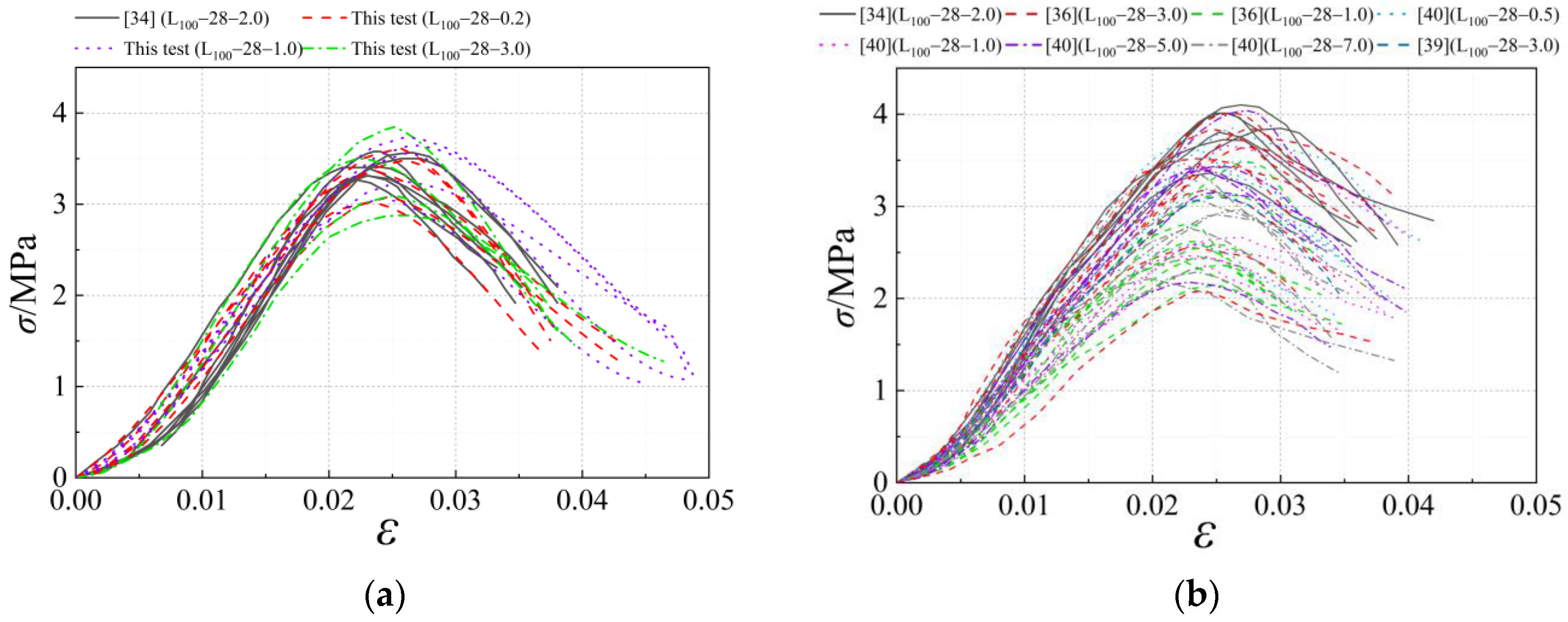
3.2. Applicability of the Modified Constitutive Equation
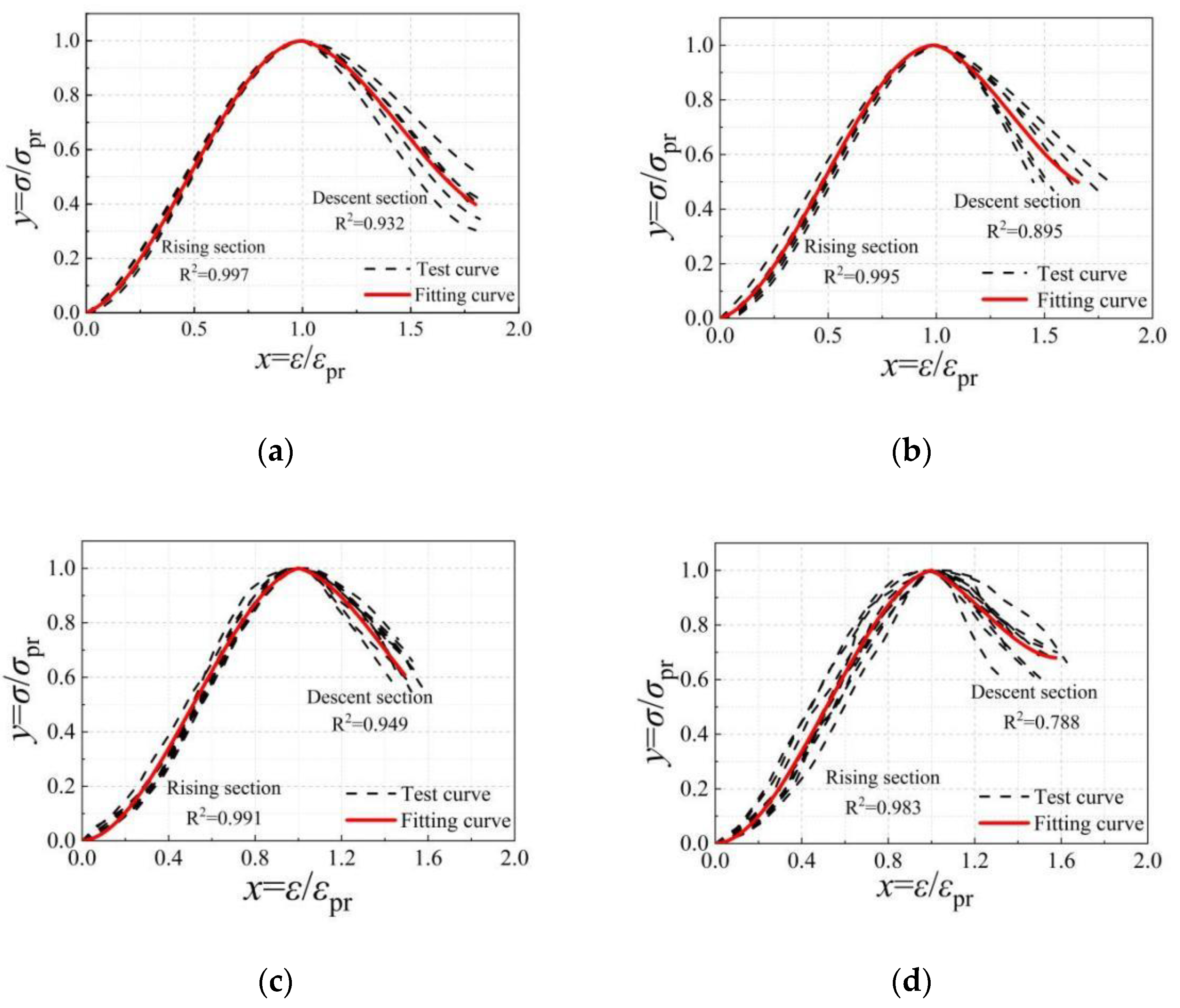
- There are certain differences in the values of the parameters of the shape of the constitutive equation curves of the standard specimens in different regions. At the same loading rate, the best-fitting results of the constitutive equation were obtained for the soil in Xinjiang. The R2 of the ascending section is 0.991, and the R2 of the descending section is 0.949. The fitting effect of the constitutive equation for the soil in Heilongjiang is relatively lower. The reason for this is that the earth material in Heilongjiang is mainly black soil, which contains more humus [40], further aggravating the inhomogeneity of the earth material. Considering that soils containing humus are not suitable for use in building structures and that the agricultural value of black soil is greater than the value of building materials, the use of black soil as a building material is not recommended.
- The present constitutive equation is a good fit for the rising section of the uniaxial compression test curve, and the descending section is relatively slightly lower. Take the Heilongjiang test data, where the fit is weakest, as an example. The R2 of the ascending section is 0.983, and the R2 of the descending section is 0.788. The main reason for the relatively low fit of the shape parameter of the descending section is the inhomogeneity of the composition of the earth material and the obvious brittle damage characteristics. Additionally, the damage development process is significantly affected by the manufacturing process and test method.
- The overall fit of the modified form of the constitutive equation to the uniaxial compressive test curves of the earth material is good. The average R2 value of the ascending segment curve is 0.991, and the average R2 value of the descending segment curve is 0.886. It shows that it has good applicability to the test data under the conditions of 100-mm-cubic standard specimens with a 28-d curing age. In addition, it can be seen from Figure 13 that the fitted curve is continuous and smooth, which can better reflect the characteristics of the initial under-concave in the rising section of the curve. The basic characteristics of x = 1 and y = 1 are met at the segment point from the rising section to the descending section, and the transition is smooth. The curve of the descending section can better reflect the stress-strain trend of the material damage process.
4. The Values of the Parameters of the Constitutive Equation
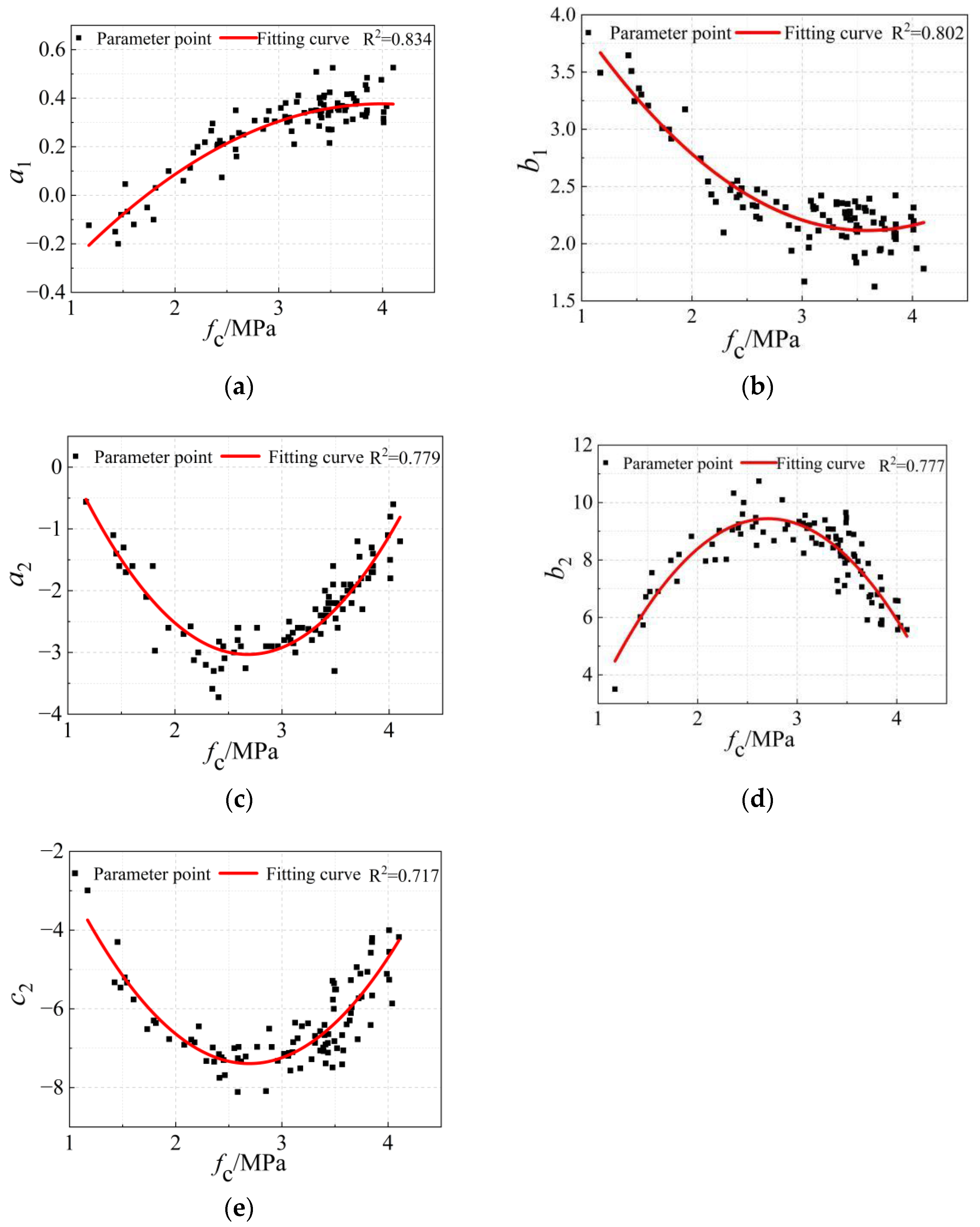
4.1. Curve Shape Parameters
4.2. Peak Compressive Strain
5. Conclusions
- The uniaxial compressive strength of earth specimens increases significantly with the increase in curing age and shows a trend of first increasing and then decreasing with the increase in size. It is relatively little influenced by the shape and loading rate of the specimen. The uniaxial compressive test with 100-mm-cubic specimens at 28 d of curing age and 1 mm∙min−1 loading rate can obtain stable test results with a small coefficient of variation of strength, which is recommended as the standard test method for the uniaxial compressive test of earth materials.
- Based on Illampas’s constitutive equation, the modified constitutive equation of earth materials under uniaxial compression can better meet the compression failure mechanics and deformation characteristics of earth materials. It is a good fit for the uniaxial compressive test data of 100-mm-cubic standard specimens maintained for 28 d. It has good applicability to soils in different regions of China.
- The calculation methods for the shape parameters of the rising and descending section curves and the peak compressive strain of the uniaxial compressive constitutive equation of the earth material under the condition of a 100-mm-cubic standard specimen at the age of 28 d of curing are established. The average values of the coefficients of determination R2 for the shape parameters of the rising and descending sections of the curve are 0.818 and 0.758, respectively, and the coefficient of determination R2 for the peak compressive strain is 0.666, which is a good overall fit.
- The modified constitutive equation and the calculation method for curve shape parameters and peak compressive strain are put forward. In the application, only the compressive strength of 100-mm-cubic standard specimens at 28 d curing age is measured, and the specific values of the relevant parameters of the constitutive equation can be calculated and determined. This is a good reference value to promote the development of computational analysis methods for earth structures and to facilitate the engineering design applications of earth structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lan, G.Q.; Wang, Y.H.; Chao, S.S. Influences of specimen geometry and loading rate on compressive strength of unstabilized compacted earth block. Adv. Mater. Sci. Eng. 2018, 2018, 5034256. [Google Scholar] [CrossRef] [Green Version]
- Dormohamadi, M.; Rahimnia, R. Combined effect of compaction and clay content on the mechanical properties of adobe brick. Case. Stud. Constr. Mat. 2020, 13, e00402. [Google Scholar] [CrossRef]
- Tan, J.Y.; Liang, J.H.; Wan, L.; Jiang, B. Influence of non-constant hygrothermal parameters on heat and moisture transfer in rammed earth walls. Buildings 2022, 12, 1077. [Google Scholar] [CrossRef]
- Van Damme, H.; Houben, H. Earth concrete. Stabilization revisited. Cement. Concrete. Res. 2018, 114, 90–102. [Google Scholar] [CrossRef]
- Abdulla, K.F.; Cunningham, L.S.; Gillie, M. Out-of-plane strengthening of adobe masonry using hemp fibre ropes: An experimental investigation. Eng. Struct. 2021, 245, 112931. [Google Scholar] [CrossRef]
- Millogo, Y.; Morel, J.C.; Aubert, J.E.; Ghavami, K. Experimental analysis of pressed adobe blocks reinforced with hibiscus cannabinus fibers. Constr. Build. Mater. 2014, 52, 71–78. [Google Scholar] [CrossRef]
- Mu, J.; Zhou, T.G. China Rural Housing Sample Survey Research Project Report; Ministry of Housing and Urban-Rural Development: Beijing, China, 2012. [Google Scholar]
- Li, Q.; Wang, W.; Wang, J.F.; Zhang, J.F.; Geng, D. Exploring the relationship between InSAR coseismic deformation and earthquake-damaged buildings. Remote. Sens. Environ. 2021, 262, 112508. [Google Scholar] [CrossRef]
- Gong, M.S.; Lin, S.B.; Sun, J.J.; Li, S.Y.; Dai, J.W.; Xie, L.L. Seismic intensity map and typical structural damage of 2010 Ms 7.1 Yushu earthquake in China. Nat. Hazards. 2015, 77, 847–866. [Google Scholar] [CrossRef] [Green Version]
- Des Roches, R.; Comerio, M.; Eberhard, M.; Mooney, W.; Rix, G.J. Overview of the 2010 Haiti Earthquake. Earthq. Spectra. 2011, 27, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Dominguez-Santos, D.; Bravo, J.A.M. Structural and mechanical performance of adobe with the addition of high-density polyethylene fibres for the construction of low-rise buildings. Eng. Fail. Anal. 2022, 139, 106461. [Google Scholar] [CrossRef]
- Momin, S.; Lovon, H.; Silva, V.; Ferreira, T.M.; Vicente, R. Seismic vulnerability assessment of portuguese adobe buildings. Buildings 2021, 11, 200. [Google Scholar] [CrossRef]
- Kumar, N.; Barbato, M. Effects of sugarcane bagasse fibers on the properties of compressed and stabilized earth blocks. Constr. Build. Mater. 2022, 315, 125552. [Google Scholar] [CrossRef]
- Eko, R.M.; Offa, E.D.; Ngatcha, T.Y.; Minsilib, L.S. Potential of salvaged steel fibers for reinforcement of unfired earth blocks. Constr. Build. Mater. 2012, 35, 340–346. [Google Scholar]
- Landrou, G.; Brumaud, C.; Habert, G. Development of a self-compacted clay based concrete-rheological, mechanical and environmental investigations. Acad. J. Civ. Eng. 2015, 33, 80–84. [Google Scholar]
- Heathcote, K.A. Durability of earthwall buildings. Constr. Build. Mater. 1995, 9, 185–189. [Google Scholar] [CrossRef]
- Fiore, A.; Marano, G.C.; Marti, C.; Molfetta, M. On the fresh/hardened properties of cement composites incorporating rubber particles from recycled tires. Adv. Civ. Eng. 2014, 2014, 876158. [Google Scholar] [CrossRef]
- Adorni, E.; Coiesson, E.; Ferretti, D. In Situ characterization of archaeological adobe bricks. Constr. Build. Mater. 2013, 40, 1–9. [Google Scholar] [CrossRef]
- Aguilar, R.; Montesinos, M.; Uceda, S. Mechanical characterization of the structural components of Pre-Columbian earthen monuments: Analysis of bricks and mortar from Huaca de la Luna in Perú. Case. Stud. Constr. Mat. 2017, 6, 16–28. [Google Scholar] [CrossRef] [Green Version]
- Illampas, R.; Ioannou, I.; Charmpis, D.C. Adobe bricks under compression: Experimental investigation and derivation of stress-strain equation. Constr. Build. Mater. 2014, 53, 83–90. [Google Scholar] [CrossRef]
- Rodríguez-Mariscal, J.D.; Solís, M.; Cifuentes, H. Methodological issues for the mechanical characterization of unfired earth bricks. Constr. Build. Mater. 2018, 175, 804–814. [Google Scholar] [CrossRef]
- GB/T 50123-2019; Standard for Geotechnical Testing Method. China Planning Press: Beijing, China, 2019.
- Danso, H.; Martinson, D.B.; Ali, M.; Williams, J. Effect of fibre aspect ratio on mechanical properties of soil building blocks. Constr. Build. Mater. 2015, 83, 314–319. [Google Scholar] [CrossRef] [Green Version]
- Salih, M.M.; Osofero, A.I.; Imbabi, M.S. Constitutive models for fibre reinforced soil bricks. Constr. Build. Mater. 2020, 240, 1–21. [Google Scholar] [CrossRef]
- Piani, T.L.; Weerheijm, J.; Peroni, M.; Koene, L.; Krabbenborg, D.; Solomos, G.; Sluys, L.J. Dynamic behaviour of adobe bricks in compression: The role of fibres and water content at various loading rates. Constr. Build. Mater. 2020, 230, 117038. [Google Scholar] [CrossRef]
- Bahar, R.; Benazzoug, M.; Kenai, S. Performance of compacted cement-stabilised soil. Cement. Concrete. Comp. 2004, 26, 811–820. [Google Scholar] [CrossRef]
- Mansour, M.B.; Jelidi, A.; Cherif, A.S.; Jabrallah, S.B. Optimizing thermal and mechanical performance of compressed earth blocks (CEB). Constr. Build. Mater. 2016, 104, 44–51. [Google Scholar] [CrossRef]
- Aymerich, F.; Fenu, L.; Meloni, P. Effect of reinforcing wool fibres on fracture and energy absorption properties of an earthen material. Constr. Build. Mater. 2012, 27, 66–72. [Google Scholar] [CrossRef]
- Houben, H.; Guillaud, H. Traité de Construction en Terre; CRATerre: Villefontaine, France; Editions Parenthèses: Marseille, France, 1989. [Google Scholar]
- ASTM D2487; Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System). de ASTM International: West Conshohocken, PA, USA, 2011.
- EN1992-1-1; Eurocode2: Design of Concrete Structures-Part 1-1: Gerneral Rules and Rules for Buildings. British Standards Institution: London, UK, 2004.
- JGJ/T 70-2009; Standard for Test Method of Performance on Building Mortar. China Architecture and Building Press: Beijing, China, 2009.
- NZS4297: 2020; Engineering Design of Earth Buildings. Building Industry Authority of New Zealand: Wellington, New Zealand, 2020.
- Zhang, K. Study on the Standard test Method of Material Strength on Raw-Soil. Ph.D. Thesis, Chang’an University, Xi’an, China, 2017. [Google Scholar]
- Zhang, Y.C.; Wang, Y.H.; Zhao, N.N.; Wang, T.Y. Experimental and stress-strain equation investigation on compressive strength of raw and modified soil in Loess Plateau. Adv. Mater. Sci. Eng. 2016, 2016, 2681038. [Google Scholar] [CrossRef] [Green Version]
- Zhong, J.Q. Study and Application on Constitutive Relationship for Earth Material and Mechanical Compressed Earth Brick Masonry. Ph.D. Thesis, Chang’an University, Xi’an, China, 2018. [Google Scholar]
- Wang, S.N.; Chen, F.Y.; Xue, Q.P.; Zhang, P. Splitting tensile strength of cement soil reinforced with basalt fibers. Materials. 2020, 13, 3110. [Google Scholar] [CrossRef]
- Liu, F. Experimental Study on Compressive Strength of Raw Soil Material Modified by Stones, Sand and Cement. Master’s Thesis, Chang’an University, Xi’an, China, 2017. [Google Scholar]
- Ding, S.Y. Experimental researches on size effect of raw-soil based materials compressive strength. Master’s Thesis, Chang’an University, Xi’an, China, 2017. [Google Scholar]
- Zhong, X.L.; Gan, Y.Q.; Deng, Y.M. Distribution, origin and speciation of soil selenium in the black soil region of Northeast China. Environ. Geochem. Hlth. 2021, 43, 1257–1271. [Google Scholar] [CrossRef]
- Gong, X.; Yu, H.F.; Wu, C.Y. Research on the constitutive relationship of concrete under uniaxial compression in freeze-thaw environment. Constr. Build. Mater. 2022, 336, 127543. [Google Scholar] [CrossRef]

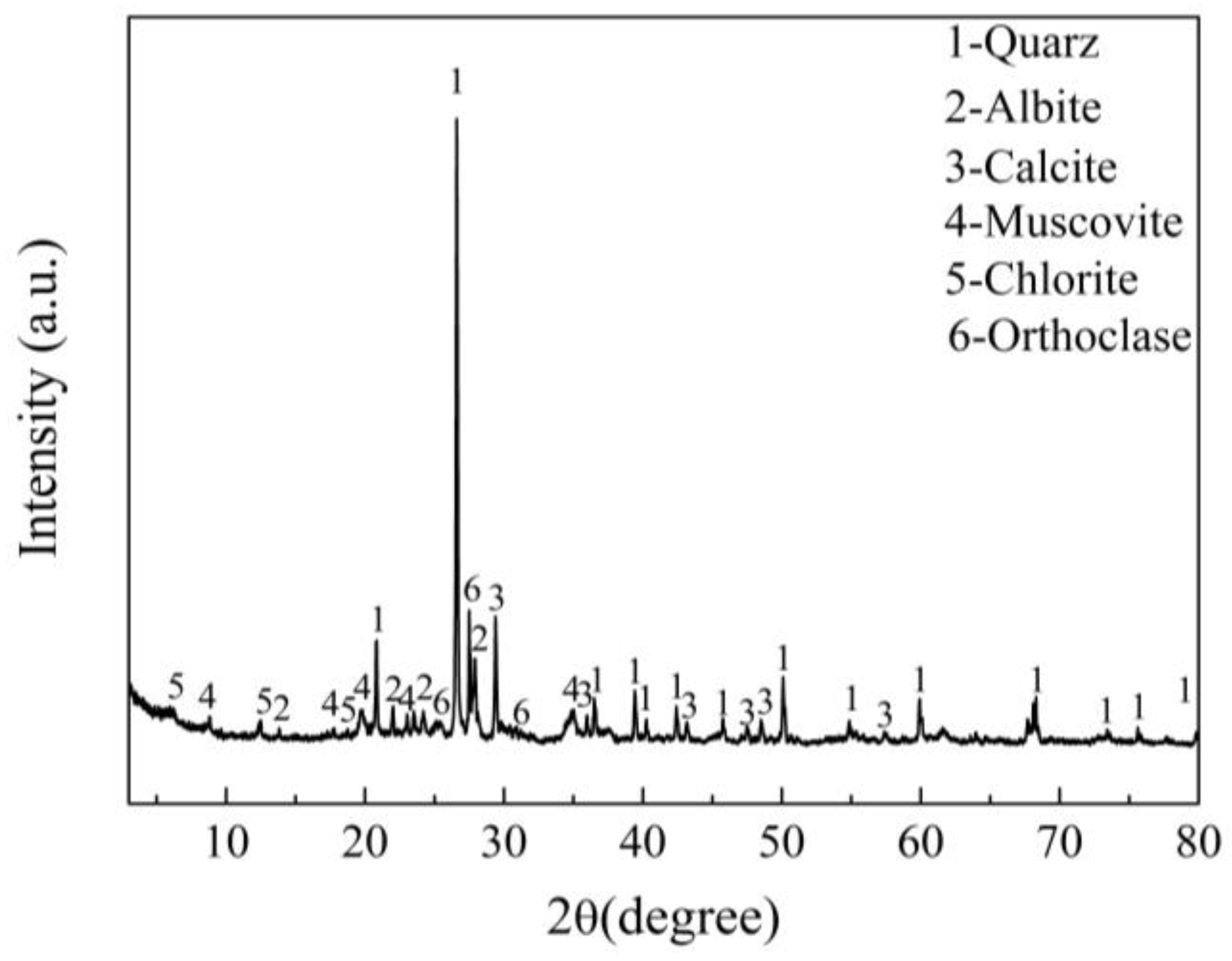
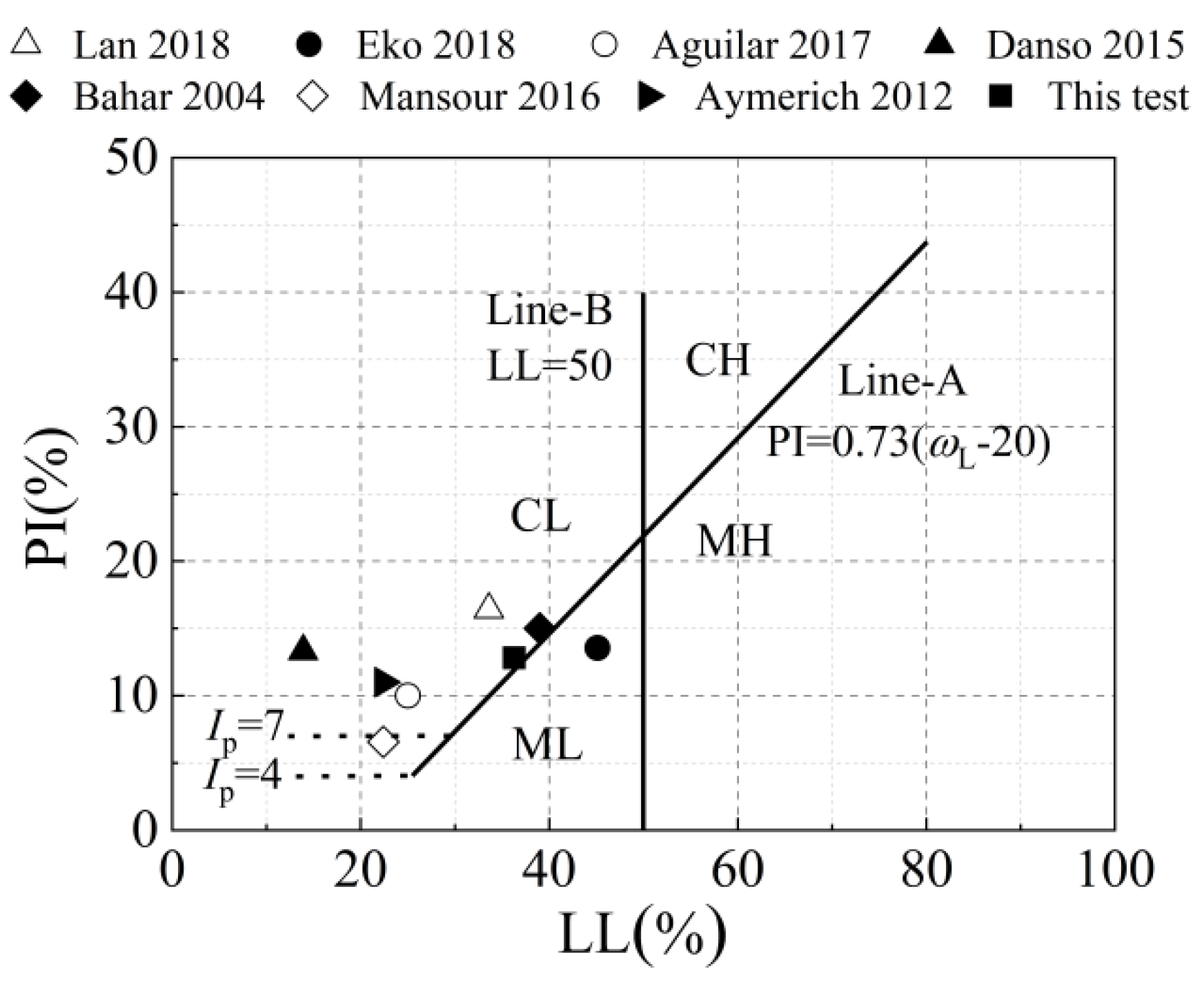




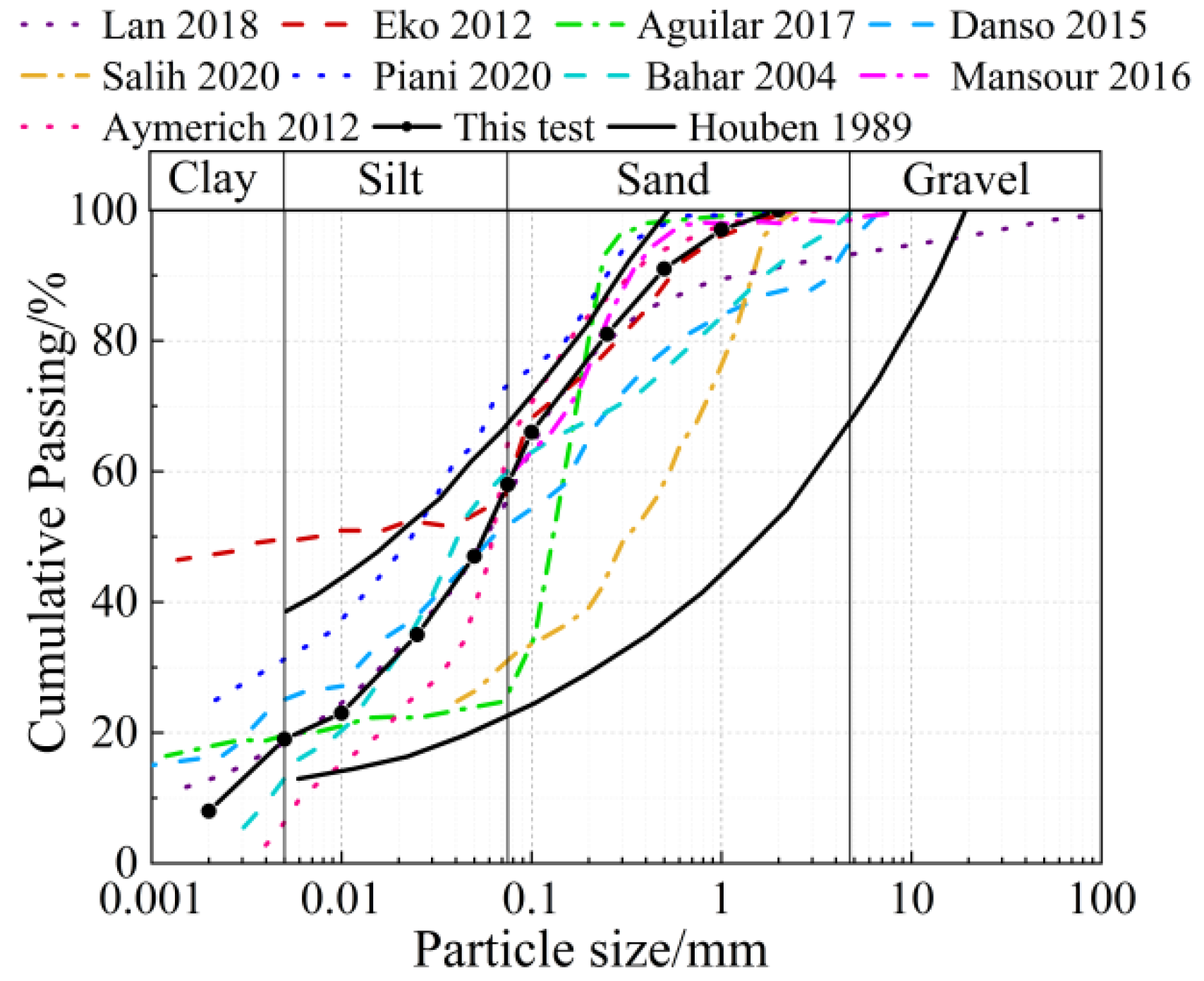
| Chemical Compositions | SiO2 | Al2O3 | CaO | Fe2O3 | MgO | K2O | Na2O | TiO2 | P2O5 | SO3 |
|---|---|---|---|---|---|---|---|---|---|---|
| Content (%) | 59.49 | 17.4 | 7.58 | 5.393 | 3.9 | 2.89 | 1.79 | 0.678 | 0.346 | 0.191 |
| Granulometry | Atterberg Limits | Maximum Dry Density (g·cm−3) | Dry Density (g·cm−3) | Optimal Water Content (%) | ||||
|---|---|---|---|---|---|---|---|---|
| Clay (%) d < 5 μm | Silt (%) 5 μm ≤ d ≤ 75 μm | Sand (%) 75 μm ≤ d ≤ 4500 μm | LL (%) | PL (%) | PI (%) | |||
| 19 | 39 | 42 | 36.3 | 23.5 | 12.8 | 2.04 | 1.66 | 23 |
| Specimen label | Specimen Type (mm) | Loading Rate (mm·min−1) | Curing Age (d) | Quantity |
|---|---|---|---|---|
| Y102-14-0.2 | Φ102 × 116 | 0.2 | 14 | 6 |
| Y102-21-0.2 | Φ102 × 116 | 0.2 | 21 | 6 |
| Y102-28-0.2 | Φ102 × 116 | 0.2 | 28 | 6 |
| L100-28-0.2 | 100 × 100 × 100 | 0.2 | 28 | 6 |
| L100-28-1.0 | 100 × 100 × 100 | 1.0 | 28 | 6 |
| L100-28-3.0 | 100 × 100 × 100 | 3.0 | 28 | 6 |
| L70.7-28-0.2 | 70.7 × 70.7 × 70.7 | 0.2 | 28 | 6 |
| L150-28-0.2 | 150 × 150 × 150 | 0.2 | 28 | 6 |
| Specimen Type (mm) | V (cm3) | n | s |
|---|---|---|---|
| Φ102 × 116 | 947.4 | 3 | 25 |
| 100 × 100 × 100 | 1000 | 3 | 26 |
| 70.7 × 70.7 × 70.7 | 353.4 | 2 | 14 |
| 150 × 150 × 150 | 3375.0 | 4 | 67 |
| Specimen Label | fcm (MPa) | σf | CV | εpr |
|---|---|---|---|---|
| Y102-14-0.2 | 1.83 | 0.206 | 0.113 | 0.0199 |
| Y102-21-0.2 | 2.33 | 0.270 | 0.116 | 0.0205 |
| Y102-28-0.2 | 3.05 | 0.314 | 0.103 | 0.0248 |
| L100-28-0.2 | 3.26 | 0.280 | 0.086 | 0.0232 |
| L100-28-1.0 | 3.42 | 0.256 | 0.075 | 0.0251 |
| L100-28-3.0 | 3.51 | 0.319 | 0.091 | 0.0225 |
| L70.7-28-0.2 | 3.11 | 0.286 | 0.092 | 0.0208 |
| L150-28-0.2 | 2.68 | 0.361 | 0.135 | 0.0275 |
| Source | Region | Atterberg Limits | Type of Soil | Forming Method | Maximum Dry Density (g·cm−3) | Optimal Moisture Content (%) | ||
|---|---|---|---|---|---|---|---|---|
| LL (%) | PL (%) | PI (%) | ||||||
| This test | Xinjiang | 36.3 | 23.5 | 12.8 | Low liquid limit clay | Light compaction method | 2.04 | 23.0 |
| [38] | Shanxi | 33.6 | 17.2 | 16.4 | Jack compaction | 1.90 | 18.2 | |
| [34] | Shanxi | 26.0 | 15.0 | 11.0 | Jack compaction | 2.04 | 18.2 | |
| [34] | Xinjiang | 25.5 | 13.6 | 11.9 | Jack compaction | 2.14 | 14.5 | |
| [34] | Fujian | 45.0 | 26.0 | 19.0 | Jack compaction | 1.74 | 29.0 | |
| [34] | Heilongjiang | 28.5 | 14.0 | 14.5 | Jack compaction | 2.00 | 16.3 | |
| [36] | Shanxi | 26.0 | 15.0 | 11.0 | Jack compaction | 2.04 | 18.2 | |
| [39] | Shanxi | 26.0 | 15.0 | 11.0 | Jack compaction | 2.04 | 18.2 | |
| Specimen Source | Region | Specimen Working Condition | Rising Section | Descending Section | |||||
|---|---|---|---|---|---|---|---|---|---|
| a1 | b1 | R2 | a2 | b2 | c2 | R2 | |||
| This test | Xinjiang | L100-28-0.2 | 0.274 | 2.363 | 0.995 | −2.505 | 8.808 | −7.013 | 0.895 |
| This test | Xinjiang | L100-28-1.0 | 0.219 | 2.332 | 0.997 | −2.010 | 7.056 | −5.190 | 0.927 |
| This test | Xinjiang | L100-28-3.0 | 0.271 | 2.319 | 0.983 | −2.204 | 7.476 | −5.056 | 0.911 |
| [38] | Shanxi | L100-28-3.0 | 0.308 | 2.302 | 0.998 | −2.850 | 9.199 | −6.845 | 0.919 |
| [34] | Shanxi | L100-28-2.0 | 0.374 | 2.208 | 0.993 | −2.801 | 10.463 | −9.125 | 0.863 |
| [34] | Xinjiang | L100-28-2.0 | 0.302 | 2.181 | 0.991 | −2.701 | 9.341 | −7.403 | 0.949 |
| [34] | Fujian | L100-28-2.0 | −0.110 | 3.193 | 0.995 | −1.720 | −7.506 | −6.495 | 0.902 |
| [34] | Heilongjiang | L100-28-2.0 | 0.250 | 2.660 | 0.984 | −2.010 | 8.402 | −7.378 | 0.788 |
| [36] | Shanxi | L100-28-3.0 | 0.402 | 2.021 | 0.994 | −2.303 | 8.768 | −7.406 | 0.873 |
| [36] | Shanxi | L100-28-1.0 | 0.201 | 2.271 | 0.986 | −2.340 | 10.493 | −10.228 | 0.841 |
| [39] | Shanxi | L100-28-0.5 | 0.330 | 2.036 | 0.987 | −2.520 | 9.436 | −7.693 | 0.834 |
| [39] | Shanxi | L100-28-1.0 | 0.420 | 1.691 | 0.983 | −2.901 | 9.938 | −7.693 | 0.929 |
| [39] | Shanxi | L100-28-5.0 | 0.302 | 2.278 | 0.993 | −2.746 | 9.523 | −7.811 | 0.925 |
| [39] | Shanxi | L100-28-7.0 | 0.346 | 2.150 | 0.996 | −2.784 | 10.096 | −8.549 | 0.846 |
| Shape Parameter | Fitting Equation |
|---|---|
| a1 | |
| b1 | |
| a2 | |
| b2 | |
| c2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, J.; Yuan, K.; Zhang, F.; Guo, L. Study on Mechanical Properties and Constitutive Equation of Earth Materials under Uniaxial Compression. Appl. Sci. 2023, 13, 19. https://doi.org/10.3390/app13010019
Yan J, Yuan K, Zhang F, Guo L. Study on Mechanical Properties and Constitutive Equation of Earth Materials under Uniaxial Compression. Applied Sciences. 2023; 13(1):19. https://doi.org/10.3390/app13010019
Chicago/Turabian StyleYan, Jianlong, Kang Yuan, Fenjie Zhang, and Longlong Guo. 2023. "Study on Mechanical Properties and Constitutive Equation of Earth Materials under Uniaxial Compression" Applied Sciences 13, no. 1: 19. https://doi.org/10.3390/app13010019
APA StyleYan, J., Yuan, K., Zhang, F., & Guo, L. (2023). Study on Mechanical Properties and Constitutive Equation of Earth Materials under Uniaxial Compression. Applied Sciences, 13(1), 19. https://doi.org/10.3390/app13010019