Effects of Imperfect Assembly and Magnetic Properties on the Three-Pole AMB System
Abstract
:Featured Application
Abstract
1. Introduction
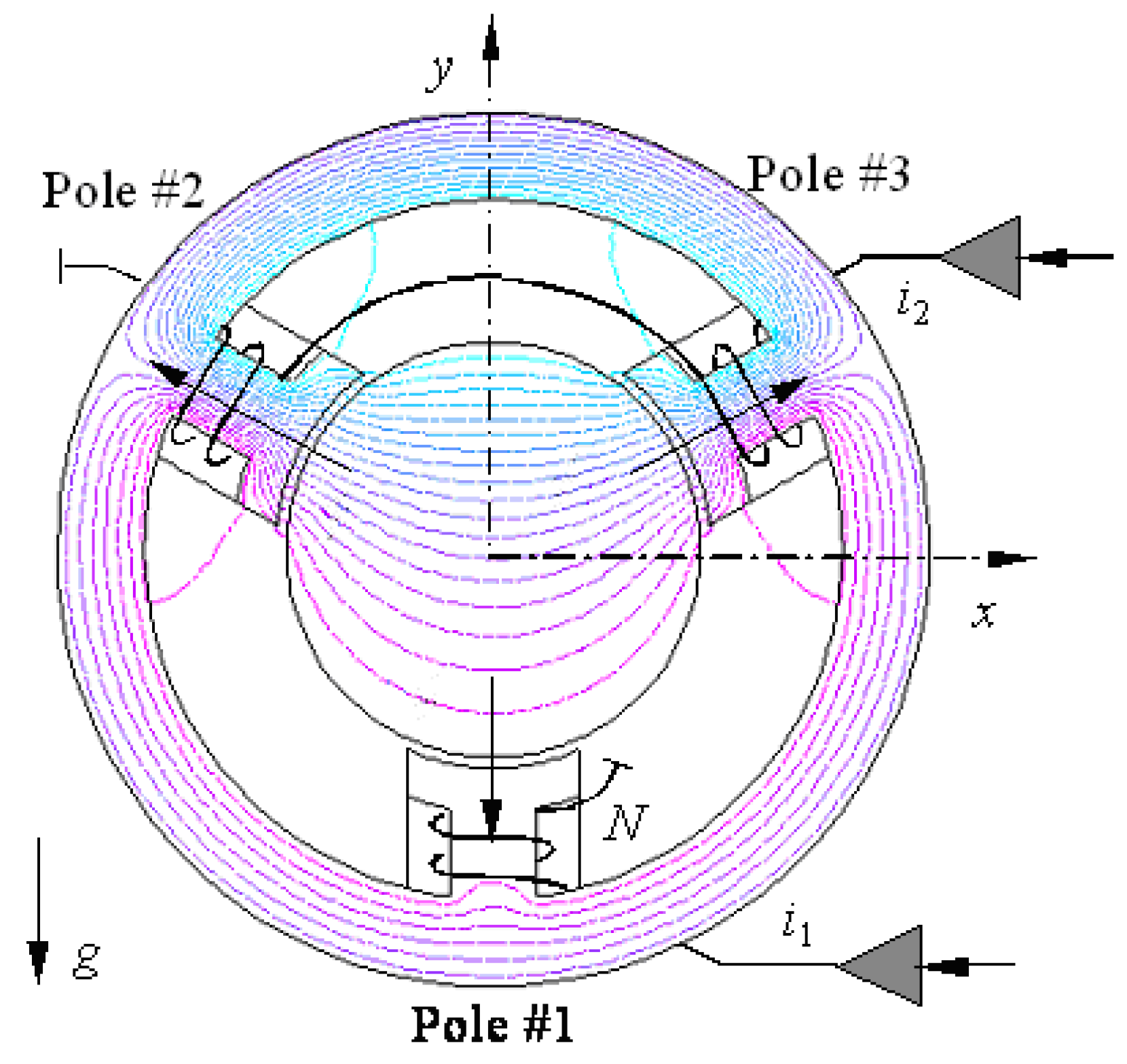
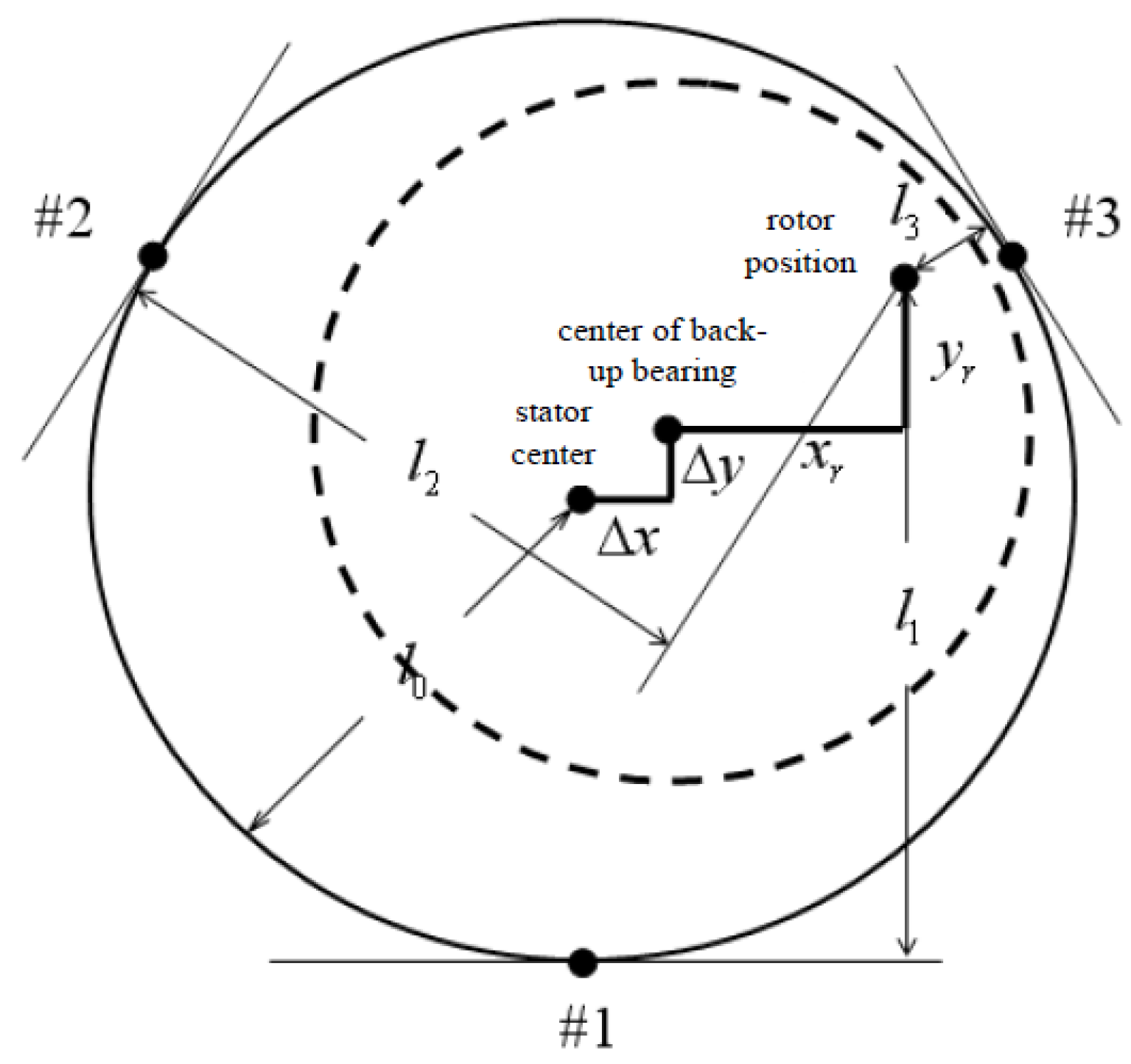
2. System Description and Dynamic Modeling
3. Design of Stable-Levitation Controller
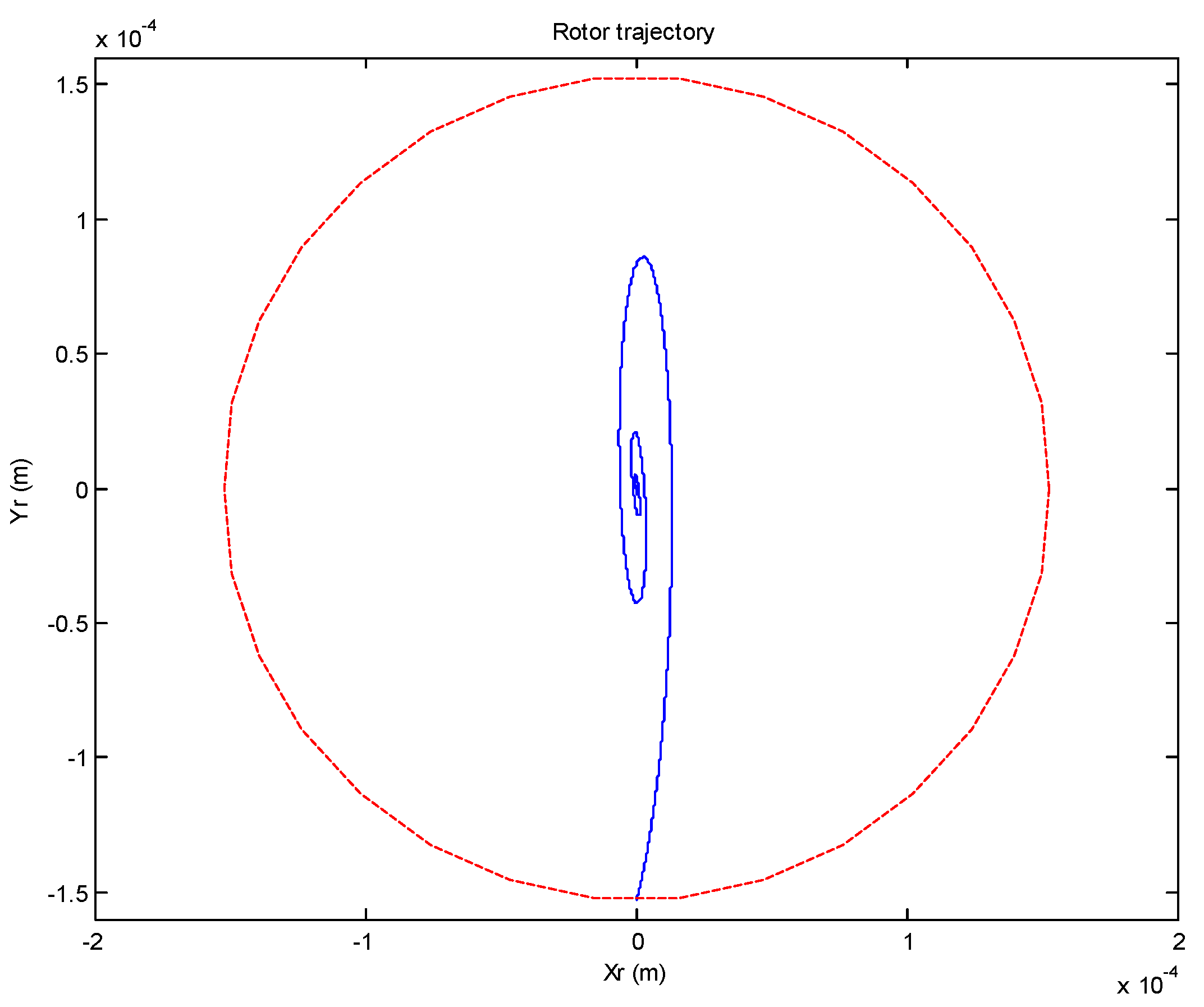
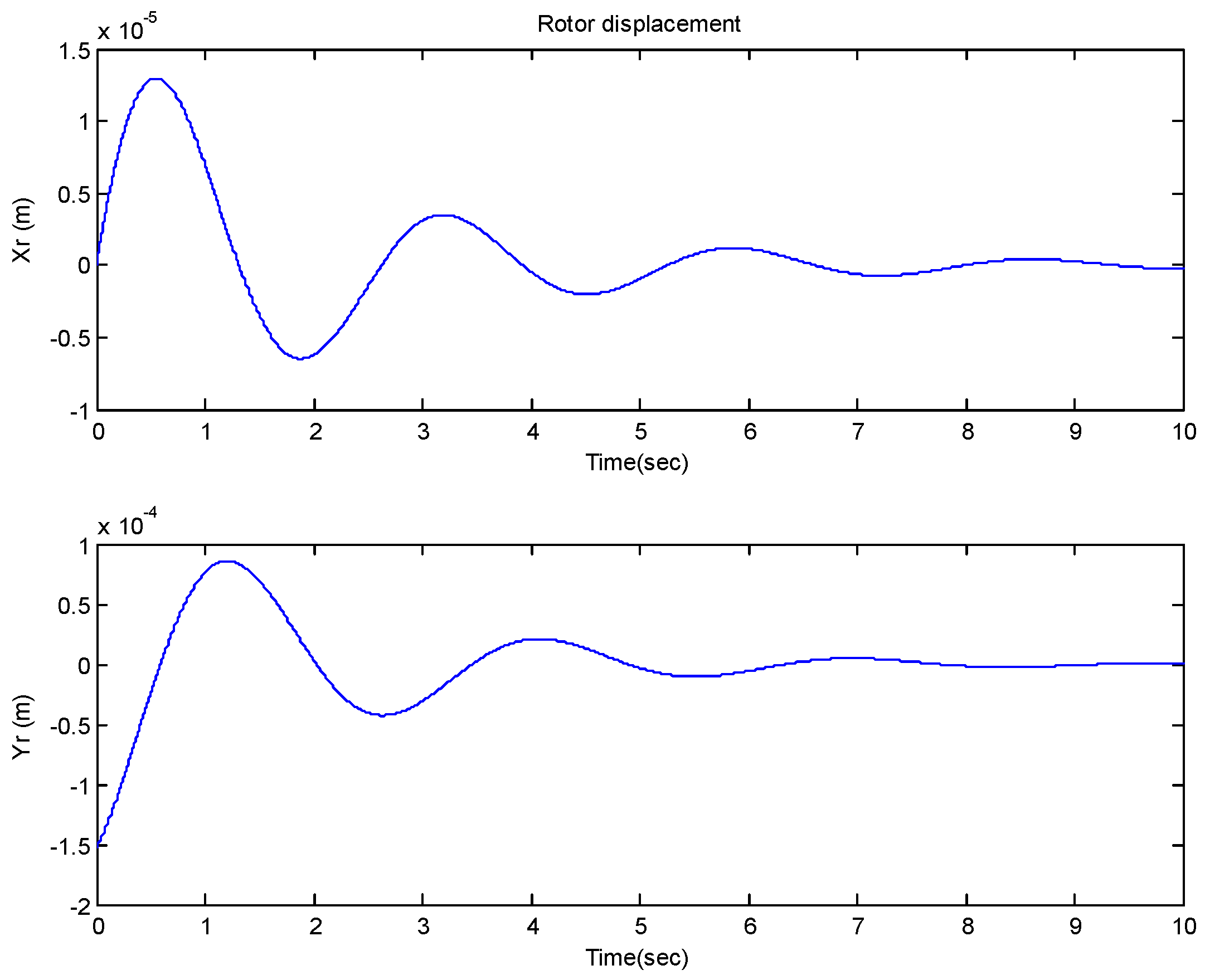
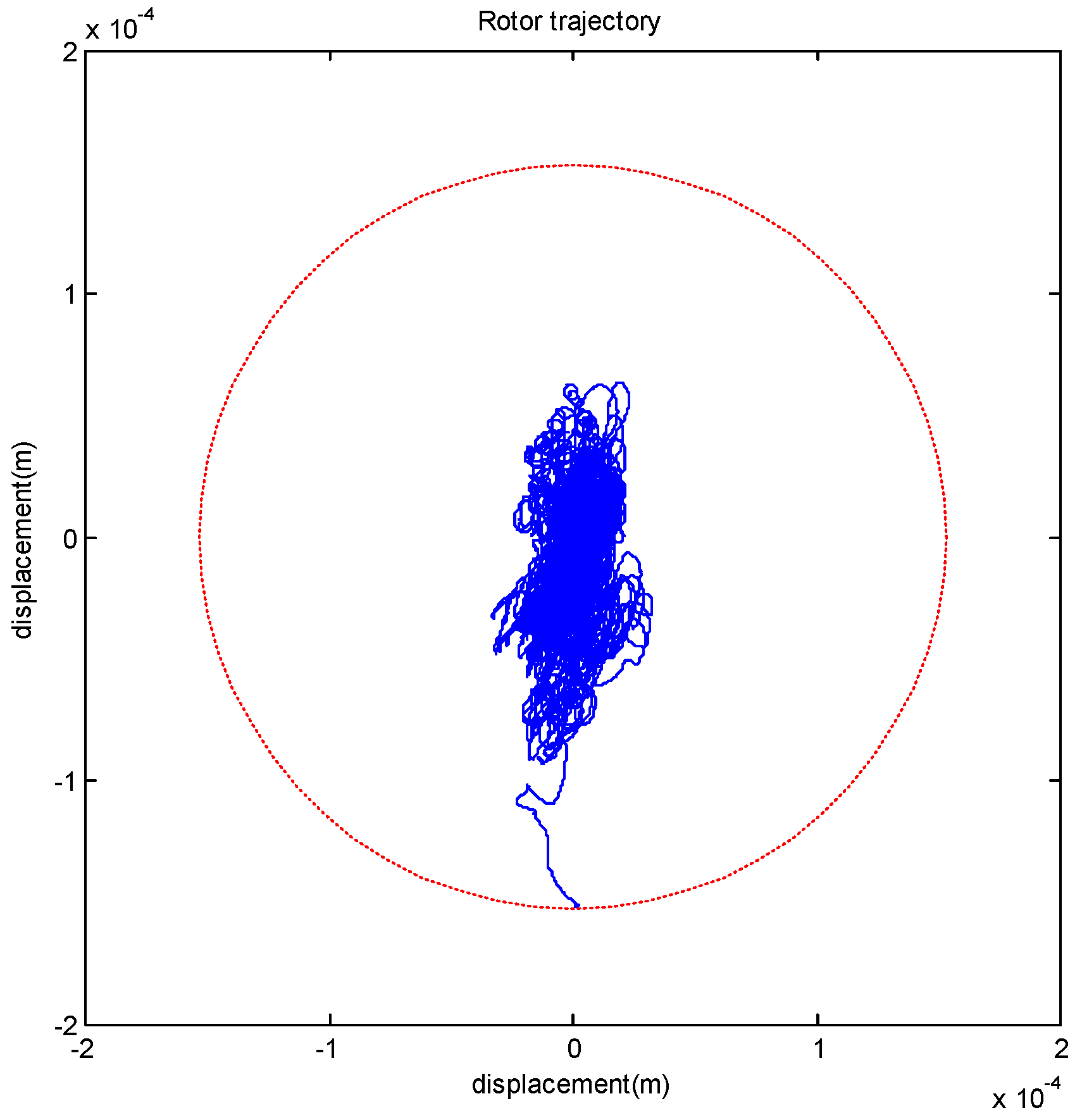
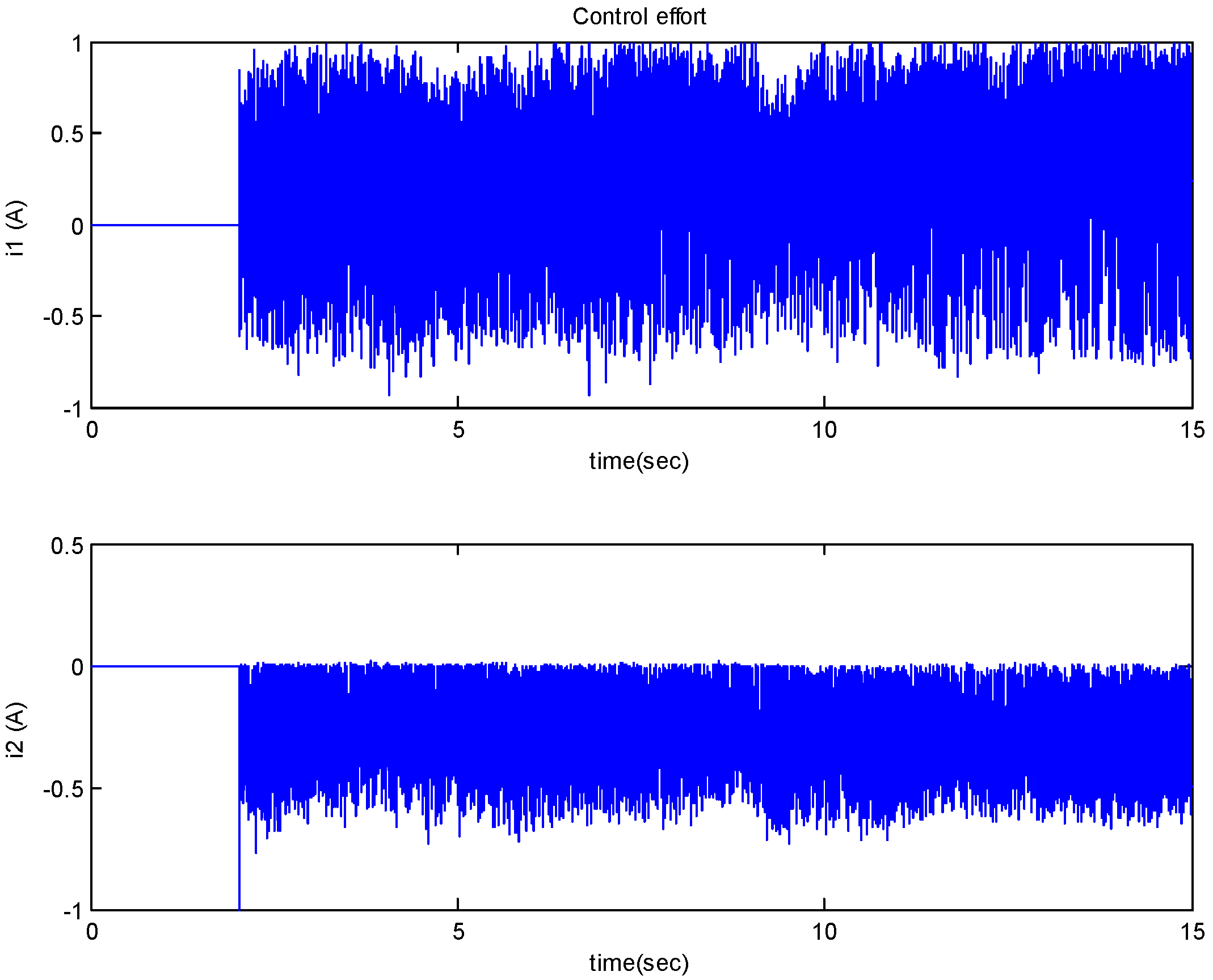
4. Simulation and Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Schweitzer, G.; Maslen, E.H. Magnetic Bearings: Theory, Design and Application to Rotating Machinery; Springer: Berlin, Germany, 2009. [Google Scholar]
- Bangcheng, H.; Zan, H.; Xu, Z.; Xu, L.; Tong, W.; Shiqiang, Z. Loss estimation, thermal analysis, and measurement of a large-scale turbomolecular pump with active magnetic bearings. IET Electr. Power Appl. 2020, 14, 1283–1290. [Google Scholar] [CrossRef]
- Prasad, K.N.V.; Narayanan, G. Electro-Magnetic Bearings with Power Electronic Control for High-Speed Rotating Machines: A Review. In Proceedings of the 2019 National Power Electronics Conference (NPEC), Tiruchirappalli, Tamil Nadu, India, 13–15 December 2019; pp. 1–6. [Google Scholar]
- Guan, X.; Zhou, J.; Jin, C.; Xu, Y.; Cui, H. Influence of different operating conditions on centrifugal compressor surge control with active magnetic bearings. Eng. Appl. Comput. Fluid Mech. 2019, 13, 824–832. [Google Scholar] [CrossRef] [Green Version]
- Toh, C.-S.; Chen, S.-L. Design, Modeling and Control of Magnetic Bearings for a Ring-Type Flywheel Energy Storage System. Energies 2016, 9, 1051. [Google Scholar] [CrossRef] [Green Version]
- Olabi, A.G.; Wilberforce, T.; Abdelkareem, M.A.; Ramadan, M. Critical Review of Flywheel Energy Storage System. Energies 2021, 14, 2159. [Google Scholar] [CrossRef]
- Wang, X.; Han, C.; Yu, Y.; Yang, Z. A modified adaptive backstepping method for shaft deflection tracking control of magnetically suspended momentum wheel with nonlinear magnetic torque. J. Frankl. Inst. 2018, 355, 3274–3287. [Google Scholar] [CrossRef]
- Park, C.H.; Yoon, T.G.; Kang, D.; Rodrigue, H. High-Precision Roller Supported by Active Magnetic Bearings. Appl. Sci. 2019, 9, 4389. [Google Scholar] [CrossRef] [Green Version]
- Lee, R.-M.; Chen, T.-C. Adaptive Control of Active Magnetic Bearing against Milling Dynamics. Appl. Sci. 2016, 6, 52. [Google Scholar] [CrossRef] [Green Version]
- Di, C.; Petrov, I.; Pyrhonen, J.J.; Bao, X. Unbalanced Magnetic Pull Compensation With Active Magnetic Bearings in a 2 MW High-Speed Induction Machine by FEM. IEEE Trans. Magn. 2018, 54, 1–13. [Google Scholar] [CrossRef]
- Chiu, H.-L. Identification Approach for Nonlinear MIMO Dynamics of Closed-Loop Active Magnetic Bearing System. Appl. Sci. 2022, 12, 8556. [Google Scholar] [CrossRef]
- Chen, S.L.; Hsu, C.T. Optimal Design of the 3-Pole Active Magnetic Bearing System. IEEE Trans. Magn. 2002, 38, 3458–3466. [Google Scholar] [CrossRef]
- El-Shourbagy, S.M.; Saeed, N.A.; Kamel, M.; Raslan, K.R.; Aboudaif, M.K.; Awrejcewicz, J. Control Performance, Stability Conditions, and Bifurcation Analysis of the Twelve-Pole Active Magnetic Bearings System. Appl. Sci. 2021, 11, 10839. [Google Scholar] [CrossRef]
- Giap, V.-N.; Huang, S.-C. Effectiveness of fuzzy sliding mode control boundary layer based on uncertainty and disturbance compensator on suspension active magnetic bearing system. Meas. Control 2020, 53, 934–942. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Gao, X.; Cui, E.; Ma, Z. State-Constraints Adaptive Backstepping Control for Active Magnetic Bearings with Parameters Nonstationarities and Uncertainties. IEEE Trans. Ind. Electron. 2020, 68, 9822–9831. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, H.; Wu, M.; Zhang, W. Active Disturbance Rejection Decoupling Control for Three-Degree-of- Freedom Six-Pole Active Magnetic Bearing Based on BP Neural Network. IEEE Trans. Appl. Supercond. 2020, 30, 1–5. [Google Scholar] [CrossRef]
- Saeed, N.A.; El-Shourbagy, S.M.; Kamel, M.; Raslan, K.R.; Awrejcewicz, J.; Gepreel, K.A. On the Resonant Vibrations Control of the Nonlinear Rotor Active Magnetic Bearing Systems. Appl. Sci. 2022, 12, 8300. [Google Scholar] [CrossRef]
- Hsu, C.-T.; Chen, S.-L. Nonlinear control of a 3-pole active magnetic bearing system. Automatica 2003, 39, 291–298. [Google Scholar] [CrossRef]
- Chen, S.-L.; Chen, S.-H.; Yan, S.-T. Experimental validation of a current-controlled three-pole magnetic rotor-bearing system. IEEE Trans. Magn. 2005, 41, 99–112. [Google Scholar] [CrossRef]
- Chen, S.L.; Lin, S.Y. Adaptive Unbalance Compensation for a Three-pole AMB System. IEEE Trans. Ind. Electron. 2020, 67, 2097–2106. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.-L.; Li, Y.-T.; Lin, C.-H.; Chen, C.-Y. Effects of Imperfect Assembly and Magnetic Properties on the Three-Pole AMB System. Appl. Sci. 2023, 13, 347. https://doi.org/10.3390/app13010347
Chen S-L, Li Y-T, Lin C-H, Chen C-Y. Effects of Imperfect Assembly and Magnetic Properties on the Three-Pole AMB System. Applied Sciences. 2023; 13(1):347. https://doi.org/10.3390/app13010347
Chicago/Turabian StyleChen, Shyh-Leh, Yi-Tsung Li, Chin-Hsiang Lin, and Chao-Yun Chen. 2023. "Effects of Imperfect Assembly and Magnetic Properties on the Three-Pole AMB System" Applied Sciences 13, no. 1: 347. https://doi.org/10.3390/app13010347
APA StyleChen, S.-L., Li, Y.-T., Lin, C.-H., & Chen, C.-Y. (2023). Effects of Imperfect Assembly and Magnetic Properties on the Three-Pole AMB System. Applied Sciences, 13(1), 347. https://doi.org/10.3390/app13010347





