Image Classification-Based Defect Detection of Railway Tracks Using Fiber Bragg Grating Ultrasonic Sensors
Abstract
:1. Introduction
2. Methodology
2.1. Working Principle of FBGs
2.2. Bulk Wave and Guided Wave Inspection Methods
3. Comparative Study
3.1. Experiment Introduction
3.1.1. The PZT/FBG Hybrid Sensing System
3.1.2. Experimental Procedures
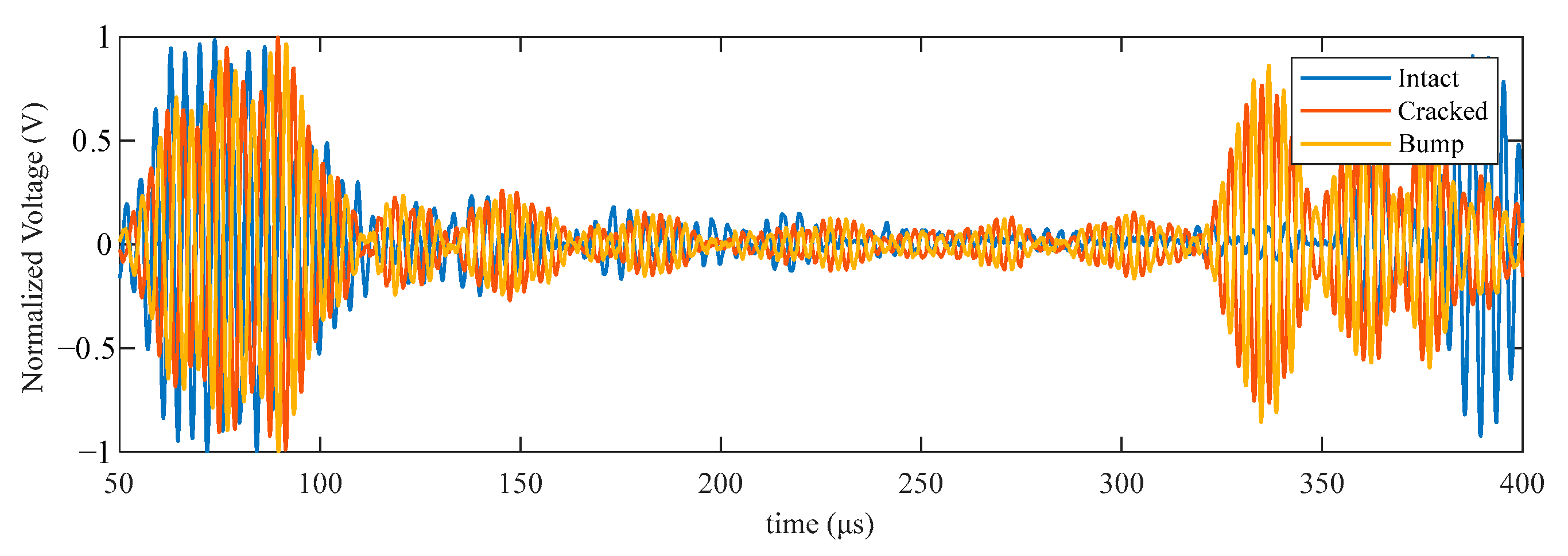
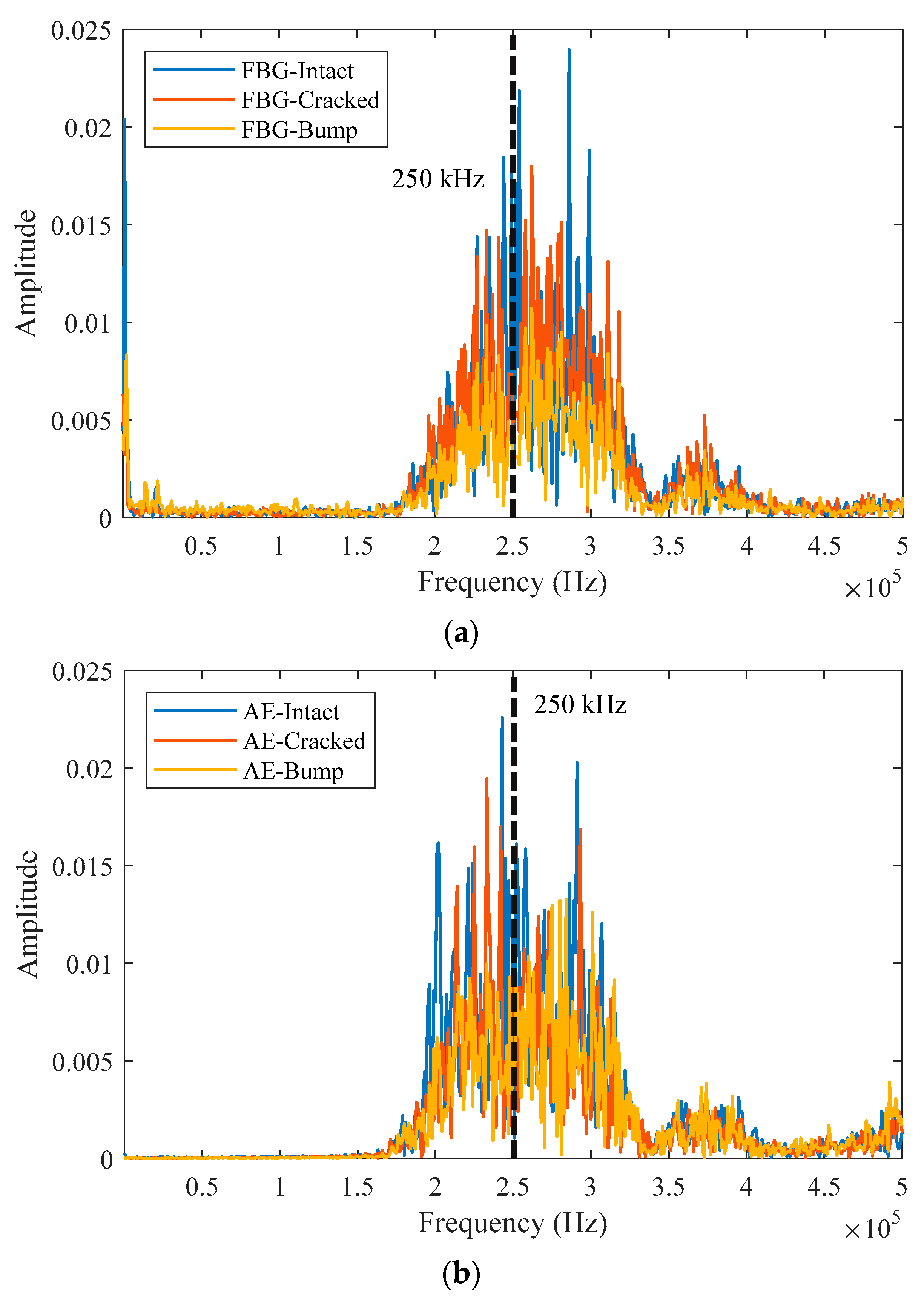
3.2. Results and Discussions
4. Image Classification-Based Rail Defect Detection
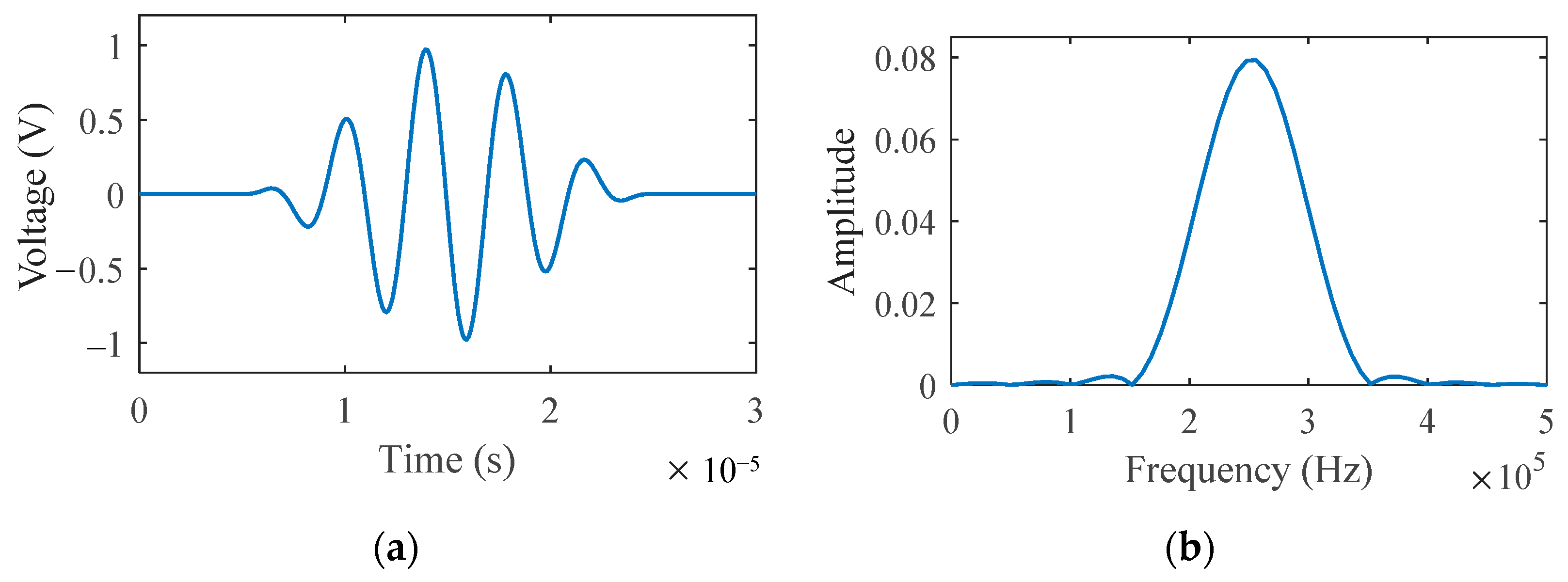
4.1. Spectrogram Image Dataset
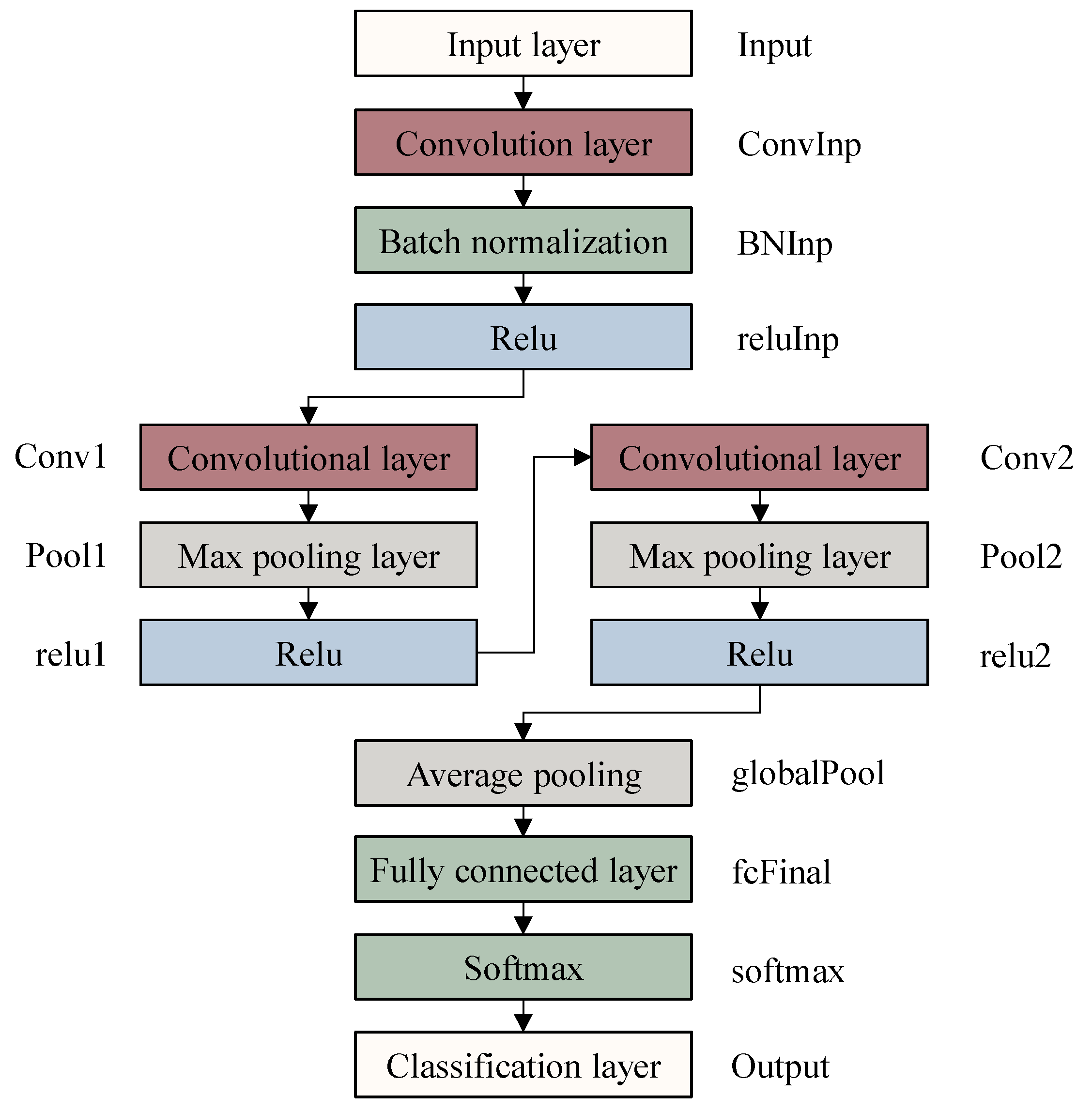
4.2. CNN
4.3. Classification Results
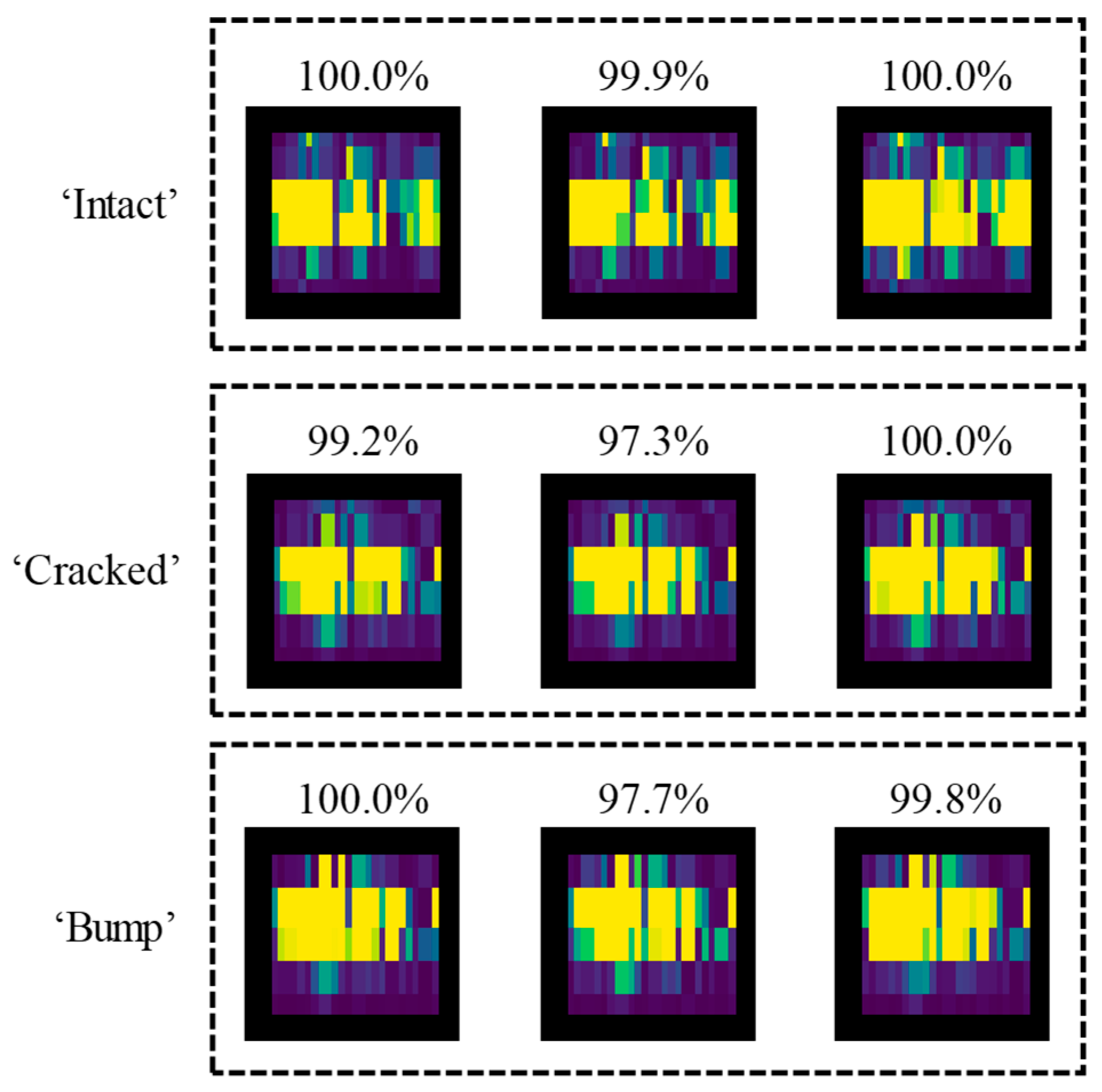
4.4. Visualization of the CNN
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, X.; Guo, C.; Yuan, L.; Kong, Q.; Ni, Y. Diffuse Ultrasonic Wave-Based Damage Detection of Railway Tracks Using PZT/FBG Hybrid Sensing System. Sensors 2022, 22, 2504. [Google Scholar] [CrossRef]
- Wilcox, P.; Evans, M.; Pavlakovic, B.; Alleyne, D.; Vine, K.; Cawley, P.; Lowe, M. Guided Wave Testing of Rail. Insight Non-Destr. Test. Cond. Monit. 2003, 45, 413–420. [Google Scholar] [CrossRef]
- Legislative Council Panel on Transport. Background Brief on the Rail Inspection Regime of the MTR Corporation Limited. Available online: https://www.legco.gov.hk/yr13-14/english/panels/tp/tp_rdp/agenda/rdp20140103.htm (accessed on 3 January 2014).
- Legislative Council Panel on Transport. Recent Railway Incidents Involving MTR Rail Cracks. Available online: https://www.legco.gov.hk/yr11-12/english/panels/tp/tp_rdp/papers/rdp_i.htm (accessed on 18 March 2011).
- Malfense Fierro, G.P.; Meo, M. Non-Linear Phased Array Imaging of Flaws Using a Dual and Tri Frequency Modulation Technique. Front. Built Environ. 2020, 6, 1–13. [Google Scholar] [CrossRef]
- Wang, P.; Xie, K.; Shao, L.; Yan, L.; Xu, J.; Chen, R. Longitudinal Force Measurement in Continuous Welded Rail with Bi-Directional FBG Strain Sensors. Smart Mater. Struct. 2015, 25, 015019. [Google Scholar] [CrossRef]
- Cano, W.F.R.; Rosolem, J.B.; Florida, C.; Lopes, P.H.D.O.; Dini, D.C.; Penze, R.S.; Costa, E.F.; Fracarolli, J.P.V. Evaluation of FBG Sensors to Measure Ultrasonic Guided Waves in Rail Transport Monitoring. In Proceedings of the 2017 SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference (IMOC), Aguas de Lindoia, Brazil, 27–30 August 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Harmanci, Y.E.; Spiridonakos, M.D.; Chatzi, E.N.; Kübler, W. An Autonomous Strain-Based Structural Monitoring Framework for Life-Cycle Analysis of a Novel Structure. Front. Built Environ. 2016, 2, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Cao, W.; Xu, L.; Yang, X.; Su, Z.; Zhang, X.; Chen, L. Diffuse Ultrasonic Wave-Based Structural Health Monitoring for Railway Turnouts. Ultrasonics 2020, 101, 106031. [Google Scholar] [CrossRef]
- Coles, A.; de Castro, B.A.; Andreades, C.; Baptista, F.G.; Meo, M.; Ciampa, F. Impact Localization in Composites Using Time Reversal, Embedded PZT Transducers, and Topological Algorithms. Front. Built Environ. 2020, 6, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Nicassio, F.; Carrino, S.; Scarselli, G. Non-Linear Lamb Waves for Locating Defects in Single-Lap Joints. Front. Built Environ. 2020, 6, 45. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Wang, Q.; Luo, Y. A Review of Applications of Visual Inspection Technology Based on Image Processing in the Railway Industry. Transp. Saf. Environ. 2019, 1, 185–204. [Google Scholar] [CrossRef]
- Wang, S.M.; Liao, C.L.; Ni, Y.Q. A Machine Vision System Based on Driving Recorder for Automatic Inspection of Rail Curvature. IEEE Sens. J. 2021, 21, 11291–11300. [Google Scholar] [CrossRef]
- Mariani, S.; Nguyen, T.; Zhu, X.; Lanza di Scalea, F. Field Test Performance of Noncontact Ultrasonic Rail Inspection System. J. Transp. Eng. A Syst. 2017, 143, 04017007. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimkhanlou, A.; Dubuc, B.; Salamone, S. A Generalizable Deep Learning Framework for Localizing and Characterizing Acoustic Emission Sources in Riveted Metallic Panels. Mech. Syst. Signal Process. 2019, 130, 248–272. [Google Scholar] [CrossRef]
- Xu, J.; Niu, X.; Ma, Q.; Han, Q. Mechanical Properties and Damage Analysis of Rubber Cement Mortar Mixed with Ceramic Waste Aggregate Based on Acoustic Emission Monitoring Technology. Constr. Build. Mater. 2021, 309, 125084. [Google Scholar] [CrossRef]
- Xu, J.; Niu, X.; Yao, Z. Mechanical Properties and Acoustic Emission Data Analyses of Crumb Rubber Concrete under Biaxial Compression Stress States. Constr. Build. Mater. 2021, 298, 123778. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, C.; Su, Z.; Yue, X.; Xiang, J.; Liu, G. Health Monitoring of Rail Structures Using Guided Waves and Three-Dimensional Diagnostic Imaging. Struct. Control Health Monit. 2017, 24, e1966. [Google Scholar] [CrossRef]
- Pathak, M.; Alahakoon, S.; Spiryagin, M.; Cole, C. Rail Foot Flaw Detection Based on a Laser Induced Ultrasonic Guided Wave Method. Measurement 2019, 148, 106922. [Google Scholar] [CrossRef]
- Loveday, P.W.; Long, C.S.; Ramatlo, D.A. Ultrasonic Guided Wave Monitoring of an Operational Rail Track. Struct. Health Monit. 2020, 19, 1666–1684. [Google Scholar] [CrossRef]
- Wee, J.; Hackney, D.; Bradford, P.; Peters, K. Experimental Study on Directionality of Ultrasonic Wave Coupling Using Surface-Bonded Fiber Bragg Grating Sensors. J. Light. Technol. 2018, 36, 932–938. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, R.; Yu, F.; Okabe, Y. Application of an Optical Fiber Sensor for Nonlinear Ultrasonic Evaluation of Fatigue Crack. IEEE Sens. J. 2019, 19, 4992–4999. [Google Scholar] [CrossRef]
- Yu, F.; Saito, O.; Okabe, Y. An Ultrasonic Visualization System Using a Fiber-Optic Bragg Grating Sensor and Its Application to Damage Detection at a Temperature of 1000 °C. Mech. Syst. Signal Process. 2021, 147, 107140. [Google Scholar] [CrossRef]
- Betz, D.C.; Thursby, G.; Culshaw, B.; Staszewski, W.J. Lamb Wave Detection and Source Location Using Fiber Bragg Gratin Rosettes. Smart Struct. Mater. 2003 Smart Sens. Technol. Meas. Syst. 2003, 5050, 117. [Google Scholar] [CrossRef]
- Yu, F.; Saito, O.; Okabe, Y. Laser Ultrasonic Visualization Technique Using a Fiber-Optic Bragg Grating Ultrasonic Sensor with an Improved Adhesion Configuration. Struct. Health Monit. 2021, 20, 303–320. [Google Scholar] [CrossRef]
- Tian, Z.; Yu, L.; Sun, X.; Lin, B. Damage Localization with Fiber Bragg Grating Lamb Wave Sensing through Adaptive Phased Array Imaging. Struct. Health Monit. 2019, 18, 334–344. [Google Scholar] [CrossRef]
- Bao, Y.; Li, H. Machine Learning Paradigm for Structural Health Monitoring. Struct. Health Monit. 2021, 20, 1353–1372. [Google Scholar] [CrossRef]
- Sloun, R.J.G.; Cohen, R.; Eldar, Y.C. Deep Learning in Ultrasound Imaging. Proc. IEEE 2020, 108, 11–29. [Google Scholar] [CrossRef] [Green Version]
- Medak, D.; Posilović, L.; Subašić, M.; Budimir, M.; Lončarić, S. Deep Learning-Based Defect Detection from Sequences of Ultrasonic B-Scans. IEEE Sens. J. 2022, 22, 2456–2463. [Google Scholar] [CrossRef]
- Mariani, S.; Rendu, Q.; Urbani, M.; Sbarufatti, C. Causal dilated convolutional neural networks for automatic inspection of ultrasonic signals in non-destructive evaluation and structural health monitoring. Mech. Syst. Signal Process. 2021, 157, 107748. [Google Scholar] [CrossRef]
- Zhang, B.; Hong, X.; Liu, Y. Distribution adaptation deep transfer learning method for cross-structure health monitoring using guided waves. Struct. Health Monit. 2022, 21, 853–871. [Google Scholar] [CrossRef]
- Tao, C.; Zhang, C.; Ji, H.; Qiu, J. Fatigue damage characterization for composite laminates using deep learning and laser ultrasonic. Compos. B Eng. 2021, 216, 108816. [Google Scholar] [CrossRef]
- Azimi, M.; Eslamlou, A.D.; Pekcan, G. Data-Driven Structural Health Monitoring and Damage Detection through Deep Learning: State-of-the-Art Review. Sensors 2020, 20, 2778. [Google Scholar] [CrossRef]
- Chen, S.X.; Zhou, L.; Ni, Y.Q.; Liu, X.Z. An Acoustic-Homologous Transfer Learning Approach for Acoustic Emission–Based Rail Condition Evaluation. Struct. Health Monit. 2021, 20, 2161–2181. [Google Scholar] [CrossRef]
- Arias-Vergara, T.; Klumpp, P.; Vasquez-Correa, J.C.; Nöth, E.; Orozco-Arroyave, J.R.; Schuster, M. Multi-channel spectrograms for speech processing applications using deep learning methods. Pattern Anal. Appl. 2021, 24, 423–431. [Google Scholar] [CrossRef]
- Lopac, N.; Hržić, F.; Vuksanović, I.P.; Lerga, J. Detection of Non-Stationary GW Signals in High Noise from Cohen’s Class of Time–Frequency Representations Using Deep Learning. IEEE Access 2022, 10, 2408–2428. [Google Scholar] [CrossRef]
- Khare, S.K.; Bajaj, V. Time–Frequency Representation and Convolutional Neural Network-Based Emotion Recognition. IEEE Trans. Neural Networks Learn. Syst. 2021, 32, 2901–2909. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Lin, J.; Song, H.; Sheng, G. Fault Identification Based on PD Ultrasonic Signal Using RNN, DNN and CNN. In Proceedings of the 2018 Condition Monitoring and Diagnosis (CMD), Perth, Australia, 23–26 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Malikov, A.K.u.; Kim, Y.H.; Yi, J.H.; Kim, J.; Zhang, J.; Cho, Y. Neural-Network-Based Ultrasonic Inspection of Offshore Coated Concrete Specimens. Coatings 2022, 12, 773. [Google Scholar] [CrossRef]
- Wild, G.; Hinckley, S. Acousto-Ultrasonic Optical Fiber Sensors: Overview and State-of-the-Art. IEEE Sens. J. 2008, 8, 1184–1193. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.R.; Tsuda, H.; Toyama, N. Impact Wave and Damage Detections Using a Strain-Free Fiber Bragg Grating Ultrasonic Receiver. NDT E Int. 2007, 40, 85–93. [Google Scholar] [CrossRef]
- Wee, J.; Hackney, D.; Bradford, P.; Peters, K. Bi-Directional Ultrasonic Wave Coupling to FBGs in Continuously Bonded Optical Fiber Sensing. Appl. Opt. 2017, 56, 7262. [Google Scholar] [CrossRef]
- Rose, J.L. A Comparison of Bulk versus Guided Waves. In Ultrasonic Guided Waves in Solid Media; Cambridge University Express: Cambridge, UK, 2014; ISBN 9781107273610. [Google Scholar]

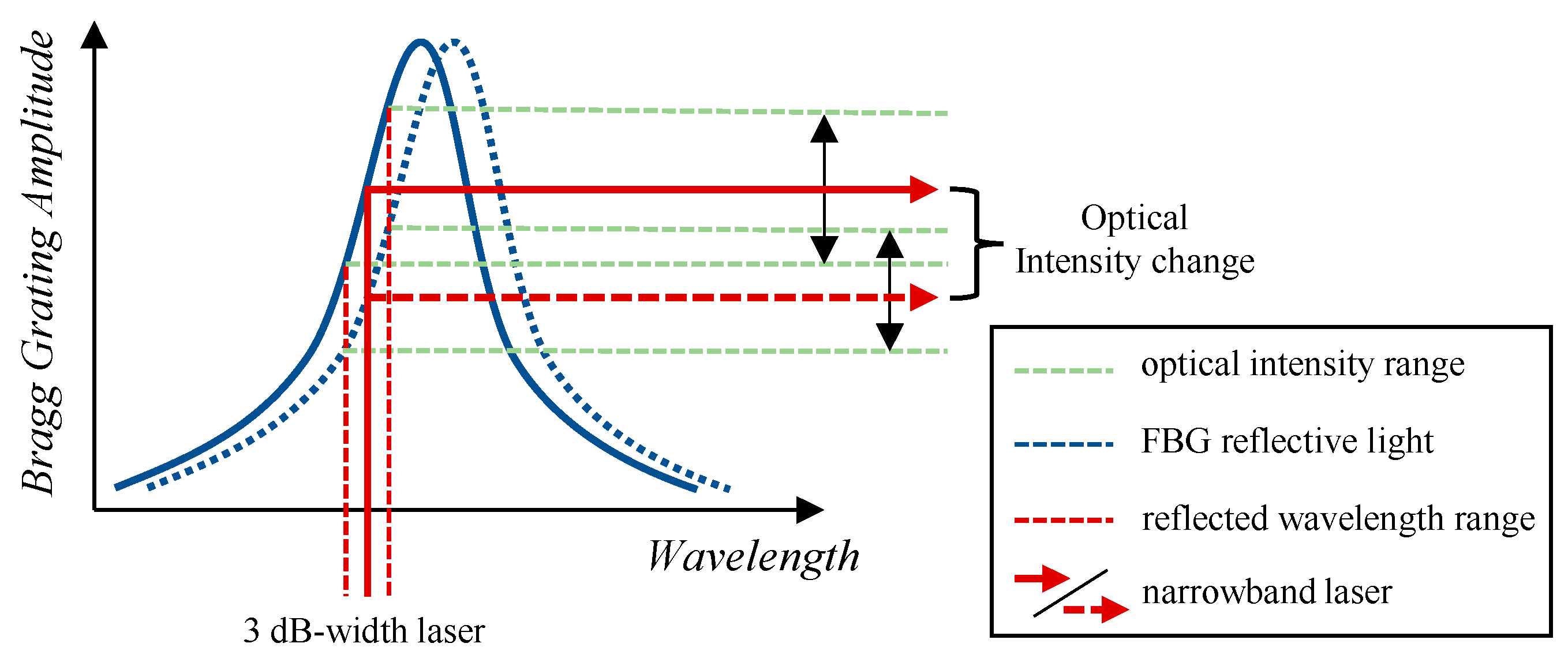









| Features | Bulk Wave Inspection | Guided Wave Inspection |
|---|---|---|
| Efficiency | Laborious and time-consuming | Fast and convenient |
| Accuracy | Point-by-point scan (accurate rectangular grid scan) | Global in nature (approximate line scan) |
| Reliability | Unreliable (can miss points) | Reliable (volumetric coverage) |
| Complexity | High-level training required for inspection | Minimal training |
| Distance | Fixed distance from reflector required | Any reasonable distance from reflector acceptable |
| Identification | The reflector must be accessible and seen | The reflector can be hidden |
| Network Layer | Layer Name | Parameters |
|---|---|---|
| Input layer | ‘Input’ | Input image size = (32, 32, 3) |
| 2-D Convolution layer | ‘ConvInp’ | net width = 16, filter size = 3, padding mode = ‘same’ |
| Batch normalization layer | ‘BNInp’ | minimum batch number = 16 |
| Relu layer | ‘reluInp’ | Relu activation function |
| 2-D Convolution layer | ‘Conv1’ | net width = 16, filter size = 1, padding mode = ‘same’ |
| 2-D Max pooling layer | ‘Pool1’ | pool size = 2 |
| Relu layer | ‘relu1’ | Relu activation function |
| 2-D Convolution layer | ‘Conv2’ | net width = 16, filter size = 1, padding mode = ‘same’ |
| 2-D Max pooling layer | ‘Pool2’ | pool size = 2 |
| Relu layer | ‘relu2’ | Relu activation function |
| Average pooling layer | ‘globalPool’ | pool size = 8 |
| Fully connected layer | ‘fcFinal’ | output size = 3 |
| Softmax layer | ‘softmax’ | Softmax activation function |
| Classification layer | ‘Output’ | number of classes = 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dang, D.-Z.; Lai, C.-C.; Ni, Y.-Q.; Zhao, Q.; Su, B.; Zhou, Q.-F. Image Classification-Based Defect Detection of Railway Tracks Using Fiber Bragg Grating Ultrasonic Sensors. Appl. Sci. 2023, 13, 384. https://doi.org/10.3390/app13010384
Dang D-Z, Lai C-C, Ni Y-Q, Zhao Q, Su B, Zhou Q-F. Image Classification-Based Defect Detection of Railway Tracks Using Fiber Bragg Grating Ultrasonic Sensors. Applied Sciences. 2023; 13(1):384. https://doi.org/10.3390/app13010384
Chicago/Turabian StyleDang, Da-Zhi, Chun-Cheung Lai, Yi-Qing Ni, Qi Zhao, Boyang Su, and Qi-Fan Zhou. 2023. "Image Classification-Based Defect Detection of Railway Tracks Using Fiber Bragg Grating Ultrasonic Sensors" Applied Sciences 13, no. 1: 384. https://doi.org/10.3390/app13010384





