Experimental Study on a Supercritical CO2 Centrifugal Compressor Used in a MWe Scale Power Cycle
Abstract
:1. Introduction
2. The Design of Single-Stage Centrifugal Compressor
2.1. The 1 MWe sCO2 Power Cycle
2.2. Throughflow Design of Compressor
2.3. Mechanical Design of Compressor
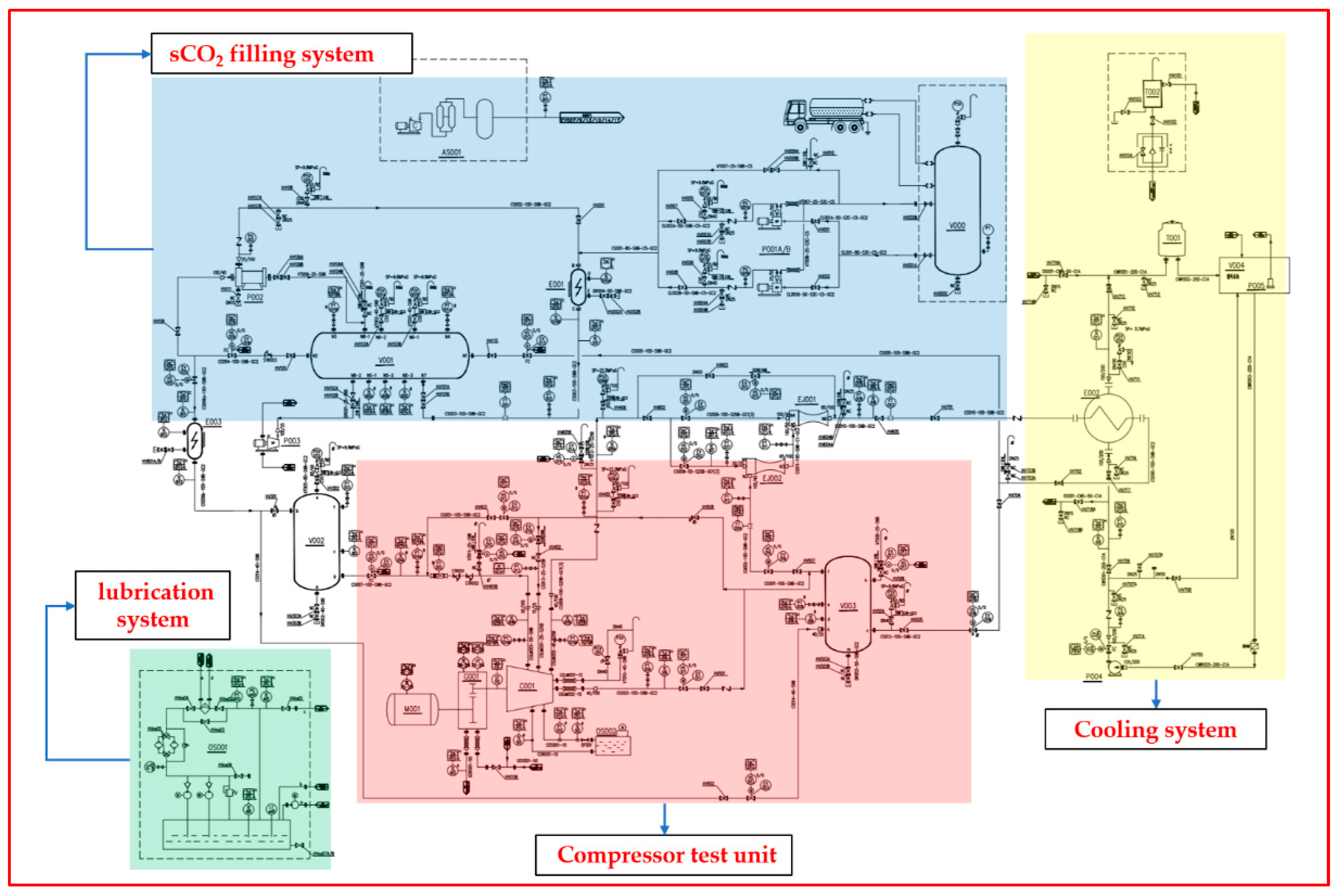
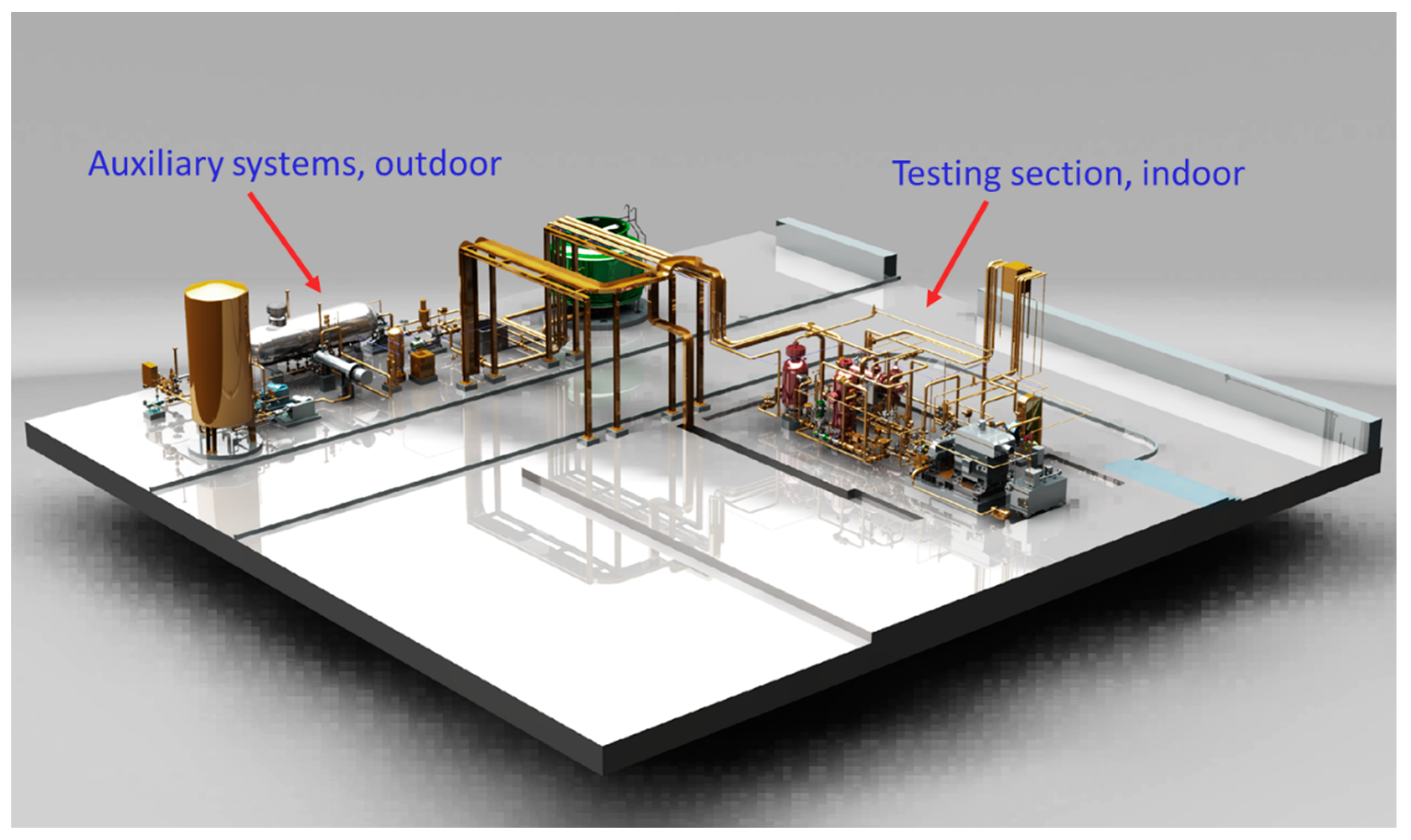
3. Experimental System
3.1. The MWe Scale sCO2 Compressor Test Loop
3.2. Measuring Instruments
4. Results
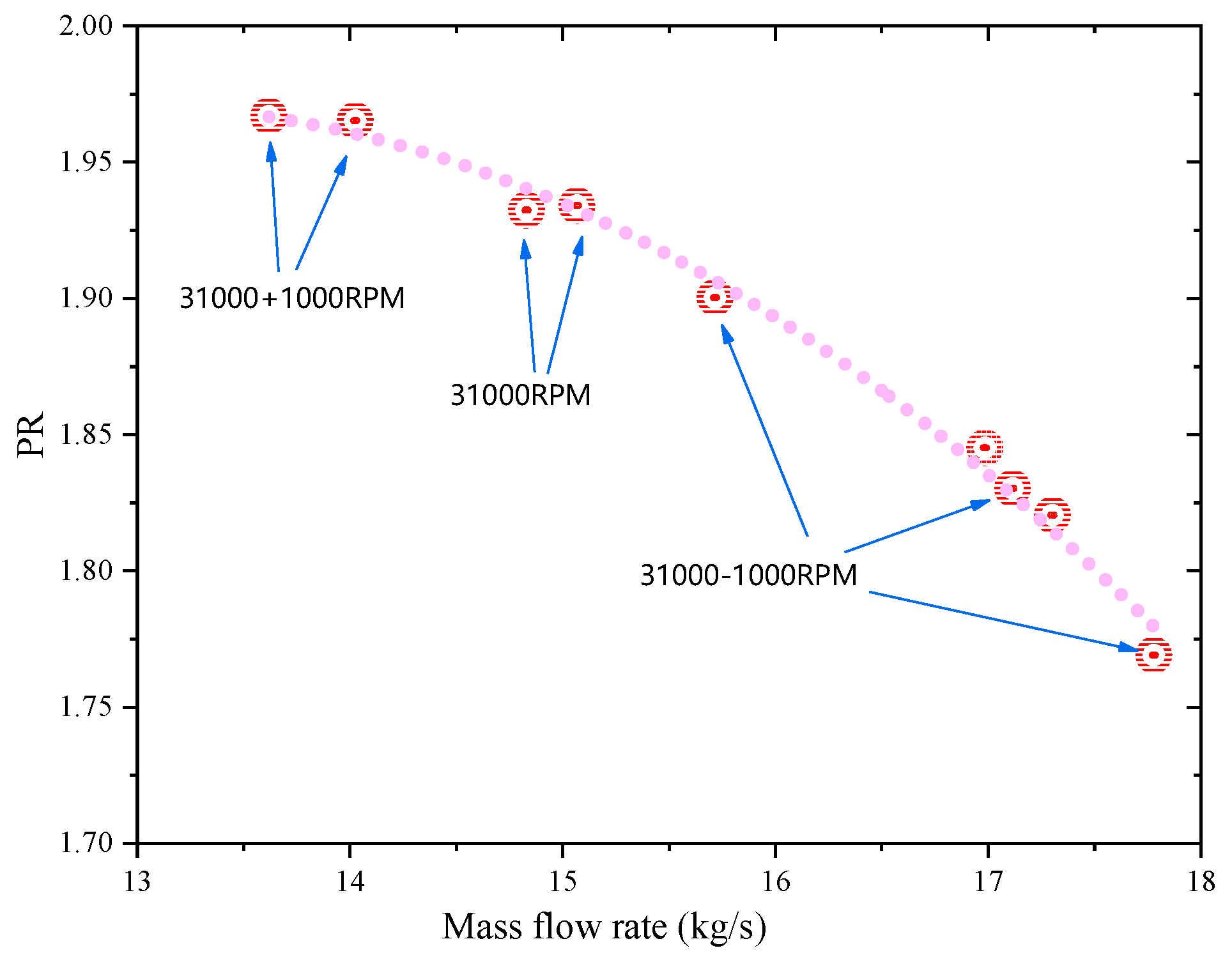
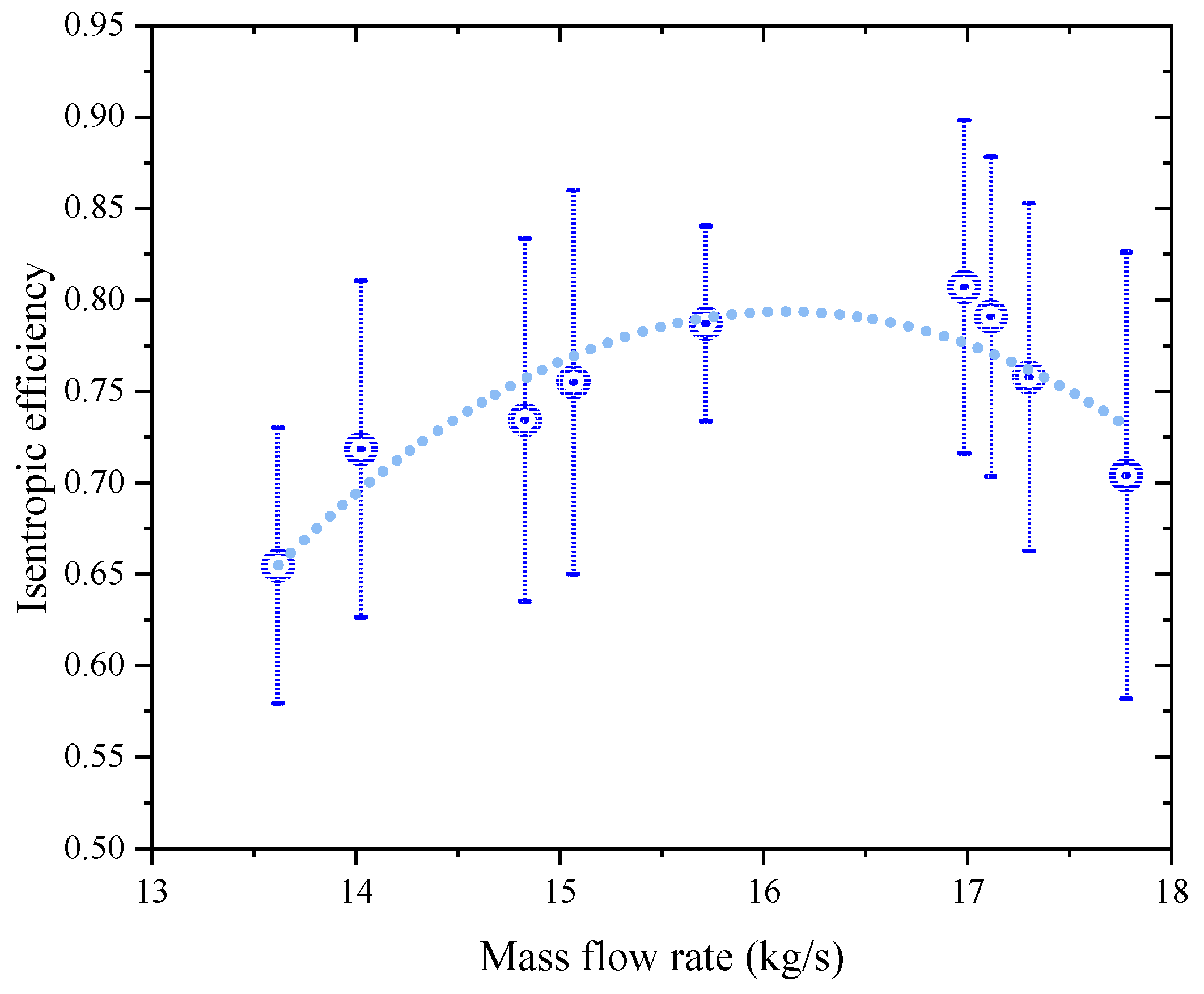
4.1. Historical Curves
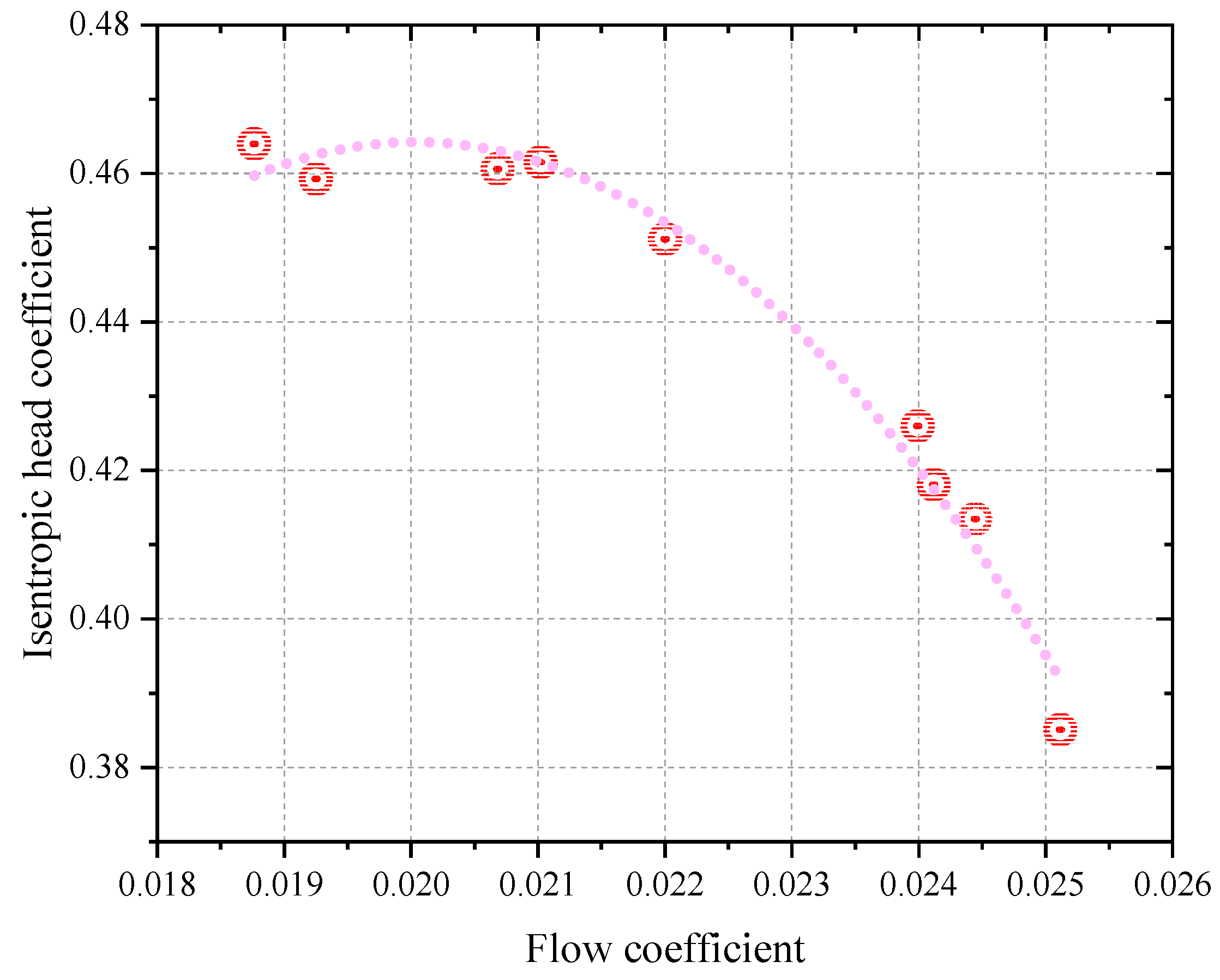
4.2. Performance Curves
5. Analysis and Discussion
5.1. Inlet Condition
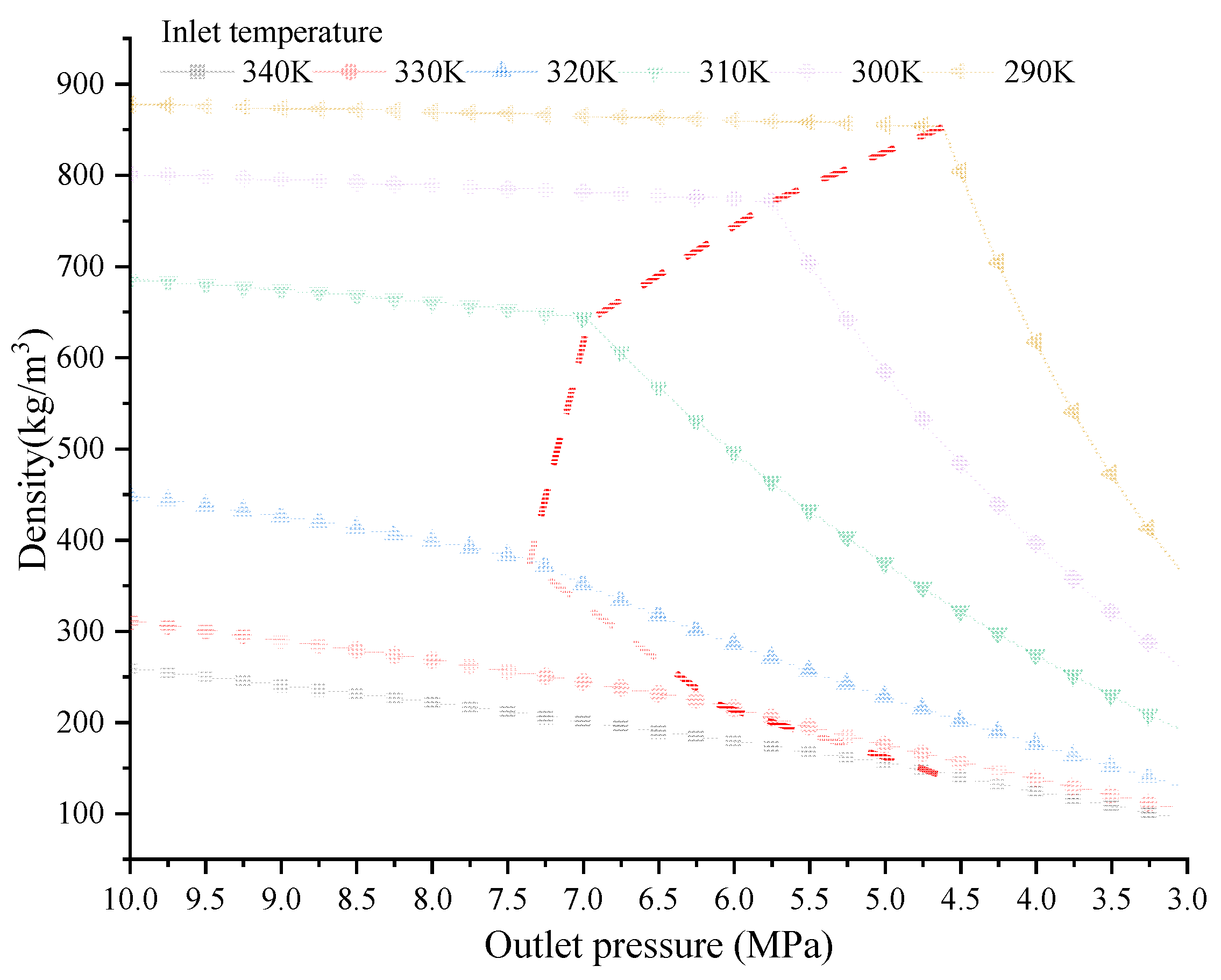
5.2. The Dimensionlessness of Experimental Results
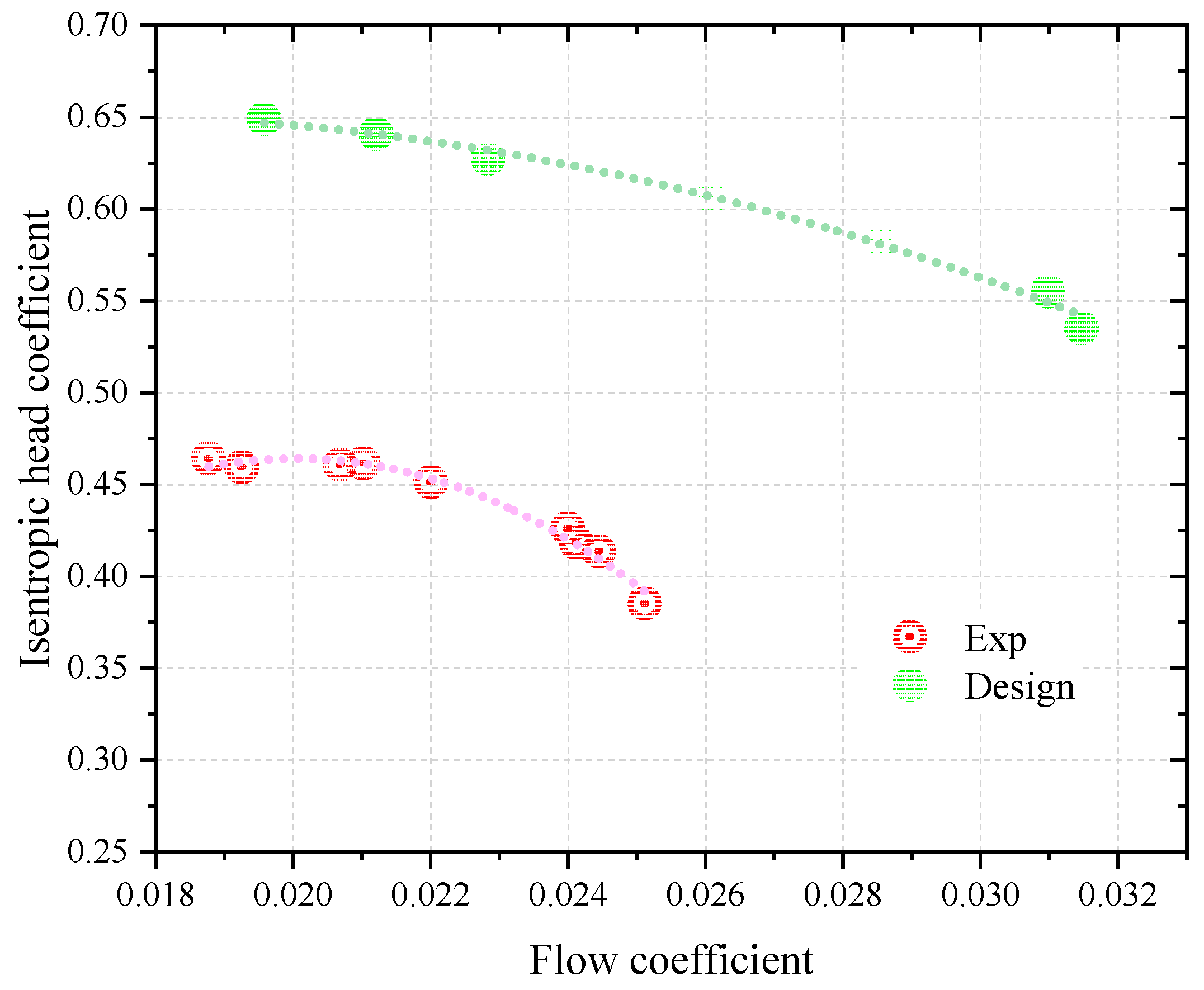
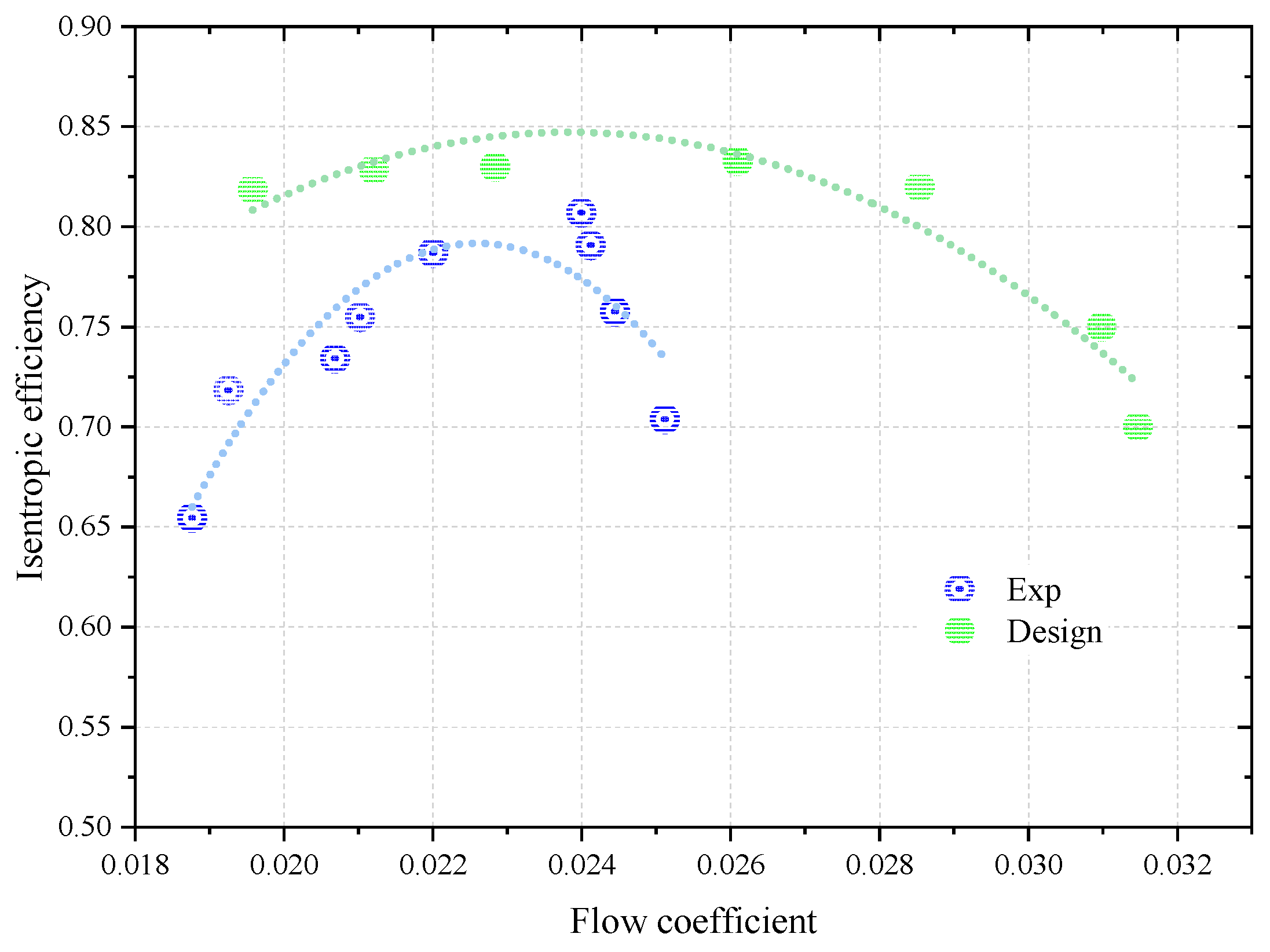
5.3. Comparison of the Experimental and Design Performance Curves
- The experimental inlet condition, located in the supercritical-liquid-like region rather than the critical line.
- The tip clearance of the experimental impeller is 0.43–0.45 mm, which is larger than the design value (0.25 mm) caused by the abrasion of the metallic coating at shroud, as is shown in Table 8.
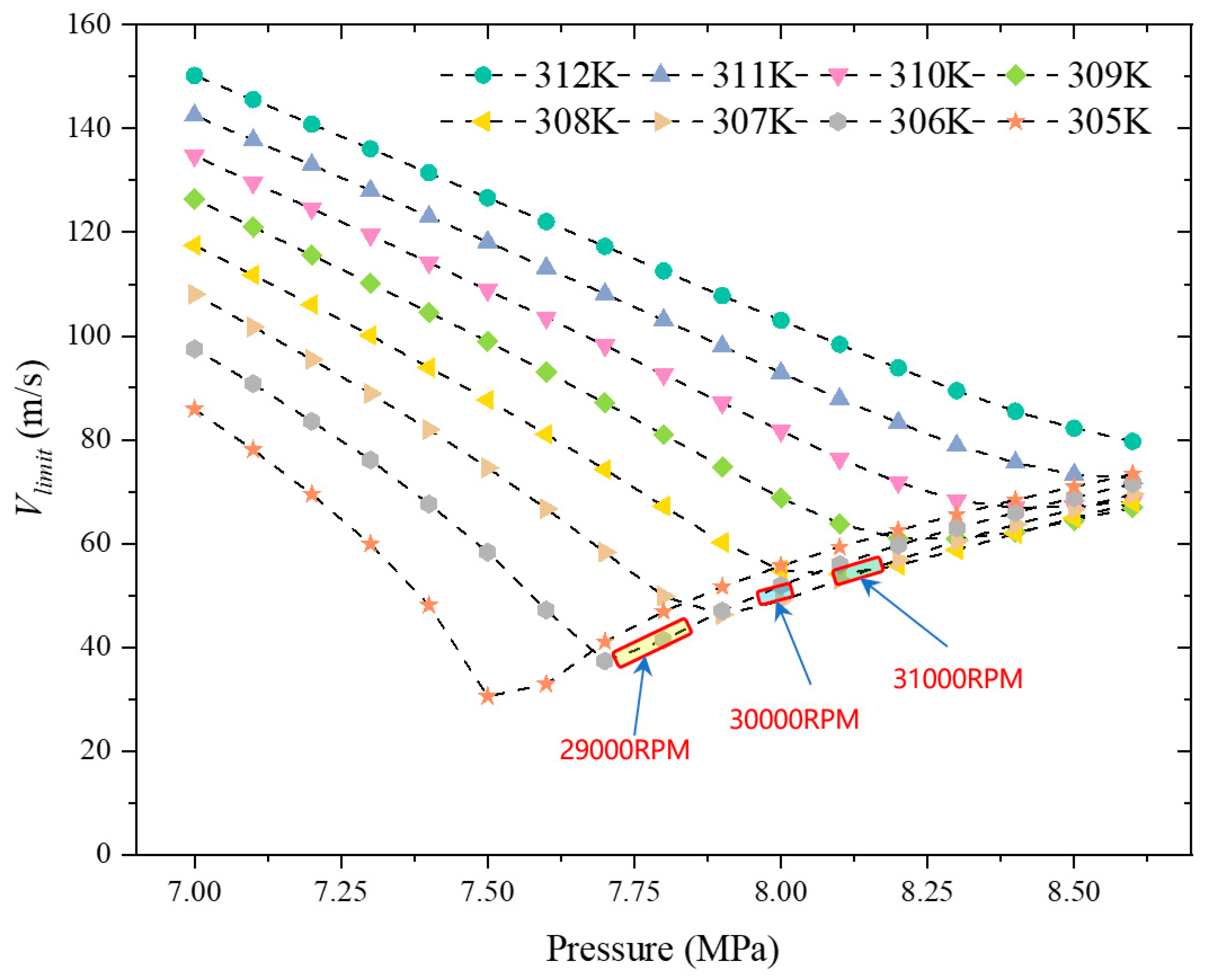
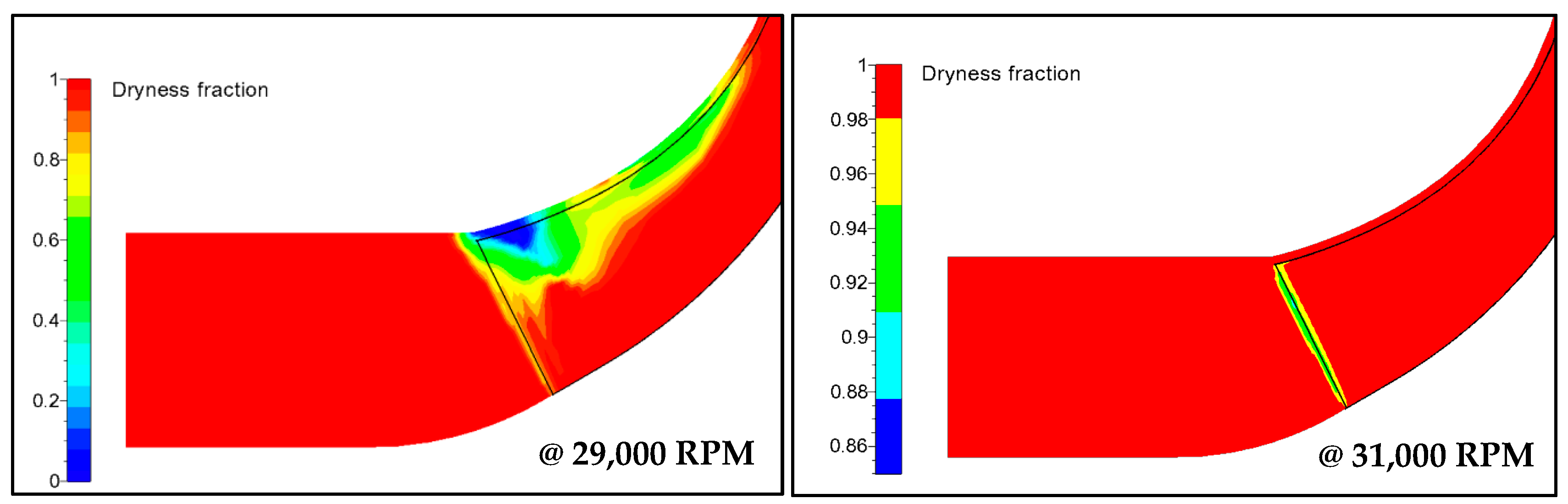
5.4. Condensation Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| units | |
| 3D | three-dimensional |
| AMC | Acceleration Margin to Condensation |
| CFD | computational fluid dynamics |
| sCO2 | Supercritical CO2 |
| Pr | pressure ratio |
| P | pressure, MPa |
| T | temperature, K |
| N | rotor speed, RPM |
| M | mass flow rate, kg/s |
| V | velocity, m/s |
| Q | flow rate, m3/s |
| H | enthalpy, kJ/kg |
| s | entropy, kJ/(kg·K) |
| Greek symbol | |
| ρ | density, kg/m3 |
| η | compressor efficiency |
| φ | flow coefficient |
| Ψ | head coefficient |
| Subscription | |
| P01 | inlet pressure, MPa |
| P02 | outlet pressure, MPa |
| T01 | inlet temperature, K |
| T02 | outlet temperature, K |
| h01 | inlet enthalpy, kJ/kg |
| h02 | outlet total enthalpy, kJ/kg |
| Vlimit | condensation acceleration Velocity, m/s |
References
- Persichilli, M.; Kacludis, A.; Zdankiewicz, E.; Held, T. Supercritical CO2 power cycle developments and commercialization: Why sCO2 can displace steam. Power-Gen India Cent. Asia 2012, 2012, 19–21. [Google Scholar]
- Fleming, D.; Holschuh, T.; Conboy, T.; Rochau, G.; Fuller, R. Scaling considerations for a multi-megawatt class supercritical CO2 Brayton cycle and path forward for commercialization. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; American Society of Mechanical Engineers Digital Collection: Copenhagen, Denmark, 2012; pp. 953–960. [Google Scholar]
- Kimball, K.J.; Clementoni, E.M. Supercritical carbon dioxide Brayton power cycle development overview. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; American Society of Mechanical Engineers Digital Collection: Copenhagen, Denmark, 2012; pp. 931–940. [Google Scholar]
- Brun, K.; Friedman, P.; Dennis, R. Fundamentals and Applications of SCO2 (sCO2) Based Power Cycles; Woodhead Publishing: Cambridge, UK, 2017. [Google Scholar]
- Utamura, M.; Hasuike, H.; Ogawa, K.; Yamamoto, T.; Fukushima, T.; Watanabe, T.; Himeno, T. Demonstration of supercritical CO2 closed regenerative Brayton Cycle in a Bench Scale Experiment. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; American Society of Mechanical Engineers Digital Collection: Copenhagen, Denmark, 2012; pp. 155–164. [Google Scholar]
- Park, J.H.; Bae, S.W.; Park, H.S.; Cha, J.E.; Kim, M.H. Transient analysis and validation with experimental data of supercritical CO2 integral experiment loop by using MARS. Energy 2018, 147, 1030–1043. [Google Scholar] [CrossRef]
- Kima, S.G.; Choa, S.K.; Leea, J.I.; Leeb, J.; Leeb, S.W.; Addadc, Y.; Chad, J.E. External loss analysis of a supercritical CO2 radial compressor. In Proceedings of the Transactions of the Korean Nuclear Society Spring Meeting, Jeju, Korea, 18–19 May 2017. [Google Scholar]
- Ahn, Y.; Lee, J.; Kim, S.G.; Lee, J.I.; Cha, J.E.; Lee, S.W. Design consideration of supercritical CO2 power cycle integral experiment loop. Energy 2015, 86, 115–127. [Google Scholar] [CrossRef]
- Bai, W.; Li, H.; Zhang, L.; Zhang, Y.; Yang, Y.; Zhang, C.; Yao, M. Energy and exergy analyses of an improved recompression supercritical CO2 cycle for coal-fired power plant. Energy 2021, 222, 119976. [Google Scholar] [CrossRef]
- Jin, Q.; Xia, S.; Chen, L. A modified recompression S–CO2 Brayton cycle and its thermodynamic optimization. Energy 2022, 263, 126015. [Google Scholar] [CrossRef]
- Krain, H.; Hoffman, W. Verification of an impeller design by laser measurements and 3D-viscous flow calculations. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 1989; p. V001T01A064. [Google Scholar]
- Wright, S.A.; Radel, R.F.; Vernon, M.E.; Pickard, P.S.; Rochau, G.E. Operation and Analysis of a Supercritical CO2 Brayton Cycle; Sandia Report SAND2010-0171; 2010; pp. 1–101. Available online: https://www.osti.gov/biblio/984129 (accessed on 21 November 2022).
- Son, S.; Cho, S.K.; Lee, J.I. Experimental investigation on performance degradation of a supercritical CO2 radial compressor by foreign object damage. Appl. Therm. Eng. 2021, 183, 116229. [Google Scholar] [CrossRef]
- Pecnik, R.; Rinaldi, E.; Colonna, P. Computational Fluid Dynamics of a Radial Compressor Operating With Supercritical CO2. ASME J. Eng. Gas Turbines Power 2012, 134, 122301. [Google Scholar] [CrossRef]
- Lettieri, C.; Baltadjiev, N.; Casey, M.; Spakovszky, Z.S. Low-Flow-Coefficient Centrifugal Compressor Design for Supercritical CO2. J. Turbomach. 2014, 136, 081008. [Google Scholar] [CrossRef]
- Ivanov, V.; Kozhukhov, Y.; Danilishin, A.; Yablokov, A.; Sokolov, M. Verification and Validation of CFD Modeling for Low-Flow-Coefficient Centrifugal Compressor Stages. Energies 2022, 15, 181. [Google Scholar] [CrossRef]
- Zhao, H.; Deng, Q.; Zhang, H.; Feng, Z. The Influence of tip clearance on supercritical CO2 centrifugal compressor performance. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 56802, p. V009T36A008. [Google Scholar]
- Uusitalo, A.; Turunen-Saaresti, T.; Grönman, A. Design and loss analysis of radial turbines for supercritical CO2 Brayton cycles. Energy 2021, 230, 120878. [Google Scholar] [CrossRef]
- Pei, J.; Zhao, Y.; Zhao, M.; Liu, G.; Yang, Q.; Li, L. Effects of leading edge profiles on flow behavior and performance of supercritical CO2 centrifugal compressor. Int. J. Mech. Sci. 2022, 229, 107520. [Google Scholar] [CrossRef]
- Monge Brenes, B. Design of Supercritical Carbon Dioxide Centrifugal Compressors. Ph.D. Thesis, Universidad de Sevilla, Sevilla, Spain, 2014. [Google Scholar]
- Rinaldi, E.; Pecnik, R.; Colonna, P. Numerical computation of the performance map of a supercritical CO2 radial compressor by means of three-dimensional CFD simulations. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2014; p. V03BT36A017. [Google Scholar]
- Rinaldi, E.; Pecnik, R.; Colonna, P. Exact Jacobians for implicit Navier–Stokes simulations of equilibrium real gas flows. J. Comput. Phys. 2014, 270, 459–477. [Google Scholar] [CrossRef]
- Shao, W.; Yang, J.; Wang, X.; Ma, Z. Accuracy study and stability control of a property-table-based CFD strategy for modeling SCO2 compressors working near the critical point of the fluid. Appl. Therm. Eng. 2021, 183, 116222. [Google Scholar] [CrossRef]
- Zhu, Y.; Jiang, Y.; Liang, S.; Guo, C.; Guo, Y.; Cai, H. One-dimensional computation method of supercritical CO2 labyrinth seal. Appl. Sci. 2020, 10, 5771. [Google Scholar] [CrossRef]
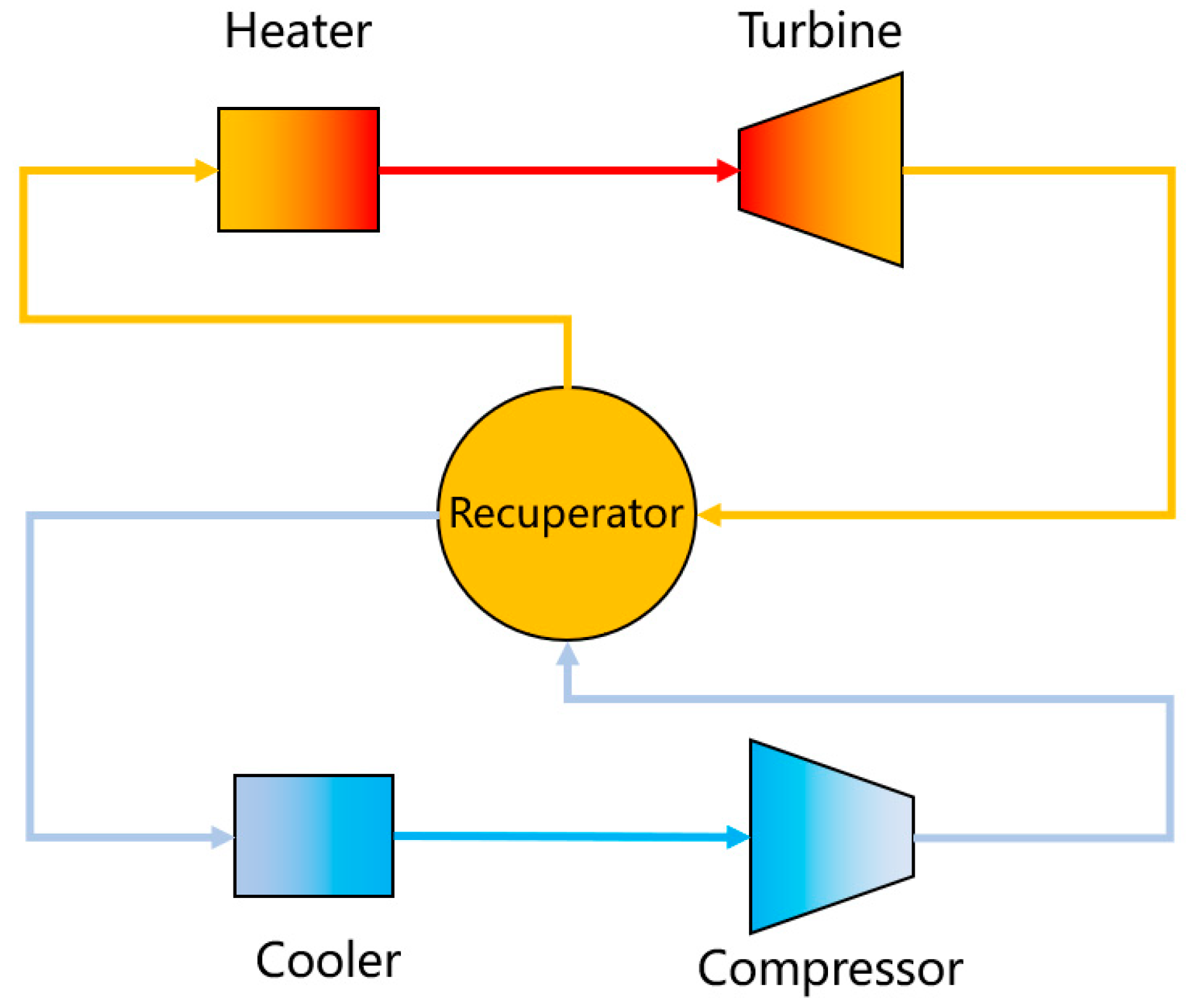
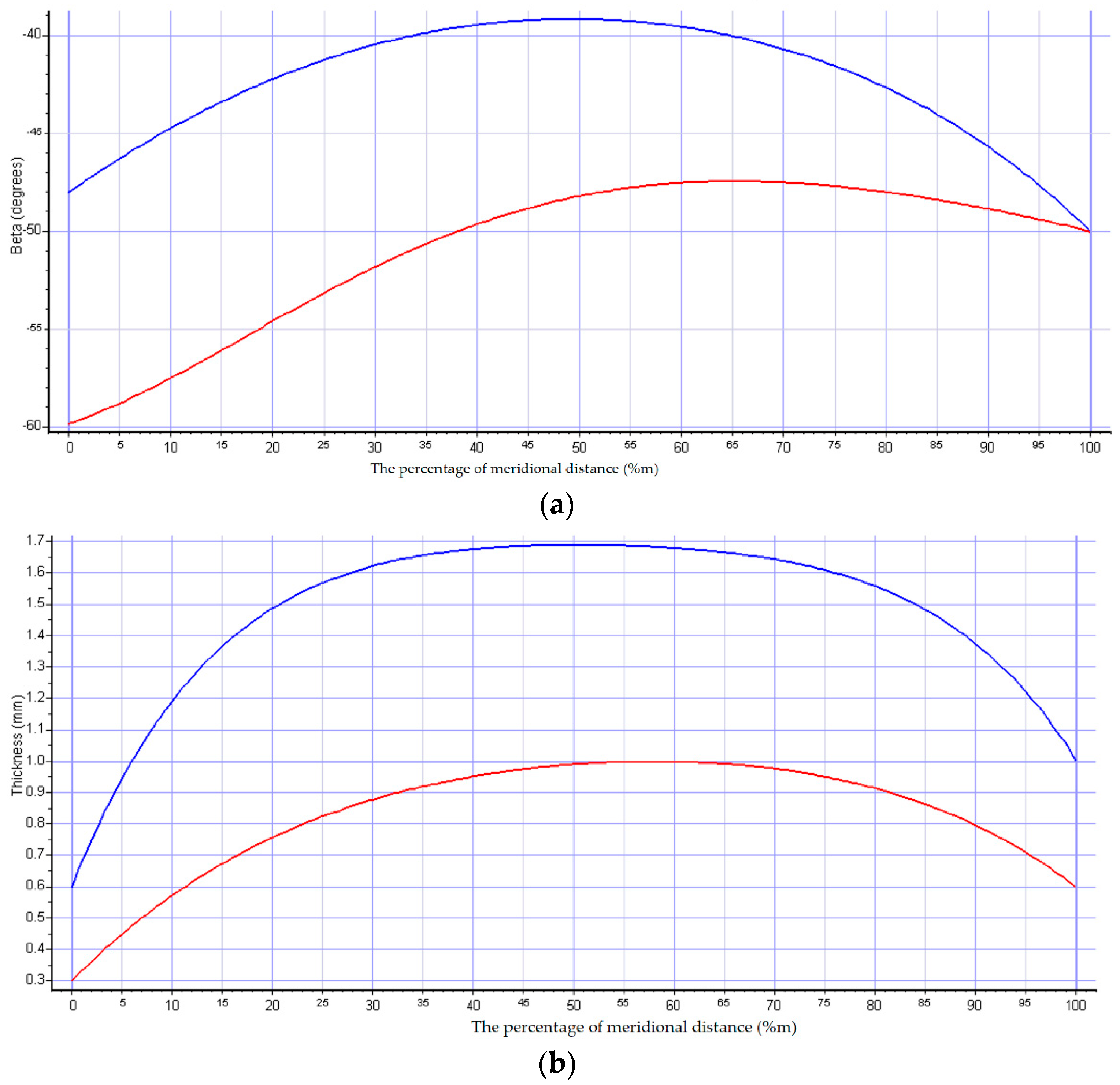
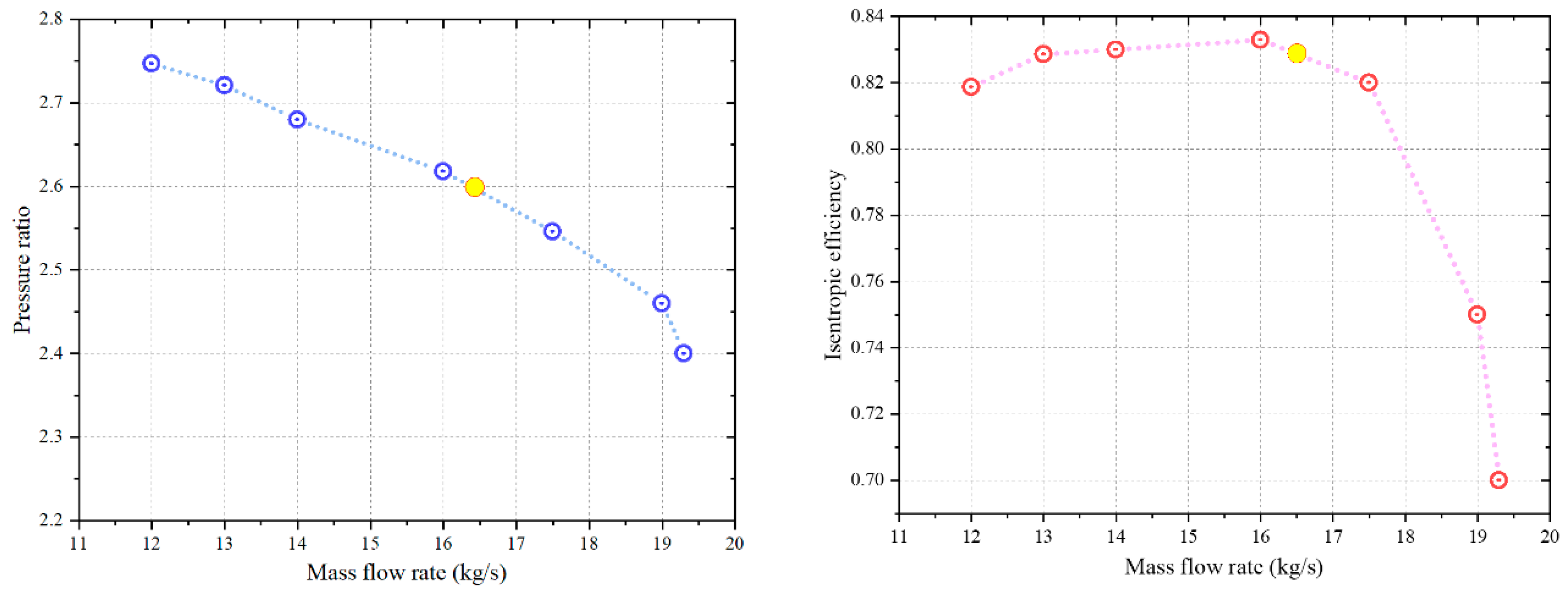
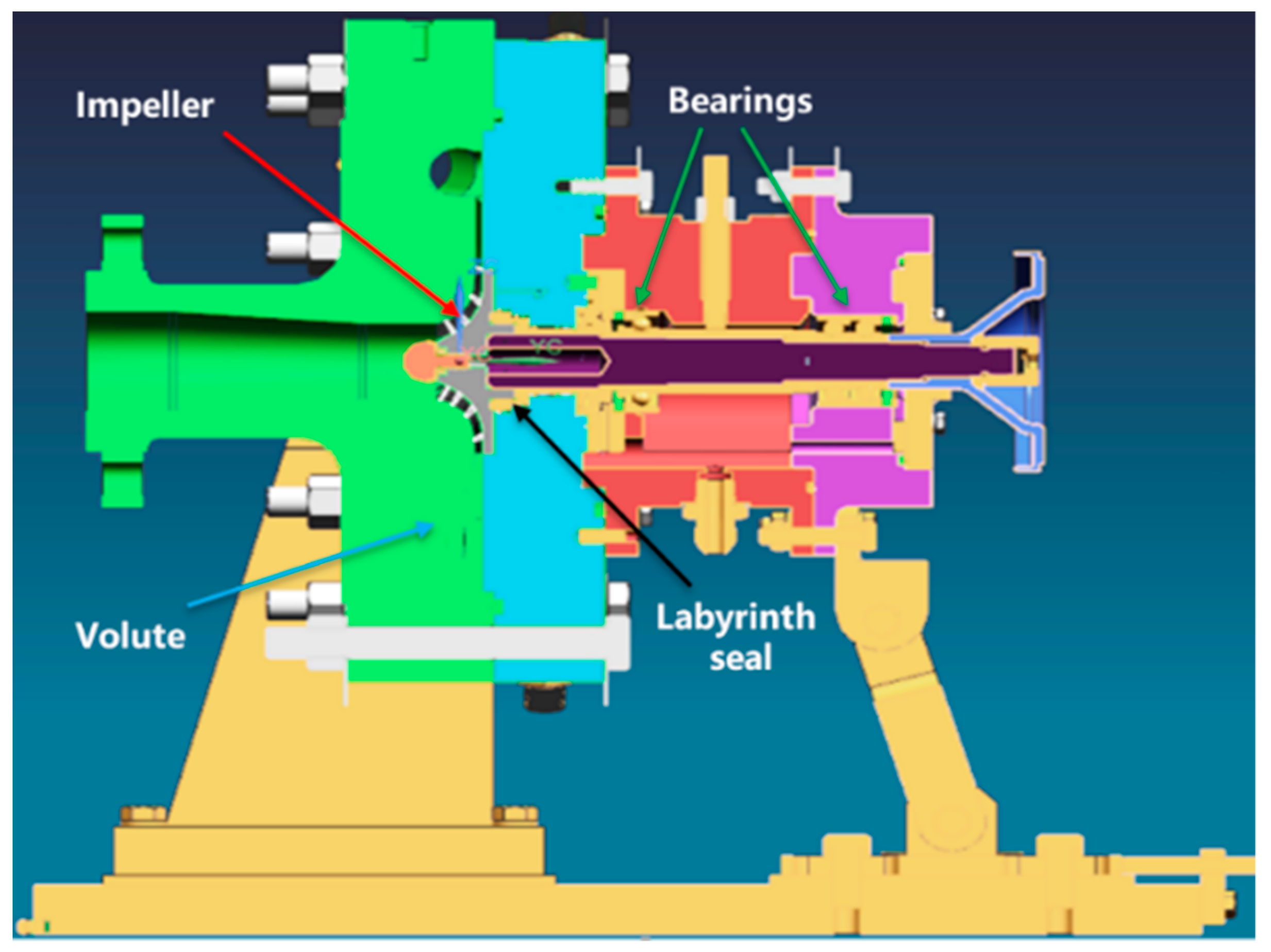






| Parameter | Value |
|---|---|
| Boiler thermal power | >5 MWth |
| Cycle efficiency | >21% |
| Turbine inlet pressure | 20 MPa |
| Turbine inlet temperature | 550 °C |
| Compressor inlet pressure | 8 MPa |
| Compressor inlet temperature | 35 °C |
| Inlet Pressure | Inlet Temperature | Mass Flow Rate | Pressure Ratio | Power | Isentropic Efficiency |
|---|---|---|---|---|---|
| 8 MPa | 35 °C | 16.3 kg/s | 2.5 | ~500 kW | >80% |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Hub radius/mm | 10 mm | Blade angle (leading-edge) | 60°/54°/48° |
| Impler radius/mm | 48 mm | Blade angle (training-edge) | 55° |
| Blade number | 15 | Blade height (leading-edge) | 7.5 mm |
| Tip clearance | 0.25 mm | Blade height (training-edge) | 3.5 mm |
| Blade inclination angle | 60° | Thickness (leading-edge) | 0.3–0.6 mm |
| Performance Index | Test Capability | |
|---|---|---|
| Experimental speed | 0~40,000 | RPM |
| Experimental mass flow | 0~25 | kg/s |
| Experimental power | 0~800 | kW |
| Compressor inlet pressure | 0~10 | MPa |
| Compressor outlet pressure | 0~22 | MPa |
| Compressor inlet temperature | 0~50 | °C |
| Compressor outlet temperature | 0~100 | °C |
| Range | Uncertainty | Type | |
|---|---|---|---|
| Inlet pressure | 0–10 MPa | <±0.075% FS | Monocrystalline Silicon |
| Outlet pressure | 0–25 MPa | <±0.075% FS | Monocrystalline Silicon |
| Inlet temperature | 0–50 °C | <±0.15 °C | PT100 |
| oulet temperature | 0–100 °C | <±0.15 °C | PT100 |
| Position | Mass Flow Range | Density Range | Mass Flow Uncertainty | Density Uncertainty |
|---|---|---|---|---|
| - | kg/s | g/cm3 | %FS | g/cm3 |
| Upstream | 2.5~25 | 400~1000 | <±0.2 | <±0.002 |
| Dimensionless Parameters | Formula |
|---|---|
| M* | M/Mref |
| N* | N/Nref |
| T01* | (T01-273.13)/(Tref -273.13) |
| T02* | (T02-273.13)/(Tref -273.13) |
| P01* | P01/Pref |
| P02* | P02/Pref |
| Design | Leading Edge (Exp) | Training Edge (Exp) | |
|---|---|---|---|
| Tip clearance | 0.25 mm | 0.43 mm | 0.45 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Liang, S.; Guo, C.; Guo, Y.; Li, Z.; Gong, X.; Jiang, Y. Experimental Study on a Supercritical CO2 Centrifugal Compressor Used in a MWe Scale Power Cycle. Appl. Sci. 2023, 13, 385. https://doi.org/10.3390/app13010385
Zhu Y, Liang S, Guo C, Guo Y, Li Z, Gong X, Jiang Y. Experimental Study on a Supercritical CO2 Centrifugal Compressor Used in a MWe Scale Power Cycle. Applied Sciences. 2023; 13(1):385. https://doi.org/10.3390/app13010385
Chicago/Turabian StyleZhu, Yuming, Shiqiang Liang, Chaohong Guo, Yongxian Guo, Zhigang Li, Xinyu Gong, and Yuyan Jiang. 2023. "Experimental Study on a Supercritical CO2 Centrifugal Compressor Used in a MWe Scale Power Cycle" Applied Sciences 13, no. 1: 385. https://doi.org/10.3390/app13010385





