Hybrid-Density Functional Calculations of Structural, Electronic, Magnetic, and Thermodynamic Properties of α-Cu2P2O7
Abstract
1. Introduction
2. Methodology
2.1. Computational Details
2.2. Elastic Properties
3. Results and Discussion
3.1. Magnetic Structure of -CuPO
3.2. Elastic Properties and Mechanical Stability of -CuPO
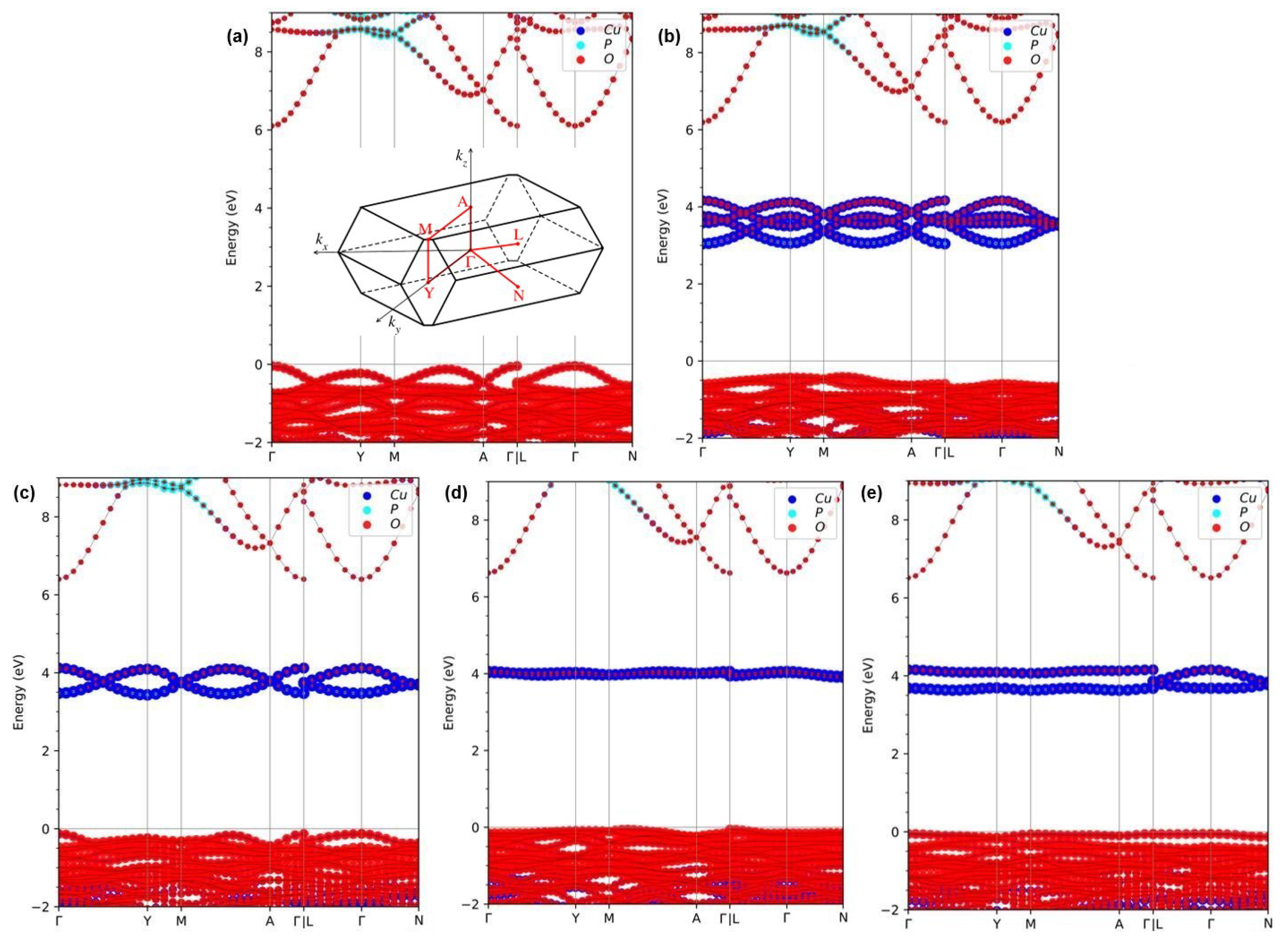
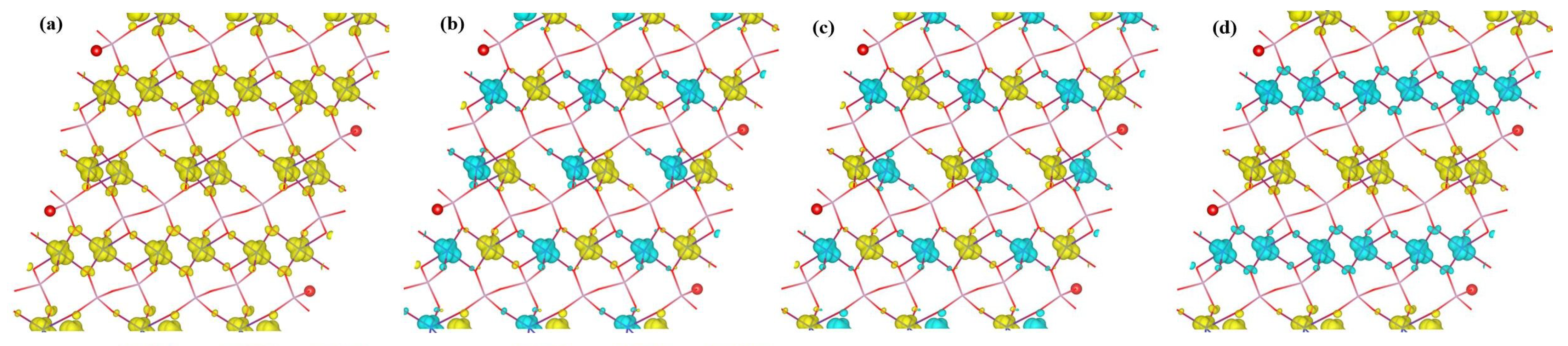
3.3. Electronic and Magnetic Structure of -CuPO
3.4. Magnetic Properties of -CuPO

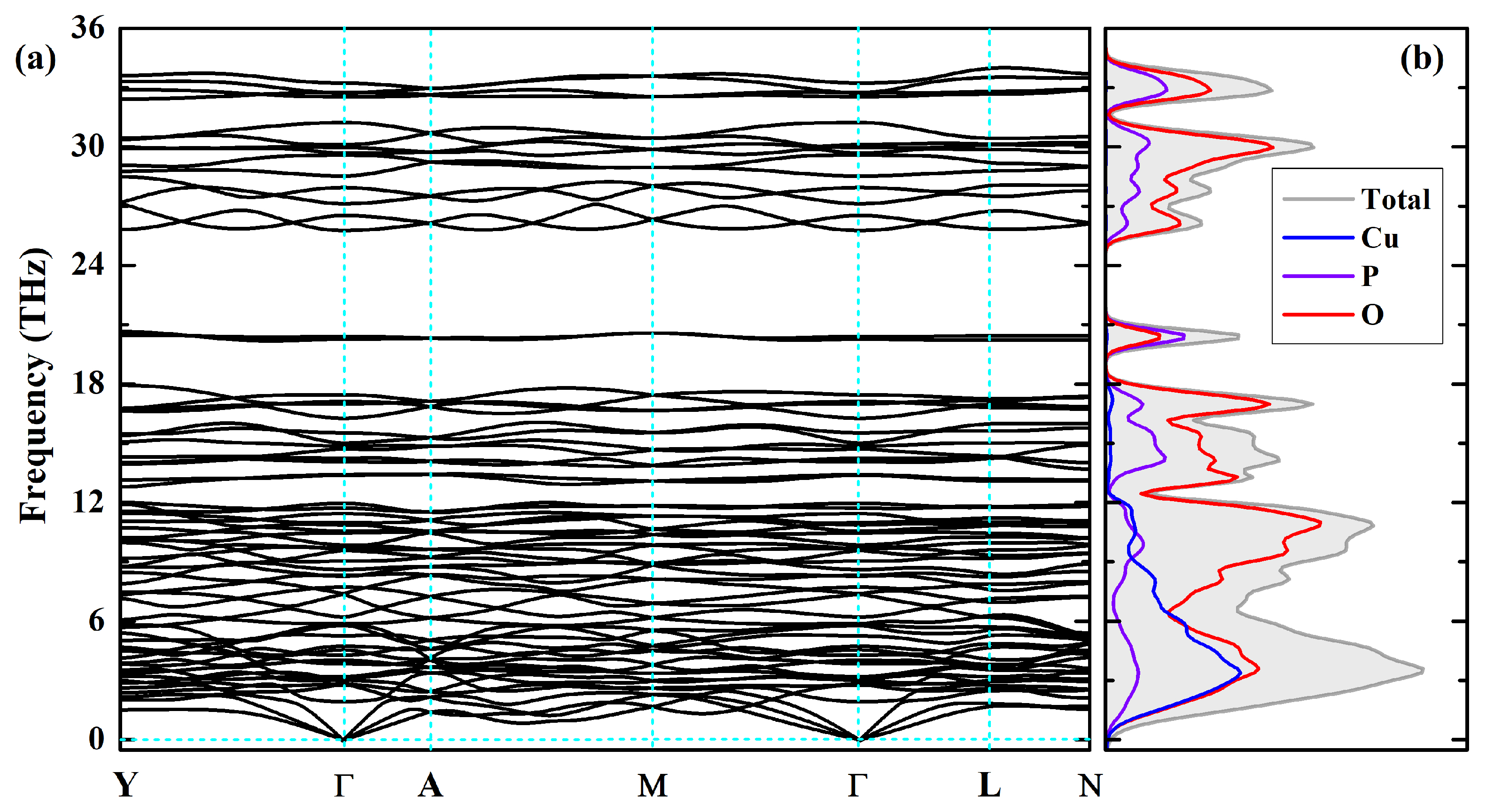
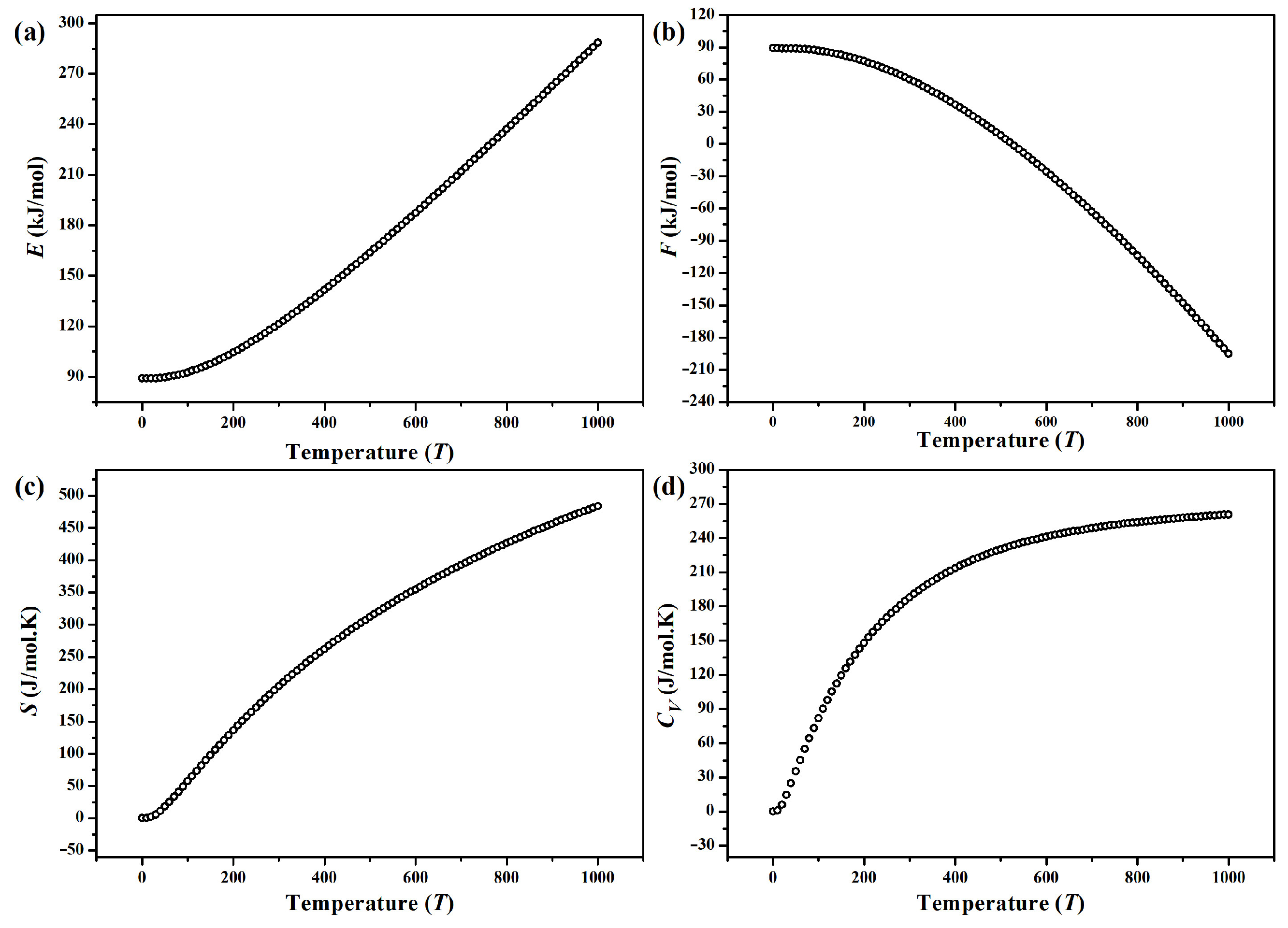
3.5. Phonon Dispersion Curves and Lattice Thermodynamic Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AFM | Antiferromagnetic |
| BZ | Brillouin zone |
| DFT | Density functional theory |
| DOS | Density of states |
| FM | Ferromagnetic |
| GGA | Generalized gradient approximation |
| HSE | Heyd-Scuseria-Ernzerhof hybrid functional |
| LDA | Local density approximation |
| PAW | Projector-augmented-wave |
| PBE | Perdew-Burke-Ernzerhof semi-local functional |
| PBE0 | Perdew-Burke-Ernzerhof hybrid functional |
| PDOS | Partial density of states |
| PhDOS | Phonon density of states |
| PM | Paramagnetic |
| QHA | Quasi-harmonic approximation |
| TDOS | Total density of states |
| VASP | Vienna Ab initio Simulation Package |
| XRD | X-ray diffraction |
References
- Dosen, A.; Marinkovic, B.A. Negative thermal expansion and cationic migration in zeolite Y used in FCC catalysts. Bull. Mater. Sci. 2019, 42, 86. [Google Scholar] [CrossRef]
- In-noi, O.; Daorattanachai, P.; Rungnim, C.; Prasitnok, K.; Rungtaweevoranit, B.; Faungnawakij, K.; Khemthong, P. Insight into Fructose Dehydration over Lewis Acid α-Cu2P2O7 Catalyst. Chem. Nano Mat. 2021, 7, 292–298. [Google Scholar]
- Li, S.Y.; Liu, Q.L.; Zhou, J.J.; Pan, T.; Gao, L.; Zhang, W.D.; Fan, L.; Lu, Y.Y. Hierarchical Co3O4 Nanofiber-Carbon Sheet Skeleton with Superior Na/Li-Philic Property Enabling Highly Stable Alkali Metal Batteries. Adv. Funct. Mater. 2019, 29, 1808847. [Google Scholar] [CrossRef]
- Agarwal, A.; Majumder, S.; Sankapal, B.R. Multi-walled carbon nanotubes supported copper phosphate microflowers for flexible solid-state supercapacitor. Int. J. Energy Res. 2022, 46, 6177–6196. [Google Scholar] [CrossRef]
- Meganathan, K.L.; BoopathiRaja, R.; Parthibavarman1, M.; Sharmila, V.; Shkir, M.; Gaikwad, S.A.; Praveenkumar, M. Design and fabrication of Cu2P2O7@Ppy electrode for extraordinary capacitance and long-term stability for ideal asymmetric supercapacitor application. J. Mater. Sci. Mater. Electron. 2021, 32, 24736–24747. [Google Scholar] [CrossRef]
- Agarwal, A.; Sankapal, B.R. Ultrathin Cu2P2O7 nanoflakes on stainless steel substrate for flexible symmetric all-solid-state supercapacitors. Chem. Eng. J. 2021, 422, 130131. [Google Scholar] [CrossRef]
- Zou, H.; Yang, X.Q.; Chen, B.; Du, Y.Y.; Ren, B.Y.; Sun, X.W.; Qiao, X.S.; Zhang, Q.W.; Wang, F. Thermal enhancement of upconversion by negative lattice expansion in orthorhombic Yb2W3O12. Angew. Chem. Int. Ed. 2019, 58, 17255–17259. [Google Scholar] [CrossRef]
- Magnusson, H.; Frisk, K. Thermodynamic evaluation of the copper-rich part of the Cu–H–O–S–P system at low temperatures. CALPHAD 2014, 47, 148–160. [Google Scholar] [CrossRef]
- Li, Y.G.; Korzhavyi, P.A. Interactions of point defects with stacking faults in oxygen-free phosphorus-containing copper. J. Nucl. Mater. 2015, 462, 160–164. [Google Scholar] [CrossRef]
- Sang, J.; Wei, P.; Liu, T.; Lv, H.; Ni, X.; Gao, D.; Zhang, J.; Li, H.; Zang, Y.; Yang, F.; et al. A Reconstructed Cu2P2O7 Catalyst for Selective CO2 Electroreduction to Multicarbon Products. Angew. Chem. 2022, 134, 202114238. [Google Scholar] [CrossRef]
- Arango, Y.C.; Vavilova, E.; Hafiez, M.A.; Janson, O.; Tsirlin, A.A.; Rosner, H.; Drechsler, S.L.; Weil, M.; Nenert, G.; Klingeler, R.; et al. Magnetic properties of the low-dimensional spin-1/2 magnet α-Cu2As2O7. Phys. Rev. B 2011, 84, 134430. [Google Scholar] [CrossRef]
- Janson, O.; Tsirlin, A.A.; Sichelschmidt, J.; Skourski, Y.; Weickert, F.; Rosner, H. Long-range superexchange in Cu2A2O7 (A = P, As, V) as a key element of the microscopic magnetic model. Phys. Rev. B 2011, 83, 094435. [Google Scholar] [CrossRef]
- Shi, N.; Sanson, A.; Gao, Q.L.; Sun, Q.; Ren, Y.; Huang, Q.Z.; de Souza, D.O.; Xing, X.R.; Chen, J. Strong Negative Thermal Expansion in a Low-Cost and Facile Oxide of Cu2P2O7. J. Am. Chem. Soc. 2020, 142, 3088–3093. [Google Scholar] [CrossRef] [PubMed]
- Effenberger, H. Structural refinement of low-temperature copper(II) pyrophosphate. Acta Cryst. C 1990, 46, 691–692. [Google Scholar] [CrossRef]
- Robertson, B.E.; Calvo, C. The crystal structure and phase transformation of α-Cu2P2O7. Acta Cryst. 1967, 22, 665–672. [Google Scholar] [CrossRef]
- Pogorzelec-Glaser, K.; Pietraszko, A.; Hilczer, B.; Poomska, M. Structure and phase transitions in Cu2P2O7. Phase. Transit. 2006, 79, 535–544. [Google Scholar] [CrossRef]
- Karaphun, A.; Chirawatkul, P.; Maensiri, S.; Swatsitang, E. Influence of calcination temperature on the structural, morphological, optical, magnetic and electrochemical properties of Cu2P2O7 nanocrystals. J. Sol.-Gel. Sci. Technol. 2018, 88, 407–421. [Google Scholar] [CrossRef]
- Yang, X.Y.; Lu, Y.; Zhang, P. First-principles study of native point defects and diffusion behaviors of helium in zirconium carbide. J. Nucl. Mater. 2015, 465, 161–166. [Google Scholar] [CrossRef]
- Ren, K.; Wang, K.; Zhang, G. Atomic Adsorption-Controlled Magnetic Properties of a Two-Dimensional (2D) Janus Monolayer. ACS Appl. Electron. Mater. 2022, 4, 4507–4513. [Google Scholar] [CrossRef]
- Ren, K.; Ma, X.; Liu, X.; Xu, Y.; Huo, W.; Li, W.; Zhang, G. Prediction of 2D IV–VI semiconductors: Auxetic materials with direct bandgap and strong optical absorption. Nanoscale 2022, 14, 8463–8473. [Google Scholar] [CrossRef]
- Bamberger, C.E.; Specht, E.D.; Anovitz, L.M. Crystalline Copper Phosphates: Synthesis and Thermal Stability. J. Am. Ceram. Soc. 1997, 80, 3133–3138. [Google Scholar] [CrossRef]
- Le, S.N.; Navrotsky, A.; Pralong, V. Energetics of copper diphosphates-Cu2P2O7 and Cu3(P2O6OH)2. Solid State Sci. 2008, 10, 761–767. [Google Scholar] [CrossRef]
- Pastukh, S.; Laskowska, M.; Dulski, M.; Krzykawski, T.; Parlinski, K.; Piekarz, P. Ab initio studies for characterization and identification of nanocrystalline copper pyrophosphate confined in mesoporous silica. Nanotechnology 2021, 32, 415701. [Google Scholar] [CrossRef] [PubMed]
- Stiles, J.A.R.; Stager, C.V. Magnetic Structure of Manganese Pyrophosphate and Copper Pyrophosphate. Can. J. Phys. 1972, 50, 3079. [Google Scholar] [CrossRef]
- Stiles, J.A.R.; Stager, C.V. Nuclear Magnetic Resonance in Antiferromagnetic Cu2P2O7. Can. J. Phys. 1973, 51, 87. [Google Scholar] [CrossRef]
- Pastukh, S.; Piekarz, P. Ab initio calculations of the structural and dynamical properties of copper pyrophosphate. Proceedings 2020, 4, 32. [Google Scholar]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Hammer, B.; Hansen, L.B.; Nørskov, J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof funtionals. Phys. Rev. B 1999, 59, 7413. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ernzerhof, M.; Bruke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 1996, 105, 9982. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew-Burke-Ernzerhof exchange-correlation functional. J. Chem. Phys. 1999, 110, 5029. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E. Assessment and validation of a screened Coulomb hybrid density functional. J. Chem. Phys. 2004, 120, 7274. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Sanville, E.; Kenny, S.D.; Smith, R.; Henkelman, G. Improved grid-based algorithm for Bader charge allocation. J. Comput. Chem. 2007, 28, 899–908. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Ewing, M.B.; Lilley, T.H.; Olofsson, G.M.; Ratzsch, M.T.; Somsen, G. Standard quantities in chemical thermodynamics. Fugacities, activities and equilibrium constants for pure and mixed phases (IUPAC Recommendations 1994). Pure Appl. Chem. 1994, 66, 533–552. [Google Scholar] [CrossRef]
- Paier, J.; Marsman, M.; Hummer, K.; Kresse, G.; Gerber, I.C.; Ángyán, J.G. Screened hybrid density functionals applied to solids. J. Chem. Phys. 2006, 124, 154709. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Movlarooy, T.; Kompany, A. First-principle calculations of the cohesive energy and electronic properties of PbTiO3. Phys. B 2007, 391, 316e21. [Google Scholar] [CrossRef]
- Yang, X.Y.; Yang, Y.; Lu, Y.; Sun, Z.Y.; Hussain, S.; Zhang, P. First-principles GGA+U calculation investigating the hydriding and diffusion properties of hydrogen in PuH2+x, 0≤x≤ 1. Int. J. Hydrogen Energy 2018, 43, 13632–13638. [Google Scholar] [CrossRef]
- Pedroza, L.; da Silva, A.J.R.; Capelle, K. Gradient-dependent density functionals of the Perdew-Burke-Ernzerhof type for atoms, molecules, and solids. Phys. Rev. B 2009, 79, 201106. [Google Scholar] [CrossRef]
- Forsyth, J.B.; Brown, P.J.; Wanklyn, B.M. Magnetism in cupric oxide. J. Phys. C Solid State Phys. 1988, 21, 2917–2929. [Google Scholar] [CrossRef]
- Watt, J.P. Hashin-Shtrikman bounds on the effective elastic moduli of polycrystals with monoclinic symmetry. J. Appl. Phys. 1980, 51, 1520–1524. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, B.T.; Zhao, X.G. Ground-state properties and high-pressure behavior of plutonium dioxide: Density functional theory calculations. Phys. Rev. B 2010, 82, 144110. [Google Scholar] [CrossRef]
- Majtyka-Pilat, A.; Wojtyniak, M.; Laskowski, L.; Chrobak, D. Structure and Properties of Copper Pyrophosphate by First-Principle Calculations. Materials 2022, 15, 842. [Google Scholar] [CrossRef]
- Hase, M.; Kohno, M.; Kitazawa, H.; Tsujii, N.; Suzuki, O.; Ozawa, K.; Kido, G.; Imai, M.; Hu, X. 1/3 magnetization plateau observed in the spin-1/2 trimer chain compound Cu3(P2O6OH)2. Phys. Rev. B 2006, 73, 104419. [Google Scholar] [CrossRef]
- Goodenough, J.B. Theory of the role of covalence in the Perovskite-Type Manganites [La, M(II)]MnO3. Phys. Rev. 1995, 100, 564. [Google Scholar] [CrossRef]
- Born, M. On the stability of crystal lattices I. Proc. Camb. Philos. Soc. 1940, 36, 160–172. [Google Scholar] [CrossRef]
- Grimvall, G.; Magyari-Köpe, B.; Ozoliņš, V.; Persson, K.A. Lattice instabilities in metallic elements. Rev. Mod. Phys. 2012, 84, 945–986. [Google Scholar] [CrossRef]
- Wu, Z.J.; Zhao, E.J.; Xiang, H.P.; Hao, X.F.; Liu, X.J.; Meng, J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B 2007, 76, 054115. [Google Scholar] [CrossRef]
- Voigt, W. Lehrburch der Kristallphysik; Teubner: Leipzig, Germany, 1928. [Google Scholar]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Lond. A 1952, 65, 350. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Phil. Mag. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Yang, X.Y.; Lu, Y.; Wei, Z.F.; Ping, Z. Mechanical, electronic, and thermodynamic properties of zirconium carbide from first-principles calculations. Chin. Phys. B 2015, 24, 116301. [Google Scholar] [CrossRef]
- Li, Y.G.; Korzhavyi, P.A. Physical and chemical properties of Cu (I) compounds with O and/or H. Dalton Trans. 2017, 46, 529–538. [Google Scholar] [CrossRef]
- Eschrig, H.; Koepernik, K. Tight-binding models for the iron-based superconductors. Phys. Rev. B 2009, 80, 104503. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: New York, NY, USA, 1990; p. 155. [Google Scholar]
- Xiang, Y.; Hao, X.; Liu, X.; Wang, M.; Tian, J.; Kang, C.; Liang, E.; Zhang, W.; Jia, Y. Tailoring Thermal Expansion of (LiFe)0.5xCu2-xxP2O7 via Codoping LiFe Diatoms in Cu2P2O7 Oxide. Inorg. Chem. 2022, 61, 1504–1511. [Google Scholar] [CrossRef]
- Yashima, M.; Suzuki, R.O. Electronic structure and magnetic properties of monoclinic β-Cu2V2O7: A GGA+U study. Phys. Rev. B 2009, 79, 125201. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Yang, X.Y.; Lu, Y.; Zhang, P. The temperature-dependent diffusion coefficient of helium in zirconium carbide studied with first-principles calculations. J. Appl. Phys. 2015, 117, 164903. [Google Scholar] [CrossRef]
- Lee, C.; Gonze, X. Ab initio calculation of the thermodynamic properties and atomic temperature factors of SiO2α-quartz and stishovite. Phys. Rev. B 1995, 51, 8610–8613. [Google Scholar] [CrossRef] [PubMed]


| State | Functional | a (Å) | b (Å) | c (Å) | () | V (Å) |
|---|---|---|---|---|---|---|
| FM | PBE | 7.245 | 8.237 | 9.411 | 111.922 | 521.060 |
| PBE0 | 7.072 | 8.115 | 9.291 | 111.003 | 497.660 | |
| HSE | 7.076 | 8.118 | 9.299 | 111.028 | 498.58 | |
| AFM-1 | PBE | 7.244 | 8.236 | 9.405 | 111.907 | 520.52 |
| PBE0 | 7.066 | 8.112 | 9.251 | 110.914 | 495.36 | |
| HSE | 7.068 | 8.121 | 9.256 | 110.910 | 496.34 | |
| AFM-2 | PBE | 7.246 | 8.231 | 9.405 | 111.925 | 520.440 |
| PBE0 | 7.063 | 8.112 | 9.252 | 110.876 | 495.260 | |
| HSE | 7.073 | 8.116 | 9.262 | 110.976 | 496.48 | |
| AFM-3 | PBE | 7.232 | 8.214 | 9.422 | 111.778 | 519.80 |
| PBE0 | 7.062 | 8.108 | 9.257 | 110.886 | 495.18 | |
| HSE | 7.063 | 8.112 | 9.262 | 110.897 | 495.82 | |
| AFM | GGA 1 | 7.217 | 8.212 | 9.429 | 111.14 | 521.20 |
| GGA+U 1 | 7.095 | 8.095 | 9.355 | 111.16 | 501.03 | |
| GGA+U+D2 1 | 6.890 | 8.104 | 9.156 | 111.09 | 476.99 | |
| PM | XRD 2 | 6.876 | 8.113 | 9.162 | 109.54 | 481.67 |
| XRD 3 | 6.895 | 8.113 | 9.164 | 109.62 | 482.86 | |
| XRD 4 | 6.887 | 8.108 | 9.156 | 109.54 | 481.59 | |
| XRD 5 | 6.901 | 8.108 | 9.176 | 109.65 | 483.53 |
| State | Functional | (∘) | (Å) | (Å) | (Å) | (Å) |
|---|---|---|---|---|---|---|
| FM | PBE | 101.735 | 3.124 | 3.354 | 6.905 | 1.921 |
| PBE0 | 100.015 | 3.052 | 3.257 | 6.580 | 1.837 | |
| HSE | 99.996 | 3.054 | 3.261 | 6.604 | 1.838 | |
| AFM-1 | PBE | 101.745 | 3.122 | 3.356 | 6.892 | 1.920 |
| PBE0 | 100.322 | 3.054 | 3.262 | 6.533 | 1.834 | |
| HSE | 100.350 | 3.059 | 3.261 | 6.553 | 1.836 | |
| AFM-2 | PBE | 101.614 | 3.120 | 3.359 | 6.906 | 1.919 |
| PBE0 | 100.284 | 3.055 | 3.259 | 6.532 | 1.836 | |
| HSE | 100.301 | 3.056 | 3.266 | 6.558 | 1.835 | |
| AFM-3 | PBE | 100.290 | 3.092 | 3.359 | 6.928 | 1.918 |
| PBE0 | 100.022 | 3.047 | 3.266 | 6.541 | 1.833 | |
| HSE | 100.028 | 3.049 | 3.267 | 6.551 | 1.835 |
| State | Functional | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| FM | PBE | −22.616 | −1.416 | 0 | −1.19 | −3.59 | 1.36 | 1.35 | 1.51 | 1.32 |
| PBE0 | −24.453 | −2.534 | 3.784 | −1.35 | −3.74 | 1.45 | 1.44 | 1.56 | 1.42 | |
| HSE | −26.741 | −2.562 | 3.084 | −1.35 | −3.74 | 1.45 | 1.44 | 1.56 | 1.42 | |
| AFM-1 | PBE | −22.671 | −1.475 | 0.390 | −1.19 | −3.64 | 1.39 | 1.36 | 1.52 | 1.32 |
| PBE0 | −24.519 | −2.604 | 4.344 | −1.35 | −3.79 | 1.46 | 1.46 | 1.58 | 1.42 | |
| HSE | −26.785 | −2.610 | 3.566 | −1.35 | −3.79 | 1.46 | 1.46 | 1.58 | 1.42 | |
| AFM-2 | PBE | −22.704 | −1.511 | 0.730 | −1.19 | −3.64 | 1.39 | 1.36 | 1.52 | 1.32 |
| PBE0 | −24.530 | −2.614 | 4.670 | −1.35 | −3.79 | 1.46 | 1.46 | 1.58 | 1.42 | |
| HSE | −26.796 | −2.620 | 3.966 | −1.35 | −3.79 | 1.46 | 1.46 | 1.58 | 1.42 | |
| AFM-3 | PBE | −22.649 | −1.447 | 0.362 | −1.20 | −3.65 | 1.39 | 1.36 | 1.52 | 1.33 |
| PBE0 | −24.530 | −2.605 | 4.395 | −1.35 | −3.79 | 1.46 | 1.46 | 1.58 | 1.42 | |
| HSE | −26.785 | −2.611 | 3.683 | −1.35 | −3.79 | 1.46 | 1.46 | 1.58 | 1.43 | |
| Previous studies | −21.725 1 | −2.892 1 | 2.85 2, 3.17 3, | |||||||
| 3.36 4, 3.79 5 | ||||||||||
| State | Functional | (eV) | (/Cell) | () | () | () |
|---|---|---|---|---|---|---|
| FM | PBE | −140.547 | 3.539 | 0.606 | 0.006 | 0.078 |
| PBE0 | −189.559 | 3.944 | 0.793 | 0.008 | 0.062 | |
| HSE | −179.043 | 3.944 | 0.791 | 0.008 | 0.063 | |
| AFM-1 | PBE | −140.664 | 0.000 | ±0.599 | ±0.002 | ±0.020 |
| PBE0 | −189.699 | 0.000 | ±0.791 | ±0.002 | ±0.033 | |
| HSE | −179.140 | 0.000 | ±0.790 | ±0.002 | ±0.029 | |
| AFM-2 | PBE | −140.736 | 0.000 | ±0.579 | ±0.003 | ±0.034 |
| PBE0 | −189.717 | 0.000 | ±0.787 | ±0.002 | ±0.028 | |
| HSE | −179.159 | 0.000 | ±0.785 | ±0.002 | ±0.028 | |
| AFM-3 | PBE | −140.609 | 0.000 | ±0.612 | ±0.004 | ±0.067 |
| PBE0 | −189.701 | 0.000 | ±0.789 | ±00.004 | ±0.052 | |
| HSE | −179.140 | 0.000 | ±0.788 | ±0.004 | ±0.052 | |
| FM | GGA [23] | −140.567 | 0.554 | |||
| GGA+U [23] | −99.822 | 0.840 | ||||
| AFM | GGA [23] | −140.598 | ±0.610 | |||
| GGA+U [23] | −99.830 | ±0.838 |
| State | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AFM-2 | 120.8 | 97.7 | 174.1 | 59.9 | 61.7 | 56.6 | 71.5 | 79.9 | 72.1 | 8.4 | −34.1 | −1.2 | −43.5 |
| Property | Averaging Method: | ||
|---|---|---|---|
| Voigt | Reuss | Hill | |
| B (GPa) | 93.298 | 80.624 | 86.961 |
| G (GPa) | 46.882 | 30.018 | 38.450 |
| Y (GPa) | 120.468 | 80.112 | 100.533 |
| 1.990 | 2.686 | 2.262 | |
| 0.285 | 0.334 | 0.300 | |
| H (GPa) | 6.413 | 3.326 | 4.819 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Zhang, P.; Korzhavyi, P. Hybrid-Density Functional Calculations of Structural, Electronic, Magnetic, and Thermodynamic Properties of α-Cu2P2O7. Appl. Sci. 2023, 13, 498. https://doi.org/10.3390/app13010498
Yang X, Zhang P, Korzhavyi P. Hybrid-Density Functional Calculations of Structural, Electronic, Magnetic, and Thermodynamic Properties of α-Cu2P2O7. Applied Sciences. 2023; 13(1):498. https://doi.org/10.3390/app13010498
Chicago/Turabian StyleYang, Xiaoyong, Ping Zhang, and Pavel Korzhavyi. 2023. "Hybrid-Density Functional Calculations of Structural, Electronic, Magnetic, and Thermodynamic Properties of α-Cu2P2O7" Applied Sciences 13, no. 1: 498. https://doi.org/10.3390/app13010498
APA StyleYang, X., Zhang, P., & Korzhavyi, P. (2023). Hybrid-Density Functional Calculations of Structural, Electronic, Magnetic, and Thermodynamic Properties of α-Cu2P2O7. Applied Sciences, 13(1), 498. https://doi.org/10.3390/app13010498








