High-Temperature Thermodynamics of Uranium from Ab Initio Modeling
Abstract
1. Introduction
2. Ab Initio Computational Methodology
3. CALPHAD Methodology
4. Results
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hofman, G.; Walters, L.; Bauer, T. Metallic fast reactor fuels. Prog. Nucl. Energy 1997, 31, 83–110. [Google Scholar] [CrossRef]
- Meyer, M.K.; Hofman, G.L.; Hayes, S.L.; Clark, C.R.; Wiencek, T.C.; Snelgrove, J.L.; Strain, R.V.; Kim, K.-H. Low-temperature irradiation behavior of uranium–molybdenum alloy dispersion fuel. J. Nucl. Mater. 2002, 304, 221–236. [Google Scholar] [CrossRef]
- Kim, Y.S.; Hofman, G.; Yacout, A. Migration of minor actinides and lanthanides in fast reactor metallic fuel. J. Nucl. Mater. 2009, 392, 164–170. [Google Scholar] [CrossRef]
- Carmack, W.J.; Porter, D.L.; Chang, I.; Hayes, S.L.; Meyer, M.K.; Burkes, D.E.; Lee, C.B.; Mizuno, T.; Delage, F.; Somers, J.; et al. Metallic fuels for advanced reactors. J. Nucl. Mater. 2009, 392, 139–150. [Google Scholar] [CrossRef]
- Todreas, N.E. Thermal-hydraulics challenges in fast reactor design. Nucl. Tech. 2009, 167, 127–144. [Google Scholar] [CrossRef]
- Janney, D.E. Metallic Fuels Handbook, Part 1: Alloys Based on U-Zr, Pu-Zr, U-Pu, or U-Pu-Zr, Including Those with Minor Actinides (Np, Am, Cm) Rare-Earth Elements (La, Ce, Pr, Nd, Gd), and Y; Idaho National Laboratory: Idaho Falls, ID, USA, 2017. [Google Scholar]
- Capriotti, L.; Bremier, S.; Inagaki, K.; Poml, P.; Papaioannou, D.; Ohta, H.; Ogata, T.; Rondinella, V.V. Characterization of metallic fuel for minor actinides trans mutation in fast reactor. Prog. Nucl. Energy 2017, 94, 194–201. [Google Scholar] [CrossRef]
- Imhoff, S.D. Uranium Density, Thermal Conductivity, Specific Heat, and Thermal Diffusivity; LA-UR-21-21810; OSTI.GOV: Idaho National Lab: Idaho Falls, ID, USA, 24 February 2021. [Google Scholar]
- Söderlind, P. Theory of the crystal structures of cerium and the light actinides. Adv. Phys. 1998, 47, 959–998. [Google Scholar] [CrossRef]
- Söderlind, P.; Johansson, B.; Yongming, L.; Nordström, L. Calculated thermal expansion of the actinide elements. Int. J. Thermophys. 1991, 12, 611–615. [Google Scholar] [CrossRef]
- Söderlind, P.; Eriksson, O.; Wills, J.M.; Boring, A.M. Elastic constants of cubic f-electron elements: Theory. Phys. Rev. B 1993, 48, 9306–9312. [Google Scholar] [CrossRef]
- Söderlind, P.; Eriksson, O.; Wills, J.; Boring, A. A unified picture of the crystal structures of metals. Nature 1995, 374, 524–525. [Google Scholar] [CrossRef]
- Söderlind, P.; Grabowski, B.; Yang, L.; Landa, A.; Björkman, T.; Souvatzis, P.; Eriksson, O. High-temperature phonon stabilization of γ-uranium from relativistic first-principles theory. Phys. Rev. B 2012, 85, 60301. [Google Scholar] [CrossRef]
- Yoo, C.-S.; Cynn, H.; Söderlind, P. Phase diagram of uranium at high pressures and temperatures. Phys. Rev. B 1998, 57, 10359. [Google Scholar] [CrossRef]
- Söderlind, P. First-principles elastic and structural properties of uranium metal. Phys. Rev. B 2002, 66, 85113. [Google Scholar] [CrossRef]
- Wills, J.M.; Eriksson, O. Crystal-structure stabilities and electronic structure for the light actinides Th, Pa, and U. Phys. Rev. B 1992, 45, 13879. [Google Scholar] [CrossRef]
- Richard, N.; Bernard, S.; Jollet, F.; Torrent, M. Plane-wave pseudopotential study of the light actinides. Phys. Rev. B 2002, 66, 235112. [Google Scholar] [CrossRef]
- Hood, R.; Yang, L.H.; Moriarty, J. Quantum molecular dynamics simulations of uranium at high pressure and temperature. Phys. Rev. B 2008, 78, 24116. [Google Scholar] [CrossRef]
- Taylor, C.D. Evaluation of first-principles techniques for obtaining materials parameters of alpha uranium and the (001) alpha uranium surface. Phys. Rev. B 2008, 77, 94119. [Google Scholar] [CrossRef]
- Xiang, S.; Huang, H.; Hsiung, L.M. Quantum mechanical calculations of uranium phases and niobium defects in γ-uranium. J. Nucl. Mater. 2008, 375, 113–119. [Google Scholar] [CrossRef]
- Bouchet, J. Lattice dynamics of α uranium. Phys. Rev. B 2008, 77, 24113. [Google Scholar] [CrossRef]
- Beeler, B.; Good, B.; Rashkeev, S.; Deo, C.; Baskes, M.; Okuniewski, M. First principles calculations for defects in U. J. Phys. Condens. Matter. 2010, 22, 505703. [Google Scholar] [CrossRef]
- Raymond, S.; Bouchet, J.; Lander, G.H.; Le Tacon, M.; Garbarino, G.; Hoesch, M.; Rueff, J.-P.; Krisch, M.; Lashley, J.C.; Schulze, R.K.; et al. Understanding the complex phase diagram of uranium: The role of electron-phonon coupling. Phys. Rev. Lett. 2011, 107, 136401. [Google Scholar] [CrossRef]
- Bouchet, J.; Albers, R. Elastic properties of the light actinides at high pressure. J. Phys. Condens. Matter. 2011, 23, 215402. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.-Y.; Wirth, B.D. First-principles study of diffusion of interstitial and vacancy in α U-Zr. J. Phys. Condens. Matter 2011, 23, 205402. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.-Y.; Wirth, B.D. First-principles study of bubble nucleation and growth behaviors in α U-Zr. J. Phys. Condens. Matter 2012, 24, 415404. [Google Scholar] [CrossRef]
- Akella, J.; Weir, S.; Wills, J.M.; Söderlind, P. Structural stability in uranium. J. Phys. Condens. Matter 1997, 9, L549–L555. [Google Scholar] [CrossRef]
- Smirnova, D.E.; Starikov, S.V.; Stegailov, V.V. Interatomic potential for uranium in a wide range of pressures and temperatures. J. Phys. Condens. Matter. 2012, 24, 15702. [Google Scholar] [CrossRef] [PubMed]
- Smirnova, D.E.; Starikov, S.V.; Stegailov, V.V. New interatomic potential for computation of mechanical and thermodynamic properties of uranium. Phys. Met. Metallogr. 2012, 113, 107–116. [Google Scholar] [CrossRef]
- Beeler, B.; Deo, C.; Baskes, M.; Okuniewski, M. Atomistic properties of γ uranium. J. Phys. Condens. Matter 2012, 24, 75401. [Google Scholar] [CrossRef]
- Pascuet, M.I.; Bonny, G.; Fernández, J.R. Many-body interatomic U and Al–U potentials. J. Nucl. Mater. 2012, 424, 158–163. [Google Scholar] [CrossRef]
- Beeler, B.; Deo, C.; Baskes, M.; Okuniewski, M. First principles calculations of the structure and elastic constants of α, β and γ uranium. J. Nucl. Mater. 2013, 433, 143–151. [Google Scholar] [CrossRef]
- Smirnova, D.E.; Kuksin, A.Y.; Starikov, S.V.; Stegailov, V.V.; Insepov, Z.; Rest, J.; Yacout, A.M. A ternary EAM interatomic potential for U–Mo alloys with xenon. Modell. Simul. Mater. Sci. Eng. 2013, 21, 35011. [Google Scholar] [CrossRef]
- Smirnova, D.E.; Kuksin, A.Y.; Starikov, S.V. Investigation of point defects diffusion in bcc uranium and U–Mo alloys. J. Nucl. Mater. 2015, 458, 304–311. [Google Scholar] [CrossRef]
- Smirnova, D.E.; Kuksin, A.Y.; Starikov, S.V.; Stegailov, V.V. Atomistic modeling of the self-diffusion in γ-U and γ-U–Mo. Phys. Met. Metallogr. 2015, 116, 445–455. [Google Scholar] [CrossRef]
- Moore, A.P.; Beeler, B.; Deo, C.; Baskes, M.I.; Okuniewski, M.A. Atomistic modeling of high temperature uranium-zirconium alloy structure and thermodynamics. J. Nucl. Mater. 2015, 467, 802–819. [Google Scholar] [CrossRef]
- Bouchet, J.; Bottin, F. Thermal evolution of vibrational properties of α-U. Phys. Rev. B 2015, 92, 174108. [Google Scholar] [CrossRef]
- Tseplyaev, V.I.; Starikov, S.V. The atomistic simulation of pressure-induced phase transition in uranium mononitride. J. Phys. Conf. Ser. 2015, 653, 012092. [Google Scholar] [CrossRef]
- Ren, Z.; Wu, J.; Ma, R.; Hu, G.; Luo, C. Thermodynamic properties of α-uranium. J. Nucl. Mater. 2016, 480, 80–87. [Google Scholar] [CrossRef]
- Kuksin, A.Y.; Starikov, S.V.; Smirnova, D.E.; Tseplyaev, V.I. The diffusion of point defects in uranium mononitride: Combination of DFT and atomistic simulation with novel potential. J. Alloys Comp. 2016, 658, 385–394. [Google Scholar] [CrossRef]
- Kolotova, L.N.; Kuksin, A.Y.; Smirnov, D.E.; Starikov, S.V.; Tseplyaev, V.I. Features of structure and phase transitions in pure uranium and U–Mo alloys: Atomistic simulation. J. Phys. Conf. Ser. 2016, 774, 12036. [Google Scholar] [CrossRef]
- Kolotova, L.N.; Starikov, S.V. Anisotropy of the U–Mo alloy: Molecular-dynamics study. Phys. Met. Metallogr. 2016, 117, 487–493. [Google Scholar] [CrossRef]
- Tseplyaev, V.I.; Starikov, S.V. The atomistic simulation of pressure-induced phase transition in uranium mononitride. J. Nucl. Mater. 2016, 480, 7–14. [Google Scholar] [CrossRef]
- Starikov, S.V.; Kolotova, L.N. Features of cubic and tetragonal structures of U–Mo alloys: Atomistic simulation. Script. Mater. 2016, 113, 27–30. [Google Scholar] [CrossRef]
- Huang, S.-Q.; Ju, X.-H. First-principles study of properties of alpha uranium crystal and seven alpha-uranium surfaces. J. Chem. 2017, 2017, 8618340. [Google Scholar] [CrossRef]
- Bouchet, J.; Bottin, F. High-temperature and high-pressure phase transitions in uranium. Phys. Rev. B 2017, 95, 54113. [Google Scholar] [CrossRef]
- Kolotova, L.N.; Starikov, S.V. Atomistic simulation of defect formation and structure transitions in U-Mo alloys in swift heavy ion irradiation. J. Nucl. Mater. 2017, 495, 111–117. [Google Scholar] [CrossRef]
- Starikov, S.; Kuksin, A.; Smirnova, D.; Dolgodvorov, A.; Ozrin, V. Multiscale modeling of uranium mononitride: Point defects diffusion, self-diffusion, phase composition. Defect Diffus. Forum 2017, 375, 101–113. [Google Scholar] [CrossRef]
- Starikov, S.V.; Kolotova, L.N.; Kuksin, A.Y.; Smirnova, D.E.; Tseplyaev, V.I. Atomistic simulation of cubic and tetragonal phases of U-Mo alloy: Structure and thermodynamic properties. J. Nucl. Mater. 2018, 499, 451–463. [Google Scholar] [CrossRef]
- Starikov, S.; Korneva, M. Description of phase transitions through accumulation of point defects: UN, UO2 and UC. J. Nucl. Mater. 2018, 510, 373–381. [Google Scholar] [CrossRef]
- Lunev, A.V.; Starikov, S.V.; Aliev, T.N.; Tseplyaev, V.I. Understanding thermally-activated glide of 1/2 110 {110} screw dislocations in UO2—A molecular dynamics analysis. Intern. J. Plast. 2018, 110, 294–305. [Google Scholar] [CrossRef]
- Torres, E.; Kaloni, T.P. Projector augmented-wave pseudopotentials for uranium-based compounds. Comp. Mater. Sci. 2020, 171, 109237. [Google Scholar] [CrossRef]
- Söderlind, P.; Landa, A.; Perron, A.; Sadigh, B.; Heo, T.W. Ground-state and thermodynamical properties of uranium mononitride from anharmonic first-principles theory. Appl. Sci. 2019, 9, 3914. [Google Scholar] [CrossRef]
- Kolotova, L.N.; Starikov, S.V.; Ozrin, V.D. Atomistic simulation of the fission-fragment-induced formation of defects in a uranium–molybdenum alloy. J. Exp. Theor. Phys. 2019, 129, 59–65. [Google Scholar] [CrossRef]
- Castellano, A.; Bottin, F.; Dorado, B.; Bouchet, J. Thermodynamic stabilization of γ-U-Mo alloys: Effect of Mo content and temperature. Phys. Rev. B 2020, 101, 184111. [Google Scholar] [CrossRef]
- Ladygin, V.V.; Korotaev, P.Y.; Yanilkin, A.V.; Shapeev, A.V. Lattice dynamics simulation using machine learning interatomic potentials. Comput. Mater. Sci. 2020, 172, 109333. [Google Scholar] [CrossRef]
- Beeler, B.; Casagranda, A.; Aagesen, L.; Zhang, Y.; Novascone, S. Atomistic calculations of the surface energy as a function of composition and temperature in γ U-Zr to inform fuel performance modeling. J. Nucl. Mater. 2020, 540, 152271. [Google Scholar] [CrossRef]
- Beeler, B.; Andersson, D.; Jiang, C.; Zhang, Y. Ab initio molecular dynamics investigation of point defects in γ-U. J. Nucl. Mater. 2020, 545, 152714. [Google Scholar] [CrossRef]
- Kolotova, L.; Gordeev, I. Structure and phase transition features of monoclinic and tetragonal phases in U–Mo alloys. Crystals 2020, 10, 515. [Google Scholar] [CrossRef]
- Söderlind, P.; Landa, A.; Perron, A.; Moore, E.E.; Wu, C. Thermodynamics of plutonium monocarbide from anharmonic and relativistic theory. Appl. Sci. 2020, 10, 6524. [Google Scholar] [CrossRef]
- Beeler, B.; Mahbuba, K.; Wang, Y.; Jokisaari, A. Determination of thermal expansion, defect formation energy, and defect-induced strain of α-U via ab initio molecular dynamics. Front. Mater. 2021, 8, 661387. [Google Scholar] [CrossRef]
- Migdal, K.; Yanilkin, A. Cold and hot uranium in DFT calculations: Investigation by the GTH pseudopotential, PAW, and APW + lo methods. Comput. Mater. Sci. 2021, 199, 110665. [Google Scholar] [CrossRef]
- Ouyang, W.; Lai, W.; Li, J.; Liu, J.; Liu, B. Atomic simulations of U-Mo under irradiation: A new angular dependent potential. Metals 2021, 11, 1018. [Google Scholar] [CrossRef]
- Söderlind, P.; Yang, L.H.; Landa, A.; Wu, A. Mechanical and thermal properties for uranium and U–6Nb alloy from first-principles theory. Appl. Sci. 2021, 11, 5643. [Google Scholar] [CrossRef]
- Söderlind, P.; Moore, E.E.; Wu, C.J. Thermodynamics modeling for actinide monocarbides and mononitrides from first principles. Appl. Sci. 2022, 12, 728. [Google Scholar] [CrossRef]
- Aly, A.; Beeler, B.; Avramova, M. Ab initio molecular dynamics investigation of γ-(U,Zr) structural and thermal properties as a function of temperature and composition. J. Nucl. Mater. 2022, 561, 153523. [Google Scholar] [CrossRef]
- Flotow, H.E.; Lohr, H.R. The heat capacity and thermodynamic functions of uranium from 5 to 350 K. J. Phys. Chem. 1960, 64, 904–906. [Google Scholar] [CrossRef]
- Jones, W.; Gordon, J.; Long, E. The heat capacities of uranium, uranium trioxide, and uranium dioxide from 15 K to 300 K. J. Chem. Phys. 1952, 20, 695–699. [Google Scholar] [CrossRef]
- Nakamura, J.-I.; Takashi, Y.; Izumi, S.-I.; Kanno, M. Heat capacity of metallic uranium and thorium from 80 to 1000 K. J. Nucl. Mater. 1980, 88, 64–72. [Google Scholar] [CrossRef]
- Grimvall, G. Thermophysical Properties of Materials; Elsevier BV: Amsterdam, The Netherlands, 1999; pp. 157–172. [Google Scholar]
- Konings, R.J.M.; Beneš, O. The thermodynamic properties of the f-elements and their compounds. I. The lanthanide and actinide metals. J. Phys. Chem. Ref. Data 2010, 39, 43102. [Google Scholar] [CrossRef]
- Marchidan, D.I.; Ciopec, M. Enthalpy of uranium to 1500 K by drop calorimetry. J. Chem. Therm. 1976, 8, 691–701. [Google Scholar] [CrossRef]
- Gathers, G. Dynamic methods for investigating thermophysical properties of matter at very high temperatures and pressures. Rep. Prog. Phys. 1986, 86, 341–396. [Google Scholar] [CrossRef]
- Belashchenko, D.K.; Smirnova, D.E.; Ostrovsky, O.I. Molecular-dynamic simulation of the thermophysical properties of liquid uranium. High Temp. 2010, 48, 363–375. [Google Scholar] [CrossRef]
- Souvatzis, P.; Eriksson, O.; Katsnelson, M.I.; Rudin, S.P. Entropy driven stabilization of energetically unstable crystal structures explained from first principles theory. Phys. Rev. Lett. 2008, 100, 95901. [Google Scholar] [CrossRef] [PubMed]
- Söderlind, P.; Landa, A.; Hood, R.Q.; Moore, E.E.; Perron, A.; McKeown, J.T. High-temperature thermodynamics modeling of graphite. Appl. Sci. 2022, 12, 7556. [Google Scholar] [CrossRef]
- Grimvall, G. Spin disorder in paramagnetic fcc iron. Phys. Rev. B 1989, 39, 12300–12301. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y. Classical mean-field approach for thermodynamics: Ab initio thermophysical properties of cerium. Phys. Rev. B 2000, 61, R11863–R11866. [Google Scholar] [CrossRef]
- Grimvall, G.; Häglund, J.; Fernández Guillermet, A. Spin fluctuations in paramagnetic chromium determined from entropy considerations. Phys. Rev. B 1993, 47, 15338–15341. [Google Scholar] [CrossRef]
- Wills, J.M.; Eriksson, O.; Andersson, P.; Delin, A.; Grechnyev, O.; Alouani, M. Full-Potential Electronic Structure Method; Springer Series in Solid-State Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 167. [Google Scholar]
- Sadigh, B.; Kutepov, A.; Landa, A.; Söderlind, P. Assessing relativistic effects and electron correlation in the actinide metals Th-Pu. Appl. Sci. 2019, 9, 5020. [Google Scholar] [CrossRef]
- Söderlind, P. First-principles phase stability, bonding, and electronic structure of actinide metals. J. Electron. Spectr. Rel. Phenom. 2014, 194, 2–7. [Google Scholar] [CrossRef]
- Söderlind, P.; Moore, K.T. When magnetism can stabilize the crystal structure of metals. Scripta Mat. 2008, 59, 1259–1262. [Google Scholar] [CrossRef]
- Söderlind, P.; Landa, A.; Sadigh, B. Density-functional theory for plutonium. Adv. Phys. 2019, 68, 1–47. [Google Scholar] [CrossRef]
- Eriksson, O.; Brooks, M.S.S.; Johansson, B. Orbital polarization in narrow-band systems: Application to volume collapses in light lanthanides. Phys. Rev. B 1990, 41, 7311(R). [Google Scholar] [CrossRef]
- Eschrig, H.; Sargolzaei, M.; Koepernik, K.; Richter, M. Orbital polarization in the Kohn-Sham-Dirac theory. EPL 2005, 72, 611–617. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Saunders, N.; Miodownik, A. CALPHAD Calculation of Phase Diagrams: A Comprehensive Guide; Elsevier Science: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Lukas, H.; Fries, S.; Sundman, B. Computational Thermodynamics: The CALPHAD Method; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Andersson, J.O.; Helander, T.; Höglund, L.; Shi, P.F.; Sundman, B. Thermo-Calc & DICTRA, computational tools for material science. Calphad 2002, 26, 273–312. [Google Scholar]
- Thermo-Calc Software PURE5/Pure Substances Database Version 5. Available online: https://thermocalc.com/products/databases/general-alloys-and-pure-substances/ (accessed on 3 February 2023).
- Dinsdale, A.T. SGTE data for pure elements. Calphad 1991, 15, 317–425. [Google Scholar] [CrossRef]
- Wilson, A.S.; Rundle, R.E. The structures of uranium metal. Acta Cryst. 1949, 2, 126–127. [Google Scholar] [CrossRef]
- Crocombette, J.; Jollet, F.; Nga, L.; Petit, T. Plane-wave pseudopotential study of point defects in uranium dioxide. Phys. Rev. B 2001, 64, 104107. [Google Scholar] [CrossRef]
- Shang, S.L.; Saengdeejing, A.; Mei, Z.G.; Kim, D.E.; Zhang, H.; Ganeshan, S.; Wang, Y.; Liu, Z.K. First-principles calculations of pure elements: Equations of state and elastic stiffness constants. Comp. Mater. Sci. 2010, 48, 813–826. [Google Scholar] [CrossRef]
- Shapiro, A.B.; Summers, L.T.; Eckels, D.J.; Sahai, V. Modeling of Casting Microstructures and Defects; UCRL-ID-128519; LLNL Internal Report: Livermore, CA, USA, 1997. [Google Scholar]
- Rohr, W.G.; Wittenberg, L.J. Density of liquid uranium. J. Phys. Chem. 1970, 74, 1151–1152. [Google Scholar] [CrossRef]
- Moore, G.E.; Kelley, K.K. High-temperature heat contents of uranium, uranium dioxide, and uranium trioxide. J. Am. Chem. Soc. 1947, 69, 2105–2107. [Google Scholar] [CrossRef] [PubMed]
- Ginnings, D.C.; Corruccini, R.J. Heat capacities at high temperatures of uranium, uranium trichloride, and uranium tetrachloride. J. Res. N. B. S. 1947, 39, 309–316. [Google Scholar] [CrossRef]
- Levinson, L.S. Heat content of molten uranium. J. Chem. Phys. 1964, 40, 3584–3585. [Google Scholar] [CrossRef]
- Rand, H.; Kubaschewski, O. Thermochemical Properties of Uranium Compounds; Oliver and Boyd; Ltd.: Edinburgh, Scotland; London, UK, 1963; p. 36. [Google Scholar]
- Fei, Y.; Saxena, S.K. An equation for the heat capacity of solids. Geochim. Cosmochim. Acta 1987, 51, 251–254. [Google Scholar] [CrossRef]
- Holley, C.E., Jr.; Storms, E.K. Thermodynamics of Nuclear Materials; Proc. IAEA.: Vienna, Austria, 1968; p. 411. [Google Scholar]
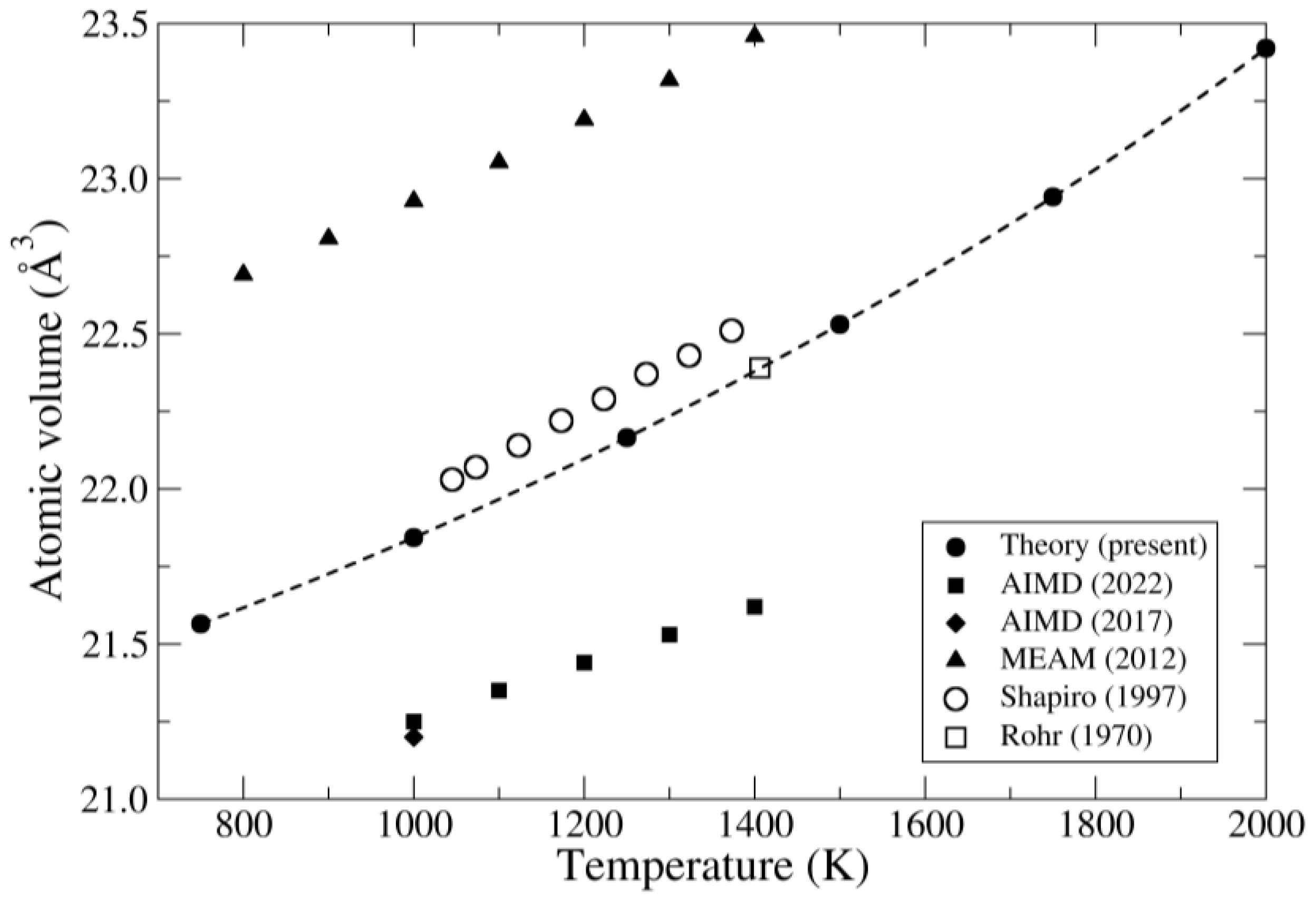

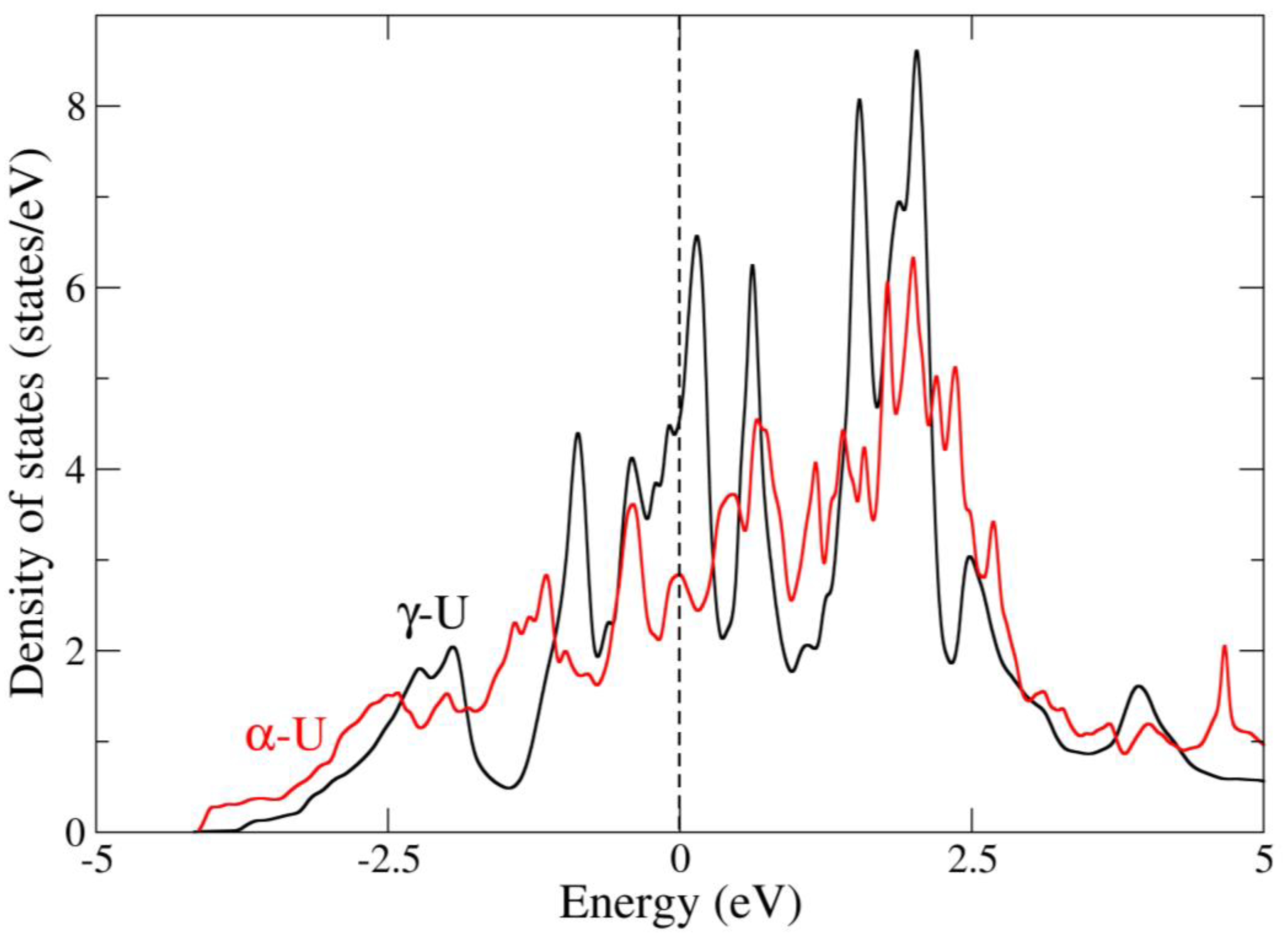

| Method | Atomic Volume (Å3) | Bulk Modulus (GPa) |
|---|---|---|
| MEAM [30] | 21.49 | 115 |
| Pseudopotential [95] | 19.06 | 170 |
| Pseudopotential [19] | 20.18 | 176 |
| Pseudopotential [96] | 20.32 | 133 |
| Pseudopotential [32] | 20.12 | 132 |
| All-electron [15] | 20.76 | 120 |
| All-electron DFT + OP + SCAILD | 21.00 | 114 |
| Experiment [14,94] | 20.89 | 113 |
| Temperature | µspin | µorbital | Fmag | Fel | Flat |
|---|---|---|---|---|---|
| 750 | 0.1150 | −0.0870 | −0.0035 | −0.0053 | −0.4342 |
| 1000 | 0.1383 | −0.1088 | −0.0049 | −0.0239 | −0.6572 |
| 1250 | 0.1580 | −0.1290 | −0.0061 | −0.0470 | −0.9005 |
| 1500 | 0.1740 | −0.1480 | −0.0066 | −0.0738 | −1.1571 |
| 1750 | 0.1860 | −0.1650 | −0.0062 | −0.1041 | −1.4362 |
| 2000 | 0.1950 | −0.1810 | −0.0048 | −0.1372 | −1.7264 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Söderlind, P.; Landa, A.; Moore, E.E.; Perron, A.; Roehling, J.; McKeown, J.T. High-Temperature Thermodynamics of Uranium from Ab Initio Modeling. Appl. Sci. 2023, 13, 2123. https://doi.org/10.3390/app13042123
Söderlind P, Landa A, Moore EE, Perron A, Roehling J, McKeown JT. High-Temperature Thermodynamics of Uranium from Ab Initio Modeling. Applied Sciences. 2023; 13(4):2123. https://doi.org/10.3390/app13042123
Chicago/Turabian StyleSöderlind, Per, Alexander Landa, Emily E. Moore, Aurélien Perron, John Roehling, and Joseph T. McKeown. 2023. "High-Temperature Thermodynamics of Uranium from Ab Initio Modeling" Applied Sciences 13, no. 4: 2123. https://doi.org/10.3390/app13042123
APA StyleSöderlind, P., Landa, A., Moore, E. E., Perron, A., Roehling, J., & McKeown, J. T. (2023). High-Temperature Thermodynamics of Uranium from Ab Initio Modeling. Applied Sciences, 13(4), 2123. https://doi.org/10.3390/app13042123








