Bedload Sediment Transport Estimation in Sand-Bed Rivers Comparing Traditional Methods and Surrogate Technologies

Abstract

Bedload sediment transport in rivers can cause impacts, such as bed erosion/deposition, sandbank formation and changes in flow capacity. Bedload sampling techniques have limitations related to spatial and temporal resolution. These constraints are more relevant in rivers with dunes and high sediment transport. This paper presents a comparison between bedload transport rates estimated with direct and indirect methods in a river with sand dunes. The case study area is a stretch of the Taquari River, in Brazil. Surveys were carried out on three consecutive days, during a flood season. A SonTek M9-ADCP with HydroSurveyor capabilities activated was used to simultaneously measure bathymetry and water velocities throughout a river reach, and also to perform moving-bed tests at six verticals along a predefined cross-section. A mechanical trap (Helley–Smith) was used to collect bedload samples at the same time and positions where the moving-bed tests were performed. Sediment transport was calculated and compared following different approaches: (1) ADCP-BT (Bottom Tracking); (2) modified ISSDOTv2 method (dune tracking); (3) HelleySmith mechanical trap; (4) and five empirical equations. The results showed good agreement between the methodologies, indicating the potential of using ADCPs for hydro sedimentological studies due to the advantages of integrating bathymetry, flow velocity and bedload data.

1. Introduction

Bedload sediment transport in rivers can interfere with hydro-morphodynamic processes, such as bed erosion/deposition, sandbank formation and changes in flow capacity. When these processes become excessive and out of balance, they might affect economic activities, such as waterway navigation, harbor installation and operation, hydroelectric power generation and water supply. It is important to understand the hydro sedimentological behavior, quantifying bedload transport, in order to establish an effective management of sediments and water resources [1].

Several bedload sampling techniques are cited in the literature. Conventional sampling procedures are based on mechanical traps deployed on the river bottom to collect sediment samples at different positions along a cross-section, during a certain time interval [2]. However, these techniques present limited spatial and temporal resolutions and high uncertainties [3]. Conventional sampling is technically difficult, time-consuming, expensive and dangerous during floods. These constraints are even more relevant in rivers with dunes and high sediment transport, as the position of the sampler on the river bottom and the heterogeneous bedload transport affect the measurements [4,5].

Surrogate technologies, such as acoustic Doppler current profilers (ADCP), provide faster and safer measurements with better resolution [6,7,8]. ADCPs were initially developed with the aim of computing water velocities and discharges. However, recent research indicates the ADCP’s potential to estimate bedload rates through a feature called bottom tracking (BT) [8,9,10].

Bottom tracking consists of sending acoustic pulses from slanted ADCP beams that reflect on the river bottom and return to the sensor. The Doppler shift in the frequency of the return pulse is related to the boat’s velocity (when the instrument is mounted on a moving boat). In rivers with a moving-bed (i.e., sediment particles in motion near the bottom), static measurements (named moving-bed tests) allow for computing spatially averaged bed particle velocities. Thereafter, bedload transport rates can be estimated from the product between moving-bed velocities, thickness of the bedload layer and sediment concentration in the bedload layer. This method is herein referred to as ADCP-BT.

Bedload may consist of fine (clays, silts and sand) to coarse (gravels and cobbles) sediment particles. The entrainment and transport of gravel beds are normally more intermittent than sand beds, due to their larger and typically less sorted particle size, providing a more spatially and temporally heterogeneous transport. Nevertheless, the supposed more homogeneous transport in sand-bed rivers tends to be restricted and local due to the transport of bed material as bedforms (ripples and dunes), which increases the spatial-temporal heterogeneity of bedload rates [11].

Additionally, to the application of ADCPs to estimate moving-bed velocities and hence bedload transport rates, the instrument with activated HydroSurveyor capabilities (in the case of SonTek M9-ADCP model) allows the collection of synchronized data of bathymetry and flow velocities, where not only the vertical beam, but also four slanted beams are used to obtain depth information. After detailed and consecutive surveys along a river reach, it is possible to analyze longitudinal bathymetric profiles, and map aggradation and degradation areas. This approach is known as dune tracking, since it evaluates dune migration rates, and has been successfully employed to estimate bedload transport [5,12,13].

Abraham et al. [14] developed a method using the dune tracking approach, which was named ISSDOTv2 (Integrated Section Surface Difference Over Time, Version 2). This method computes bedload based on the difference in time-sequenced three-dimensional bathymetric data. Scour volumes calculated from the difference plots of bed level are related to the average bedload transport due to the dune’s movement. A systemic bias inherent in the methodology is related to dune migration not being captured due to insufficient temporal sampling frequency, which tends to underestimate bedload transport as the time interval between consecutive surveys increases. Shelley et al. [15] implemented a procedure to correct scour volumes and bedload estimates using information about dune characteristics (wavelength, height and celerity) and the time interval between the surveys.

Currently, there is no standard procedure for the identification and discrimination of geometric bedform characteristics. Many researchers apply different methodologies, obtaining variable results, which confirms the present lack of a consistent and nonarbitrary quantitative descriptor of bed morphology. With the aim to fulfill this gap, Gutierrez et al. [16] proposed the application of robust spline filters and continuous wavelet transforms to discriminate these morphodynamic features, allowing for a quantitative recognition of bedform hierarchies. This methodology was applied in this work to reduce subjectivity in establishing the parameter values needed in the ISSDOTv2 correction term (proposed by Shelley et al. [15]).

The present paper shows a comparison between different direct and indirect methods applied to estimate bedload transport rates in a river with sand dunes, during a flood season. Two approaches were carried out using an ADCP: (1) moving-bed tests using the bottom tracking feature; and (2) dune tracking. Moreover, a Helley-Smith (HS) mechanical trap was used to collect bedload samples at six verticals along a predefined cross-section. The field measurements were carried out during one campaign (31 January 2018 to 2 February 2018), on a daily basis, obtaining pairs of data sets for each methodology. Additionally, five empirical transport equations were used with hydraulic and sedimentometric parameters averaged for the river cross-section: Einstein [17], Einstein-Brown [18], Kalinske [19], Meyer-Peter-Müller [20] and Van Rijn [21]. Bedload rates were compared to evaluate the accuracy of all methodologies.

2. Study Site

The Taquari River drains a catchment area of 65,000 km² and is located in the midwestern region of Brazil, in the Upper Paraguay Basin, whose watershed area is approximately 600,000 km², spreads across three countries (Brazil, Bolivia and Paraguay) and includes Pantanal, one of the world’s largest freshwater wetlands (140,000 km² [22]). Known for its biodiversity, Pantanal is considered a World Natural Heritage site by UNESCO, reinforcing the importance of better understanding sediment dynamics in the region.

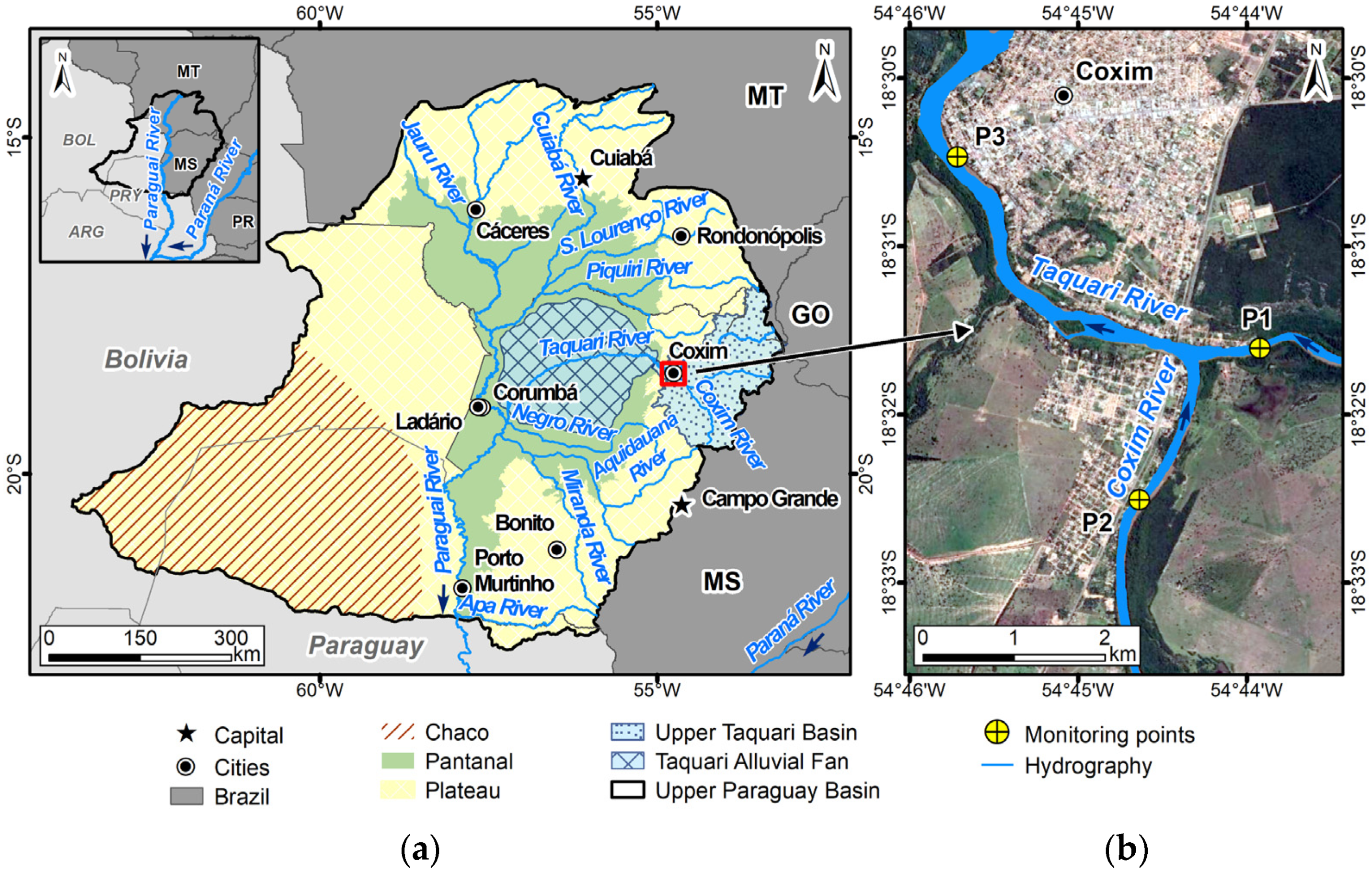
The study site is located in the upper reach of the Taquari River (18°31′36.26″S, 54°43′56.90″W), in the city of Coxim, Brazil. In Figure 1, P1 is the monitored cross-section within the surveyed river reach, P2 is a control point at the Coxim River and P3 is a stream gauging station called Coxim (code 66870000, in the Brazilian National Water and Sanitation Agency) at the Taquari River. Historical data available at P3 include water level, water discharge and cross-section bathymetric profiles.

Sediment transport (in suspension and bedload) in the study area is high during floods, increasing the morphology dynamics and frequently altering the bedforms geometries. At the Coxim gauging station (P3, located 4.5 km downstream of the study site and after the confluence with the Coxim River), the drainage area is 27,600 km² and the annual average discharge is 350 m³/s. Floods normally occur during the summer (December–March), with maximum discharges higher than 1600 m³/s at extreme events. During the drought season (July–September), flow is near 250 m³/s. The annual average rainfall in the region is 1230 mm/year, and the monthly average rainfall during the summer is 200 mm/month.

At the monitored cross-section (P1), during the field campaign, in a flood season, the river width was approximately 110 m, mean water depth was near 2.0 m, mean flow velocity was 1.2 m/s and the water level slope was 15–25 cm/km. The riverbed is mobile, and bedload is formed by fine and medium sand (125 μm < d < 500 μm). Along the 1.0 km surveyed reach, upstream of the confluence of the Taquari and Coxim Rivers, the morphology is dynamic, with the interaction of bars, ripples and dunes of varying sizes.

3. Materials and Methods

3.1. Field Measurements

Hydrodynamics, bedload transport and morphological changes were monitored using an acoustic Doppler current profiler (SonTek M9-ADCP) on 3 consecutive days in the first trimester of 2018. An external real-time kinematic global positioning system (RTK-GPS) was coupled with the ADCP to improve vessel positional precision (subdecimetric in horizontal). The RTK system used was formed by two Leica 1200 GX GNSS dual frequency GPS receivers (L1 and L2) and a Pacific Crest PDL radio. The GPS mobile station was attached to the ADCP through a metal pole, directly above the ADCP sensor. The GPS base station was fixed at a random point on the right margin (approximately 15 m away from the riverbank), tracked throughout the field campaign.

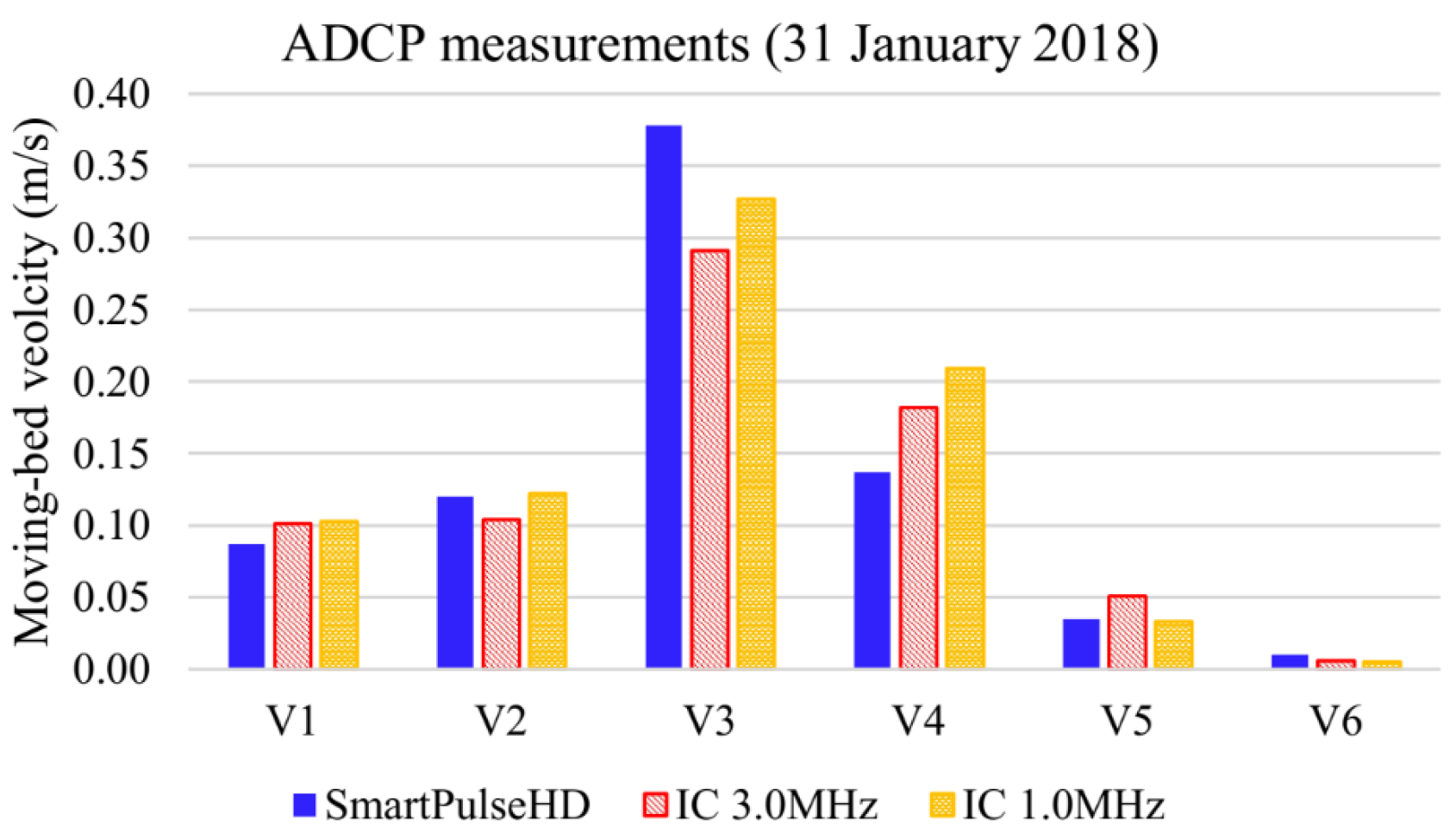
The M9-ADCP was applied to measure water discharges at cross-section P1, following procedures regarding quality control [23]. Static ADCP moving-bed tests were also performed at 6 verticals locations along the cross-section P1 (Figure 2a), to evaluate the average velocity of sediment particles moving close to the riverbed. These results were used to estimate bedload transport rates.

In addition to discharge measurements and moving-bed tests, the ADCP was used for two bathymetric surveys (integrated with simultaneous flow velocity collection), using the HydroSurveyor software capabilities [24]. The surveyed reach was approximately 1 km long (380 m upstream and 620 m downstream of the cross-section P1) (Figure 2b). Each bathymetric survey lasted 3 h and the time interval between them was near 24 h. The collection frequency was 1 Hz, with 5 depth points measured per second (from the ADCP vertical beam and its 4 slanted beams). During the survey, navigation was conducted with longitudinal, transversal and oblique track lines, trying to cover the biggest possible area of the river. At regions of higher river width, e.g., near the confluence with the Coxim River (downstream), the transversal distance between longitudinal track lines reached 30 m. However, near the region where the modified ISSDOT method was applied, the transversal distance was below 20 m.

The distances between consecutive depth points (1 Hz frequency) measured with the ADCP varied according to the boat speed and local depth. Since maximum depths were approximately 5–6 m and boat speed did not exceed 20 km/h (normally less than 15 km/h), the distance between successive measured points was less than one meter (usually some decimeters), with overlapping data due to the 5-beam scheme. The width of each surveyed “swath” varied mainly between 1 m and 3 m.

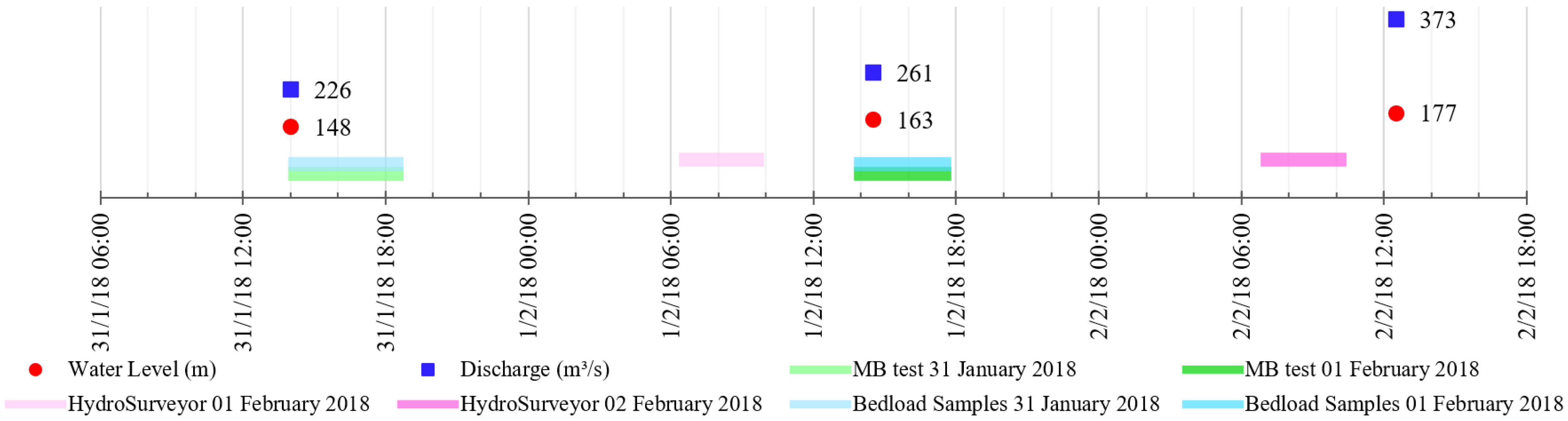
For logistic reasons, it was not possible to conduct all types of surveys (water discharges, moving-bed tests, bathymetry, flow velocities, and bedload samples) on the same days.

Table 1. Surveys carried out during the field campaign.

Survey	Equipment	31 January 2018	1 February 2018	2 February 2018
Water discharges	ADCP + RTK	X	X	X
Moving-bed tests	ADCP + RTK	X	X
Bathymetry	ADCP + RTK		X	X
Flow velocities field	ADCP + RTK		X	X
Bedload samples	Helley-Smith	X	X
Bed material samples	USBM-54	X

“X”—indicates the days when the measurements were made.

and Figure 3 summarize the temporal resolution and the equipment used.

3.2. Digital Elevation Model

After post-processing the bathymetric data (eliminating outliers and smoothing the water level), an underwater digital elevation model (DEM) was generated for each survey day (Figure 4). For this purpose, the processed bathymetry was interpolated in a curvilinear grid with an average resolution of 1.4 m, using methods available on the QuickIn module of the Delft3D software [25]: grid cell averaging, triangular interpolation and internal diffusion. The two DEMs (1 February 2018 and 2 February 2018) were used to investigate and analyze bedforms along the river reach and to extract longitudinal bed elevation profiles (application of the modified ISSDOTv2 method). The justification for the choice of the grid and Delft3D software capabilities was due to subsequent morphodynamical simulations (not shown in this paper).

3.3. Bed Material and Bedload Samples

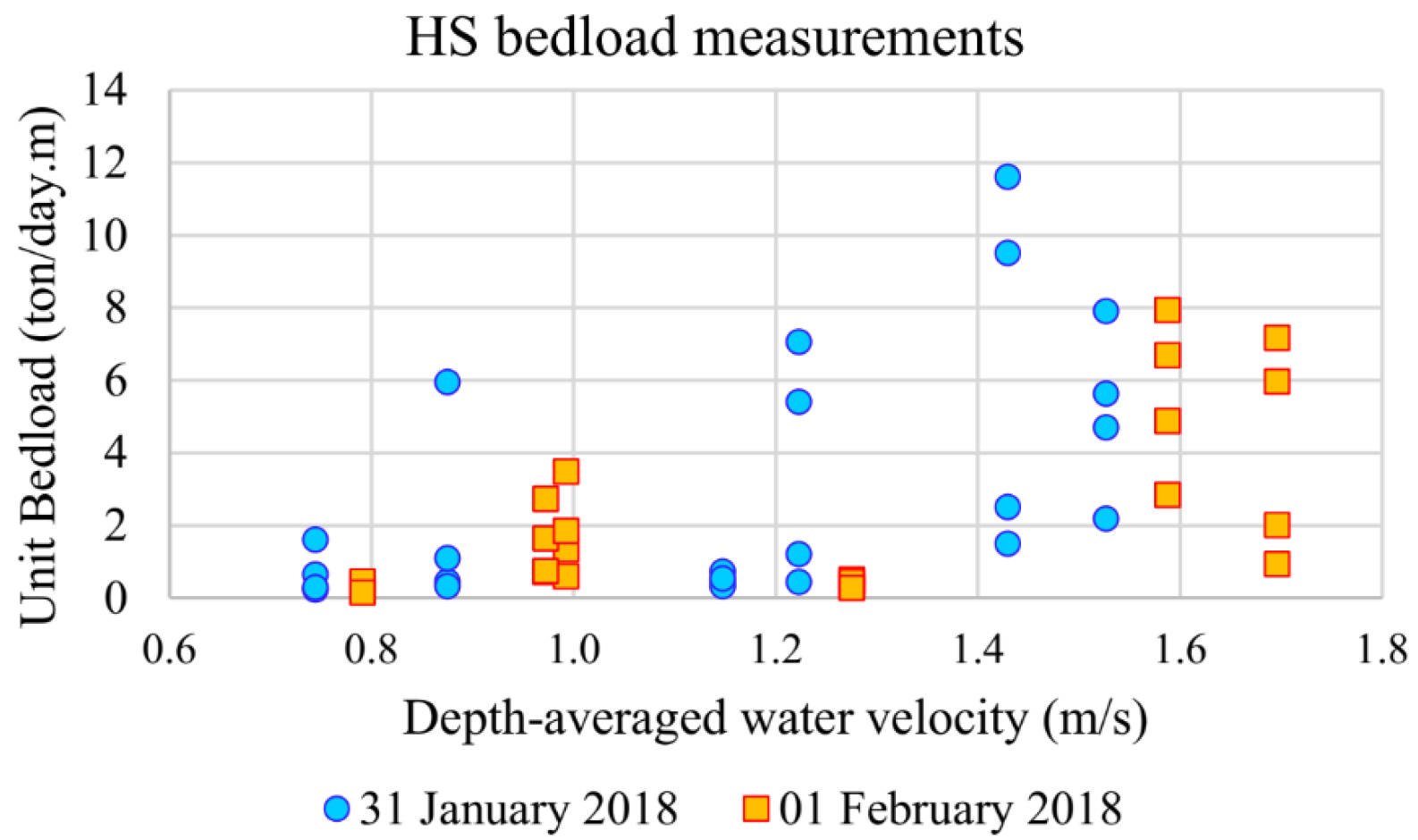
Bed material and bedload samples were collected with an USBM-54 sampler and with a Helley-Smith (HS) mechanical trap, respectively, on two consecutive days. The samplers were handled from an anchored boat at the same 6 verticals at the cross-section P1 where moving-bed tests were performed. The distances between verticals varied from 9 m to 25 m and the duration of each HS sampling was 2 min. Samples were analyzed in a laboratory using laser diffraction technology, and particle size distribution curves were obtained.

In order to reduce the uncertainties associated with the HS sampling, four samples were collected in each vertical. In total, 48 bedload samples were obtained, 24 on each measurement day. Unfortunately, it was not possible to use a video camera to monitor the inlet of sediment into the HS sampler nozzle due to the high turbidity of the river, caused by the high concentration of suspended sediments in the water column. Complementary measurements performed with a USD-49 sampler indicated an average suspended sediment concentration (SSC) of 190 mg/L at 20% of depth and 310 mg/L at 80% of depth, calculated following the filtration method [26].

Therefore, despite the caution during bedload sampling, e.g., slowly lowering and raising the sampler through the water column, it was not possible to monitor the entrainment of sediments into the HS trap. This constraint, thus, hampered the assessment of a potential decrease in the quality and reliability of the bedload samples.

After drying and weighing all 48 sediment samples, unit bedload transport rates at each vertical were computed as the average of 4 daily samples. The total bedload transport at the cross-section was calculated by integrating the unit rates with the increment widths of each vertical.

A method proposed by Frings and Vollmer [3] was applied to estimate the uncertainties related to HS samplings. The uncertainty was determined based on parameters, such as the number of subsections along the cross-section (n_s = 6), the number of samples per subsection (n_m = 4), the temporal-spatial variation of bedload transport (z₁ = 0.15 and z₂ = 8) and the proportion of the total cross-section in which transport occurs (k = 1). From these values, a relative uncertainty of 63% was calculated for HS estimates of total bedload transport. Details about the method can be found in the aforementioned reference.

3.4. Moving-Bed Tests (ADCP-BT)

The ADCP-BT method, also called the kinematic model, computes bedload transport rate based on Equation (1), where $v_{MB}$ is the average moving-bed velocity, ${\delta }_b$ is the thickness of the bedload active layer and $c_b$ is the sediment concentration in the bedload layer [27,28,29].

$$q_{b, ADCP}=v_{MB}·{\delta }_b·c_b$$

(1)

Moving-bed tests (MB) were performed with ADCP to measure $v_{MB}$, using the bottom tracking feature. Measurements were carried out at the same verticals where HS samples were collected. Tests lasted 5 min.

The ADCP-BT method was applied following two different approaches: (1) based on Einstein [17], hereafter called ADCP-BTe; and (2) based on Van Rijn [27], hereafter called ADCP-BTvr. In the ADCP-BTe method, the thickness of the bedload layer (${\delta }_{b\_e}$) in each vertical was adopted as twice the median diameter ($d_{50}$) of HS samples (Equation (2) [17]) and the sediment concentration in the bedload layer ($c_{b\_e}$) followed Equation (3), both classical formulae from the literature [1]. In the ADCP-BTvr method, ${\delta }_{b\_vr}$ and $c_{b\_vr}$ were computed based on the formulations proposed by Van Rijn [27], (Equations (4)–(8)). Density was adopted as ${\rho }_s=2650$ kg/m³ and porosity as $p=0.4$ (usual values for sand [1]).

$${\delta }_{b\_e}=2\times d_{50}$$

(2)

$$c_{b\_e}=\left(1-p\right)\times {\rho }_s$$

(3)

$${\delta }_{b\_vr}=0.3\times d_{50}\times D_{*}^{0.7}\times T^{0.5}$$

(4)

$$D_{*}=d_{50}\times {\left[\frac{\left(s-1\right)g}{{\upsilon }^2}\right]}^{\frac{1}{3}}$$

(5)

$$T=\frac{{\left(u_{*}^{\prime }\right)}^2-{\left(u_{\ast cr}\right)}^2}{{\left(u_{\ast cr}\right)}^2}$$

(6)

$$u_{*}^{\prime }=\frac{\overline{u}}{5.75\times \log \left(\frac{12h}{3d_{90}}\right)}$$

(7)

$$\frac{c_{b\_vr}}{c_0}=0.18\times \frac{T}{D_{*}}$$

(8)

where ${\rho }_s$ is the density of sand (kg/m³); $p$ is the porosity of sand (dimensionless); $D_{*}$ is the dimensionless particle parameter; $T$ is the transport stage parameter (or excess shear parameter) (dimensionless); $\upsilon$ is the kinematic viscosity of water (m²/s); $u_{*}^{\prime }$ is the bed shear velocity related to grains (m/s); $u_{\ast cr}$ is the critical bed shear velocity (m/s) according to Shields; $\overline{u}$ is the depth-averaged flow velocity (m/s); $h$ is the water depth (m); $d_{90}$ represents the grain size (m) of the superficial bed sediment for which 90% of the particles are lower in weight; $c_0$ is the maximum (bed) concentration (=0.65).

Due to the arrangement of the equipment on the boat, it was not possible to track exactly the same point (in each vertical) with the ADCP and the Helley-Smith sampler. This contributes to the uncertainties related to the sampling procedures and the variability of the results. However, the distance between both devices was kept the shortest as possible, not exceeding 3 m. The results of MB tests were used to estimate unit bedload transport rates at the 6 verticals and then integrate them along the cross-section.

3.5. Empirical Formulae

Five empirical formulae (

Table 2. Empirical formulae applied to estimate bedload transport rates.

Reference	Equations
Kalinske [19]	$\frac{q_b}{u_{*}\times d}=10\times {{\Psi }^{\prime }}^2$
Meyer-Peter-Müller [20]	$\varphi ={\left(4\times {\Psi }^{\prime }-0.188\right)}^{3/2}$
Einstein [17]	${\Psi }_E=\frac{\left(s-1\right)\times d}{R\prime \times I}$
	$$\begin{gathered} \hspace{1em}\hspace{1em}\hspace{1em}R\prime ={\left(ks/ks\prime \right)}^{3/2}\times R \\ \varphi vs {\Psi }_E\to see chart in the reference \end{gathered}$$
Einstein-Brown [18]	$\varphi =40\times \Psi {\prime }^3$
Van Rijn [21]	$q_b=0.015\times v\times h\times {\left(d/h\right)}^{1.2}\times M_e^{1.5}$
	$M_e=\frac{v-v_{cr}}{\sqrt{\left(s-1\right)\times g\times d}}$
General formulae	$\varphi =\frac{q_b}{d^{3/2}\times \sqrt{\left(s-1\right)\times g}}$
	$\Psi =\frac{{\tau }_0}{\left(s-1\right)\times \rho \times g\times d}$
	${\Psi }^{\prime }=\frac{{\tau }_0^{\prime }}{\left(s-1\right)\times \rho \times g\times d}={\left(ks/k{s}^{\prime }\right)}^{3/2}\times \Psi =\frac{1}{{\Psi }_E}$
	$q_{b1}=q_b\times {\rho }_s$
	$ks=\frac{1}{n}$
	${\tau }_0=\rho \times g\times R\times I$

) were applied to estimate bedload transport at Taquari River cross-section: Kalinske [19], Meyer-Peter-Müller [20], Einstein [17], Einstein-Brown [18] and Van Rijn [21]. The equations presented at the end of Table 2 are general formulae used to compute some of the parameters needed in the empirical transport equations. From now on, the mentioned methods are referred to by the following acronyms, respectively: K, MPM, E, EB and VR.

All the equations developed by these researchers use information about hydraulic parameters and bed material characteristics to evaluate bedload transport capacity. The values applied in the equations are space and time averaged, showing a more general and simplified approach than other methods that account for local effects. The presented formulae were selected for this study because they have been found to provide accurate bedload transport estimates in large sand rivers with dunes.

In Table 2, $q_b$ is the unit bedload transport rate in volume (m³/s·m); $q_{b1}$ is the unit bedload transport rate in mass (kg/s·m); ${\tau }_0$ is the bed shear stress (N/m²); $u_{*}$ is the shear velocity, also called friction velocity (m/s); $\Psi$ is the shields parameter, also called flow parameter (dimensionless); ${\Psi }^{\prime }$ is the flow parameter related to grains, not influenced by bedforms roughness (dimensionless); ${\Psi }_E$ is the flow parameter used by Einstein, inverse of ${\Psi }^{\prime }$ (dimensionless); $\varphi$ is called transport parameter (dimensionless); the apostrophe $\prime$ refers to the influence of grains, (disregarding bedforms); $g$ is the acceleration due to gravity (m/s²); $d$ is the sediment diameter (m); $\rho$ is the density of water (kg/m³); ${\rho }_s$ is the density of sediments (kg/m³); $I$ is the water surface slope of the study reach (m/m); $h$ is the flow depth (m); $R$ is the hydraulic radius (m) of the cross-section (ratio of the cross-sectional area to the wetted perimeter); $M_e$ is a mobility parameter which represents the excess mobility of sediments (dimensionless); $s$ is the specific gravity of sediments (dimensionless); $v$ is the depth-averaged flow velocity (m/s); $v_{cr}$ is the critical water velocity for currents based on shields (initiation of motion) (m/s); $ks$ is a roughness coefficient of the bed (m^1/3/s), equivalent to the inverse of Manning’s $n$ roughness coefficient (s·m^−1/3).

Kalinske [19] developed a simple theory of bedload transport where the main driver was particle velocity. He assumed that particle velocity adapted instantaneously to fluid velocity (linear relationship), which is the main shortcoming of his approach because of the different processes of particle motion (sliding, rolling and saltating). In his model, bedload transport rate is computed from the volume of particles in motion (per unit streambed area) and their mean velocity.

The Meyer-Peter-Müller formula is normally restricted to 0.4 to 28.6 mm uniform sediments or mixtures in steep rivers with high rates of bedload transport [4,30]. Despite the fact that the data upon which the formula was based were obtained in flows with little or no suspended load, the MPM equation is commonly employed to predict bedload transport in a wide range of fluvial systems, even for flows with appreciable suspended loads.

For Einstein [17], bedload transport reflects the random nature of particle paths and exchanges between the bed and stream. In his approach, the main driver of bedload transport is the number of sediment particles entrained. Although he used probabilistic concepts, his bedload equation is deterministic (and in good agreement with the MPM equation). The concepts of his work are in use today, e.g., bedload transport as an intermittent process, dimensional analysis, probabilities of entrainment and deposition, influence of turbulence on incipient motion [31,32].

The Einstein-Brown formula is a modification developed by H. Rouse, M.C. Boyer and E.M. Laursen of a formula by Einstein [33], presented in Brown [18]. The equation was based on flume data with well-sorted sediments (d = 0.3–28.6 mm). The Einstein and the Einstein-Brown formulae are based on the concept that the fluid forces on the bed sediment fluctuate randomly due to the turbulence of the flow. They consider that a small amount of sediment moves randomly in jumps or steps even when the mean hydraulic forces at the bed are very small, resulting in continuous values of bedload at low transport rates [34].

The Van Rijn [21] formula was developed for particle sizes ranging between 0.2 and 2 mm. The bedload transport model for steady flow proposed by the author is a parameterization of a detailed grain saltation model representing the basic forces acting on a bedload particle. The Van Rijn model is appropriate for rivers transporting sandy sediments in conditions of subcritical flow.

3.6. Modified ISSDOTv2 Method

In rivers with bedforms, dune tracking is considered an effective way for estimating bedload transport. In this case, successive surveys were performed along a longitudinal bathymetric profile and, based on sediment and bedform characteristics, unit bedload was calculated [5,12,35,36].

The integrated section surface difference over time method (ISSDOTv2) uses the scour volumes computed from the difference plots of time-sequenced bathymetric data to estimate bedload transport [14,15,37]. This method is represented by Equation (9), which is mathematically equivalent and dimensionally homogeneous to Equation (10), developed by Richardson et al. [38]. The main advantage of the ISSDOTv2 method is that Equation (9) is applied over a longitudinal profile, while Equation (10) requires averaged wave heights and velocities.

$$q_{b,\mathrm{ISSDOTv}2}=\frac{\left(1-p\right)\times {\rho }_s\times V}{1.82\times \Delta t_{bat}\times N_d}$$

(9)

$$q_b=\frac{\left(1-p\right)\times v_d\times H_d\times {\rho }_s}{2}$$

(10)

where $q_{b,\mathrm{ISSDOTv}2}$ is the bed-material load moving in the sand wave computed by the ISSDOTv2 method (in kg/s); ${\rho }_s$ is the density of sand (=2650 kg/m³); $p$ is the porosity of sand (adopted as 0.4); 1.82 is a constant that accounts for the nontriangular shape of dunes; $N_d$ is the number of dunes along the longitudinal profile; $V$ is the scoured volume (m³) during the time interval $\Delta t_{bat}$ between the bathymetric surveys (s); $v_d$ is the dune speed (celerity, in m/s); and $H_d$ is the dune height (m).

The condition for applying the methodology is that the scoured volumes are equal to (or very close to) the depositional volumes. In rivers, unlike laboratory experiments, this condition is rarely observed, since flow is unsteady and the interaction between turbulence and high shear stresses results in the suspension of bed-material. Some of these suspended sediment particles might travel downstream and deposit on a different dune from which they originated, thus, adding depositional volume to another dune. Abraham et al. [37] recommend scour-deposition ratios between 0.8 and 1.2 (20% variation); otherwise, the profile is considered unsuitable for the method.

Furthermore, a systemic bias inherent in the methodology underestimates the bedload rates. This error is related to the dune celerity and to the time interval between the surveys. In the process of subtracting longitudinal bathymetric profiles, some scour volumes are not computed (triangles C and D in Figure 5). The larger the time interval and the dune celerity, the greater the not computed volumes and the lower the calculated bedload. Shelley et al. [15] proposed a procedure to correct this systemic bias, represented by Equation (11), allowing the application of the ISSDOTv2 method with large time intervals.

$$q_{b,\mathrm{ISSDOTv}2,corr}=q_{b,\mathrm{ISSDOTv}2}+\frac{v_d^2\times \Delta t_{bat}\times H_d}{2\times \lambda }$$

(11)

where $q_{b,\mathrm{ISSDOTv}2,corr}$ is the corrected dune transport rate (kg/s); and $\lambda$ is the dune wavelength (m).

Originally, the ISSDOTv2 method was developed to be applied over longitudinal bathymetric profiles surveyed with multibeam echosounders. The higher spatial resolution of the depth points measured with multibeam yields high accuracy in the interpolated digital elevation models (DEMs), thus, improving the quality of bedload estimates. In the present study, the lower resolution resulting from the ADCP survey (using only 5 beams) increases the uncertainties in the DEMs’ construction and in the subsequent profiles’ extraction. This modified approach, regarding the difference in bathymetric data collection and its spatial resolution, motivated the authors to test a modified ISSDOTv2 method, hereafter called mISSDOTv2.

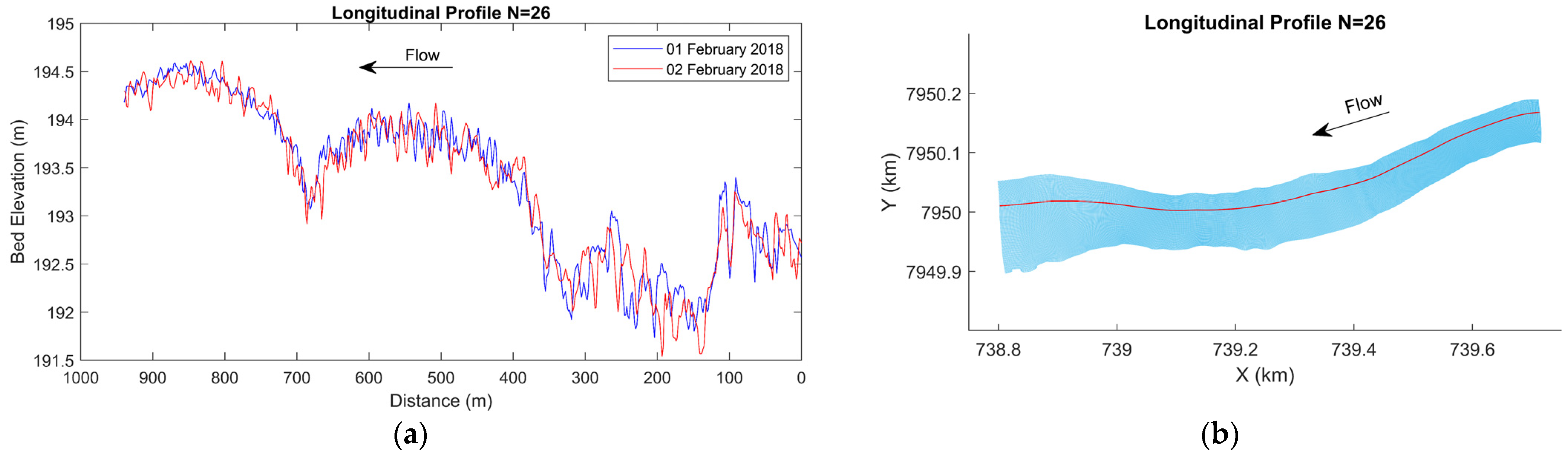
The mISSDOTv2 method was applied in the central region of the study area (Figure 6), in a reach approximately 300 m long and with 85 longitudinal profiles spaced approximately 1.15 m apart. This area comprises the cross-section P1. Only 33 profiles were selected (39%) because they presented scour-deposition ratios within the range of 20% (0.8 to 1.2). Bedload rate was calculated for each selected profile and subsequently corrected according to dune geometric characteristics obtained from wavelet-spline analysis and to the time interval between the bathymetries ($\Delta t_{bat}=24 \mathrm{h}$). The results were extrapolated to the region where profiles were discarded. The total bedload transport at the cross-section was computed by integrating all longitudinal swaths.

3.7. Spline Filters and Wavelet Transforms

Since bedforms can be interpreted as harmonic variations, they can be decomposed through mathematical analysis for waves or oscillatory systems. Available techniques include spectral analysis, moving average smoothing techniques, fractal theory and logistic regression, among others.

In this work, a methodology based on the use of robust spline filters and continuous wavelet transforms to discriminate bedform geometry was applied [16]. This technique overcomes the limitations of the Fourier transform used in spectral analysis, as it can be applied to nonstationary, intermittent, aperiodic, discontinuous, nonlinear and three-dimensional processes, such as riverbed morphology.

The algorithm of the spline filter uses the penalized least squares method and smoothes uniformly sampled data through the discrete cosine transform. The wavelet function used is the Morlet function, which can capture frequencies in the ripple scale (wavelength less than 60 cm), although the measurement resolution is lower.

In this methodology, continuous wavelet analysis is performed on the original signal (bathymetric longitudinal profile: elevation or depth), generating a global wavelet spectrum that provides information about bedform wavelengths with greater frequency and intensity. Then, the spline filter is applied sequentially to the original signal and its derivatives, using the transformed wavelet analysis with the characteristic lengths obtained from the global spectrum to decompose and hierarchize the bedform profile into three categories.

Usually, the first hierarchy corresponds to ripples or small dunes (wavelengths in the order of 5 m), the second hierarchy is associated with medium (10 m) or large (100 m) dunes and the third hierarchy comprises mega-dunes or bars. The sum of the three hierarchies’ signals results in the original signal. More details about the methodology can be found in Gutierrez et al. [16,39] and Torrence and Compo [40].

4. Results

4.1. Discharges, Flow Velocity, Grain Size and DEM

During the field campaign (31 January 2018, 1 February 2018 and 2 February 2018), measurements were carried out at cross-section P1 (Figure 7,

Table 3. Measured and estimated hydraulic parameters at Taquari River, cross-section P1.

Parameters	31 January 2018	1 February 2018	2 February 2018
Water Level (cm)	148	163	177
Discharge (m3/s)	226	261	373
Mean Flow Velocity (m/s)	1.13	1.18	1.33
Cross-Section Area (m2)	200.3	221.4	280.4
Width (m)	101.3	109.4	120.8
Mean Depth (m)	1.98	2.02	2.32
Hydraulic Radius (m)	1.85	1.81	2.30
Water Level Slope (cm/km)	15	25	25
d50 (mm) (bedload)	0.268	0.274	-
d90 (mm) (bedload)	0.397	0.406	-
d50 (mm) (bed material)	0.302	-	-
d90 (mm) (bed material)	0.418	-	-
Transport Stage	11.4	12.5	15.7
Manning’s n (s/m1/3)	0.016	0.020	0.021

). On these days, discharges were 226 m³/s, 261 m³/s and 373 m³/s, respectively. The mean flow velocity varied from 1.1 m/s to 1.3 m/s, mean water depth varied from 2.0 m to 2.3 m and cross-section width was approximately 110 m. Bedload consists of fine sand (125 μm < d < 250 μm) and medium sand (250 μm < d < 500 μm). Figure 8 shows depth-averaged velocities mapped along the river reach after ADCP surveys on two consecutive days.

Figure 9a illustrates a DEM (1 February 2018) of the region where the modified ISSDOTv2 method was applied. By the plot difference of the two DEMs (2 February 2018–1 February 2018), the areas with aggradation and degradation during the time interval between the surveys were identified (Figure 9b). Analyzing the vertical variation at all grid points, 96% of the points presented erosion/deposition heights in the range ±50 cm, and 81% in the range ±25 cm. The distribution of the morphological variation was reasonably symmetrical, with 48% of the points undergoing aggradation and 52% undergoing degradation.

4.2. Unit Bedload Transport

Unit bedload rates were computed at the six verticals along the cross-section P1, where HS samples were collected, and MB tests were performed with ADCP. Despite the highest resolution in water velocities obtained with SmartPulseHD (automatically variable frequency: 1.0 MHz and/or 3.0 MHz), the moving-bed velocities measured with this feature were very similar to those obtained with the two manual configuration schemes (1.0 MHz and 3.0 MHz fixed frequencies). The average standard deviation of measurements performed on 31 January 2018 (Figure 10), for example, was 0.019 m/s. On that day, the highest standard deviation happened in Vertical 3 (Std Dev = 0.044 m/s).

Figure 11 presents the unit bedload rates estimated with HS versus the depth-averaged water velocities measured at each vertical. The low correlation of the plotted data (R = 0.29 for 31 January 2018 and R = 0.44 for 1 February 2018) reinforces the high uncertainties associated with the HS samplings in sand-bed rivers.

Comparing the unit bedload rates based on ADCP-BTe and ADCP-BTvr (Figure 12), there is no trend where one method yields higher bedload rates than the other. For example, at some verticals, the ADCP-BTe unit rates were higher than the ADCP-BTvr estimates, but at other verticals, the opposite happened. This suggests that a compensation of differences exists, influenced by the necessary parameters to apply Equation (1) in each vertical: the thickness of the bedload layer (${\delta }_b$) and the sediment concentration in the bedload layer ($c_b$). In general, the estimates of $c_{b\_vr}$ were lower than $c_{b\_e}$ (which was constant), with an average ratio of 35%. On the other hand, estimates of ${\delta }_{b\_vr}$ were in average twice of ${\delta }_{b\_e}$, with higher deviations observed at the verticals where flow velocities and bedload transport were more intense.

4.3. Bedform Characteristics and mISSDOTv2

After correcting and interpolating the bathymetric data on the curvilinear grid, longitudinal bed profiles were extracted from the underwater DEM. Figure 13 shows a pair of longitudinal bed profiles (at grid position N = 26) of 1 February 2018 (blue) and 2 February 2018 (red). This pair of profiles met the selection criteria for use in the mISSDOTv2 method, i.e., presented erosion-deposition ratios within the range [0.8–1.2]. Inconsistencies observed in some profiles might be related to bathymetric data interpolations on the grid, which is a constraint of the modified ISSDOTv2 in comparison to the original methodology based on multibeam surveys.

Despite the feasibility of identifying bedforms along the illustrated profiles, it is challenging to determine by visual inspection the height, wavelength and celerity of the dunes. Intending to decrease subjectiveness of personal interpretation while determining geometries and dimensions, the methodology developed by Gutierrez et al. [16,39] was applied.

The first wavelet analysis was performed on the original signal (longitudinal bed elevation profile) and generated a global wavelet spectrum indicating the most frequent bedform wavelengths. Figure 14 presents the first step results for the profile N = 26 (1 February 2018). The wavelet power spectrum contours show the spatial distribution of wavelengths (λ), with a 95% confidence interval, and the cone of influence (dashed blue line) discriminates reliable from spurious local power spectrum results. The global wavelet power spectrum indicates the main wavelength frequencies found at the analyzed profile (peaks located to the right of the dotted red line correspond to wavelengths at 95% of the confidence level). Characteristic wavelengths for the presented profile are: 14 m, 32 m, 100 m, 168 m and 387 m.

On the second step, longitudinal bedforms were decomposed and hierarchized based on the wavelengths previously found. Three hierarchies were defined: the first referring to small dunes; the second, associated with medium or large dunes; and the third hierarchy, comprising mega-dunes or bars. Figure 15 illustrates the decomposition of the longitudinal profile N = 26 (1 February 2018).

The results from the wavelet transforms provided information to analytically quantify bedform dimensions so that the mISSDOTv2 method could be applied with the correction term (Equation (11)). Nevertheless, it was necessary to visually assess the dune celerity for each selected longitudinal profile pair, computing the ratio of the distance between the dune’s crests to the time interval of 24 h. As there were many dunes with varying sizes and speeds over a single profile path, it was necessary to average the individual estimates to establish a unique dune celerity value for use in Equation (11). Thus, it was not possible to use the same objectivity as in the wavelet-spline methodology.

The second hierarchy (h_2,3) resulting from the wavelet-spline discrimination was adopted as the bedform reference to evaluate the systemic loss of area and correct the dune transport rate using Equation (11). For each selected profile, one numeric value was determined for each parameter: dune wavelength ($\lambda$), dune height ($H_d$) and dune celerity ($v_d$). The variations observed between the profiles were: 30 < $\lambda$ < 80 (m); 0.2 < $H_d$ < 0.8 (m); 1 < $v_d$ < 20 (m/day). The average area loss of the selected profiles was 35% of the total corrected dune transport rate.

4.4. Total Bedload Transport

The total bedload transport is the mass (or volume) of bedload that passes through a cross-section during a defined time interval. Figure 16a shows the total bedload transport at cross-section P1 computed based on Helley-Smith (HS) samples, moving-bed tests (ADCP-BTe and ADCP-BTvr), the modified ISSDOTv2 method and five empirical equations (K, MPM, E, EB and VR). The predictions were created for the three consecutive survey days. The result of the mISSDOTv2 method (776 tons/day), however, represents the mean bedload transport between the last two days (1 February 2018 and 2 February 2018), since it uses longitudinal profiles from two DEMs generated with bathymetric data measured under two distinct hydraulic conditions.

The average total bedload transport rates of all methods are: 528 ton/day (31 January 2018), 742 ton/day (1 February 2018) and 1182 ton/day (2 February 2018) (Figure 16a). The accuracy of the methods was evaluated in terms of a discrepancy ratio, defined as the ratio of the computed total bedload of each method and the average of all methods. Figure 16b shows the discrepancy ratios as a function of the transport stage (Equation (6)). Several authors consider the methods to give consistent sediment transport rates when the discrepancy ratio is between 0.5 and 2 [4,27,30,41,42,43]. This condition was met for all estimates on the three days, except for the HS measurements, which were probably underestimated.

The lowest sediment transport rates were estimated by HS on the first two days (this method was not applied on the third day) and by the MPM equation on the third day (disregarding the mISSDOTv2 method, which represents the mean bedload between the last two days).

The maximal sediment transport rates on the first two days were accomplished with ADCP-BTe and ADCP-BTvr (which were not applied on the third day). Despite the variations in unit bedload rates computed with these two approaches, the total bedload transport was similar: (A) 31 January 2018–829 tons/day with ADCP-BTe and 794 tons/day with ADCP-BTvr; (B) 1 February 2018–926 tons/day with ADCP-BTe and 1046 tons/day with ADCP-BTvr.

On 2 February 2018, the maximal rate was predicted by the EB equation. When the Shields parameter ($\Psi$) is high, the EB equation begins to consider a portion of the suspended (fine) sediment as bedload (on last day, Shields parameter was calculated as $\Psi =1.3$). This is the main reason for the higher bedload computed on that day, when the discharge severely increased (+43% in relation to the previous day).

5. Discussion

The presence of a sampling device on the river bottom alters the pattern of the flow and sediment transport in its vicinity [44]. The Helley-Smith sampler was developed to perform collections in environments carrying coarse sediments; however, when used in sand-bed rivers (d < 0.5 mm), the samples can be overestimated [45]. For example, samplings with HS at the East Fork River near Pinedale, Wyoming, USA, where particle sizes varied between 0.25 mm and 0.5 mm, were overestimated by 150% [46].

Studies have shown that the effectiveness of HS for bedload sampling is influenced by mesh size [47,48], nozzle wall thickness [49], flow turbulence and bedform dynamics [44]. The position of the device on the river bottom (above or below the bedload layer; and aligned or not with the flow) can cause oversampling or undersampling of bedload rates [50,51]. In rivers with bedforms, the spatial variability of bedload transport is a source of uncertainty for the physical samples, since the bedload rate at a specific cross-section tends to decrease temporally from a maximum near the crest to a minimum in the trough as dunes migrate downstream [52].

Even for pressure-difference samplers with hydraulic efficiency near 100%, the sampling efficiency is affected by errors and uncertainties as mentioned above [53]. Therefore, caution is needed when considering the difficulties of obtaining accurate measurements with mechanical traps, especially when recognizing the drawbacks of the HS sampler when used in sand-bed rivers. Although it was not possible to identify the specific factors that caused the lower rates of the HS estimates in the Taquari River, the magnitude of the computed total transport was useful for comparison with the other methods.

Considering the surrogate method ADCP-BT, it is interesting to point out that Villard et al. [8] have also estimated bedload transport with ADCP (bottom-tracking), testing the Einstein [17] and Van Rijn [27] approaches. After a linear functional analysis comparing bedload estimates from the ADCP-BT method, the Helley-Smith sampler and the Van Rijn formulae [27], they concluded that there was no improvement in either relation, when modeled values (based on Van Rijn [27]) of bedload layer thickness (${\delta }_b$) and bedload concentration ($c_b$) were used.

A possible reason for the high bedload rates estimated with ADCP-BTe is related to $c_b$ determination using Equation (3) with $p=0.4$, which is equivalent to adopting the maximum possible concentration in the bedload layer. Actually, the expected porosity should be higher than 0.4, even with coarser bed particles. The ADCP-BTvr, in turn, considers a bed particle’s saltation height (${\delta }_b$) that, although does exist in sand-bed streams subjected to bed shear velocities, is very small, in the order of a few diameters.

Latosinski et al. [1] assessed bedload rates in a large sand-bed river (Paraná river, in Argentina) using ADCP-BT, combining theoretical parameters and apparent velocity of bed-particles from ADCP. Comparing ADCP-BTe and ADCP-BTvr, they concluded that there is indeed a compensation of differences between the methodologies, in such a way that the ADCP-BTe approach yields better results, even though it lacks a clear physical meaning.

From Villard et al. [8] and Latosinski et al. [1] findings, the adoption of constant values of ${\delta }_b$ and $c_b$ (based on Einstein [17]) seem to be quite appropriate to explore the ADCP-BT capability. The results from the present work at Taquari River endorse this statement, despite the lack of a physically based foundation in the definition of variables.

Regarding the complementary use of the ADCP sensor (exploiting its 5 beams) for collecting bathymetric data should be recognized for its lower spatial resolution in comparison to a multibeam echosounder survey. While errors in depth measurements and RTK-GPS positioning contribute to errors in estimated bed elevations, the interpolation step to create the DEMs is considered to be the dominant source of error [54]. Nonetheless, the presented study intended to test a simpler, cheaper and easier approach to evaluate the capability to estimate bedload transport using a modified ISSDOTv2 method.

The ADCP application (with HydroSurveyor capabilities activated to measure bathymetry) shows great potential, despite the spatial resolution constraints. However, since the bathymetry interpolation applied to create DEMs increases noise and uncertainties in the longitudinal profiles, the application of mISSDOTv2, although promising, must be carried out with caution.

During the field campaign, it was not possible to repeat the bathymetric survey more than once, preventing the establishment of a linear relationship between lost area and time interval to evaluate the computed corrected values [15] in the modified ISSDOTv2 method. During the second bathymetry, the pilot of the boat tried to follow the original track lines, maintaining the boat speed as constant as possible, but in general it was not possible to cover the same exact paths. Then, the visual inspection of longitudinal profile pairs (before interpolation) and the recognition of equivalent dunes at different times were hampered by the limited time-spatial resolution of the ADCP bathymetric surveys.

Two pieces of evidence were considered to evaluate if bedforms traveled less than 50% of their wavelength in the time interval between the consecutive surveys (24 h). The first evidence was based on dune-tracking measurements performed with an ADCP in the Paraná River [55], where bed material and flow velocities are similar to those found at the Taquari River, which resulted in dune velocities of approximately 1 m/day. The second piece of evidence was based on the results of a computational morphological modeling of the study site with the Delft3D software [25]. Simulations were performed, testing different sediment transport formulations and providing longitudinal bed profiles that pointed out that dunes traveled less than 50% of their wavelength in 24 h (Figure 17).

Despite these efforts, it was not possible to guarantee that dunes did not travel more than their wavelength in the 24-h interval between the ADCP surveys. This is the main uncertainty related to the application of the mISSODTv2 in the presented research. Nevertheless, the authors considered it useful to present the results to illustrate the potential of the methodology, and to warn about the necessary precautions. A major piece of advice is to perform several transects along a fixed longitudinal path before the bathymetric surveys, with the aim of recognizing bedform features at different time steps. From the analysis of the distance traveled by these bedforms, the proper time interval between the bathymetric surveys should be chosen, considering the equipment used, the extension of the area, and the local sand wave velocities for a specific hydrologic condition.

It is worth mentioning that the bedload empirical formulations applied in this paper (Table 2) predict the maximum bedload transport rate that a flow in equilibrium can produce, given the local hydraulic and sedimentological conditions. This transport capacity may not be equal to the actual transport if the channel is undergoing aggradation or degradation processes. Since it is not trivial to determine when this capacity is reached, the use of field-measured data to check the validity of bedload transport equations (and vice versa) should be carried out carefully.

Table 4. Advantages and disadvantages of methods applied to estimate bedload sediment transport in sand-bed rivers with bedforms.

Method	Advantages	Disadvantages
Helley-Smith Sampler	Physical sampling allowing bed material analysis. Cheaper instrument.	Limited spatial resolution. Limited temporal resolution. Intrusive method, causing bed disturbance. High uncertainties related to the sampler (hydraulic) efficiency and the sampling efficiency. Time-consuming and dangerous during floods. The representativeness of the sample is affected by the presence of bedforms. Originally developed for environments carrying coarse sediments.
ADCP-BT	Faster and safer measurements. Higher spatial and temporal resolutions compared to physical sampling. Nonintrusive method. Simultaneous measurement of flow velocity at each vertical point. Results are useful to correct water discharges estimates based on the bottom-tracking feature.	The measured average moving-bed velocity is influenced by the ADCP frequency and the acoustic pulse length. The measured average moving-bed velocity is influenced by bedload particle grain size. Uncertainties related to the determination of the parameters: thickness of the bedload active layer and sediment concentration in the bedload layer. The representativeness of the sample is affected by the presence of bedforms. Specialized (and expensive) equipment and trained staff are needed.
Modified ISSDOTv2	Nonintrusive method. Useful in rivers with bedforms. Simultaneous measurement of flow velocities throughout the river reach. The method is applied over longitudinal bathymetric profiles. Bedload estimates tend to be more accurate, since they consider a wide area and the spatial variability of bedload transport.	There must be bedforms (especially dunes). A systemic bias related to dune migration not captured in different time-sequenced 3D bathymetric data must be corrected. Necessity to determine the geometric bedforms characteristics and celerity to correct the scour volumes and bedload estimates. Specialized (and expensive) equipment and trained staff are needed. Require detailed and consecutive surveys along a river reach (time-consuming). Difficulties in consecutively tracking the same boat paths in large rivers. Uncertainties related to the bathymetry resolution (spatial and temporal). Uncertainties related to the interpolation applied to create the digital elevation models (DEMs). Requires that the scoured volumes be equal to the depositional volumes (steady regime).
Empirical Formulae	Easy to implement. Wide use and discussion in the literature.	Field measurements are necessary for the determination of hydraulic and sedimentometric parameters. Parameters are space-time averaged for the river cross-section, not accounting for local effects. Each equation is developed for specific site conditions. The formulations predict the maximum bedload transport rate that a flow in equilibrium can produce.

summarizes the main advantages and disadvantages of the methods analyzed in this paper. As seen, it is not possible to choose one method as the most efficient and recommended of all. Each one has its own constraints and is more suitable for specific conditions concerning economic costs, hydraulic/sedimentologic characteristics, equipment availability, field staff capacity, desired spatial-temporal resolution and hydrological regime.

6. Conclusions

Field measurements were carried out during a flood season on a sand-bed river with high sediment transport (bedload and suspended load), when transport stages were between 11 and 16. A SonTek M9-ADCP was employed for different purposes during the field campaign: (a) measure discharges at the main cross-section; (b) perform moving-bed tests at six verticals along the cross-section; and (c) simultaneously map bathymetry and flow velocities throughout the 1.0-km length of the study reach.

Bedload sediment transport rates were estimated using the following four approaches: (1) physical sampling, using the Helley-Smith mechanical trap; (2) moving-bed tests with ADCP (bottom tracking feature); (3) dune tracking, based on a modified ISSDOTv2 method; and (4) five empirical equations (Einstein [17]; Einstein-Brown [18]; Kalinske [19]; Meyer-Peter and Müller [20]; Van Rijn [21]). Results were consistent, with discrepancy ratios between 0.5 and 2, except for the HS measurements that underestimated the bedload transport.

Data collected with ADCP may be used for purposes other than those used in the present work. Williams et al. [56], for instance, employed dense observations of depths and flow velocities acquired from an ADCP to calibrate and validate a hydrodynamic model implemented for a braided river. In this regard, the data collected at the Taquari River were also used in three-dimensional hydrosedimentological modeling with Delft3D software [25], the results of which are presented in the author’s thesis [57].

The simultaneously collected and spatially distributed depths and flow velocities are extremely useful for mapping hydrodynamic and sedimentological behaviors and increasing our understanding of local physical processes. The application of these datapoints with empirical formulations, such as Van Rijn [21], allows the analysis of bedload transport distribution throughout the monitored area, overcoming the limitations inherent to cross-section averaged estimates. Although this procedure was not shown in this paper, some preliminary results indicate good agreement with the total bedload rates presented here [57].

The calculation of moving-bed particle velocity from the difference in bottom-tracking and RTK-GNSS-derived velocities, for the case when the boat is in motion, is a routine not yet available, neither on RiverSurveyor software nor on HydroSurveyor software. The development of a tool integrated into HydroSurveyor that encompasses this issue would be a great contribution to mapping bedload velocities and their spatial variability throughout a river reach. It was suggested to the ADCP manufacturer.

Another promising approach to estimate bedload rates in rivers with bedforms is the acoustic mapping velocimetry (AMV) method [58]. The technique combines components and processing protocols from two contemporary nonintrusive approaches: acoustic and image-based. The bedform mapping is conducted with acoustic surveys (preferably multibeam-echo soundings), while the estimation of the velocity of the bedforms is obtained with processing techniques pertaining to image-based velocimetry. The bedload rates are then computed by applying Equation (10) [38], where dune heights can be calculated manually and individually for each dune or by using an automated technique [59].