A Robust Intelligent Controller for Autonomous Ground Vehicle Longitudinal Dynamics

Abstract

In this paper, a novel adaptive sliding mode controller (SMC) was designed based on a robust law considering disturbances and uncertainties for autonomous ground vehicle (AGV) longitudinal dynamics. The robust law was utilized in an innovative method involving the upper bounds of disturbances and uncertainties. Estimating this lumped uncertainty upper limit based on a neural network approach allowed its online knowledge. It guided the controller to withstand the disturbance and to compensate for the uncertainties. A stability analysis, according to Lyapunov, was completed to confirm the asymptotic convergence of the states to the desired state. The effectiveness and benefits of the planned approach were scrutinized by simulations and comparative studies.

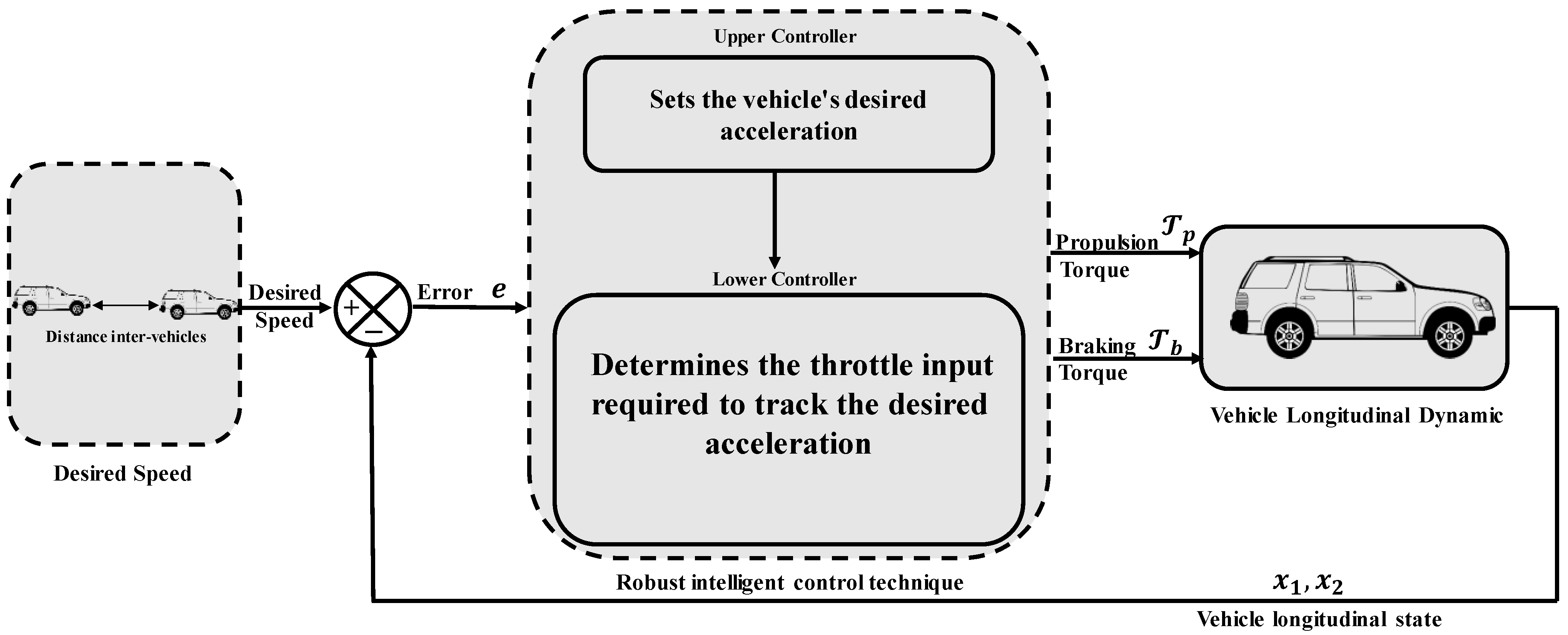
1. Introduction

The current huge jump in self-driving stems from evolutionary development since the birth of the autonomous-driving concept. This concept is based not only on the substitution of the human driver but also a reduction in fatal accidents due to human factors. Indeed, carmakers search to meet the challenge by designing sophisticated and fully automated guidance systems. The development of an autonomous vehicle involves three key phases: environment perception, path planning, and path tracking [1]. The first phase permits one to perceive the vehicle’s external surroundings; the second phase exploits the data issued from the first phase, while the third phase is charged with decision-making. In other words, it tries to impose on the vehicle dynamics the path arising from the second phase. The third phase focuses on the control systems, which are in charge of tracking the target path and enforcing it on the vehicle. The fundamental mission of the control unit is to maintain the vehicle’s dynamic stability. This unit has two layers; the first is dedicated to the control algorithm, and the second is dedicated to the actuators. The latter is responsible for the execution of the orders issued by the first layer. These orders are algorithms that concern lateral and longitudinal control [2].

The concepts and physics of longitudinal vehicle control strategies have been studied since the late 1960s. Various longitudinal control approaches have been elaborated [3]. Longitudinal control can be characterized as the system of control strategies that are applied to control the behavior of a vehicle on its longitudinal trajectory via the various actuators assigned to acceleration and braking [4]. These longitudinal control techniques target advanced driver assistance system (ADAS) features. Adaptive cruise control (ACC) and intelligent speed assistance (ISA) are ADAS features that are relevant to longitudinal control. As mentioned earlier, the nucleus of the control is either based on conventional control theory approaches, strategies based on automatic learning theory, or a combination of both.

Autonomous ground vehicles (AGV) longitudinal dynamics are a long-standing challenge in the automotive area. A variety of control methods are offered; the sliding mode control (SMC) is recognized as the dominant approach to controlling the dynamics of autonomous systems in general [5,6,7,8] and AGVs in particular [1,9,10]. In this light, the authors of [11] offered a second-order sliding mode controller. This technique has been used to conceive a longitudinal controller that can adjust the inter-obstacle distance. Experimental tests have been conducted to verify the effectiveness of this approach. This study addressed the improvement of the ACC and stop-and-go features of ADASs. In the same vein, the authors of [12] intended to provide the best control performances of the ACC feature based on an optimal super-twisting sliding mode control design. In a similar fashion, sliding mode control combined with a fuzzy control technique was elaborated in [13]. The SMC drove the vehicle from a random primary position to a potential parking place. At the same time, the fuzzy controller took over to park the vehicle in this desired position. This strategy was designed to improve autonomous parking algorithms. A backstepping controller merged with an extended Luenberger observer was discussed in [14]. Based on a quarter-vehicle model, the states observer provided online estimations of the brake torque, angular wheel speed, and vehicle speed. This design was intended to enhance the performance of the antilock braking system (ABS). An MPC tracking algorithm incorporating longitudinal velocity compensation to minimize tracking error and ensure vehicle stability was discussed in [15]. This method managed the lateral and longitudinal dynamics concurrently to achieve the vehicle’s complete stability.

Over and above conventional proposals, combinations of deterministic and intelligent methods are omnipresent in the literature. The authors of [16] proposed beetle antenna searching (BAS) and particle swarm optimization (PSO) algorithms to determine the appropriate PID parameter settings to control a dual-wheel AGV robot. In the same vein, an intelligent approach based on an optimization technique was proposed in [17]. The butterfly optimization algorithm (BOA) was used to set the optimal parameters of a PID controller. A coupled strategy including an EMRAN architecture with an extended Kalman filter, PID cruise, and a Stanley controller was suggested in [18]. This EMRAN-based method’s performance concerning RMS tracking errors has shown its superiority over the Stanley controller, fuzzy-based PID, and conventional PID. On top of providing great robustness, the EMRAN-assisted controller has demonstrated its ability to cope in extreme situations. This process focused on the improvement of ADASs’ ACC feature. An intelligent robust adaptive exponential-like sliding mode was offered by [19]. A type-2 fuzzy neural network (T2FNN) was proposed to estimate the unidentified vehicle dynamics. The T2FNN-based hierarchical controller aiming at the closed-loop stability of the system has guaranteed the convergence of the heading error to zero. Intelligent high-speed trains incorporating backstepping control and deep learning were investigated in [20]. A long short-term memory network (LSTM) merged with a fully connected neural network has been utilized. The approach has presented an excellent follow-up of the high-speed profile while providing a suitable steady-state separation within the safety band. This technique aims at improving the ACC feature. To innovate within the scope of the same function, a hybrid structure combining the PID, MPC, and adaptive-network fuzzy inference system (ANFIS) was provided in [21]. This technique exhibited a good indicator in terms of acceleration comfort due to being less aggressive than the other controllers involved in this study; moreover, its tracking error reached 95% of the reference. Beyond that, the ANFIS controller showed an average error of 0.07 m/s² when the acceleration was at its maximum. The authors of [22] proposed a multi-objective model predictive control (MPC) design targeting improving a vehicle’s active suspension control. The proposed approach has shown promising results through experimental tests related to the suspension system on a quarter car in laboratory conditions. A combination of MPC, feedforward, and PID feedback was discussed in [23]. MPC was designed to determine longitudinal acceleration under the driver’s expectations. The built-in PID feedback and anticipation were adopted to ensure the desired longitudinal acceleration tracking by acting on the longitudinal actuators; this approach aimed to contribute to the ACC feature of ADASs. Along the same lines, [24] discussed a self-organizing neuro-fuzzy controller. This intelligent technique incorporated a neural network and a fuzzy system to automatically adapt the vehicle’s speed by learning from the human pilot and utilizing anticipation. This process targeted the innovation at the level of the ISA feature of the ADAS. The authors of [25] sought to address the contribution to the autonomous emergency braking (AEB) feature through the proposed approach of a PID and a Kalman filter. This strategy aimed to determine adequate speed profiles to prevent collisions.

For low-friction roads, a single neural PID combined with a Kalman filter was offered to find the maximum deceleration, whereas for high-friction roads the desired deceleration was achieved according to comfort and safety. This approach was presented as a non-traditional AEB model. The authors of [26] discussed a radial basis functions neural network (RBNN)-based SMC control structure that contributed to both ACC and ISA. In this study, the upper limit of disturbance was estimated with the RBNN. On this basis, the SMC was deployed to design a longitudinal velocity controller. The combination has proven its superiority, with an average tracking error of 0.718 kph in various driving conditions. Moreover, the RBNN was deployed by [27] in order to design an intelligent braking system while contributing to the brake assist system (BA) as an ADAS feature. A self-adaptive PID using the RBNN was proposed by [28] for improving the ACC and stop-and-go features. The vehicle dynamic model utilized in this study included an engine model, a transmission system model, and a brake model. This approach has proven to be very reliable, with low-speed tracking errors of less than 0.203 (m/s), which leads to better driving comfort. In addition, a hybrid solution involving the mentioned NN algorithm and a fuzzy system was investigated in [29] by designing an ANFIS strategy to diagnose centrifugal pumps’ fault types.

Famous for its ability to approximate and identify nonlinear quantities in modeling and control, the RBNN is widely involved in different aspects of AGV control. The vast majority of these studies focused on contributing to lateral stability issues [1,18,30,31]. Notwithstanding its utility for longitudinal control purposes, it remains underutilized, with a tiny portion of the research addressing the longitudinal control of the AGVs. Consequently, this study was intended to bridge this gap by suggesting a novel robust intelligent control technique for addressing AGV longitudinal dynamics.

This study proposes an adaptive SMC law taking advantage of the RBNN for the robust stability of AGV longitudinal dynamics, considering uncertainties and external disturbances. The salient distinguishing points of this research are as follows:

• The proposed design contributes to the ADASs in general and ACC with ISA in particular.
• An adaptive control design provides disturbance rejection and uncertainty compensation.
• The novel robust law is a function of the upper bounds of lumped uncertainties and does not require any prior knowledge of the latter.
• An immediate adaptation identifies the upper bounds of perturbations and uncertainties via estimating the neural architecture’s parameters.

The current study is arranged as follows: The vehicle modeling is displayed in Section 2. The proposed control strategy, with the necessary derivations and stability proof, is specified in Section 3. Section 4 exemplifies the performance of the suggested method through a simulation study. A conclusion is then reached in Section 5.

2. Vehicle Modeling

As a vehicle is in motion, it is exposed to the following extraneous longitudinal forces: longitudinal tire grip forces, aerodynamic drag forces, climbing resistance forces, and rolling resistance forces (see Figure 1).

The aggregate effect of the forces along the vehicle’s longitudinal axis is expressed as follows:

$$m\ddot{x}={\mathfrak{f}}_{xf}+{\mathfrak{f}}_{xr}-{\mathfrak{f}}_{aero}-{\mathcal{R}}_{xf}-{\mathcal{R}}_{xr}-mgsin\left(\theta \right)$$

(1)

where ${\mathfrak{f}}_{xf}$ and ${\mathfrak{f}}_{xr}$ are the longitudinal forces arising from the encounter between the tire and the road, ${\mathfrak{f}}_{aero}$ is the longitudinal aerodynamic drag force, and ${\mathcal{R}}_{xf}$ and ${\mathcal{R}}_{xr}$ are the forces resulting from the rolling resistance of the front and rear tires, respectively. $m$ is the vehicle mass, $g$ is the acceleration caused by gravity, and $\theta$ is the road’s angle of inclination.

2.1. Longitudinal Aerodynamic Drag Force

The following expression describes the aerodynamic drag force:

$${\mathfrak{f}}_{aero}=\frac{1}{2}\rho c_{ad}{\mathcal{A}}_f{\left({\upsilon }_w\pm {\upsilon }_x\right)}^2$$

(2)

where $\rho$ is the air density, $c_{ad}$ is the coefficient of aerodynamic drag, ${\mathcal{A}}_f$ is the area of the vehicle’s front surface, ${\upsilon }_w$ is the wind velocity, and ${\upsilon }_x$ denotes the vehicle’s longitudinal velocity.

2.2. Rolling Resistance

Typically, rolling resistance is denominated as having an approximate proportional dependence on the vertical force exerted on each tire [32].

$${\mathcal{R}}_{xf}=\mathcal{F}\left({\mathfrak{f}}_{zf},r_{sat},{\upsilon }_x\right)$$

(3)

$${\mathcal{R}}_{xr}=\mathcal{F}\left({\mathfrak{f}}_{zr},r_{sat},{\upsilon }_x\right)$$

(4)

where ${\mathfrak{f}}_{zf}$ and ${\mathfrak{f}}_{zr}$ are the vertical forces and $r_{sat}$ is the tire’s statically loaded radius.

2.3. Longitudinal Tire Forces

The literature provides a spectrum of the longitudinal force of nonlinear tire models such as Pacejka, Dugoff, and others [32,33]. These models were developed via half-empirical or empirical studies that have given a mathematical characterization of the tire/road contact forces along the longitudinal direction and are expressed in terms of the slip rate, the coefficient of friction, and the normal load.

Pacejcka’s model remains the most widely used model since it gives an in-depth description of the tire–road interaction via the magic formula described below:

$${\mathfrak{f}}_{xf}=\mu {\mathfrak{f}}_z{}_{f,r}\sin \left(C_{x_{f,r}}{\tan }^{-1}\left(B_{x_{f,r}}{\mathcal{S}}_{x_{f,r}}-E_{x_{fr}}\left(\begin{array}{l}{B}_{x_{f,r}}{\mathcal{S}}_{x_{f,r}}\\ -{\tan }^{-1}{B}_{x_{f,r}}{\mathcal{S}}_{x_{f,r}}\end{array}\right)\right)\right)$$

(5)

where $\mu$ is the friction coefficient, ${\mathfrak{f}}_z$ indicates the vertical forces, and ${\mathcal{S}}_{xf}$ and ${\mathcal{S}}_{xr}$ denote the front and rear longitudinal pure slip ratio, respectively. For a complete overview, the reader can follow [34,35].

Using Equation (5), the nonlinear behavior of the longitudinal contact forces is plotted in Figure 2 for different vertical forces and a range of longitudinal slip ratio values from −100% to +100%. This figure demonstrates that the relation between the longitudinal contact forces and the longitudinal slip is linear in the area indicated by the two dotted straight lines. The proportionality coefficients ${\complement }_{xf}$ and ${\complement }_{xr}$ are the longitudinal tire stiffness values related to the front and rear tires. These linear relationships, which will be opted for in the following section, can be expressed as:

$${\mathfrak{f}}_{xf}={\complement }_{xf}{\mathcal{S}}_{xf}$$

(6)

$${\mathfrak{f}}_{xr}={\complement }_{xr}{\mathcal{S}}_{xr}$$

(7)

2.4. Simplified Vehicle Longitudinal Model

To synthesize the controllers, the bicycle model, which presents a simplified version of the four-wheel model, is often used (see Figure 3).

By considering only of the vehicle’s front wheel, using Equation (1) the bicycle model front-wheel dynamics are expressed as [34]:

$${\mathfrak{l}}_{\mathcal{W}}{\dot{\mathcal{W}}}_f=-{\mathfrak{f}}_{xf} {\mathfrak{r}}_w+{\mathcal{T}}_p-{\mathcal{T}}_b$$

(8)

where ${\mathcal{W}}_f$ is front-wheel rotation speed, ${\mathfrak{l}}_{\mathcal{W}}$ is the front-wheel moment of inertia, ${\mathfrak{r}}_w$ is the front-wheel radius, and ${\mathcal{T}}_p$ and ${\mathcal{T}}_b$ are the propulsion and braking torque, respectively.

From Equation (9), we can write ${\mathfrak{f}}_{xf}$ as:

$${\mathfrak{f}}_{xf}=\frac{1}{{\mathfrak{r}}_w}\left({\mathcal{T}}_p-{\mathcal{T}}_b-{\mathfrak{l}}_{\mathcal{W}}{\dot{\mathcal{W}}}_f\right)$$

(9)

Based on the hypothesis defined in [34], Equations (10) and (11) are given:

$${\upsilon }_x={\mathfrak{r}}_w{\mathcal{W}}_f$$

$${\mathcal{W}}_f={\mathfrak{r}}_g{\mathcal{W}}_e$$

(10)

$${\mathcal{T}}_e={\mathfrak{r}}_g{\mathcal{T}}_p$$

(11)

where ${\mathfrak{r}}_g$ denotes the transmission gear ratio, ${\mathcal{W}}_e$ is the engine speed, and ${\mathcal{T}}_e$ is the engine torque.

Based on Equations (9)–(11), Equation (1), which represents the longitudinal vehicle dynamics, is written as:

$$\ddot{x}=-\frac{{\mathfrak{r}}_w}{m{\mathfrak{r}}_w^2+{\mathfrak{l}}_{\mathcal{W}}}\left({\mathcal{T}}_p+{\mathfrak{r}}_w\left({\mathfrak{f}}_{aero}+{\mathcal{R}}_{xf}+mg\sin \theta \right)\right)+\frac{{\mathfrak{r}}_w}{{\mathfrak{r}}_g\left(m{\mathfrak{r}}_w^2+{\mathfrak{l}}_{\mathcal{W}}\right)}{\mathcal{T}}_e$$

(12)

3. Controller Development

3.1. Motivation

In the nonlinear systems control area, neural network controllers (NNCs) are generally made by a combination of classical or modern control techniques and neural network algorithms. This hybrid structure was initially proposed by Kawato et al. and Psaltis et al. in 1988 [36,37,38]. Since then, a torrent of NNCs have been introduced in the literature, especially in robotics [39,40,41]. Based on the ANN algorithms, the NNCs are often used to identify or approximate unmodeled dynamics, nonlinearities, unmeasurable noise, and multi-loops [42]. However, for autonomous vehicle control, the challenges of designing an intelligent control structure are attracting considerable attention from researchers. In this context, a design of longitudinal control approaches based on neural networks is elaborated in the following subsections.

3.2. Problem Formulation

In view of preparing the vehicle model for the controller development as well as the expression arrangement, the following re-expression was chosen:

$$\begin{array}{l} {\dot{x}}_1=\dot{x}\\ {\dot{x}}_2=\mathcal{F}\left(x,t\right)+\mathfrak{S}\left(x,t\right)\mathfrak{U}+\mathfrak{O}\left(x,t\right) \end{array}$$

(13)

with

$$\begin{array}{l} \mathcal{F}\left(x,t\right)=-\frac{{\mathfrak{r}}_w}{m{\mathfrak{r}}_w^2+{\mathfrak{l}}_{\mathcal{W}}}\left({\mathcal{T}}_p+{\mathfrak{r}}_w\left(\frac{1}{2}\rho c_{ad}{\dot{x}}_1{}^2+{\mathcal{R}}_{xf}+mgsin\theta \right)\right)\\ \mathfrak{S}\left(x,t\right)=\frac{{\mathfrak{r}}_w}{{\mathfrak{r}}_g\left(m{\mathfrak{r}}_w^2+{\mathfrak{l}}_{\mathcal{W}}\right)}\end{array}$$

Remark 1.

The  $\mathfrak{S}$ function depends on the vehicle’s speed via the change in the transmission ratio (${\mathfrak{r}}_g$), as described in Equations (11) and (12). Therefore, it is set, $\mathfrak{S}\left(x,t\right)$, as a function of longitudinal position and time.

$x$ is the longitudinal position, $\mathfrak{U}$ is the control input, and $\mathfrak{O}\left(x,t\right)$ is the vehicle uncertainty and the outdoor disturbances. This lumped uncertainty of the vehicle, $\mathfrak{O}\left(x,t\right)$, is considered to be constrained by a positive upper limit value ($\mathfrak{M}$), as follows:

$$\mathfrak{O}\left(x,t\right)\le \mathfrak{M}$$

(14)

3.3. Robust Adaptive RBNN-SMC

3.3.1. Sliding Surfaces

Based on the tracking error ($e$), the sliding surface ($\mathcal{Z}$) is given as:

$$\begin{gathered} e\left(t\right)=x_d-x \\ \mathcal{Z}\left(t\right)=\mathfrak{p}e+\dot{e} \end{gathered}$$

(15)

where $\mathfrak{p}$ is a positive constant.

3.3.2. Equivalent Control Law

After forcing the sliding surface’s time derivative to zero, the equivalent law is given as:

$${\mathfrak{U}}_{eq}=-\frac{\mathfrak{p}\dot{e}+\mathcal{F}\left(x,t\right)}{\mathfrak{S}\left(x,t\right)}$$

(16)

3.3.3. Robust Law

To accommodate disturbances and parametric uncertainties, a robust law is given in terms of the upper limit of lumped uncertainty, as follows:

$${\mathfrak{U}}_r=\frac{1}{\mathfrak{S}\left(x,t\right)}\left(-q\mathcal{Z}-\mathcal{K}sign\left(\mathcal{Z}\right)\right)$$

(17)

where $q$ and $\mathcal{K}$ indicate the switching gains and $\mathcal{K}$ is chosen as [43,44] $\mathcal{K}=\mathfrak{M}+o$, where $\mathfrak{M}$ is the upper limit of the lumped uncertainty, given in [43], and $o$ is a positive constant.

The idea of designing a control law considering the upper limits of disturbances and uncertainties is insufficient to guarantee high performance against real non-static disturbances. To solve this problem, a neuronal architecture was adopted to approximate the upper limit ($\mathfrak{M}$) depending on the variation in these critical factors. Hence, the subdivision of the robust law (${\mathfrak{U}}_r$) into two terms, ${\mathfrak{U}}_{sw}$ and ${\mathfrak{U}}_{rbnn}$, was as follows:

$$\left\{\begin{array}{l}{\mathfrak{U}}_r={\mathfrak{U}}_{sw}+{\mathfrak{U}}_{rbnn}\\ {\mathfrak{U}}_{sw}=\frac{1}{\mathfrak{S}\left(x,t\right)}\left(-q\mathcal{Z}-osign\left(\mathcal{Z}\right)\right)\\ {\mathfrak{U}}_{rbnn}= \frac{-\widehat{\mathfrak{M}}sign\left(\mathcal{Z}\right)}{\mathfrak{S}\left(x,t\right)}\end{array}\right.$$

(18)

As it is expressed in the Equation (18), the term ${\mathfrak{U}}_{rbnn}$ contains the approximation of the lumped uncertainty upper bound by the RBNN, as described in Figure 4.

$\widehat{\mathfrak{M}}$ is the output of RBNN and presents the estimation of $\mathfrak{M}$ according to the expression

$$\widehat{\mathfrak{M}}\left(\mathcal{Z},\mathfrak{y},c\right)={{\displaystyle \sum }}_{j=1}^n{\widehat{\omega }}_j{\mathcal{H}}_j(\mathcal{Z})={\widehat{\omega }}^T\mathcal{H}\left(\mathcal{Z}\right)$$

(19)

where $\mathcal{H}$ is the Gaussian activation function constituted by the radial basis function defined as

$${\mathcal{H}}_j\left(\mathcal{Z}\right)=e^{\left(-\frac{{\left(\mathcal{Z}-{\mathfrak{y}}_j\right)}^2}{ c_j^2}\right)}, j=1,2\dots n$$

(20)

The input of the RBNN structure is the sliding variable $\mathcal{Z}$. Each hidden node has a center parameter vector and an input vector of the same dimension.

On the other hand, $\mathfrak{M}$ can be expressed using RBNN’s ideal parameters ${\omega }^{*}$, ${\mathfrak{y}}^{*}$, and $c^{*}$, given as [42,45]:

$$\mathfrak{M}={\mathfrak{M}}^{*}+{\gimel }_1={\omega }^{*}{}^T{\mathcal{H}}^{*}\left(\mathcal{Z}\right)+{\gimel }_2$$

(21)

${\gimel }_1$ denotes the approximation error of the RBNN, which is assumed to be limited by the non-zero positive constant ${\gimel }_n$ as $\left|{\gimel }_1\right|<{\gimel }_n$ [42,45].

The estimated weight vector ($\widehat{\omega }$), the estimated center vector ($\widehat{\mathfrak{y}}$), and the estimated width vector ($\widehat{c}$) are defined as

$$\widehat{\omega }=\left[\begin{array}{c}\begin{array}{c}{\widehat{\omega }}_1\\ {\widehat{\omega }}_2\\ ..\\ {\widehat{\omega }}_n\end{array}\end{array}\right];\mathcal{H}=\left[\begin{array}{c}{\mathcal{H}}_1\\ {\mathcal{H}}_2\\ ..\\ {\mathcal{H}}_n\end{array}\right];\widehat{c}=\left[\begin{array}{c}{\widehat{c}}_1\\ {\widehat{c}}_2\\ ..\\ {\widehat{c}}_n\end{array}\right]$$

(22)

where $n$ is the hidden-layer node number.

Obtaining the expression allows the adaptation of the parameters $\widehat{\omega }$, $\widehat{\mathfrak{y}}$, and $\widehat{c}$, which provides the adjustment of $\mathfrak{M}$ according to external factors and uncertainties. To achieve this, the Gaussian function is linearized as in [46]. This leads to the differentiation of Equation (20) as:

$$\mathsf{\Delta }{\widehat{\mathfrak{M}}}_j\left(\mathcal{Z}\right)=\mathsf{\Delta }{\widehat{\omega }}_j{\mathcal{H}}_j\left(\mathcal{Z}\right)+{\widehat{\omega }}_j\frac{\partial {\mathcal{H}}_j}{\partial {\widehat{\mathfrak{y}}}_j}\mathsf{\Delta }{\widehat{\mathfrak{y}}}_j+{\widehat{\omega }}_j\frac{\partial {\mathcal{H}}_j}{\partial {\widehat{c}}_j}\mathsf{\Delta }{\widehat{c}}_j+{\gimel }_2{}_j$$

(23)

The linearization neglects the high-order terms of the Taylor expansion of $\widehat{\mathfrak{M}}\left(\mathcal{Z}\right)$, which causes a ${\gimel }_2$ error quantity of ${\gimel }_2={\displaystyle {\displaystyle \sum }_{j=1}^n}{\gimel }_2{}_j$, which is assumed to be constrained by the positive constant ${\gimel }_n$ as $\left|{\gimel }_2\right|<{\gimel }_2{}_n$ [46].

The vectors of the partial derivative of $\mathcal{H}$ with respect to $\widehat{\mathfrak{y}}$ and $\widehat{c}$, $\frac{\partial {\mathcal{H}}_j}{\partial {\widehat{\mathfrak{y}}}_j}$ and $\frac{\partial {\mathcal{H}}_j}{\partial {\widehat{c}}_j}$, are expressed as

$${\mathcal{H}}_{\widehat{c}}^{\prime }=\left[\begin{array}{cccc}\frac{\partial {\mathcal{H}}_1}{\partial {\widehat{c}}_1}& 0& \dots & 0\\ 0& \frac{\partial {\mathcal{H}}_2}{\partial {\widehat{c}}_2}& \cdots & 0\\ ⋮& 0& \ddots & ⋮\\ 0& 0& \cdots & \frac{\partial {\mathcal{H}}_n}{\partial {\widehat{c}}_n}\end{array}\right]\in {ℝ}^{n\times n}$$

$${\mathcal{H}}_{\widehat{\mathfrak{y}}}^{\prime }=\left[\begin{array}{cccc}\frac{\partial {\mathcal{H}}_1}{\partial {\widehat{\mathfrak{y}}}_1}& 0& \dots & 0\\ 0& \frac{\partial {\mathcal{H}}_2}{\partial {\widehat{\mathfrak{y}}}_2}& \cdots & 0\\ ⋮& 0& \ddots & ⋮\\ 0& 0& \cdots & \frac{\partial {\mathcal{H}}_n}{\partial {\widehat{\mathfrak{y}}}_n}\end{array}\right] \in {ℝ}^{n\times n}$$

$\tilde{\omega }$, $\tilde{\mathfrak{y}}$, and $\tilde{c}$ denote the estimation error as

$$\left\{\begin{array}{l}\tilde{\mathfrak{M}}={\mathfrak{M}}^{*}-\widehat{\mathfrak{M}}\\ \tilde{\omega }={\omega }^{*}-\widehat{\omega } \\ \tilde{\mathfrak{y}}={\mathfrak{y}}^{*}-\widehat{\mathfrak{y}} \\ \tilde{c}=c^{*}-\widehat{c}\end{array}\right.$$

(24)

Subsequently, $\mathsf{\Delta }\tilde{\mathfrak{M}}$ can be written as

$$\mathsf{\Delta }\tilde{\mathfrak{M}}={\mathfrak{M}}^{*}-\widehat{\mathfrak{M}}+{\gimel }_1=\mathsf{\Delta }\widehat{\mathfrak{M}}+{\gimel }_1$$

(25)

where $\mathsf{\Delta }\widehat{\mathfrak{M}}={\displaystyle {\displaystyle \sum }_{j=1}^n}\mathsf{\Delta }\widehat{\mathfrak{M}}\left(\mathcal{Z}\right)$.

Then, based on Equations (23) and (25), we can obtain the following:

$$\tilde{\mathfrak{M}}\left(\mathcal{Z}\right)={\tilde{\omega }}^T\mathcal{H}\left(\mathcal{Z}\right)+{\omega }^T{\mathcal{H}}_{\widehat{\mathfrak{y}}}^{\prime }\left(\tilde{\mathfrak{y}}\right)\tilde{\mathfrak{y}}+{\omega }^T{\mathcal{H}}_{\widehat{\mathrm{c}}}^{\prime }\left(\tilde{\mathrm{c}}\right)\tilde{\mathrm{c}}+{\gimel }_1+{\gimel }_2$$

(26)

Under the condition $\left|{\gimel }_1+{\gimel }_2\right|\le o$, the parameters $\widehat{\omega }$, $\widehat{\mathfrak{y}}$, and $\widehat{\mathrm{c}}$ can be adjusted by following adaptive laws:

$$\left\{\begin{array}{c}\dot{\widehat{\omega } }=-a_1\left|\mathcal{Z}\right|H\left(\mathcal{Z}\right)\\ \dot{\widehat{\mathfrak{y}} }=-a_2\left|\mathcal{Z}\right|{\mathcal{H}}_{\widehat{\mathfrak{y}}}^{\prime }\omega \\ \dot{\widehat{c} }=-a_3\left|\mathcal{Z}\right|{\mathcal{H}}_{\widehat{c}}^{\prime }\omega \end{array}\right.\left\{\begin{array}{c}{\dot{\widehat{\omega } }}_j=-a_1\left|\mathcal{Z}\right|{\mathcal{H}}_j\left(\mathcal{Z}\right)\\ {\dot{\widehat{\mathfrak{y}} }}_j=-a_2\left|\mathcal{Z}\right|\frac{\partial {\mathcal{H}}_j}{\partial {\widehat{\mathfrak{y}}}_j}{\omega }_j\\ {\dot{\widehat{c} }}_j=-a_3\left|\mathcal{Z}\right|\frac{\partial {\mathcal{H}}_j}{\partial {\widehat{c}}_j}{\omega }_j\end{array}\right.$$

(27)

where $a_k,k=\left\{1,2,3\right\}$ are non-zero-positive constants.

Proposition 1.

Considering the system expressed by Equation (13), the lumped uncertainties are coherent with the inequality$\mathfrak{O}\left(x,t\right)\le \mathfrak{M}$.

If the sliding surface is set as

$$\mathcal{Z}\left(t\right)=\mathfrak{p}e+\dot{e}$$

(28)

the control law is defined as

$$\mathfrak{U}={\mathfrak{U}}_{eq}+{\mathfrak{U}}_{sw}+{\mathfrak{U}}_{rbnn}$$

(29)

with

$$\begin{array}{l}{\mathfrak{U}}_{eq}=-\frac{\mathfrak{p}\dot{e}+\mathcal{F}\left(x,t\right)}{\mathfrak{S}\left(x,t\right)}\\ {\mathfrak{U}}_{sw}=\frac{1}{\mathfrak{S}\left(x,t\right)}\left(-q\mathcal{Z}-osign\left(\mathcal{Z}\right)\right)\\ {\mathfrak{U}}_{rbnn}=\frac{-\widehat{\mathfrak{M}}sign\left(\mathcal{Z}\right)}{\mathfrak{S}\left(x,t\right)}\end{array}$$

Accordingly, by choosing this sliding surface, given this control law, the tracking error converges to zero.

Proof. 

Consider the candidate Lyapunov function as

$$\mathcal{L}=\frac{1}{2}\left({\mathcal{Z}}^2+\frac{1}{a_1}{\tilde{\omega }}^T\tilde{\omega }+\frac{1}{a_2}{\tilde{\mathfrak{y}}}^T\tilde{\mathfrak{y}}+\frac{1}{a_3}{\tilde{\mathrm{c}}}^T\tilde{\mathrm{c}}\right)$$

(30)

The time derivative of $\mathcal{L}$ is

$$\dot{\mathcal{L}}=\mathcal{Z}\dot{\mathcal{Z}}+\frac{1}{{\mathrm{a}}_1}{\tilde{\omega }}^T\dot{\tilde{\omega }}+\frac{1}{{\mathrm{a}}_2}{\tilde{\mathfrak{y}}}^T\dot{\tilde{\mathfrak{y}}}+\frac{1}{{\mathrm{a}}_3}{\tilde{\mathrm{c}}}^T\dot{\tilde{\mathrm{c}}}$$

$$\dot{\mathcal{L}}=\mathcal{Z}\left(\mathfrak{p}\dot{e}+\mathcal{F}\left(x,t\right)+\mathfrak{S}\left(x,t\right)\mathfrak{U}+\mathfrak{O}\left(x,t\right)\right)+\frac{1}{a_1}{\tilde{\omega }}^T\dot{\tilde{\omega }}+\frac{1}{a_2}{\tilde{\mathfrak{y}}}^T\dot{\tilde{\mathfrak{y}}}+\frac{1}{a_3}{\tilde{\mathrm{c}}}^T\dot{\tilde{\mathrm{c}}}$$

(31)

By substituting (29) into (31), $\dot{\mathcal{L}}$ becomes:

$$\dot{\mathcal{L}}=\mathcal{Z}\left(\mathfrak{O}\left(x,t\right)-q\mathcal{Z}-\left(\widehat{\mathfrak{M}}+o\right)sign\left(\mathcal{Z}\right)\right)+\frac{1}{a_1}{\tilde{\omega }}^T\dot{\tilde{\omega }}+\frac{1}{a_2}{\tilde{\mathfrak{y}}}^T\dot{\tilde{\mathfrak{y}}}+\frac{1}{a_3}{\tilde{c}}^T\dot{\tilde{c}}$$

(32)

□

Remark 2.

It is important to mention this mathematical property:$\forall \left(\alpha ,\beta \right)\in {ℝ}^2,\left(\alpha +\beta \right)\le \left|\alpha +\beta \right|\le \left|\alpha \right|+\left|\beta \right|$.

Using Remark 2, we can obtain the following:

$$\dot{\mathcal{L}}\le \left(\left|\mathfrak{O}\left(\mathcal{X},t\right)\right|-\left|\widehat{\mathfrak{M}}\right|\right)\left|\mathcal{Z}\right|-q{\mathcal{Z}}^2-o\left|\mathcal{Z}\right|+\left|\frac{1}{a_1}{\tilde{\omega }}^T\dot{\tilde{\omega }}+\frac{1}{a_2}{\tilde{\mathfrak{y}}}^T\dot{\tilde{\mathfrak{y}}}+\frac{1}{a_3}{\tilde{c}}^T\dot{\tilde{c}}\right|$$

(33)

From Equations (25) and (26), we can obtain the following:

$$\begin{array}{l}\dot{\mathcal{L}}\le -q{\mathcal{Z}}^2-o\left|\mathcal{Z}\right|+\left|\tilde{\mathfrak{M}}\right|\left|\mathcal{Z}\right|+\left|\frac{1}{q_1}{\tilde{\omega }}^T\dot{\tilde{\omega }}+\frac{1}{q_2}{\tilde{\mathfrak{y}}}^T\dot{\tilde{\mathfrak{y}}}+\frac{1}{q_3}{\tilde{c}}^T\dot{\tilde{c}}\right|\\ =-q{\mathcal{Z}}^2-o\left|\mathcal{Z}\right|+\left|{\tilde{\omega }}^T\mathcal{H}\left(\mathcal{Z}\right)+{\omega }^T{\mathcal{H}}_{\widehat{\mathfrak{y}}}^{\prime }\left(\tilde{\mathfrak{y}}\right)\tilde{\mathfrak{y}}+{\omega }^T{\mathcal{H}}_{\widehat{c}}^{\prime }\left(\tilde{c}\right)\tilde{c}+{\gimel }_1+{\gimel }_2\right|\left|\mathcal{Z}\right|\\ +\left|\frac{1}{a_1}{\tilde{\omega }}^T\dot{\tilde{\omega }}+\frac{1}{a_2}{\tilde{\mathfrak{y}}}^T\dot{\tilde{\mathfrak{y}}}+\frac{1}{a_3}{\tilde{c}}^T\dot{\tilde{c}}\right|\end{array}$$

(34)

According to Equation (24), Equation (34) becomes:

$$\begin{array}{l}\dot{\mathcal{L}}\le -\mathrm{q}{\mathcal{Z}}^2-o\left|\mathcal{Z}\right|+\left|{\gimel }_1+{\gimel }_2\right|\left|\mathcal{Z}\right|+\left|{\tilde{\omega }}^T\right|\left(\left|\mathcal{H}\left(\mathcal{Z}\right)\right|\left|\mathcal{Z}\right|-\frac{1}{{\mathrm{a}}_1}\left|\dot{\widehat{\omega }}\right|\right)\\ +\left|{\tilde{\mathfrak{y}}}^T\right|\left({\omega }^T\left|{\mathcal{H}}_{\widehat{\mathfrak{y}}}^{\prime }\left(\tilde{\mathfrak{y}}\right)\right|\left|\mathcal{Z}\right|-\frac{1}{{\mathrm{a}}_2}\left|\dot{\widehat{\mathfrak{y}}}\right|\right)+{\tilde{\mathrm{c}}}^T\left({\omega }^T{\mathcal{H}}_{\widehat{\mathrm{c}}}^{\prime }\left(\tilde{\mathrm{c}}\right)\left|\mathcal{Z}\right|-\frac{1}{{\mathrm{a}}_3}\left|\dot{\tilde{c}}\right|\right)\end{array}$$

(35)

From Equation (27), we can achieve:

$$\begin{array}{l}\dot{\mathcal{L}}\le -\mathrm{q}{\mathcal{Z}}^2-o\left|\mathcal{Z}\right|+\left|{\gimel }_1+{\gimel }_2\right|\left|\mathcal{Z}\right|\\ =-q{\mathcal{Z}}^2-\left(o-\left|{\gimel }_1+{\gimel }_2\right|\right)\left|\mathcal{Z}\right|\end{array}$$

(36)

Using the condition $\left|{\gimel }_1+{\gimel }_2\right|\le o$ results in $\dot{\mathcal{L}}\le 0$. Asymptotic stability is guaranteed under Lyapunov’s theory.

The proof is thus complete.

To conclude this conceptual section, the new proposed process is outlined visually in Figure 5.

4. Results and Discussion

The performance of the proposed strategy was evaluated by tracking a speed scenario while accounting for unknown disturbances and uncertainties. A comparison with the super-twisting SMC [12] was made in this context.

Since the tire is the primary ground contact, the parametric uncertainty considered in this simulation was 50% and acted on the front-wheel moment of inertia (${\mathfrak{l}}_{\mathcal{W}}$) [10,43]. Moreover, the disturbance’s nature was random and frequent. The vehicle parameters used were similar to [12]. The proposed control scheme settings were given as follows: $\mathfrak{p}=0.001$, $o=0.0001$, $q=100$, $a_1=15, a_{1,2}=0,5$, and $n=6$.

All simulations were performed using MATLAB R2021a software, with a fixed sample time of 10 ms and an automatic solver on a Lenovo machine characterized by a 2.7 GHz processor, 16 GB of RAM, and a 512 GB SSD.

The simulation outcomes of the proposed method and that of [12] are presented in Figure 6 and Figure 7.

In Figure 6, it can be observed that the suggested longitudinal controller directed the vehicle speed to perfectly reach the desired speed. However, at first sight, the simulation results of the super-twisting SMC approach were not as satisfactory as the proposed approach. To further analyze the performance of both approaches, it was important to study the results in transient and steady states. Indeed, in the transient regime the proposed approach showed zero rise time, whereas the response time was extremely insignificant. However, for the super-twisting SMC the rise time and the response time were highly significant and the overshoot was considerable, even in the steady state, particularly in the speed range, indicating the onset of slow motion. Moreover, a quantitative study was undertaken to underline the offered method’s success utilizing the integral of the absolute error ($\mathfrak{i}\mathfrak{a}\mathfrak{e}$), as written in Equation (37), as a performance index of the absolute error of the longitudinal displacement. These numerical values are presented in

Table 1. Quantitative performance assessment.

Approaches	$\mathfrak{i}\mathfrak{a}\mathfrak{e}$ Performance Index
Proposed method	0.825
Super-twisting SMC	64.419

.

$$\mathfrak{i}\mathfrak{a}\mathfrak{e}={{\displaystyle \int }}_0^{t_f}\left| e\right|dt$$

(37)

where $t_f$ indicates the final simulation time.

Figure 7 shows the engine torque acting on the wheel; this parameter exactly indicates the controller output. In fact, it is obvious that, at each speed step, the discussed control structure reacted simultaneously by imposing a torque that caused the vehicle’s wheels to turn.

In the acceleration steps, the torque resulting from the proposed method and that resulting from the super-twisting SMC did not occur in an increasing sense. As can be seen, the torque reached its maximum in the second speed step, and then decreased, returning to a lower value, even when the requested speed in the next step was higher than in the previous step. It can be stated that the controllers reacted intelligently by adding or subtracting the requested quantities to achieve the desired speed. Nevertheless, when the speed decreased, the controllers reacted in a decreasing rhythm, which is logical since the vehicle started to reduce its speed.

The execution of the orders issued by the control algorithm was performed by the actuators, requiring sufficient energy for their operation. To this end, a comparative study gave numerical data regarding the energy consumption of the control strategies involved in this study. The integral of the square value ($ISV$) of the absolute error of the longitudinal acceleration provided this information related to the energy consumed by the acceleration/braking actuators [43]. The $ISV$ is expressed in Equation (38). These results are illustrated in

Table 2. Quantitative performance analysis.

Approaches	$\mathit{I}\mathit{S}\mathit{V}$ Performance Index
Proposed method	27.719
Super-twisting SMC	196.8197

.

$$ISV={{\displaystyle \int }}_0^{t_f}{\left|e_{acc}\right|}^{2}dt$$

(38)

Table 2 also shows that the proposed approach is optimal in terms of the power usage by the actuators moving the vehicle forward and backward and braking.

Remark 3.

This note mentions and describes the equipment for the experimental validation of the proposed control approach for a potential implementation on the lateral level. The following are the principal elements, shown in Figure 8, involved in the process of carrying out the field experiment:

1. 

A Toyota Prius first-level autonomous vehicle

2. 

An automatic steering wheel robot.

3. 

A Lenovo computer.

5. Conclusions

ADAS are vehicle control systems that improve driving comfort and road safety by using the vehicle’s sensing capabilities and control algorithms. In this sense, this work has contributed to longitudinal autonomous control. Throughout this research, a novel approach based on a conventional sliding mode and RBNN has been developed, verified theoretically in the sense of Lyapunov, and validated in a simulation compared to the super-twisting SMC. Accordingly, it is necessary to summarize the following conclusions:

• Offering a robust law considering the disturbance and uncertainty upper limit as well as adapting it to each sampling time has been proven to provide outstanding results over and above the super-twisting SMC that often dominated the conventional SMC in terms of performance.
• Providing an algorithm that was able to estimate the upper limit of uncertainties and disturbances allowed the proposed design scheme to be utilized with no need for information regarding upper-limit external disturbances.
• Orienting the proposed design toward a real nonlinear system, such as longitudinal vehicle dynamics, can not only confirm the proposed method’s sovereignty but can also be embedded to contribute to the ADASs in general and ACC and ISA in particular.

In short, since the proposed technique has revealed its superiority, this will lead to further examination and testing using other driving conditions and scenarios while performing this technique for lateral control objectives, followed by implementation and testing using the above-mentioned steering robot, all of which constitute the perspectives of this manuscript.