Investigating the Influence of Embedment Length on the Anchorage Force of Rock Bolts with Modified Pile Elements

Abstract

The embedment length (EL) of full-grouting rock bolts is a core factor in rock bolt reinforcement. Therefore, understanding the influence of EL on the reinforcement performance of rock bolts benefits the rock reinforcement quality. To realise this purpose, this paper adopted the numerical modelling method. In this numerical modelling method, the structural elements of modified piles were used. The elastic debonding law was incorporated into the modified pile elements to model the debonding behaviour of the surface between rock bolts and grout. The results showed that the sliding of modified pile elements had a marginal influence on the reinforcement performance of rock bolts. Moreover, the EL has a paramount influence on the reinforcement performance of rock bolts. Before the rock bolts reached the largest anchorage force, there was a linear relation between the largest anchorage force and the EL. It was effective to use the linear regression analysis method to predict the critical EL of rock bolts. This finding was also applicable to fibre-reinforced polymer (FRP) rock bolts. Additionally, the rock bolt type had a paramount influence on the reinforcement performance of rock bolts. Before the rock bolts reached the largest anchorage force, metal rock bolts showed much larger initial stiffness than FRP rock bolts.

1. Introduction

Rock reinforcement exerts a paramount role in underground excavating engineering [1]. This is more apparent in mining engineering. This is because, in mining engineering, the underground openings are normally located in jointed rock masses, such as coal, mudstone, shale and sandstone [2]. The stability of those jointed rock masses is usually poor. Therefore, once the underground roadways or chambers are excavated in those jointed rock masses, the surrounding rock masses are likely to converge [3]. This may lead to a collapse of the roof, leading to underground disasters [4].

To prevent the paramount convergence of underground openings and underground roof collapsing disasters, many methods can be used, such as grouting. Li et al. [5] demonstrated that using grouting could improve the shear strength of jointed rock mass. Additionally, rock reinforcement methods can be used [6]. Among kinds of rock reinforcement methods, using rock bolts to improve the strength and stability of rock masses accounts for a major part [7]. Therefore, it is quite necessary to understand the rock reinforcement mechanism of rock bolts.

To realise this target, previous researchers and engineers conducted numerous experimental tests, analytical modelling, numerical modelling and in situ tests. For example, Krukovskyi et al. [8] used the numerical modelling method to analyse the changing in the dimension and shape of a rock mass zone reinforced with injection rock bolts. It was demonstrated that increasing the number of injection rock bolts was likely to create the rock bolt arch in the mine roof. Moreover, Matayev et al. [9] used a two-dimensional finite element program to predict the stress–strain state of the rock mass under the stope operations. Their study can be used to create an in situ geomechanical model to optimise the parameters for the mining support.

Although the selected investigating methods are diverse in evaluating the anchorage force of rock bolts, the investigating protocol is quite similar. It uses the pull-out (PO) method to investigate the anchorage force of rock bolts [10]. Moreover, with this method, the load transfer process between the rock bolts, grout column and rock masses can be evaluated.

According to this concept, the anchorage force of rock bolts under various geological and loading environments has been investigated. The influence of numerous parameters on the anchorage force of rock bolts has been revealed, such as grout strength, bolt diameter, rock mass strength and stress condition. Among kinds of parameters, researchers and engineers paid much attention to the parameter of embedment length (EL). The EL is defined as the length in which the rock bolt is bonded with the surrounding rock masses with grout.

The EL is significant to the rock bolt reinforcement. If the EL is too short, the rock bolts are not able to maintain the stability of excavated rock mass. However, if the EL is too long, it will increase the economic cost and resource waste. Therefore, optimising the EL of rock bolts is important to maintain the safety of underground openings and reduce economic costs.

To fulfil the optimising of the rock bolts’ EL, how the EL influences the anchorage force of rock bolts should be clearly understood. Therefore, this paper adopted the modified pile elements to reveal the relationship between the EL and the rock bolt anchorage force.

For full-grouting rock bolts, the EL is almost identical to the rock bolt length. Apparently, optimising the EL is conducive to determining the proper length of rock bolts. Moreover, optimising the EL is conducive to reducing the grouting cost in rock reinforcement.

To investigate how the EL influenced the anchorage force of rock bolts, Benmokrane et al. [11] conducted PO tests on ribbed rock bolts. The EL ranged between seven times the bolt diameter and fourteen times the bolt diameter. It showed that the largest anchorage force increased directly with the EL. Similarly, Kilik et al. [12] conducted PO tests on rock bolts with the EL ranging between 150 mm and 320 mm. They found that there was a linear relationship between the largest anchorage force and the EL. Mortazavi [13] investigated how the EL influenced the anchorage force of three diverse rock bolts: weld grip, single Arapree and double Arapree. It showed that the largest anchorage force increased linearly with the EL.

Li et al. [14] investigated the critical EL with laboratory tests. The tested bolt had a diameter of 20 mm. It showed that the critical EL was directly related to the water–cement ratio. With this ratio increasing, the critical EL also increased. Ma et al. [15] compared the reinforcement performance of rock bolts when the EL increased from 100 mm to 300 mm. They found that with the EL increasing, the rock bolts were likely to show yielding behaviour under the PO environment. Lu et al. [16] tested the reinforcement performance of a bamboo rock bolt. The EL ranged between 800 mm and 3000 mm. It showed that the largest anchorage force increased linearly with the EL. Vlachopoulos, Cruz and Forbes [1] investigated the reinforcement performance of rock bolts under diverse loading conditions. During testing, the EL was changed from 100 mm to 1000 mm. They found that the EL was the key factor in determining the reinforcement performance of rock bolts. Moreover, they found that critical EL was around 430 mm. Skrzypkowski et al. [17] compared the reinforcement performance of rock bolts when the EL was 0.1 m and 0.2 m. Apparently, the EL had an apparent influence on the largest anchorage force of rock bolts. No matter which hole diameter was used, the rock bolts had a higher anchorage force when the EL was longer. Skrzypkowski et al. [18] conducted laboratory tests to investigate the reinforcement performance of rock bolts when the EL increased from 100 mm to 200 mm. In this case, a constant borehole diameter of 28 mm was used. It showed that the largest anchorage force increased directly with the EL. Høien et al. [19] conducted laboratory PO tests on rock bolts to reveal the critical EL. They indicated that the critical EL was composed of three parts: the cone broken length, the plastic deformation length and the elastic deformation length.

The above experimental study exerts a paramount role in helping underground operators to better understand the rock reinforcement mechanism. However, compared with that, when referring to the EL influence, much less work has been conducted with the numerical modelling method.

Recently, modified pile elements have been proposed to investigate the reinforcement performance of rock bolts [20]. The advantages of modified pile elements are that there is a rock bolt flag. Once this rock bolt flag is turned on, it can be used to model point-anchored rock bolts and full-grouting rock bolts. Moreover, modified pile elements accept the revision of the original constitutive model. Therefore, users can revise the original constitutive model of the modified pile elements. The credibility of the modified pile elements has been validated with experimental PO tests in previous research [21].

However, until now, little research has been conducted to use the modified pile elements with an elastic debonding law to investigate the reinforcement performance of rock bolts. Therefore, the research gap is that little research has been conducted to use this numerical modelling method to study the reinforcement performance of rock bolts.

To solve this gap, this paper used the numerical software of FLAC3D 6.0 to conduct the numerical simulation. The modified pile elements were used to simulate the rock bolts. More importantly, an elastic debonding law was substituted into the modified pile elements to replace the original constitutive model.

The task of this paper is to reveal the relationship between the EL and anchorage force of full-grouting rock bolts with modified pile elements. To fulfil this task, the following objectives are prepared:

–

To determine the sliding influence of modified pile elements on the reinforcement performance of rock bolts;

–

To evaluate the influence of the EL on the reinforcement performance of metal rock bolts;

–

To evaluate the influence of the EL on the reinforcement performance of FRP rock bolts;

–

To compare the tensile performance of metal rock bolts and FRP rock bolts.

2. Methods

This study focuses on the reinforcement performance of full-grouting rock bolts under the uniaxial loading environment. Therefore, the traditional PO method was used. Specifically, a rock bolt was installed in a rock block and a low PO rate was applied on the external end of the rock bolt. This test was continued until the rock bolt anchorage system failed. During the whole test process, the PO force and displacement were recorded to indicate the reinforcement performance of rock bolts.

In this study, the numerical software FLAC3D 6.0 was used. The reason to use this program is that it is an advanced commercial program. Previous research indicated that this program is robust in modelling kinds of mining engineering issues [22]. More importantly, in FLAC3D 6.0, various structure elements are embedded. Therefore, users can adopt those structure elements to model rock reinforcement bolts.

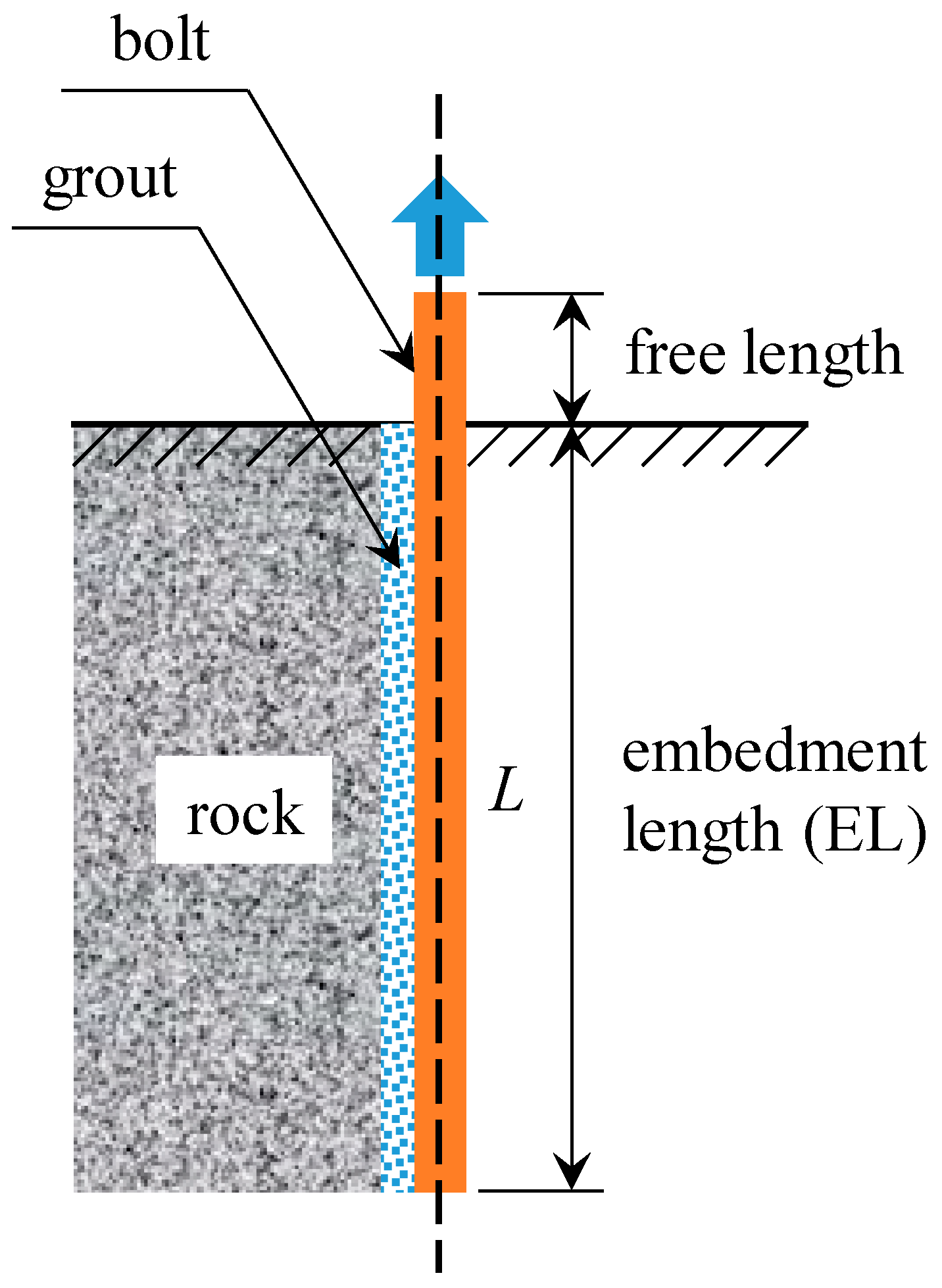
When using the FLAC3D 6.0, a numerical PO scenario was created, as shown in Figure 1. It is basically composed of three parts: the rock bolt, the grout column and the surrounding rock. The rock bolt can be divided into two parts: the free length and the EL. The free length is only 0.1 m. The purpose of this free length is to simulate the protruding section of rock bolts in experimental PO tests. Below the free length, it is the EL. More importantly, the EL can be adjusted by users. Since the numerical software has the convenience of creating numerical blocks, the EL can be easily increased or decreased by users. In this study, the EL was changed between 0.5 m and 3 m.

To model the PO influence, a low PO rate of 5 × 10⁻⁷ m/s was applied at the external end of the rock bolt. Moreover, this low PO rate was fixed during the whole PO process.

In this study, two kinds of rock bolts were used. One was metal rock bolts and the other was FRP rock bolts. The basic information of those two rock bolts is tabulated in

Table 1. Basic information of tested rock bolts.

No.	1	2
Rock bolt type	Metal rock bolt	FRP rock bolt
Elastic modulus (GPa)	220	50
Rock bolt diameter (mm)	22	22
Rock bolt perimeter (mm)	69.1	69.1
Cross-sectional area of rock bolts (mm2)	380.1	380.1
Tensile rupture force (kN)	220	220
Tensile failure strain	1 × 10−4	1 × 10−4

.

The modified pile elements can simulate tensile rupture of rock bolts. It indicates that after the tensile force in the rock bolt reaches 220 kN and the corresponding tensile strain in the bolt reaches 1 × 10⁻⁴, tensile rupture of the rock bolt will occur.

As for the surface between rock bolts and grout, an elastic debonding law was used to model it. It is defined that before the shear slip of the surface between rock bolts and grout reaches 1 mm, the bonding stress at the surface increases linearly to the strength of 2 MPa. After that, the bonding stress at the surface declines directly to the residual strength of 1 MPa. Since then, the bonding stress of the surface between rock bolts and grout remains constant.

The rock bolt is installed in a numerical rock block. The rock block had an elastic modulus (EM) of 25 GPa and Poisson’s ratio of 0.25. It is admitted that in reality, the rock is an elastoplastic material. Therefore, the rock may generate plastic deformation. Then, in rock mechanics, the elastoplastic models are always used to simulate the rock mass, such as the Mohr–Coulomb model or the strain-softening model. However, in this study, attention is concentrated on the bonding failure of rock bolts. Therefore, no failure of the rock mass occurs. Then, an elastic model is used to simulate the numerical rock block. Moreover, when using the elastoplastic models, more input parameters are needed. This decreases the practicability of this numerical calculation.

During the whole PO process, the PO force and displacement at the external end of the rock bolt were monitored. After the numerical PO test ended, the recorded results can be used to reflect and compare the reinforcement performance of rock bolts.

2.1. Numerical PO Tests on Metal Rock Bolts

Numerical PO tests were first conducted on metal rock bolts. Two series of tests were conducted.

The first series of tests is to reveal the sliding influence of modified pile elements. In this scenario, three diverse ELs were used: 1.5 m, 2.5 m and 3 m. For the modified pile elements in FLAC3D 6.0, there is a sliding switch. However, its function on the reinforcement performance of rock bolts is not clear. Therefore, numerical PO tests on rock bolts with the EL ranging from 1.5 m to 3 m were conducted. For each EL, two diverse PO tests were conducted. In one PO test, the sliding switch was turned on while in other PO tests, the sliding switch was turned off.

Then, the second series of tests is to investigate how the EL influenced the reinforcement performance of metal rock bolts. During the PO process, the EL was changed between 0.5 m and 3 m.

2.2. Numerical PO Tests on FRP Rock Bolts

Further work was continued to investigate the reinforcement performance of FRP rock bolts. Specifically, how the EL influenced the reinforcement performance of FRP rock bolts was investigated.

In this study, the EM of rock bolts was regarded as the parameter to distinguish FRP rock bolts from metal rock bolts. Previous experimental studies showed that the FRP rock bolts usually had an EM of around 50 GPa, which was much smaller than that of metal rock bolts [23]. Therefore, in this study, an EM of 50 GPa was used to model the FRP rock bolts. Additionally, a number of PO tests were conducted on FRP rock bolts with the EL ranging between 0.5 m and 3 m.

3. Results

3.1. Sliding Influence of the Modified Pile Elements

When the EL was 1.5 m, the PO results are shown in Figure 2. It shows that the anchorage force increased non-linearly with the PO displacement. When the PO displacement reached around 2.3 mm, the anchorage force reached the maximum. After that, the PO force declined gently. Then, it remained almost constant. More interestingly, the sliding of modified pile elements had a marginal influence on the reinforcement performance of metal rock bolts. The overall performance of metal rock bolts was consistent and independent of the sliding switch.

When the EL was 2.5, the reinforcement performance of metal rock bolts is shown in Figure 3. Apparently, in this case, the sliding of modified pile elements had no paramount influence on the reinforcement performance of rock bolts.

Finally, when the EL was 3 m, the modelling results are shown in Figure 4. In this case, the reinforcement performance of metal rock bolts was almost identical.

The above analysis showed that the sliding of modified pile elements had almost no influence on the reinforcement performance of metal rock bolts. Therefore, in the following numerical PO tests, the sliding switch of modified pile elements was always set off.

3.2. Influence of the EL on the Reinforcement Performance of Metal Rock Bolts

After numerical PO tests were conducted on metal rock bolts, the reinforcement performance of metal rock bolts is shown in Figure 5.

It showed that the EL had a paramount influence on the reinforcement performance of metal rock bolts. With the EL increasing, the largest anchorage force of metal rock bolts increased apparently. However, the increasing trend was apparently diverse.

When the EL was smaller than 0.7 m, the anchorage force of metal rock bolts increased almost linearly with the PO displacement before the anchorage force reached the maximum. However, when the EL was longer than 1 m, there was a non-linear relation between the anchorage force and the PO displacement. This was more apparent when the EL was longer than 2 m.

To better reveal the relation between the largest anchorage force and the EL, the largest anchorage force was extracted and plotted, as shown in Figure 6. It should be noted that in this scenario, when the EL was 3 m, the PO force reached the tensile rupture force of metal rock bolts. Consequently, tensile rupture of metal rock bolts occurred. Therefore, when the EL was 3 m, the failure mode of the anchorage system was diverse from the others.

When the EL ranged between 0.5 m and 2.5 m, the anchorage system had a consistent failure mode of bonding failure at the surface between rock bolts and grout. To investigate how the EL influenced the reinforcement performance of metal rock bolts, linear fitting was conducted. It showed that when the EL ranged between 0.5 m and 2.5 m, the following equation was obtained:

$$y=52.12x+68.55$$

(1)

where y: the largest anchorage force of metal rock bolts; x: the EL.

The corresponding correlation coefficient was 0.9769. Apparently, the correlation coefficient was not ideal since it was even less than 0.98. As for the reason, it was found that when the EL was smaller than 0.7 m, the largest anchorage force of metal rock bolts was not stable. Specifically, when the EL was 0.5 m, the largest anchorage force was 101.8 kN. Then, when the EL increased to 0.7 m, the largest anchorage force was 106.2 kN, which was quite close to 101.8 kN. This indicated that when the EL was short enough, the anchorage force of metal rock bolts was not stable. According to this finding, it is recommended that when conducting the PO tests on metal rock bolts, the EL should not be too short. In this way, the obtained results can be more accurate and reliable.

One more linear regression was conducted. In this case, the largest anchorage force when the EL was 0.5 m was eliminated. The reason is that when the EL was 0.5 m, it was too short to guarantee the accuracy of the anchorage force results. Therefore, the linear regression was conducted on the results when the EL ranged between 0.7 m and 2.5 m. The obtained equation is shown below:

$$y=55.63x+61.71$$

(2)

In this case, the corresponding correlation coefficient was 0.9841. It showed that when the EL ranged between 0.7 m and 2.5 m, there was a paramount linear relation between the largest anchorage force and the EL. Moreover, this obtained equation can be used to predict the critical EL.

To realise this, the tensile rupture force of the metal rock bolts was substituted into Equation (2). Then, the critical EL can be obtained. For this scenario, the predicted critical EL was 2.85 m.

To confirm whether the predicted critical EL was accurate, further numerical PO tests were conducted. In this case, the EL was increased from 2.5 m. When the failure mode of the anchorage system changed from the bonding failure of the surface to the tensile rupture of rock bolts, the corresponding EL was regarded as the critical EL. It showed that when the EL increased to 2.76 m, the failure mode of the anchorage system changed to tensile rupture of rock bolts, as shown in Figure 7.

With this analysis, for this scenario, the critical EL was 2.76 m. Apparently, the predicted critical EL of 2.84 m was larger than the exact critical EL of 2.76 m. However, the difference between them is quite small. Specifically, the relative difference between them is only 2.9%. This confirmed that using this linear regression analysis method to predict the critical EL of rock bolts was effective.

The debonding behaviour of the surface between rock bolts and grout was also investigated. Specifically, the relation between the bonding stress and shear slip of the surface between rock bolts and grout was recorded. Then, it was exported and plotted. When the EL was 1.5 m and 2.5 m, the bonding stress versus shear slip of the surface between rock bolts and grout was shown in Figure 8. Apparently, although the EL was diverse, the debonding behaviour of the surface between rock bolts and grout was identical. This confirmed that the elastic debonding law was successfully incorporated into the modified pile elements. Moreover, this incorporation was independent of the EL.

3.3. Influence of the EL on the Reinforcement Performance of FRP Rock Bolts

When the EM of rock bolts was set as 50 GPa, the corresponding reinforcement performance of FRP rock bolts is shown in Figure 9. Apparently, the reinforcement performance of FRP rock bolts was much more diverse than metal rock bolts. For FRP rock bolts, even when the EL was short as 0.5 m, there was a non-linear relation between the anchorage force of rock bolts and the PO displacement. This non-linear relation was more apparent when the EL was long.

To investigate how the EL influenced the largest anchorage force of FRP rock bolts, the largest anchorage force of FRP rock bolts was extracted and plotted. It should be noted that when the EL was 3 m, the anchorage system failed by tensile rupture of FRP rock bolts. In this case, the failure mode of the anchorage system was diverse from the others. Therefore, when the EL was smaller than 3 m, the largest anchorage force of FRP rock bolts was plotted together, as shown in Figure 10.

Apparently, for FRP rock bolts, there was a strong linear relation between the largest anchorage force and EL. The correlation coefficient was 0.9997. Moreover, the corresponding linear regression equation was shown below:

$$y=66.27x+18.19$$

(3)

Relying on this equation, the critical EL of FRP rock bolts can be predicted. For FRP rock bolts, the tensile rupture force was still 220 kN. Therefore, after substituting this tensile rupture force into Equation (3), the corresponding critical EL can be obtained. It showed that under this scenario, for FRP rock bolts, the predicted critical EL was 3.03 m.

Further numerical simulation was conducted to confirm the exact critical EL. To realise this, the EL was increased gradually from 2.5 m. When the failure mode of the anchorage system changed from bonding failure at the surface between rock bolts and grout to the tensile rupture of the FRP rock bolts, the corresponding EL was regarded as the critical EL. It was coincident that when the EL increased to 3 m, tensile rupture of FRP rock bolts occurred. Therefore, in this scenario, for FRP rock bolts, the critical EL was 3 m. Compared with the predicted critical EL of 3.03 m, there was a quite small difference between them. This further confirmed that using the linear regression analysis method to predict the critical EL of rock bolts was effective.

3.4. Comparison between Metal Rock Bolts and FRP Rock Bolts

A comparison was conducted between metal rock bolts and FRP rock bolts. First, the reinforcement performance of rock bolts when the EL was 1.5 m is shown in Figure 11. Apparently, the rock bolt type had a paramount influence on the reinforcement performance of rock bolts. The initial stiffness of metal rock bolts was much larger than that of FRP rock bolts. This indicated that the anchorage system reinforced with the metal rock bolts was more brittle than the anchorage system reinforced with the FRP rock bolts. Thirdly, the post-failure performance of metal rock bolts was apparently diverse from that of FRP rock bolts. For metal rock bolts, after the largest anchorage force, the anchorage force of metal rock bolts oscillated. By contrast, for FRP rock bolts, after the largest anchorage force, the anchorage force of FRP rock bolts decreased smoothly. Additionally, there was no oscillation in the anchorage force of FRP rock bolts.

A comparison was also conducted on metal rock bolts and FRP rock bolts when the EL was 2.5 m. The results are shown in Figure 12. It is apparent that the stiffness of the rock bolt anchorage system was still larger than that of the FRP rock bolt anchorage system. When the steel rock bolt reached the largest anchorage force, the corresponding PO displacement was 4.59 mm. By contrast, when the FRP rock bolt reached the largest anchorage force, the corresponding PO displacement was 14.72 mm. This value was more than three times the corresponding PO displacement that occurred in the steel rock bolt test.

Last, the reinforcement performance of metal rock bolts and FRP rock bolts was compared when the EL was 3.5 m, as shown in Figure 13. In this scenario, the anchorage system consistently failed by the tensile rupture of rock bolts. There was still a paramount difference in the reinforcement performance of metal rock bolts and FRP rock bolts. The initial stiffness of FRP rock bolts was much smaller than that of metal rock bolts.

4. Discussion

In this study, how the EL influenced the reinforcement performance of rock bolts was investigated with numerical modelling. First, numerical modelling work was conducted on metal rock bolts. It is interesting to see that when the EL was short, there was no paramount increase in the largest anchorage force. For example, in this study, for metal rock bolts, when the EL increased from 0.5 m to 0.7 m, the largest anchorage force of metal rock bolts increased from 101.8 kN to 106.2 kN. This indicated that when the EL increased by 40%, the largest anchorage force of metal rock bolts increased by 4.32%. For the reason, it was inferred that when the EL was too short, the obtained anchorage force results were not reliable. Specifically, a scatter of results may occur. This finding was consistent with the conclusion obtained by Stillborg [24]. When Stillborg [24] conducted experimental PO tests on cable bolts, he found that when the EL was short enough, the obtained anchorage force was not reliable. This was because there was an apparent scatter of the anchorage force. Therefore, for this point, the numerical modelling results were consistent with the previous experimental results.

Then, this numerical study revealed that when the anchorage system failed by bonding failure at the surface between rock bolts and grout, there was generally a linear relation between the largest anchorage force and the EL. This was more apparent if the too-short EL was eliminated. This finding was applicable to both metal rock bolts and FRP rock bolts. This finding agreed well with the experimental work conducted by Kilik, Yasar and Celik [12]. In their study, the correlation coefficient was 0.9936. In this study, the correlation coefficient was 0.9841 for metal rock bolts and 0.9997 for FRP rock bolts. Overall, the numerical investigating results were consistent with the previous experimental work. Moreover, according to this study, it was inferred that using the linear regression analysis method to predict the critical EL of rock bolts was reliable.

It is noted that the relationship between the anchorage force and the EL is obtained based on considering the elastoplastic behaviour of the surface between rock bolts and grout. Before the shear stress reaches the peak, the shear stress increases linearly. After it reaches the peak, the shear stress drops to the residual shear strength and remains constant.

Last, this study revealed that the initial stiffness of metal rock bolts was larger than that of FRP rock bolts, as shown in Figure 11, Figure 12 and Figure 13. This finding was consistent with the in situ test results obtained by Bai et al. [25]. Specifically, Bai, Zhang and Yan [25] compared the reinforcement performance of two rock bolts. One was the traditional metal rock bolts and the other one was the FRP rock bolts. The in situ experimental PO tests were conducted. It showed that the metal rock bolts had similar anchorage force compared with the FRP rock bolts. However, at the initial loading stage, the initial stiffness was diverse. For metal rock bolts, the initial slope of the force–displacement curve was much larger. Therefore, the experimental results indicated that the metal rock bolts had larger initial stiffness than FRP rock bolts. This further confirmed that the current numerical modelling approach was robust in analysing the reinforcement performance of rock bolts.

It is also acknowledged that this current paper is not able to fit all rock bolt application cases in mining engineering. The reason is that in the in situ environment, there are many uncertainties. The previous research indicates that these uncertainties can lead to the complexity of mining engineering cases and difficulty in solving the mining engineering issues [26,27]. Because of these uncertainties, when this study is applied to an engineering case, the findings may be adjusted to fit new cases. Nevertheless, this current study can still provide a theoretical basement for engineering cases.

Furthermore, the quality of the rock bolting may be influenced by the loading condition. For example, Liu and Li [28] demonstrated that in tunnelling, compared with the conventional loading method, when the unloading confining pressure was used, fewer plastic zones occurred. For this study, the influence of unloading conditions was not considered. However, further work can be continued to evaluate the rock bolting quality under the unloading condition.

5. Conclusions

This study conducted numerical modelling work on investigating the reinforcement performance of full-grouting rock bolts. A number of numerical PO tests were conducted on rock bolts. Two diverse types of rock bolts were used. One was the traditional metal rock bolts and the other one was the FRP rock bolts. During the PO process, the PO force and displacement were recorded. The force–displacement results were summarised and compared. According to this study, the following conclusions were obtained.

(1)

The sliding function of modified pile elements had a marginal influence on the reinforcement performance of rock bolts. This was independent of the EL of rock bolts. No matter whether the sliding function was considered, the metal rock bolts and FRP rock bolts showed consistent reinforcement performance.

(2)

The EL has a paramount influence on the reinforcement performance of rock bolts. When the EL was too short, the reinforcement performance of rock bolts was not reliable. The largest anchorage force of rock bolts was not stable. Therefore, when conducting PO tests of rock bolts, it is recommended that the EL should be relatively long enough.

(3)

Before the rock bolts reached the largest anchorage force, there was generally a linear relation between the largest anchorage force and the EL. This linear relation was applicable for both metal rock bolts and FRP rock bolts. Moreover, the linear regression analysis method was robust in predicting the critical rupture force of rock bolts.

(4)

The FRP rock bolts showed a paramount difference in reinforcement performance compared with metal rock bolts. For the force–displacement curve, the FRP rock bolts showed a much smaller initial stiffness. Consequently, when the FRP rock bolts reached the largest anchorage force, the corresponding PO displacement was much smaller.