Power Flow Optimization by Integrating Novel Metaheuristic Algorithms and Adopting Renewables to Improve Power System Operation
Abstract
1. Introduction
- Hybridizing teaching and learning algorithms with turbulent flow optimizations developed a novel, efficient, and robust optimization algorithm named TLTFWO. This method is used to optimize optimal power flow (OPF) problems involving conventional thermal power plants, solar photovoltaics, and distributed wind power.
- This work addresses the uncertainties of renewable generation by using the Weibull probability density function to model wind distribution and the lognormal probability density function to model solar radiation.
- In addition to fuel costs, emissions, power losses, and voltage deviations, OPF also considers fuel costs, emissions, power losses, and voltage deviations. Factors such as economics, technology, and safety limit these functions. Furthermore, this study examined reserve, direct, and penalty costs in addition to thermal power unit production costs.
- An optimal scheduling of thermal power plants based on renewable energy is determined by the amount of carbon tax associated with the goal function.
2. Description of the Problem
- The active power output of WT–PV is uncertain and time-varying [50],
- The OPF is executed ten times in a period of 10 min. So, irradiance and wind speed are sampled periodically at each 1 min.
- Noting that WT/PV units can also generate reactive power, the voltage magnitudes of WT/PV buses have been assumed to be control parameters [51].
2.1. Constraints
2.2. Objective Functions
2.3. Modelling of WT and PV Generation
2.3.1. Modelling of WT Generation
2.3.2. Modelling of PV Output Power
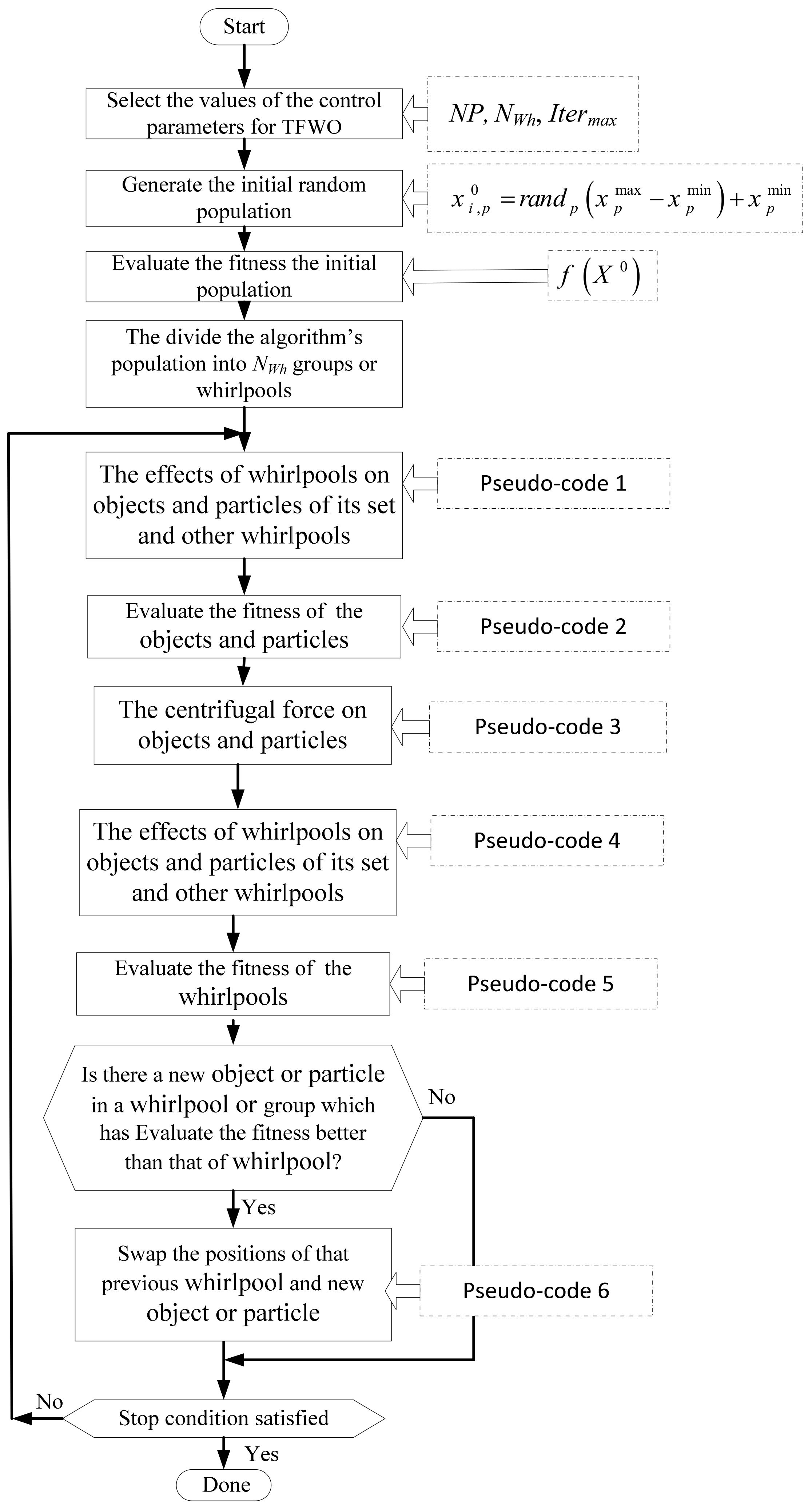
3. The Proposed Optimization Hybrid Algorithm
3.1. TFWO
3.1.1. How Are Whirlpools Made?
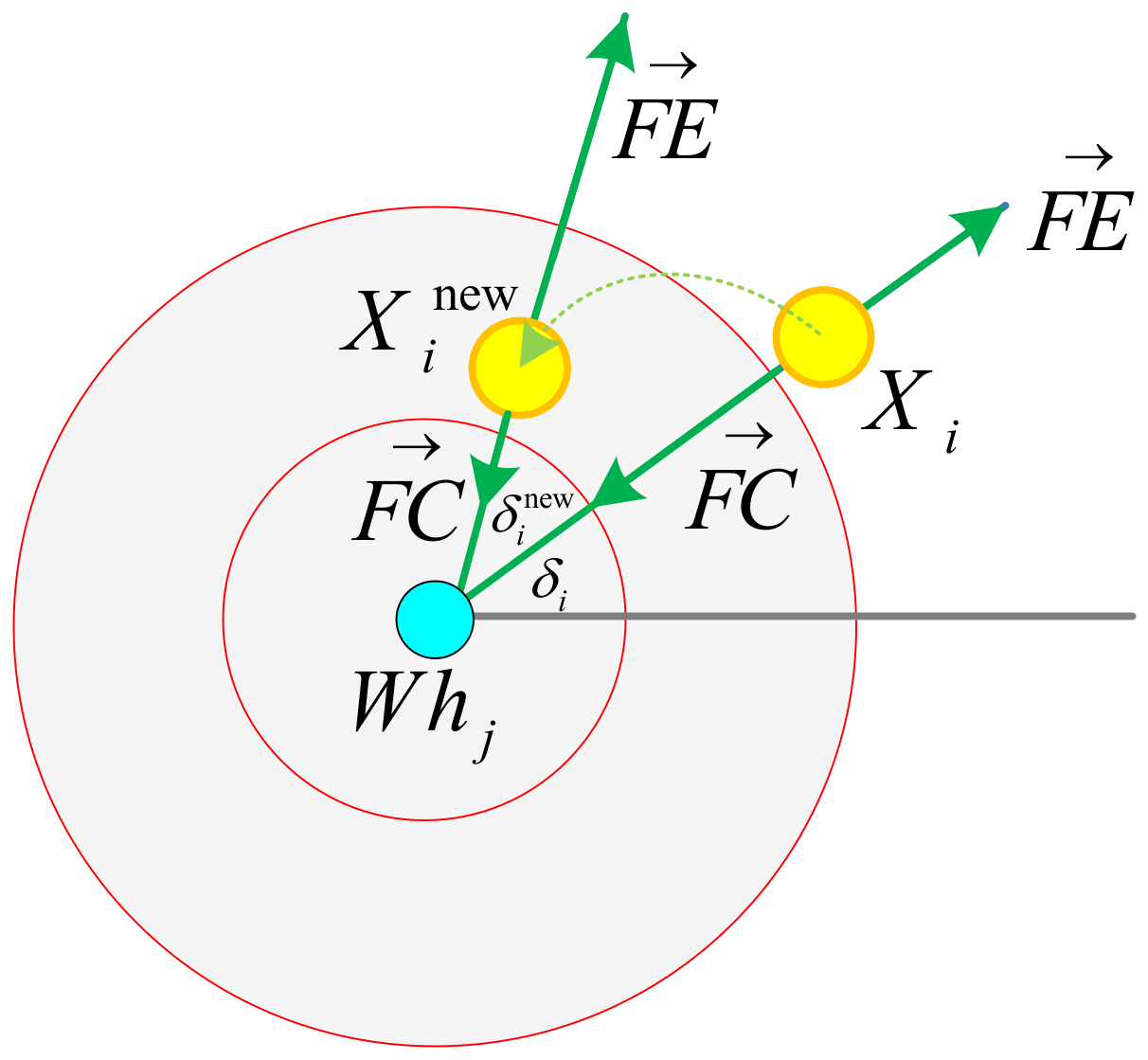
3.1.2. How Whirlpools Impact Their Own and other Whirlpools’ Objects and Particles
| Algorithm 1. Generating the new position (Pseudo-code 1) | |
| 1: | for |
| 2: | Calculate using Equation (30) |
| 3: | end |
| 4: | with the minimum value of |
| 5: | with the maximum value of |
| 6: | |
| 7: | Calculate using Equation (31) |
| 8: | |
| Algorithm 2. Updating the new position (Pseudo-code 2) | |
| 1: | |
| 2: | if |
| 3: | |
| 4: | |
| 5: | end |
3.1.3. Centrifugal Force
| Algorithm 3. Updating pth position using the centrifugal force (Pseudo-code 3) | |
| 1: | Evaluate the centrifugal force ( using Equation (33) |
| 2: | |
| 3: | |
| 4: | Update using Equation (34) |
| 5: | |
| 6: | end |
3.1.4. Interactions between Whirlpools
| Algorithm 4. Whirlpools’ interaction process (Pseudo-code 4) | |
| 1: | for |
| 2: | Calculate using Equation (35) |
| 3: | |
| 4: | with the minimum value of |
| 5: | Evaluate using Equation (36) |
| 6: | |
| 7: | |
| Algorithm 5. Whirlpools’ updating process (Pseudo-code 5) | |
| 1: | |
| 2: | |
| 3: | |
| 4: | |
| 5: | |
| Algorithm 6. Selection mechanism (Pseudo-code 6) | |
| 1: | |
| 2: | |
| 3: | |
| 4: | |
3.2. TLBO Algorithm
3.2.1. Teaching Phase
3.2.2. Learning Phase
3.3. The Proposed TLTFWO Algorithm
4. TLTFWO for Different OPF Problems
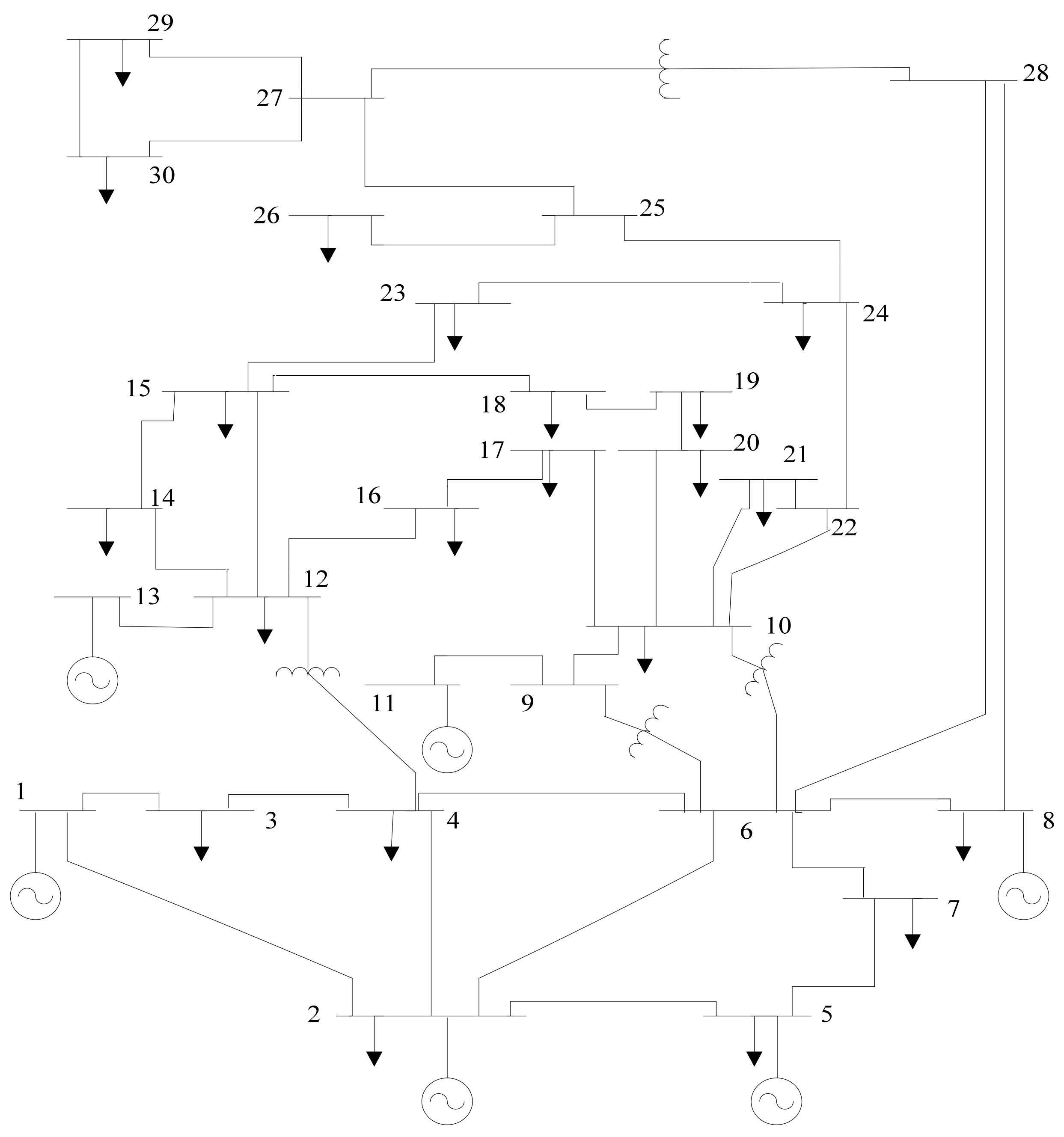
4.1. OPF Solutions IEEE 30-Bus Network [56]
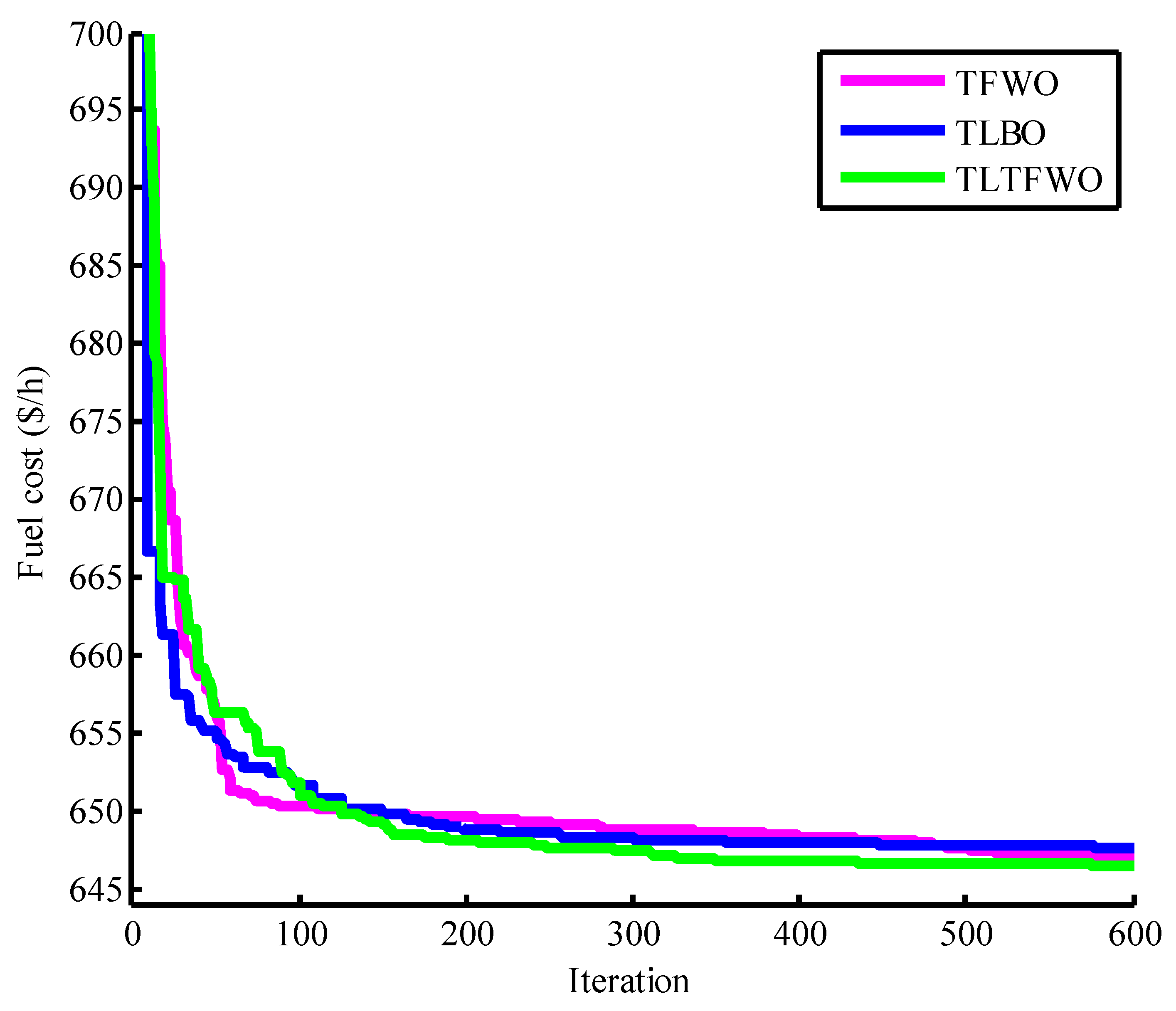
4.1.1. Case 1: Minimization of Fuel Cost
4.1.2. Case 2: Minimization of Piecewise Quadratic Fuel Cost
4.1.3. Case 3: Minimization of Fuel Cost Considering VPEs
4.1.4. Case 4: Minimization of Real Power Loss and Fuel Cost
4.1.5. Case 5: Minimization of Fuel Cost and Voltage Deviation
4.1.6. Case 6: Minimization of Fuel Cost, Emissions, Voltage Deviation and Losses
4.2. OPF Problem Solution in the Presence of WT and PV Units
4.2.1. Case 7: Minimizing the Generation Cost When Incorporating WT and PV Generation
4.2.2. Case 8: Minimizing Generation Cost in the Presence of WT and PV Units with the Carbon Tax
4.3. Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pourakbari-Kasmaei, M.; Mantovani, J.R.S. Logically constrained optimal power flow: Solver-based mixed-integer nonlinear programming model. Int. J. Electr. Power Energy Syst. 2018, 97, 240–249. [Google Scholar] [CrossRef]
- Momoh, J.A.; Adapa, R.; El-Hawary, M.E. A review of selected optimal power flow literature to 1993. I. Nonlinear and quadratic programming approaches. IEEE Trans. Power Syst. 1999, 14, 96–104. [Google Scholar] [CrossRef]
- Momoh, J.A.; El-Hawary, M.E.; Adapa, R. A review of selected optimal power flow literature to 1993. II. Newton, linear programming and interior point methods. IEEE Trans. Power Syst. 1999, 14, 105–111. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Gitizadeh, M.; Akbari, E. An improved teaching–learning-based optimization algorithm using Lévy mutation strategy for non-smooth optimal power flow. Int. J. Electr. Power Energy Syst. 2015, 65, 375–384. [Google Scholar] [CrossRef]
- Dasgupta, K.; Roy, P.K.; Mukherjee, V. Power flow based hydro-thermal-wind scheduling of hybrid power system using sine cosine algorithm. Electr. Power Syst. Res. 2020, 178, 106018. [Google Scholar] [CrossRef]
- Attia, A.-F.; el Sehiemy, R.A.; Hasanien, H.M. Optimal power flow solution in power systems using a novel Sine-Cosine algorithm. Int. J. Electr. Power Energy Syst. 2018, 99, 331–343. [Google Scholar] [CrossRef]
- Güçyetmez, M.; Çam, E. A new hybrid algorithm with genetic-teaching learning optimization (G-TLBO) technique for optimizing of power flow in wind-thermal power systems. Electr. Eng. 2016, 98, 145–157. [Google Scholar] [CrossRef]
- Pham, L.H.; Dinh, B.H.; Nguyen, T.T. Optimal power flow for an integrated wind-solar-hydro-thermal power system considering uncertainty of wind speed and solar radiation. Neural Comput. Appl. 2022, 34, 10655–10689. [Google Scholar] [CrossRef]
- El-Fergany, A.A.; Hasanien, H.M. Single and Multi-objective Optimal Power Flow Using Grey Wolf Optimizer and Differential Evolution Algorithms. Electr. Power Compon. Syst. 2015, 43, 1548–1559. [Google Scholar] [CrossRef]
- Maheshwari, A.; Sood, Y.R. Solution approach for optimal power flow considering wind turbine and environmental emissions. Wind Eng. 2022, 46, 480–502. [Google Scholar] [CrossRef]
- Narimani, M.R.; Azizipanah-Abarghooee, R.; Zoghdar-Moghadam-Shahrekohne, B.; Gholami, K. A novel approach to multi-objective optimal power flow by a new hybrid optimization algorithm considering generator constraints and multi-fuel type. Energy 2013, 49, 119–136. [Google Scholar] [CrossRef]
- Duman, S.; Wu, L.; Li, J. Moth swarm algorithm based approach for the ACOPF considering wind and tidal energy. In The International Conference on Artificial Intelligence and Applied Mathematics in Engineering; Springer: Cham, Switzerland, 2019; pp. 830–843. [Google Scholar]
- Herbadji, O.; Slimani, L.; Bouktir, T. Optimal power flow with four conflicting objective functions using multi-objective ant lion algorithm: A case study of the algerian electrical network. Iran. J. Electr. Electron. Eng. 2019, 15, 94–113. [Google Scholar] [CrossRef]
- Nguyen, T.T. A high performance social spider optimization algorithm for optimal power flow solution with single objective optimization. Energy 2019, 171, 218–240. [Google Scholar] [CrossRef]
- Riaz, M.; Hanif, A.; Hussain, S.J.; Memon, M.I.; Ali, M.U.; Zafar, A. An optimization-based strategy for solving optimal power flow problems in a power system integrated with stochastic solar and wind power energy. Appl. Sci. 2021, 11, 6883. [Google Scholar] [CrossRef]
- Sarda, J.; Pandya, K.; Lee, K.Y. Hybrid cross entropy—Cuckoo search algorithm for solving optimal power flow with renewable generators and controllable loads. Optim. Control. Appl. Methods 2021, 1–25. [Google Scholar] [CrossRef]
- Sarhan, S.; El-Sehiemy, R.; Abaza, A.; Gafar, M. Turbulent Flow of Water-Based Optimization for Solving Multi-Objective Technical and Economic Aspects of Optimal Power Flow Problems. Mathematics 2022, 10, 2106. [Google Scholar] [CrossRef]
- Khan, I.U.; Javaid, N.; Gamage, K.A.A.; Taylor, C.J.; Baig, S.; Ma, X. Heuristic algorithm based optimal power flow model incorporating stochastic renewable energy sources. IEEE Access 2020, 8, 148622–148643. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, P.N.; Amaratunga, G.A.J. Optimal power flow solutions incorporating stochastic wind and solar power. Energy Convers. Manag. 2017, 148, 1194–1207. [Google Scholar] [CrossRef]
- Ali, Z.M.; Aleem, S.H.E.A.; Omar, A.I.; Mahmoud, B.S. Economical-environmental-technical operation of power networks with high penetration of renewable energy systems using multi-objective coronavirus herd immunity algorithm. Mathematics 2022, 10, 1201. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Akbari, E.; Vahed, A.A. Solving nonlinear, non-smooth and non-convex optimal power flow problems using chaotic invasive weed optimization algorithms based on chaos. Energy 2014, 73, 340–353. [Google Scholar] [CrossRef]
- Elattar, E.E. Optimal power flow of a power system incorporating stochastic wind power based on modified moth swarm algorithm. IEEE Access 2019, 7, 89581–89593. [Google Scholar] [CrossRef]
- Ma, R.; Li, X.; Luo, Y.; Wu, X.; Jiang, F. Multi-objective dynamic optimal power flow of wind integrated power systems considering demand response. CSEE J. Power Energy Syst. 2019, 5, 466–473. [Google Scholar] [CrossRef]
- Salkuti, S.R. Optimal power flow using multi-objective glowworm swarm optimization algorithm in a wind energy integrated power system. Int. J. Green Energy 2019, 16, 1547–1561. [Google Scholar] [CrossRef]
- Ahmad, M.; Javaid, N.; Niaz, I.A.; Almogren, A.; Radwan, A. A Bio-Inspired Heuristic Algorithm for Solving Optimal Power Flow Problem in Hybrid Power System. IEEE Access 2021, 9, 159809–159826. [Google Scholar] [CrossRef]
- Kyomugisha, R.; Muriithi, C.M.; Edimu, M. Multi-objective optimal power flow for static voltage stability margin improvement. Heliyon 2021, 7, e08631. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, B.; Wang, P.; Liang, J.; Yuan, Y.; Huang, Y.; Lei, X. Multi-objective optimal power flow based on improved strength Pareto evolutionary algorithm. Energy 2017, 122, 70–82. [Google Scholar] [CrossRef]
- Maheshwari, A.; Sood, Y.R.; Jaiswal, S.; Sharma, S.; Kaur, J. Ant Lion Optimization Based OPF Solution Incorporating Wind Turbines and Carbon Emissions. In Proceedings of the 2021 Innovations in Power and Advanced Computing Technologies (i-PACT), Kuala Lumpur, Malaysia, 27–29 November 2021; pp. 1–6. [Google Scholar]
- Elattar, E.E.; ElSayed, S.K. Modified JAYA algorithm for optimal power flow incorporating renewable energy sources considering the cost, emission, power loss and voltage profile improvement. Energy 2019, 178, 598–609. [Google Scholar] [CrossRef]
- El-Sattar, S.A.; Kamel, S.; Ebeed, M.; Jurado, F. An improved version of salp swarm algorithm for solving optimal power flow problem. Soft Comput. 2021, 25, 4027–4052. [Google Scholar] [CrossRef]
- Abdo, M.; Kamel, S.; Ebeed, M.; Yu, J.; Jurado, F. Solving non-smooth optimal power flow problems using a developed grey wolf optimizer. Energies 2018, 11, 1692. [Google Scholar] [CrossRef]
- Mouassa, S.; Althobaiti, A.; Jurado, F.; Ghoneim, S.S.M. Novel Design of Slim Mould Optimizer for the Solution of Optimal Power Flow Problems Incorporating Intermittent Sources: A Case Study of Algerian Electricity Grid. IEEE Access 2022, 10, 22646–22661. [Google Scholar] [CrossRef]
- Chen, G.; Qian, J.; Zhang, Z.; Sun, Z. Multi-objective optimal power flow based on hybrid firefly-bat algorithm and constraints-prior object-fuzzy sorting strategy. IEEE Access 2019, 7, 139726–139745. [Google Scholar] [CrossRef]
- Naderipour, A.; Davoudkhani, I.F.; Abdul-Malek, Z. New modified algorithm: θ-turbulent flow of water-based optimization. Environ. Sci. Pollut. Res. 2021, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.; Qi, X.; Lei, R.; Li, J. Slope reliability evaluation using an improved Kriging active learning method with various active learning functions. Arab. J. Geosci. 2022, 15, 1–13. [Google Scholar] [CrossRef]
- Sallam, M.E.; Attia, M.A.; Abdelaziz, A.Y.; Sameh, M.A.; Yakout, A.H. Optimal Sizing of Different Energy Sources in an Isolated Hybrid Microgrid Using Turbulent Flow Water-Based Optimization Algorithm. IEEE Access 2022, 10, 61922–61936. [Google Scholar] [CrossRef]
- Eid, A.; Kamel, S. Optimal allocation of shunt compensators in distribution systems using turbulent flow of waterbased optimization Algorithm. In Proceedings of the 2020 IEEE Electric Power and Energy Conference (EPEC), Edmonton, AB, Canada, 9–10 November 2020; pp. 1–5. [Google Scholar]
- Wahab, A.M.A.B.; Kamel, S.; Hassan, M.H.; Mosaad, M.I.; AbdulFattah, T.A. Optimal Reactive Power Dispatch Using a Chaotic Turbulent Flow of Water-Based Optimization Algorithm. Mathematics 2022, 10, 346. [Google Scholar] [CrossRef]
- Said, M.; Shaheen, A.M.; Ginidi, A.R.; El-Sehiemy, R.A.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. Estimating parameters of photovoltaic models using accurate turbulent flow of water optimizer. Processes 2021, 9, 627. [Google Scholar] [CrossRef]
- Abdelminaam, D.S.; Said, M.; Houssein, E.H. Turbulent flow of water-based optimization using new objective function for parameter extraction of six photovoltaic models. IEEE Access 2021, 9, 35382–35398. [Google Scholar] [CrossRef]
- Nasri, S.; Nowdeh, S.A.; Davoudkhani, I.F.; Moghaddam, M.J.H.; Kalam, A.; Shahrokhi, S.; Zand, M. Maximum Power point tracking of Photovoltaic Renewable Energy System using a New method based on turbulent flow of water-based optimization (TFWO) under Partial shading conditions. In Fundamentals and Innovations in Solar Energy; Springer: Berlin/Heidelberg, Germany, 2021; pp. 285–310. [Google Scholar]
- Fayek, H.H.; Abdalla, O.H. Optimal Settings of BTB-VSC in Interconnected Power System Using TFWO. In Proceedings of the 2021 IEEE 30th International Symposium on Industrial Electronics (ISIE), Kyoto, Japan, 20–23 June 2021; pp. 1–6. [Google Scholar]
- Kurban, R.; Durmus, A.; Karakose, E. A comparison of novel metaheuristic algorithms on color aerial image multilevel thresholding. Eng. Appl. Artif. Intell. 2021, 105, 104410. [Google Scholar] [CrossRef]
- Sakthivel, V.P.; Thirumal, K.; Sathya, P.D. Quasi-oppositional turbulent water flow-based optimization for cascaded short term hydrothermal scheduling with valve-point effects and multiple fuels. Energy 2022, 251, 123905. [Google Scholar] [CrossRef]
- Suresh, G.; Prasad, D.; Gopila, M. An efficient approach based power flow management in smart grid system with hybrid renewable energy sources. Renew. Energy Focus 2021, 39, 110–122. [Google Scholar]
- Deb, S.; Houssein, E.H.; Said, M.; Abdelminaam, D.S. Performance of turbulent flow of water optimization on economic load dispatch problem. IEEE Access 2021, 9, 77882–77893. [Google Scholar] [CrossRef]
- Gnanaprakasam, C.N.; Brindha, G.; Gnanasoundharam, J.; Devi, E.A. An efficient MFM-TFWO approach for unit commitment with uncertainty of DGs in electric vehicle parking lots. J. Intell. Fuzzy Syst. 2022, 43, 1–26. [Google Scholar] [CrossRef]
- Sakthivel, V.P.; Thirumal, K.; Sathya, P.D. Short term scheduling of hydrothermal power systems with photovoltaic and pumped storage plants using quasi-oppositional turbulent water flow optimization. Renew. Energy 2022, 191, 459–492. [Google Scholar] [CrossRef]
- Witanowski, Ł.; Breńkacz, Ł.; Szewczuk-Krypa, N.; Dorosińska-Komor, M.; Puchalski, B. Comparable analysis of PID controller settings in order to ensure reliable operation of active foil bearings. Eksploat. Niezawodn. 2022, 24, 377–385. [Google Scholar] [CrossRef]
- Swief, R.A.; Hassan, N.M.; Hasanien, H.M.; Abdelaziz, A.Y.; Kamh, M.Z. Multi-regional optimal power flow using marine predators algorithm considering load and generation variability. IEEE Access 2021, 9, 74600–74613. [Google Scholar] [CrossRef]
- Khamees, A.K.; Abdelaziz, A.Y.; Eskaros, M.R.; Alhelou, H.H.; Attia, M.A. Stochastic Modeling for Wind Energy and Multi-Objective Optimal Power Flow by Novel Meta-Heuristic Method. IEEE Access 2021, 9, 158353–158366. [Google Scholar] [CrossRef]
- Fathy, A.; Abdelaziz, A. Single-objective optimal power flow for electric power systems based on crow search algorithm. Arch. Electr. Eng. 2018, 67. [Google Scholar] [CrossRef]
- Ullah, Z.; Wang, S.; Radosavljević, J.; Lai, J. A Solution to the Optimal Power Flow Problem Considering WT and PV Generation. IEEE Access 2019, 7, 46763–46772. [Google Scholar] [CrossRef]
- Panda, A.; Tripathy, M.; Barisal, A.K.; Prakash, T. A modified bacteria foraging based optimal power flow framework for Hydro-Thermal-Wind generation system in the presence of STATCOM. Energy 2017, 124, 720–740. [Google Scholar] [CrossRef]
- Alghamdi, A.S. Optimal Power Flow in Wind–Photovoltaic Energy Regulation Systems Using a Modified Turbulent Water Flow-Based Optimization. Sustainability 2022, 14, 16444. [Google Scholar] [CrossRef]
- Mohamed, A.-A.A.; Mohamed, Y.S.; El-Gaafary, A.A.M.; Hemeida, A.M. Optimal power flow using moth swarm algorithm. Electr. Power Syst. Res. 2017, 142, 190–206. [Google Scholar] [CrossRef]
- Abido, M.A. Optimal Power Flow Using Tabu Search Algorithm. Electr. Power Compon. Syst. 2002, 30, 469–483. [Google Scholar] [CrossRef]
- Abaci, K.; Yamacli, V. Differential search algorithm for solving multi-objective optimal power flow problem. Int. J. Electr. Power Energy Syst. 2016, 79, 1–10. [Google Scholar] [CrossRef]
- Niknam, T.; Narimani, M.r.; Jabbari, M.; Malekpour, A.R. A modified shuffle frog leaping algorithm for multi-objective optimal power flow. Energy 2011, 36, 6420–6432. [Google Scholar] [CrossRef]
- Sayah, S.; Zehar, K. Modified differential evolution algorithm for optimal power flow with non-smooth cost functions. Energy Convers. Manag. 2008, 49, 3036–3042. [Google Scholar] [CrossRef]
- Hazra, J.; Sinha, A.K. A multi-objective optimal power flow using particle swarm optimization. Eur. Trans. Electr. Power 2011, 21, 1028–1045. [Google Scholar] [CrossRef]
- Niknam, T.; Narimani, M.R.; Aghaei, J.; Tabatabaei, S.; Nayeripour, M. Modified Honey Bee Mating Optimisation to solve dynamic optimal power flow considering generator constraints. IET Gener. Transm. Distrib. 2011, 5, 989. [Google Scholar] [CrossRef]
- Sood, Y. Evolutionary programming based optimal power flow and its validation for deregulated power system analysis. Int. J. Electr. Power Energy Syst. 2007, 29, 65–75. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Ghanbarian, M.M.; Gitizadeh, M. Multi-objective optimal electric power planning in the power system using Gaussian bare-bones imperialist competitive algorithm. Inf. Sci. 2015, 294, 286–304. [Google Scholar] [CrossRef]
- Khamees, A.K.; Abdelaziz, A.Y.; Eskaros, M.R.; El-Shahat, A.; Attia, M.A. Optimal Power Flow Solution of Wind-Integrated Power System Using Novel Metaheuristic Method. Energies 2021, 14, 6117. [Google Scholar] [CrossRef]
- Radosavljević, J.; Klimenta, D.; Jevtić, M.; Arsić, N. Optimal Power Flow Using a Hybrid Optimization Algorithm of Particle Swarm Optimization and Gravitational Search Algorithm. Electr. Power Compon. Syst. 2015, 43, 1958–1970. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Rahmani, S.; Roosta, A.; Falah, H. A novel hybrid algorithm of imperialist competitive algorithm and teaching learning algorithm for optimal power flow problem with non-smooth cost functions. Eng. Appl. Artif. Intell. 2014, 29, 54–69. [Google Scholar] [CrossRef]
- Kumar, A.R.; Premalatha, L. Optimal power flow for a deregulated power system using adaptive real coded biogeography-based optimization. Int. J. Electr. Power Energy Syst. 2015, 73, 393–399. [Google Scholar] [CrossRef]
- Guvenc, U.; Bakir, H.; Duman, S.; Ozkaya, B. Optimal Power Flow Using Manta Ray Foraging Optimization. In The International Conference on Artificial Intelligence and Applied Mathematics in Engineering; Springer: Cham, Switzerland, 2020; pp. 136–149. [Google Scholar]
- Pulluri, H.; Naresh, R.; Sharma, V. A solution network based on stud krill herd algorithm for optimal power flow problems. Soft Comput. 2018, 22, 159–176. [Google Scholar] [CrossRef]
- Ongsakul, W.; Tantimaporn, T. Optimal Power Flow by Improved Evolutionary Programming. Electr. Power Compon. Syst. 2006, 34, 79–95. [Google Scholar] [CrossRef]
- Alghamdi, A.S. A Hybrid Firefly-JAYA Algorithm for the Optimal Power Flow Problem Considering Wind and Solar Power Generations. Appl. Sci. 2022, 12, 7193. [Google Scholar] [CrossRef]
- Warid, W.; Hizam, H.; Mariun, N.; Abdul-Wahab, N.I. Optimal power flow using the Jaya algorithm. Energies 2016, 9, 678. [Google Scholar] [CrossRef]
- Roy, R.; Jadhav, H.T. Optimal power flow solution of power system incorporating stochastic wind power using Gbest guided artificial bee colony algorithm. Int. J. Electr. Power Energy Syst. 2015, 64, 562–578. [Google Scholar] [CrossRef]
- Jebaraj, L.; Sakthivel, S. A new swarm intelligence optimization approach to solve power flow optimization problem incorporating conflicting and fuel cost based objective functions. e-Prime-Adv. Electr. Eng. Electron. Energy 2022, 2, 100031. [Google Scholar]
- Biswas, P.P.; Suganthan, P.N.; Mallipeddi, R.; Amaratunga, G.A.J. Optimal power flow solutions using differential evolution algorithm integrated with effective constraint handling techniques. Eng. Appl. Artif. Intell. 2018, 68, 81–100. [Google Scholar] [CrossRef]
- Bouchekara, H.R.E.H.; Chaib, A.E.; Abido, M.A.; El-Sehiemy, R.A. Optimal power flow using an Improved Colliding Bodies Optimization algorithm. Appl. Soft Comput. 2016, 42, 119–131. [Google Scholar] [CrossRef]
- Bentouati, B.; Khelifi, A.; Shaheen, A.M.; El-Sehiemy, R.A. An enhanced moth-swarm algorithm for efficient energy management based multi dimensions OPF problem. J. Ambient Intell. Humaniz. Comput 2020, 12, 9499–9519. [Google Scholar] [CrossRef]
- Warid, W.; Hizam, H.; Mariun, N.; Wahab, N.I.A. A novel quasi-oppositional modified Jaya algorithm for multi-objective optimal power flow solution. Appl. Soft Comput. 2018, 65, 360–373. [Google Scholar] [CrossRef]
- Ghoneim, S.S.M.; Kotb, M.F.; Hasanien, H.M.; Alharthi, M.M.; El-Fergany, A.A. Cost Minimizations and Performance Enhancements of Power Systems Using Spherical Prune Differential Evolution Algorithm Including Modal Analysis. Sustainability 2021, 13, 8113. [Google Scholar] [CrossRef]
- El Sehiemy, R.A.; Selim, F.; Bentouati, B.; Abido, M.A. A novel multi-objective hybrid particle swarm and salp optimization algorithm for technical-economical-environmental operation in power systems. Energy 2020, 193, 116817. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Ghanbarian, M.M.; Gharibzadeh, M.; Vahed, A.A. Multi-objective optimal power flow considering the cost, emission, voltage deviation and power losses using multi-objective modified imperialist competitive algorithm. Energy 2014, 78, 276–289. [Google Scholar] [CrossRef]
- Shilaja, C.; Ravi, K. Optimal power flow using hybrid DA-APSO algorithm in renewable energy resources. Energy Procedia 2017, 117, 1085–1092. [Google Scholar] [CrossRef]
- Ouafa, H.; Linda, S.; Tarek, B. Multi-objective optimal power flow considering the fuel cost, emission, voltage deviation and power losses using Multi-Objective Dragonfly algorithm. In Proceedings of the International Conference on Recent Advances in Electrical Systems, Tunisia, North Africa, 22–24 December 2017. [Google Scholar]
- Gupta, S.; Kumar, N.; Srivastava, L.; Malik, H.; Marugán, A.P.; Márquez, F.G. A Hybrid Jaya-Powell’s Pattern Search Algorithm for Multi-Objective Optimal Power Flow Incorporating Distributed Generation. Energies 2021, 14, 2831. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, S.; Tang, Q.; Zhou, Y.; Zeng, T. An improved NSGA-III integrating adaptive elimination strategy to solution of many-objective optimal power flow problems. Energy 2019, 172, 945–957. [Google Scholar] [CrossRef]
- Ghasemi, M.; Akbari, E.; Rahimnejad, A.; Razavi, S.E.; Ghavidel, S.; Li, L. Phasor particle swarm optimization: A simple and efficient variant of PSO. Soft Comput. 2019, 23, 9701–9718. [Google Scholar] [CrossRef]
- Pizzuti, C. Ga-net: A genetic algorithm for community detection in social networks. In International Conference on Parallel Problem Solving from Nature; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1081–1090. [Google Scholar]






| Reference | The proposed Methods | Studied Power Systems | Objectives |
|---|---|---|---|
| [4] | Teaching-learning-based optimization (TLBO) and Lévy TLBO (LTLBO) | IEEE 30-bus and IEEE 57-bus | Minimization of fuel cost without and with valve point loadings, improvement of voltage profile, piecewise quadratic fuel cost functions, and emission. |
| [5] | Sine cosine algorithm (SCA) | Standard 9-bus system | Hydrothermal scheduling (HTS) problem for optimizing fuel cost, emission and combined cost emission |
| [6] | A modified sine cosine algorithm (MSCA) | IEEE-30 bus and IEEE 118-bus systems | Minimizing the overall fuel cost, the active power transmission losses, and improving the voltage profile at load buses by reducing the voltage deviation |
| [7] | TLBO and genetic algorithm (GA) | 19 bus 7336 MW Turkish-wind-thermal power system | Fuel costs for three different loading situations. |
| [8] | An effective cuckoo search algorithm (ECSA) | IEEE-30 bus system | Minimizing the overall fuel cost, the active power transmission losses, and improving the voltage profile at load buses by reducing the voltage deviation |
| [9] | Grey wolf optimizer (GWO) and differential evolution (DE) | IEEE-30 bus and IEEE 118-bus systems | Minimizing the overall fuel cost, the active and reactive power transmission losses, and the voltage security index |
| [10] | Ant lion optimization (ALO) | IEEE 30 and IEEE 57-bus systems | Operating cost, voltage profile, and transmission power losses |
| [11] | Particle Swarm Optimization (PSO) and Shuffle Frog Leaping algorithms (SFLA) | IEEE 30, IEEE 57 and IEEE 118-bus systems | Power generation involving the prohibited zones, valve point effect and multi-fuel type of generation units, voltage profile, voltage security index, and transmission power losses |
| [12] | Moth Swarm Algorithm (MSA) | IEEE 30-bus test system | Operating cost with and without the consideration of prohibited operating zones |
| [13] | Multi-objective ant lion algorithm (MOALA) | IEEE 30-bus, IEEE 57-bus, IEEE 118-bus, IEEE 300-bus systems and on practical Algerian DZ114-bus system | Generation cost, environmental pollution emission, active power losses, and voltage deviation |
| [14] | Social spider optimization (SSO) algorithms | IEEE 30, IEEE 57 and IEEE 118-bus systems | Fuel cost, power loss, polluted emission, voltage deviation and voltage security index |
| [15] | A hybridization of PSO with GWO | Modified IEEE 30 bus test system | Generation costs without and with considering valve point effects, and carbon tax |
| [16] | Cross entropy-cuckoo search algorithm (CE-CSA) | Modified IEEE 57 bus system | Generation costs with wind energy and solar PV generators and controllable loads |
| [17] | Turbulent flow of water-based optimization (TFWO) | IEEE 30-, 57-bus test system and four large-scale power systems called IEEE, 300-bus, 1354pegase, 3012wp, and IEEE 9241pegase power systems. | Minimize the fuel cost, emission, active power loss, voltage deviation at the load buses, and voltage stability index (VSI) |
| [18] | Grey wolf optimizer (GWO) | Modified IEEE-30 and IEEE-57 bus test systems | Generation cost considering renewable energy sources (RES) |
| [19] | Success history-based adaptive differential evolution (SADE) | Modified IEEE 30 bus system | Generation cost considering renewable energy sources (RES) |
| [20] | Coronavirus herd immunity optimizer (CHIO), salp swarm algorithm (SSA), and ant lion optimizer (ALO) | IEEE 30-bus and IEEE 57-bus systems | Total fuel costs, emissions level, power losses, voltage deviation, and voltage stability |
| [21] | Chaotic invasive weed optimization algorithms (CIWOs) | IEEE 30 bus test system | Power generation involving the prohibited zones, valve point effect and multi-fuel type of generation units |
| [22] | Modified moth swarm algorithm (MMSA) | Modified IEEE-30 and IEEE-118 bus test systems | Total fuel costs considering renewable energy sources (RES), power losses, voltage deviation |
| [23] | A hybrid of a non-dominated sorting genetic algorithm-II (NSGA-II) and fuzzy satisfaction-maximizing method | IEEE 6-units\30-nodes system | Multi-objective dynamic OPF (MDOPF) considering wind generation (WG) and demand response (DR) with fuel cost, carbon emission and active power losses |
| [24] | Multi-objective glowworm swarm optimization (MOGSO) | Modified IEEE 30 and 300 bus systems | Total generation cost, transmission losses, and voltage stability enhancement index |
| [25] | Bird swarm algorithm (BSA) | IEEE 30 bus system | Total fuel costs and emissions |
| [26] | Multi-objective PSO (MOPSO) | IEEE 30-bus and IEEE 57-bus systems | Generation cost, transmission loss, and the maximum voltage collapse proximity index (VCPI) |
| [27] | Modified strength Pareto evolutionary algorithm | IEEE 30-bus and IEEE 57-bus systems | Fuel cost and emission |
| [28] | Ant lion optimization (ALO) | Modified IEEE 30 bus system | Operational costs, voltage profile, and system-wide transmission power losses |
| [29] | Modified Jaya | IEEE 30-bus and IEEE 118-bus systems | Operational costs, emission, power loss and voltage profile improvement |
| [30] | Improved salp swarm algorithm (ISSA) in compared with moth-flame optimization (MFO), improved harmony search (IHS), genetic algorithm (GA) | IEEE 30-bus, IEEE 57-bus and IEEE 118-bus systems | Minimize quadratic fuel cost, piecewise and quadratic fuel cost, considering the valve-point effect and prohibited zones. |
| [31] | Developed GWO (DGWO) | IEEE 30 bus system | Quadratic fuel cost minimization, piecewise quadratic cost minimization, and quadratic fuel cost minimization considering the valve point effect. |
| [32] | Slime mould algorithm (SMA) in compared with gorilla troops optimizer (GTO), orca predation algorithm (OPA), artificial ecosystem optimizer (AEO), hunger games search (HGS), jellyfish search (JS) optimizer, and success-history-based parameter adaptation for DE. | IEEE 30-bus test system and Algerian power system, DZA 114-bus | The overall cost of the system, including reserve cost for over-estimation and penalty cost for under-estimation of both PV-solar and wind energy. |
| [33] | A novel hybrid firefly-bat algorithm with constraints-prior object-fuzzy sorting strategy (HFBA-COFS) | IEEE 30-bus, IEEE 57-bus and IEEE 118-bus systems | Active power loss, total emission and fuel cost |
| Reference | Year | Contribution | Area of the Application |
|---|---|---|---|
| [34] | 2021 | θ-turbulent flow of water-based optimization (θ-TFWO) | Reactive power control of a power system |
| [35] | 2022 | TFWO | Slope reliability evaluation, estimate the correlation parameter of Kriging method |
| [36] | 2022 | TFWO | Optimal sizing of different energy sources in an isolated hybrid micro-grid |
| [37] | 2020 | TFWO | Optimal placement of parallel compensators at the distribution level |
| [38] | 2022 | Chaotic TFWO | Optimal reactive power dispatch (ORPD) problems in the power systems |
| [39,40,41] | 2021 | TFWO | Estimating parameters of photovoltaic models |
| [42] | 2021 | TFWO | Finding optimal parameters of the back-to-back voltage source converters (BTB-VSC) |
| [43] | 2021 | TFWO | Color aerial image multilevel thresholding |
| [44] | 2022 | Quasi-oppositional TFWO | Short-term hydrothermal scheduling (SHTS) |
| [45] | 2021 | A hybrid of TFWO and battle royale optimization (BRO), called TFW-BRO | Power flow in smart grids using renewables |
| [46] | 2021 | TFWO | Economic load dispatch (ELD) problems in the power systems |
| [47] | 2022 | A combined of multi-fidelity meta-optimization (MFM) and TFWO (MFM-TFWO) | Unit commitment (UC) in the power systems |
| [48] | 2022 | Quasi-oppositional TFWO | Short term planning of hydrothermal power systems with PVs and pumped-storage plants |
| [49] | 2022 | TFWO | Selecting the parameters of a proportional-integral-derivative (PID) controller |
| Parameters | Cases: | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| PG1 | 177.1398 | 139.9991 | 198.7424 | 102.6131 | 176.2434 | 122.1760 |
| PG2 | 48.7069 | 55.0000 | 44.8704 | 55.5533 | 48.8509 | 52.5571 |
| PG5 | 21.3886 | 24.0889 | 18.4725 | 38.1107 | 21.6373 | 31.4806 |
| PG8 | 21.2540 | 34.9994 | 10.0001 | 35.0000 | 22.2667 | 35.0000 |
| PG11 | 11.9311 | 18.3672 | 10.0000 | 30.0000 | 12.2386 | 26.7497 |
| PG13 | 12.0000 | 17.6834 | 12.0002 | 26.6524 | 12.0008 | 21.0234 |
| VG1 | 1.0839 | 1.0744 | 1.0816 | 1.0698 | 1.0421 | 1.0731 |
| VG2 | 1.0607 | 1.0572 | 1.0581 | 1.0576 | 1.0226 | 1.0574 |
| VG5 | 1.0340 | 1.0312 | 1.0309 | 1.0359 | 1.0137 | 1.0327 |
| VG8 | 1.0383 | 1.0392 | 1.0372 | 1.0438 | 1.0057 | 1.0409 |
| VG11 | 1.0996 | 1.0869 | 1.0986 | 1.0835 | 1.0732 | 1.0402 |
| VG13 | 1.0513 | 1.0666 | 1.0629 | 1.0573 | 0.9875 | 1.0244 |
| T6–9 | 1.0707 | 1.0249 | 1.0412 | 1.0857 | 1.0998 | 1.0999 |
| T6–10 | 0.9183 | 0.9590 | 0.9730 | 0.9000 | 0.9001 | 0.9512 |
| T4–12 | 0.9762 | 1.0015 | 0.9952 | 0.9901 | 0.9385 | 1.0326 |
| T28–27 | 0.9737 | 0.9731 | 0.9782 | 0.9750 | 0.9711 | 1.0047 |
| QC10 | 2.4939 | 3.6587 | 4.5988 | 4.5252 | 4.9938 | 3.1650 |
| QC12 | 1.0909 | 0.0003 | 1.9342 | 0.1672 | 0.0542 | 0.0312 |
| QC15 | 4.4547 | 3.9139 | 4.3825 | 4.4646 | 4.9993 | 3.8300 |
| QC17 | 5.0000 | 5.0000 | 4.9907 | 5.0000 | 0 | 4.9997 |
| QC20 | 4.2352 | 4.2499 | 4.3793 | 4.2524 | 5.0000 | 4.9999 |
| QC21 | 5.0000 | 5.0000 | 4.9994 | 5.0000 | 4.9981 | 5.0000 |
| QC23 | 3.2543 | 3.3075 | 3.1515 | 3.2616 | 4.9980 | 4.2227 |
| QC24 | 5.0000 | 5.0000 | 4.9987 | 5.0000 | 4.9999 | 5.0000 |
| QC29 | 2.6470 | 2.6285 | 2.6856 | 2.5559 | 2.6457 | 2.6067 |
| Cost (USD/h) | 800.4780 | 646.4715 | 832.1584 | 859.0075 | 803.6829 | 830.2863 |
| Emission (t/h) | 0.3663 | 0.2835 | 0.4378 | 0.2289 | 0.3636 | 0.2529 |
| Power losses (MW) | 9.0204 | 6.7380 | 10.6856 | 4.5295 | 9.8377 | 5.5868 |
| V.D. (p.u.) | 0.9084 | 0.9152 | 0.8618 | 0.9279 | 0.0950 | 0.2976 |
| Optimizer | Fuel cost (USD/h) | Emission (t/h) | Power Losses (MW) | V.D. (p.u.) |
|---|---|---|---|---|
| TS [57] | 802.29 | - | - | - |
| ABC [58] | 800.660 | 0.365141 | 9.0328 | 0.9209 |
| SFLA-SA [59] | 801.79 | - | - | - |
| DE [60] | 802.39 | - | 9.466 | - |
| AGSO [61] | 801.75 | 0.3703 | - | - |
| MSA [56] | 800.5099 | 0.36645 | 9.0345 | 0.90357 |
| GWO [62] | 801.41 | - | 9.30 | - |
| EP [63] | 803.57 | - | - | - |
| MGBICA [64] | 801.1409 | 0.3296 | - | - |
| AO [65] | 801.83 | - | - | - |
| PSOGSA [66] | 800.49859 | - | 9.0339 | 0.12674 |
| MICA-TLA [67] | 801.0488 | - | 9.1895 | - |
| ARCBBO [68] | 800.5159 | 0.3663 | 9.0255 | 0.8867 |
| MHBMO [9] | 801.985 | - | 9.49 | - |
| MRFO [69] | 800.7680 | - | 9.1150 | - |
| FPA [56] | 802.7983 | 0.35959 | 9.5406 | 0.36788 |
| SKH [70] | 800.5141 | 0.3662 | 9.0282 | - |
| IEP [71] | 802.46 | - | - | - |
| HFAJAYA [72] | 800.4800 | 0.3659 | 9.0134 | 0.9047 |
| JAYA [73] | 800.4794 | - | 9.06481 | 0.1273 |
| FA [72] | 800.7502 | 0.36532 | 9.0219 | 0.9205 |
| MFO [56] | 800.6863 | 0.36849 | 9.1492 | 0.75768 |
| PPSOGSA [55] | 800.528 | - | 9.02665 | 0.91136 |
| MPSO-SFLA [11] | 801.75 | - | 9.54 | - |
| TFWO | 800.8426 | 0.3668 | 9.3207 | 0.9044 |
| TLBO | 800.9923 | 0.3369 | 9.4892 | 0.9026 |
| TLTFWO | 800.4780 | 0.3663 | 9.0204 | 0.9084 |
| Optimizer | Fuel cost (USD/h) | Emission (t/h) | Power Losses (MW) | V.D. (p.u.) |
|---|---|---|---|---|
| MSA [56] | 646.8364 | 0.28352 | 6.8001 | 0.84479 |
| GABC [74] | 647.03 | - | 6.8160 | 0.8010 |
| MFO [56] | 649.2727 | 0.28336 | 7.2293 | 0.47024 |
| MPSO-SFLA [11] | 647.55 | - | - | - |
| FPA [56] | 651.3768 | 0.28083 | 7.2355 | 0.31259 |
| LTLBO [4] | 647.4315 | 0.2835 | 6.9347 | 0.8896 |
| SSO [14] | 663.3518 | - | - | - |
| MDE [60] | 647.846 | - | 7.095 | - |
| SSA [75] | 646.7796 | 0.2836 | 6.5599 | 0.5320 |
| IEP [71] | 649.312 | - | - | - |
| MICA-TLA [67] | 647.1002 | - | 6.8945 | - |
| TFWO | 646.9425 | 0.2840 | 6.8026 | 0.9136 |
| TLBO | 647.5263 | 0.2838 | 6.8375 | 0.9102 |
| TLTFWO | 646.4715 | 0.2835 | 6.7380 | 0.9152 |
| Optimizer | Fuel Cost (USD/h) | Emission (t/h) | Power Losses (MW) | V.D. (p.u.) |
|---|---|---|---|---|
| HFAJAYA [72] | 832.1798 | 0.4378 | 10.6897 | 0.8578 |
| FA [72] | 832.5596 | 0.4372 | 10.6823 | 0.8539 |
| SP-DE [76] | 832.4813 | 0.43651 | 10.6762 | 0.75042 |
| PSO [77] | 832.6871 | - | - | - |
| TFWO | 832.6598 | 0.4382 | 10.9105 | 0.8410 |
| TLBO | 832.7624 | 0.4380 | 10.9397 | 0.8322 |
| TLTFWO | 832.1584 | 0.4378 | 10.6856 | 0.8618 |
| Optimizer | Fuel Cost (USD/h) | Emission (t/h) | Power Losses (MW) | V.D. (p.u.) | |
|---|---|---|---|---|---|
| EMSA [78] | 859.9514 | 0.2278 | 4.6071 | 0.7758 | 1044.2354 |
| MOALO [13] | 826.4556 | 0.2642 | 5.7727 | 1.2560 | 1057.3636 |
| MJaya [79] | 827.9124 | - | 5.7960 | - | 1059.7524 |
| MSA [56] | 859.1915 | 0.2289 | 4.5404 | 0.92852 | 1040.8075 |
| SpDEA [80] | 837.8510 | - | 5.6093 | 0.8106 | 1062.223 |
| QOMJaya [79] | 826.9651 | - | 5.7596 | - | 1402.9251 |
| TFWO | 860.1514 | 0.2292 | 4.5335 | 0.9145 | 1041.4914 |
| TLBO | 860.2684 | 0.2295 | 4.6002 | 0.9096 | 1044.2764 |
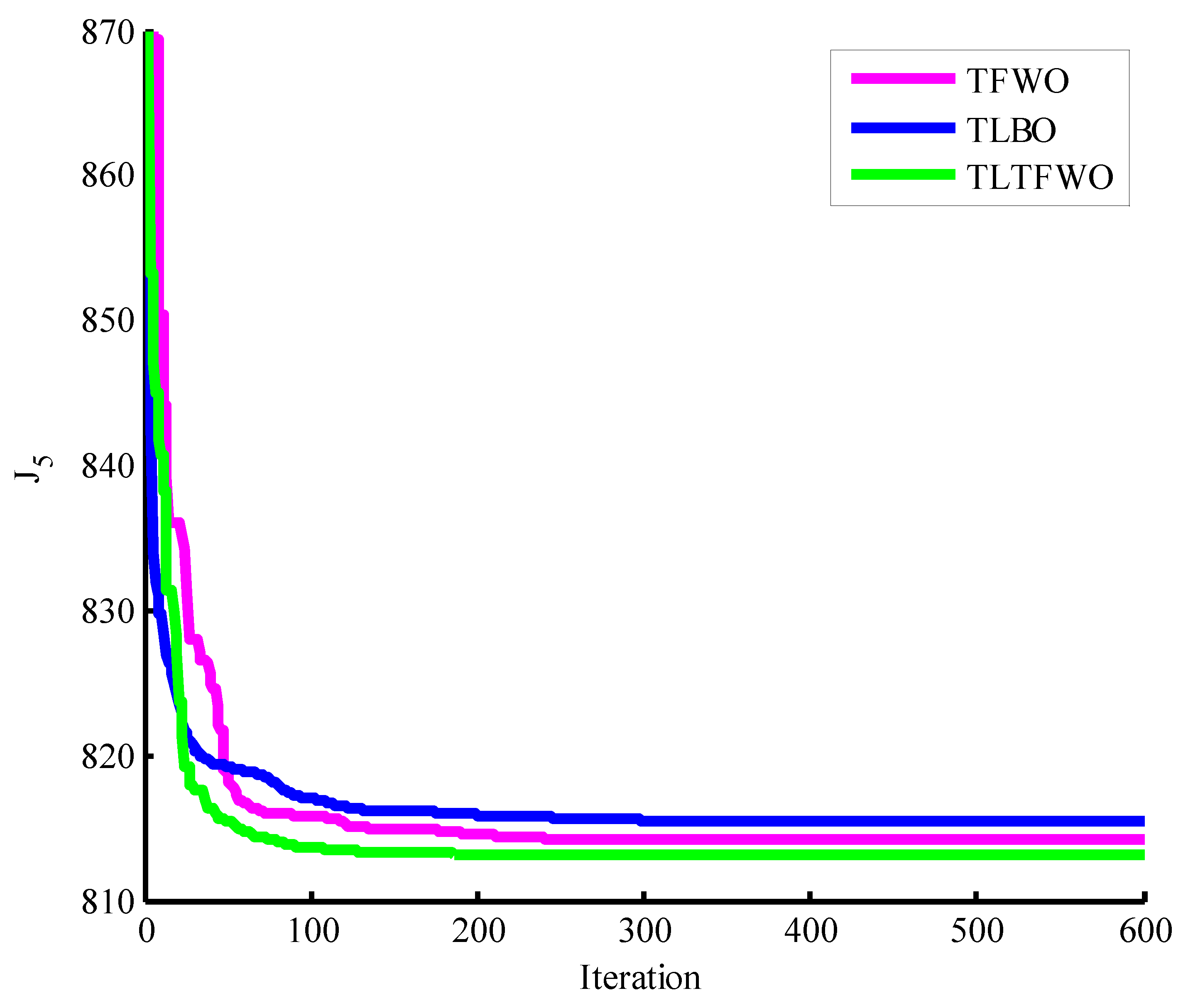
| TLTFWO | 859.0075 | 0.2289 | 4.5295 | 0.9279 | 1040.1875 |
| Optimizer | Fuel Cost (USD/h) | Emission (t/h) | Power Losses (MW) | V.D. (p.u.) | |
|---|---|---|---|---|---|
| PSO [81] | 804.477 | 0.368 | 10.129 | 0.126 | 817.0770 |
| PSO-SSO [81] | 803.9899 | 0.367 | 9.961 | 0.0940 | 813.3899 |
| BB-MOPSO [82] | 804.9639 | - | - | 0.1021 | 815.1739 |
| EMSA [78] | 803.4286 | 0.3643 | 9.7894 | 0.1073 | 814.1586 |
| TFWO [17] | 803.416 | 0.365 | 9.795 | 0.101 | 813.5160 |
| SpDEA [80] | 803.0290 | - | 9.0949 | 0.2799 | 831.0190 |
| MFO [56] | 803.7911 | 0.36355 | 9.8685 | 0.10563 | 814.3541 |
| DA-APSO [83] | 802.63 | - | - | 0.1164 | 814.2700 |
| SSO [81] | 803.73 | 0.365 | 9.841 | 0.1044 | 814.1700 |
| MOMICA [82] | 804.9611 | 0.3552 | 9.8212 | 0.0952 | 814.4811 |
| MPSO [56] | 803.9787 | 0.3636 | 9.9242 | 0.1202 | 815.9987 |
| MNSGA-II [82] | 805.0076 | - | - | 0.0989 | 814.8976 |
| TFWO | 804.2510 | 0.3639 | 10.1563 | 0.0998 | 814.2310 |
| TLBO | 804.7380 | 0.3671 | 9.9995 | 0.1065 | 815.3880 |
| TLTFWO | 803.6829 | 0.3636 | 9.8377 | 0.09450 | 813.1829 |
| Algorithm | Fuel Cost (USD/h) | Emission (t/h) | Power Losses (MW) | V.D. (p.u.) | |
|---|---|---|---|---|---|
| SSO [81] | 829.978 | 0.25 | 5.426 | 0.516 | 964.9360 |
| MODA [84] | 828.49 | 0.265 | 5.912 | 0.585 | 975.8740 |
| MNSGA-II [82] | 834.5616 | 0.2527 | 5.6606 | 0.4308 | 972.9429 |
| PSO [81] | 828.2904 | 0.261 | 5.644 | 0.55 | 968.9674 |
| J-PPS3 [85] | 830.3088 | 0.2363 | 5.6377 | 0.2949 | 965.0228 |
| I-NSGA-III [86] | 881.9395 | 0.2209 | 4.7449 | 0.1754 | 994.2078 |
| MFO [56] | 830.9135 | 0.25231 | 5.5971 | 0.33164 | 965.8080 |
| J-PPS2 [85] | 830.8672 | 0.2357 | 5.6175 | 0.2948 | 965.1201 |
| MOALO [13] | 826.2676 | 0.2730 | 7.2073 | 0.7160 | 1005.0512 |
| MSA [56] | 830.639 | 0.25258 | 5.6219 | 0.29385 | 965.2907 |
| BB-MOPSO [82] | 833.0345 | 0.2479 | 5.6504 | 0.3945 | 970.3379 |
| J-PPS1 [85] | 830.9938 | 0.2355 | 5.6120 | 0.2990 | 965.2159 |
| TFWO | 831.7219 | 0.2540 | 5.6523 | 0.2981 | 967.1586 |
| TLBO | 831.2634 | 0.2602 | 5.8517 | 0.3111 | 971.4777 |
| TLTFWO | 830.2863 | 0.2529 | 5.5868 | 0.2976 | 964.2506 |
| Wind Power Generating Plants | Solar PV Plant | ||||||
|---|---|---|---|---|---|---|---|
| Wind Farm | No. of Turbines | Rated Power, Pwr (MW) | Weibull PDF Parameters | Weibull Mean, Mwbl | Rated Power, Psr (MW) | Lognormal PDF Parameters | Lognormal Mean, Mlgn |
| 1 (bus 5) | 25 | 75 | c = 9, k = 2 | v = 7.976 m/s | 50 (bus 13) | σ = 0.6, µ = 6 | G = 483 W/m2 |
| 2 (bus 11) | 20 | 60 | c = 10, k = 2 | v = 8.862 m/s | |||
| Variables | TFWO | TLBO | TLTFWO |
|---|---|---|---|
| PG1 (MW) | 134.90791 | 134.90791 | 134.90793 |
| PG2 (MW) | 29.0275 | 28.2868 | 27.0466 |
| Pws1 (MW) | 44.0282 | 43.6213 | 42.9326 |
| PG3 (MW) | 10 | 10 | 10 |
| Pws2 (MW) | 37.1649 | 36.8238 | 36.2236 |
| Pss (MW) | 34.0406 | 35.5344 | 38.0833 |
| VG1 (p.u.) | 1.0718 | 1.0723 | 1.072 |
| VG2 (p.u.) | 1.0568 | 1.0573 | 1.057 |
| VG5 (p.u.) | 1.0349 | 1.0352 | 1.0348 |
| VG8 (p.u.) | 1.0702 | 1.0398 | 1.0395 |
| VG11 (p.u.) | 1.0981 | 1.0996 | 1.0999 |
| VG13 (p.u.) | 1.0489 | 1.0548 | 1.0559 |
| QG1 (MVAR) | −2.31923 | −1.91971 | −1.91987 |
| QG2 (MVAR) | 11.8198 | 13.2443 | 13.2115 |
| Qws1 (MVAR) | 22.4185 | 23.1879 | 23.2748 |
| QG3(MVAR) | 40 | 35.0704 | 34.6188 |
| Qws2 (MVAR) | 30 | 30 | 30 |
| Qss (MVAR) | 15.0849 | 17.4102 | 17.8624 |
| Fuelvlvcost (USD/h) | 442.3257 | 439.8602 | 435.7669 |
| Wind gen cost (USD/h) | 247.9662 | 245.3840 | 240.9739 |
| Solar gen cost (USD/h) | 92.0150 | 97.2115 | 105.2384 |
| Total Cost (USD/h) | 782.3068 | 782.4558 | 781.9791 |
| Emission (t/h) | 1.76196 | 1.76213 | 1.76245 |
| Power losses (MW) | 5.7692 | 5.7741 | 5.7941 |
| V.D. (p.u.) | 0.45405 | 0.46348 | 0.46546 |
| Variables | TFWO | TLBO | TLTFWO |
|---|---|---|---|
| PG1 (MW) | 123.11028 | 123.50416 | 123.32853 |
| PG2 (MW) | 31.9607 | 33.0291 | 32.5297 |
| Pws1 (MW) | 45.4523 | 46.0158 | 45.7041 |
| PG3 (MW) | 10 | 10 | 10 |
| Pws2 (MW) | 38.2959 | 38.7483 | 38.5267 |
| Pss (MW) | 39.8618 | 37.4806 | 38.629 |
| VG1 (p.u.) | 1.0696 | 1.071 | 1.0697 |
| VG2 (p.u.) | 1.0561 | 1.0514 | 1.0561 |
| VG5 (p.u.) | 1.035 | 1.1 | 1.0954 |
| VG8 (p.u.) | 1.0686 | 1.1 | 1.0402 |
| VG11 (p.u.) | 1.1 | 1.1 | 1.0985 |
| VG13 (p.u.) | 1.0514 | 1.0594 | 1.054 |
| QG1 (MVAR) | −3.21843 | 12.1278 | −2.96534 |
| QG2 (MVAR) | 10.7334 | −20 | 4.09265 |
| Qws1 (MVAR) | 22.2319 | 35 | 35 |
| QG3(MVAR) | 40 | 40 | 32.6276 |
| Qws2 (MVAR) | 30 | 30 | 30 |
| Qss (MVAR) | 15.9599 | 18.8826 | 16.9538 |
| Fuelvlvcost (USD/h) | 424.8316 | 429.4076 | 427.2849 |
| Wind gen cost (USD/h) | 256.9048 | 260.5086 | 258.6126 |
| Solar gen cost (USD/h) | 112.2470 | 103.7997 | 107.3181 |
| Total Cost (USD/h) | 793.9835 | 793.7159 | 793.2156 |
| Emission (t/h) | 0.87057 | 0.89030 | 0.88144 |
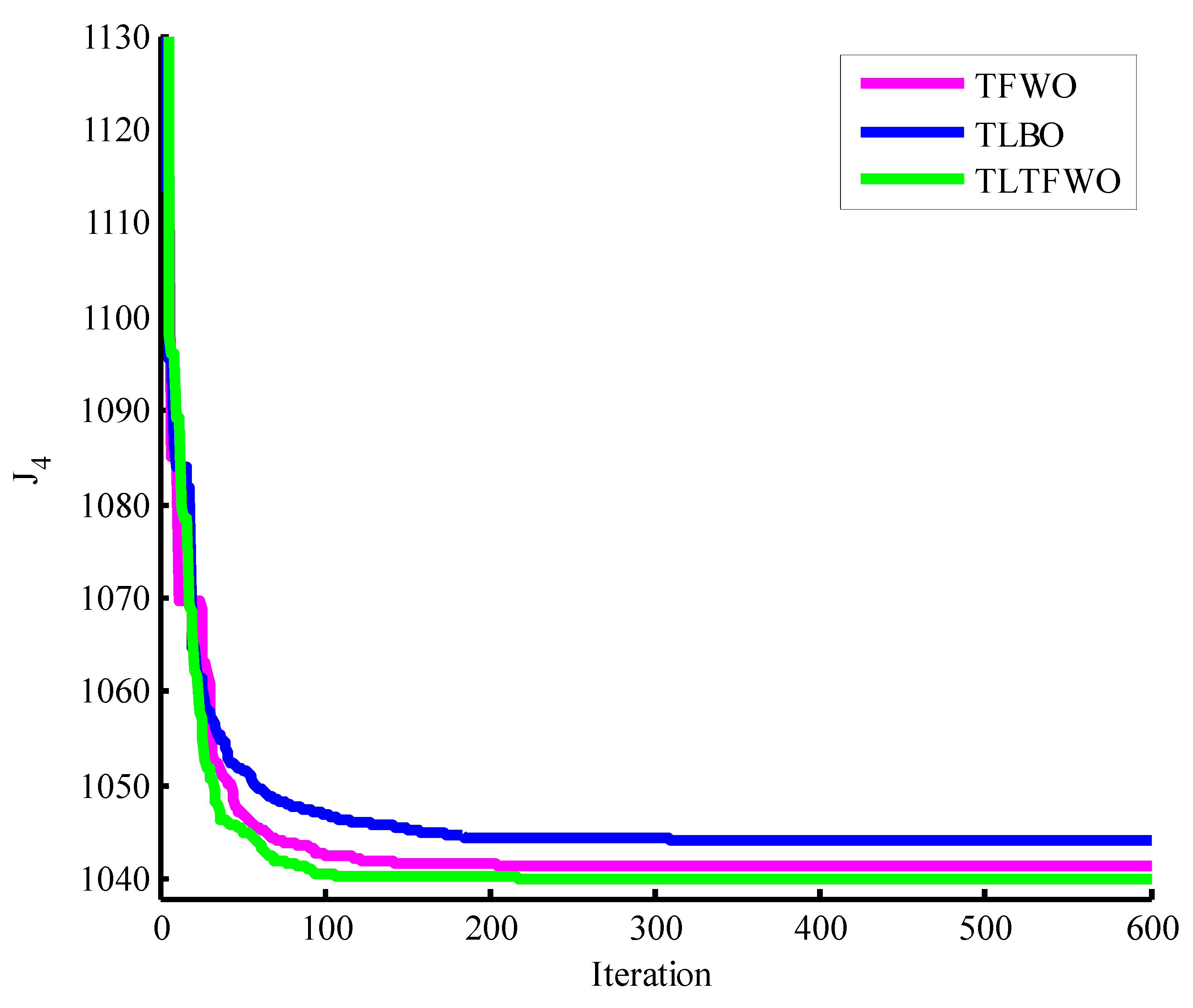
| J8 | 811.3949 | 811.5219 | 810.8444 |
| Power losses (MW) | 5.2809 | 5.3780 | 5.3180 |
| V.D. (p.u.) | 0.46214 | 0.49157 | 0.47299 |
| Carbon tax (USD/h) | 17.4114 | 17.806 | 17.6288 |
| Method | Min | Mean | Max | Std. | Time (s) |
|---|---|---|---|---|---|
| Case 1 | |||||
| PSO | 801.1419 | 801.8326 | 802.9401 | 1.03 | 28 |
| GA | 801.6345 | 802.5472 | 803.2009 | 1.48 | 36 |
| TFWO | 800.8426 | 801.2513 | 801.5878 | 0.56 | 30 |
| TLBO | 800.9923 | 801.2958 | 801.6004 | 0.45 | 33 |
| TLTFWO | 800.4780 | 800.6012 | 800.7639 | 0.14 | 30 |
| Case 2 | |||||
| PSO | 647.5328 | 647.9796 | 648.6117 | 0.74 | 31 |
| GA | 647.9935 | 648.7213 | 649.5020 | 1.21 | 35 |
| TFWO | 646.9425 | 647.3011 | 647.7208 | 0.42 | 30 |
| TLBO | 647.5263 | 647.8730 | 648.4102 | 0.38 | 33 |
| TLTFWO | 646.4715 | 646.5819 | 646.7009 | 0.17 | 30 |
| Case 3 | |||||
| PSO | 832.9628 | 833.4139 | 833.8996 | 1.01 | 32 |
| GA | 833.6085 | 834.8323 | 836.0047 | 1.95 | 38 |
| TFWO | 832.6598 | 832.9418 | 833.3994 | 0.61 | 29 |
| TLBO | 832.7624 | 832.9771 | 833.4825 | 0.72 | 34 |
| TLTFWO | 832.1584 | 832.2837 | 832.4035 | 0.19 | 30 |
| Case 4 | |||||
| PSO | 1045.3157 | 1046.7329 | 1047.3214 | 1.61 | 33 |
| GA | 1045.9559 | 1047.1046 | 1048.3610 | 1.14 | 40 |
| TFWO | 1041.4914 | 1042.5326 | 1043.4218 | 1.52 | 31 |
| TLBO | 1044.2764 | 1045.4579 | 1046.8018 | 1.49 | 35 |
| TLTFWO | 1040.1875 | 1040.3267 | 1040.4793 | 0.23 | 29 |
| Case 5 | |||||
| PSO | 815.3592 | 816.5410 | 817.7862 | 1.75 | 32 |
| GA | 816.6919 | 817.7764 | 819.2102 | 2.32 | 35 |
| TFWO | 814.2310 | 815.6249 | 816.5998 | 1.40 | 30 |
| TLBO | 815.3880 | 816.4528 | 817.6781 | 1.44 | 34 |
| TLTFWO | 813.1829 | 813.3613 | 813.4817 | 0.15 | 30 |
| Case 6 | |||||
| PSO | 970.9024 | 973.1466 | 974.1565 | 1.39 | 36 |
| GA | 973.4101 | 975.6303 | 976.8919 | 2.16 | 40 |
| TFWO | 967.1586 | 967.8543 | 968.4628 | 0.55 | 30 |
| TLBO | 971.4777 | 972.0647 | 972.9847 | 0.81 | 33 |
| TLTFWO | 964.2506 | 964.3928 | 964.5224 | 0.15 | 32 |
| Case 7 | |||||
| PSO | 782.7100 | 783.2148 | 783.7969 | 0.89 | 33 |
| GA | 783.2565 | 784.6206 | 786.7536 | 1.37 | 41 |
| TFWO | 782.3068 | 782.6754 | 783.2645 | 0.63 | 35 |
| TLBO | 782.4558 | 782.9740 | 783.8231 | 0.94 | 38 |
| TLTFWO | 781.9791 | 782.2216 | 782.4136 | 0.20 | 35 |
| Case 8 | |||||
| PSO | 811.4062 | 812.5325 | 813.5510 | 0.57 | 33 |
| GA | 812.6163 | 813.7541 | 815.4792 | 2.25 | 40 |
| TFWO | 811.3949 | 812.3127 | 813.1720 | 1.16 | 35 |
| TLBO | 811.5219 | 812.3812 | 813.2546 | 1.43 | 39 |
| TLTFWO | 810.8444 | 810.9632 | 811.2148 | 0.18 | 35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alanazi, M.; Alanazi, A.; Abdelaziz, A.Y.; Siano, P. Power Flow Optimization by Integrating Novel Metaheuristic Algorithms and Adopting Renewables to Improve Power System Operation. Appl. Sci. 2023, 13, 527. https://doi.org/10.3390/app13010527
Alanazi M, Alanazi A, Abdelaziz AY, Siano P. Power Flow Optimization by Integrating Novel Metaheuristic Algorithms and Adopting Renewables to Improve Power System Operation. Applied Sciences. 2023; 13(1):527. https://doi.org/10.3390/app13010527
Chicago/Turabian StyleAlanazi, Mohana, Abdulaziz Alanazi, Almoataz Y. Abdelaziz, and Pierluigi Siano. 2023. "Power Flow Optimization by Integrating Novel Metaheuristic Algorithms and Adopting Renewables to Improve Power System Operation" Applied Sciences 13, no. 1: 527. https://doi.org/10.3390/app13010527
APA StyleAlanazi, M., Alanazi, A., Abdelaziz, A. Y., & Siano, P. (2023). Power Flow Optimization by Integrating Novel Metaheuristic Algorithms and Adopting Renewables to Improve Power System Operation. Applied Sciences, 13(1), 527. https://doi.org/10.3390/app13010527








