Networked Control System Based on PSO-RBF Neural Network Time-Delay Prediction Model
Abstract
1. Introduction
- A time-delay prediction model based on RBF neural networks is proposed and optimized using the PSO algorithm. A nonlinear adjustment formula for the weights based on particle fitness is proposed for the characteristics of particle swarm algorithms that tend to fall into local optimality, and the speed of the particles is dynamically adjusted in combination with the taboo search algorithm (TS). The connection weights of the RBF neural network, the centers of the neural nodes in the hidden layer, and the amplitudes of the neural nodes are confirmed by the improved PSO algorithm to ensure the prediction accuracy of the prediction model.
- An online predictive controller based on RBF neural networks is proposed. A gradient descent method regulates each parameter of the online RBF neural network. An objective function with differential components is proposed to evaluate the optimization effect in the rolling optimization phase to ensure adequate compensation of the system transmission delay.
- The PSO-RBF neural network prediction model was simulated and compared with the RBF neural network prediction model and the BP neural network prediction model.
- The network control system designed in this paper has been simulated and analyzed, and the control system has been compared with existing control strategies.
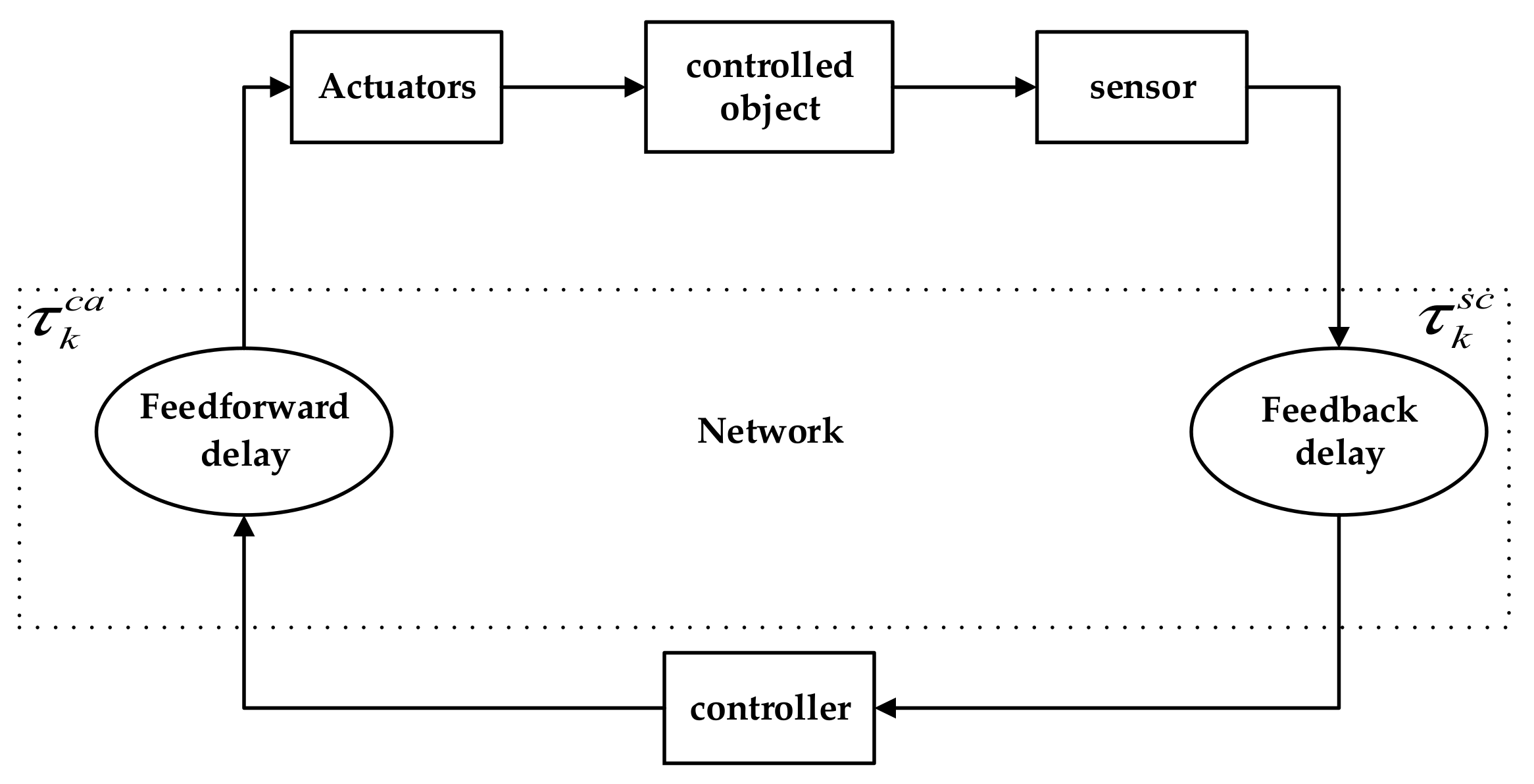
2. Networked Control System Modeling for Time-Delay Problems
- The sensor nodes are clock-driven, meaning the sampling period of the control system is the same.
- The controller node and actuator node are both driven by events, meaning that the time at which information arrives at the node is the time of operation of the device at the corresponding node.
- There is no packet loss or timing error.
- The network transmission delay at each moment is less than the sampling period.
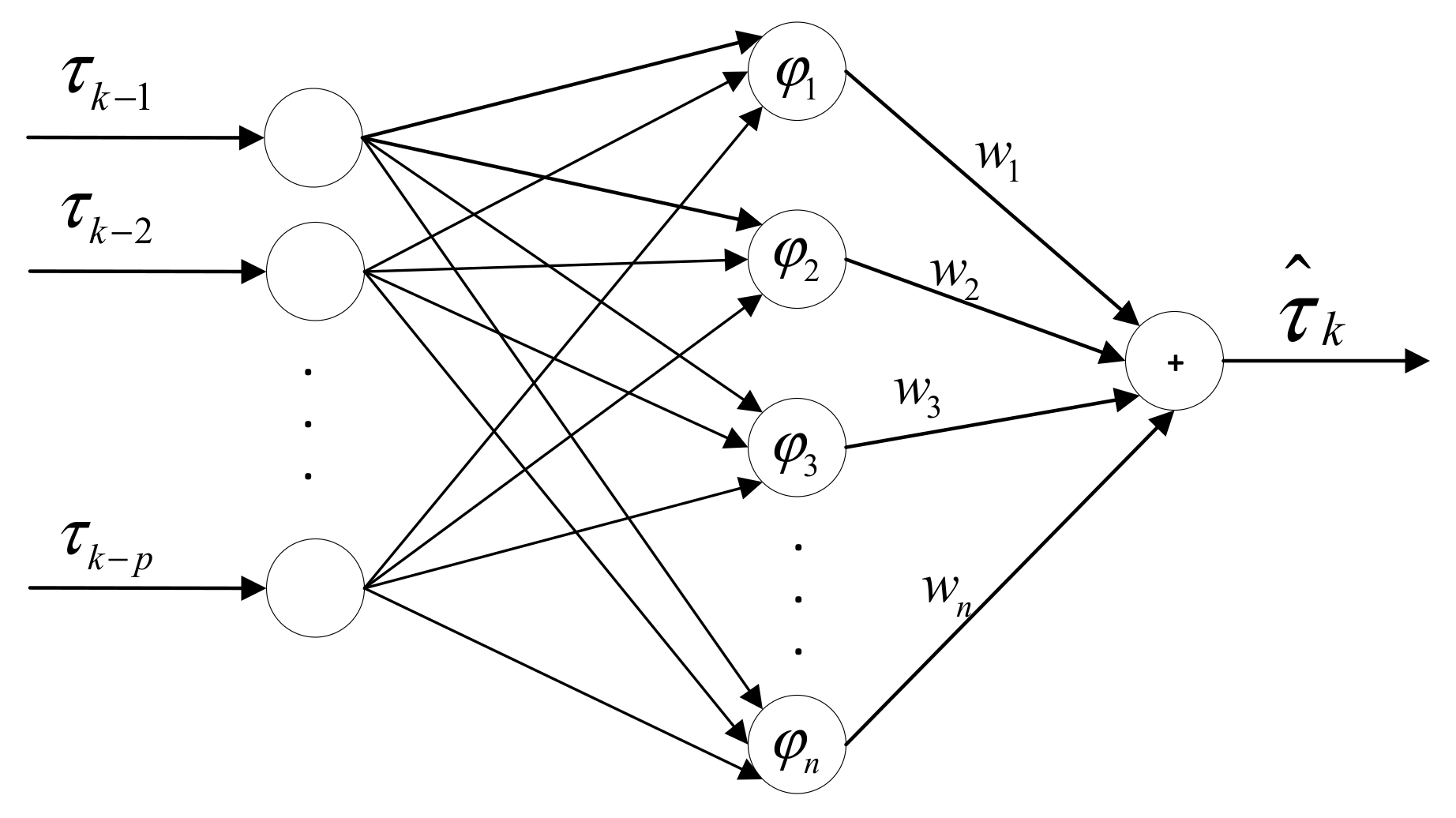
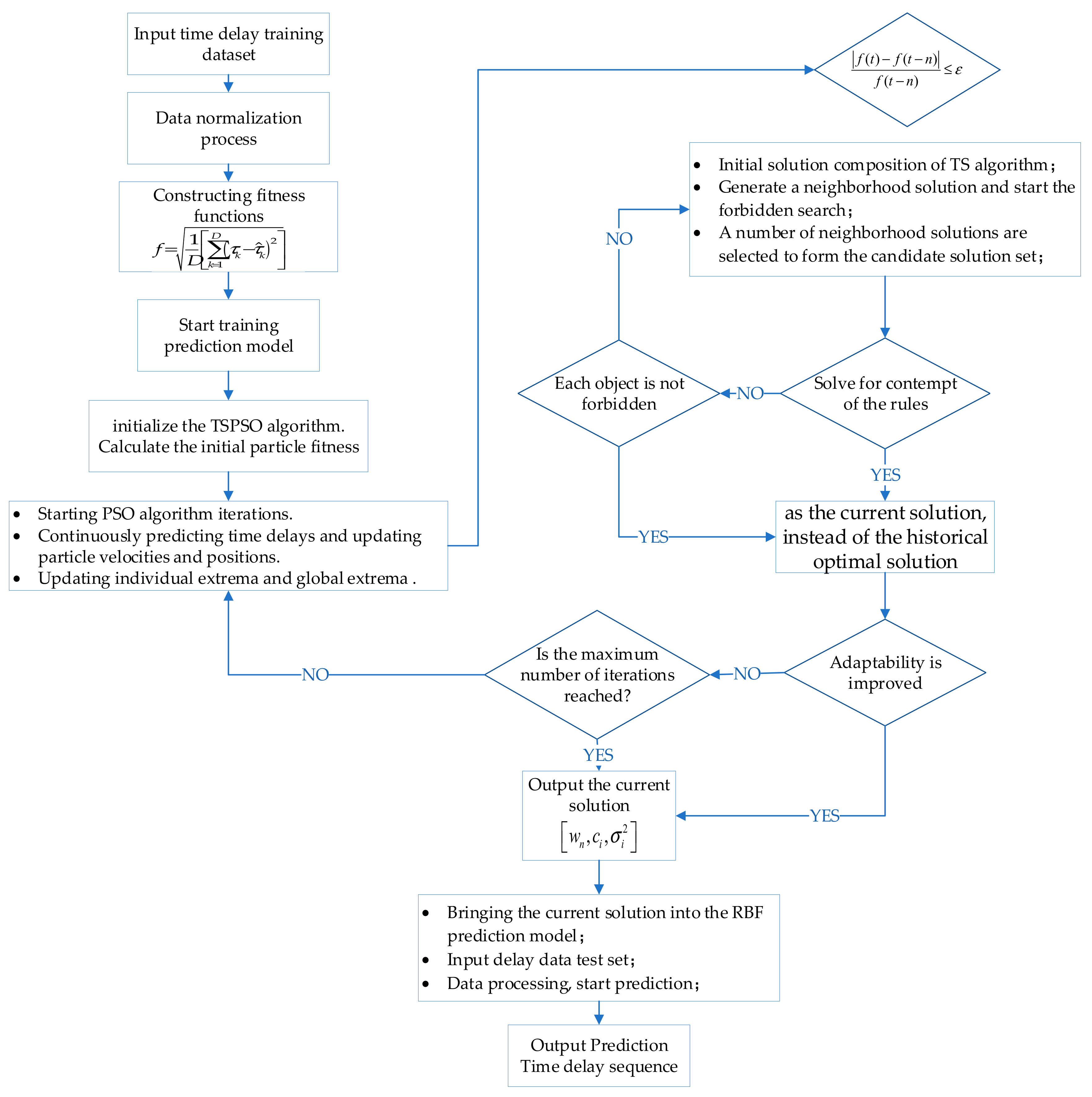
3. An Offline RBF Neural Network Delay Prediction Model Based on the Improved PSO Algorithm
3.1. Offline RBF Neural Network Prediction Model
3.2. Particle Swarm Optimization Algorithm
3.3. PSO-RBF Time-Delay Prediction Model
4. Online RBF Model Predictive Controller Design
4.1. Online RBF Network Single-Step Predictive Controller Design
- The online RBF neural network is trained one by one with unknown maximum, minimum, and mean values, which cannot be normalized.
- Online RBF neural networks are trained data-by-data and cannot be corrected using the global error guidance function for weights and thresholds. However, thanks to this feature, the online RBF neural network is somewhat resistant to interference when applied to the controller design.
- The nodes of the hidden layer cannot be found using the K-means algorithm because the data set is not available in advance for online RBF neural networks.
4.2. Rolling Optimization and Feedback Correction
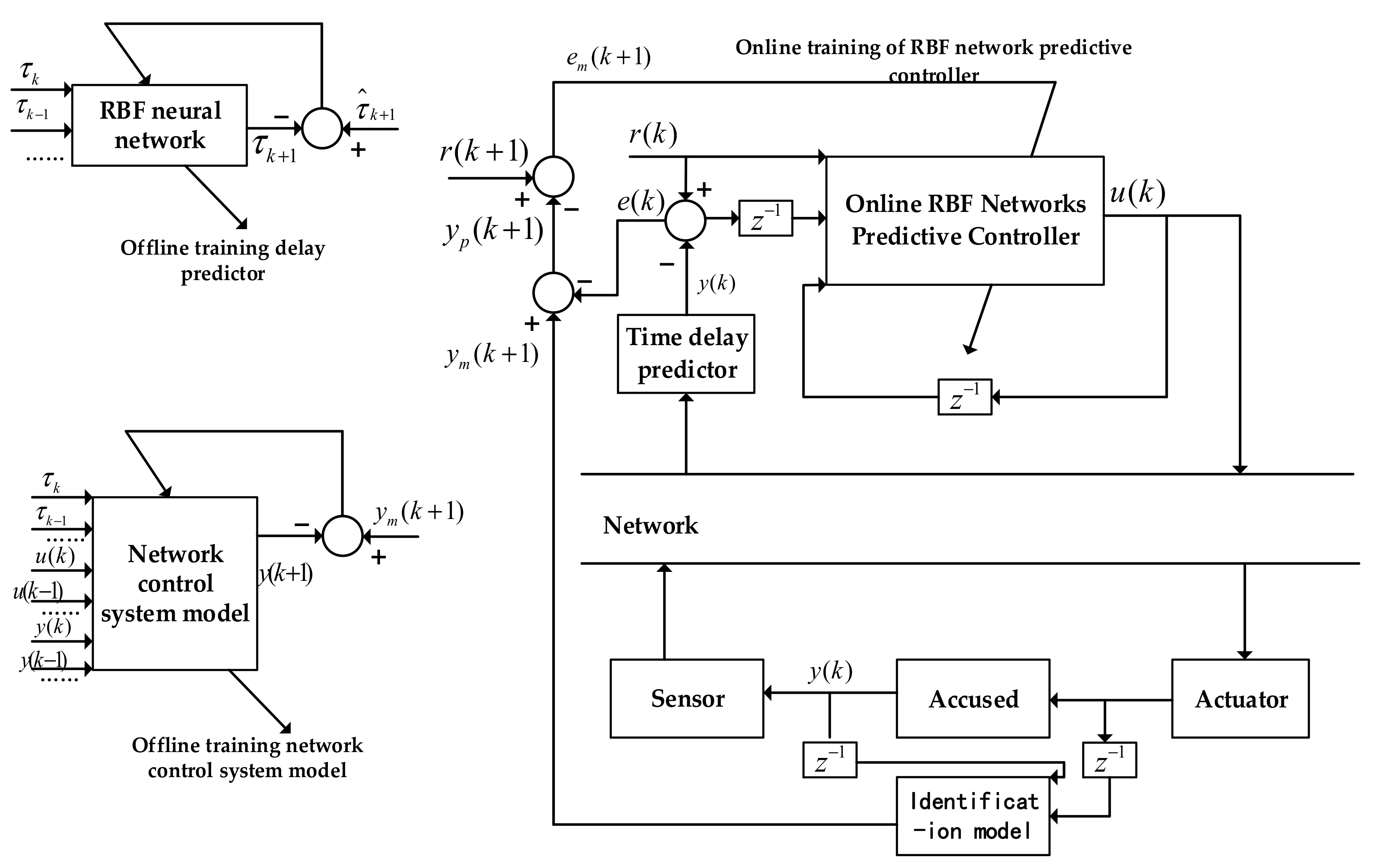
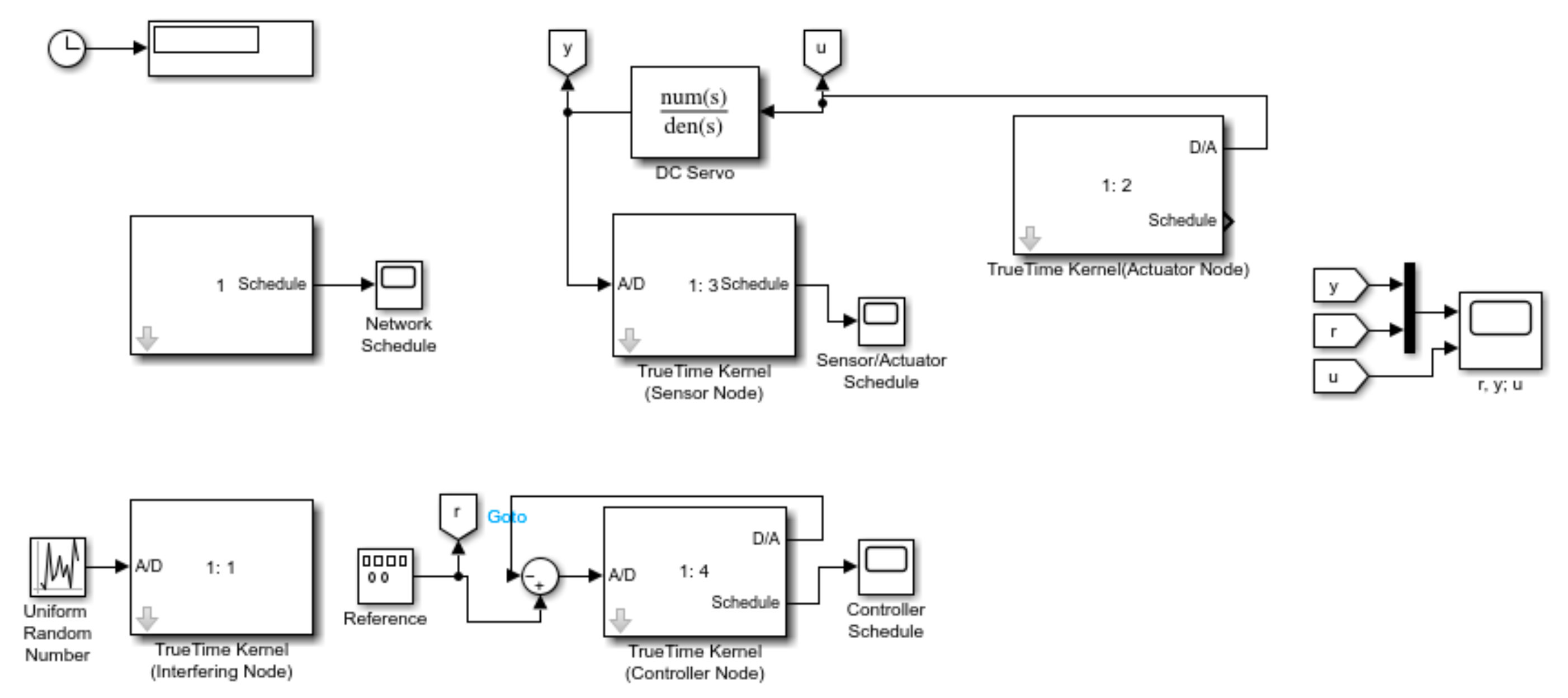
5. Networked Control Systems Based on RBF Neural Networks
- Design goal: the system is a networked control system with stochastic time-delay prediction and compensation, for situations where the time-delay model is known or unknown.
- Controlled objects: for nonlinear control objects.
- Delay models: for random delays, fixed delays and random delays that satisfy the Markov chain model.
- System structure: straightforward structure.
- Stochastic delay prediction model: an offline RBF network delay prediction model based on an improved PSO algorithm, i.e., the content in Section 3 of this paper.
- Controller: online RBF neural network single-step predictive controller, i.e., what is in Section 4 of this paper.
- Identification model: a network control system based on stochastic time delays, i.e., the contents of Section 2 of this paper.
- System nodes are driven: the controller nodes and actuator nodes are event-driven, and sensor nodes are clock-driven.
- Sampling period: The sampling period is greater than the network transmission delay at any given moment .
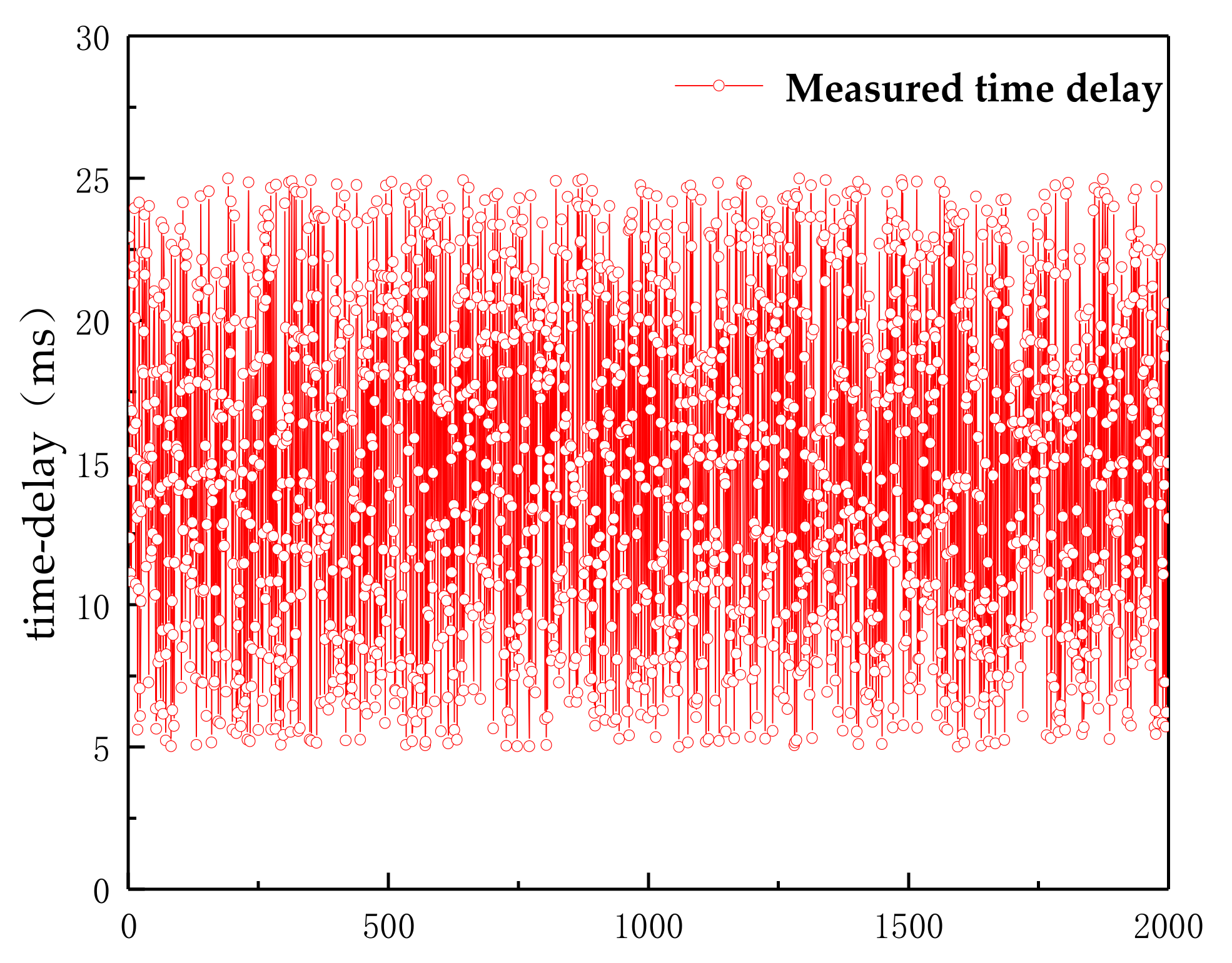
- Sampling of data for offline training of RBF neural networks. The training data for the time-delay prediction model is the actual measurement data of the time delay, sampled and used to train the time-delay prediction; the input and output of the controlled object are collected and used to train the recognition model.
- Determining the number of input nodes and the number of nodes in the hidden layer for the RBF neural network. The number of input nodes and the number of nodes in the hidden layer of the time-delay prediction model and online RBF network controller are problem-specific and need to be tested for errors to determine the number of nodes for said problem. Typically, satisfying the equation
- where: is the overall system time delay; is the time-delay difference generated by the system after time-delay compensation; is the number of steps; and is the sampling frequency.
- In the case that the sampling frequency is set appropriately, and the delay can be accurately predicted in most cases, single-step predictive control is used, and is taken as 1.
- Initialization of the delay prediction model, the controller, and the recognition model.
- Controller response. The amount of control at the current moment of the controlled object is calculated by , , and ; the time-delay prediction is performed by a time-delay prediction model with the completion of offline training, and the time delay is compensated.
- After predicting and compensating for time delay, actuator response, controlled object response, sensor response, and sample completion, the system returns to step (4).
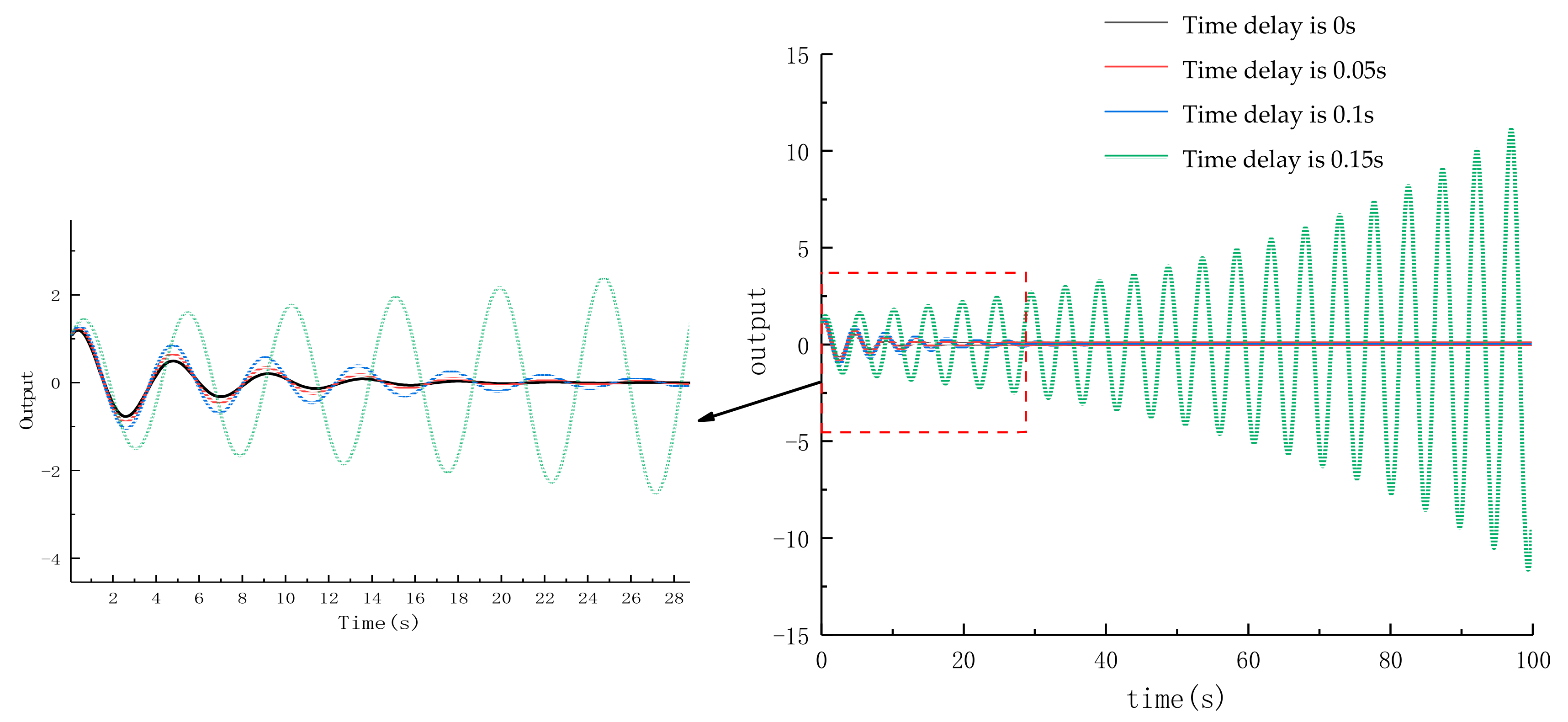
6. System Simulation and Analysis of Results
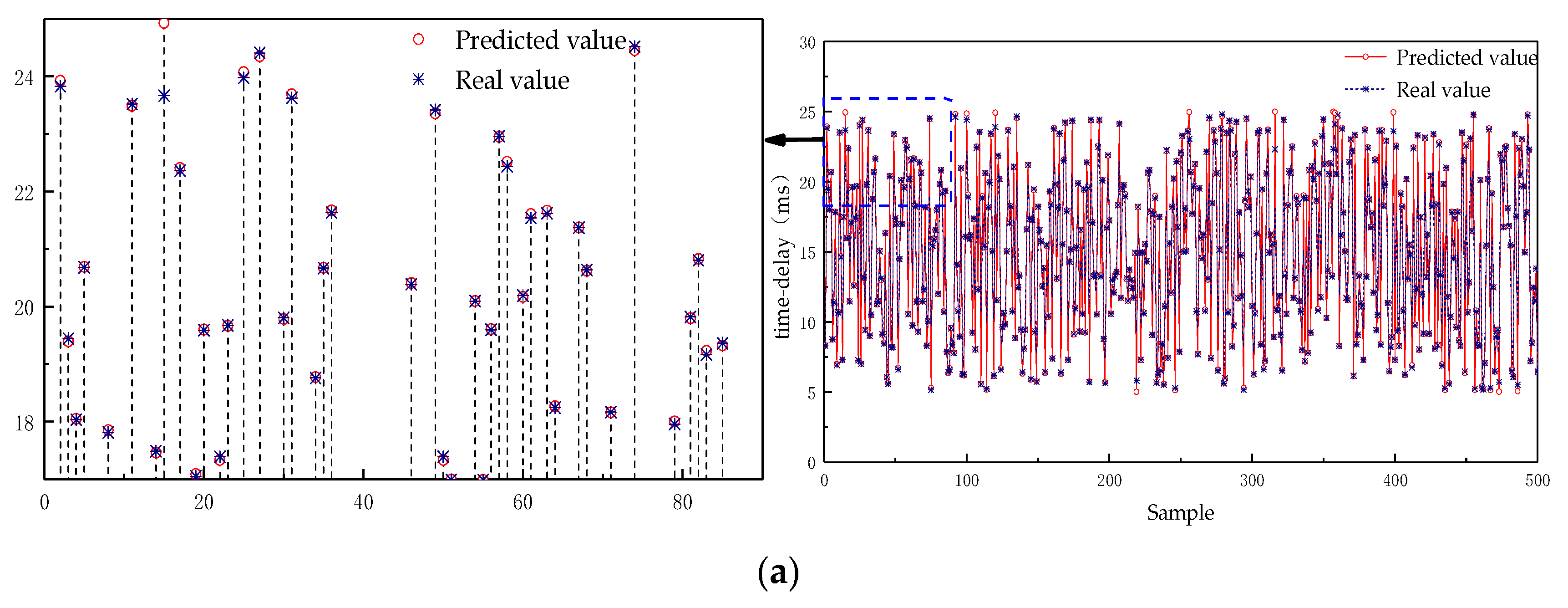
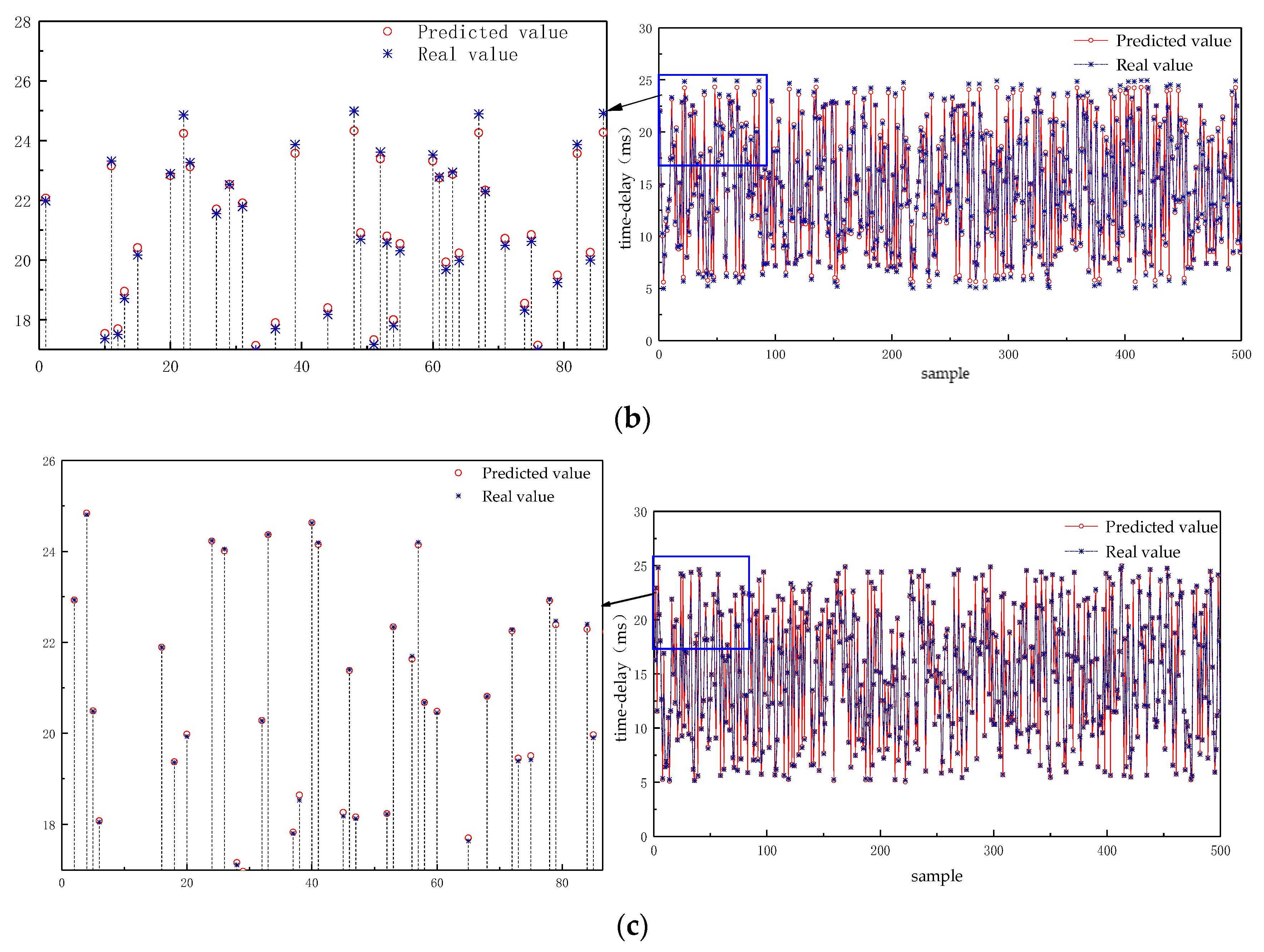
6.1. Validation of the Offline Delay Prediction Model
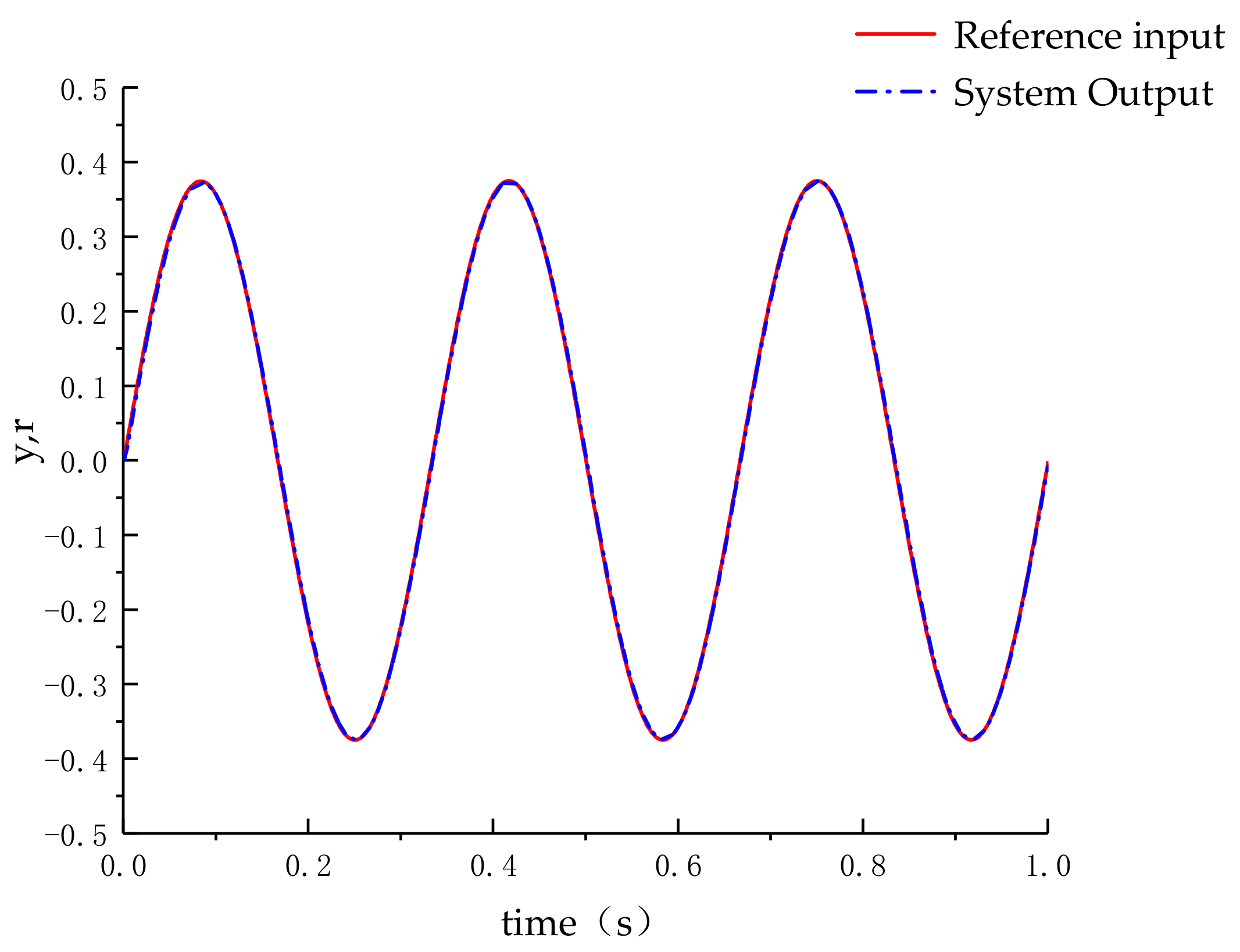
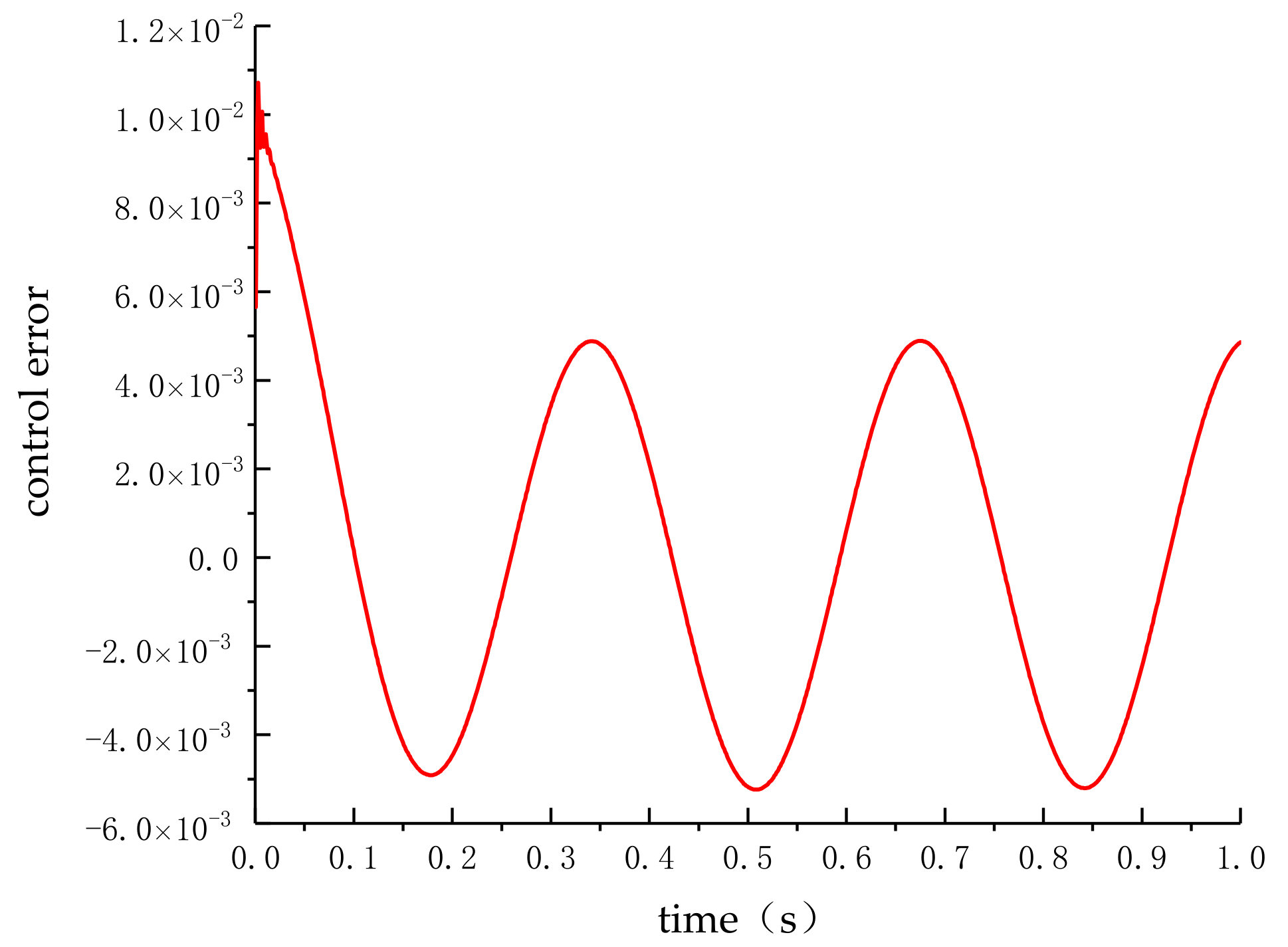
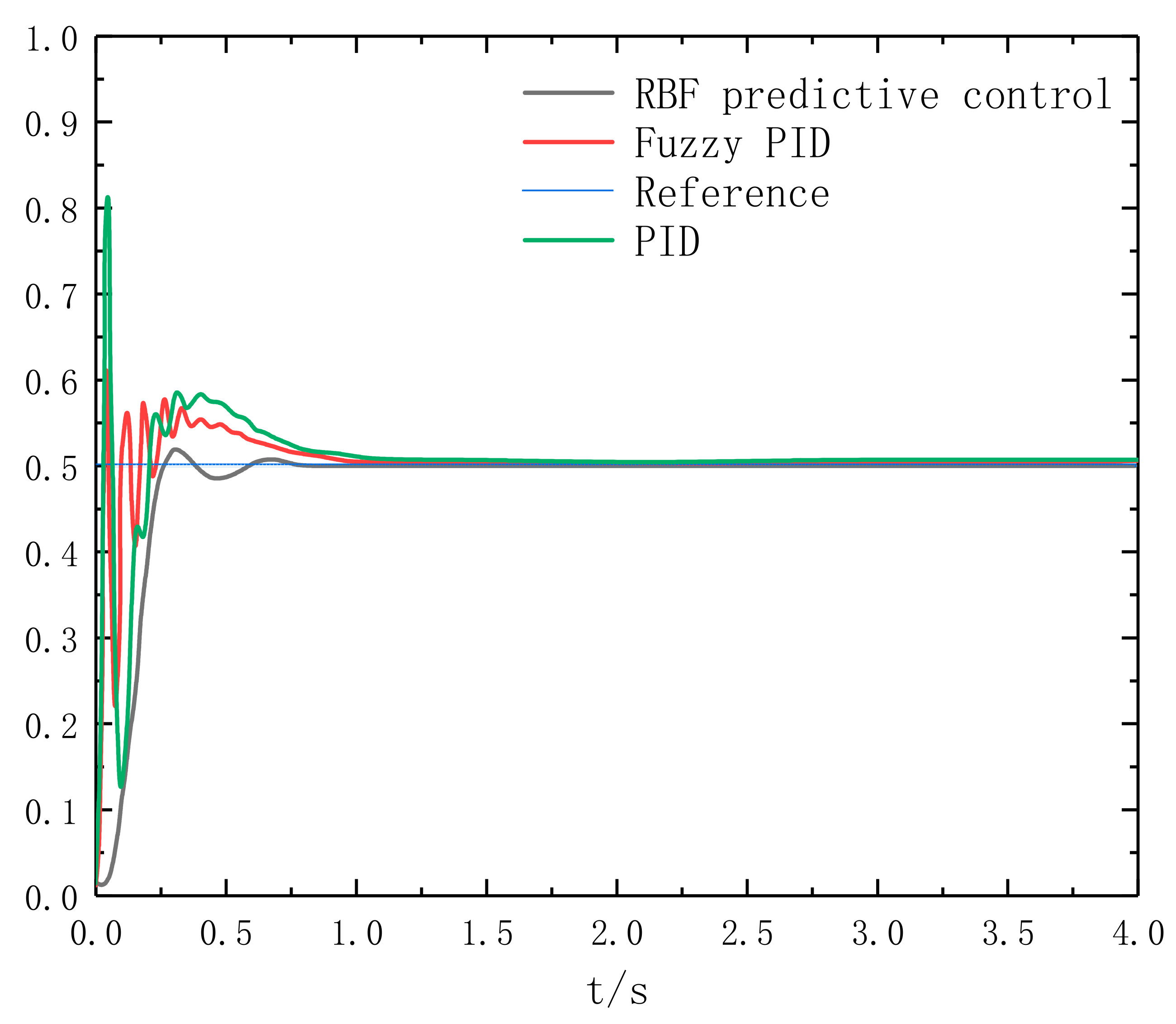
6.2. Control Performance Analysis of Network Control Systems Based on Rbf Neural Networks
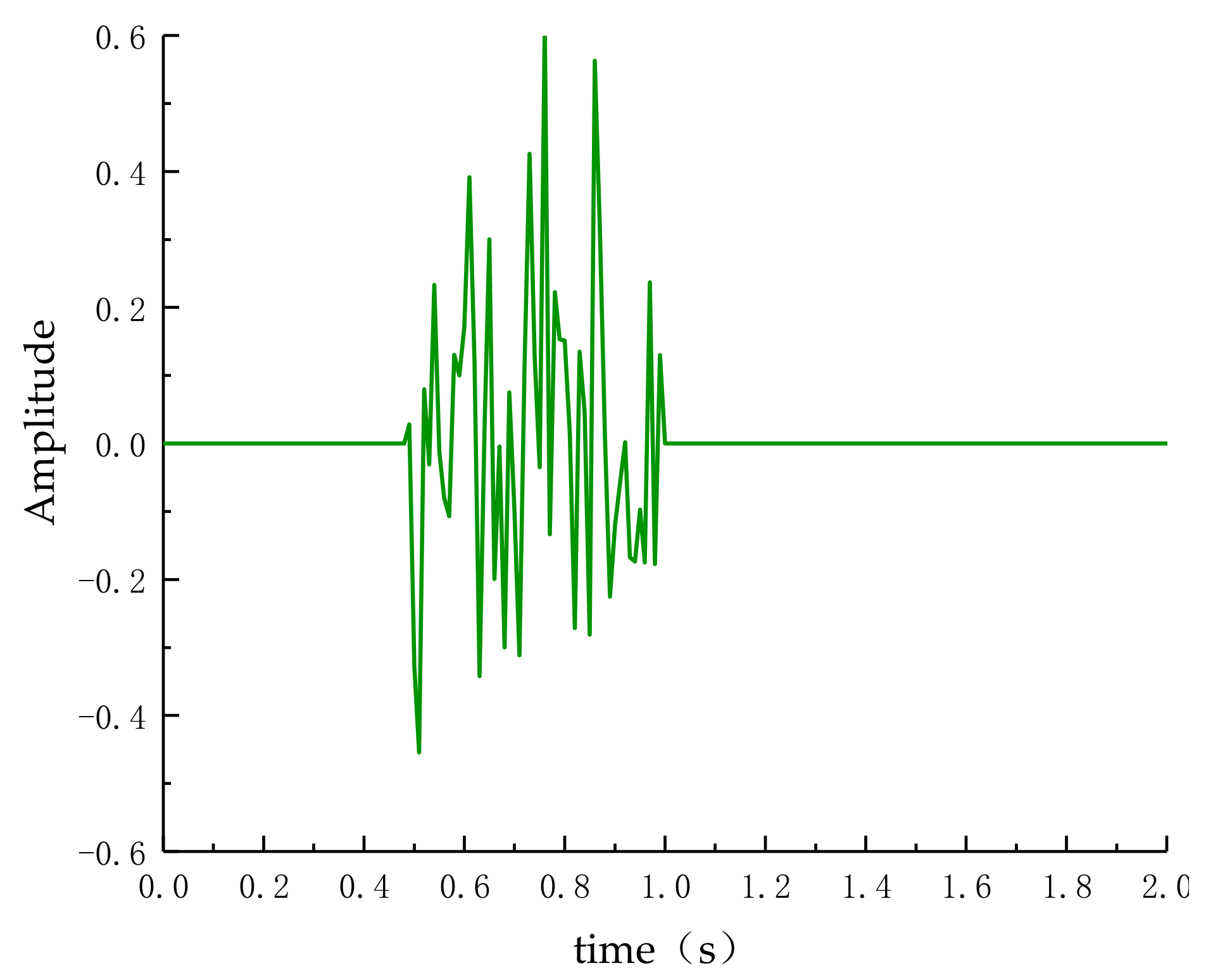
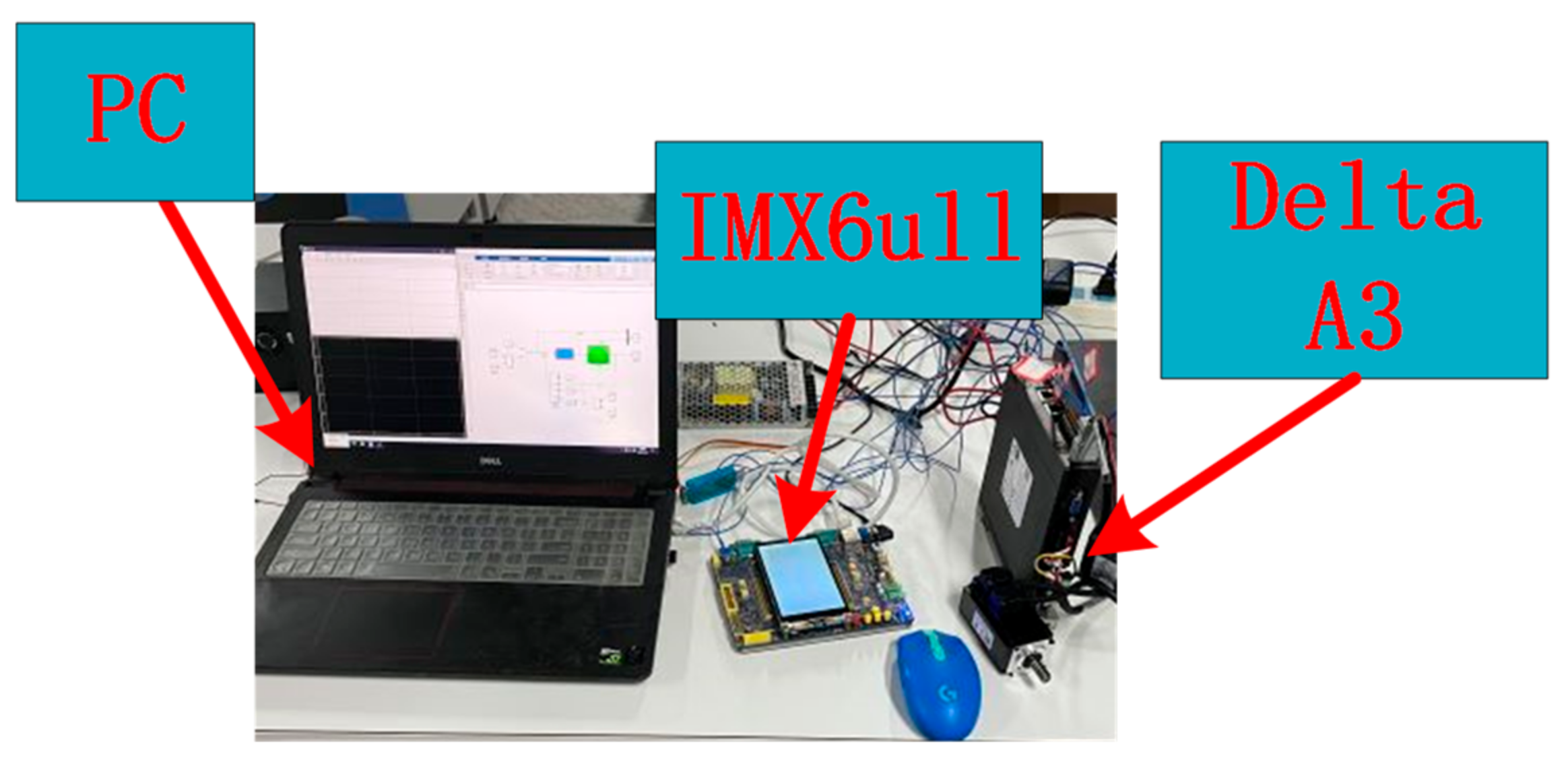
6.3. Physical Verification of Network Control System Based on RBF Neural Network
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mahmoud, M.S.; Sabih, M. Experimental Investigations for Distributed Networked Control Systems. IEEE Syst. J. 2014, 8, 717–725. [Google Scholar] [CrossRef]
- Ding, L.; Han, Q.-L.; Wang, L.Y.; Sindi, E. Distributed Cooperative Optimal Control of DC Microgrids With Communication Delays. IEEE Trans. Ind. Inform. 2018, 14, 3924–3935. [Google Scholar] [CrossRef]
- Sandberg, H.; Amin, S.; Johansson, K. Cyberphysical Security in Networked Control Systems: An Introduction to the Issue. IEEE Control Syst. 2015, 35, 20–23. [Google Scholar] [CrossRef]
- Wang, Y.-L.; Han, Q.-L. Network-Based Modelling and Dynamic Output Feedback Control for Unmanned Marine Vehicles in Network Environments. Automatica 2018, 91, 43–53. [Google Scholar] [CrossRef]
- Zhang, X.-M.; Han, Q.-L. Network-Based H-Infinity Filtering Using a Logic Jumping-like Trigger. Automatica 2013, 49, 1428–1435. [Google Scholar] [CrossRef]
- Zhang, X.-M.; Han, Q.-L.; Ge, X.; Ding, D.; Ding, L.; Yue, D.; Peng, C. Networked Control Systems: A Survey of Trends and Techniques. IEEE/CAA J. Autom. Sin. 2020, 7, 1–17. [Google Scholar] [CrossRef]
- Hu, Z.; Deng, F.; Xing, M.; Li, J. Modeling and Control of Itô Stochastic Networked Control Systems With Random Packet Dropouts Subject to Time-Varying Sampling. IEEE Trans. Automat. Contr. 2017, 62, 4194–4201. [Google Scholar] [CrossRef]
- Zhiwen, W.; Ge, G. Fundamental Issues and Prospective Directions in Networked Multirate Control Systems. Math. Probl. Eng. 2014, 2014, 1–10. [Google Scholar] [CrossRef]
- Qiu, J.; Gao, H.; Ding, S.X. Recent Advances on Fuzzy-Model-Based Nonlinear Networked Control Systems: A Survey. IEEE Trans. Ind. Electron. 2016, 63, 1207–1217. [Google Scholar] [CrossRef]
- Ge, X.; Yang, F.; Han, Q.-L. Distributed Networked Control Systems: A Brief Overview. Inf. Sci. 2017, 380, 117–131. [Google Scholar] [CrossRef]
- Yuan, H.; Bi, J.; Tan, W.; Zhou, M.; Li, B.H.; Li, J. TTSA: An Effective Scheduling Approach for Delay Bounded Tasks in Hybrid Clouds. IEEE Trans. Cybern. 2017, 47, 3658–3668. [Google Scholar] [CrossRef] [PubMed]
- Yuan, H.; Bi, J.; Tan, W.; Li, B.H. Temporal Task Scheduling With Constrained Service Delay for Profit Maximization in Hybrid Clouds. IEEE Trans. Autom. Sci. Eng. 2017, 14, 337–348. [Google Scholar] [CrossRef]
- Bi, J.; Yuan, H.; Tan, W.; Zhou, M.; Fan, Y.; Zhang, J.; Li, J. Application-Aware Dynamic Fine-Grained Resource Provisioning in a Virtualized Cloud Data Center. IEEE Trans. Autom. Sci. Eng. 2017, 14, 1172–1184. [Google Scholar] [CrossRef]
- Bi, J.; Yuan, H.; Zhou, M. Temporal Prediction of Multiapplication Consolidated Workloads in Distributed Clouds. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1763–1773. [Google Scholar] [CrossRef]
- Bi, J.; Feng, T.; Yuan, H. Real-Time and Short-Term Anomaly Detection for GWAC Light Curves. Comput. Ind. 2018, 97, 76–84. [Google Scholar] [CrossRef]
- Assali, E.A. Predefined-Time Synchronization of Chaotic Systems with Different Dimensions and Applications. Chaos Solitons Fractals 2021, 147, 110988. [Google Scholar] [CrossRef]
- Tian, Z. Networked Control System Time-Delay Compensation Based on PI-Based Dynamic Matrix Control. At-Automatisierungstechnik 2021, 69, 41–51. [Google Scholar] [CrossRef]
- Medjiah, S.; Taleb, T.; Ahmed, T. Sailing over Data Mules in Delay-Tolerant Networks. IEEE Trans. Wirel. Commun. 2014, 13, 5–13. [Google Scholar] [CrossRef]
- Li, H.; Xiong, N.; Park, J.H.; Cao, Q. Predictive Control for Vehicular Sensor Networks Based on Round-Trip Time-Delay Prediction. IET Commun. 2010, 4, 801–809. [Google Scholar] [CrossRef]
- Lv, Z.; Wang, L.; Han, Z.; Zhao, J.; Wang, W. Surrogate-Assisted Particle Swarm Optimization Algorithm with Pareto Active Learning for Expensive Multi-Objective Optimization. IEEE/CAA J. Autom. Sin. 2019, 6, 838–849. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, W.; Xiao, Z.; Yang, W.; Peng, Y.; Chen, J.; Li, J. Novel Quantitative Structure Activity Relationship Models for Predicting Hexadecane/Air Partition Coefficients of Organic Compounds. J. Environ. Sci. 2023, 124, 98–104. [Google Scholar] [CrossRef] [PubMed]
- Guan, S.; Huang, D.; Guo, S.; Zhao, L.; Chen, H. An Improved Fault Diagnosis Approach Using LSSVM for Complex Industrial Systems. Machines 2022, 10, 443. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, Y.; Song, W.; Liu, S.; Tian, B. A Hybrid Forecasting Model for Depth-Averaged Current Velocities of Underwater Gliders. Acta Oceanol. Sin. 2022, 41, 182–191. [Google Scholar] [CrossRef]
- Liu, J.-X.; Jia, Z.-H. Telecommunication Traffic Prediction Based on Improved LSSVM. Int. J. Pattern Recognit. Artif. Intell. 2018, 32, 1850007. [Google Scholar] [CrossRef]
- Kong, X.; Zhang, T. Improved Generalized Predictive Control for High-Speed Train Network Systems Based on EMD-AQPSO-LS-SVM Time Delay Prediction Model. Math. Probl. Eng. 2020, 2020, 1–19. [Google Scholar] [CrossRef]
- Treviso, F.; Trinchero, R.; Canavero, F.G. Multiple Delay Identification in Long Interconnects via LS-SVM Regression. IEEE Access 2021, 9, 39028–39042. [Google Scholar] [CrossRef]
- Liu, J.; Tao, X.; Ma, X.; Feng, K.; Chen, J. Fuzzy Controllers With Neural Network Predictor for Second-Order Linear Systems With Time Delay. IEEE Access 2020, 8, 206049–206062. [Google Scholar] [CrossRef]
- Lian, B.; Zhang, Q.; Li, J. Integrated Sliding Mode Control and Neural Networks Based Packet Disordering Prediction for Nonlinear Networked Control Systems. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2324–2335. [Google Scholar] [CrossRef]
- Lopez-Echeverria, D.; Magana, M.E. Variable Sampling Approach to Mitigate Instability in Networked Control Systems With Delays. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 119–126. [Google Scholar] [CrossRef]
- Li, X.; Zhao, T.; Zhang, J.; Chen, T. Predication Control for Indoor Temperature Time-Delay Using Elman Neural Network in Variable Air Volume System. Energy Build. 2017, 154, 545–552. [Google Scholar] [CrossRef]
- Xu, P.; Wu, J. A Novel Method for Time Delay Prediction in Networked Control Systems. Int. J. Ad Hoc Ubiquitous Comput. 2019, 32, 99–109. [Google Scholar] [CrossRef]
- Tian, Z. A Method to Predict Random Time-Delay of Networked Control System. IETE J. Res. 2020, 68, 3503–3513. [Google Scholar] [CrossRef]
- Chen, D.-Y.; Liu, Y.; Ma, X.-Y. Parameter Joint Estimation of Phase Space Reconstruction in Chaotic Time Series Based on Radial Basis Function Neural Networks. Acta Phys. Sin. 2012, 61, 7623–7629. [Google Scholar] [CrossRef]
- Fu, Y.; Guo, D.; Li, Q.; Liu, L.; Qu, S.; Xiang, W. Digital Twin Based Network Latency Prediction in Vehicular Networks. Electronics 2022, 14, 2217. [Google Scholar] [CrossRef]
- Qian, Y.; Zeng, J.; Zhang, S.; Xu, D.; Wei, X. Short-Term Traffic Prediction Based on Genetic Algorithm Improved Neural Network. Teh. Vjesn. Tech. Gaz. 2020, 27, 1270–1276. [Google Scholar] [CrossRef]
- Hamdi, H.; Ben Regaya, C.; Zaafouri, A. Real-Time Study of a Photovoltaic System with Boost Converter Using the PSO-RBF Neural Network Algorithms in a MyRio Controller. Sol. Energy 2019, 183, 1–16. [Google Scholar] [CrossRef]


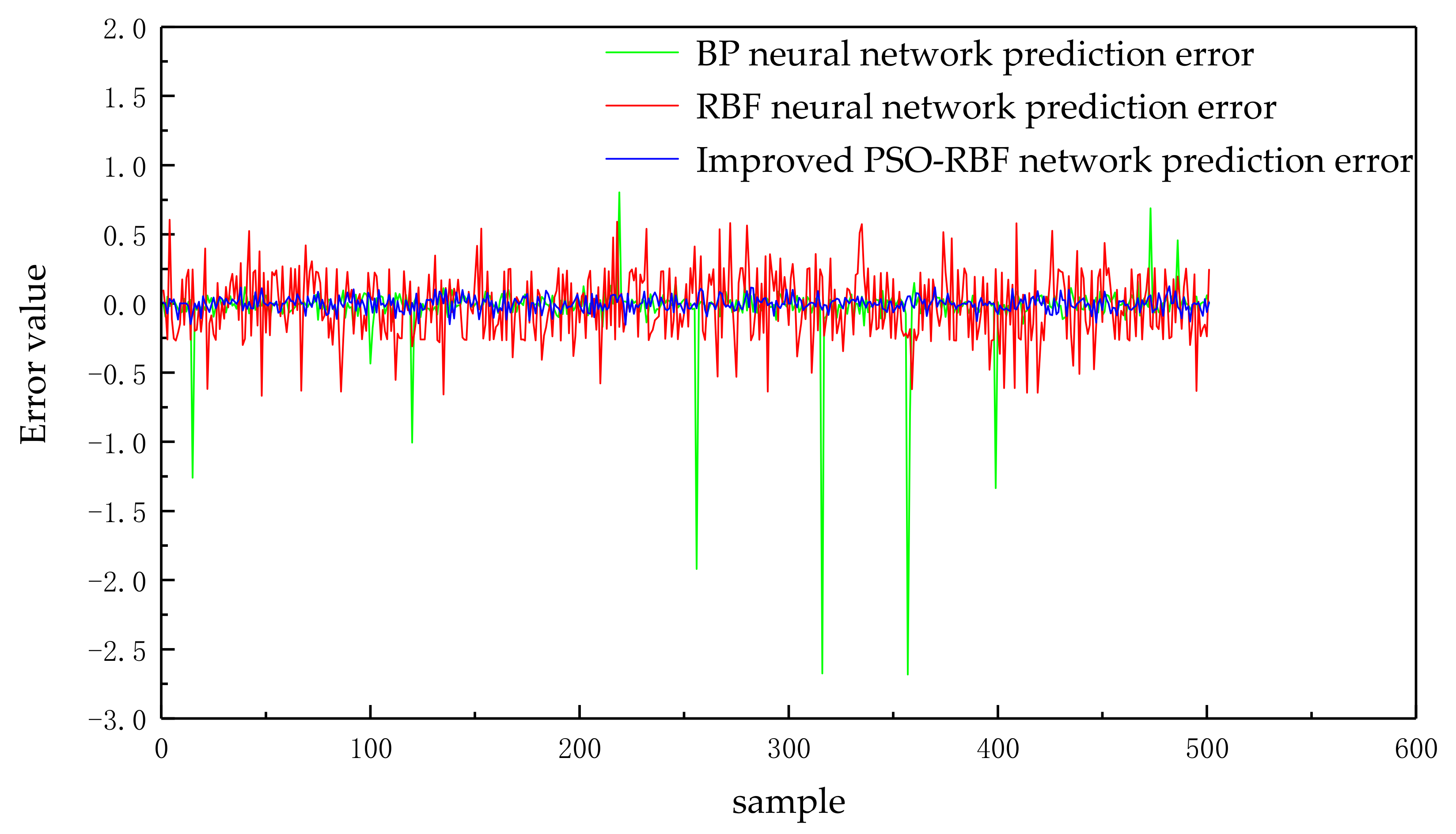


| Time-Delay Prediction Methods | RMSE | MAE | Cycle Forecast Time (ms) |
|---|---|---|---|
| BP Neural Networks | 0.0242 | 0.0688 | 5.47 |
| RBF Neural Networks | 0.0188 | 0.2045 | 0.94 |
| Improving PSO-RBF networks | 0.0105 | 0.0383 | 1.38 |
| Control Algorithms | IAE | ITAE |
|---|---|---|
| PID algorithms | 0.2616 | 0.2467 |
| Fuzzy PID control | 0.1196 | 0.1069 |
| RBF predictive control | 0.0831 | 0.0734 |
| Control Algorithms | IAE | ITAE |
|---|---|---|
| PID algorithms | 0.3109 | 0.3623 |
| Fuzzy PID control | 0.1826 | 0.1657 |
| RBF predictive control | 0.1248 | 0.1196 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, D.; Lei, Y.; Liu, S.; Zhang, Y.; Zhang, M. Networked Control System Based on PSO-RBF Neural Network Time-Delay Prediction Model. Appl. Sci. 2023, 13, 536. https://doi.org/10.3390/app13010536
You D, Lei Y, Liu S, Zhang Y, Zhang M. Networked Control System Based on PSO-RBF Neural Network Time-Delay Prediction Model. Applied Sciences. 2023; 13(1):536. https://doi.org/10.3390/app13010536
Chicago/Turabian StyleYou, Dazhang, Yiming Lei, Shan Liu, Yepeng Zhang, and Min Zhang. 2023. "Networked Control System Based on PSO-RBF Neural Network Time-Delay Prediction Model" Applied Sciences 13, no. 1: 536. https://doi.org/10.3390/app13010536
APA StyleYou, D., Lei, Y., Liu, S., Zhang, Y., & Zhang, M. (2023). Networked Control System Based on PSO-RBF Neural Network Time-Delay Prediction Model. Applied Sciences, 13(1), 536. https://doi.org/10.3390/app13010536





