Featured Application
Provide the compressive strength of fiber reinforced polymer confined concrete specimens with machine learning tools based on real, experimental measurements.
Abstract
Accurate estimation of the mechanical properties of concrete is important for the development of new materials to lead construction applications. Experimental research, aided by empirical and statistical models, has been commonly employed to establish a connection between concrete properties and the resulting compressive strength. However, these methods can be labor-intensive to develop and may not always produce accurate results when the relationships between concrete properties, mixture composition, and curing conditions are complex. In this paper, an experimental dataset based on uniaxial compression experiments conducted on concrete specimens, confined using fiber-reinforced polymer jackets, is incorporated to predict the compressive strength of confined specimens. Experimental measurements are bound to the mechanical and physical properties of the material and fed into a machine learning platform. Novel data science techniques are exploited at first to prepare the experimental dataset before entering the machine learning procedure. Twelve machine learning algorithms are employed to predict the compressive strength, with tree-based methods yielding the highest accuracy scores, achieving coefficients of determination close to unity. Eventually, it is shown that, by carefully manipulating experimental datasets and selecting the appropriate algorithm, a fast and accurate computational platform is created, which can be generalized to bypass expensive, time-consuming, and susceptible-to-errors experiments, and serve as a solution to practical problems in science and engineering.
1. Introduction
The incorporation of novel computational techniques in industrial and construction applications has made a major breakthrough during the last decade, driven by sustainability and environmentally friendly solutions [1]. The effectiveness of these methods has been assessed in a variety of contexts due to the complexity and nonlinear behavior of structural elements [2]. Various numerical and analytical models, based on either experimental or simulation results, have been proposed and improved our understanding of phenomena taking place during the life cycle of a material [3]. At the heart of each model, there is data science. The wealth of data produced has opened the way to scientists and engineers to incorporate it on new statistical techniques and methods and suggest novel functional materials that perform best under specific environmental conditions due to their user-defined inherent characteristics, and which may be exploited by most scientific and technological domains [4]. The majority of data-driven methods being incorporated rely on concepts derived from artificial intelligence (AI) theory.
Machine learning (ML), as a subfield of AI, refers to the extraction of computational models able to reveal linear/non-linear relationships and patterns directly from data that would be difficult to obtain using common statistical methods. Predictive models are drawn, and the key is to remain bound on established physical laws [5]. Available ML algorithms dive deep into data, are being trained on data behavior and are capable of providing accurate predictions either in a supervised or an unsupervised learning approach. In supervised ML, input data characteristics are known a priori, while in unsupervised learning, the algorithm seeks hidden patterns inside unlabeled data, first [6]. ML algorithms are evolving on the basis of capturing data behavior while, in parallel, trying to eliminate less relevant input features, driven by explainability, which is currently a prerequisite for novel AI techniques [7].
The question of whether data-driven methods and ML fit to a problem or not is a subject of investigation. The existence of a certain amount of problem-specific data is critical in order to conduct the investigation. In practical applications, such as those in the construction and building sector, research data are acquired via expensive and time-consuming experiments, providing only a portion of the amount of data needed for an ML model to function effectively [8]. When simulation data are incorporated and data seem sufficient, excessive computational cost may arise if the number of input features entering the model is large. Moreover, possible input correlations may also exist, and further statistical analysis tools must be exploited [9].
This is a popular field for ML, suggesting efficient data preprocessing methods, application-specific algorithms based on simple architectures [10] or deep neural networks [11], and various output configurations, from numerical predictions to differential equation solving [12] and analytical equation extraction [13]. More specifically, in the field of construction and building industry, ML techniques have been employed to predict concrete properties that affect its strength and quality measures, such as the compressive strength, [14]. The compressive strength may be affected by the concrete mix proportion [15], the addition of various substances, such as fly ash or ground granulated blast furnace slag [16], the amount of steel or polymer fibers in its content [17] or its structural and mechanical properties [18]. In all cases, the available databases have been widely exploited to apply novel ML methods to extract the properties of interest.
Care has to be taken so that only high-quality data are exploited, preventing the consideration of erroneous, missing or redundant information [19]. In this paper, an extensive statistical analysis on the implied dataset and advanced feature engineering concepts for data curation are incorporated before data enter the ML computational flowchart. Feature engineering is capable of extracting relevant features from raw data and transforming them into a suitable format for ML models. It involves selecting, creating, and transforming variables that can be used to predict the outcome of interest in order to improve the performance of the model by making the data more relevant, informative, and predictive.
The ML stage involves the application of 12 different ML algorithms, from purely linear to highly non-linear implementations, to predict values only from data. A key issue is the algorithm choice, which is vital for achieving increased prediction accuracy for the model. From an extensive computational analysis, it is concluded that the random forest (RF) algorithm has shown low error and superiority over prediction accuracy, reaching a value for the coefficient of determination of R2 = 0.957, while linear-based algorithms fail to fit on the specific dataset.
This paper suggests an integrated framework of predicting construction material properties which may be complementary to experiments or traditional simulation techniques and complex mathematical analysis, and, in many cases, replace them, only by considering input information related to structural and mechanical parameters of the specimen. Therefore, unknown property values can be instantly obtained by ML in cases where experiments are difficult to perform, for example, in extreme pressure conditions. Apart from the prediction of the concrete compressive strength, this method can be expanded to the prediction of other properties of interest, as well, and attain a central role in guiding construction applications.
Next, the description of the dataset is given, containing an adequate number of real experimental measurements, more than any relevant study in the field (to our knowledge). The pre-processing stage is also analyzed, presenting a computational approach that considers the input correlations report, a partial dependence analysis, an overfitting test, a feature importance estimation, and a dimensionality reduction technique that aims to minimize the number of input parameters to further reduce calculation time and simplify the model. The ML computational framework is finally presented, with measures of accuracy to guide the appropriate algorithmic implementation.
2. Experimental Database and Methods
2.1. System Model
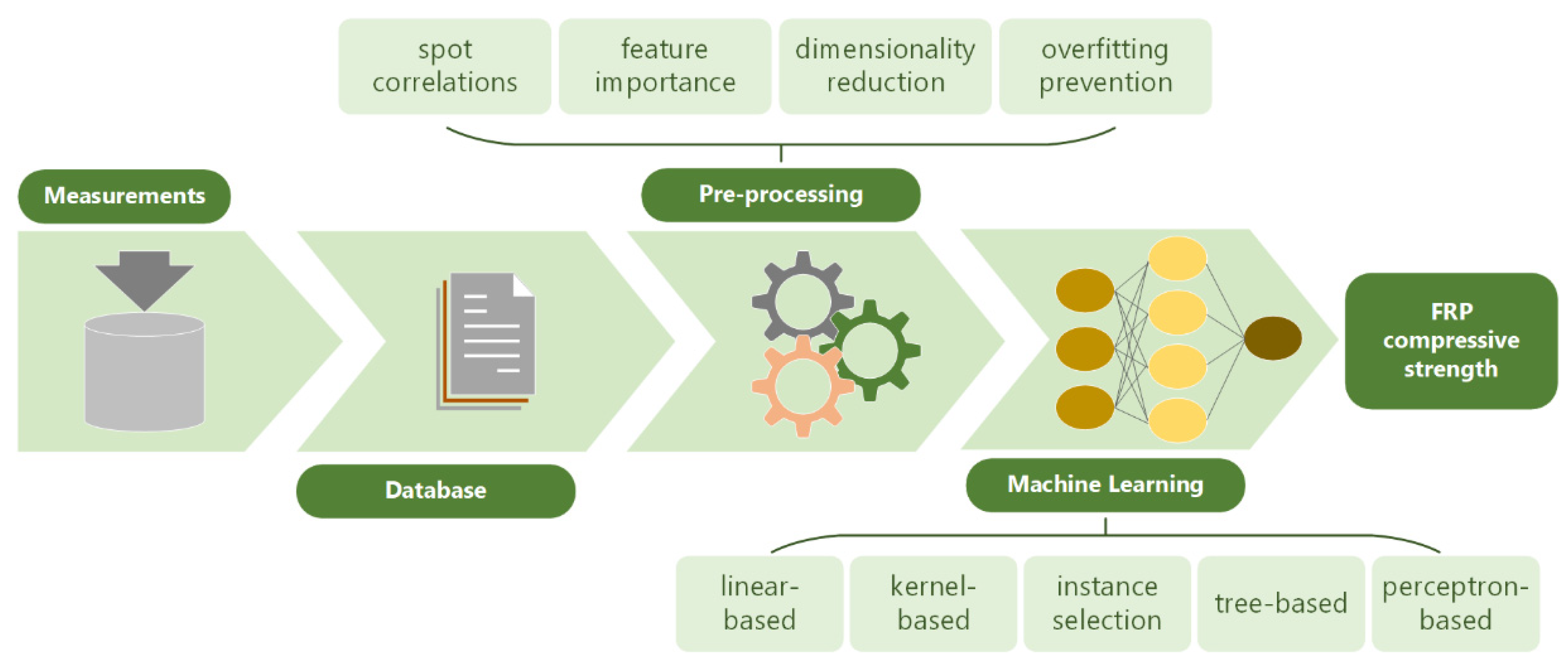
A database of 1476 experimental measurements has been incorporated in this paper, focusing on the fiber-reinforced polymer (FRP) confined concrete compressive strength, , as a function of specimen geometric parameters and mechanical properties of FRP and concrete [20]. In a similar work, has been predicted by ML methods with satisfying accuracy based on 780 literature results [21]. Our approach (Figure 1) integrates feature engineering concepts for effective data curation and novel ML algorithms to decide on the mapping between input parameters and the output variable, along with fundamental concepts to argue the results.
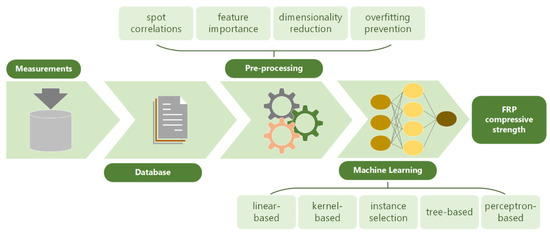
Figure 1.
ML approach to predict concrete compressive strength from experimental data.
More specifically, the experimental database is created by tabulating eight independent input parameters that can be used to evaluate the compressive strength of the material. Feature engineering concepts are exploited before data enters the ML flow. After extensive testing, all eight inputs are examined on their correlation with each other, and their partial effect on the output is evaluated. Care is also taken on overfitting prevention. Overfitting is a common problem in supervised ML, where a model becomes too closely tailored to training data, resulting in poor generalization to new, unseen data [22]. To address this issue, it is important to carefully monitor the model’s fit during training and use techniques such as regularization and the chi-squared test to prevent overfitting. The pre-processing stage also involves dimensionality reduction techniques, such as the Principal Component Analysis (PCA). This method linearly transforms the given inputs to a smaller number of new inputs, which, oftentimes, produce almost similar accuracy to the original inputs when fed to an ML model, but with less computational burden.
A total of 12 different ML algorithms are evaluated on their performance for the specific dataset. These algorithms are divided into five categories: based on their architecture, linear-based, kernel-based, instance selection, tree-based, and neural network-based. Apart from selecting the optimal choice for compressive strength prediction, this detailed investigation is an additional tool for overfitting prevention, as conclusions on their applications are drawn upon their different behavior on data.
2.2. Dataset Characteristics
The process of concrete confinement with FRP composites has been found to significantly improve compressive strength. Concrete is known to significantly expand when subjected to uniaxial unconfined compression. It has been shown that when a material with high axial strength such as a fiber reinforced polymer is used for confinement, the unconfined concrete compressive strength increases significantly [23,24]. The increase is related to the confining material properties since it reacts to concrete’s lateral expansion and gets axially stressed. Therefore, higher concrete confined strength is obtained when FRPs with higher tensile strength are used for confinement [23,25]. The most common composites used for confinement are based on aramid, carbon, and glass fibers. Data points used in this study originate from a purely experimental dataset covering various FRP confined concrete cylindrical specimens [15]. The experimental database incorporates all concrete strength categories, along with different types of confining FRP materials. The total number of conducted experiments made for each category is provided in the last column of Table 1. The experiments were all conducted in short, circular, column-like specimens with diameters varying from 50 to 100 mm and lengths from 100 to 316 mm.

Table 1.
Specimen characteristics.
There are eight possible input parameters that affect the output of confined compressive strength. Table 2 provides a brief description and statistical information on the inputs and the output. These refer to geometrical characteristics of the concrete specimens (diameter, D, and height, H), FRP layer properties (thickness of the FRP, t, and number of FRP layers, L), as well as measures of mechanical properties, such as the respective unconfined concrete strength, fco, (without FRP layers), the elastic modulus, Ef, and the FRP ultimate tensile stress and strain, ff and εfu, respectively.

Table 2.
Dataset parameters and statistical properties.
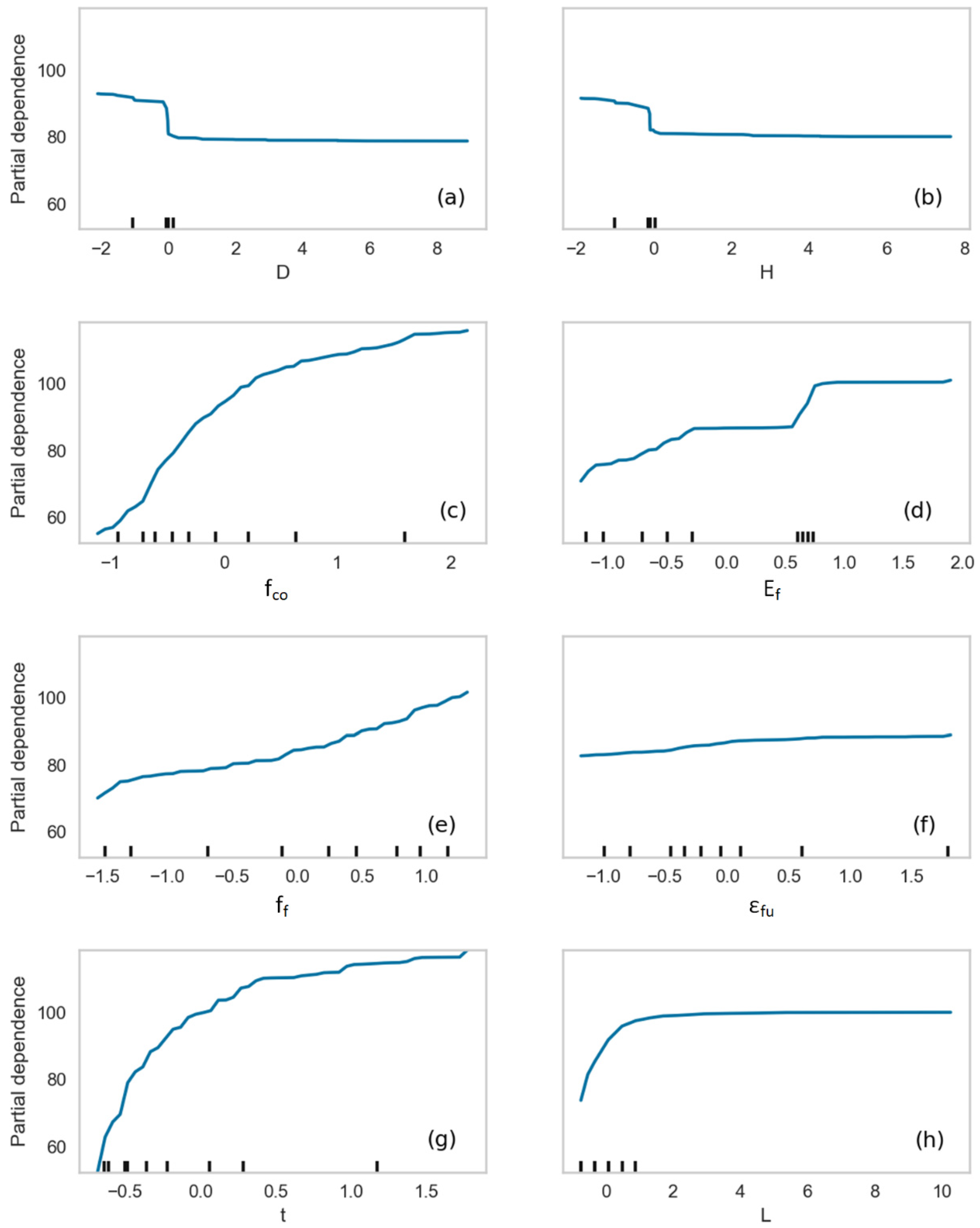
The partial dependence plot given in Figure 2 expresses the average marginal effect on the compressive strength when each one of the eight input variables changes, while, in parallel, the remaining inputs are fixed. It is observed that the effect of fco on fcc is crucial, since, if all other inputs remain constant, as fco spans from its minimum to its maximum value, fcc is significantly altered (Figure 2c). Similar fcc behavior is acquired for the t parameter (Figure 2g). These two parameters denote that the unconfined concrete strength and the FRP thickness, i.e., the main structural components of the specimen, mostly characterize the compressive strength. The number of FRP layers, L, seems important only for the first layers, while its increase after a certain value does not provide extra strength (Figure 2h). Geometrical characteristics D and H, (Figure 2a,b, respectively) are only negatively affecting fcc when they have small values (i.e., small specimens), while this effect is no longer valid for larger specimens. FRP elastic modulus, Ef, and tensile strength, ff, are two features that have an important impact on fcc, as can be seen from the respective Figure 2d,e. On the other hand, fcc is only slightly affected by the change of the FRP ultimate tensile strain, εfu (Figure 2f).
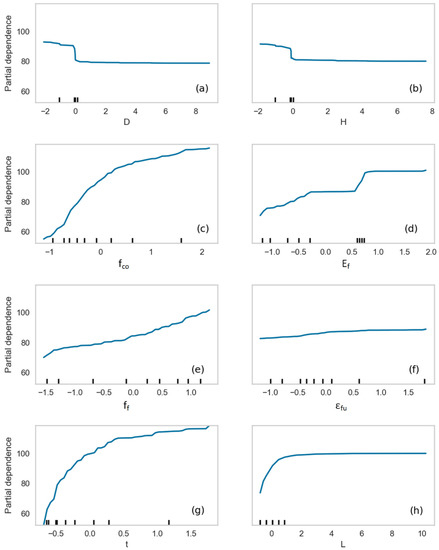
Figure 2.
Partial dependence plots, presenting the fcc dependence on each one of the eight input variables (a–h).
2.3. Input Correlations
The 1476 points dataset is divided into two parts, a training set (80%) to feed the model and a testing set (20%) for comparison with ML predicted values. Input data are pre-processed before being fed to the ML pipeline. This normalization stage aims to restrict the input parameters in the range given by
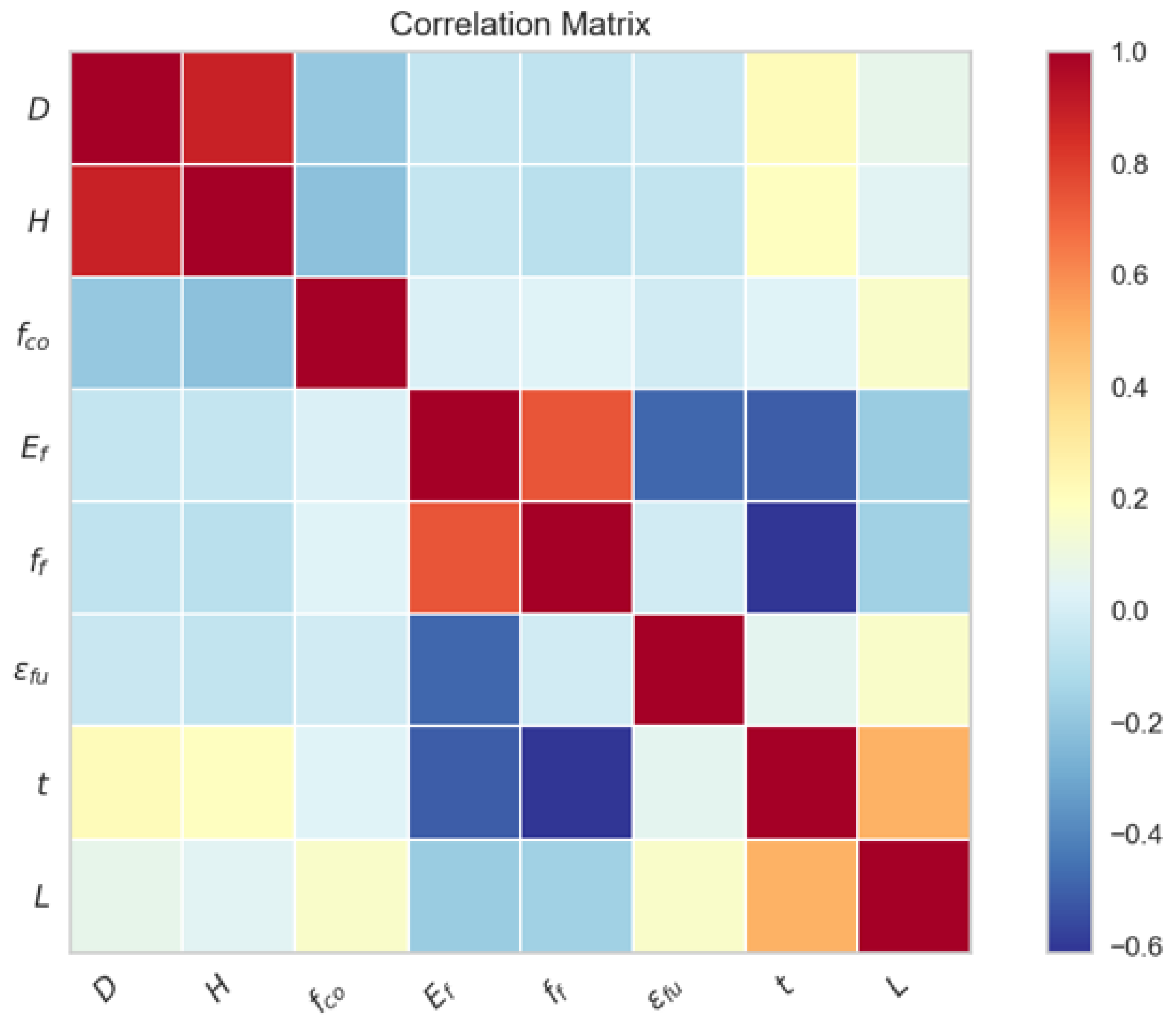
and, next, a correlation test is applied for all input features to check for independency. Figure 3 is the correlation matrix, which depicts the correlation coefficients between input variables. Values range from −1 to 1, where −1 indicates a strong negative correlation, 0 indicates no correlation, and 1 indicates a strong positive correlation. If two variables are highly correlated (negatively or positively), it may be necessary to remove one of them from the model to avoid overfitting or to improve the model’s performance. It is observed that some kind of correlation exists between D and H, Ef and ff, and t and ff, though further investigation is needed to clear out if these input pairs may be omitted from the model.
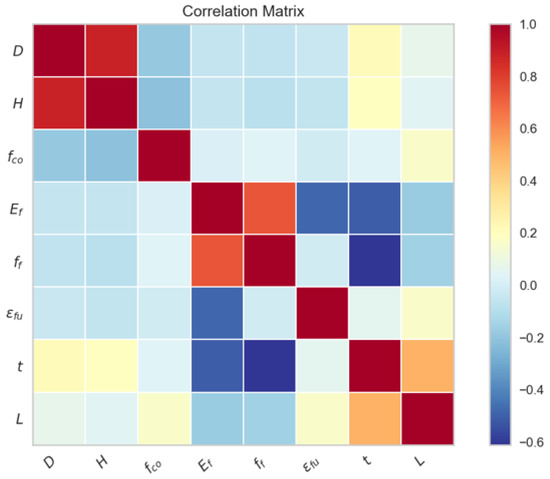
Figure 3.
Correlation matrix for the eight inputs.
The variation inflation factor (VIF) is a popular measure and is employed to provide an estimate of high-multicollinearity between variables
where the coefficient of determination. As a general rule, if VIF > 10 for a specific input, then this input can be omitted from the model. Our calculations have given the values presented in Table 3, where it is shown the ML model is to run with all eight available input parameters.

Table 3.
Values for the VIF.
2.4. Chi-Squared Test
Various techniques have been employed to eliminate overfitting in prediction methods. Overfitting occurs when a data-driven model sticks on training data and fails to predict when new data are introduced. Even though algorithmic metrics may show increased accuracy, this may be a false result. The chi-squared test is utilized to ensure that all input features are statistically significant [26] and a difference that may be observed between observed and expected values is due to a hidden relationship between them or at random. It is given by:
where, Eij the expected value, Oij the observed value, and RxK the total outcome number. The test has given all p-values below the 0.05 threshold, above which it would be implied that there exists a relationship between the observed and the expected value.
2.5. Dimensionality Reduction
The incorporation of a dimensionality reduction technique such as principal component analysis (PCA) [27] can harness the vast number of input parameters observed in data science applications. PCA acts on data by diminishing the number of input features into fewer, without significant loss of information compared to the all-feature instance, and is an important pre-processing step before feeding data to the appropriate algorithm. This may be a challenging task, since one would have to incorporate both domain knowledge and a good understanding of the algorithmic learning procedure [28]. It has been successfully applied to construction data [29].
PCA is employed to approximate the variation in p prediction variables using k < p transformed components. The result is a smaller number of input variables that still explain most of the data variance. The eight-input data set, after the application of the PCA algorithm, is transformed into a six-component set. PCA component values are shown in Table 4. Every PCAi component (i = 1–6) is given by

Table 4.
PCA components, with PCA1-6 having impact on data calculations. Grey-shaded cells are removed from calculations.
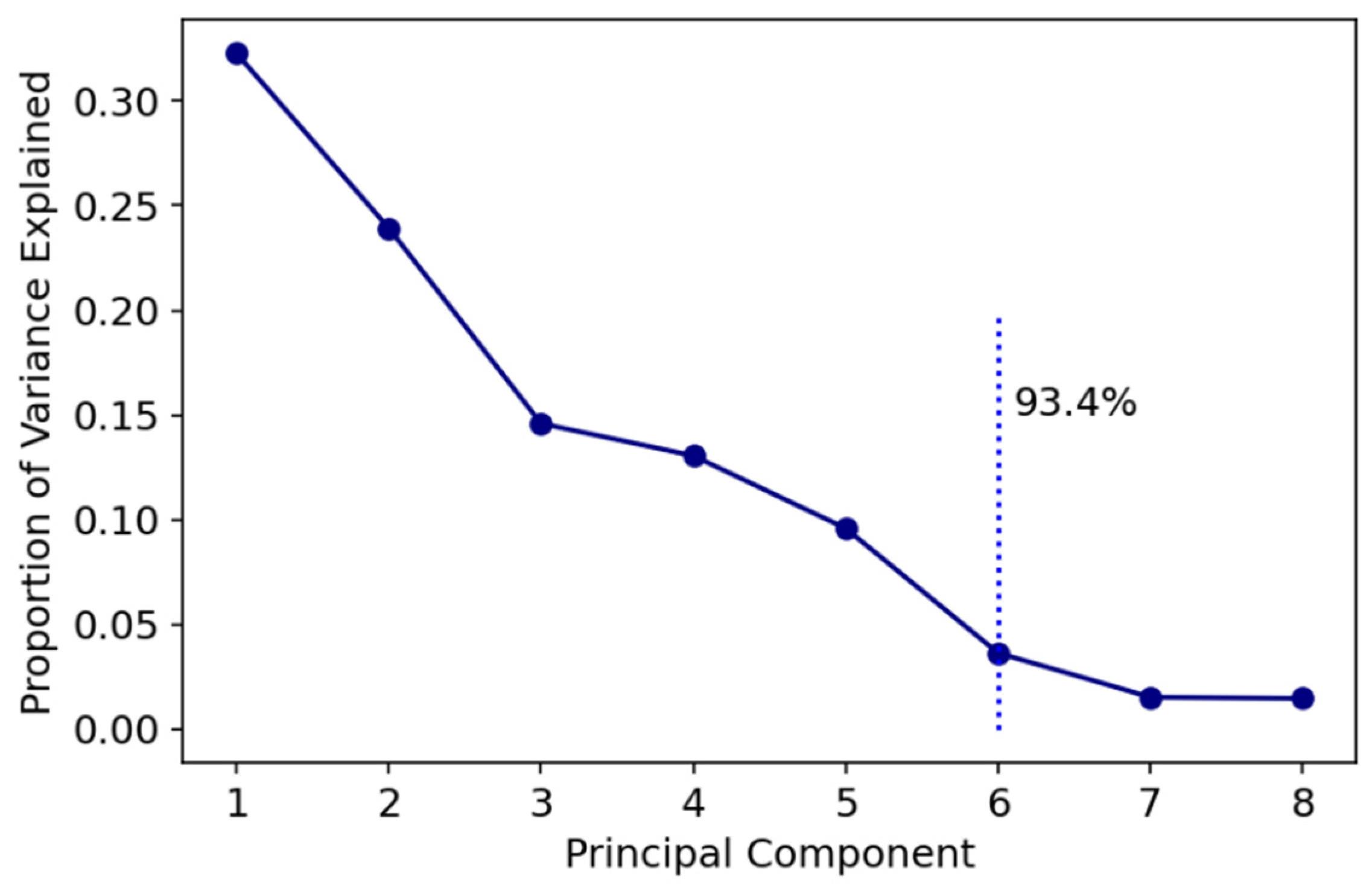
The elbow criterion of a scree plot has been incorporated to depict the desired number of inputs. The scree plot in Figure 4 presents the number of components vs. the proportion of the variance explained. The first six out of the total eight components are selected since they achieve 93.4% variance.
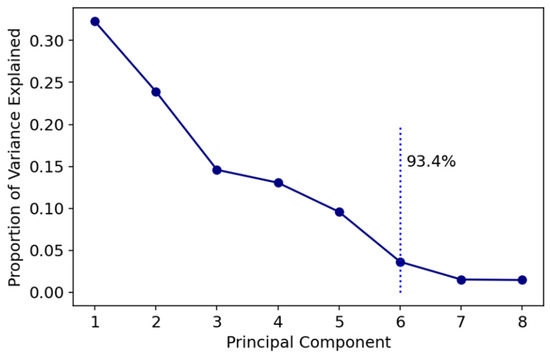
Figure 4.
Scree plot, indicating that by incorporating 6 PCA inputs instead of the original eight, our model can achieve up to 93.4% of the input variance.
3. Machine Learning Algorithms
Some of the well-established ML algorithms which have found fields of applicability in material science and engineering presented here lie in five major categories [30]: (a) linear-based, (b) kernel-based, (c) tree-based, (d) perceptron-based, and (e) instance selection. The choice of twelve different ML algorithms that have different mechanisms to be trained on data is a further step towards overfitting elimination.
3.1. Linear-Based Algorithms
3.1.1. Multiple Linear Regression
Regression analysis is incorporated to examine the relationship between a dependent variable and one or more independent variables. In the case of only one independent variable, it is referred as univariate regression, while multiple linear regression (MLR) is considered when multiple independent variables are concerned [31]. MLR involves the linear combination of n independent input variables to determine the dependent variable Y as
where are weights imposed on the respective independent input and a bias term.
3.1.2. Ridge Regression
Ridge regression is a regularization, linear regression technique, incorporated for estimating multiple linear regression coefficients when linear regression fails to capture the behavior of the data. If there are cases where the input variables are non-orthogonal, MLR fails to give proper weight to the individual explanatory variables used as predictors [32]. Ridge Regression may produce accurate predictions with less training data compared to MLR [33,34].
3.1.3. LASSO Regression
The least absolute shrinkage and selection operator (LASSO) regression technique is also a type of linear regression. Its methodology relies on using shrinkage and feature selection to select a small, predictive subset of features from a high-dimensional data set [35].
3.2. Kernel-Based Algorithms
3.2.1. Support Vector Machines
Support vector machines (SVMs) are a well-established and effective method for classification and regression analysis [36]. They utilize kernel functions to transform the input data into a higher dimensional space, allowing for easy generalization despite the increased computational demands. Kernel functions may be linear, polynomial, or radial basis functions (RBF). SVM’s versatility makes it effective for a wide range of data analysis problems. However, due to its multi-parametric nature and error sensitivity, advanced schemes, such as the fuzzy weighted SVM, have been proposed [37].
3.2.2. Gaussian Process Regression
Gaussian process (GP) regression is based on Gaussian probability distribution and can be incorporated for non-linear data analysis problems. It utilizes input data as evidence to predict an unknown function [38]. It originates from Bayesian probability theory, where the search methodology involves centering around a prior function in the beginning, and a posterior function, after evidence has been extracted from the process, and is closely connected to other regression techniques.
A GP model, before conditioning on data, is unanimously specified by its mean and covariance functions (e.g., the kernel) [39]. Covariance employs the assumptions about the function to learn and it is the main ingredient to guide the GP predictor. Popular kernels incorporated are the squared exponential, the linear, and the radial basis function (RBF).
3.3. Tree-Based Algorithms
3.3.1. Decision Trees
Decision trees (DT) is a tree-based technique, where each node represents a decision/calculation function, which, depending on the outcome, passes its output either towards a leaf (a final node) or another node where a new decision is taken. By following the path from the upper node to the final decision leaf, the desired predicted output is reached. Input features are randomly selected to enter each node and new features enter the decision procedure as the tree evolves. The DT algorithm is easily applied to ML problems; nevertheless, oftentimes, overfitting might come up and additional statistical data curation techniques are needed to confront this [40].
3.3.2. Random Forest
An RF algorithmic structure is made up of multiple decision trees working together. Each tree makes its own prediction, and the final prediction is determined by taking their average. Increasing the number of trees in the forest typically leads to higher accuracy, as it reduces the likelihood of overfitting. This makes the RF algorithm a very effective tool that has been used in many successful applications [41,42,43].
3.3.3. Gradient Boosting
Gradient boosting (GB) is also a very popular family of tree-based algorithms. The unique aspect of this method is that it combines different individual functions, or learners, to create an ensemble function that has enhanced prediction capabilities. GB acts in three steps during the tree creation: The process optimizes the performance of the loss function by identifying the weaker learner and improving its accuracy through the addition of more trees [44].
3.4. Perceptron-Based Algorithms
Multi-Layer Perceptron
The Multi-Layer Perceptron (MLP) is a type of neural network that consists of multiple layers, including the input, output, and hidden layers. The number of hidden layers is typically determined through experimentation. The flow of data between neurons in an MLP is driven by the activation functions applied to each internal node and the weight function applied to each input. These weights are adjusted during training to minimize the error between the predicted and the expected output. MLP training is performed iteratively, using backward computation and gradient-based learning (e.g., the Stochastic Gradient Descent).
Notwithstanding the fact that MLPs are probably the most favorable choices in ML concrete properties prediction applications [45,46], their multi-parametric implementation may, on the other hand, pose difficulties in model convergence, trapping local minima and overfitting [47].
3.5. Instance-Selection
k-Nearest Neighbors
The k-Nearest Neighbors (k-NN) algorithm decides on the classification of a new data point by looking at the k closest training data points and using a distance metric to determine their similarity. In this case, the Euclidean distance is used to calculate the distances between the test data point and the training data points. The distances are then sorted and the most commonly occurring label among the first k distances is chosen as the prediction. Each sample includes both the input vector and the desired output [42]. Mainly incorporated in classification problems, k-NN lacks in generalization and can be significantly slow in regression problems. From a technical aspect, k-NN stores all training data during testing, and this can lead to slower execution times and increased memory load, especially for big data applications [48].
3.6. Measures of Accuracy
An ML algorithm is tested on its accuracy with several calculated metrics that generally describe the fitting of input data to the proposed ML output. To evaluate the success of the proposed algorithm, one can use various error statistics, such as the coefficient of determination, , mean absolute error, MAE, root mean squared error, RMSE, average absolute deviation, AAD, and the Akaike information criterion, AIC, as shown in Table 5.

Table 5.
Metrics used to characterize a method’s accuracy.
The coefficient of determination is a measure of the goodness of fit of a regression model. It represents the proportion of the variance in the dependent variable that is explained by the model. It ranges from 0 to 1, with a higher value indicating a better fit. MAE is a measure of the difference (absolute) between predicted values and observed values, while RMSE is calculated by taking the square root of the average of the squared differences between the predicted and the observed values. AAD is calculated by taking the average of the absolute differences between the predicted and the observed values. AIC measures the relative quality of a statistical model. It is used to compare multiple models and select the one that best fits the data, where lower AIC value indicates a better model.
All these statistic measures clearly depict how well the proposed method predicts the actual values.
4. Results and Discussion
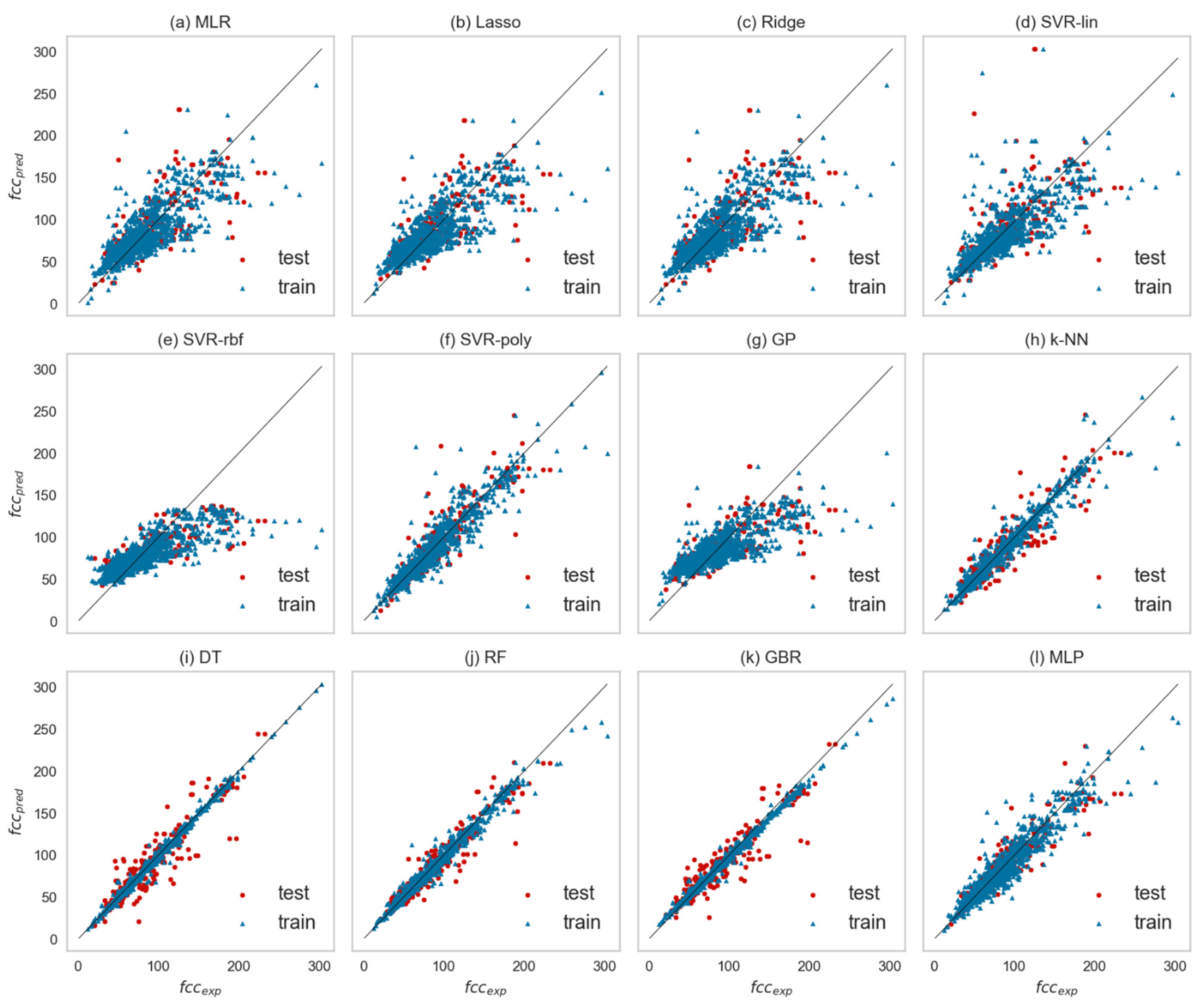
Measures of accuracy for the confined compressive strength (fcc) dataset employed for every algorithm are provided in Table 6. They can be examined in parallel to the identity plots of Figure 5, where fcc experimental values are compared to fcc predicted values, in terms of how close to the 45° line they stand. In cases where training and testing points are shown scarcely distributed away from the 45° line, this is evidence of poor fitting to the specific algorithm. It has been found that algorithms with a tree-like structure, such as RF, GBR, and DT, have demonstrated the best performance for all metrics for the compressive strength prediction, since all data points examined are set close to the 45° line. Satisfying results have also been calculated through the k-means and the MLP models.

Table 6.
Calculated metrics for all ML algorithms applied to the dataset for all eight inputs.
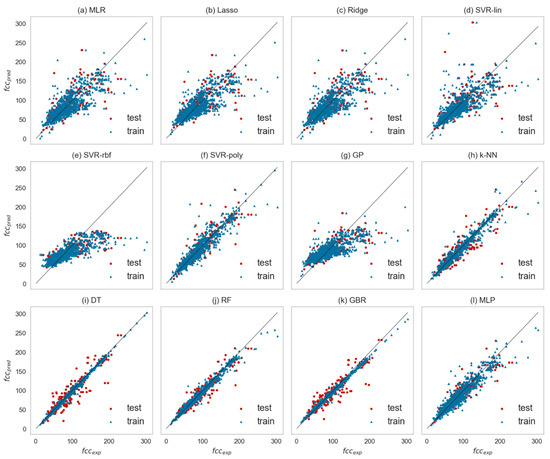
Figure 5.
Experimental versus predicted values for fcc (both training and test data) in identity plots being the output of 12 different algorithms, (a) MLR, (b) LASSO, (c) Ridge, (d) SVR-linear kernel, (e) SVR-RBF, (f) SVR-polynomial, (g) GP, (h) k-NN, (i) DT, (j) RF, (k) GBR, and (l) MMLP. The 45° line shows the perfect match.
More specifically, the RF algorithm (Figure 5j) achieves the highest R2 score, and this verifies that the implied regression model achieves fine fitting. This outcome agrees to the results obtained in [49], where RF has been found to provide accurate predictions in similar applications even with no parameter tuning. Fine fitting is further verified by the minimum values obtained for the absolute and the squared error, MAE and RMSE, respectively. The calculated AAD metric denotes that the variability of RF predicted values around the experimental ones is low. Another important evidence is the AIC value, which estimates the unknown parameters in terms of the Maximum Likelihood Principle [50]. In search of the best regression model, it is proposed that it is preferable to choose the one with minimum AIC value [51]. It is also important to note that our RF model achieves one of the highest accuracy metrics, compared to what is shown in the literature (more details can be found in the recent review of Chaabene et al. [52]).
The tree-based, ensemble GBR algorithm (Figure 5k), along with the DT (Figure 5i), have also performed similarly to RF, with high R2 score and low MAE, RMSE, and AAD values. The AIC criterion denotes slightly better performance for GBR compared to DT. Apart from the tree-based methods, the instance selection algorithm, k-NN, is also a good choice for predicting the compressive strength, followed by the polynomial-SVR. On the other hand, the remaining linear-based algorithms (MLR, Ridge, Lasso, in Figure 5a–c) and kernel-based (SVR-linear, SVR-rbf, GP, in Figure 5d,e,g, respectively) have shown smaller accuracy metrics.
At first sight, this is evidence that the dataset incorporated clearly presents non-linear behavior. All linear ML algorithms have failed to reproduce the experimental data. On the other hand, kernel-based methods cannot be excluded from such applications, since they have shown remarkable performance in various material prediction models, especially in computationally intensive applications near the atomic scale [53,54]. For the GP algorithm, of particular importance is how to select the kernel function and model parameters need to be recursively optimized to achieve the optimal result [38].
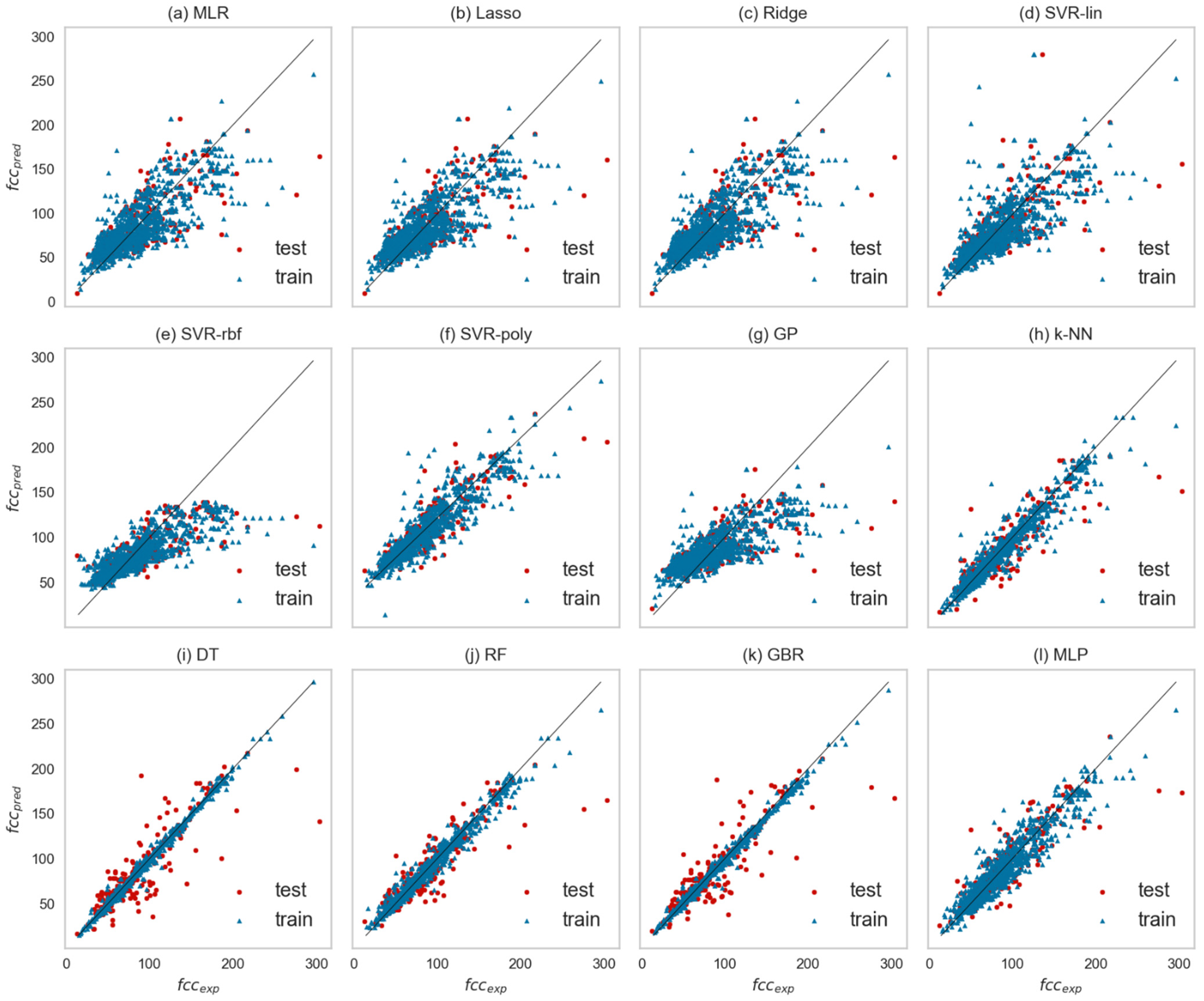
Measures and predictions obtained after the incorporation of the PCA technique, which reduces the initial eight parameter space to six, are shown in Table 7 and Figure 6. If examined individually, Table 7 follows the same trend as the values in Table 6. The tree-based algorithms have achieved maximum measures of accuracy compared to linear- and kernel-based ones. If these values are compared to the eight-input case in Table 6, it is observed that R2 scores are slightly lower for all cases. From a general point of view, PCA has trivial impact on linear- and kernel-based algorithms, e.g., the algorithms that have shown poor performance during the eight-input data flow (see Table 6 and Figure 5).

Table 7.
Calculated metrics for all ML algorithms applied to the dataset for the reduced case with six PCA inputs.
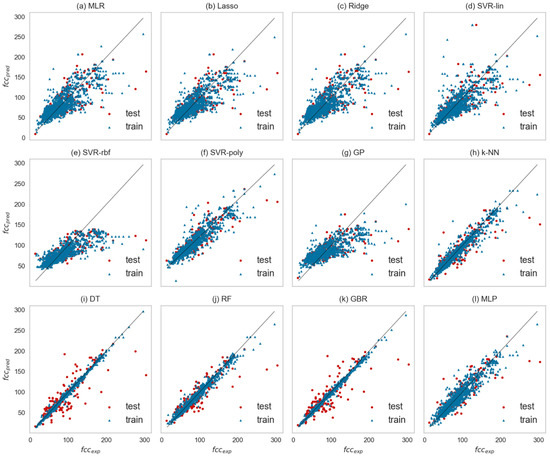
Figure 6.
Experimental versus predicted values for fcc (both training and test data, after the incorporation of six PCA inputs instead of the original eight) in identity plots being the output of 12 different algorithms, (a) MLR, (b) LASSO, (c) Ridge, (d) SVR-linear kernel, (e) SVR-RBF, (f) SVR-polynomial, (g) GP, (h) k-NN, (i) DT, (j) RF, (k) GBR, and (l) MMLP. The 45° line shows the perfect match.
Nevertheless, there is significant loss of accuracy in terms of RMSE, MAE, and AAD and for RF, DT, GBR, MLP, and SVR-poly (see Table 8). The k-NN has also shown significant RMSE increase.

Table 8.
Measures of accuracy comparison. Values for each measure correspond to the percentage of loss when the all-input case is substituted by the six PCA inputs case.
It has to be noted that the application of the PCA technique here is given for comparison reasons. The number of available experimental data and the eight input features do not primarily demand increased computational time to run on modern hardware sources, and all inputs can be processed effectively. However, it is clearly depicted that during a computational process of predicting material properties, when and if needed, PCA can be successfully introduced. The experimental research efforts from our team continue and future work is going to enrich the dataset with more input and output properties, and this is certainly a field of application.
As one of the primary goals of materials science and engineering research is to develop novel materials that perform optimally under specific conditions, it’s important to understand how and which features affect its behavior. Results can be found in sensitivity analysis to identify the importance of each input variable in the prediction process. Taking in mind all (eight) model input parameters, characteristic feature importance plots to argue on each input significance on the final prediction are presented next. This investigation is made on an algorithmic basis.
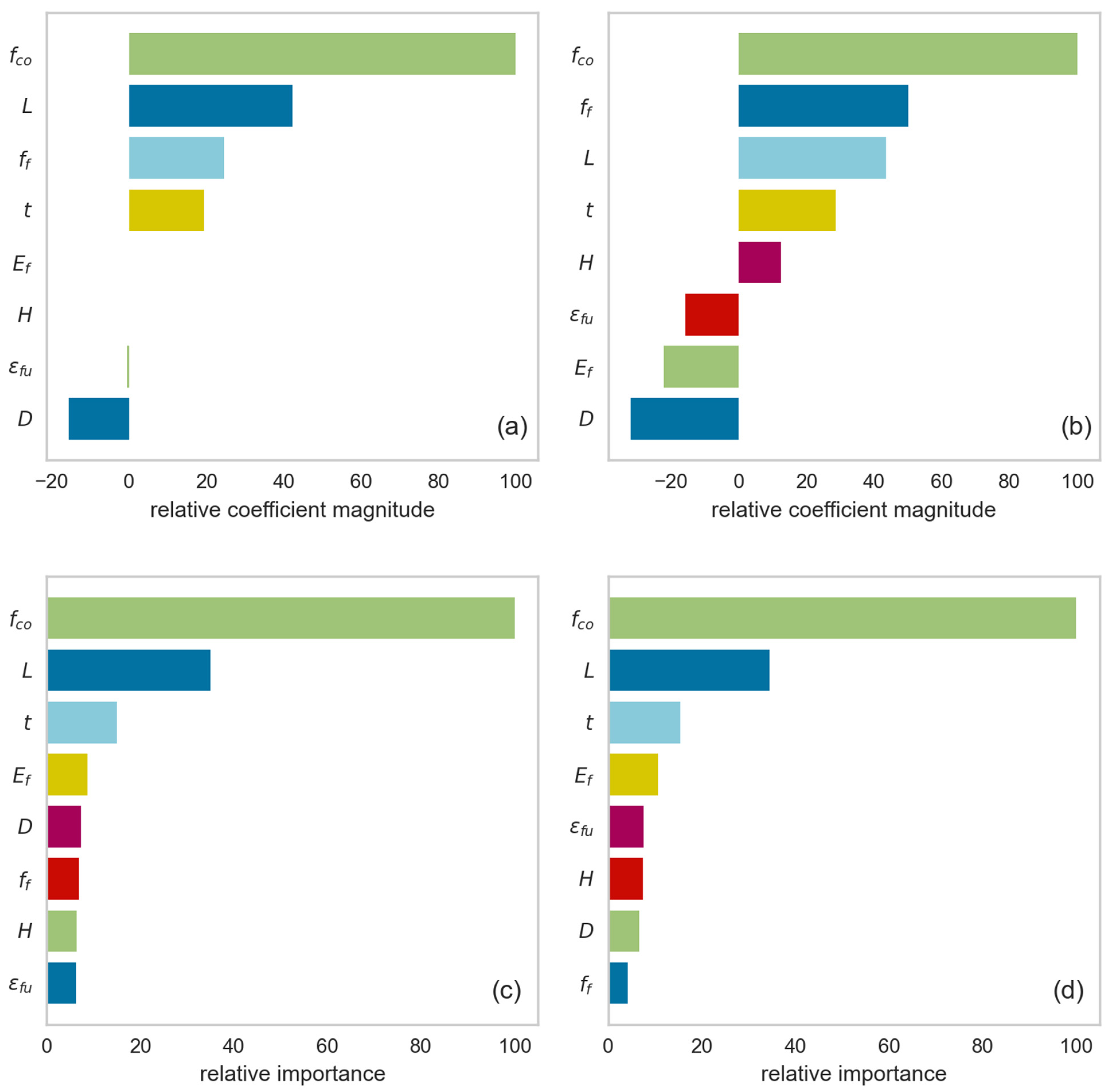
Figure 7 presents the most important input features for four of the algorithms investigated here by incorporating the FeatureImportances() function from the YellowBrick python package [55]. All algorithms agree that the most significant feature is fco, i.e., the unconfined concrete strength. The two more accurate tree-based algorithms according to Table 6 and Table 7, RF and GBR (in Figure 7c,d, respectively), also consider the number of FRP layers, L, and the FRP ultimate axial strength, ff, of increased importance.
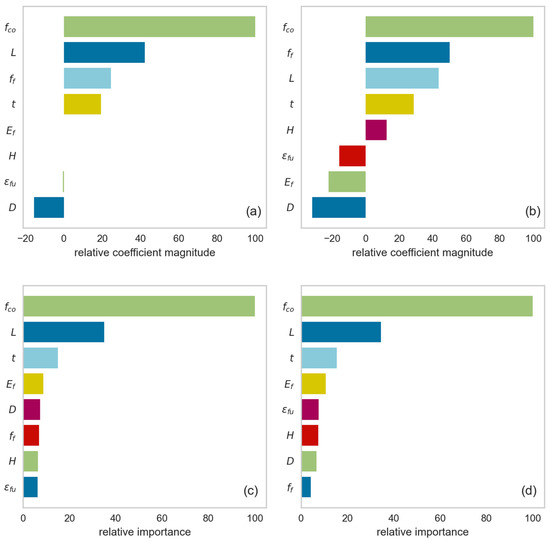
Figure 7.
Feature importance for the (a) LASSO, (b) Ridge, (c) RF, and (d) GBR algorithms.
These findings are very important, as they may be a valuable tool for application engineers, as it can depict the proper material to use in relevant applications. The unconfined concrete strength, being the basis for the calculations before the layered composite material is applied around the cylindrical specimen, is of outmost importance, followed by the number of layers, L, (carbon, glass or aramid) to be wrapped around it. To reach even more accurate predictions on the obtained confined compressive strength, one has to further take in mind the effect of the FRP thickness, t, and the FRP Young’s modulus, Ef. The remaining input parameters, such as the specimen diameter, D, and height, H, the ultimate tensile strength of the FRP, ff, and the ultimate FRP strain, εfu, are of small importance.
5. Conclusions
Structural engineering applications can be analyzed and processed through structure–property relations that are clearly dependent on the input variables. When analytical models are not at hand, ML and statistical methods may be an effective alternative to describe these dependencies using purely data driven methods, overcoming timely and expensive experimental procedures. This paper employs an extended database of experimental measurements that fully describe the mechanical and physical properties of FRP confined concrete specimens and suggests an ML platform to predict the compressive strength of confined concrete.
Feature engineering concepts are first explored to prepare the dataset and make it more relevant, informative, and predictive. Correlation tests, in the form of a correlation matrix and a VIF test, have spotted no correlations between input features. Moreover, a partial dependence calculation has been performed. This has shown that the effect of the structural FRP parameters, i.e., the unconfined concrete strength, fco, and the FRP thickness, t, are the primary components affecting mostly the FRP compressive strength. This can be useful to drive future optimization of specimens considered for relevant applications. Furthermore, dimensionality reduction techniques such as PCA are also leveraged to minimize the number of independent input features, providing a means of calculation boost. It has been shown that by considering six independent input features derived from PCA, one can replace the original eight-input dataset, achieving 93.4% variance.
The key element of the proposed model is the ML algorithm. All algorithms presented here have shown that they are capable of providing accurate predictions in a wide-parameter space, even in the presence of noise in the observations, which is due to the experimental measurements. The suggested tree-based ML algorithms investigated on the problem perform well and may be incorporated in similar applications without evidence of overfitting, as also verified using a statistical chi-squared test. More specifically, the RF algorithm has achieved optimal measures of prediction accuracy. As for the implied trees inside the RF structure, the feature importance procedure exploited here has revealed that decisions are mainly driven by the significant parameter fco. The remaining input parameters, such as the number of FRP layers, FRP thickness, FRP ultimate tensile stress, diameter and height of the cylindrical concrete specimens, FRP ultimate tensile strain, and FRP elastic modulus, can be employed for the model refinement.
Overall, the detailed data science and ML procedure suggested in this paper can aid scientific and engineering applications towards imbuing existing and newly created knowledge into computational models by overcoming the traditional pathway, which often demands either expensive experimental procedures or computationally and hardware-intensive techniques.
Author Contributions
Conceptualization, F.S., C.G.P., T.E.K.; methodology, F.S., T.E.K.; software, F.S.; validation, C.G.P., T.E.K., M.V.; formal analysis, C.G.P.; investigation, M.V., C.G.P.; resources, M.V., C.G.P.; data curation, F.S.; writing—original draft preparation, F.S., C.G.P.; writing—review and editing, T.E.K.; visualization, F.S.; supervision, C.G.P., T.E.K.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data may be available upon reasonable request from the authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sbahieh, S.; Tahir, F.; Al-Ghamdi, S.G. Environmental and Mechanical Performance of Different Fiber Reinforced Polymers in Beams. Mater. Today: Proc. 2022, 62, 3548–3552. [Google Scholar] [CrossRef]
- Mirrashid, M.; Naderpour, H. Recent Trends in Prediction of Concrete Elements Behavior Using Soft Computing (2010–2020). Arch. Comput. Methods Eng. 2021, 28, 3307–3327. [Google Scholar] [CrossRef]
- Bhuvaneswari, V.; Priyadharshini, M.; Deepa, C.; Balaji, D.; Rajeshkumar, L.; Ramesh, M. Deep Learning for Material Synthesis and Manufacturing Systems: A Review. Mater. Today Proc. 2021, 46, 3263–3269. [Google Scholar] [CrossRef]
- Chakraborty, D.; Awolusi, I.; Gutierrez, L. An Explainable Machine Learning Model to Predict and Elucidate the Compressive Behavior of High-Performance Concrete. Results Eng. 2021, 11, 100245. [Google Scholar] [CrossRef]
- Dimiduk, D.M.; Holm, E.A.; Niezgoda, S.R. Perspectives on the Impact of Machine Learning, Deep Learning, and Artificial Intelligence on Materials, Processes, and Structures Engineering. Integr. Mater. Manuf. Innov. 2018, 7, 157–172. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, C.; Snoussi, H.; Zhang, G. Machine Learning Approaches for Thermoelectric Materials Research. Adv. Funct. Mater. 2020, 30, 1906041. [Google Scholar] [CrossRef]
- Kailkhura, B.; Gallagher, B.; Kim, S.; Hiszpanski, A.; Han, T.Y.-J. Reliable and Explainable Machine-Learning Methods for Accelerated Material Discovery. NPJ Comput. Mater. 2019, 5, 108. [Google Scholar] [CrossRef]
- Hu, Z.; Li, Q.; Yan, H.; Wen, Y. Experimental Study on Slender CFRP-Confined Circular RC Columns under Axial Compression. Appl. Sci. 2021, 11, 3968. [Google Scholar] [CrossRef]
- Gao, C.; Min, X.; Fang, M.; Tao, T.; Zheng, X.; Liu, Y.; Wu, X.; Huang, Z. Innovative Materials Science via Machine Learning. Adv. Funct. Mater. 2022, 32, 2108044. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.E. Machine Learning Techniques for Fluid Flows at the Nanoscale. Fluids 2021, 6, 96. [Google Scholar] [CrossRef]
- Kashefi, A.; Rempe, D.; Guibas, L.J. A Point-Cloud Deep Learning Framework for Prediction of Fluid Flow Fields on Irregular Geometries. Phys. Fluids 2021, 33, 027104. [Google Scholar] [CrossRef]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A Deep Learning Library for Solving Differential Equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Sofos, F.; Charakopoulos, A.; Papastamatiou, K.; Karakasidis, T.E. A Combined Clustering/Symbolic Regression Framework for Fluid Property Prediction. Phys. Fluids 2022, 34, 062004. [Google Scholar] [CrossRef]
- Cook, R.; Lapeyre, J.; Ma, H.; Kumar, A. Prediction of Compressive Strength of Concrete: Critical Comparison of Performance of a Hybrid Machine Learning Model with Standalone Models. J. Mater. Civ. Eng. 2019, 31, 04019255. [Google Scholar] [CrossRef]
- Young, B.A.; Hall, A.; Pilon, L.; Gupta, P.; Sant, G. Can the Compressive Strength of Concrete Be Estimated from Knowledge of the Mixture Proportions?: New Insights from Statistical Analysis and Machine Learning Methods. Cem. Concr. Res. 2019, 115, 379–388. [Google Scholar] [CrossRef]
- Asteris, P.G.; Skentou, A.D.; Bardhan, A.; Samui, P.; Pilakoutas, K. Predicting Concrete Compressive Strength Using Hybrid Ensembling of Surrogate Machine Learning Models. Cem. Concr. Res. 2021, 145, 106449. [Google Scholar] [CrossRef]
- Abdulhameed, A.A.; Al-Zuhairi, A.H.; Al Zaidee, S.R.; Hanoon, A.N.; Al Zand, A.W.; Hason, M.M.; Abdulhameed, H.A. The Behavior of Hybrid Fiber-Reinforced Concrete Elements: A New Stress-Strain Model Using an Evolutionary Approach. Appl. Sci. 2022, 12, 2245. [Google Scholar] [CrossRef]
- da Silva, S.R.; Cimadon, F.N.; Borges, P.M.; Schiavon, J.Z.; Possan, E.; de Oliveira Andrade, J.J. Relationship between the Mechanical Properties and Carbonation of Concretes with Construction and Demolition Waste. Case Stud. Constr. Mater. 2022, 16, e00860. [Google Scholar] [CrossRef]
- Wei, J.; Chu, X.; Sun, X.; Xu, K.; Deng, H.; Chen, J.; Wei, Z.; Lei, M. Machine Learning in Materials Science. InfoMat 2019, 1, 338–358. [Google Scholar] [CrossRef]
- Valasaki, M.; Papakonstantinou, C.G. Confined Circular Columns: An Experimental Overview. Buildings. submitted.
- Keshtegar, B.; Gholampour, A.; Thai, D.-K.; Taylan, O.; Trung, N.-T. Hybrid Regression and Machine Learning Model for Predicting Ultimate Condition of FRP-Confined Concrete. Compos. Struct. 2021, 262, 113644. [Google Scholar] [CrossRef]
- Ying, X. An Overview of Overfitting and Its Solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Vincent, T. Axial Compressive Behavior of Circular High-Strength Concrete-Filled FRP Tubes. J. Compos. Constr. 2014, 18, 04013037. [Google Scholar] [CrossRef]
- Michael, N. Fardis and Homayoun Khalili Concrete Encased in Fiberglass-Reinforced Plastic. ACI J. Proc. 1981, 78, 440–446. [Google Scholar] [CrossRef]
- Papakonstantinou, C.G. Fiber Reinforced Polymer (FRP) Confined Circular Columns: Compressive Strength Assessment. JESTR 2020, 13, 1–13. [Google Scholar] [CrossRef]
- Behnke, M.; Briner, N.; Cullen, D.; Schwerdtfeger, K.; Warren, J.; Basnet, R.; Doleck, T. Feature Engineering and Machine Learning Model Comparison for Malicious Activity Detection in the DNS-Over-HTTPS Protocol. IEEE Access 2021, 9, 129902–129916. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.E. Nanoscale Slip Length Prediction with Machine Learning Tools. Sci. Rep. 2021, 11, 12520. [Google Scholar] [CrossRef]
- Wang, M.; Wang, T.; Cai, P.; Chen, X. Nanomaterials Discovery and Design through Machine Learning. Small Methods 2019, 3, 1900025. [Google Scholar] [CrossRef]
- Dobgegah, R.; Owusu-Manu, D.-G.; Omoteso, K. A Principal Component Analysis of Project Management Construction Industry Competencies for the Ghanaian. Constr. Econ. Build. 2011, 11, 26–40. [Google Scholar] [CrossRef]
- Sofos, F.; Stavrogiannis, C.; Exarchou-Kouveli, K.K.; Akabua, D.; Charilas, G.; Karakasidis, T.E. Current Trends in Fluid Research in the Era of Artificial Intelligence: A Review. Fluids 2022, 7, 116. [Google Scholar] [CrossRef]
- Uyanık, G.K.; Güler, N. A Study on Multiple Linear Regression Analysis. Procedia -Soc. Behav. Sci. 2013, 106, 234–240. [Google Scholar] [CrossRef]
- McDonald, G.C. Ridge Regression. WIREs Comput. Stat. 2009, 1, 93–100. [Google Scholar] [CrossRef]
- Gareth James, D.W.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer: New York, NY, USA, 2013. [Google Scholar]
- Bibas, K.; Fogel, Y.; Feder, M. A New Look at an Old Problem: A Universal Learning Approach to Linear Regression. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; pp. 2304–2308. [Google Scholar]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Society Ser. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Sonnenburg, S.; Rätsch, G.; Schäfer, C.; Schölkopf, B. Large Scale Multiple Kernel Learning. J. Mach. Learn. Res. 2006, 7, 1531–1565. [Google Scholar]
- Fan, Z.; Chiong, R.; Hu, Z.; Lin, Y. A Fuzzy Weighted Relative Error Support Vector Machine for Reverse Prediction of Concrete Components. Comput. Struct. 2020, 230, 106171. [Google Scholar] [CrossRef]
- Deringer, V.L.; Bartók, A.P.; Bernstein, N.; Wilkins, D.M.; Ceriotti, M.; Csányi, G. Gaussian Process Regression for Materials and Molecules. Chem. Rev. 2021, 121, 10073–10141. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Gaussian Processes in Machine Learning. In Advanced Lectures on Machine Learning: ML Summer Schools 2003, Canberra, Australia, 2–14 February 2003, Tübingen, Germany, 4–16 August 2003, Revised Lectures; Bousquet, O., von Luxburg, U., Rätsch, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 63–71. ISBN 978-3-540-28650-9. [Google Scholar]
- Schmidt, J.; Marques, M.R.G.; Botti, S.; Marques, M.A.L. Recent Advances and Applications of Machine Learning in Solid-State Materials Science. NPJ Comput. Mater. 2019, 5, 83. [Google Scholar] [CrossRef]
- Allers, J.P.; Harvey, J.A.; Garzon, F.H.; Alam, T.M. Machine Learning Prediction of Self-Diffusion in Lennard-Jones Fluids. J. Chem. Phys. 2020, 153, 034102. [Google Scholar] [CrossRef]
- Rahman, J.; Ahmed, K.S.; Khan, N.I.; Islam, K.; Mangalathu, S. Data-Driven Shear Strength Prediction of Steel Fiber Reinforced Concrete Beams Using Machine Learning Approach. Eng. Struct. 2021, 233, 111743. [Google Scholar] [CrossRef]
- Xiong, J.; Zhang, T.Y.; Shi, S.Q. Machine Learning of Mechanical Properties of Steels. Sci. China Technol. Sci. 2020, 63, 1247–1255. [Google Scholar] [CrossRef]
- Sandhu, A.K.; Batth, R.S. Software Reuse Analytics Using Integrated Random Forest and Gradient Boosting Machine Learning Algorithm. Softw. Pract. Exp. 2021, 51, 735–747. [Google Scholar] [CrossRef]
- Ikumi, T.; Galeote, E.; Pujadas, P.; de la Fuente, A.; López-Carreño, R.D. Neural Network-Aided Prediction of Post-Cracking Tensile Strength of Fibre-Reinforced Concrete. Comput. Struct. 2021, 256, 106640. [Google Scholar] [CrossRef]
- Roberson, M.M.; Inman, K.M.; Carey, A.S.; Howard, I.L.; Shannon, J. Probabilistic Neural Networks That Predict Compressive Strength of High Strength Concrete in Mass Placements Using Thermal History. Comput. Struct. 2022, 259, 106707. [Google Scholar] [CrossRef]
- Nguyen, H.; Vu, T.; Vo, T.P.; Thai, H.-T. Efficient Machine Learning Models for Prediction of Concrete Strengths. Constr. Build. Mater. 2021, 266, 120950. [Google Scholar] [CrossRef]
- Song, Y.; Liang, J.; Lu, J.; Zhao, X. An Efficient Instance Selection Algorithm for k Nearest Neighbor Regression. Neurocomputing 2017, 251, 26–34. [Google Scholar] [CrossRef]
- Han, Q.; Gui, C.; Xu, J.; Lacidogna, G. A Generalized Method to Predict the Compressive Strength of High-Performance Concrete by Improved Random Forest Algorithm. Constr. Build. Mater. 2019, 226, 734–742. [Google Scholar] [CrossRef]
- Cavanaugh, J.E.; Neath, A.A. The Akaike Information Criterion: Background, Derivation, Properties, Application, Interpretation, and Refinements. WIREs Comput. Stat. 2019, 11, e1460. [Google Scholar] [CrossRef]
- Baguley, T.S. Serious Stats: A Guide to Advanced Statistics for the Behavioral Sciences; Palgrave Macmillan: New York, NY, USA, 2012; p. xxiii. ISBN 0-230-57718-0. [Google Scholar]
- Ben Chaabene, W.; Flah, M.; Nehdi, M.L. Machine Learning Prediction of Mechanical Properties of Concrete: Critical Review. Constr. Build. Mater. 2020, 260, 119889. [Google Scholar] [CrossRef]
- Bartók, A.P.; Payne, M.C.; Kondor, R.; Csányi, G. Gaussian Approximation Potentials: The Accuracy of Quantum Mechanics, without the Electrons. Phys. Rev. Lett. 2010, 104, 136403. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, Z.; Qian, P.; Ala-Nissila, T.; Caro, M.A. Structure and Pore Size Distribution in Nanoporous Carbon. Chem. Mater. 2022, 34, 617–628. [Google Scholar] [CrossRef]
- Bengfort, B.; Bilbro, R. Yellowbrick: Visualizing the Scikit-Learn Model Selection Process. J. Open Source Softw. 2019, 4, 1075. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).