Experimental and Empirical Studies to Evaluate Liquefaction Resistance of Partially Saturated Sands
Abstract
:1. Introduction
2. Prediction Models for Partially Saturated Soils
2.1. Previous Literature
2.2. Adopted Empirical Methodology
3. Materials and Methods
3.1. Testing Device and Test Material
3.2. Specimen Preparation
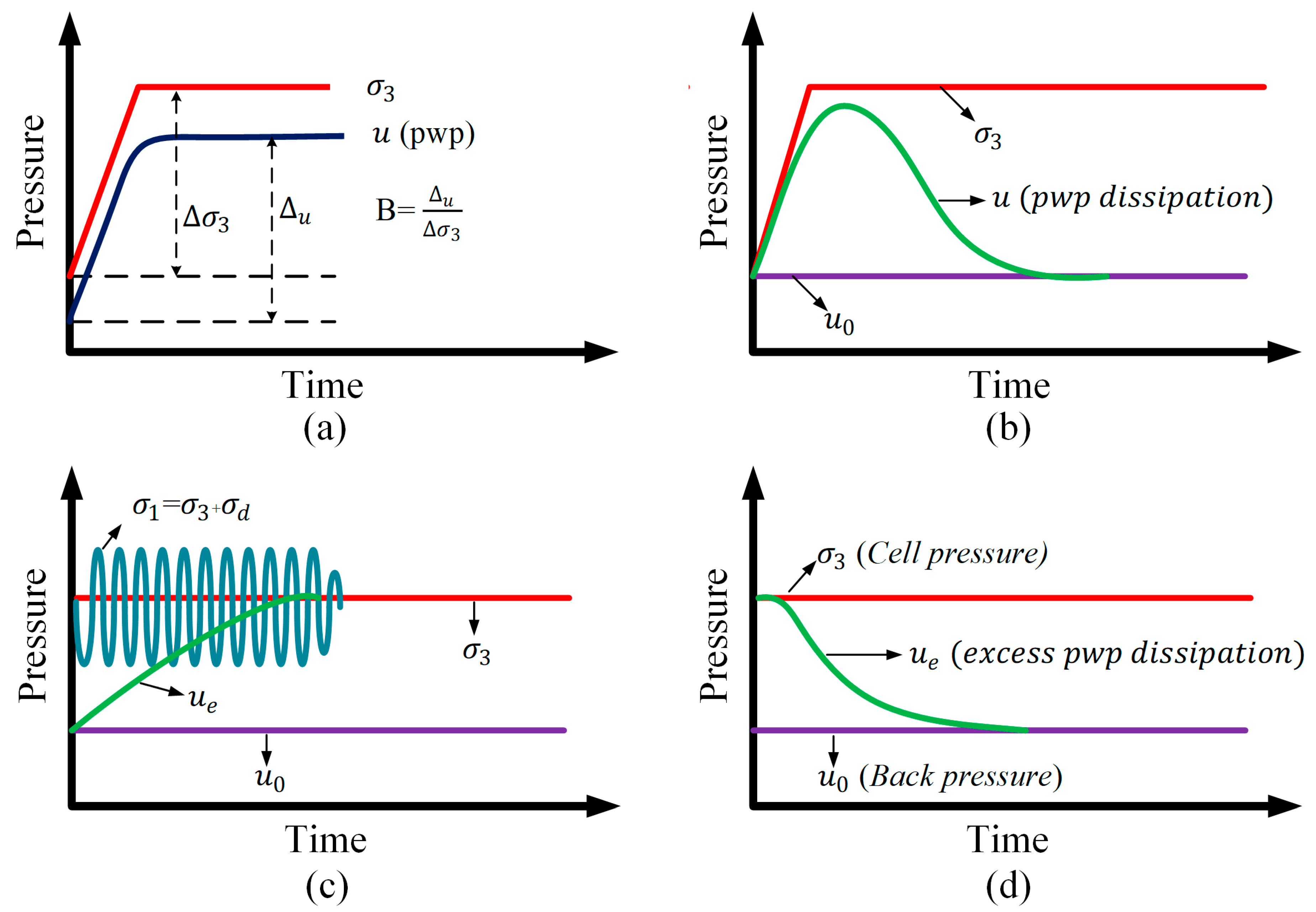
3.3. Testing Stages and Test Program
4. Experimental Results
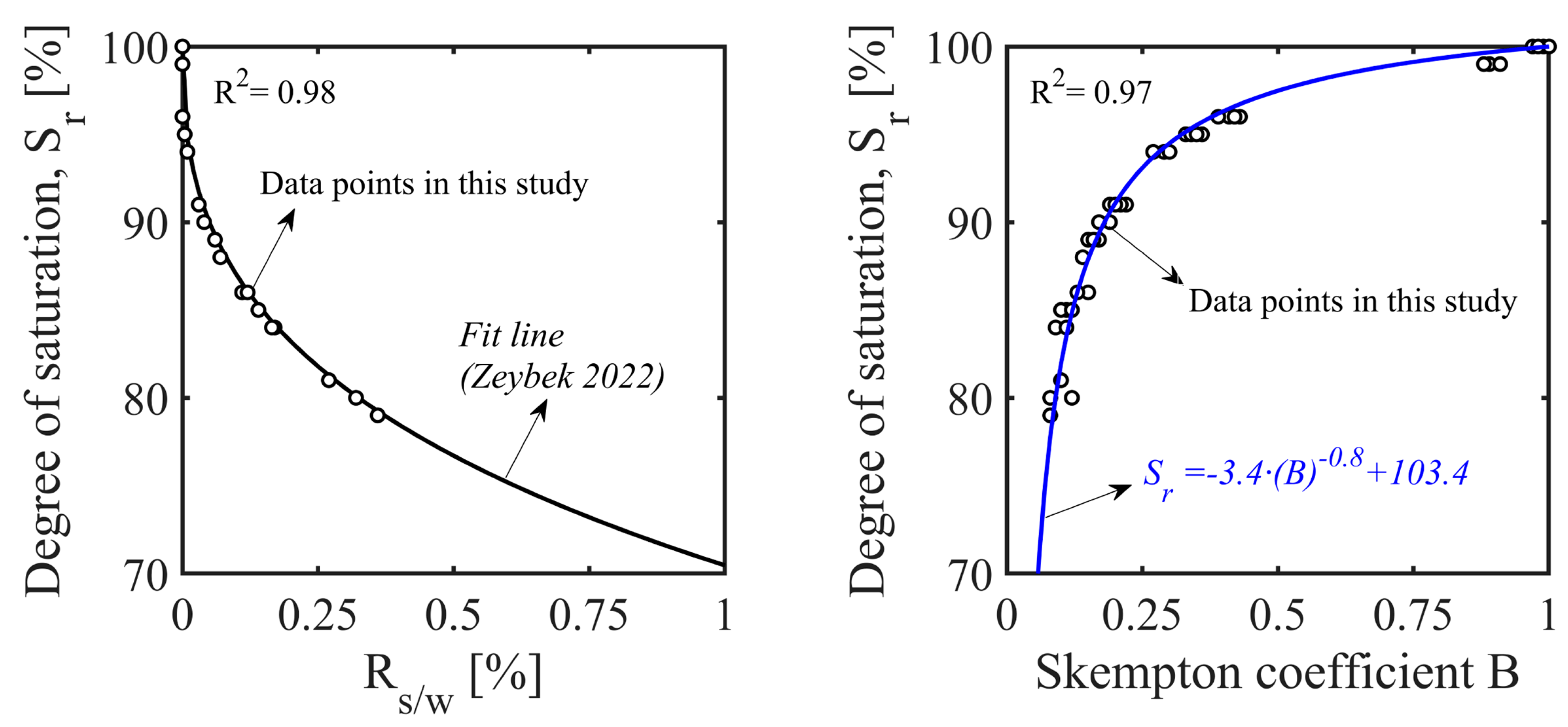
4.1. Relationship between Degree of Saturation and B Parameter
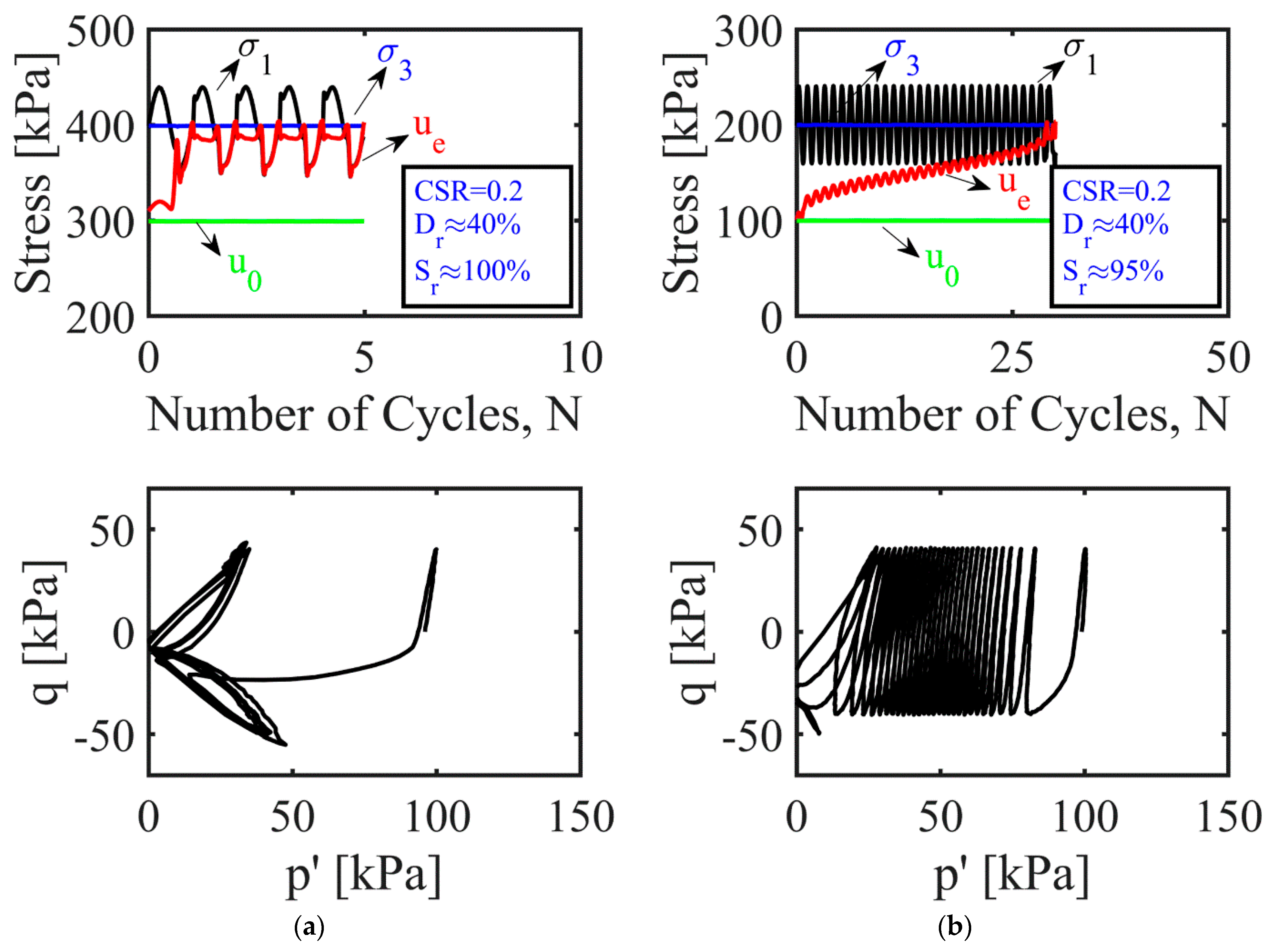
4.2. Excess Pore-Pressure Generation and Stress Degradation
4.3. Parameters Affecting Liquefaction Behavior of Partially Saturated Sands
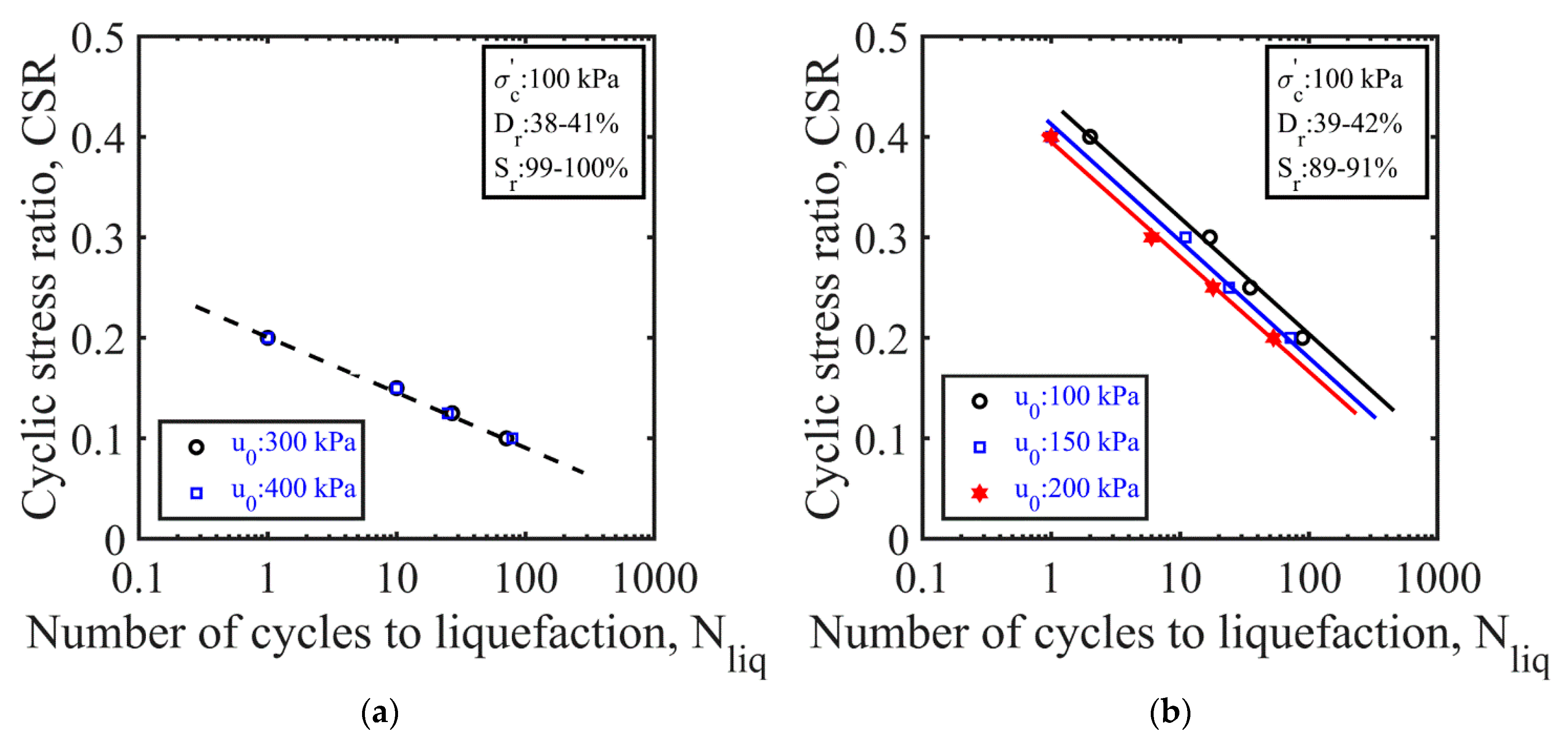
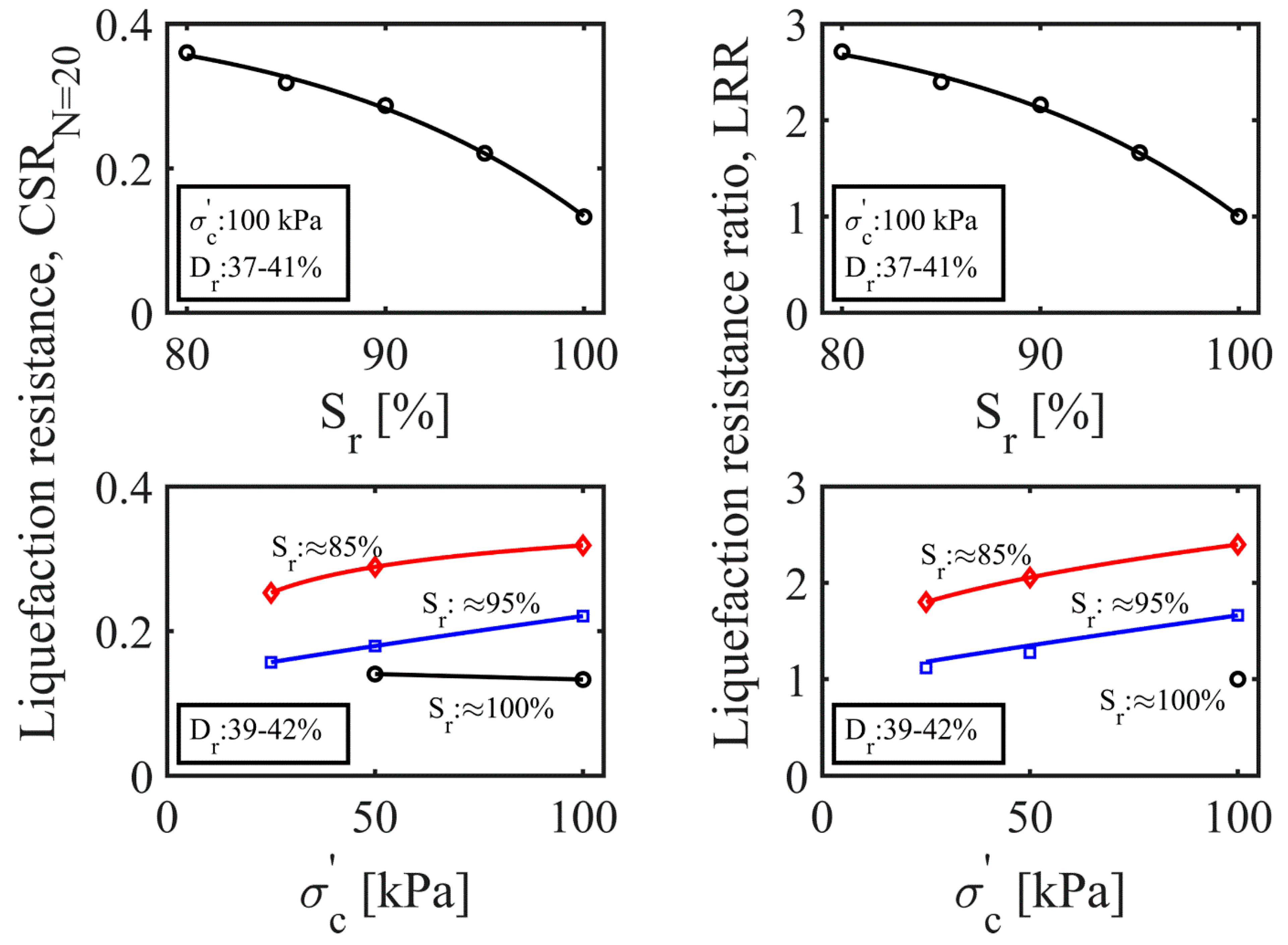
4.3.1. Effective Confining Stress
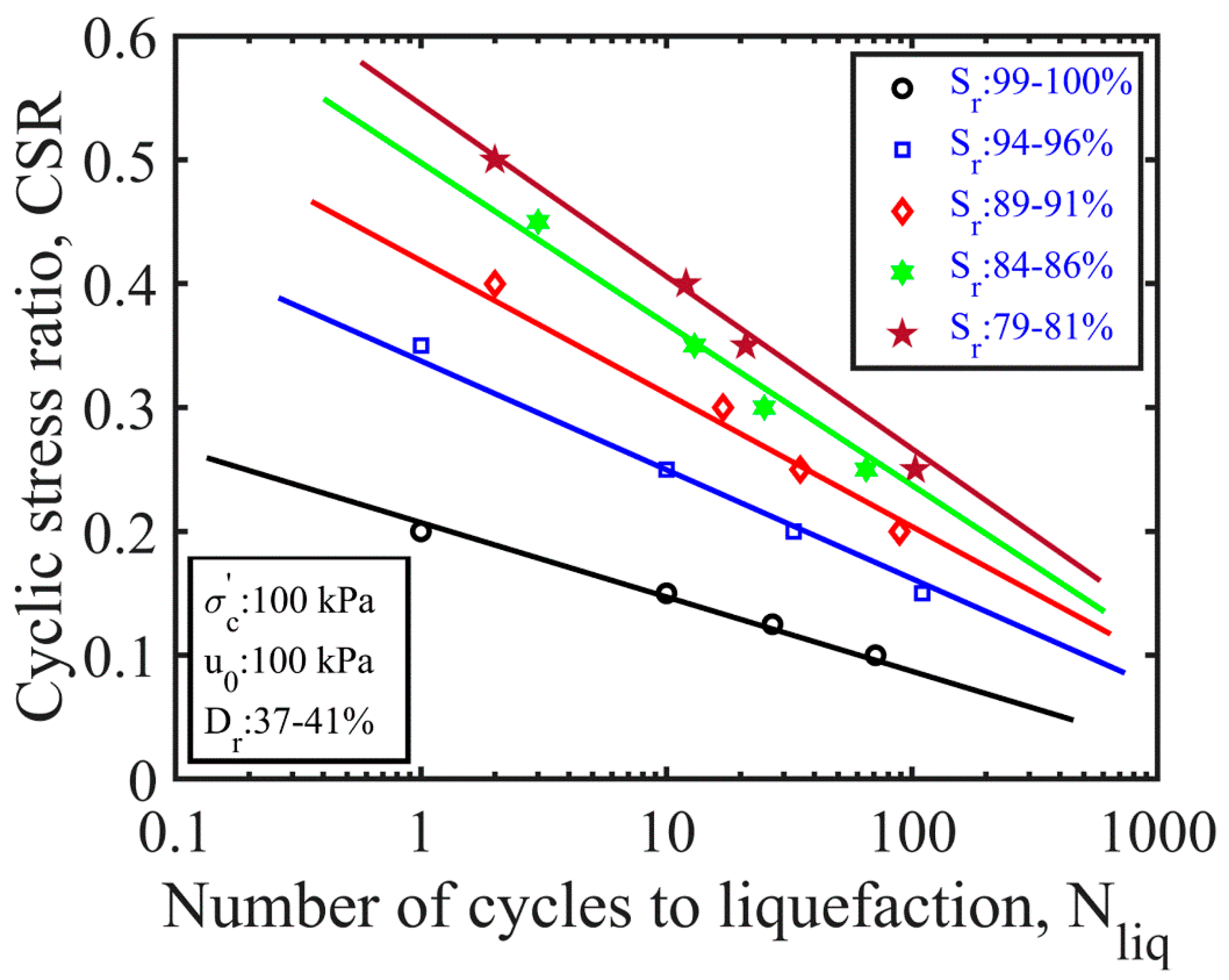
4.3.2. Degree of Saturation
4.3.3. Back Pressure
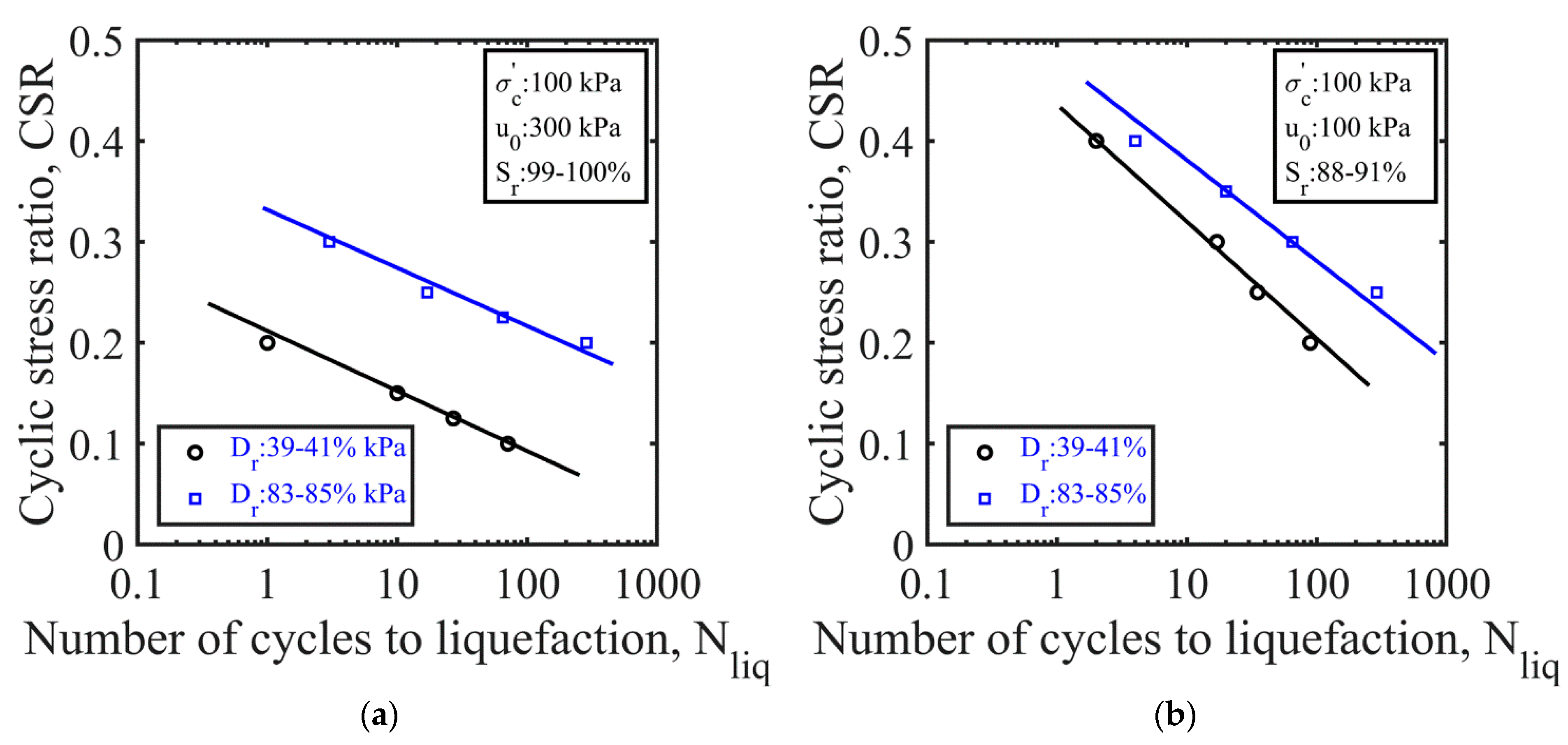
4.3.4. Relative Density
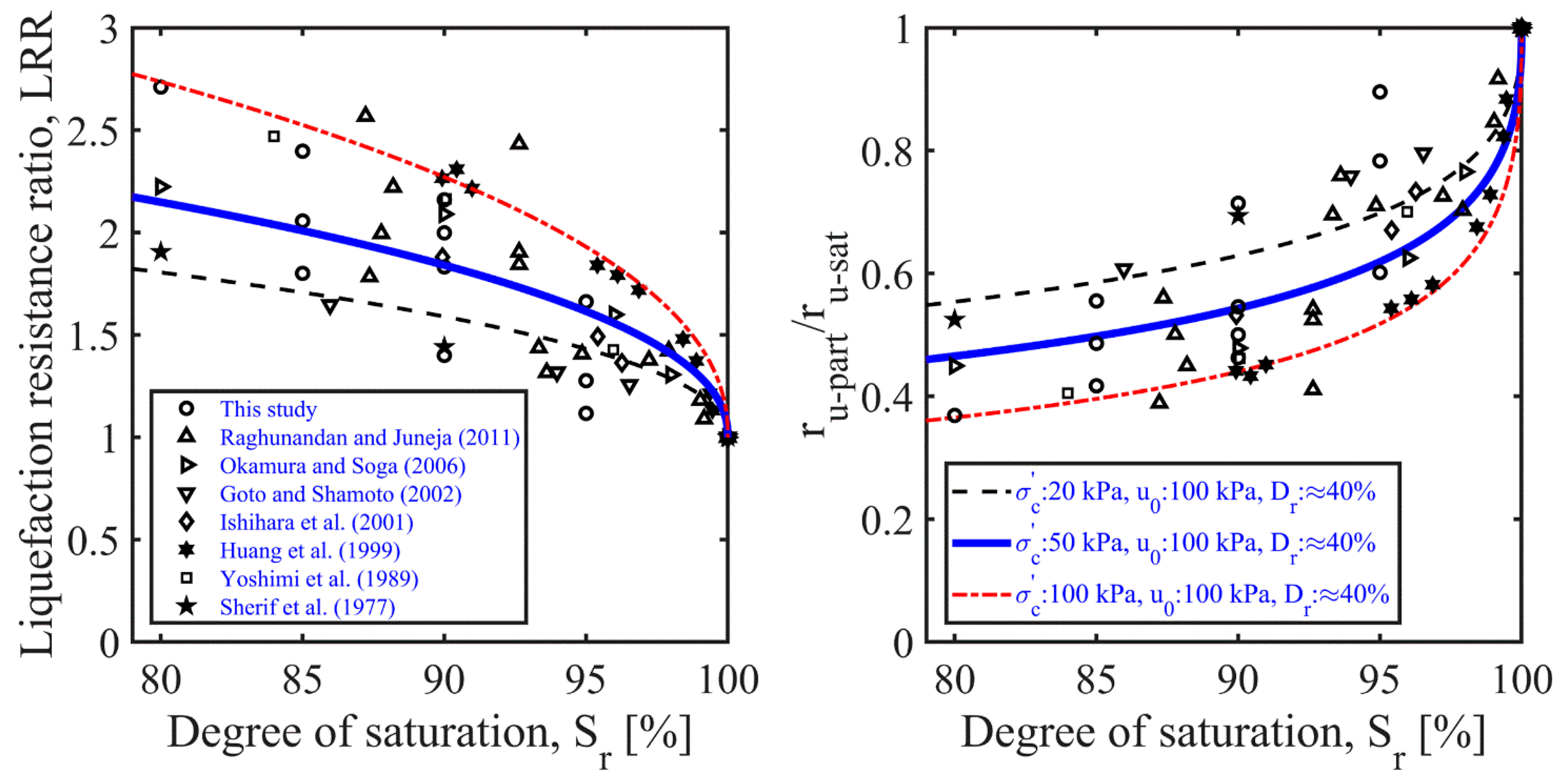
4.4. Liquefaction-Resistance Ratio
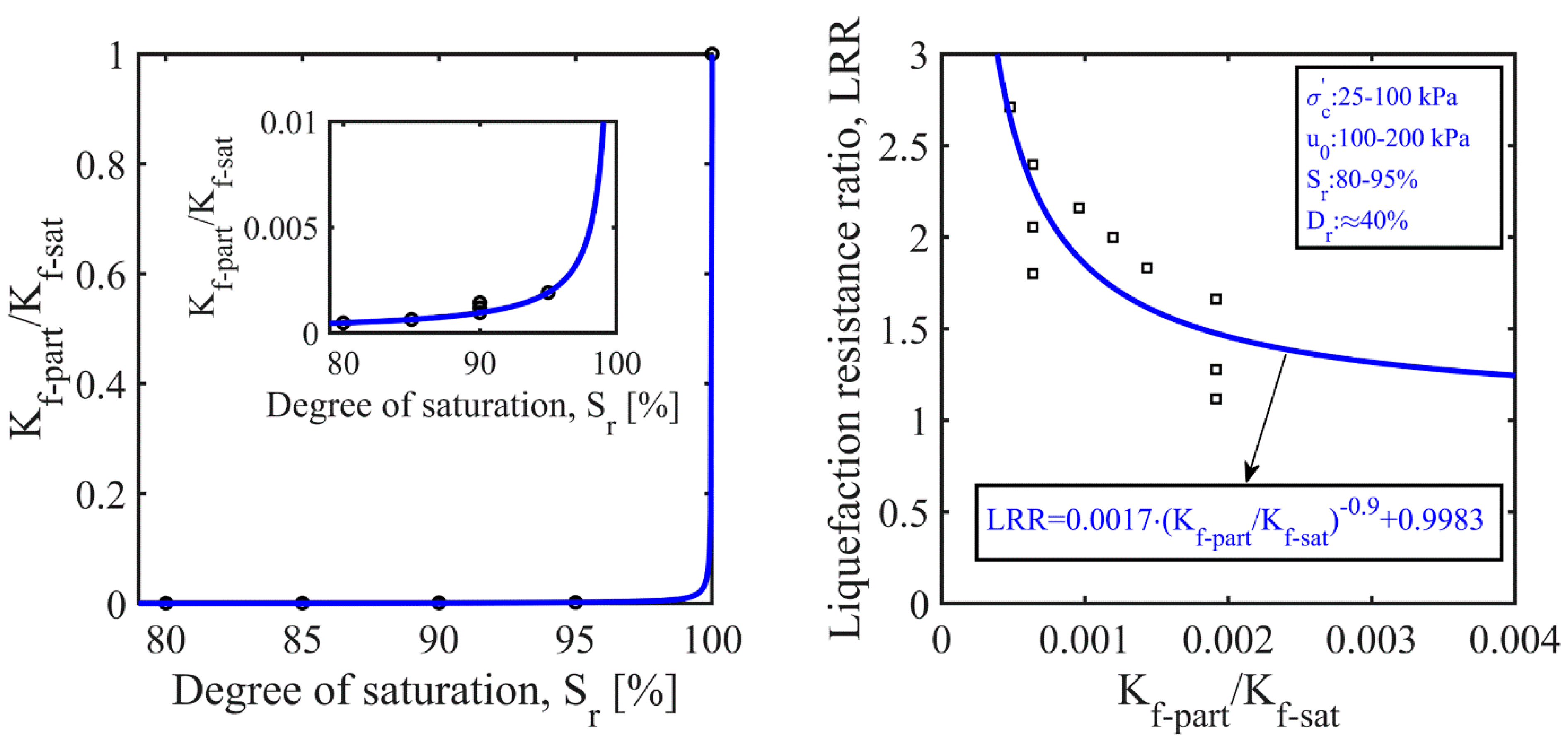
5. Proposed Empirical Functions
5.1. Bulk Modulus
5.2. Maximum Volumetric Strains
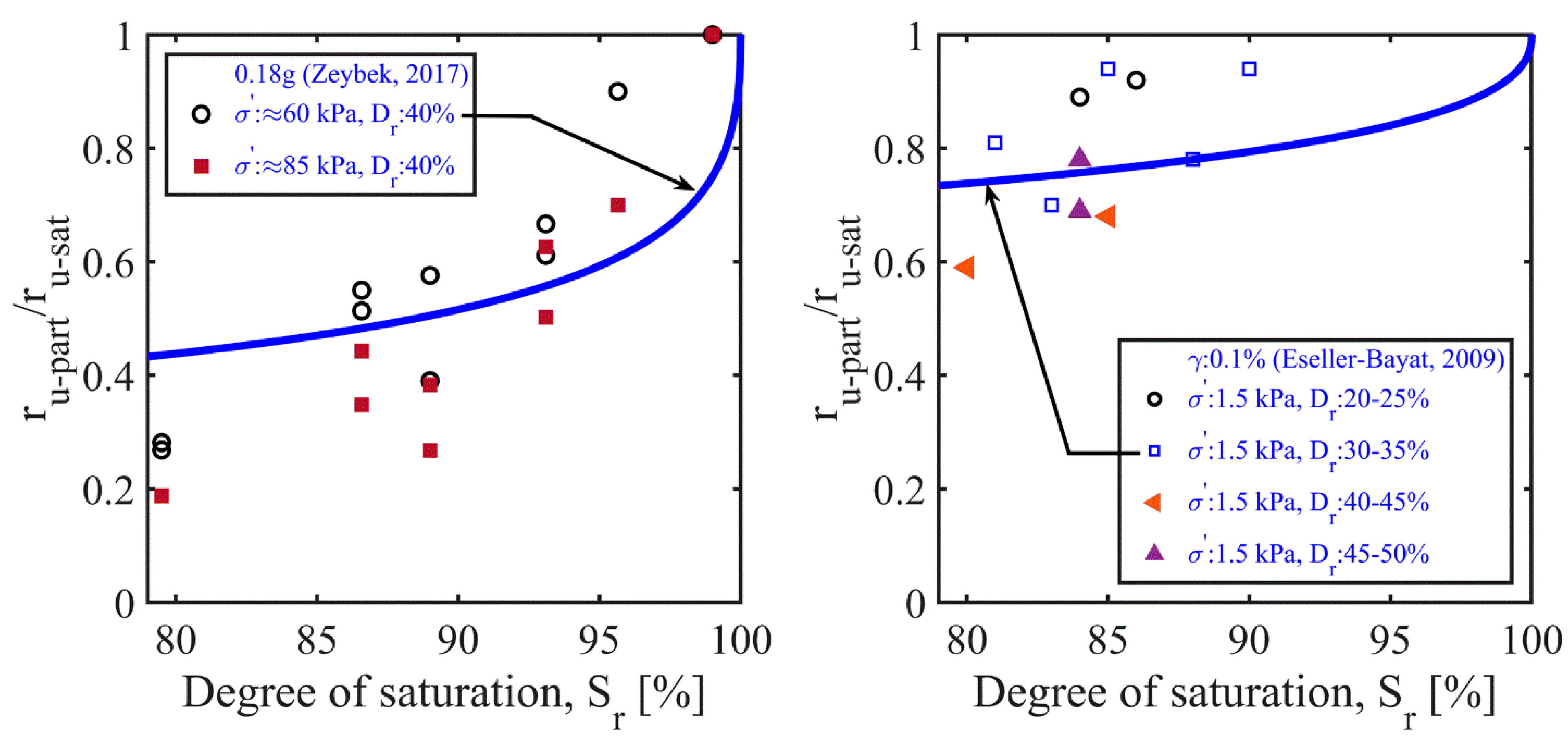
5.3. Excess Pore-Pressure Ratios
6. Conclusions and Recommendations
- (1)
- The liquefaction behavior of sand was observed to change as the triaxial specimens were turned from nearly/fully saturated to a partially saturated state. The liquefaction resistance of the partially saturated sand specimens appeared to increase as the degree of saturation was reduced.
- (2)
- The undrained cyclic behavior of the partially saturated sand was not only sensitive to the degree of saturation but also to the level of the initial effective confining stress and back pressure (or initial pore water pressure) acting on the sand. At the same degrees of saturation, the partially saturated sands showed a greater resistance to liquefaction under larger initial effective confining stresses and lower back pressures. Amongst these parameters, the effect of the back pressure was less significant than those of the degrees of saturation and confining stress.
- (3)
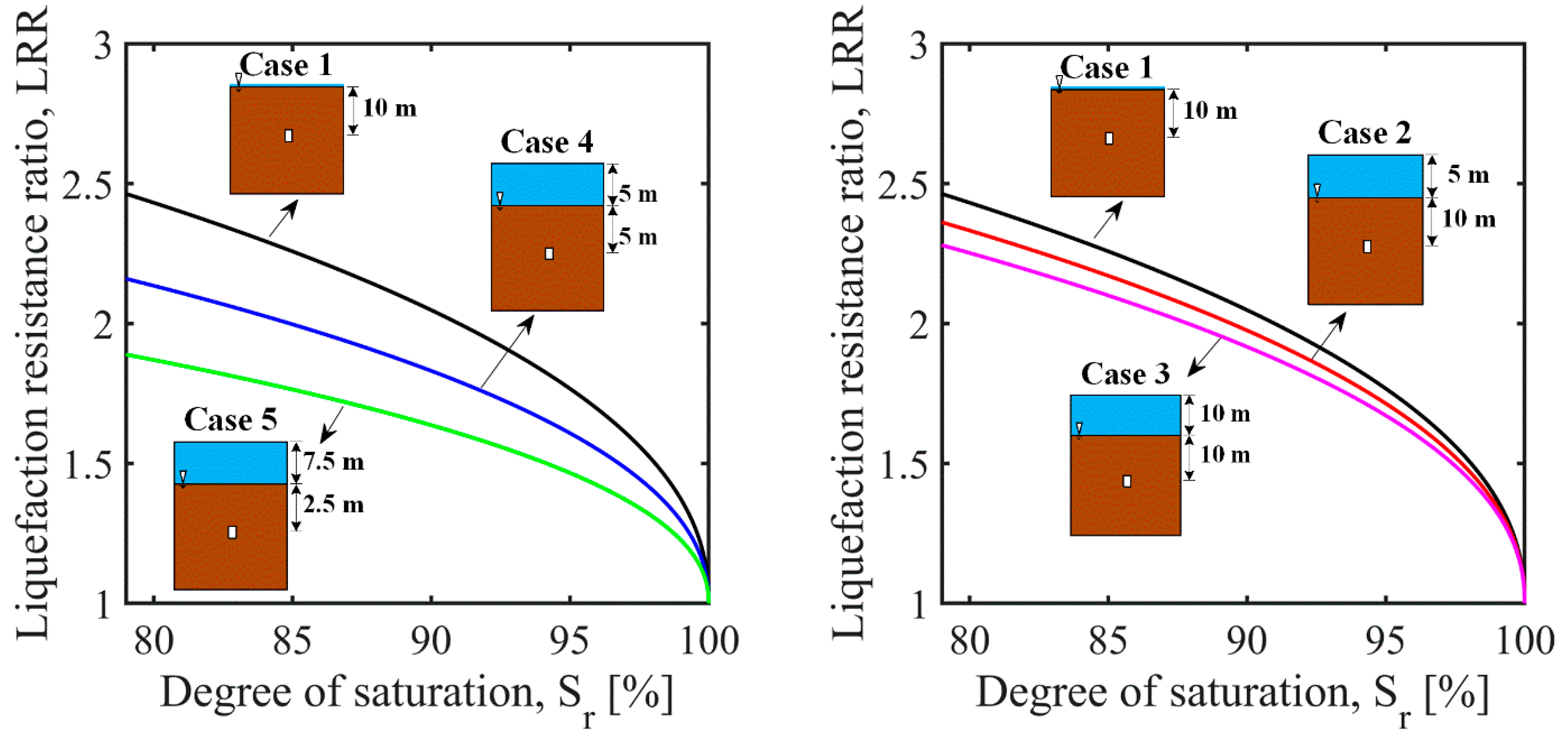
- The positive effect of the confining stress and the adverse effect of the back pressure require consideration in design practice. During the practical application of IPS methods for the treatment of liquefiable deposits in the field, the shallower layers should be desaturated more than the deeper layers.
- (4)
- The proposed empirical approach was shown to enable a practical assessment of the normalized liquefaction resistance of partially saturated sands as a function of the pore-fluid bulk modulus, maximum volumetric strains, and normalized excess pore-pressure ratios. The model seemed to successfully capture the trends followed by the experimental data and produced physically sensible estimations for a complex topic of geotechnical earthquake engineering.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seed, H.B.; Idriss, I.M. Analysis of soil liquefaction: Niigata earthquake. J. Soil Mech. Found. Div. 1967, 93, 83–108. [Google Scholar] [CrossRef]
- Hamada, M.; O’ Rourke, T.D. Japanese case studies. In NCEER-92-0001: Case Studies of Liquefaction and Lifeline Performance during Past Earthquakes; Hamada, M., O’Rourke, T.D., Eds.; University of Buffalo: New York, NY, USA, 1992; Volume 1, pp. 31–199. [Google Scholar]
- Bray, J.; Sancio, R.; Durgunoglu, T.; Onalp, A.; Youd, T.; Stewart, J.; Seed, R.; Cetin, O.; Bol, E.; Baturay, M.; et al. Subsurface characterization at ground failure sites in Adapazari, Turkey. J. Geotech. Geoenviron. Eng. 2004, 130, 673–685. [Google Scholar] [CrossRef] [Green Version]
- Olson, S.M.; Green, R.A.; Lasley, S.; Martin, N.; Cox, B.R.; Rathje, E.; Bachhuber, J.; French, J. Documenting liquefaction and lateral spreading triggered by the 12 January 2010 Haiti Earthquake. Earthq. Spectra 2011, 27, 93–116. [Google Scholar] [CrossRef] [Green Version]
- Bertalot, D.; Brennan, A.J.; Villalobos, F.A. Influence of bearing pressure on liquefaction-induced settlement of shallow foundations. Géotechnique 2013, 63, 391–399. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Hyodo, M.; Goda, K.; Tazoh, T.; Taylor, C.A. Liquefaction of soil in the Tokyo Bay area from the 2011 Tohoku (Japan) earthquake. Soil Dyn. Earthq. Eng. 2011, 31, 1618–1628. [Google Scholar] [CrossRef]
- Cubrinovski, M.; Bray, J.D.; Taylor, M.; Giorgini, S.; Bradley, B.; Wotherspoon, L.; Zupan, J. Soil liquefaction effects in the Central Business District during the February 2011 Christchurch Earthquake. Seismol. Res. Lett. 2011, 82, 893–904. [Google Scholar] [CrossRef]
- Avilés-Campoverde, D.; Chunga, K.; Ortiz-Hernández, E.; Vivas-Espinoza, E.; Toulkeridis, T.; Morales-Delgado, A.; Delgado-Toala, D. Seismically induced soil liquefaction and geological conditions in the city of Jama due to the M7.8 Pedernales Earthquake in 2016, NW Ecuador. Geosciences 2021, 11, 20. [Google Scholar] [CrossRef]
- Ortiz-Hernández, E.; Chunga, K.; Toulkeridis, T.; Pastor, J.L. Soil liquefaction and other seismic-associated phenomena in the city of Chone during the 2016 Earthquake of Coastal Ecuador. Appl. Sci. 2022, 12, 7867. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M. Simplified procedure for evaluating soil liquefaction potential. J. Soil Mech. Found. Div. 1971, 97, 1249–1273. [Google Scholar] [CrossRef]
- Tokimatsu, K.; Seed, H.B. Evaluation of settlements in sands due to earthquake shaking. J. Geotech. Geoenviron. Eng. 1987, 113, 861–878. [Google Scholar] [CrossRef]
- Ishihara, K.; Yoshimine, M. Evaluation of settlements in sand deposits following liquefaction during earthquakes. Soils Found. 1992, 32, 173–188. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Dobry, R. Seismic response of shallow foundation on liquefiable sand. J. Geotech. Geoenviron. Eng. 1997, 123, 557–567. [Google Scholar] [CrossRef]
- Tsukamoto, Y.; Kawabe, S.; Matsumoto, J.; Hagiwara, S. Cyclic resistance of two unsaturated silty sands against soil liquefaction. Soils Found. 2014, 54, 1094–1103. [Google Scholar] [CrossRef] [Green Version]
- Zeybek, A.; Madabhushi, S.P.G. Closure to “Simplified procedure for prediction of earthquake-induced settlements in partially saturated soils” by Abdülhakim Zeybek and Santana Phani Gopal Madabhushi. J. Geotech. Geoenviron. Eng. 2021, 147, 07020027. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils, 1st ed.; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Okamura, M.; Soga, Y. Effects of pore fluid compressibility on liquefaction resistance of partially saturated sand. Soils Found. 2006, 46, 695–700. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, J.K.; Santamarina, J.C. Biological considerations in geotechnical engineering. J. Geotech. Geoenviron. Eng. 2005, 131, 1222–1233. [Google Scholar] [CrossRef] [Green Version]
- Rebata-Landa, V.; Santamarina, J.C. Mechanical effects of biogenic nitrogen gas bubbles in soils. J. Geotech. Geoenviron. Eng. 2012, 138, 128–137. [Google Scholar] [CrossRef]
- Okamura, M.; Takebayashi, M.; Nishida, K.; Fujii, N.; Jinguji, M.; Imasato, T.; Yasuhara, H.; Nakagawa, E. In-situ desaturation test by air injection and its evaluation through field monitoring and multiphase flow simulation. J. Geotech. Geoenviron. Eng. 2011, 137, 643–652. [Google Scholar] [CrossRef]
- Zeybek, A.; Madabhushi, S.P.G. Influence of air injection on the liquefaction induced deformation mechanisms beneath shallow foundations. Soil Dyn. Earthq. Eng. 2017, 97, 266–276. [Google Scholar] [CrossRef] [Green Version]
- Zeybek, A.; Madabhushi, S.P.G.; Pelecanos, L. Seismic response of partially saturated soils beneath shallow foundations under sequential ground motions. Bull. Earthquake Eng. 2020, 18, 1987–2002. [Google Scholar] [CrossRef]
- Yegian, M.K.; Eseller-Bayat, E.; Alshawabkeh, A.; Ali, S. Induced partial saturation (IPS) for liquefaction mitigation: Experimental investigation. J. Geotech. Geoenviron. Eng. 2007, 133, 372–380. [Google Scholar] [CrossRef] [Green Version]
- He, J.; Chue, J.; Ivanov, V. Mitigation of liquefaction of saturated sand using biogas. Géotechnique 2013, 63, 267–275. [Google Scholar] [CrossRef]
- O’Donnell, S.T.; Rittmann, B.E.; Kavazanjian, E. MIDP: Liquefaction mitigation via microbial denitrification as a two-stage process. I: Desaturation. J. Geotech. Geoenviron. Eng. 2017, 143, 04017094. [Google Scholar] [CrossRef]
- Eseller-Bayat, E.E.; Yegian, M.K.; Alshawabkeh, A.; Gokyer, S. Liquefaction response of partially saturated sands. I: Experimental results. J. Geotech. Geoenviron. Eng. 2013, 139, 863–871. [Google Scholar] [CrossRef] [Green Version]
- Zeybek, A. Shaking table tests on seismic performance of shallow foundations resting on partially saturated sands. Arab. J. Geosci. 2022, 15, 774. [Google Scholar] [CrossRef]
- Okamura, M.; Ishihara, M.; Tamura, K. Degree of saturation and liquefaction resistances of sand improved with sand compaction pile. J. Geotech. Geoenviron. Eng. 2006, 132, 258–264. [Google Scholar] [CrossRef]
- Zeybek, A.; Madabhushi, S.P.G. Durability of partial saturation to counteract liquefaction. Proc. Inst. Civ. Eng. Ground Improv. 2017, 170, 102–111. [Google Scholar] [CrossRef]
- Takemura, J.; Igarashi, R.; Izawa, J.; Okamura, M.; Masuda, M. Centrifuge Model Tests on Soil Desaturation as a Liquefaction Countermeasure. In Proceedings of the 17th International Conference on Soil Mechanics and Geotechnical Engineering, Alexandria, Egypt, 5–9 October 2009; Hamza, M., Shahien, M., El-Mossallamy, Y., Eds.; IOS Press: Amsterdam, The Netherlands, 2009; pp. 502–505. [Google Scholar] [CrossRef]
- Ghayoomi, M.; McCartney, J.S.; Ko, H.-Y. Centrifuge test to assess the seismic compression of partially saturated sands. Geotech. Test. J. 2011, 34, 321–331. [Google Scholar] [CrossRef]
- Marasini, N.P.; Okamura, M. Air injection to mitigate liquefaction under light structures. Int. J. Phys. Model Geotech. 2015, 15, 129–140. [Google Scholar] [CrossRef]
- Zeybek, A.; Madabhushi, S.P.G. Centrifuge testing to evaluate the liquefaction response of air-injected partially saturated soils beneath shallow foundations. Bull. Earthq. Eng. 2017, 15, 339–356. [Google Scholar] [CrossRef]
- Sherif, M.A.; Tsuchiya, C.; Ishibashi, I. Saturation effects on initial soil liquefaction. J. Geotech. Eng. Div. 1977, 103, 914–917. [Google Scholar] [CrossRef]
- Yoshimi, Y.; Tanaka, K.; Tokimatsu, K. Liquefaction resistance of a partially saturated sand. Soils Found. 1989, 29, 157–162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, Y.; Tsuchiya, H.; Ishihara, K. Estimation of Partial Saturation Effect on Liquefaction Resistance of Sand Using P-Wave Velocity. Proc. Jpn. Geotech. Soc. 1999, 113, 431–434. [Google Scholar]
- Goto, S.; Shamoto, Y. Estimation Method for the Liquefaction Strength of Unsaturated Sandy Soil (Part2). In Proceedings of the Thirty-Seventh Japan National Conference on Geotechnical Engineering, Osaka, Japan, 14–16 July 2002; pp. 1985–1986. [Google Scholar] [CrossRef]
- Tsukamoto, Y.; Ishihara, K.; Nakazawa, H.; Kamada, K.; Huang, Y. Resistance of partly saturated sand to liquefaction with reference to longitudinal and shear wave velocities. Soils Found. 2002, 42, 93–104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, J.; Savidis, S.; Roemer, M. Evaluating liquefaction strength of partially saturated sand. J. Geotech. Geoenviron. Eng. 2004, 130, 975–979. [Google Scholar] [CrossRef]
- Raghunandan, M.E.; Juneja, A. A study on the liquefaction resistance and dynamic properties of de-saturated sand. Electron. J. Geotech. Eng. 2011, 16, 109–123. [Google Scholar]
- Eseller-Bayat, E.E.; Gulen, D.B. Undrained dynamic response of partially saturated sands tested in a DSS-C device. J. Geotech. Geoenviron. Eng. 2020, 146, 04020118. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M.; Makdisi, F.; Banerjee, N. EERC 75-29 Report: Representation of Irregular Stress Time Histories by Equivalent Uniform Stress Series in Liquefaction Analyses; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1975. [Google Scholar]
- Polito, C.P.; Green, R.A.; Lee, J. Pore pressure generation models for sands and silty soils subjected to cyclic loading. J. Geotech. Geoenviron. Eng. 2008, 134, 1490–1500. [Google Scholar] [CrossRef]
- Dobry, R.; Ladd, R.S.; Yokel, F.Y.; Chung, R.M.; Powell, D. Prediction of Pore Water Pressure Buildup and Liquefaction of Sands during Earthquakes by the Cyclic Strain Method. In NBS Building Science Series; Department of Commerce, National Bureau of Standards: Washington, DC, USA, 1982; pp. 138–150. [Google Scholar]
- Green, R.A.; Mitchell, J.K.; Polito, C.P. Energy-Based Excess Pore Pressure Generation Model for Cohesionless Soils. In Proceedings of Developments in Theoretical Geomechanics—The John Booker Memorial Symposium (Smith DW Carter JP, eds), Sydney, NSW, Australia, 16–17 November 2000; A.A. Balkema Publishers: Rotterdam, The Netherlands, 2000; pp. 383–390. [Google Scholar]
- Martin, G.R.; Finn, W.L.; Seed, H.B. Fundamentals of liquefaction under cyclic loading. J. Geotech. Geoenviron. Eng. 1975, 101, 423–438. [Google Scholar] [CrossRef]
- Finn, W.D.L.; Martin, G.R.; Byrne, P.M. Seismic response and liquefaction of sands. J. Geotech. Eng. Div. ASCE 1976, 102, 841–856. [Google Scholar] [CrossRef]
- Koning, H. Some Observations on the Modulus of Compressibility of Water. In Proceedings of the European Conference on SMFE; 1963; Volume 1, pp. 33–36. [Google Scholar]
- Mousavi, S.; Ghayoomi, M. A Semi-Empirical Model to Predict Excess Pore Pressure Generation in Partially Saturated Sand. In Proceedings of 4th European Conference on Unsaturated Soils (E-UNSAT 2020), E3S Web Conference; 2020; Volume 195, p. 02026. [Google Scholar] [CrossRef]
- Ghayoomi, M.; McCartney, J.S.; Ko, H.-Y. Empirical methodology to estimate seismically induced settlement of partially saturated sand. J. Geotech. Geoenviron. Eng. 2013, 139, 367–376. [Google Scholar] [CrossRef] [Green Version]
- Zeybek, A.; Madabhushi, S.P.G. Simplified procedure for prediction of earthquake-induced settlements in partially saturated soils. J. Geotech. Geoenviron. Eng. 2019, 145, 04019100. [Google Scholar] [CrossRef]
- Tsuchida, H. Prediction and Countermeasure against the Liquefaction in Sand Deposits. In Abstract of the Seminar at the Port and Harbour Research Institute; Ministry of Transport, 1970; pp. 3.1–3.33. [Google Scholar]
- ASTM D6913/D6913M-17; Standard Test Methods for Particle-Size Distribution (Gradation) of Soils Using Sieve Analysis. ASTM International: West Conshohocken, PA, USA, 2017.
- ASTM D854-14; Standard Test Methods for Specific Gravity of Soil Solids by Water Pycnometer. ASTM International: West Conshohocken, PA, USA, 2014.
- ASTM D4253-16e1; Standard Test Methods for Maximum Index Density and Unit Weight of Soils Using a Vibratory Table. ASTM International: West Conshohocken, PA, USA, 2019.
- ASTM D4254-16; Standard Test Methods for Minimum Index Density and Unit Weight of Soils and Calculation of Relative Density. ASTM International: West Conshohocken, PA, USA, 2016.
- Zeybek, A. Suggested method of specimen preparation for triaxial tests on partially saturated sand. Geotech. Test. J. 2022, 45, 20210168. [Google Scholar] [CrossRef]
- ASTM D5311/D5311M-13; Standard Test Method for Load Controlled Cyclic Triaxial Strength of Soil. ASTM International: West Conshohocken, PA, USA, 2013.
- Vaid, Y.P.; Chern, J.C.; Tumi, H. Confining pressure, grain angularity, and liquefaction. J. Geotech. Geoenviron. Eng. 1985, 111, 1229–1235. [Google Scholar] [CrossRef]
- Papadopoulou, A.; Tika, T. The effect of fines on critical state and liquefaction resistance characteristics of non-plastic silty sands. Soils Found. 2008, 48, 713–725. [Google Scholar] [CrossRef] [Green Version]
- Mousavi, S.; Ghayoomi, M. Liquefaction Mitigation of Silty Sands via Microbial Induced Partial Saturation. In Proceedings of the 8th International Conference on Case Histories in Geotechnical Engineering, Geo-Congress 2019: Earthquake Engineering and Soil Dynamics, Philadelphia, PA, USA, 24–27 March 2019; pp. 304–312. [Google Scholar] [CrossRef]
- Świdziński, W.; Smyczyński, M. Modelling of static liquefaction of partially saturated non-cohesive soils. Appl. Sci. 2022, 12, 2076. [Google Scholar] [CrossRef]
- Cordeiro, D.; Molina-Gómez, F.; Ferreira, C.; Rios, S.; Viana da Fonseca, A. Cyclic liquefaction resistance of an alluvial natural sand: A comparison between fully and partially saturated conditions. Geotechnics 2022, 2, 1–13. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Shen, J.; Zhu, C. Particle size and confining-pressure effects of shear characteristics of coral sand: An experimental study. Bull. Eng. Geol. Environ. 2022, 81, 97. [Google Scholar] [CrossRef]
- Zeybek, A. Air Injection Technique to Mitigate Liquefaction beneath Shallow Foundations. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2017. [Google Scholar]
- Eseller-Bayat, E.E. Seismic Response and Prevention of Liquefaction Failure of Sands Partially Saturated through Introduction of Gas Bubbles. Ph.D. Thesis, Northeastern University, Boston, MA, USA, 2009. [Google Scholar]

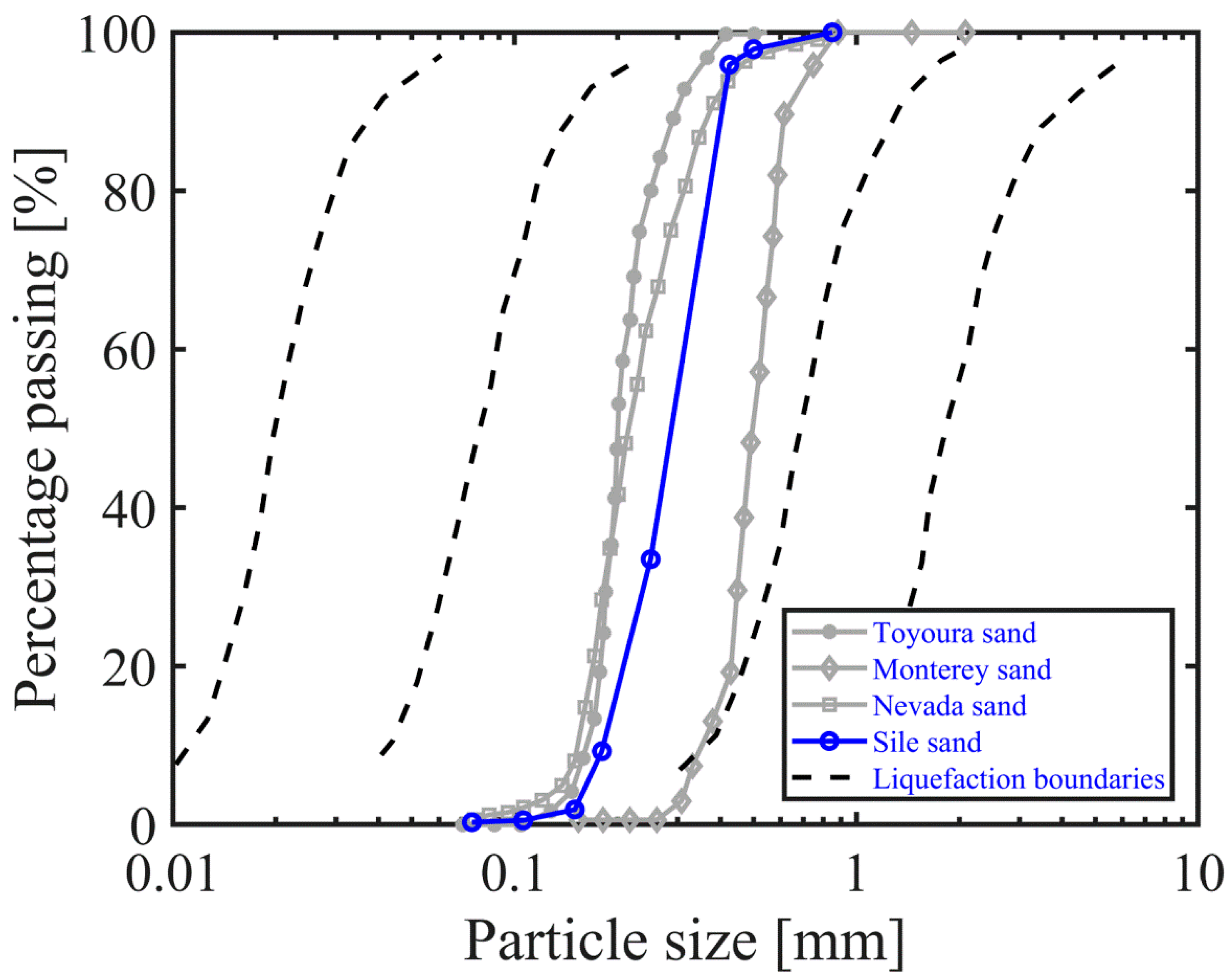



| Properties of Sand | Value | Test Standard |
|---|---|---|
| Average particle size, (mm) | 0.296 | |
| Coefficient of gradation, | 0.974 | ASTM, D6913/D6913M-17 [53] |
| Uniformity coefficient, | 1.352 | |
| Specific gravity, | 2.65 | ASTM, D854-14 [54] |
| Minimum void ratio, | 0.574 | ASTM, Method 1A, D4253-16e1 [55] |
| Maximum void ratio, | 0.885 | ASTM, Method A in D4254-16 [56] |
| Soil classification | SP | Unified Soil Classification System (USCS) |
| Test No. | Test ID | (%) | (%) | B | (kPa) | (kPa) | (kPa) | CSR | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | FS1 | 39 | 100 | 0.98 | 400 | 300 | 100 | 0.10 | 71 |
| 2 | FS2 | 39 | 100 | 0.99 | 400 | 300 | 100 | 0.125 | 27 |
| 3 | FS3 | 40 | 100 | 1.00 | 400 | 300 | 100 | 0.15 | 10 |
| 4 | FS4 | 41 | 99 | 0.89 | 400 | 300 | 100 | 0.20 | 1 |
| 5 | FS5 | 40 | 100 | 0.97 | 350 | 300 | 50 | 0.10 | 85 |
| 6 | FS6 | 39 | 100 | 0.99 | 350 | 300 | 50 | 0.125 | 32 |
| 7 | FS7 | 39 | 99 | 0.91 | 350 | 300 | 50 | 0.15 | 15 |
| 8 | FS8 | 40 | 100 | 0.98 | 350 | 300 | 50 | 0.20 | 1 |
| 9 | FS9 | 39 | 100 | 0.99 | 500 | 400 | 100 | 0.10 | 79 |
| 10 | FS10 | 38 | 100 | 1.00 | 500 | 400 | 100 | 0.125 | 25 |
| 11 | FS11 | 41 | 100 | 0.98 | 500 | 400 | 100 | 0.15 | 10 |
| 12 | FS12 | 40 | 100 | 0.99 | 500 | 400 | 100 | 0.20 | 1 |
| 13 | FS13 | 83 | 100 | 1.00 | 400 | 300 | 100 | 0.20 | 285 |
| 14 | FS14 | 84 | 100 | 0.97 | 400 | 300 | 100 | 0.225 | 65 |
| 15 | FS15 | 83 | 100 | 0.98 | 400 | 300 | 100 | 0.25 | 17 |
| 16 | FS16 | 85 | 99 | 0.88 | 400 | 300 | 100 | 0.30 | 3 |
| Test No. | Test ID | (%) | (%) | B | (kPa) | (kPa) | (kPa) | CSR | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | PS1 | 39 | 95 | 0.33 | 200 | 100 | 100 | 0.15 | 110 |
| 2 | PS2 | 40 | 94 | 0.29 | 200 | 100 | 100 | 0.20 | 33 |
| 3 | PS3 | 41 | 96 | 0.41 | 200 | 100 | 100 | 0.25 | 10 |
| 4 | PS4 | 40 | 96 | 0.39 | 200 | 100 | 100 | 0.35 | 1 |
| 5 | PS5 | 39 | 89 | 0.16 | 200 | 100 | 100 | 0.20 | 89 |
| 6 | PS6 | 38 | 90 | 0.17 | 200 | 100 | 100 | 0.25 | 35 |
| 7 | PS7 | 41 | 91 | 0.19 | 200 | 100 | 100 | 0.30 | 17 |
| 8 | PS8 | 40 | 89 | 0.15 | 200 | 100 | 100 | 0.40 | 2 |
| 9 | PS9 | 39 | 85 | 0.11 | 200 | 100 | 100 | 0.25 | 65 |
| 10 | PS10 | 40 | 86 | 0.13 | 200 | 100 | 100 | 0.30 | 25 |
| 11 | PS11 | 41 | 85 | 0.11 | 200 | 100 | 100 | 0.35 | 13 |
| 12 | PS12 | 39 | 84 | 0.09 | 200 | 100 | 100 | 0.45 | 3 |
| 13 | PS13 | 37 | 80 | 0.08 | 200 | 100 | 100 | 0.25 | 103 |
| 14 | PS14 | 41 | 80 | 0.12 | 200 | 100 | 100 | 0.35 | 21 |
| 15 | PS15 | 40 | 79 | 0.08 | 200 | 100 | 100 | 0.40 | 12 |
| 16 | PS16 | 41 | 81 | 0.10 | 200 | 100 | 100 | 0.50 | 2 |
| 17 | PS17 | 41 | 96 | 0.43 | 150 | 100 | 50 | 0.15 | 69 |
| 18 | PS18 | 42 | 95 | 0.35 | 150 | 100 | 50 | 0.20 | 14 |
| 19 | PS19 | 39 | 95 | 0.36 | 150 | 100 | 50 | 0.25 | 3 |
| 20 | PS20 | 40 | 94 | 0.27 | 150 | 100 | 50 | 0.35 | 1 |
| 21 | PS21 | 40 | 94 | 0.3 | 125 | 100 | 25 | 0.15 | 29 |
| 22 | PS22 | 41 | 95 | 0.34 | 125 | 100 | 25 | 0.20 | 5 |
| 23 | PS23 | 40 | 95 | 0.35 | 125 | 100 | 25 | 0.25 | 2 |
| 24 | PS24 | 39 | 96 | 0.42 | 125 | 100 | 25 | 0.35 | 1 |
| 25 | PS25 | 41 | 85 | 0.11 | 150 | 100 | 50 | 0.25 | 37 |
| 26 | PS26 | 40 | 84 | 0.11 | 150 | 100 | 50 | 0.30 | 15 |
| 27 | PS27 | 39 | 86 | 0.13 | 150 | 100 | 50 | 0.35 | 8 |
| 28 | PS28 | 40 | 85 | 0.10 | 150 | 100 | 50 | 0.45 | 1 |
| 29 | PS29 | 42 | 85 | 0.12 | 125 | 100 | 25 | 0.25 | 21 |
| 30 | PS30 | 41 | 86 | 0.15 | 125 | 100 | 25 | 0.3 | 9 |
| 31 | PS31 | 40 | 84 | 0.11 | 125 | 100 | 25 | 0.35 | 4 |
| 32 | PS32 | 40 | 86 | 0.13 | 125 | 100 | 25 | 0.45 | 1 |
| 33 | PS33 | 39 | 90 | 0.19 | 250 | 150 | 100 | 0.20 | 72 |
| 34 | PS34 | 40 | 91 | 0.22 | 250 | 150 | 100 | 0.25 | 24 |
| 35 | PS35 | 39 | 89 | 0.17 | 250 | 150 | 100 | 0.30 | 11 |
| 36 | PS36 | 40 | 89 | 0.16 | 250 | 150 | 100 | 0.40 | 1 |
| 37 | PS37 | 39 | 90 | 0.17 | 300 | 200 | 100 | 0.20 | 53 |
| 38 | PS38 | 42 | 91 | 0.21 | 300 | 200 | 100 | 0.25 | 18 |
| 39 | PS39 | 39 | 89 | 0.16 | 300 | 200 | 100 | 0.30 | 6 |
| 40 | PS40 | 41 | 90 | 0.17 | 300 | 200 | 100 | 0.40 | 1 |
| 41 | PS41 | 84 | 89 | 0.16 | 200 | 100 | 100 | 0.25 | 289 |
| 42 | PS42 | 85 | 88 | 0.14 | 200 | 100 | 100 | 0.30 | 65 |
| 43 | PS43 | 83 | 91 | 0.20 | 200 | 100 | 100 | 0.35 | 20 |
| 44 | PS44 | 84 | 90 | 0.17 | 200 | 100 | 100 | 0.40 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeybek, A. Experimental and Empirical Studies to Evaluate Liquefaction Resistance of Partially Saturated Sands. Appl. Sci. 2023, 13, 81. https://doi.org/10.3390/app13010081
Zeybek A. Experimental and Empirical Studies to Evaluate Liquefaction Resistance of Partially Saturated Sands. Applied Sciences. 2023; 13(1):81. https://doi.org/10.3390/app13010081
Chicago/Turabian StyleZeybek, Abdülhakim. 2023. "Experimental and Empirical Studies to Evaluate Liquefaction Resistance of Partially Saturated Sands" Applied Sciences 13, no. 1: 81. https://doi.org/10.3390/app13010081
APA StyleZeybek, A. (2023). Experimental and Empirical Studies to Evaluate Liquefaction Resistance of Partially Saturated Sands. Applied Sciences, 13(1), 81. https://doi.org/10.3390/app13010081