Numerical Analysis of New Stainless-Steel Corrugated-Plate Reinforcement of Shield-Tunnel Segmental Joints Based on Virtual-Tracking-Element Technology

Abstract

Shield tunnels inevitably endure various forms of damage as their service times increase. Steel corrugated plates have been used extensively under multiple conditions and have proven effective in strengthening segmental joints, according to full-scale tests. A numerical model is proposed to probe the feasibility of using a new stainless-steel corrugated plate (SSCP) to reinforce shield-tunnel segments. A new method, called virtual-tracking-element technology, is employed to achieve the simulation of a realistic stress state of the segmental joint. Moreover, a segmental-joint-component analysis and a parametric study were conducted based on the numerical model. The results demonstrate that: (1) the virtual-tracking-element technology is a valid and efficient approach to the simulation of the secondary-stress state of segmental joints; (2) SSCP reinforcement is not fully utilized when the grade of segmental concrete is C50, and it has a wide safety margin for potential overload; (3) SSCP reinforcement performs well regardless of the burial depth, and reinforcement in advance is recommended.

1. Introduction

As the service times of shield tunnels increase, it is common for segments to have deficiencies, such as seepage, cracking, and spalling [1,2,3], leading to large lateral deformation and lower bearing capacity in tunnels, which poses a potential threat to their operation and maintenance. It is necessary to repair and strengthen current shield tunnel segments.

A variety of reinforcement technologies have been applied in shield-segment reinforcement, such as a steel plate–UHPC composite structure [4], a steel plate–short bolt composite structure [5], filament-wound profiles (FWP) [6], an ultra-high-toughness cementitious composite [7], etc. However, the current reinforcement technologies have limitations, such as complex procedures, large steel consumption, and limited reinforcement effects. The new stainless-steel corrugated plate (SSCP) has many advantages in the field of tunnel-segment reinforcement due to its novel structure, light weight, high strength, convenient construction, and corrosion resistance [8].

Corrugated steel has been widely used in pipelines, culverts, and utility tunnels [9,10,11,12]. Regarding the construction of tunnels, corrugated steel plates have been used as support structures, and they were proven to be capable of resisting the surrounding rock deformation [13]. In addition, attempts have been made to use corrugated steel plates to strengthen shield tunnels. Ren et al. [14] investigated the ultimate bearing capacity and failure mode of a corrugated-steel-reinforced segment through a mechanical test, but the tunnel segmental joint was not considered. A full-scale test (the details of which are introduced in Section 2) was carried out to investigate the mechanical behaviors of the segmental joint, unreinforced and reinforced by a stainless-steel corrugated plate (SSCP), and the latter manifested higher strength and stiffness, a longer hardening phase, and better ductility.

Full-scale mechanical tests can reflect the mechanical properties of specimens with high precision, but there are problems, such as high cost, and the loading conditions are limited and not entirely representative. Numerical models can simulate various working conditions at low cost, but these models need to be calibrated by a mechanical test. To investigate the effect of segmental joint reinforcement, numerical methods have been developed, which usually establish refined models of the segmental joint comprising grooves, bolt-hand holes, gaskets, etc. Simultaneously, in order to improve efficiency, a reasonable simplification of the constitutive model and contact relationship is taken into account.

In numerical analyses, the removal and activation of elements are generally used to perform the simulation of the secondary stress process of reinforcement [15]. Elements of reinforcement components (such as reinforced steel plates, the interface, etc.) are removed before the calculation starts, and they are activated after the deformation is generated by applying loads on the original structure. Although this method is theoretically feasible, the activated element often appears at the initial position, resulting in an overlap with the deformed structure, which is not consistent with reality [6,16,17]. Therefore, a new method, called virtual-tracking-element technology [18], is adopted to allow the reinforcement element to deform along with the structure, without affecting the stress or strain. Hence, the reinforcement element can be activated at a deformed position and bear the load normally within the damaged structure, allowing the simulation of secondary stress.

This paper is organized as follows: Section 2 contains the experimental data from the full-scale test on a segmental joint reinforced by SSCP. Section 3 is devoted to the development method and the parameters of the numerical modeling. Section 4 introduces the principle and methodology of using virtual-tracking-element technology to simulate the secondary stress state. Section 5 presents the verification of the validity of the numerical model and the analysis of the numerical results and parametric study.

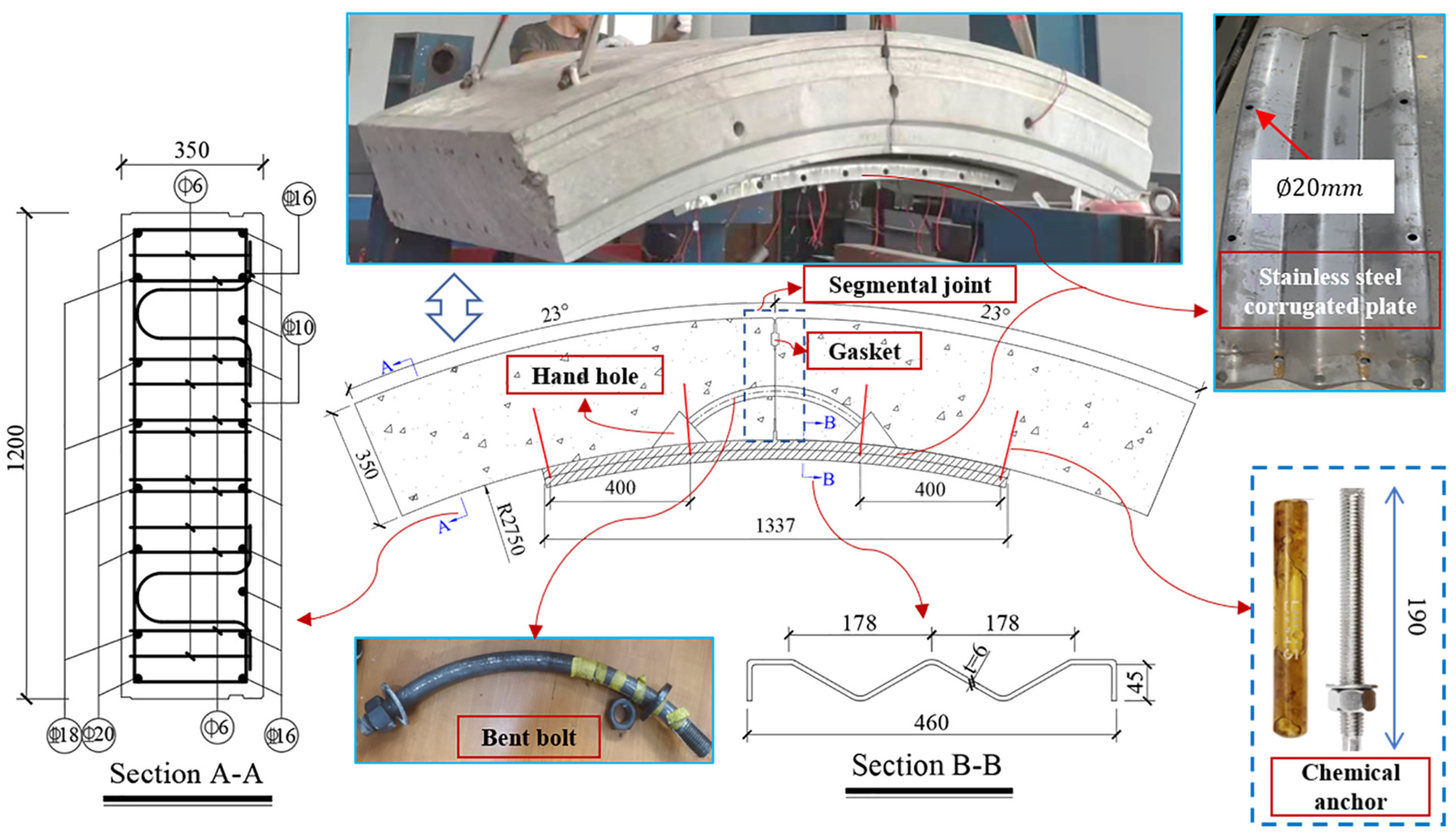
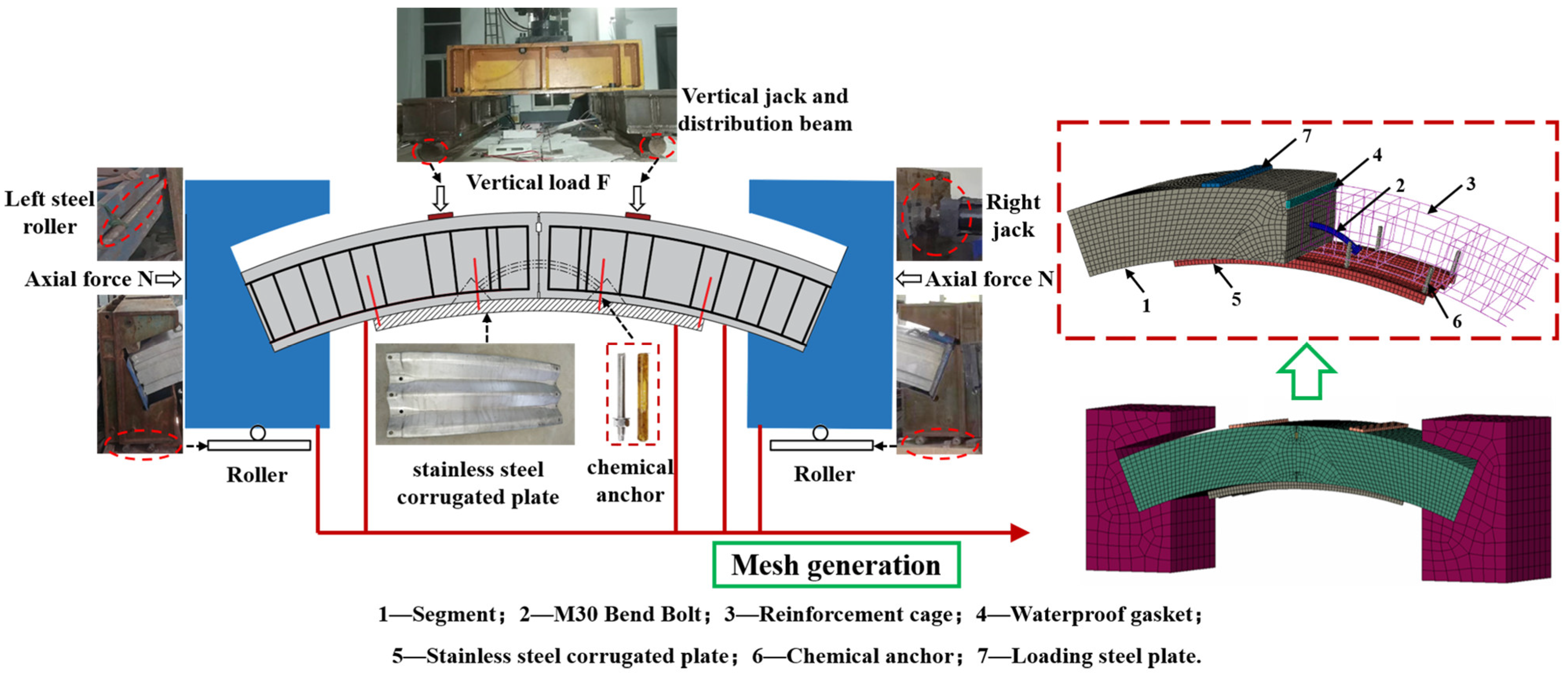
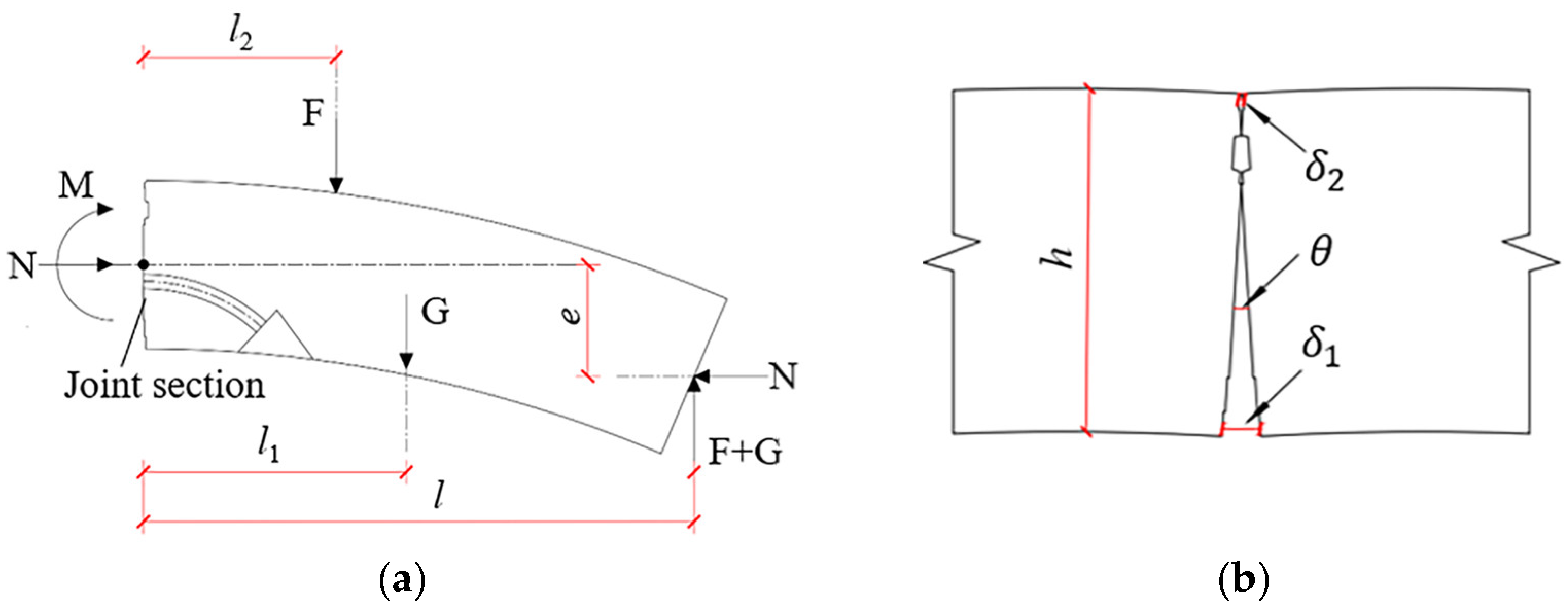
2. Data from the Full-Scale Test

The experiment included two full-scale segmental joint specimens designated as SP-0 and SP-1, referring to the unreinforced and reinforced segmental joint specimen, respectively, in order to represent a typical joint configuration in a subway shield-tunnel-lining structure.

Both specimens were assembled by two segments with a central angle of 23°. The internal and external diameters of the segments were 5500 mm and 6200 mm, respectively, and the width and thickness of the segments were 1200 mm and 350 mm, respectively. Two 5.8-grade M30 bent bolts (center-line-arc radius 380 mm, arc length 530 mm) were used to assemble the segments to form the joint specimen.

Figure 1 shows the stainless-steel corrugated plate (SSCP) reinforced segmental joint specimen (SP-1). The segments and bent bolts used in the strengthened segmental joint specimen were the same as those used in the unreinforced segmental joint specimen. Chemical anchors made of 2205 stainless steel with a diameter of 16 mm were used to fix SSCP on the segmental joint, and holes with a diameter of 20 mm were punched on SSCP. The ends of the joint specimens were erected on two steel components and their bottoms were supported by two rollers, which means they were simply supported. No preload was applied to the unreinforced specimens (SP-0).

The segmental joints of tunnels in service undergo stress before reinforcement, and reinforcement does not bear load until the load continues to develop or segmental material degrades. Therefore, the joint is actually under secondary stress when the reinforcement starts to share the load. In order to simulate realistic reinforcement conditions, on the full-scale test, the secondary stress state of the specimen was achieved by applying a vertical load F_k, corresponding to the load of the elastic-deformation limit point of unreinforced specimen (SP-0) on the segmental joint before reinforcement. When the load was lower than F_k, the nut of chemical anchor, which connected the specimen (SP-1) and SSCP, was not tightened; hence, SSCP did not share the load borne by the specimen. In other words, the reinforcement was applied by tightening the chemical-anchor bolt nut when the load reached F_k (see Figure 2).

3. Numerical Modeling

3.1. Geometry and Element Mesh

The numerical model is made up of the following components: the segment, corrugated steel plate, chemical anchor, reinforcement cage, bent bolt, loading plate, and support. Apart from the fact that the longitudinal width of the segment taken as half the structure was 600 mm, the sizes of other components were the same as those on the test.

The element type of the components except rebars was the eight-node solid reduced integral element, referred to as C3D8R in ABAQUS, and the reinforcement cage used the truss element.

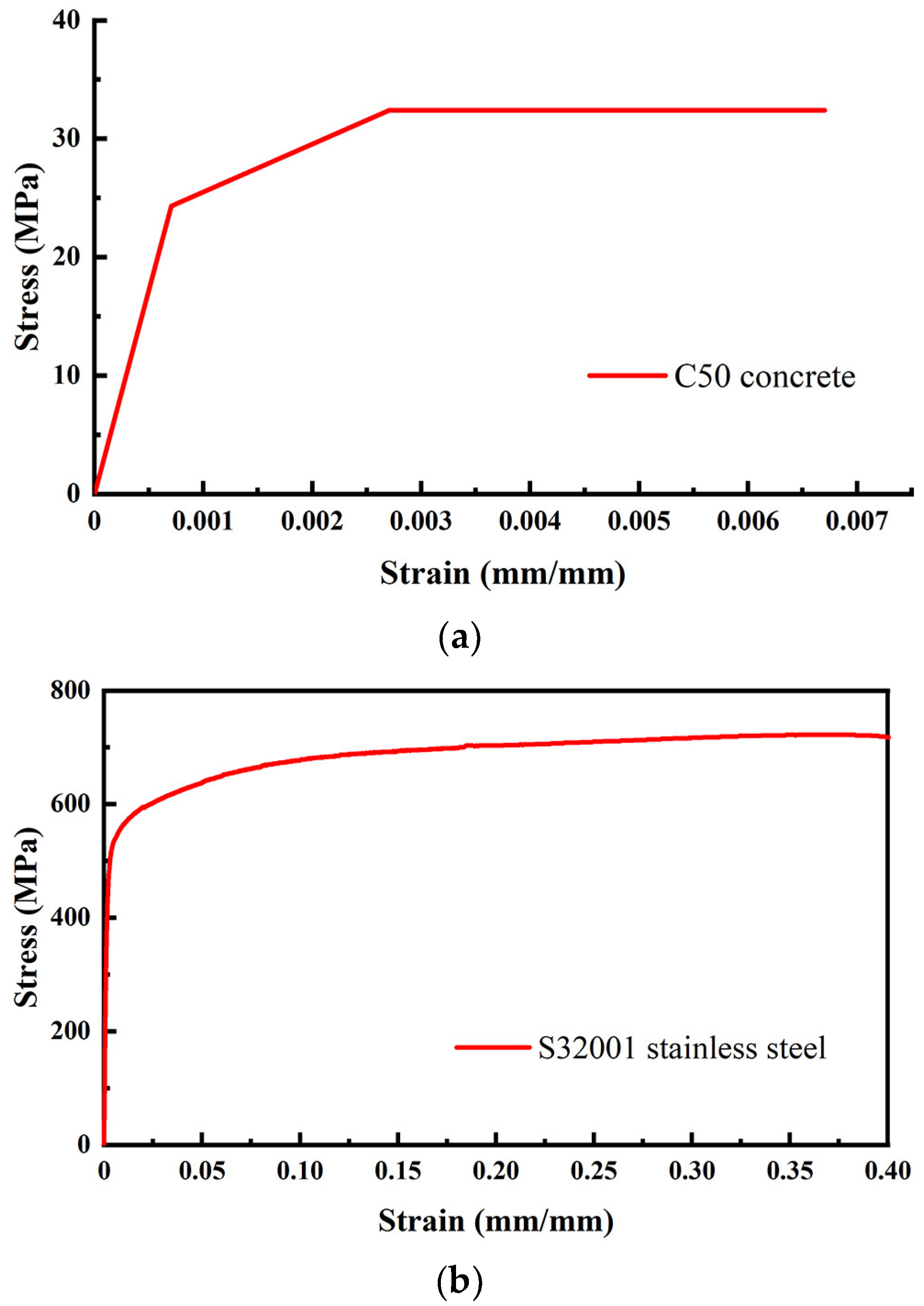
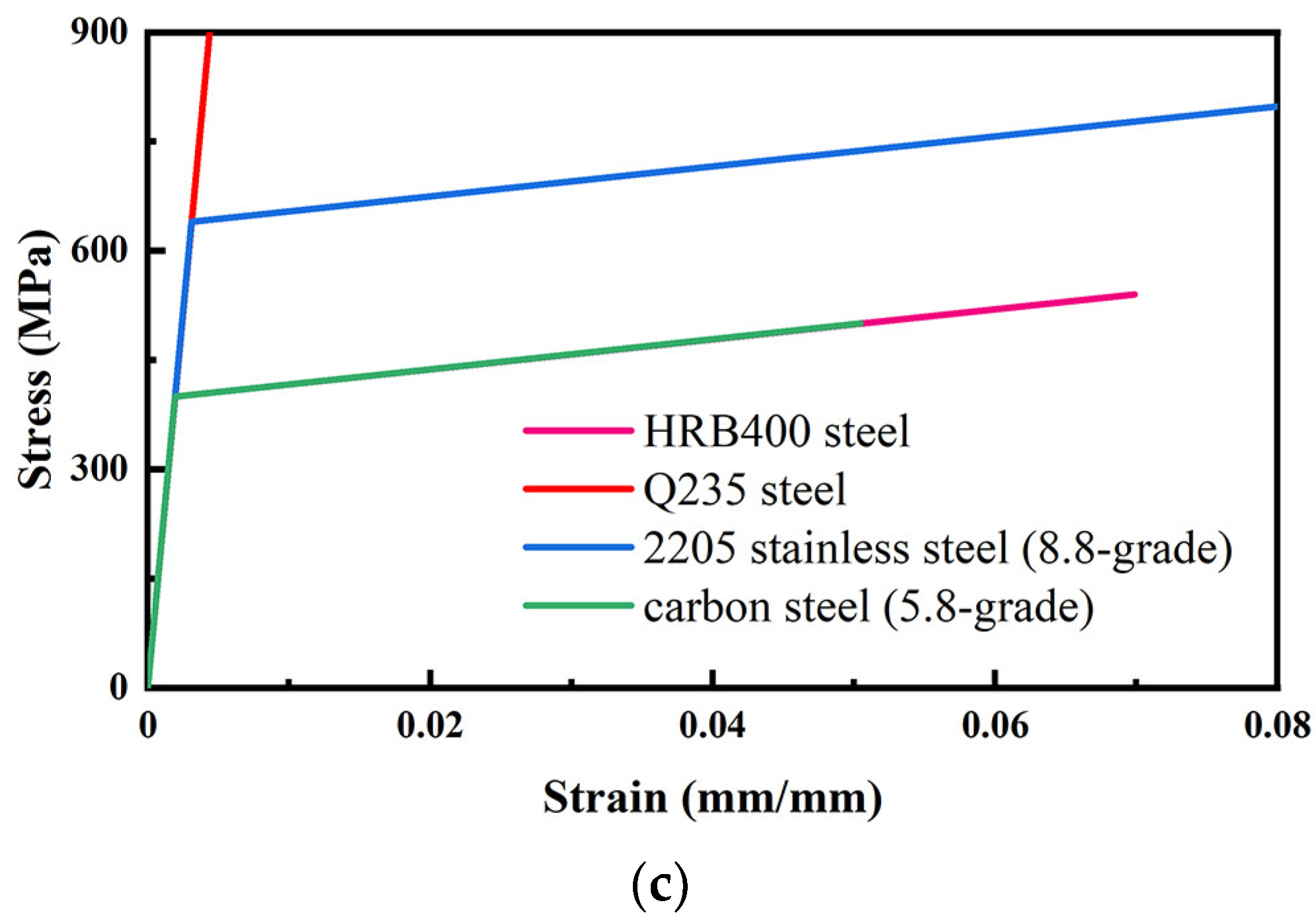
3.2. Constitutive Models of Materials

Saenz model [19] is widely used in FE analysis of concrete, and a simplified tri-fold Saenz constitutive curve [20] was adopted to improve the efficiency (Figure 3a). The waterproof gasket is generally considered as elastic in the FE model, in which the elastic modulus E is 1 GPa and Poisson’s ratio ν is 0.45 [21]. The material of the corrugated steel plate used in the test was a new type of duplex stainless steel, S32001 (Figure 3b). The bent bolts, chemical anchors, rebars, backing plates, and supports were modeled by a double-slash elastic–plastic model (Figure 3c). The parameters of the materials were selected according to Chinese code [22,23], and are listed in

Table 1. Materials parameters of the components.

Component	Material	E (GPa)	fy (MPa)	εy	fu (MPa)	ν
Concrete	C50	34.5	24.3	0.0007	32.4	0.2
SSCP	S32001 stainless steel	206	490	0.0024	720	0.3
Bent bolt	carbon steel (5.8-grade)	206	400	0.0019	500	0.3
Chemical anchor	2205 stainless steel (8.8-grade)	206	640	0.0031	800	0.3
Reinforcement cage	HRB400 steel	206	400	0.0019	540	0.3
Backing plate	Q235 steel	206	-	-	-	0.3
Support	Q235 steel	206	-	-	-	0.3

E denotes the elastic modulus; f_y denotes the yield stress; ε_y denotes the yield strain; f_u denotes ultimate stress; ν denotes Poisson’s ratio.

.

3.3. Contact Relationships

Hard contact can transmit any level of pressure until the two components are separated and penetration does not occur. Tied constraint means that the contact surfaces were firmly bonded and separation is not allowed, as the segment, the support, and the backing plate were kept in close contact during the loading process, and the connection between the groove and the gasket is firm, since they are pasted with glue. The embedded region was extensively used to simulate the contact between the concrete and rebars, since it allows overlap between the parts without deducting space. The contact relationships in the model are summarized in

Table 2. Contact types between components in the FE model.

Number	Contact Pairs	Type
1	Segment and segment	Hard contact
2	Segment and reinforcement cage	Embedded region
3	Segment bent-bolt hole wall and bent bolts	Hard contact
4	Segment and backing plate	Tie
5	Segment and support	Tie
6	Segment and gasket	Tie
7	Segment-hand-hole face and bent-bolt nut	Tie
8	Segment and chemical anchor	Embedded region
9	Segment and SSCP	Hard contact
10	SSCP and chemical anchor	Tie
11	Gasket and gasket	Hard contact

and demonstrated in Figure 4.

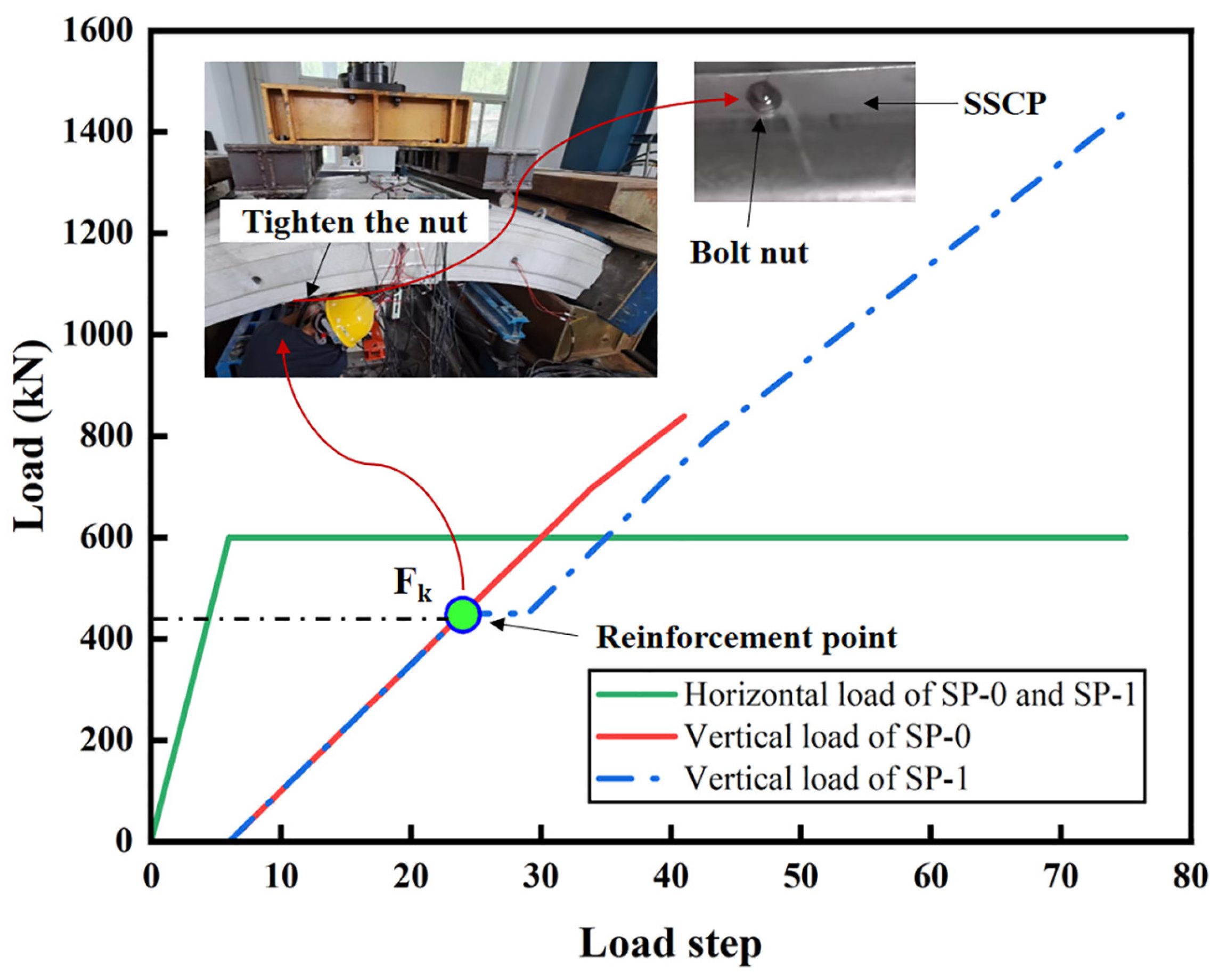
3.4. Load and Boundary Conditions

On the mechanical test, the vertical force provided by the actuator acted on the two loading plates on the top of the segment through the distribution beam, and the horizontal force acted directly on the support through the horizontal actuator. In the FE model, reference points corresponding to the acting surfaces of the actuators were created, and the concentrated loads were applied on them.

The round steel rod at the bottom and on the left side limited the vertical and horizontal displacement of the specimen, respectively. Constraints were imposed at the corresponding positions. The 3D FE model is illustrated in Figure 4.

4. Secondary-Stress Simulation

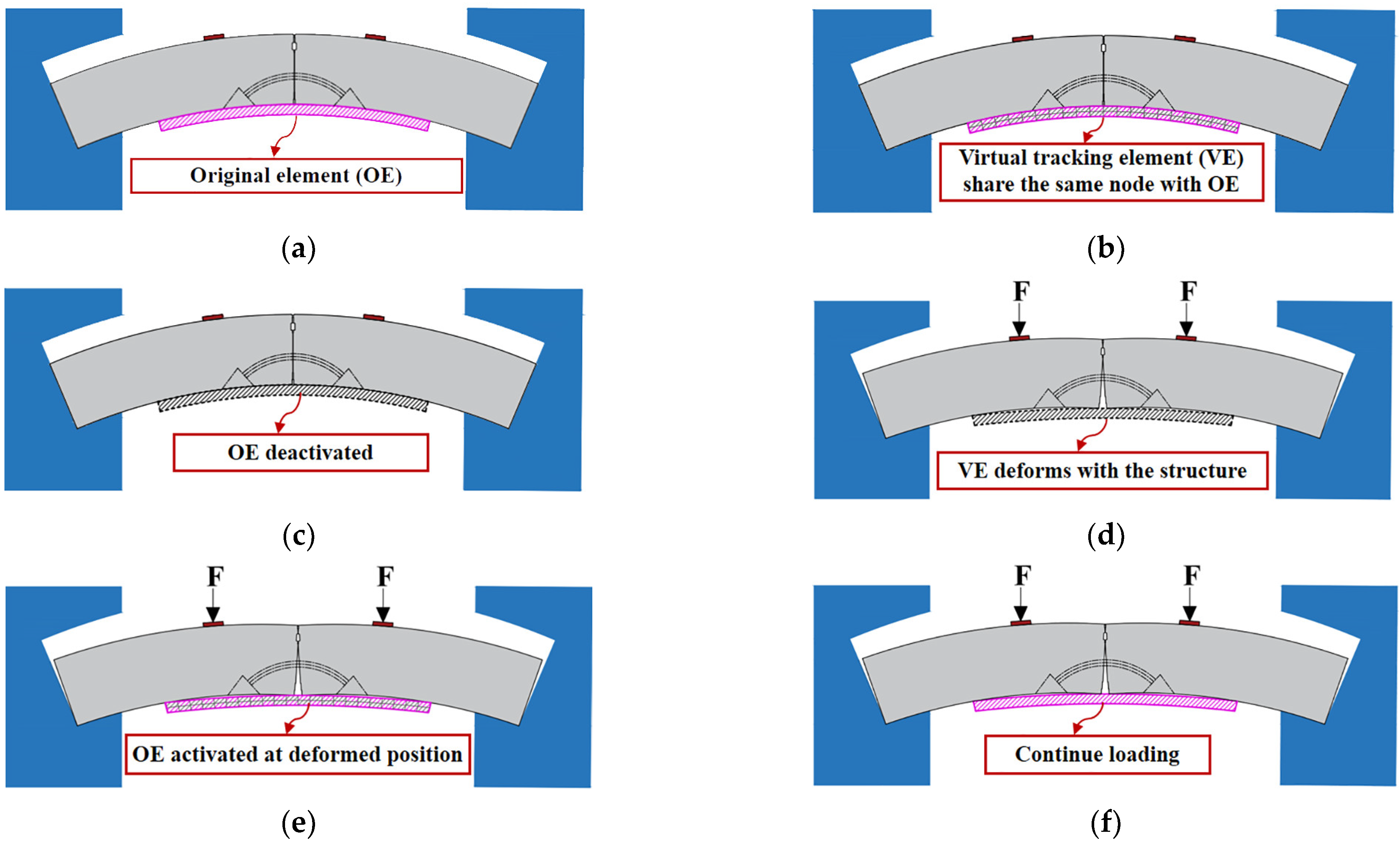
4.1. Principle of Virtual-Tracking-Element Technology

The ABAQUS 2020 software can be used to perform the removal (deactivated) and activation (reactivated) of elements. During the simulation of the reinforcement installation, the position of the segmental joint changes after the initial load is applied. However, in ABAQUS, the activation of the corresponding element is activated at the original position, resulting in the activated reinforcement element partially overlapping with the deformed joint, which is inconsistent with reality.

In order to simulate realistic reinforcement under secondary stress, the activated element needs to appear in the deformed position without strain, so as to bear the load normally after reinforcement. The original element (abbreviated as OE), which is an element of SSCP and the chemical anchor in this model, needs to be copied as an element with a tracking function (called virtual tracking element, abbreviated as VE) at the same location, i.e., VE is actually a backup of OE, with exactly the same nodes. Moreover, VE is required to have no influence on the original structure; thus, the position of VE can be obtained along with the deformation of the structure. When OE is activated, its elements are generated at the deformed position as they have the same nodes as VE. Subsequently, OE shares the load with the deformed structure as the loading continues. Considering the principle above, the requirements for VE are summarized as follows:

i.

The VE should have the same shape and contact relationship as OE and share all nodes, but have a different element number;

ii.

The stiffness of VE should be extremely low, so that its influence on the stress of the original structure can be ignored;

iii.

The mass of VE should be especially small to prevent potential displacement caused by the weight.

4.2. Simulation Methodology

Based on the principle of the virtual tracking element, the secondary-stress simulation of the segmental joint reinforcement was performed. The methodology of virtual-tracking-element technology in ABAQUS can be divided into following steps:

i.

Establish the initial 3D FE model (Figure 5a) and create VE; VE shares the node with OE (Figure 5b);

ii.

Remove OE (Figure 5c), apply load and allow VE to deform, along with the structure (Figure 5d);

iii.

Activate OE (Figure 5e) and continue loading to failure (Figure 5f).

Specifically, the method for creating VE is as follows. Export the model file and use the “Elcopy” command to copy the corresponding original element. Next, import the modified model file and set the properties of VE. Notably, the elastic modulus should be set 4 to 5 orders of magnitude lower than the original structure. The density can be set as 0, and contact relationship need not to be reset, since it is the same as OE.

5. Results and Analysis

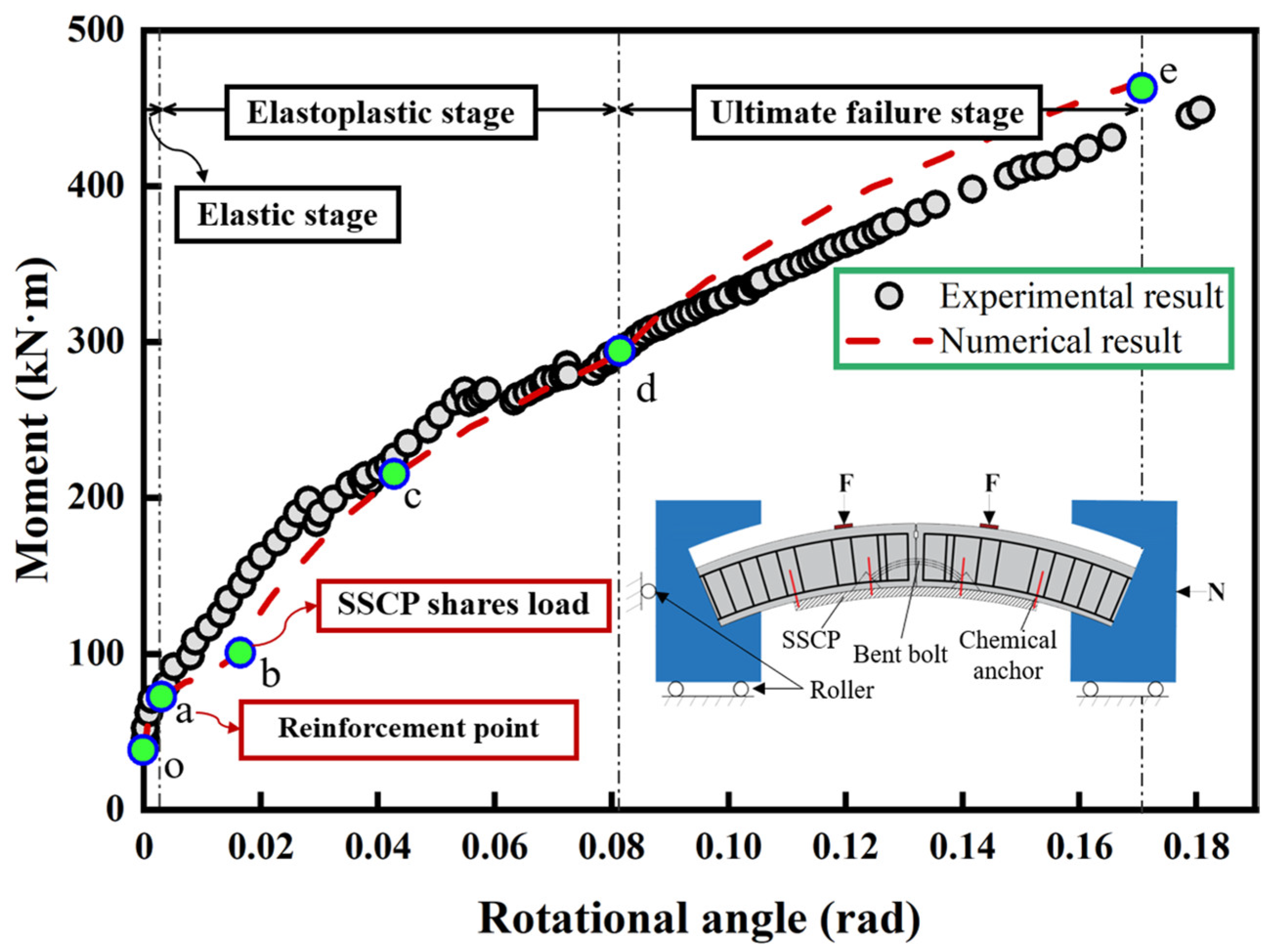
5.1. Model Validation

In order to verify the validity of the numerical model, the comparison between the numerically calculated and experimentally obtained bending moment–rotational angle curve is conducted. The schematic diagrams of the calculation of the moment and rotational angle are illustrated in Figure 6 and they can be calculated using Equations (1) and (2), respectively.

$$M=\left(F+G\right)\times l-G\times l_1-F\times l_2-N\times e$$

(1)

where M is bending moment of the joint section, F is the vertical load, G is the self-weight of the segment, N is the horizontal load, and $e$ is the vertical eccentric distance of N. The $l$, $l_1$, and $l_2$ are the horizontal distances of the three forces from the joint section, respectively.

$$\theta =2arctan\frac{{\delta }_1-{\delta }_2}{2h}$$

(2)

where, θ is the rotational angle (unit: radians), ${\delta }_1$ is the joint-opening change at the internal surface (unit: mm), ${\delta }_2$ is the joint-closing change at the external surface (unit: mm), and $h$ is the thickness of the segment, which is 350 mm.

The corresponding comparison between the numerical and experimental results of the unreinforced and reinforced specimens are shown in Figure 7 and Figure 8, respectively. It can be seen that both numerical curves are in good agreement with the experimental results, and that the curves can be divided into a couple of sections.

As demonstrated in Figure 7, in the OA section, the specimen is in the elastic stage, with low deformation and high stiffness. This result was slightly larger than the test result due to the manufacturing errors in the experiment. The deformation accelerated in the AB section, since the bent bolts began to yield. In the BC section, a temporary increase in the stiffness occurred, since the external concrete was squeezed and in close contact, and the plastic zone started to form; in the ultimate-failure stage (CD section), the compression stress exceeded the bearing capacity of the concrete and led to failure (the plastic zone penetrated through the concrete), and the ultimate moment was 193 kN∙m.

Regarding the reinforced specimen (Figure 8), the point a is the reinforcement point, corresponding to the elastic limit (point a in Figure 7), and the stiffness in the OA section is the same as the unreinforced specimen, indicating that the virtual tracking element had no effect on the specimen. The AB section manifested similar stiffness from the unreinforced specimen, which was attributed to the interspace between the punched-hole wall of the SSCP and the chemical anchor, making SSCP unable to share the load. When the chemical anchor made contact with the hole wall (point b), the stiffness had a notable increase due to the high reinforcement capability of the SSCP. Therefore, the increase in stiffness often lagged behind the reinforcement point. In the CD section, the stiffness gradually decreased because the trough of the SSCP entered the yielding stage, which undermined its capacity to resist deformation. In the final stage, the failure mode was the same as that in the unreinforced specimen (concrete cracked), and the ultimate moment was 464 kN∙m, which increased by 140.4% compared to the unreinforced specimen.

5.2. Component Analysis

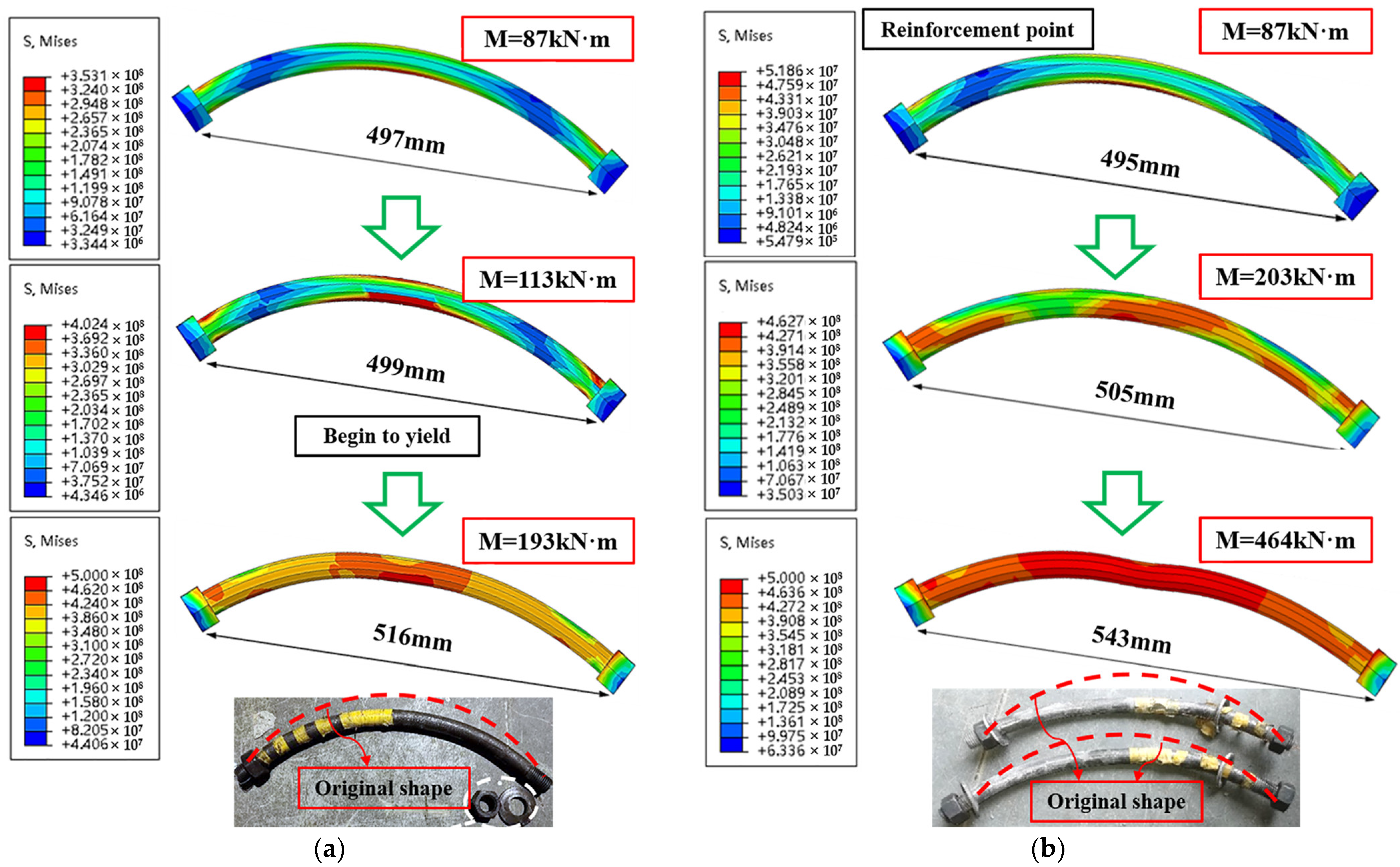
5.2.1. Bent Bolt

The stress contour and deformation of the bent bolts of the unreinforced specimen are shown in Figure 9a. The internal surface began to yield (the Mises stress exceeded 400 MPa) when the moment increased to 113 kN∙m, and the deformation grew quickly after yielding. When the moment reached 193 kN∙m, most of the bent bolt entered the plastic stage, but only a limited region (the mid-span internal surface) reached the ultimate stress (500 MPa).

As shown in Figure 9b, with the SSCP sharing the load, the stress and deformation of the bent bolt were relatively low under the same moment (M = 87 kN∙m). Moreover, the ultimate moment was obviously increased (464 kN∙m) and the stress in the ultimate stage was higher. Nearly the whole bolt yielded and the midrange reached the ultimate stress, resulting in considerably larger deformation (543 mm) than that of the unreinforced specimen (516 mm).

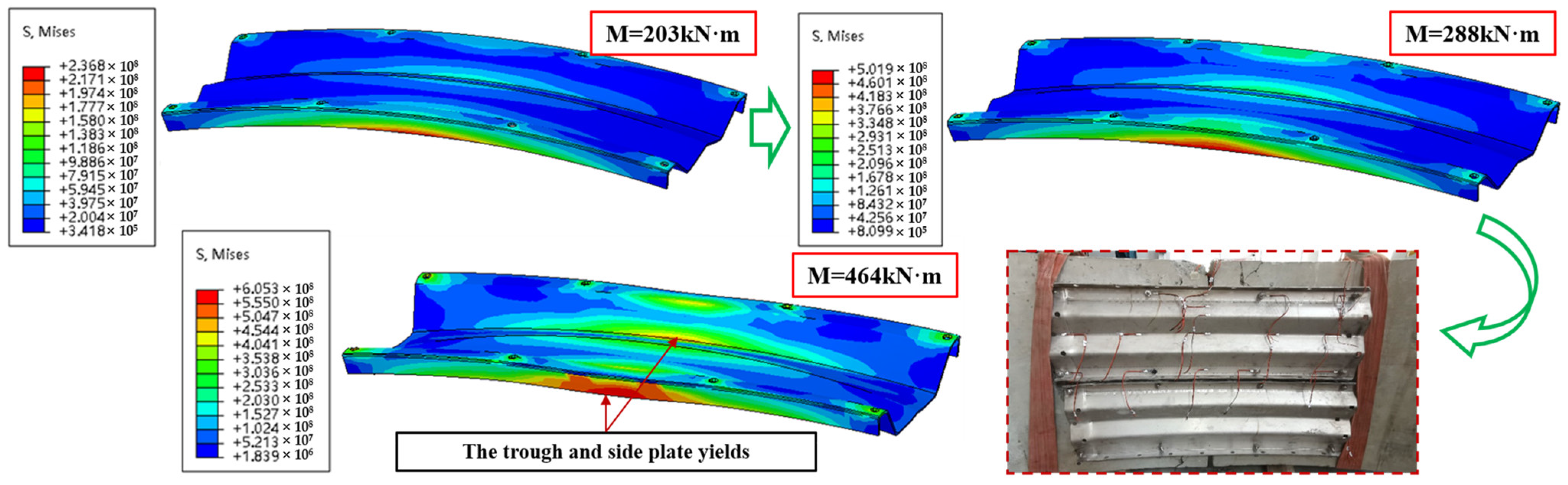
5.2.2. Stainless-Steel Corrugated Plate (SSCP)

Figure 10 is the stress contour of the SSCP at different stages. When the moment increased to 288 kN∙m, the stress of the trough and side plate partially reached the yield stress (490 MPa), leading to a decrease in the stiffness of the reinforced specimen. When the specimen reached the ultimate stage (concrete cracking), no SSCP buckling occurred, and the maximum stress (605 MPa) was far from reaching the ultimate strength (720 MPa), suggesting that the reinforcement capacity of the SSCP was not fully utilized when the grade of the concrete is C50. On the other hand, the relatively low utilization meant an adequate safety margin for unexpected conditions.

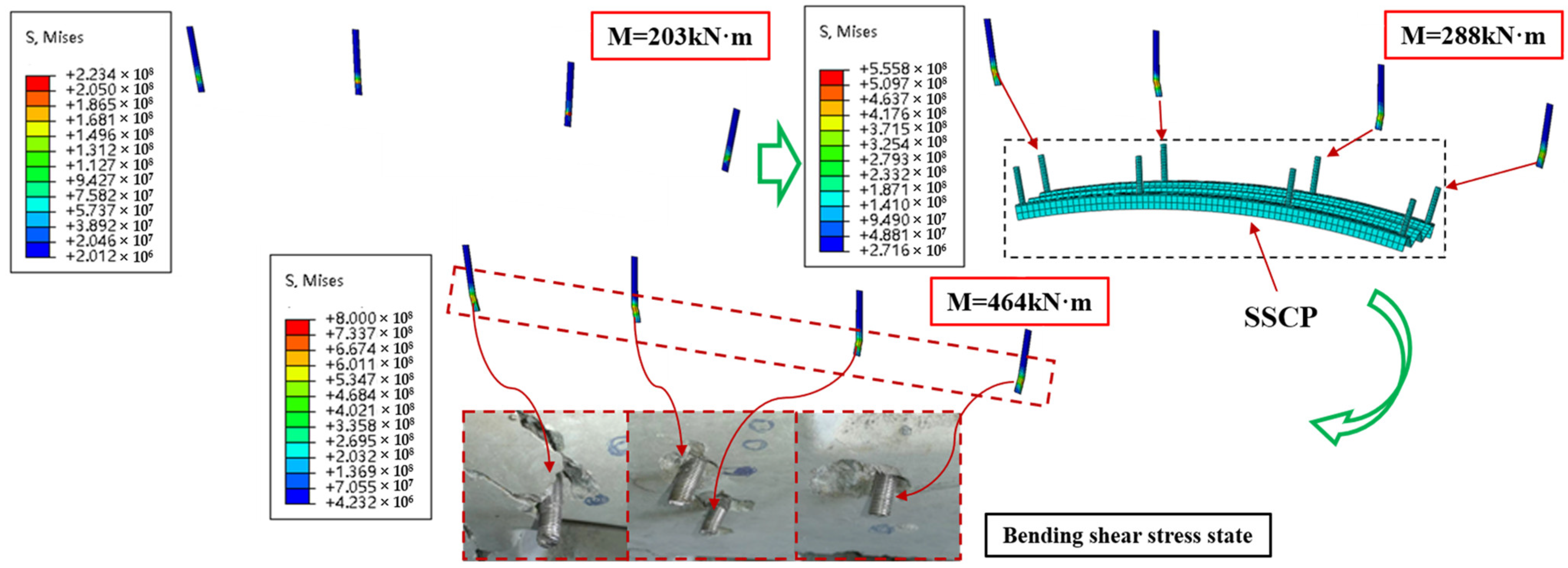
5.2.3. Chemical Anchor

As can be seen in Figure 11, the chemical anchor was under shear stress. When the moment reached 288 kN∙m, there was a localized region of high stress at the joint between the chemical anchor and the hole wall of the SSCP, and the anchor showed obvious bending-shear behavior. When the specimen entered the ultimate failure stage (the moment reached 464 kN∙m), the lower part of the anchor yielded (the Mises stress was larger than 640 MPa) and the joint region reached the ultimate stress (800 MPa). Nevertheless, no shear failure occurred during the loading process, owing to the superior ductility of the chemical anchor.

5.3. Parametric Study

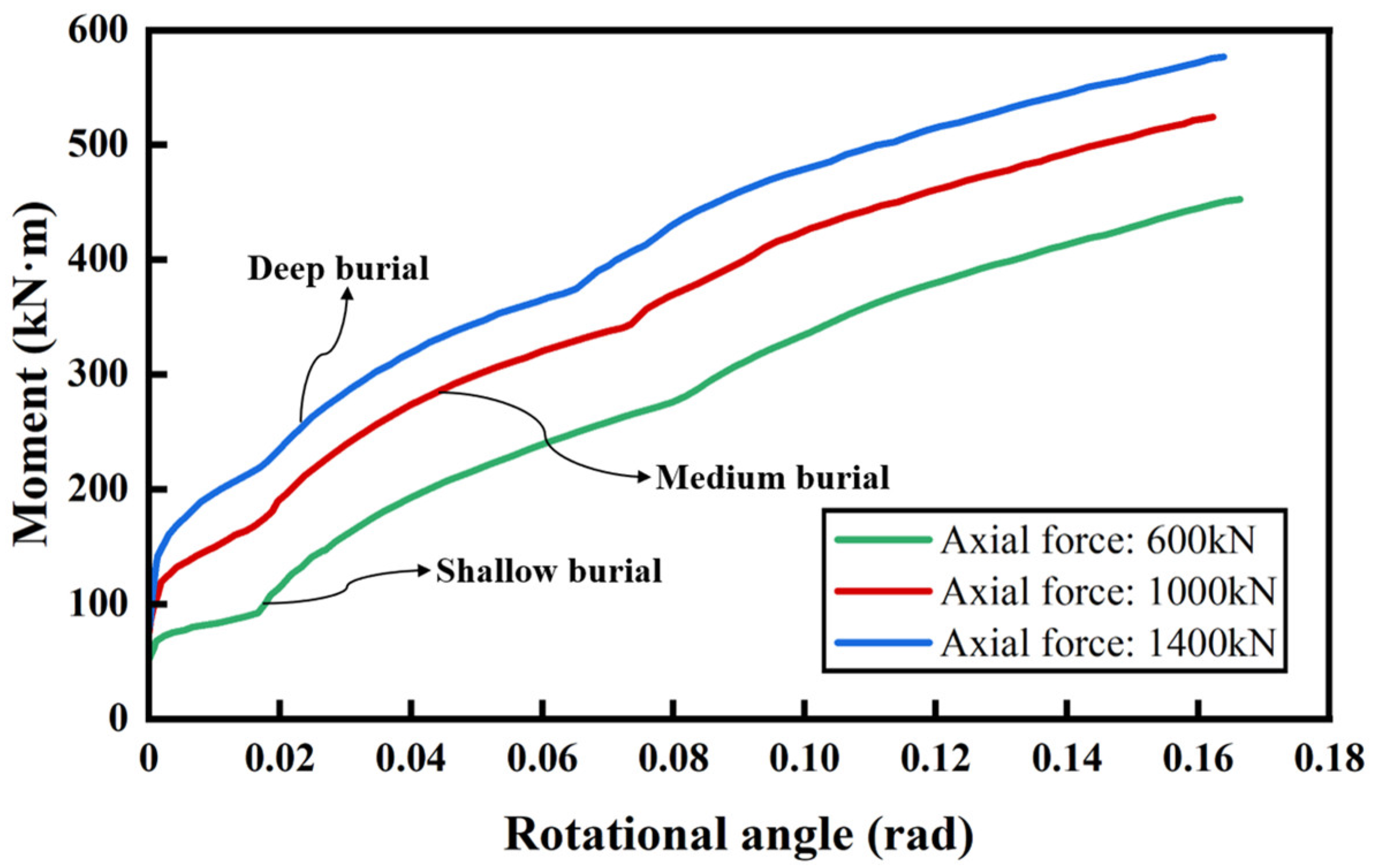
5.3.1. Axial Force

According to the different burial depths of the tunnels in the Shanghai metro, the axial force is divided into three conditions: 600 kN, 1000 kN, and 1400 kN. These correspond to three burial-depth types, shallow burial, medium burial, and deep burial, respectively (see Figure 12). With the axial force increasing, the stiffness in the initial stage was higher due to the closer contact of the external concrete. Nevertheless, the slope of the curves was generally the same in the ultimate stage. The underlying cause is that the stiffness was entirely provided by SCCP, since the concrete had almost completely cracked at this point. In other words, the strength of the SSCP was sufficiently high to ensure that the SSCP could sustain its reinforcement effect until the concrete failed under different axial forces, which indicates the extensive applicability of SSCP reinforcement in tunnels with different burial depths.

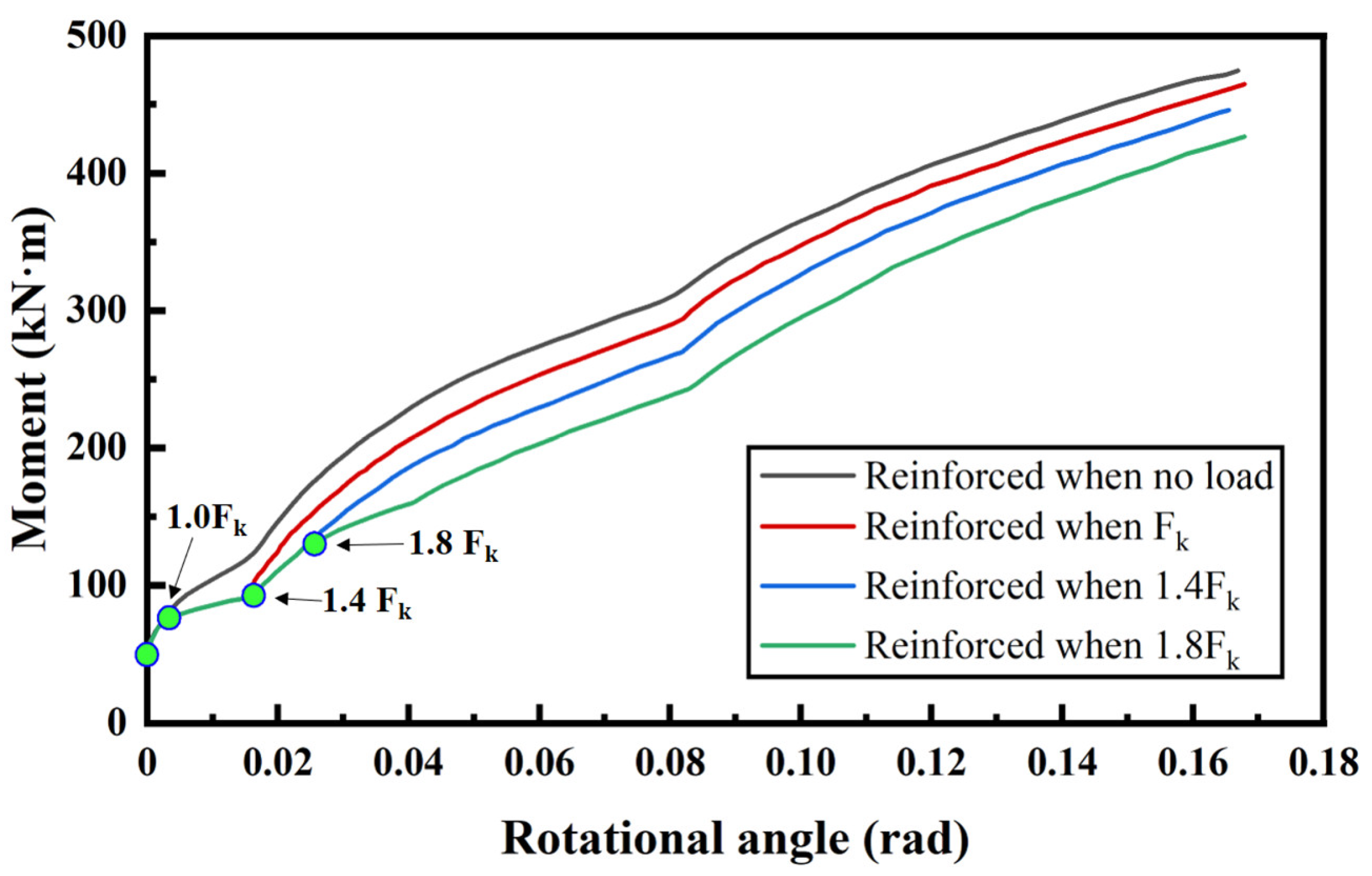
5.3.2. Reinforcement Timing

The reinforcement was conducted when the load reached 1.0 F_k (corresponding to the elastic’s limit point) on the full-scale test, and the ultimate load of the unreinforced specimen was 2.2 F_k. In order to investigate the appropriate reinforcement timepoint, different reinforcement timings were considered by activating the reinforcement elements under different loads: 1.0 F_k, 1.4 F_k, 1.8 F_k, and no pre-applied load (see Figure 13). There was no obvious improvement in the ultimate bending moment, and the ultimate rotational angles were also generally the same, indicating that the utilization of SSCP was comparable. Although the stiffness was similar in that in the ultimate stage, the increase in the initial stiffness was more evident with reinforcement conducted in advance. Considering that the tunnels in service are typically in the elastic or elastoplastic stage, reinforcement in advance is recommended.

6. Conclusions

In this paper, the finite-element software ABAQUS was used to establish a numerical model of the new SSCP reinforcement for the segmental joints of a shield tunnel, and the virtual tracking element was used to conduct a secondary-stress simulation of the segmental joint. The validity of the numerical model was confirmed by the full-scale test. The main conclusions are as follows:

• The use of the virtual-tracking-element technology is feasible for simulating the secondary-stress state of segmental joint reinforcement. The virtual tracking element is similar to a backup of the original element, and it has no influence on the stress or the strain as the structure deforms. By removing and activating the corresponding elements in different steps, the current deformation and secondary-stress characteristics of the segmental joint can be taken into account.
• The reinforcement capacity of SSCP is not fully utilized when segmental concrete is of the C50 grade. Hence, the utilization of SSCP is greater when reinforcing segmental joint of high-grade concrete. On the other hand, the relatively low level of utilization indicates that SSCP reinforcement has a sufficient safety margin for potential excessive loads.
• The SSCP can sustain its reinforcement capability under different axial forces. Thus, SSCP is applicable to tunnel reinforcement regardless of the burial depth. In addition, reinforcement in advance is recommended, since the increase in stiffness is more obvious when the tunnel is in the elastic or elastoplastic stage.