Lightweight Omnidirectional Radiation Protection for a Photon-Counting Imaging System in Space Applications
Abstract
:1. Introduction
2. Materials and Methods
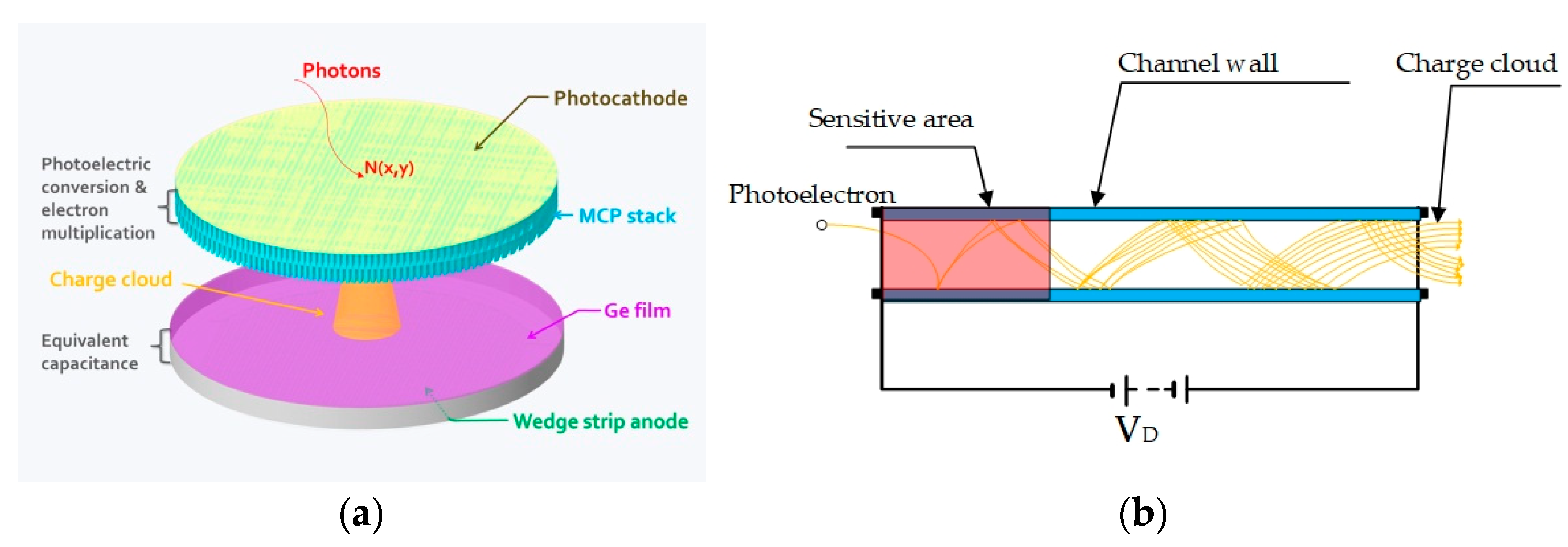
2.1. Protection for Detector
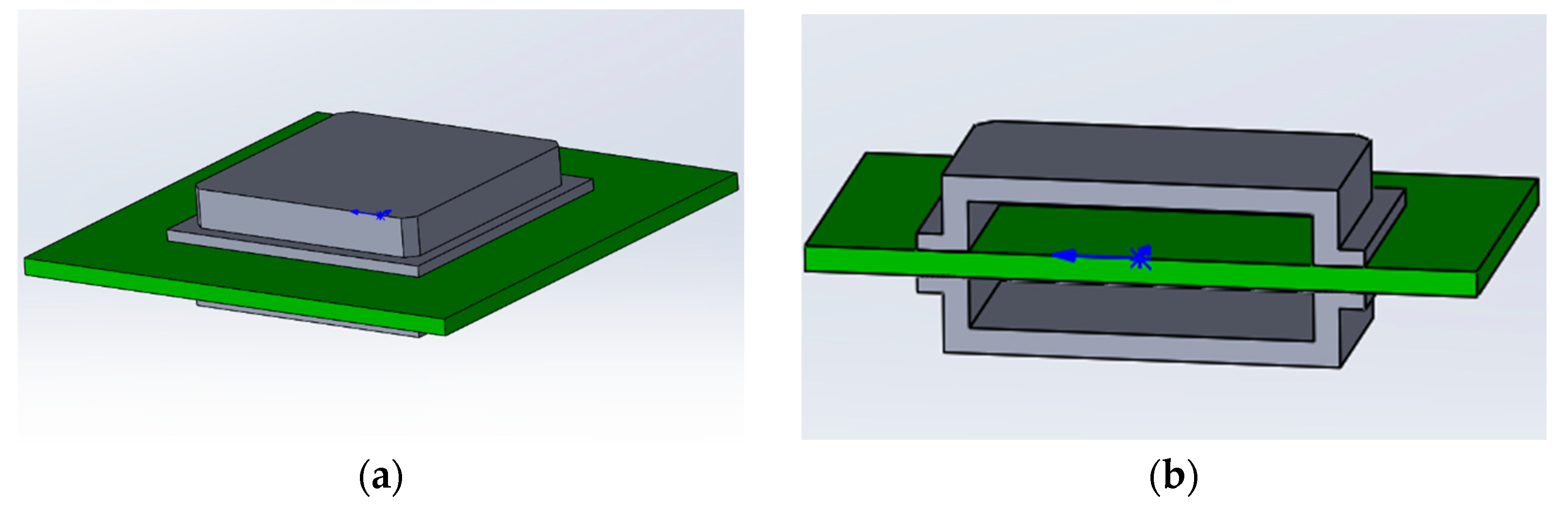
2.2. Local Protective Structure of Electronic Devices
2.3. Shielding Materials
3. Results and Discussion
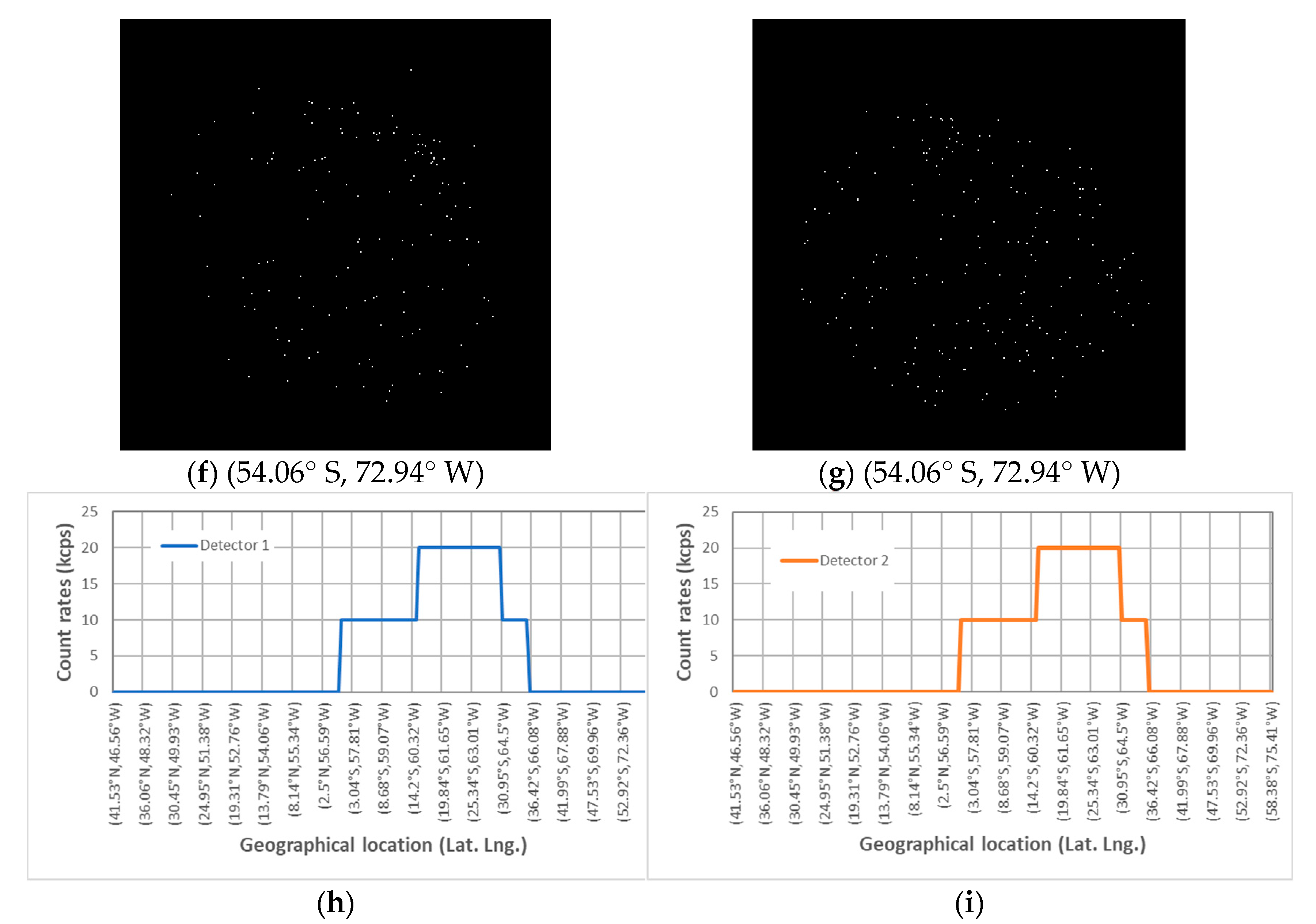
3.1. Test of Photon Counting Imaging in Space
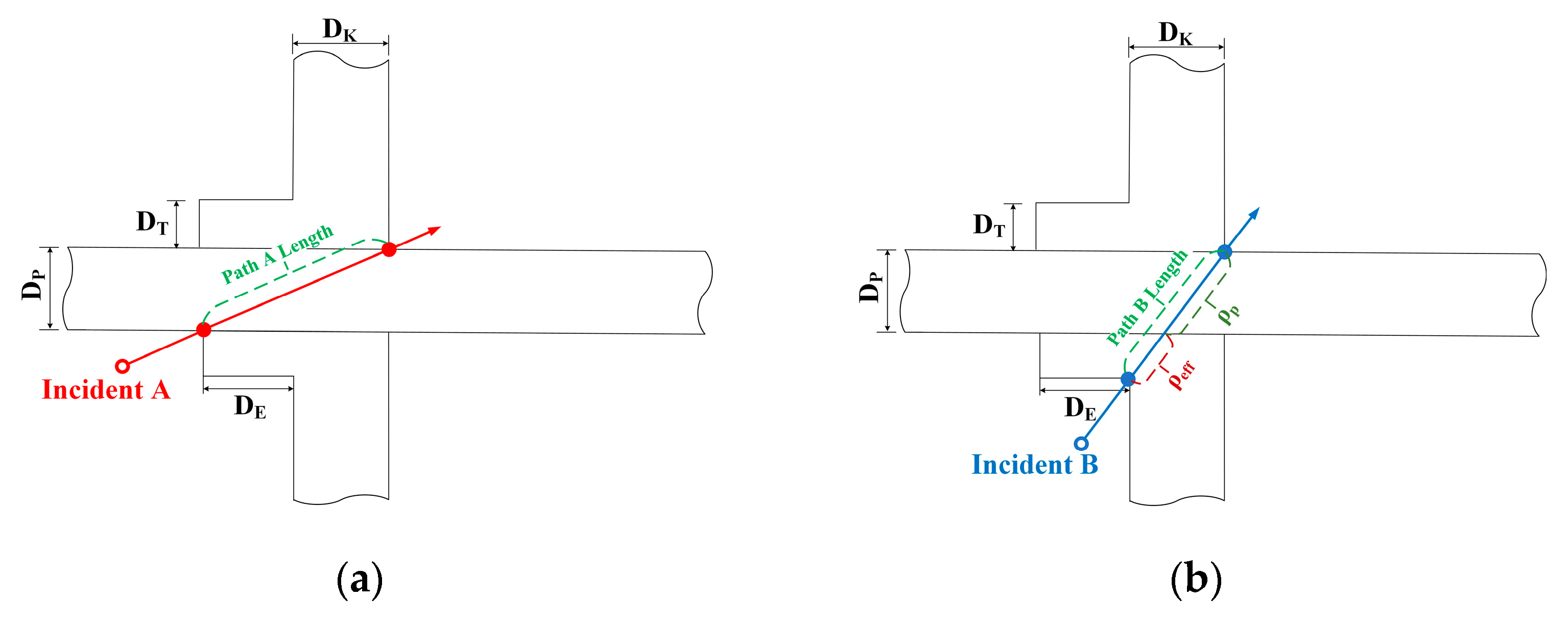
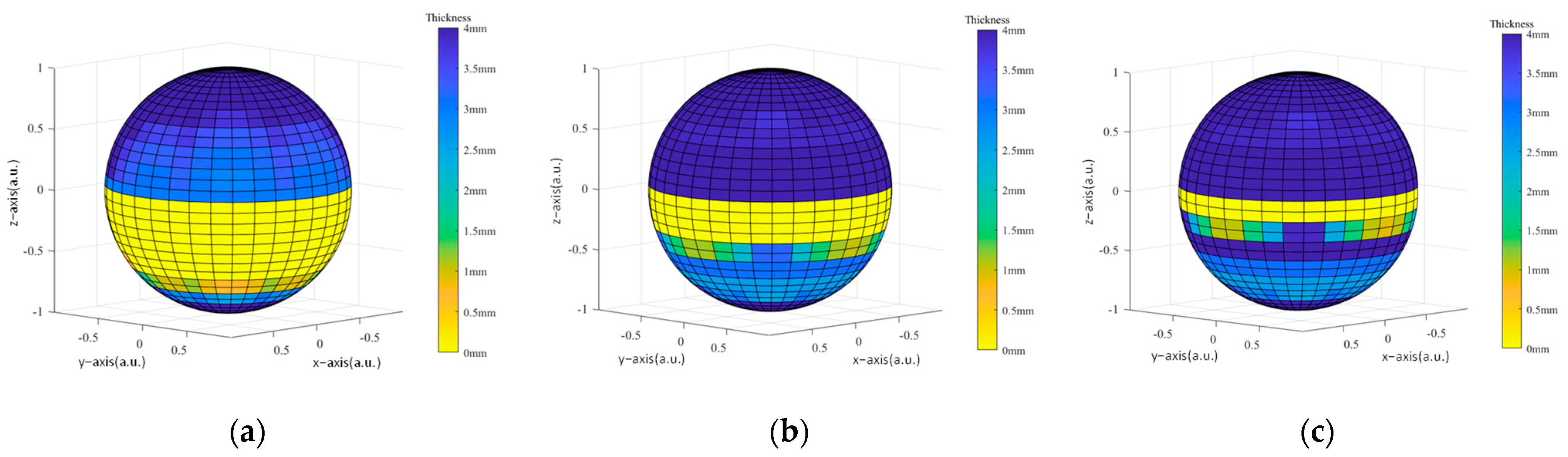
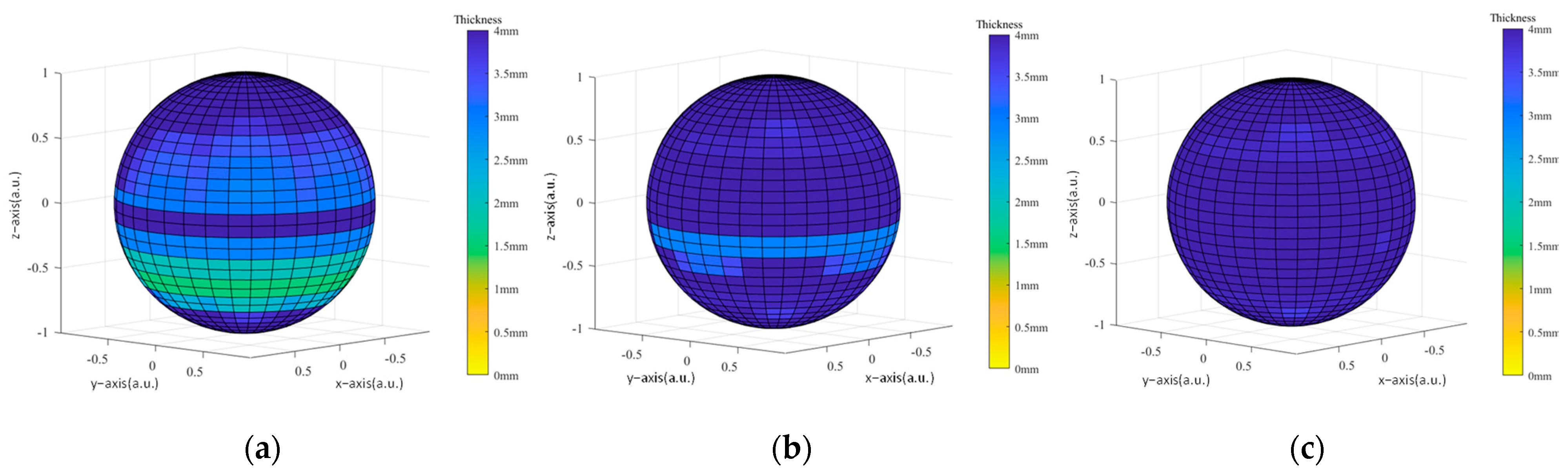
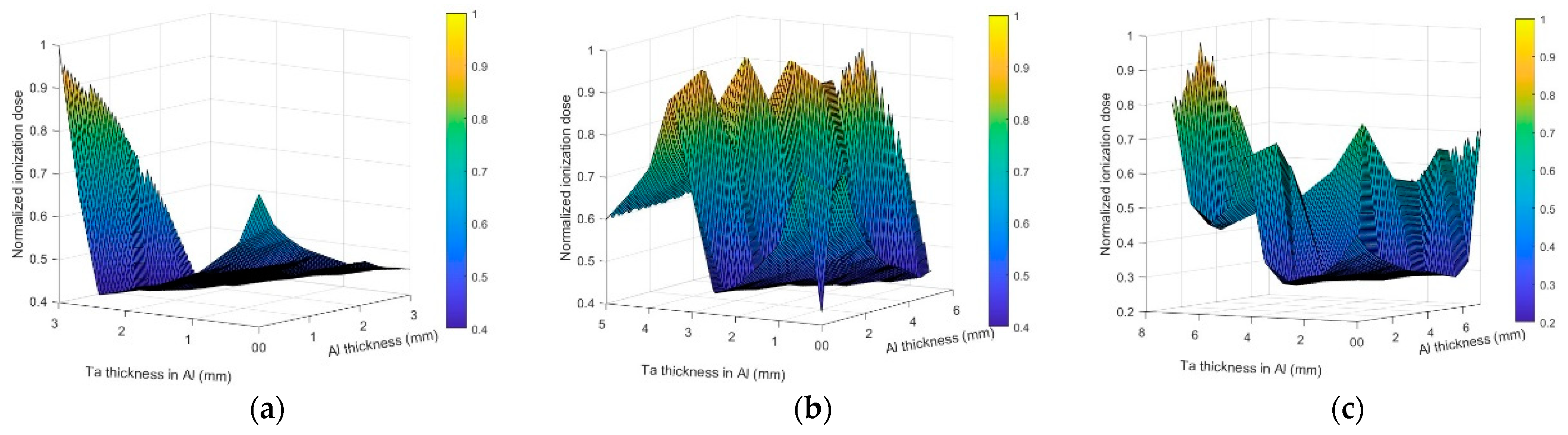
3.2. Uniformity of Protection
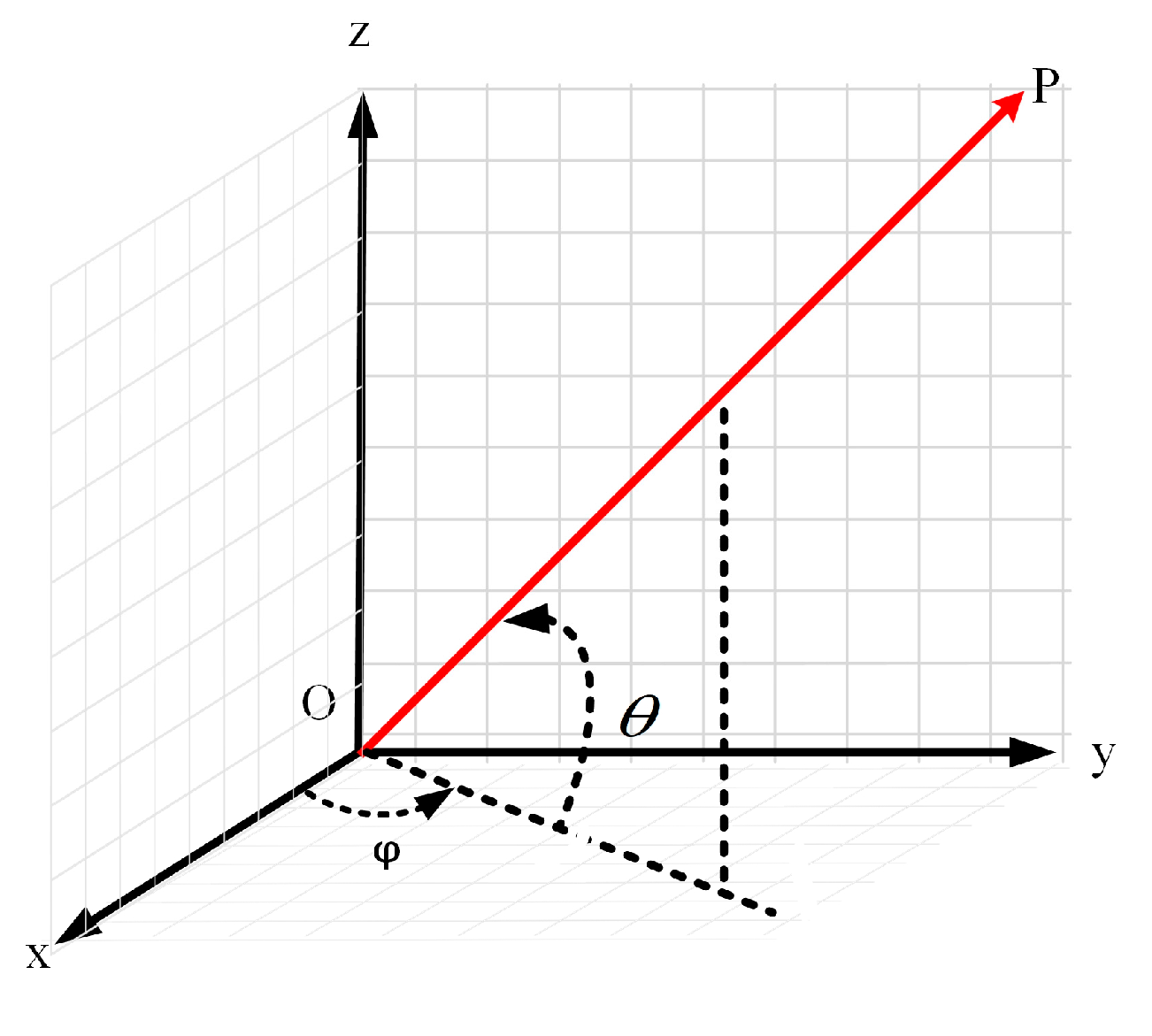
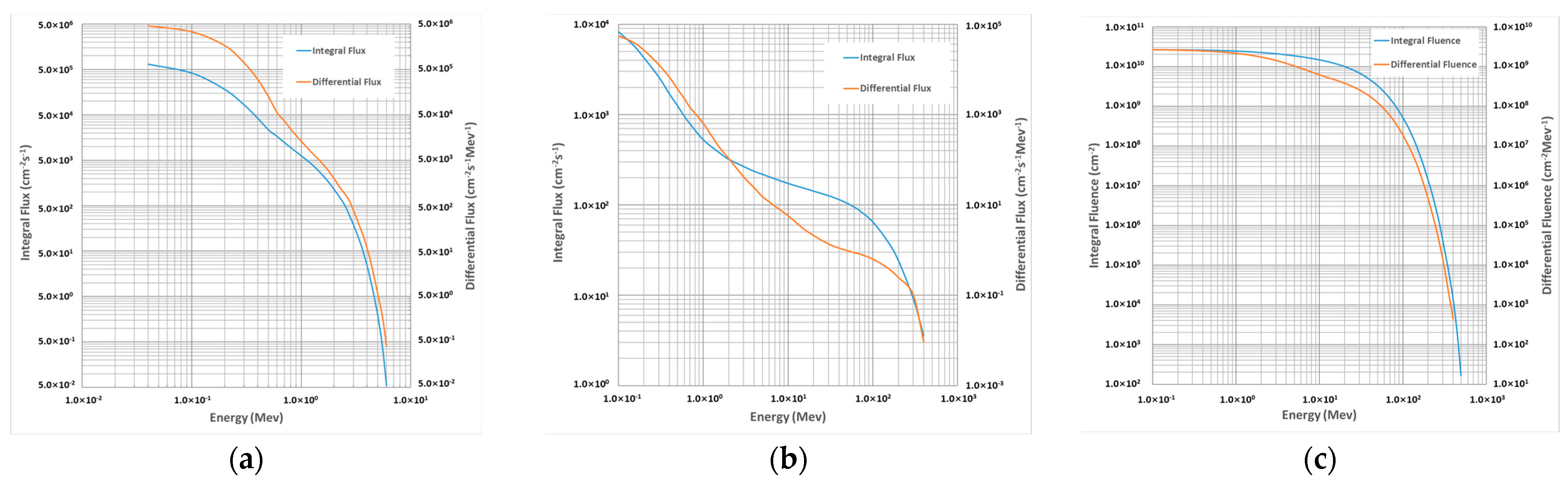
3.3. Simulation of Multilayer Shield
4. Conclusions
5. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bourdarie, S.; Xapsos, M. The near-earth space radiation environment. IEEE Trans. Nucl. Sci. 2008, 55, 1810–1832. [Google Scholar] [CrossRef]
- Ripoll, J.F.; Claudepierre, S.G.; Ukhorskiy, A.Y.; Colpitts, C.; Li, X.; Fennell, J.F.; Crabtree, C. Particle dynamics in the Earth’s radiation belts: Review of current research and open questions. J. Geophys. Res. Space Phys. 2020, 125, e2019JA026735. [Google Scholar] [CrossRef]
- Anderson, P.C.; Rich, F.J.; Borisov, S. Mapping the South Atlantic Anomaly continuously over 27 years. J. Atmos. Sol. Terr. Phys. 2018, 177, 237–246. [Google Scholar] [CrossRef]
- Heirtzler, J.R. The future of the South Atlantic anomaly and implications for radiation damage in space. J. Atmos. Sol. Terr. Phys. 2002, 64, 1701–1708. [Google Scholar] [CrossRef]
- Topper, A.D.; Casey, M.C.; Wilcox, E.P.; Campola, M.J.; Cochran, D.J.; O’Bryan, M.V.; Pellish, J.A.; Majewicz, P.J. Compendium of Radiation Effects Test Results from NASA Goddard Space Flight Center. In Proceedings of the Nuclear and Space Radiation Effects Conference (NSREC), Ottawa, ON, Canada, 17–23 July 2021. [Google Scholar]
- Rahman, M.M.; Shankar, D.; Santra, S. Analysis of radiation environment and its effect on spacecraft in different orbits. In Proceedings of the International Astronautical Congress (IAC2017), Adelaide, Australia, 25–29 September 2017. [Google Scholar]
- Ferraro, R.; Alía, R.G.; Danzeca, S.; Masi, A. Analysis of Bipolar Integrated Circuit Degradation Mechanisms Against Combined TID–DD Effects. IEEE Trans. Nucl. Sci. 2021, 68, 1585–1593. [Google Scholar] [CrossRef]
- Marcelot, O.; Goiffon, V.; Raine, M.; Duhamel, O. Radiation effects in CCD on CMOS devices: First analysis of TID and DDD effects. IEEE Trans. Nucl. Sci. 2015, 62, 2965–2970. [Google Scholar] [CrossRef]
- Samwel, S.W.; El-Aziz, E.A.; Garrett, H.B.; Hady, A.A.; Ibrahim, M.; Amin, M.Y. Space radiation impact on smallsats during maximum and minimum solar activity. Adv. Space Res. 2019, 64, 239–251. [Google Scholar] [CrossRef]
- Morton, T.; Lyons, V. Estimation of the radiation environment based on the NASA AP-8 and AE-8 Models. In Proceedings of the 5th International Workshop on Radiation Effects on Semiconductor Devices for Space Applications, Dushanbe, Tajikistan, 1 October 2002. [Google Scholar]
- Chunqin, W.; Yueqiang, S.; Guangwei, C.; Zhang, X.; Li, J.; Zhang, X.; Jing, T.; Shen, G.; Zhang, S.; Huang, C.; et al. Radiation dose evaluation and analysis inside FY-3A satellite. Chin. J. Space. Sci. 2015, 35, 56–63. (In Chinese) [Google Scholar]
- Wang, C.Q.; Zhang, X.G.; Shen, G.H.; Zhang, S.; Zhang, X.; Huang, C.; Li, X. Dynamic results of electron flux in radiation belt from 2011 to 2015 based on FY-3B satellite observation. Chin. J. Geophys. 2021, 64, 1831–1841. [Google Scholar]
- Cepeda-Rizo, J.; Gayle, J.; Ravich, J. Thermal and Structural Electronic Packaging Analysis for Space and Extreme Environments, 1st ed.; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Dacko, A.; Kowalski, T.; Baran, J.; Barciński, T. Electronic box structural analyses for a space flight. In Photonics Applications in Astronomy, Communications, Industry, and High-Energy Physics Experiments, Proceedings of the Wilga 2019—Photonics Applications and Web Engineering, Wilga, Poland, 6 November 2019; SPIE: Paris, France, 2019. [Google Scholar]
- Fenske, M.T.; Barth, J.L.; Didion, J.R.; Mule, P.; The Development of Lightweight Electronics Enclosures for Space Applications. NASA Technical Reports Server. Available online: https://ntrs.nasa.gov/citations/20030022659 (accessed on 26 January 2023).
- Daneshvar, H.; Milan, K.G.; Sadr, A.; Sedighy, S.H.; Malekie, S.; Mosayebi, A. Multilayer radiation shield for satellite electronic components protection. Sci. Rep. 2021, 11, 20657. [Google Scholar] [CrossRef] [PubMed]
- Fetzer, A. Radiation Shielding Simulations for Small Satellites on Geostationary Transfer Orbit. Master’s Thesis, Aalto University, Espoo, Finland, 25 April 2022. [Google Scholar]
- Chen, B.; Song, K.F.; Li, Z.H.; Wu, Q.-W.; Ni, Q.-L.; Wang, X.-D.; Xie, J.-J.; Liu, S.-J.; He, L.-P.; He, F. Development and calibration of the Moon-based EUV camera for Chang’e-3. Res. Astron. Astrophys. 2014, 12, 1654–1663. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, H.N.; He, H.; He, F.; Chen, B.; Feng, J.-Q.; Ping, J.-S.; Shen, C.; Xu, R.-L.; Zhang, X.-X. Analysis of observational data from Extreme Ultra-Violet Camera onboard Chang’E-3 mission. Astrophys. Space Sci. 2016, 361, 76. [Google Scholar] [CrossRef]
- Zhang, X.X.; Chen, B.; He, F.; Song, K.; He, L.; Liu, S.; Guo, Q.; Li, J.; Wang, X.; Zhang, H.; et al. Wide-field auroral imager onboard the Fengyun satellite. Light. Sci. Appl. 2019, 8, 47. [Google Scholar] [CrossRef] [PubMed]
- Ding, G.; Li, J.; Zhang, X.; He, F.; He, L.; Song, K.; Sun, L.; Dai, S.; Liu, S.; Chen, B.; et al. Wide-field aurora imager onboard Fengyun satellite: Data products and validation. Earth Planet. Phys. 2021, 5, 73–78. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, X.X.; He, L.P.; Song, K.; Liu, S.; Ding, G.; Dun, J.; Li, J.; Li, Z.; Guo, Q.; et al. Solar X-ray and EUV imager on board the FY-3E satellite. Light. Sci. Appl. 2022, 11, 329. [Google Scholar] [CrossRef] [PubMed]
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.; et al. Recent developments in Geant4. Nucl. Instrum. Methods Phys. Res. A 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Kalospyros, S.A.; Gika, V.; Nikitaki, Z.; Kalamara, A.; Kyriakou, L.; Emfietzoglou, D.; Kokkoris, M.; Georgakilas, A.G. Monte Carlo Simulation-Based Calculations of Complex DNA Damage for Incidents of Environmental Ionizing Radiation Exposure. Appl. Sci. 2021, 11, 8985. [Google Scholar] [CrossRef]
- Han, Z.W.; Song, K.F.; Zhang, H.J.; Yu, M.; He, L.; Guo, Q.; Wang, X.; Liu, Y.; Chen, B. Photon Counting Imaging with Low Noise and a Wide Dynamic Range for Aurora Observations. Sensors 2020, 20, 5958. [Google Scholar] [CrossRef] [PubMed]
- Tulej, M.; Meyer, S.; Lüthi, M.; Lasi, D.; Galli, A.; Piazza, D.; Desorgher, L.; Reggiani, D.; Hajdas, W.; Karlsson, S.; et al. Experimental investigation of the radiation shielding efficiency of a MCP detector in the radiation environment near Jupiter’s moon Europa. Nucl. Instrum. Methods Phys. Res. Sect. B 2016, 383, 21–37. [Google Scholar] [CrossRef]
- Sigmund, P. Particle Penetration and Radiation Effects; Springer Series in Solid-State Sciences; Springer: Berlin/Heidelberg, Germany, 2014; Volume 2, p. 179. [Google Scholar]


| Materials | Density | Atomic Number (Z) | Atomic Weight (A) | Z/A |
|---|---|---|---|---|
| Aluminum (Al) | 2.7 g/cm3 | 13 | 26.98 g/mol | 0.48 |
| High-Density Polyethylene (HDPE) | 0.95 g/cm3 | 2.25 | * | * |
| Tantalum (Ta) | 16.6 g/cm3 | 73 | 180.95 g/mol | 0.40 |
| Group | ||||||
|---|---|---|---|---|---|---|
| 1 | 3 mm | 3 mm | 2 mm | 0 mm | 2.8 g/cm3 | 0.93 g/cm3 |
| 2 | 3 mm | 3 mm | 2 mm | 3 mm | 2.8 g/cm3 | 0.93 g/cm3 |
| 3 | 3 mm | 3 mm | 2 mm | 6 mm | 2.8 g/cm3 | 0.93 g/cm3 |
| Index | Parameters |
|---|---|
| Categories | NPSSO |
| Orbital altitude | 836.0 km |
| Orbital inclination | 98.75° |
| Orbital eccentricity | ≤0.0025 |
| Orbital period | 101.5 min |
| Longitude of ascending node | 14:00 PM |
| Shielding Configurations | Sensitivity | Maximum Counting Rates | Dark Count Rates |
|---|---|---|---|
| Whole shielding with three layers | 8.79 count s−1 Rayleigh−1 | 350 kcps | 0.068 * |
| Local shielding with three layers | 8.78 count s−1 Rayleigh−1 | 351 kcps | 0.079 * |
| Single-layer shielding using aluminum | 8.80 count s−1 Rayleigh−1 | 350 kcps | 1 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Z.-W.; Song, K.-F.; Liu, S.-J.; Guo, Q.-F.; Ding, G.-X.; He, L.-P.; Li, C.-W.; Zhang, H.-J.; Liu, Y.; Chen, B. Lightweight Omnidirectional Radiation Protection for a Photon-Counting Imaging System in Space Applications. Appl. Sci. 2023, 13, 5905. https://doi.org/10.3390/app13105905
Han Z-W, Song K-F, Liu S-J, Guo Q-F, Ding G-X, He L-P, Li C-W, Zhang H-J, Liu Y, Chen B. Lightweight Omnidirectional Radiation Protection for a Photon-Counting Imaging System in Space Applications. Applied Sciences. 2023; 13(10):5905. https://doi.org/10.3390/app13105905
Chicago/Turabian StyleHan, Zhen-Wei, Ke-Fei Song, Shi-Jie Liu, Quan-Feng Guo, Guang-Xing Ding, Ling-Ping He, Cheng-Wei Li, Hong-Ji Zhang, Yang Liu, and Bo Chen. 2023. "Lightweight Omnidirectional Radiation Protection for a Photon-Counting Imaging System in Space Applications" Applied Sciences 13, no. 10: 5905. https://doi.org/10.3390/app13105905
APA StyleHan, Z.-W., Song, K.-F., Liu, S.-J., Guo, Q.-F., Ding, G.-X., He, L.-P., Li, C.-W., Zhang, H.-J., Liu, Y., & Chen, B. (2023). Lightweight Omnidirectional Radiation Protection for a Photon-Counting Imaging System in Space Applications. Applied Sciences, 13(10), 5905. https://doi.org/10.3390/app13105905





