A Survey of An Intelligent Multi-Agent Formation Control

Abstract

We present an overview of formation control for multi-agent systems. Multi-agent formation cooperation is important to accomplish assigned tasks more efficiently and safely compared to a single agent. For the way information flows between agents, we divide the available results into communication-based topologies as well as vision-based formation controls. Then, we summarize the problem formulation, discuss the differences, and review the latest results on formation control schemes. Lastly, we give research recommendations for multi-intelligent agent controls in a certain period in the future.

1. Introduction

In recent years, with the continuous development of material technology as well as artificial intelligence technology, agents such as UAVs, unmanned boats, and robots have been widely used in search and rescue [1], navigation, and other livelihood tasks as well as military tasks such as surveillance [2], target tracking [3], and aerial refueling [4]. With the widespread use of intelligent bodies, the great challenge of controlling them to perform various tasks efficiently and safely to realize their great application potential has made the theory of multi-intelligent body formation control gradually become a research hotspot.

The purpose of intelligent agent formation control is to drive multiple intelligent agents to achieve the desired state or to form a specified distance between intelligent agents. There have been many review papers addressing intelligent body formation control. In [5], Yu et al. provide an overview for fault detection in unmanned formation control and give methods to achieve the reconfiguration of formations after different obstacles. In [6], Elijah surveyed the current state of research on the cooperative control of fixed-wing UAVs, covering formation control, and control methods for adjusting the tail, rotor, and wings of fixed-wing UAVs for maneuvering. Unlike the previous ones, Anderson et al. in [7] classified the intelligent body formations according to distance, displacement, and position, and gave the basic control methods and ideas. In addition to various types of control strategies, multiple formation fault-tolerant fault detection methods were investigated by Kamel et al. and presented in [8]. However, after that, scholars have conducted a lot of research on formation control, so we believe it is time to carry out a survey on multi-intelligence control methods.

Since there is a large body of research literature addressing formation control, it would be a challenge to exhaustively review the existing research results. Therefore, in this paper, we do not provide an exhaustive account of all the literature, but rather focus on the types of information that agents interact with and the characteristics of the interaction topology, as we believe that both determine the strategies and methods of multi-agent formation control.

Formation control schemes are essentially about controlling the agent to reach the desired position in a limited time, and the type of information the agent interacts with and the characteristics of a stable communication link in the interaction naturally lead to the agent’s requirements for sensors and the type of sensing variables to achieve the target formation. The mission environment and the agent’s own load limit the type and number of sensors carried, thus specifying the type of information to be interacted with and determining whether a stable communication link can be formed. Specifically, if the agent can form a stable communication link by the sensors it carries, the agent can actively control itself to form the desired formation through stable information interaction. In contrast, if a stable communication link cannot be formed, the agent can only rely on the data sensors it carries to passively receive relative information and thus use the relative information to achieve control of its position and attitude to form a formation. In short, the formation of a stable communication link determines the topology of the information exchange and also the type of information exchange. Based on the above observations, we classify the existing stratigraphic control into a communication-based formation control and a visual servo-based formation control according to whether a stable communication link can be formed. To the best of our knowledge, there is no relevant classification and investigation method in the previous studies.

Communication-based formation control is where the intelligent agent is not only able to sense its state information, but also able to sense the state information of other intelligent agents in the formation through the inter-agent communication topology. By comparing the difference between itself and other agents in the formation, the agent controls its state through the controller and finally achieves the desired state.

Vision-based formation control is where intelligent agents cannot communicate with each other to achieve an accurate state information transfer, and can only obtain the state of other intelligent agents through on-board sensors, and realize the estimation of state information and calculate the error to achieve the formation control through 3D reconstruction or an image conversion matrix.

The above classification leads to the conclusion that communication-based formation control techniques require the least sensor capability, but a more stable sensor performance. When the communication sensors are stable, the ability to transmit information is higher. In vision-based formation control techniques, although not much information is required to be measured by the sensors, the requirements for information accuracy are increased. The advantages and disadvantages of the two types of methods are shown in

Table 1. Control method comparison.

	Types of Sensors	Accurate Status Transfer	Interaction Requirements	Interaction Capability
Communication-based formation control	Communication sensors GPS, etc.	Highly accurate status	Stable messaging topology	High interaction ability
Vision-based formation control	Vision sensors GPS, etc.	Sensor-dependent accuracy	No communication required	One-way information delivery

.

Due to a large amount of the literature available on formation control, it is impractical to give an exhaustive account of each one of them, so this paper focuses on intelligent body modeling, formation control methods under different information transfer methods, and the future development prospects of intelligent body formations. The main contributions of this paper are as follows:

(a)

We summarize the agent models used in the process of implementing formation control. The content covers a variety of agent models to provide some references for the reader to choose the appropriate model for their research.

(b)

Starting from the basic concepts of formation control, this paper classifies formation control methods into communication-based formation control methods and visual servo-based formation control methods, according to whether a stable communication link can be established, and reviews related works. The basic concepts of different methods are briefly outlined and some typical formation architectures, as well as algorithms, are provided to the readers.

(c)

The paper summarizes and discusses some limitations of the existing research work and outlines some potential ideas that can be addressed shortly.

This paper is structured as follows: the major models used in agent formation control and the classification of control states are presented in Section 2. In Section 3 and Section 4, communication topology-based and vision servo-based formation control methods are discussed and existing results are reviewed. The current problems faced by agent formation controls and the possible development directions are discussed in Section 5. Section 6 concludes and discusses the paper.

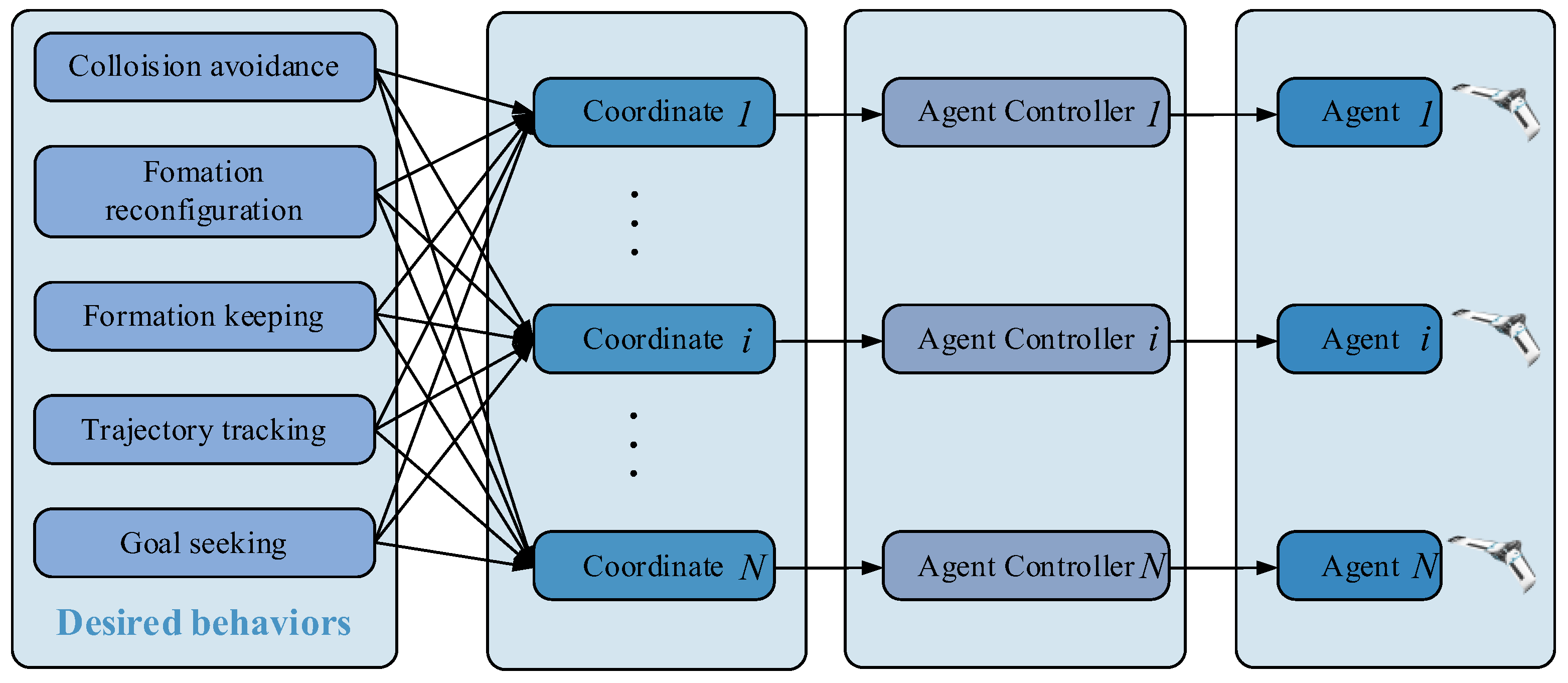
2. The Intelligent Agent Formation Control Problem

Intelligent agent formation can be described as a process in which the agent completes the attitude (IL) control as well as the position (OL) control to achieve the desired position under the formation controller. The control process (taking a fixed-wing UAV as an example) is shown in Figure 1.

Firstly, a definition of formation control is given. In [9,10,11], for a cluster with $N$ intelligence agents, the formation can be described as:

$$\left\{\begin{array}{c}{\dot{x}}_i=f_i\left(x_i,u_i\right)\\ y_i=g_i\left(x_1,\dots ,x_N\right)\\ z_i=h_i\left(x_i\right)\end{array}\right.,i=1,..,N$$

(1)

where $x_i,y_i,z_i$ are the state, metric, and output of the $i$ agent in the cluster. The formation is achieved as the constraint that is achieved as $\left(z\right)=F\left(z^{\ast }\right)$. This formation control is to design the control law that assures that the outputs stably converge to the desired set of $z^{\ast }=x:F\left(z\right)=F\left(z^{\ast }\right)$. In order to better describe the formation control method, the following first describes the various types of individual intelligent agent control models commonly used in the study.

2.1. The Linear Intelligent Agent Model

In early studies, researchers mostly used linear models of first-order intelligence [12,13], then the $i$ intelligence model in a cluster with $N$ agents can be expressed as

$${\dot{x}}_t^i=u_t^i$$

(2)

where $x_t^i\in ℝ$ represents the state information of the $i$ intelligent agent and $u_t^i\in ℝ$ is the input of the agent at that moment. After subsequent intensive research and the development of techniques, second-order linear models were widely used in studies [14,15] with a model formulated as:

$$\left\{\begin{array}{c}{\dot{x}}_t^i=v_t^i\\ {\dot{v}}_t^i=u_t^i\end{array}\right.$$

(3)

where $x_t^i\in ℝ$ represents the $i$-th intelligent agent state information, $v_t^i\in ℝ$ represents the agent velocity, and $u_t^i\in ℝ$ is the input at that moment. Although the above second-order linear model can be well applied to the consensus calculation, the linear system does not respond well to the motion patterns of other agents such as vehicles. Therefore, some scholars propose nonlinear equations of the motion for agents in the two-dimensional plane.

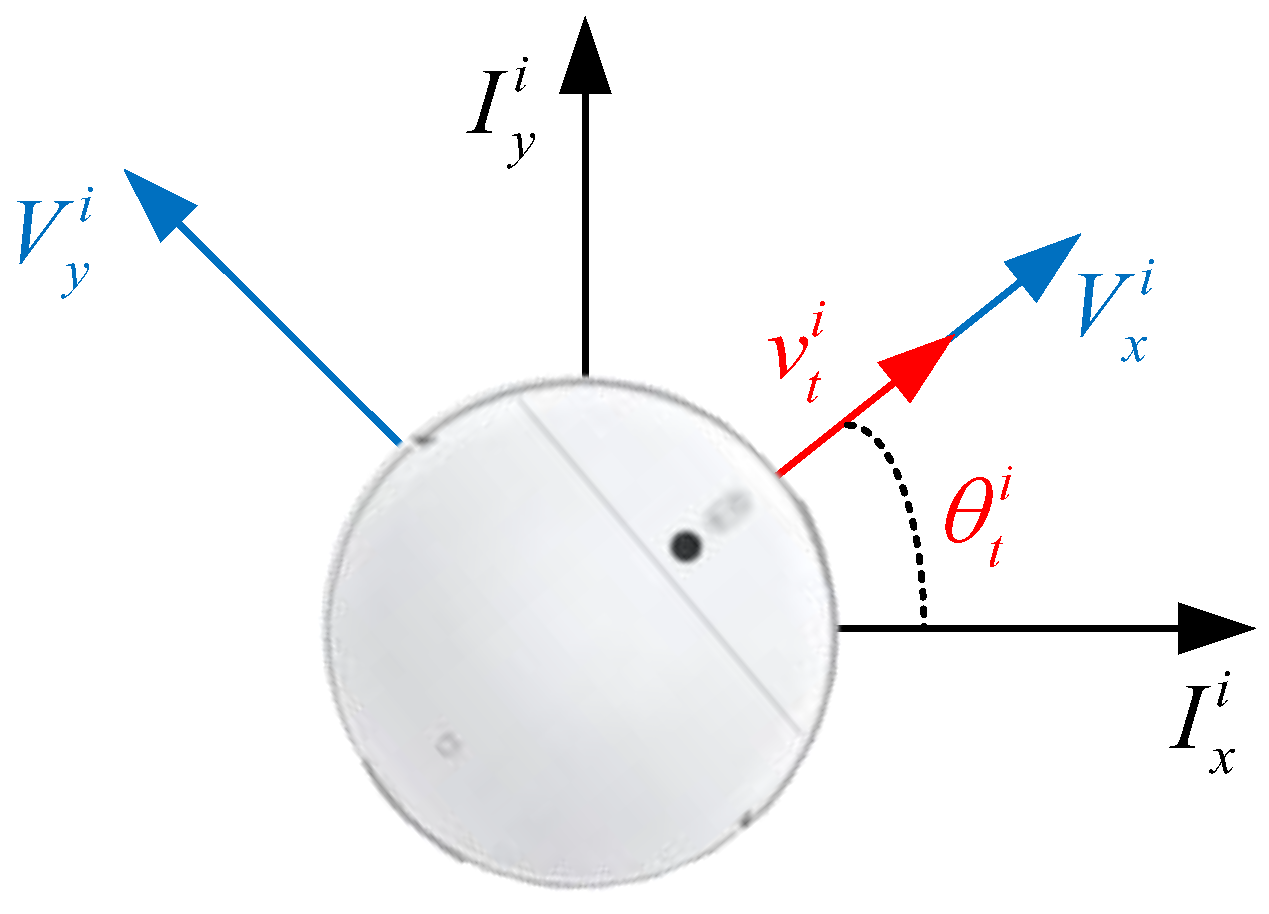
2.2. The 2D Intelligent Agent Motion Model

In order to better describe the equations of motion of agents in the two-dimensional plane, two coordinate systems are proposed. Suppose that in a formation with $N$ agents, $V^i$ denotes the $i$-th agent velocity coordinate frame with the origin at the center of mass of the agent, $V_x^i$ points to the velocity direction, and $V_y^i$ points to be perpendicular to $V_x^i$ according to the right-handed spiral rule, then the velocity of the agent at time $t$ in the velocity coordinate frame can be expressed as a vector $v={\left[\begin{array}{cc}{v}_t^i& 0\end{array}\right]}^T$. Assuming that the angle between the velocity direction and the inertial system is ${\theta }_t^i$, the relationship between the velocity coordinate system $V^i$ and its relationship with the inertial frame $I$ is shown in Figure 2.

Then, the agent equation of motion can be expressed [14,15] as:

$$\left[\begin{array}{c}{\dot{x}}_t^i\\ {\dot{y}}_t^i\\ {\dot{\theta }}_t^i\end{array}\right]=\left[\begin{array}{cc}\cos {\theta }_t^i& 0\\ \sin {\theta }_t^i& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}{v}_t^i\\ {\omega }_t^i\end{array}\right]$$

(4)

where $u_t^i={\left[\begin{array}{cc}{v}_t^i& {\omega }_t^i\end{array}\right]}^T$ is the input of the agent, and ${\mathit{x}}_t^i=\left[\begin{array}{ccc}{x}_t^i& y_t^i& {\theta }_t^i\end{array}\right]$ is the status information. However, the kinematic model of the two-wheeled agent, considering the noncomplete constraints of pure rolling, anti-skid, and vehicle wheelbase, can be described as [16]:

$$\left[\begin{array}{c}{\dot{x}}_t^i\\ {\dot{y}}_t^i\\ {\dot{\theta }}_t^i\end{array}\right]=\left[\begin{array}{cc}\cos {\theta }_t^i& -d\sin {\theta }_t^i\\ \sin {\theta }_t^i& d\cos {\theta }_t^i\\ 0& 1\end{array}\right]\left[\begin{array}{c}{v}_t^i\\ {\omega }_t^i\end{array}\right]$$

(5)

where $d$ represents the distance between the center of mass of the agent and the center of the wheel axis.

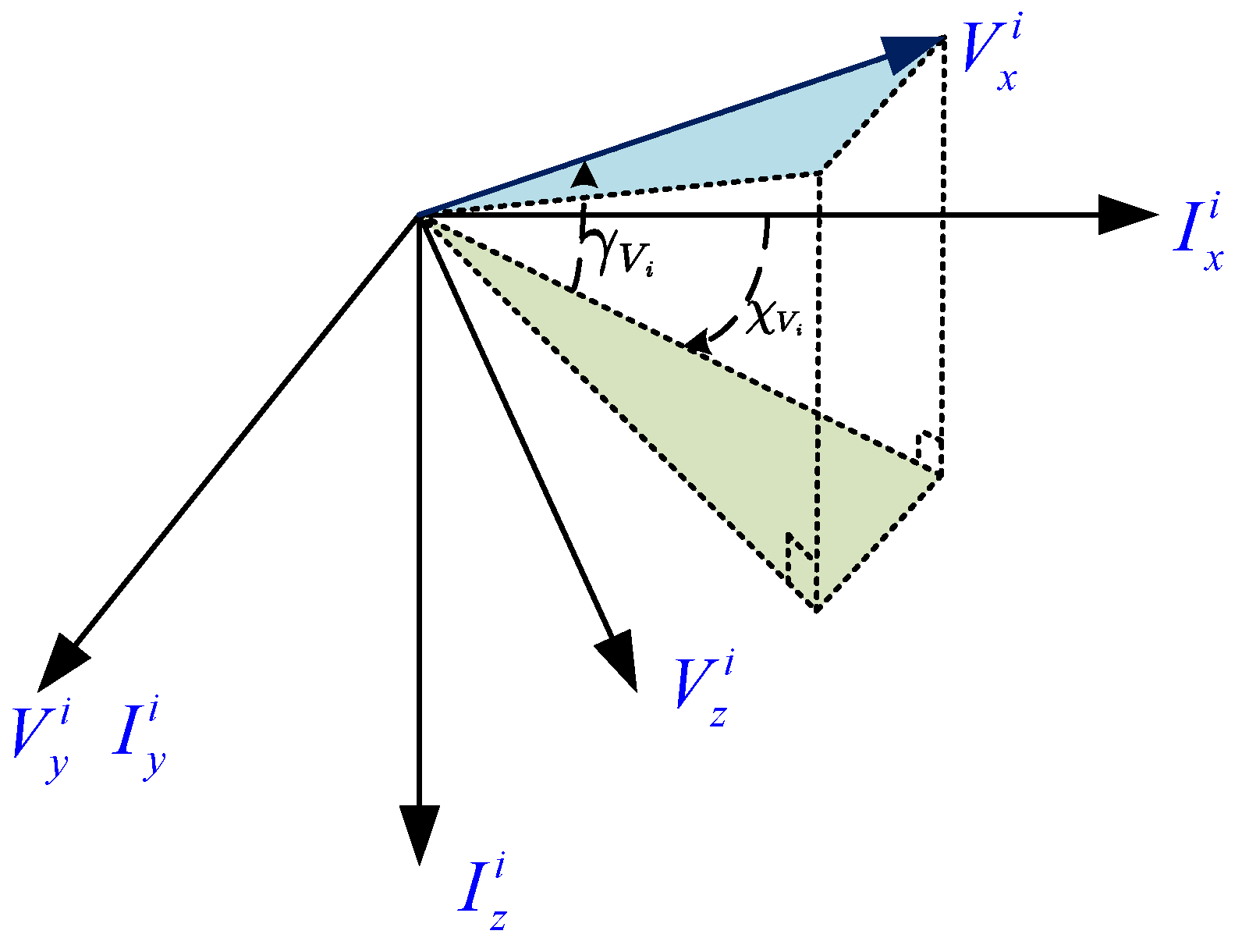
2.3. The 3D Intelligent Agent Model

The motion of the intelligent agent does not only stay in the two-dimensional plane, and the above model does not reflect the motion of the intelligent body in the three-dimensional environment, and the following presents the model of the nonlinear motion of the intelligent agent in the three-dimensional environment. In order to describe the modeling process of the UAV in 3D space, the geodesic coordinate frame $I$ is introduced, and the body coordinate frame $V^i$ of the Follower agent, $V_x^i$ points to the velocity direction, $V_z^i$ is vertically down along the center of mass direction of the intelligent body, and $V_y^i$ is determined according to the right-hand rule, and the relationship is shown in Figure 3.

It is assumed that in a formation with $N$ agents, the inter-agent dynamics are decoupled, while the effect of agent roll is not considered and the effect of external wind speed is neglected. Assuming that the intelligent body velocity vector is $v={\left[\begin{array}{ccc}{v}_t^i& 0& 0\end{array}\right]}^T$, the acceleration vector is $a_t^i={\left[\begin{array}{ccc}{a}_{xt}^i& a_{yt}^i& a_{zt}^i\end{array}\right]}^T$, ${\gamma }_t^i$ is the pitch angle, ${\chi }_t^i$ is the yaw angle, and $p_t^i={\left[\begin{array}{ccc}{x}_t^i& y_t^i& z_t^i\end{array}\right]}^T$ is the position vector of the intelligent body in the inertial frame at moment $t$ of the $i$-th UAV, the intelligent agent 3D model can be expressed as [17]:

$$\left[\begin{array}{c}{\dot{x}}_t^i\\ {\dot{y}}_t^i\\ {\dot{z}}_t^i\\ {\dot{v}}_t^i\\ {\dot{\chi }}_t^i\\ {\dot{\gamma }}_t^i\end{array}\right]=\left[\begin{array}{c}{v}_t^i\cos {\gamma }_t^i\cos {\chi }_t^i\\ v_t^i\cos {\gamma }_t^i\sin {\chi }_t^i\\ -v_t^i\sin {\gamma }_t^i\\ a_{xt}^i\\ a_{zt}^i/v_t^i\\ -a_{yt}^i/v_t^i\end{array}\right]$$

(6)

In three dimensions, it is sometimes necessary to consider the wing vortices, when the agent model can be formulated as [18]:

$$\left[\begin{array}{c}{\dot{x}}_t^i\\ {\dot{y}}_t^i\\ {\dot{z}}_t^i\\ {\dot{v}}_t^i\\ {\dot{\chi }}_t^i\\ {\dot{\gamma }}_t^i\end{array}\right]=\left[\begin{array}{c}{v}_t^i\cos {\gamma }_t^i\cos {\chi }_t^i\\ v_t^i\cos {\gamma }_t^i\sin {\chi }_t^i\\ -v_t^i\sin {\gamma }_t^i\\ \left(T_t^i-D_t^i\right)/m_i-g\sin {\gamma }_t^i+d_{v_t^i}\\ L_t^i\sin {\mu }_i/\left(m_i{v}_t^i\cos {\gamma }_t^i\right)+d_{{\chi }_t^i}\\ L_t^i\cos {\mu }_i/\left(m_i{v}_t^i\right)-g\cos {\gamma }_t^i/v_t^i+d_{{\gamma }_t^i}\end{array}\right]$$

(7)

where $p_t^i={\left[\begin{array}{ccc}{x}_t^i& y_t^i& z_t^i\end{array}\right]}^T$ is the position vector of the agent in the inertial coordinate system at moment $t$, $v_t^i$ is the velocity of the agent in tight formation, i.e., the synthetic velocity of airspeed and wake vortex-induced wake velocity, ${\chi }_t^i$ and ${\gamma }_t^i$ are the yaw and pitch angles, respectively, $m_i$ is the mass, $g$ is the gravitational acceleration, $T_t^i$ is the engine thrust, $D_t^i$ is the drag, $L_t^i$ is the lift, ${\mu }_i$ is the bank angle, and $d_{v_t^i}$,$d_{{\chi }_t^i}$,$d_{{\gamma }_t^i}$ is the set sum term of the model uncertainty as well as the wake vortex perturbation.

In order to describe the three-dimensional agent motion model under load, researchers have also proposed an agent motion model [6]:

$$\left[\begin{array}{c}{\dot{x}}_t^i\\ {\dot{y}}_t^i\\ {\dot{z}}_t^i\\ {\dot{v}}_t^i\\ {\dot{\chi }}_t^i\\ {\dot{\gamma }}_t^i\end{array}\right]=\left[\begin{array}{c}{v}_t^i\cos {\gamma }_t^i\cos {\chi }_t^i\\ v_t^i\cos {\gamma }_t^i\sin {\chi }_t^i\\ -v_t^i\sin {\gamma }_t^i\\ g{n}_x^i-g\sin {\gamma }_t^i\\ \frac{g}{v_t^i\cos {\gamma }_t^i}{n}_y^i\\ \frac{-g}{v_t^i}\left(n_z^i+\cos {\gamma }_t^i\right)\end{array}\right]$$

(8)

where $p_t^i={\left[\begin{array}{ccc}{x}_t^i& y_t^i& z_t^i\end{array}\right]}^T$ is the position vector of the agent in the inertial coordinate frame, $v_t^i$ is the velocity. $g$ is the gravitational acceleration. $n^i=\left[\begin{array}{ccc}{n}_x^i& n_y^i& n_z^i\end{array}\right]$ is the load vector in the three directions in the agent’s inertial frame.

In addition to the common models introduced above, there are also intelligent agent motion models for different requirements, such as agent models under wind field perturbation [19,20], intelligent agent motion models for water surfaces [21,22], and intelligent agent models for cosmic space [23,24].

2.4. Other Formation Control Categories

Depending on the application scenarios and requirements of agent formation, the methods of formation control can also be classified into many categories. Therefore, several other classification methods are introduced in this subsection based on the classifications in the previous review article.

Depending on the control content, in [10], the researchers classified formation control into position-based formation control, displacement-based formation control, and distance-based formation control.

Position-based formation control is where the agent takes its own final ideal position in the global frame as a reference and actively controls its own position to reach the ideal position to achieve formation control.

Displacement-based formation control is where the agent in the formation controls the relative displacement of itself and the agents in the neighborhood to reach the ideal position. Unlike the former, the individual does not need to know its absolute position in the inertial coordinate frame, but only needs to know its position relative to the neighboring intelligences.

Distance-based formation control is based on the displacement-based formation control, the directional requirement of the relative position is reduced, and the amount of agent-controlled variable is changed to the distance between the agents.

Formations can be further classified into rigid formation structures as well as flexible formation structures, depending on whether the relative distance between the agents within the formation can vary according to the task [25].

Rigid formation structure is where the reference trajectory of each agent is determined by giving a constant relative linear vector to a single agent, enabling the agents within the cluster to maintain a fixed-distance formation, while keeping track of the ideal trajectory.

Flexible formation structure is where formation control is achieved by determining a curvilinear relative vector of agents relative to the ideal position, ensuring that the agents can change their relative positions as needed while maintaining their distances.

Compared with the above classification methods, this paper classifies and contrasts the discussion in terms of information acquisition methods as well as types, highlighting the impact of the communication link formation or not on formation control, especially on the types of interaction information. In addition, the kind of information determines the formation control strategy, so we believe it is necessary to write this paper and will present and summarize the comparison according to the communication-based formation control method and the visual servo-based formation control method.

Remark 1. 

The references of this paper are all from Web of Science. Some of them are the first literature in which the techniques covered in the paper were proposed and applied, and some of them are the latest or representative research results.

3. Communication-Based Formation Control Methods

Communication-based formation control is more conducive to the implementation of different formation control strategies because it enables mutual communication between the agents in a cluster. Therefore, in this section, the communication-based formation control methods are introduced according to different formation strategies. Among them, the comparison of various strategies is shown in

Table 2. Control strategy comparison.

Control Strategies	Advantages	Disadvantages
Leader–Follower	1. Simple design and implementation, easy to expand the formation 2. Better formation tracking performance 3. Simple communication topology	1. Formation stability is too dependent on the leader 2. No information interaction between the leader and the follower, poor robustness 3. Poor formation stability when there is a communication delay
Virtual Structure	High stability of intelligent agent formation	1. Poor flexibility, poor obstacle avoidance ability 2. Poor robustness against external interference 3. Excessive communication load can cause node failure
Behavior Based	Strong ability to respond to multiple targets and mission requirements in formations	1. Difficult to express the formation behavior by a mathematical model 2. Poor stability 3. Poor robustness in the face of an unknown environment because the formation behavior is loading first
Consensus Based	Enables formation control in limited and varying communication topologies	1. Simple intelligent agent model, only the first-order or second-order linear model is considered 2. Insufficient consideration for the motion form of a single agent, poor robustness
Intelligent Control	1. Less difficult to model 2. Robustness in dealing with location environment	1. Long computation time and high complexity 2. Calculation is a black box, difficulty to describe the control process mathematically and estimate accurately

.

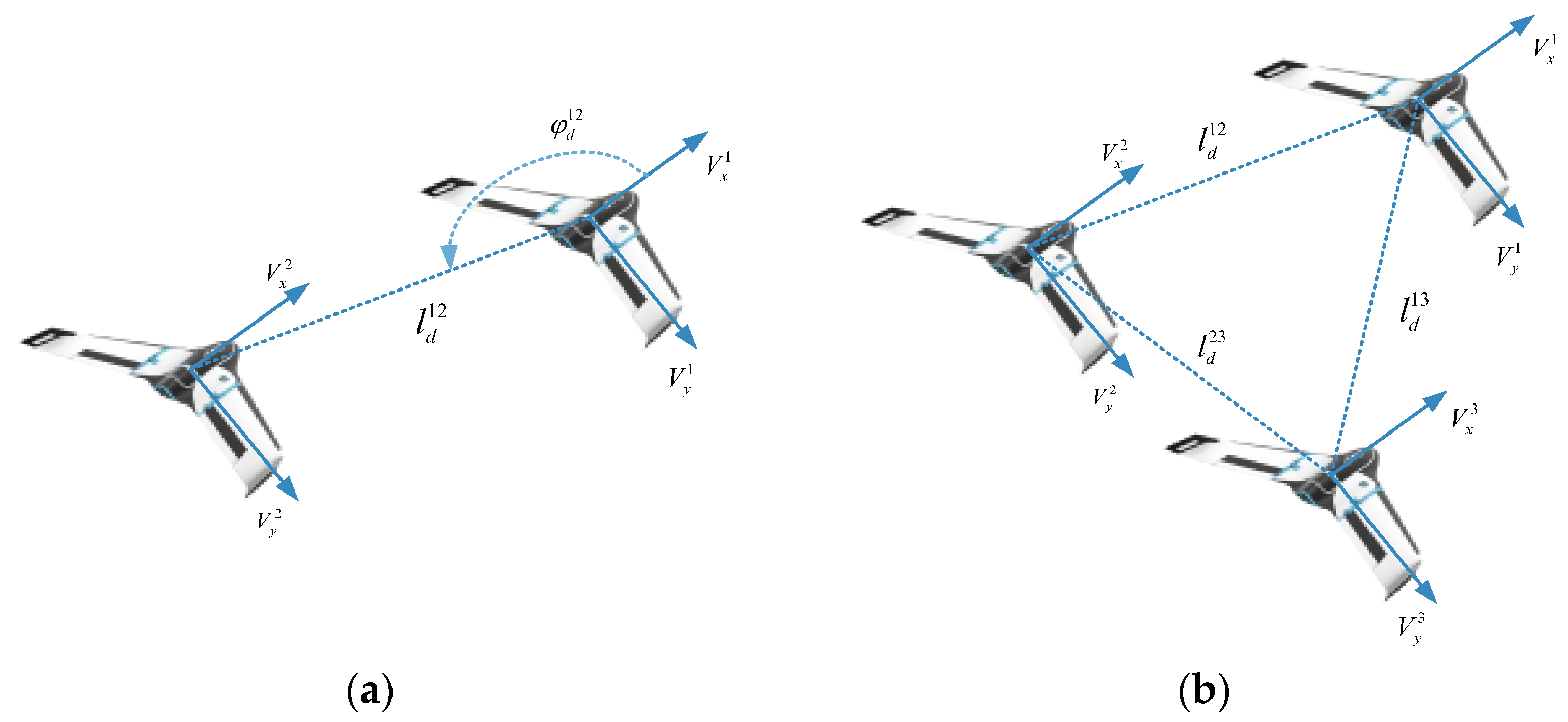
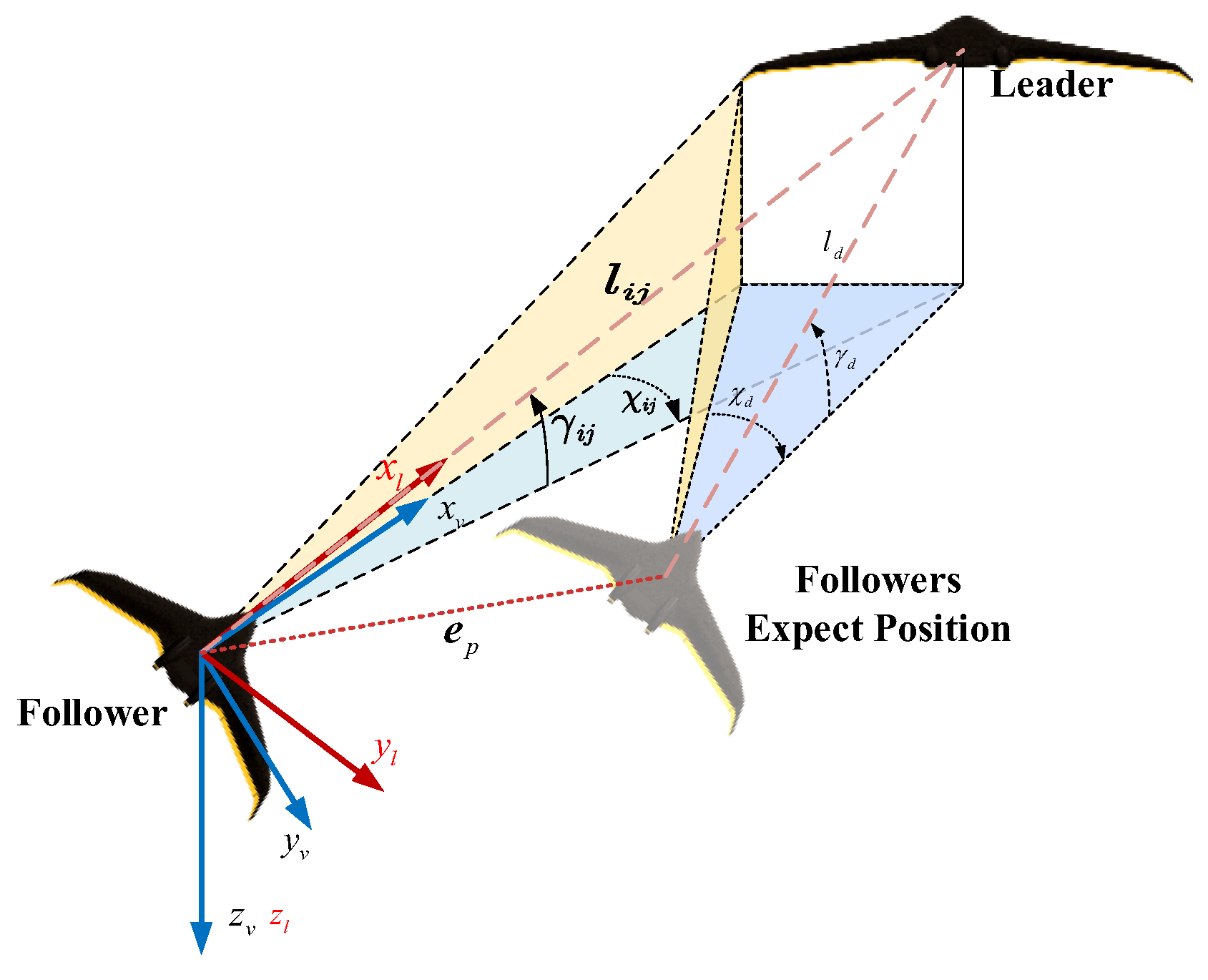
3.1. Leader–Follower

In the Leader-Follower formation control strategy, one or several agents in the formation will be designated as the leaders, or to enhance the robust performance of the formation, instead of designating an actual leader, a virtual leader will possible be implemented in advance in the controller of each intelligent agent. After the system is given the desired trajectory, the controller on the follower agent will follow the designed control law to reach the specified position in the formation, transforming the formation control problem into a trajectory-tracking problem to achieve the overall desired motion. This strategy was first proposed in 1978 by Cruz [26] and used in non-complete restraint robot systems and has since been widely used in intelligent agent formation control. In [27], the Leader-Follower is divided into two main types, $l-\phi$ as well as $l-l$. In the $l-\phi$ type, the controller will control the formation of the desired distance between the follower and the leader as well as the desired angle. In the $l-l$ type the ideal distance between the agents of the formation members is achieved.

In the literature [28], Roldao et al. have designed a formation control for rotor agents using a Lyapunov nonlinear controller, which differs from previous formation control methods by being able to provide multiple alternative paths. In [29], a distributed sliding mode control method is given that uses only its own information as well as the pilot information to achieve formation control, and the speed of the follower does not need to be strictly greater than the pilot. In [30], a formation controller based on a second-order kinematic model with a sliding mode compensator design was proposed for coping with the parameter uncertainty while ensuring an error reduction and improving the system robustness. In [31], Zhao et al. have considered constraints, such as state as well as input constraints, during the intelligent agent formation flight to achieve rotary wing intelligent body formation control using a model predictive control and give simulation experiments for the multi-agent 3D case. In [32], Kim et al. have designed a dynamic compensation control law using the target heading angle and target velocity as feedforward terms.

Researchers [33] have designed different control laws using both strategies of Leader–Follower. The backstepping control method has also been applied to formation control, and in the literature [34], load factors are used instead of rudder angles as multi-intelligent body formation inputs to achieve the formation control, while [35] differentiates the UAV mathematical model into a linear attitude control system as well as a nonlinear position control loop to design the control laws for formation control. In [36], Ghamry et al. have used sliding mode control to achieve stabilization as well as attitude angle adjustment and a linear quadratic regulator to achieve trajectory tracking. In the literature [37], a high-order sliding mode controller is designed for the formation control in the presence of bounded unknown disturbances. In [38], Olfati-Saber uses a fusion of three algorithms to achieve an intelligent agent formation trajectory tracking and obstacle avoidance based on the line of adherence to Reynolds’ law.

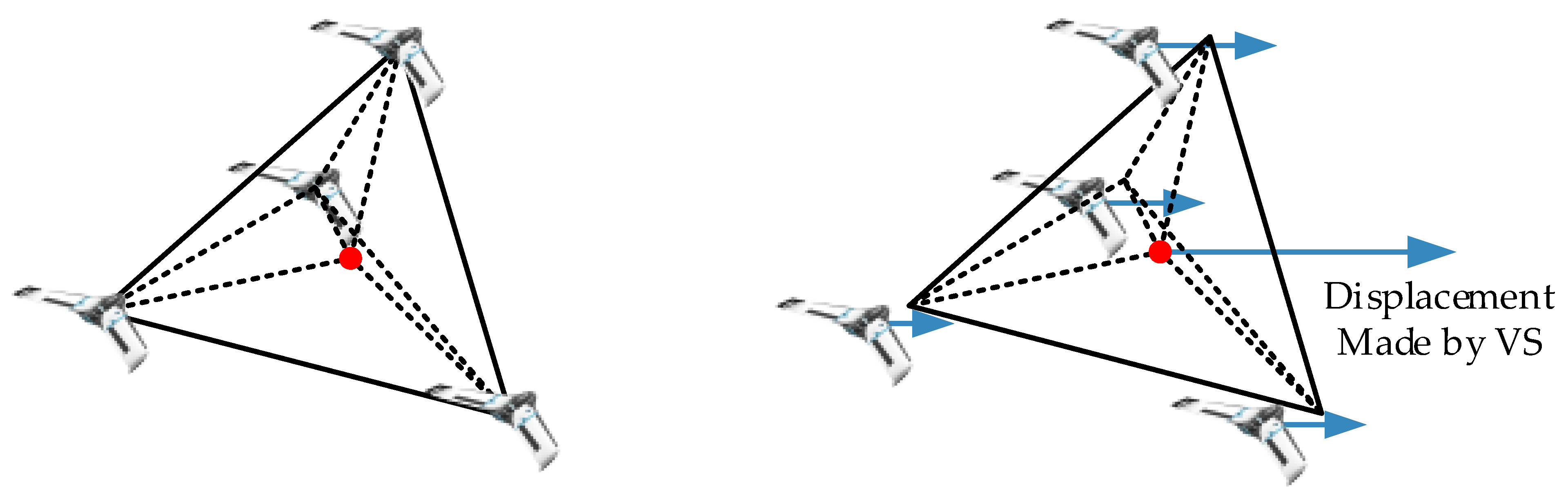
3.2. Virtual Structure

The virtual structure (VS) views the formation as a whole and deploys the desired position for each agent. When the agent reaches the desired position in the structure in the process of achieving the trajectory tracking, it means that formation control is achieved(shown in Figure 4). When the algorithm was first proposed in 1997, Lewis and Tan et al. had already considered the agents as particles in a rigid structure and achieved formation maintenance by the particles maintaining geometry [39,40] and formation and maintenance by the particle movement (as shown in Figure 5).

Virtual structure is sub-divided into a “rigid” virtual structure and “flexible” virtual structure according to whether the agents within the group can achieve a change in a relative position [25]. Rigid structures have better stability, and in order to solve the performance constraints of rigid structures during turns and the degradation of formation performance [41], Moscovitz et al. have proposed the flexible virtual structure formation control method. The virtual structure reference point is defined using constant curve coordinates relative to the formation reference point to optimize the robustness of the formation during turns.

In [42], Barfoot et al. have derived equations to determine the velocity and turn rate of the reference point of a flexible virtual structure based on the relative curvilinear coordinates of the reference point and the formation trajectory. A control law based on the virtual structure and angle design of the formation has been proposed in [43], making it easier for the formation to deal with the time-varying scale and scaling of the structure. Wei Ren et al. have proposed a control law based on neighborhood individual information for the formation-keeping and attitude alignment problem of a spacecraft [44]. Shahbazi has developed a control law in the presence of external disturbances, model uncertainties, sensor noise, and actuation saturation constructing controllers to achieve formation stabilization control under external disturbances, model uncertainty, sensor noise, and actuation saturation [24]. To enable formation switching between fixed and temporary formations, as well as to provide an operational interface to large-scale formation control, a controller that enables a single operator to control 3–5 agents or even larger formations was proposed and validated in [45].

A robust controller is proposed in [46,47] for solving the virtual leader design problem in missions. An improved virtual structure approach for spacecraft formation control is presented in [48]. Askari [49] has integrated feedback into the control structure to improve the stability and robustness of the formation. In [50], researchers used a synchronous position tracking controller for a multi-wing formation flight control in combination with a virtual structure approach to effectively improve the method proposed by Peterson et al. [51] for formation control under wind speed perturbations. To cope with intelligent body formation control with variable communication delays, Feng et al. in [52] first established formation affine rules and implemented the formation control of large-scale intelligent agents in a short time, according to these rules. Decentralized estimators as well as model predictive control methods were proposed by Wang et al. in [53] to achieve a virtual target state estimation as well as formation control under constraints.

3.3. Behavior Based

The behavior-based formation control method is inspired by the behavior of clusters in nature (e.g., flocks of pigeons and schools of fish, etc.). The desired several classes of behaviors are first set for each intelligent agent within the cluster, and the final control law is derived based on the importance weights of each behavior. The possible behaviors include obstacle avoidance, formation reconstruction, formation retention, trajectory tracking, and target search. When the behaviors receive feedback from the intelligent agents through the sensors, the control inputs are generated based on the different weights of the behaviors, and the inputs are transmitted to the agent actuators, and first applied to formation control in [54] (the algorithm flow is shown in Figure 6).

In [55], a position error-based trajectory controller is proposed to achieve the trajectory tracking of agents as well as formation shape keeping. In [52], they have designed agents as spheres with a safe radius to achieve collision avoidance within a cluster, velocity matching, and applying search maneuvers to achieve the formation movement in the desired direction. Sharma et al. [56] have simultaneously studied formation control algorithms in different dimensions, developed several basic clustering laws for intelligent bodies within a cluster, applied cohesion rules to move the formation on a circle of fixed radius, and proposed a decentralized autonomous algorithm to achieve intra-formation collision avoidance. In [57], Kim et al. have derived feedback linearization rules with differential transfer graphs and obtained a weight matrix corresponding to two desired behaviors by solving a cost function for a three-degrees-of-freedom point mass model after considering the coupled dynamics of multiple agents.

Jonathan et al. [58] have designed three control strategies for three cases and implemented hardware-in-the-loop formation control simulations. To achieve formation control with local information as well as minimal communication, a control law based on the sensor translation angle has been proposed in [59] and applied in formation control experiments for large-scale agents. Xu, Zhang et al. have proposed a control law based on a classification search method for large-scale intelligent body formation initialization as well as obstacle avoidance [60]. In [61], Lee and Chwa combined a behavior-based formation control approach to achieve the control and retention of agents in complex environments. In [62], the authors quantify the performance metrics of agents, have designed control laws based on agent performance metrics, and have performed experimental simulations using RT Messenger.

3.4. Consensus Based

Consensus algorithms are an effective approach to address agent formation control. The goal of consensus control is to drive the states of agents in a formation to an identical expectation [63]. Under different linear models, the classical consensus algorithms can be represented in different ways [64]. Under the first-order linear integral model, the consensus protocol can be represented as:

$$u_t^i={\displaystyle \sum _{j\in N}{a}_{ij}\left(x_j-x_i\right)}$$

(9)

When the first-order integral dynamic model is extended to the second-order dynamic model, the system consensus protocol can be formulated as:

$$u_t^i={\displaystyle \sum _{j\in N}{a}_{ij}\left(\left(x_j-x_i\right)+\gamma \left(v_j-v_i\right)\right)}$$

(10)

where $\gamma >0$ is a scaling factor. The exchange of information between agents in consensus algorithm-based formations is achieved through the communication topology.

In [65], the authors have shown that formation consensus control can be achieved in the case of formations in which the communication topology can interact frequently with the system. In [66], researchers have extended the case of first-order models with a constant fixed topology at interconnection to second-order integral models. In [65], scholars imposed a constraint on the weight factor in the information update scheme, but considering that the constraint can be extended to more general cases, researchers in [13] extended the above constraint to directed graphs and explored the minimum requirements for reaching consensus control using a graph theory as well as a matrix theory. In [12], researchers have investigated the problem of achieving an average consensus for topological graphs in a strongly connected and balanced state study to achieve the consensus control problem in the presence of communication delays. Ren and Beard have applied dynamic evolutionary consensus to the formation flight of multiple space-based interferometers [67]. In [68], Slotine and Wang et al. have studied consensus applications using nonlinear contraction theory. Olfati et al. have used second-order dynamical formation-keeping algorithms to achieve a set mass attitude alignment, the consensus control of position deviation, and the cluster obstacle avoidance [69]. However, all the above studies assume that the intelligent body formation implements the algorithm in a unidirectional information exchange topology, while in [70], the authors give the necessary conditions for reaching a formation consensus in the context of a unidirectional information exchange topology.

Zuo and Tie et al. have used Lyapunov functions to design continuous time-invariant consensus protocols for each first-order integral agent in [71] to implement the problem of the finite time control of intelligence in undirected topological networks. Feng et al. have divided the agent formation information into global and local information and designed a class of nonlinear consensus protocols to implement formation control in a finite time [72]. A control law to achieve finite-time consensus control with local information interaction is proposed in [73] and implements the formation control of agents. Researchers in [74,75] implement the formation control of intelligence within a formation with the same time delay. Compared to the previous literature, more improvements were proposed in [76] by Wang et al.; based on [71], Wang et al. extended the topology of information interaction between intelligence from an undirected topology to a directed topology. Compared with [72,73,74,75], Wang et al. further considered formation control under different communication delays.

In addition to the above studies, other studies address consensus algorithms. A consensus controller based on the Lagrangian approach was proposed in [77]. Xiao et al. have used a neural dynamics optimized nonlinear model predictive control to implement a distributed master-slave consensus multi-agent formation system control [78]. In [79], Rezaei designed a decentralized adaptive output consensus protocol to implement—in undirected or equilibrium—heterogeneous linear multi-intelligent systems with unknown parameters. In [80], Qin et al. designed a continuous sliding mode tracking protocol with an adaptive mechanism to implement agent system formation control with perturbations and actuator failures. In [81], the authors use a consensus sliding mode formation control algorithm to cope with the formation in the case of disturbance problems.

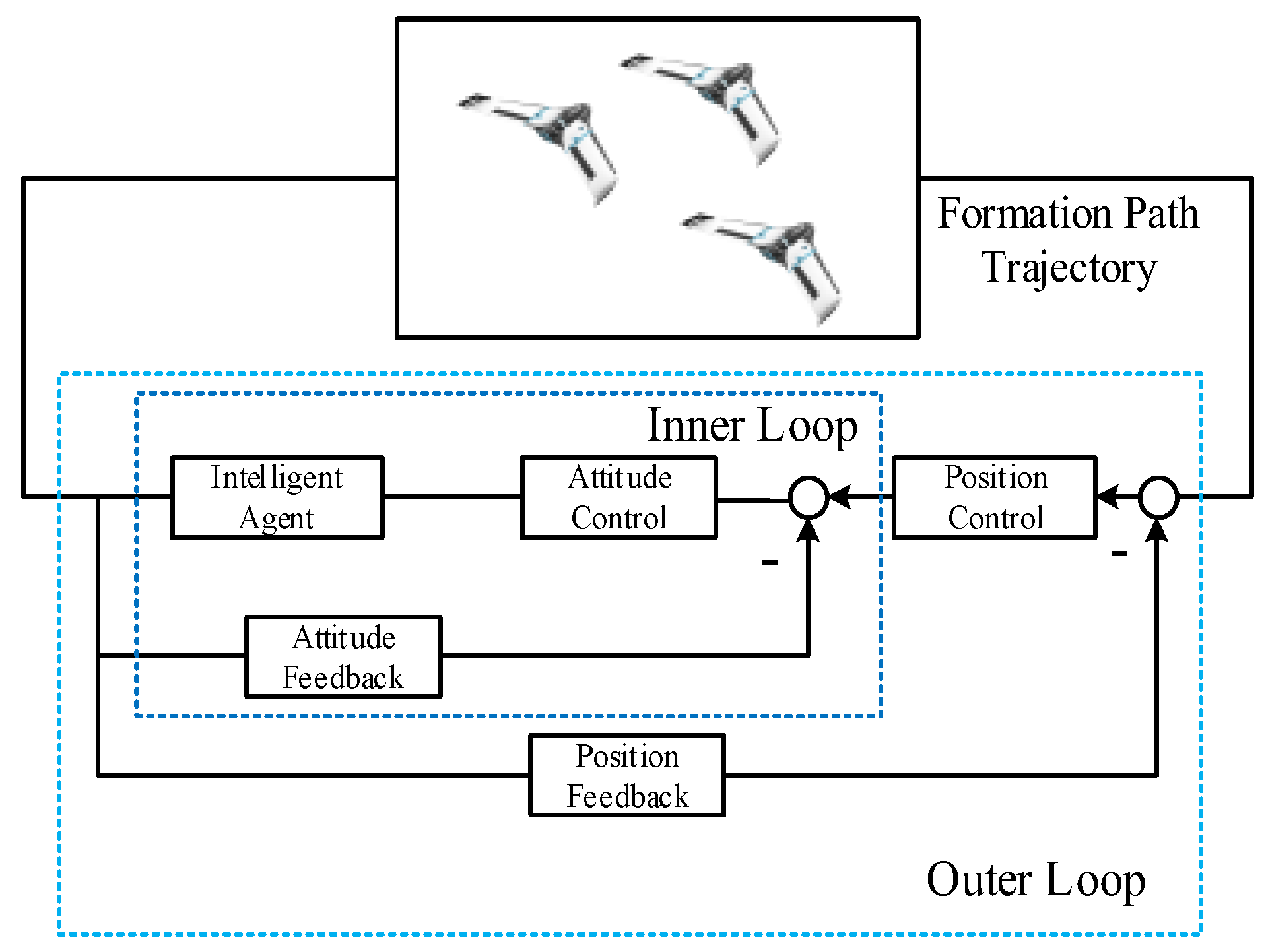
3.5. Intelligent Control

With the development and advancement of computer intelligence algorithms, intelligent control techniques have also become an effective means of solving problems in formation control, especially in formation control with unmodelled dynamics and when there are unmodelled disturbances. Intelligent formation control techniques mainly include fuzzy control theory [82], neural network control algorithms [83] (the basic algorithmic process is shown in Figure 7), adaptive control algorithms [84], model predictive control algorithms based on reinforcement learning [85], and various other intelligent algorithms.

A fuzzy control protocol for the unpredictable disturbance terms in formation flight has been proposed in [82] by Y. Li et al. In [86], Abbsai et al. have used fuzzy control to achieve self-tuning of controller gains and to realize simulation tests on three UAVs in six degrees of freedom conditions. Neural network-based and fuzzy system-based design controllers have been proposed in [87,88,89] and [90,91,92], respectively. Guo et al. have used adaptive neural networks to offset the system uncertainty caused by position nonlinear dynamics and to achieve formation control by designing Lyapunov–Krasovskii functions to compensate for state delays [84]. Wang et al. have used distributed inverse control in [93,94] to achieve the formation control of multiple agents in the presence of input saturation, but the increase in the number of system stages makes the complexity explode. Cui et al. have introduced auxiliary systems to offset the effect of input saturation in the control law design process and reduce the number of scalars to be estimated and the burden of network communication [95].

Although formation control under stable communication links is easier to implement and apply, it is also increasingly difficult to form effective and stable communication links between agents as the intelligent agent formation task area becomes more complex. This has led to the emergence of another visual servo-based formation control method.

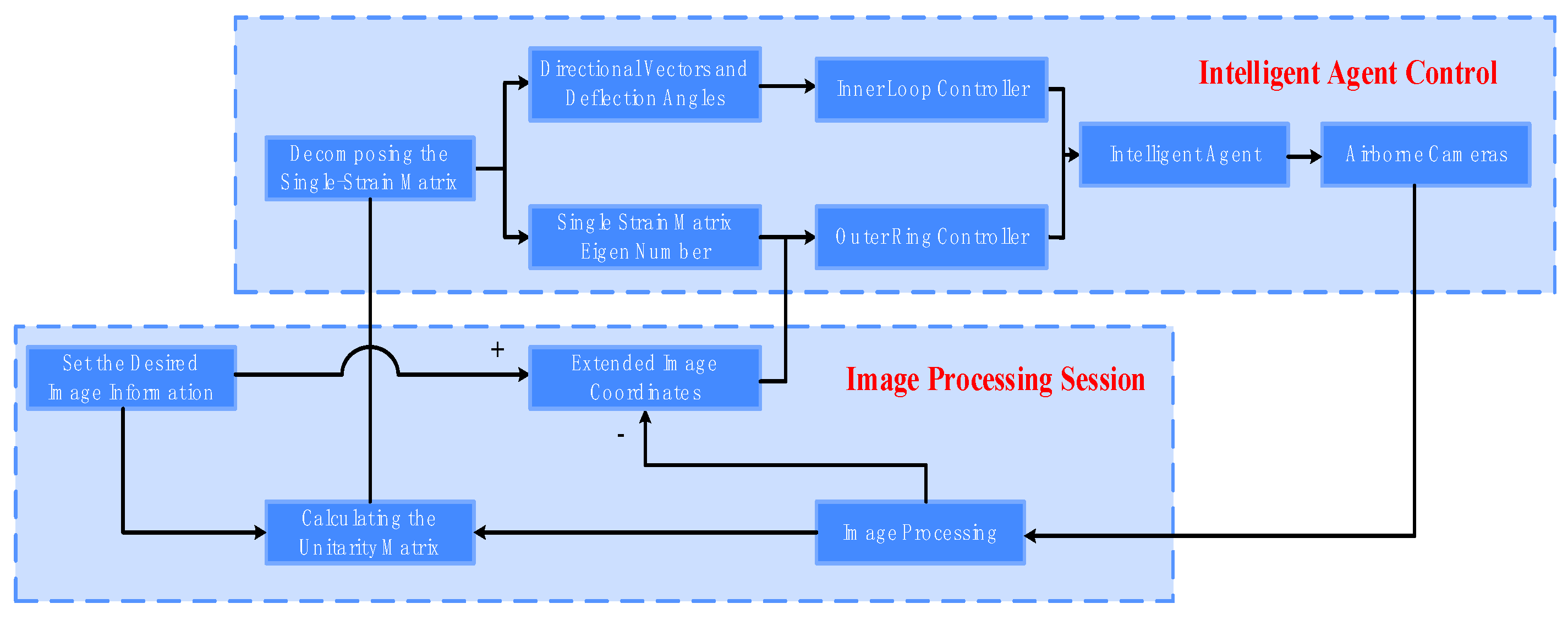
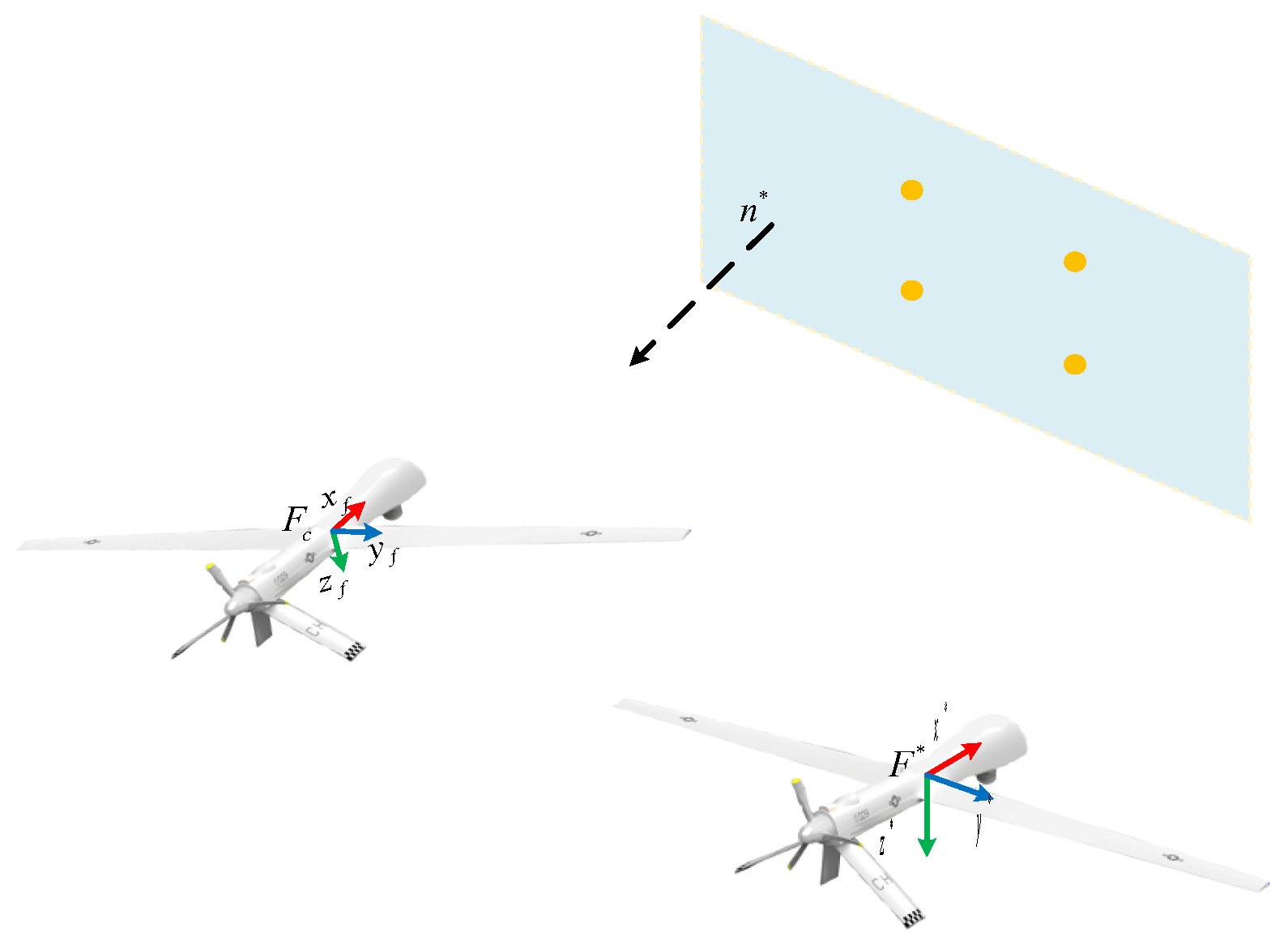
4. Vision-Based Formation Control

With the continuous development of intelligent agent technology and the increasing diversity of tasks performed by formations, formation control methods relying on vision sensors are gradually becoming a hot research topic. Vision sensors have the advantage of stable information transmission and contain a large amount of information compared to communication sensors. The concept of vision control seems to have been first proposed by Hill and Park in order to distinguish their approach from the earlier “blocks world” [96], and was first applied to the control of robotic arms. A good review of the application of vision-based servo control on robotic arms is given in [97].

With the progress of science and technology, it seems that Stella et al. first applied this technology to formation control in 1995 to solve the formation control problem under communication constraints [98]. Vision-based formation control uses vision sensors to detect the current state of the agent as well as the state of the target agent to achieve formation control based on the state error of both, and is a fusion technique for multiple disciplines whose control objectives can be described by the following functions:

$$e_i\left(t\right)=x_i\left(t,a\right)-x_d\left(t\right)$$

(11)

where $x_i\left(t\right)$ is the state vector of the $i$-th intelligent body in the formation, $x_d\left(t\right)$ is the desired state of the intelligent body or the pilot intelligent body state, and $a$ is the relevant modeling parameter. From the above equation, it can be seen that the selection of the agent states and the design of the controller to achieve error minimization are the main tasks. Based on this section, the vision-based formation control algorithm is introduced. The basic control strategy for vision-based formation control is the Leader–Follower mode and, depending on the input airborne camera acquisition state characteristics and the type of controller role, Hutchinson et al. in their paper [99] given the first definition of vision-based control and classified it into position-based visual servo formation control algorithm (PBVS), Image-Based Visual Servo Formation Control algorithm (IBVS), and Hybrid-Based Vision Servo Formation Control (HBVS). The following is a description of the application of the three methods to intelligent body formation control.

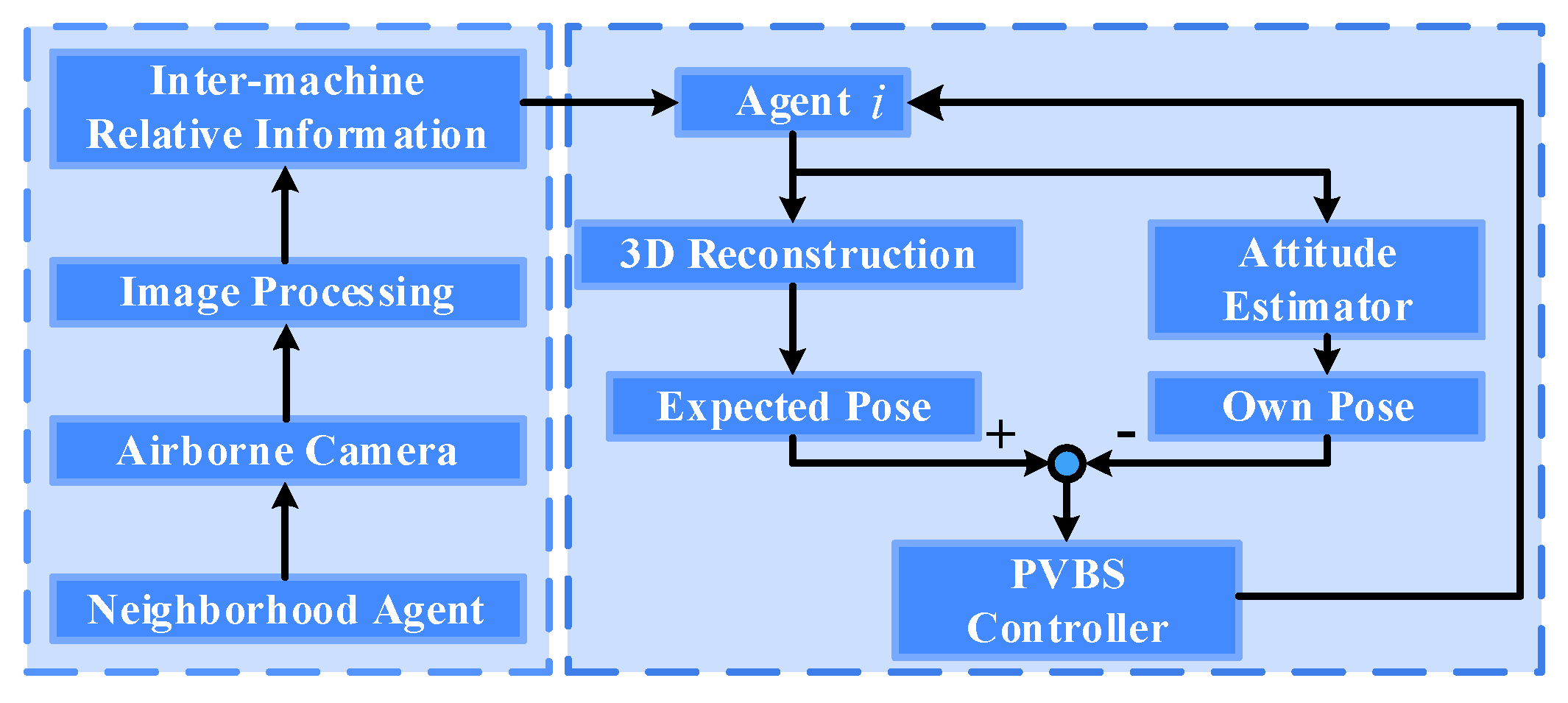
4.1. Position-Based Visual Servoing

For the position-based visual servo (PBVS) formation control algorithm, the control process can be expressed as follows: using the on-board camera to obtain the relative information between the agent and the pilot agent in the neighborhood, reconstructing the pilot agent in three dimensions or two dimensions through the agent model as well as the spatial model, and designing the formation control law based on this to obtain the expected positional attitude of the agent and the positional attitude of the agent itself, whose general control rate can be expressed as follows:

$$u_i={\widehat{u}}_d+f\left(x_i\left(t\right),x_d\left(t\right),{\dot{\mathit{x}}}_i\left(t,a\right),{\dot{\mathit{x}}}_d\left(t\right)\right)+g\left(x_i\left(t\right)\right)$$

(12)

where ${\widehat{u}}_d$ is the estimated desired input, $x_d\left(t\right)$ is the desired distance, and ${\dot{\mathit{x}}}_d\left(t\right)$ is the desired velocity. The control flow and control results of the intelligent body formation achieved by the control rate involved in the above equation are shown in Figure 8 and Figure 9.

The PBVS formation algorithm is characterized by Cartesian spatial trajectory optimality in achieving control because of the use of the visual sensor as a 3D positional information sensor. Because the accuracy of the PBVS controller depends on its own state estimation and on the 3D reconstruction for the desired state, the PBVS algorithm is highly dependent on the accuracy of modeling, 3D model reconstruction, the measurement error of the agent’s positional sensor, and the accuracy of the on-board camera parameters. In 1999, it seemed that Kim et al. [100] had already, for the first time in order to apply nano-robots to a robot soccer tournament, used PBVS for robot formation control. In [101], Spletzer et al. then applied PBVS to formation control and cooperative localization for target tracking and control. A controller innovation based on tracking curve theory and velocity was proposed in [102] for the control of incomplete agents under communication constraints. It seems to be the first time that Moshtagh et al. implemented formation control in the 3D case based on visual information [103]. The approach of classifying followers to achieve tracking was proposed in [104] to implement a triangular formation model for intelligent agents. The concept of PBVS was first presented precisely in [105] and was applied to formation control algorithms.

For a more accurate estimation of the neighborhood agent states, Kalman filtering is used for state estimation. Intelligent body formation control was implemented using only monocular cameras [106]. Ramachandra et al. have proposed in [107] an acceleration guidance law in the absence of large turning angle maneuvers for UAV formations, and to compensate for the errors introduced by modeling using adaptive neural networks to enhance the feedback controller. In [108], the researchers provide a formation control method based on visual sensor information in close proximity. While Johnson et al. in [109] used an adaptive design to enhance the estimation of the Kalman filter for system immunity. Sattigeri et al. in [110] have proposed to estimate the relative distance and direction with an airborne camera and designed an adaptive acceleration control law for formation control. To improve the applicability of the algorithm, Lin et al. in [14] have designed control laws based on the inverse height of the camera’s optical center and a single feature point on the guide body to achieve formation control under visibility constraints.

In recent years, adaptive and intelligent control has been used in PBVS formation control algorithms to improve the robustness of formation systems against uncertainties such as constraints, modeling errors, and perturbations. In [111], Liu et al. have designed adaptive robust control algorithms to achieve distributed control of quadrotor formations. Mostafa et al. have used perspective cameras to consider the image and physical space constraints while optimizing the formation flight trajectory using the prediction range [112]. A Nussbaum gain adaptive controller and a static nonlinear gain controller were proposed by Ti Miao et al. [113] for the control of uncertain agent systems. To reduce the effect of noise as well as discontinuous information when estimating the pilot, particle filtering was used for the estimation of attitude, and a multi-objective control law was proposed in [114]. In addition, Guan et al. have proposed a particle swarm optimization neural network-based control algorithm to improve the accuracy of formation control [115].

The current research based on PBVS to achieve formation control started early and the research has achieved certain research results, but disadvantages of requiring a high modeling accuracy and being sensitive to noise still exist. Therefore, some scholars have shifted their attention to the IBVS algorithm for improving the shortcomings in the PBVS algorithm and enhancing the formation control performance.

4.2. Image-Based Visual Servoing (IBVS)

In order to improve the deficiencies in PBVS, IBVS has been used for formation control in recent years. Compared with the PBVS algorithm, IBVS has a simpler structure and can directly use the image error to achieve formation control. The basic flow of the algorithm and the control objectives are shown in Figure 10 and Figure 11.

The basic controller of the IBVS control algorithm can be expressed as follows:

$$u_i={\widehat{u}}_d+J_{image}f\left(\left(m_i,n_i\right)-\left(m_d,n_d\right)\right)+g\left(e_i\right)$$

(13)

where ${\widehat{u}}_d$ is the pilot estimation input and $J_{image}$ is the Image Jacobi Matrix (IJM). Since the image captured in the algorithm is two-dimensional information, it enables the utilization of point features in relation to the change in the agent as it moves. Therefore, in the initial formation control, the method of using point feature extraction to achieve formation control became the researchers’ first choice. At the same time, researchers usually use more than four feature points as target features considering the computational complexity, as well as the possible image Jacobi matrix singularity and system stability in practical applications [116]. A method to achieve target tracking by point feature extraction was proposed by Mondragon et al. in [117], and the verification of the algorithm was achieved using intelligent agent formations. In practical applications, it is found that it is difficult to extract point features. In contrast, it is easier to extract the proxy line features. In addition, when the image is not clear, the line features have better robustness, and it can better represent the polyhedral properties of the agent. It seems that Malis was the first in [118] to consider already extracting line features to achieve formation control when the camera parameters are unknown. Wang et al. [119] have considered agent dynamics to achieve visual control and to achieve localization of static targets. The method where line features are extracted and achieve formation control was proposed and applied in [106]. To further extend the usefulness of IBVS and improve the robustness, scholars proposed to extract more irregular feature moments from images to achieve visual servo control [120].

The initial application of IBVS to formation control was mostly the problem of the formation for localization of static targets or path tracking. It seems that in [121], Aveek et al. have implemented formation control using panoramic cameras. Dani et al. have explicitly used the IBVS algorithm in [122] to implement the formation control problem under the Leader–Follower strategy. In Min et al.’s paper [123], a formation control algorithm for multiple machines in the presence of a restricted field of view has been proposed and the algorithm information acquisition has been implemented with only monocular cameras and the effectiveness of the algorithm has been verified on a solid robot. Franchi et al., on the other hand, have implemented an innovative nonlinear control design to achieve formation control [124]. In [125], Stacey et al. in [121,124] have applied the principles of port Hamiltonian theory and bond graph modeling to the formation control problem to prove the asymptotic stability of the system. Later, in [126], the authors improved their previous architecture proposed in [121] by designing observers that enable formation control for the case where orientation measurements are available but the associated distance measurements are not. In addition, to implement the IBVS-based formation control algorithm in the distance-free state, Chen et al. in [127] have designed a controller using an adaptive update law to achieve formation control while ensuring the stable observation of feature points.

In recent years, to improve the applicability of the IBVS algorithm, the case of unmeasurable parameters in the algorithm has received increasing attention from scholars. For formation control in the case of an unpredictable navigator speed and an uncalibrated airborne camera, Bastourous et al. in [128] have proposed a predictive compensation method to achieve formation control. Felicetti et al. in [129], to achieve task objectives such as formation acquisition, formation reorganization, and formation retention with optimal control, have designed an optimal control framework based on the minimization of driving forces. To reduce the impact of the depth of feature point information on the controller design, Miao et al. have [130] designed adaptive controllers based on the Nussbaum gain to handle unknown control systems. Similarly, to reduce the control error due to uncertainty, Hu et al. in [131] have introduced a coordination term to reduce the coordination error and added adaptive techniques to improve the algorithm robustness. However, when designing control algorithms based on IBVS, there are still design flaws such as the singularity of the IJM is difficult to circumvent, only local convergence is guaranteed, there are local minima and spatial trajectory problems, and the hybrid vision servoing formation control algorithm can prevent the above problems very well.

4.3. Hybrid Vision-Based Servoing

To solve the problems of PBVS being highly dependent on camera calibration and accuracy for modeling, as well as high IBVS requirements for the initial position and singular values of the image Jacobi matrix, Malis et al. in [131] have proposed a vision-based control algorithm using both partial 3D information and 2D image information, with a core idea to transform the Euclidean single-response matrix in the classical HBVS algorithm into a projective single-response matrix that can be obtained by using only the image information and achieving stable control by establishing an adaptive control law. If one wants to compare the use of the three methods under different tasks, one can refer to [132], where Gans et al. first proposed evaluation criteria for the algorithms PBVS, IBVS, and HBVS and evaluated the algorithm performance under different situations. The basic formulation can be summarized as follows: if the camera intrinsic matrix $K$ is known, the Euclidean single-response matrix $H$ at the core of the algorithm can be calculated as:

$$H=K^{-1}GK$$

(14)

To obtain the scaled Euclidean position and the rotation of the camera, the single-responsibility matrix $H$ can be decomposed as:

$$H=R+t{n}^{*T}$$

(15)

as shown in [132]. The basic flow of the algorithm and the control objectives are shown in Figure 12 and Figure 13.

In the following, different expressions of HBVS and classical applications are first described. Currently, classical expressions as well as quaternion expressions are generally used to achieve the description of the error for the position error and attitude error during HBVS control. It seems that Chen et al. in [133] were the first to design adaptive controllers to achieve an adaptive estimation in the absence of depth information as well as in the absence of camera parameters. Fang et al. have used a hybrid position controller to achieve an error convergence based on classical expressions [134]. In [135,136], Hu et al. obtained estimates of the rotation matrix directly with the help of image features in the infinity plane and used quaternion descriptions and extended image coordinates to achieve a description of the pose and position errors.

To combine the advantages of both PBVS and IBVS algorithms, Fang et al. in [137] designed a time-varying controller, the first application of HBVS to the stabilization control of agent. Zhang et al. [137,138] have defined a new hybrid error vector and used a smooth time-varying feedback controller to handle the incomplete constraint to achieve global stability of closed-loop systems in the absence of depth information. In [139], Li et al. have defined error vectors containing image signals and rotation angles, and achieved error convergence by introducing auxiliary variables and parameter update laws. For the formation control of a large number of agents, Lopez et al. [140] have proposed a novel framework and proposed control laws to drive the agent to the desired position by imposing stiffness constraints.

At present, there are few applications of intelligent agent formation using HBVS, and only part of the application examples are given in this paper as an introduction. When the algorithm is further applied in formation control, we will conduct further investigation and give a related report. Meanwhile, the incomplete statistics for the advantages and disadvantages of the above three visual servo applications are shown in

Table 3. Control strategy comparison.

Vision-Based Servo Strategy	Advantages	Disadvantages
PBVS	Optimal with Cartesian space trajectory	1. High dependence on the calibration of the model, the accuracy of the 3D model 2. when reconstructed. 3. Slow calculation speed during 3D reconstruction. 4. Dependence on the accuracy of intelligent agent positional information and camera parameters. 5. Loss of feature points can lead to controller failure.
IBVS	1. Simpler structure 2. Higher robustness to calibration errors 3. No longer dependent on the system parameters of the camera or robot 4. The possibility of using multiple features. 5. Wider range of application	1. The singularities of the IJM are difficult to circumvent. 2. Only local convergence is guaranteed. 3. The existence of local minima. 4. The possibility of spatial trajectory problems. 5. Requires a priori information at the target location. 6. Giving up the control of Cartesian velocity. 7. Difficult to apply in complex environments.
HBVS	1. Higher robustness to calibration errors. 2. Absence of the case where the Jacobi matrix is singular. 3. A wider range of applications.	Some reliance on offline calibration

.

5. Discussion

In this paper, the existing research results are classified into two categories, communication link-based formation control and visual servo-based formation control, concerning whether the existing agents can form effective communication links, where the references involved in each type of method are shown in

Table 4. Control strategy corresponding references.

	Control Strategies	References
Communication-link based	Leader–Follower	[26,27,28,29,30,31,32,33,34,35,36,37,38]
	Virtual Structure	[24,25,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53]
	Behavior Based	[54,55,56,57,58,59,60,61,62]
	Consensus Based	[12,13,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81]
	Intelligent Control	[82,83,84,85,86,87,88,89,90,91,92,93,94,95]
Vision-based servo	PBVS	[14,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115]
	IBVS	[106,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130]
	HBVS	[131,132,133,134,135,136,137,138,139,140,141,142]

. Some research proposals for the above methods are presented next as well.

(1)

Fixed-time formation control. In the current types of formation control algorithms, most of them are based on achieving the formation control within an infinite time. Considering the time limitation of some tasks, the formation control method in fixed time should be given by considering the task time limit when designing the formation controller, especially the formation control for a fixed time under arbitrary initial conditions. In addition, to achieve a fixed-time formation control, the state information of the intelligent agent has a great influence on the control effect, so according to the access to the state information of the agent, this can also be divided into fixed-time formation control under global information and fixed-time formation control under local state information.

(2)

Formation control under noise and other perturbations. When the formation control algorithm is applied, the system perturbation caused by noise cannot be avoided. Specifically, whether the noise is bounded or not can be divided into bounded noise (such as sensor measurement noise, wind speed, calibration error of the airborne camera, etc.) and unbounded noise (such as unknown obstacles in the formation movement process). Therefore, in the subsequent research, more attention should be paid to the formation control under the disturbance situation. The research directions that can be considered are, first, to improve the accuracy of the modeling and the accuracy of the formation control model, which can effectively improve the control effect; second, to design an adaptive control for different bounded noises; and third, the design of the filter, so that the noise data can be applied to the system as ideal data after passing through the filter.

(3)

Scalability of intelligent agent formations. The formations need to be readily scalable or scalable to fit the mission and environment, for example:

(a)

Reconfiguration and decomposition of multi-intelligence formations, using the reconfiguration of formation agents to realize and maintain formations of various types and in different initial states, especially the withdrawal of agents in the formation when they are damaged and in the replenishment of new agents. At the same time, the formation decomposition can realize the reduction in its size in the mission area and the obstacle avoidance and flight in the narrow area.

(b)

Control of heterogeneous agent clusters. Take air intelligent agent formation control as an example, due to the different agent performance and initial state, the control of heterogeneous formation control can be divided into air–air heterogeneous speed intelligent agent formation control, air–ground, or air–sea heterogeneous agent control, etc.

(4)

Formation control under state information transfer constraints. Subject to the performance constraints of various types of sensors, the way of transferring the state information of intelligent agents is often restricted in the actual formation control, which requires us to realize the formation control problem under the state information transfer constraint. The possible research directions are:

(a)

Realizing a bidirectional state information transfer between the leader and the follower. Currently, only consensus-based formation control methods are designed with information interaction channels between the leader and the follower according to the communication topology. However, in other methods, the information state can only be transferred from the leader agent to the follower agent in one direction regardless of the existence of communication links, so it is necessary to achieve a bidirectionality of state information transfer between the leader agent and the follower agent.

(b)

Formation control under sensor constraint or data loss. In the actual formation control process, the sensors receive the production process and technical limitations, there are inevitably detection angle distance and signal limitations (such as GPS signal loss), so it is challenging to achieve the formation control under sensor constraints.

(5)

Intelligent control technology to achieve formation control. In recent years, with the continuous development of artificial intelligence, its application in various fields has gradually increased, and intelligent control can effectively complement the modeling uncertainty as well as achieve the impact of various types of disturbances not modeled to the formation control. However, in practice, there are relatively few methods to achieve formation control with intelligent control techniques.

(6)

Multi-target formation control. Although there are many types of tasks that intelligent agents can perform, there are few control methods for an intelligent agent formation to perform multiple tasks at the same time, and it is challenging to add formation control algorithms to cope with multi-task situations appropriately in subsequent research.

6. Conclusions

In this paper, we divide the existing research results into communication-based formation control methods and visual servo-based formation control methods according to the presence or absence of a stable communication link, and analyze them in comparison. To the best of our knowledge, this is not available in previous research. We summarize the agent model in the context of the literature, discuss the basic formulation of the problem, and compare the advantages and disadvantages of various types of control methods. In the discussion, we provide concluding remarks and discuss the current limitations and challenges. This will inform researchers in their choice of methods.

However, this survey is far from an exhaustive literature review, and also this paper has limitations. Most of summaries of agent models in this paper apply only to ideal environments, but there are fewer descriptions of models in engineering applications. There are fewer presentations on the environment of agent applications, which will be the next step of our investigation. Although we hope that this paper has provided a useful overview of intelligent agent formation control, many important results may have been missed.