Adaptive Fusion Sampling Strategy Combining Geotechnical and Geophysical Data for Evaluating Two-Dimensional Soil Liquefaction Potential and Reconsolidation Settlement
Abstract
:1. Introduction
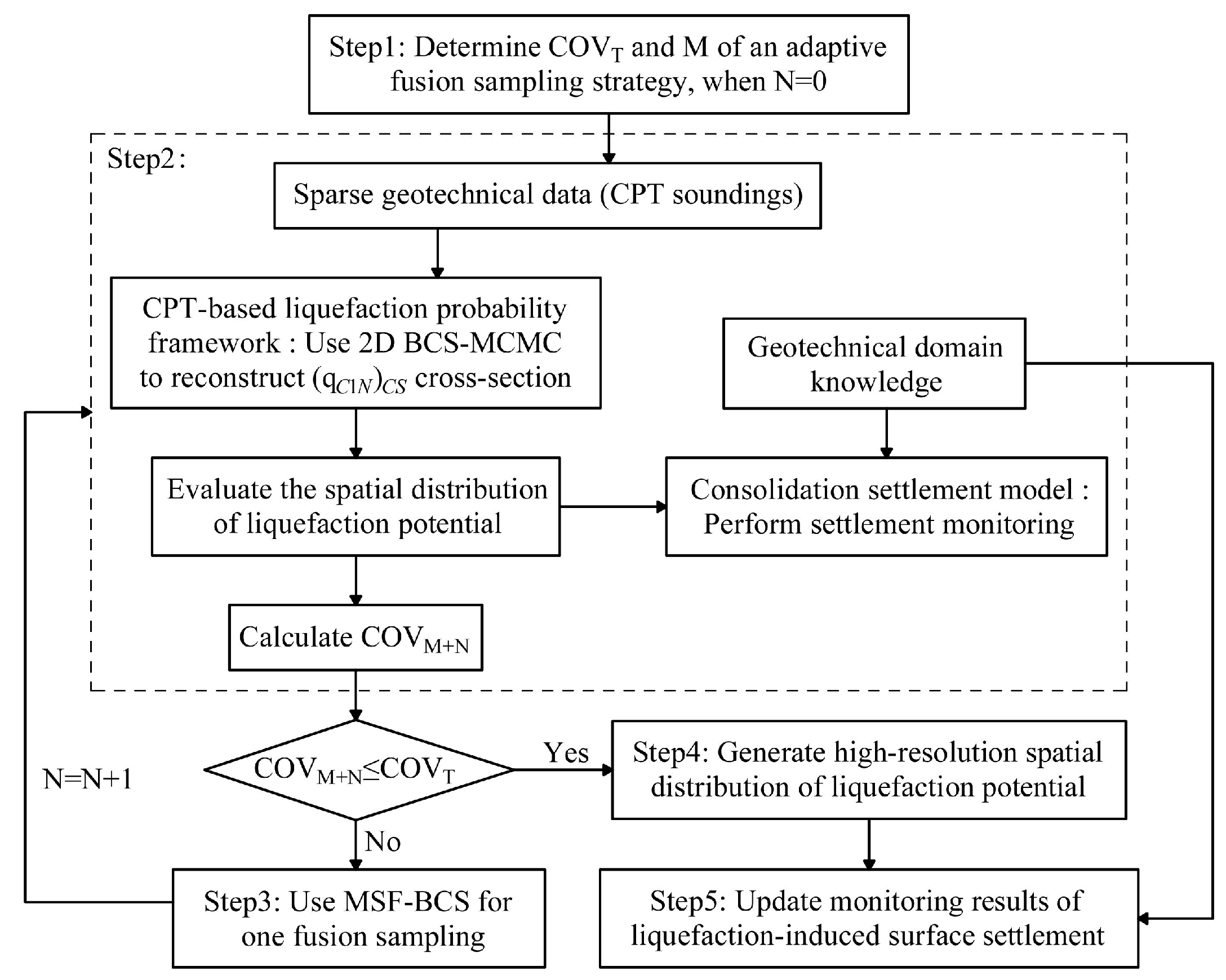
2. Framework of Adaptive Fusion Sampling Strategy
3. CPT-Based Simplified Liquefaction Procedure and Consolidation Settlement Model
3.1. CPT-Based Liquefaction Probability Assessment Framework
3.2. Assessment of Liquefaction-Induced Site Settlement
4. 2D Bayesian Compressive Sampling (2D BCS)
5. Multi-Source Fusion Bayesian Compressed Sampling (MSF-BCS)
5.1. Multi-Source Bayesian Compressive Sampling (MS-BCS)
5.2. Determination of the Optimal Location for Fusion Sampling
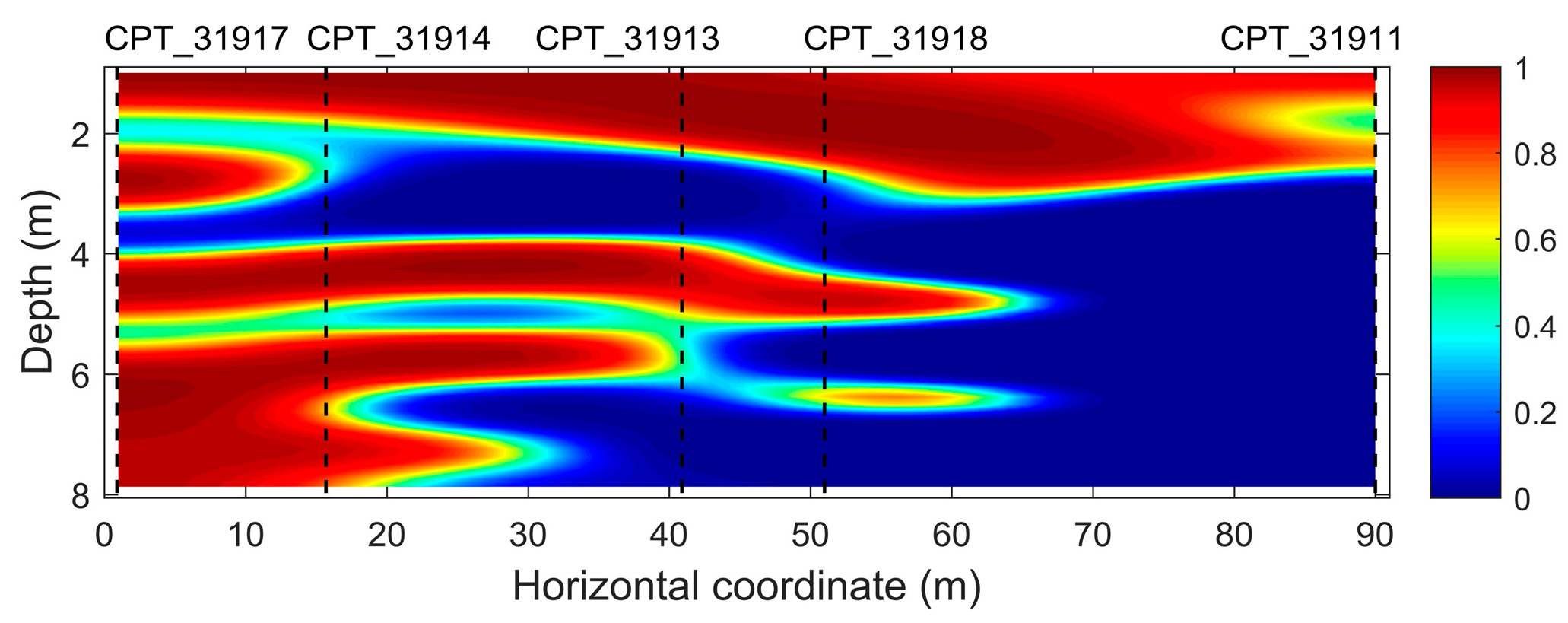
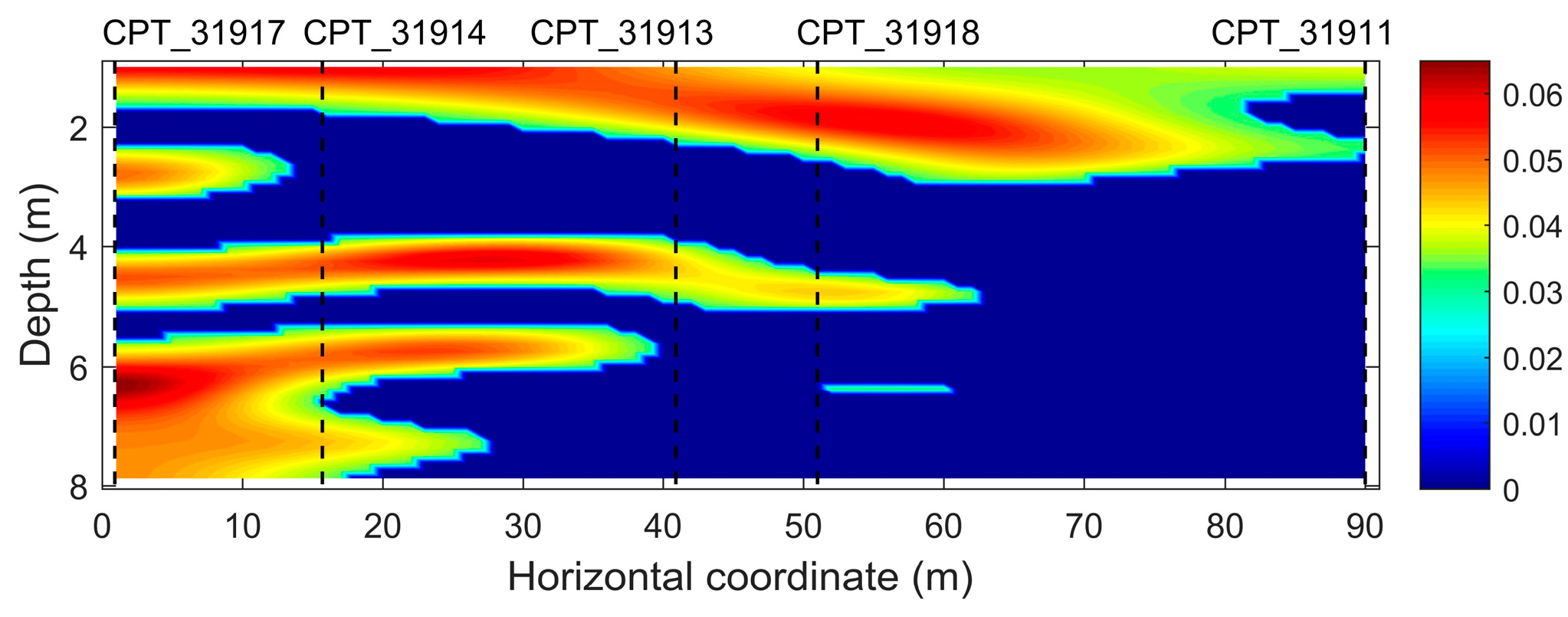
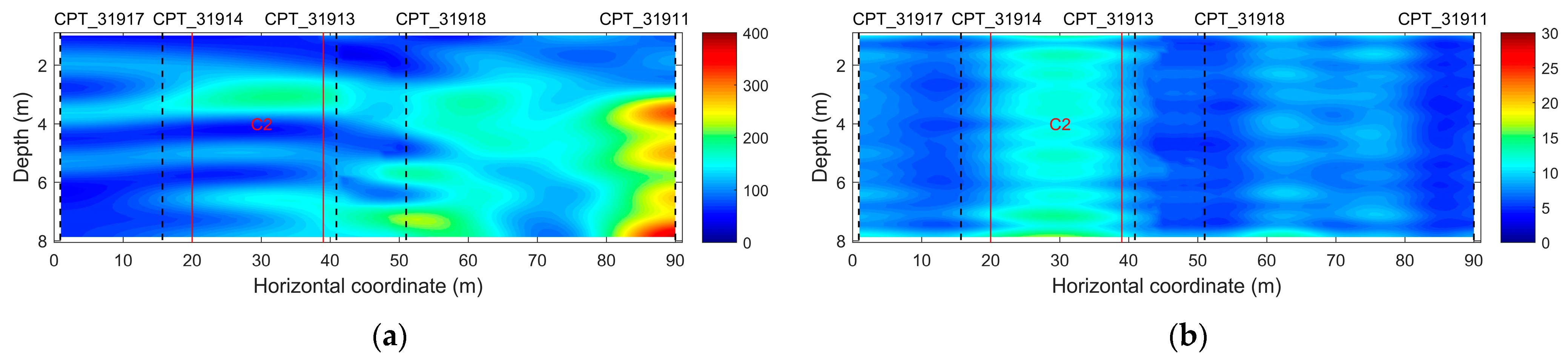
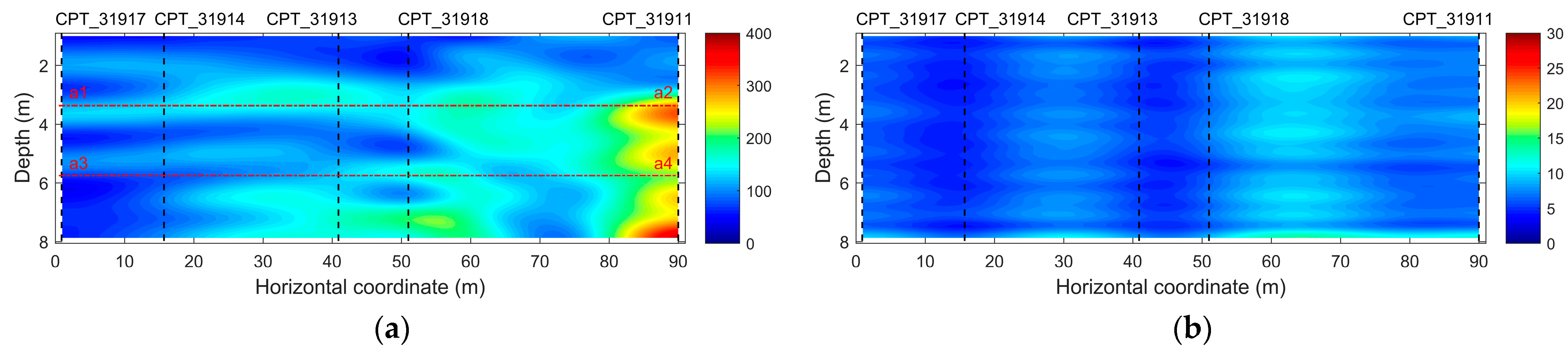
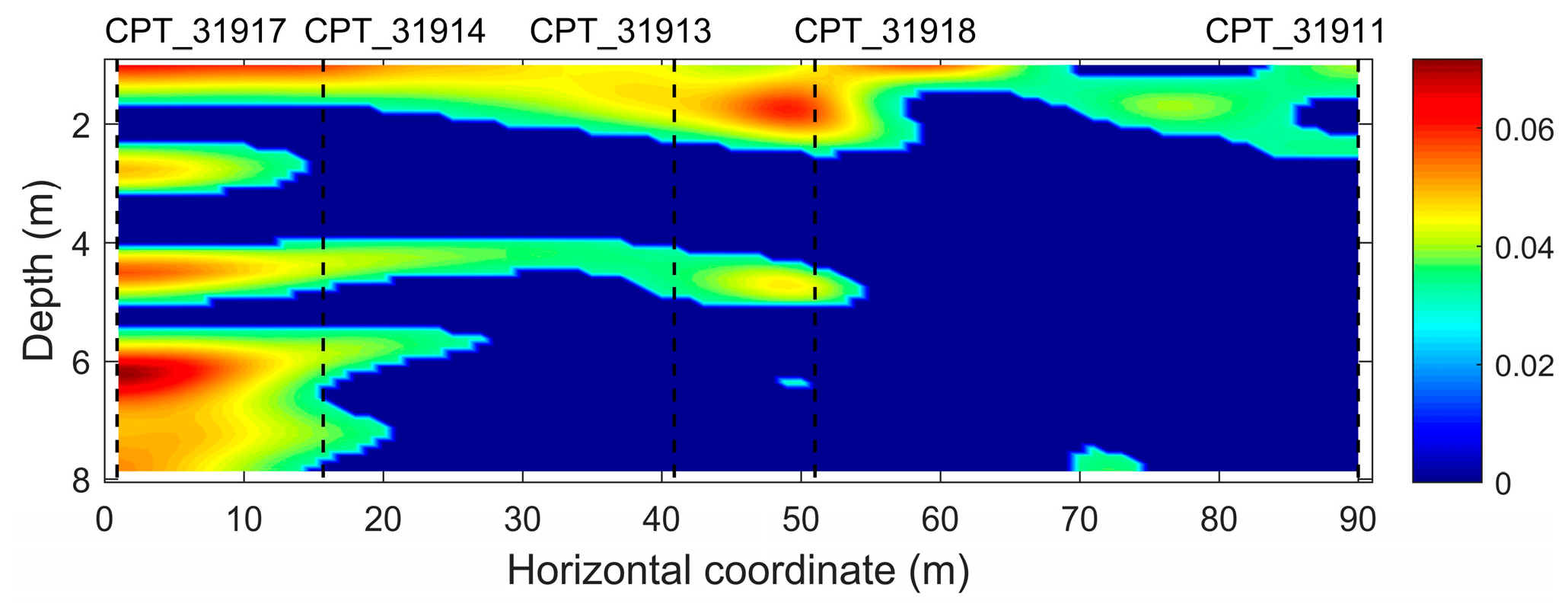
6. Real Data Example
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation
| CPT | cone penetration test |
| 2D BCS | two-dimensional Bayesian Compressive Sampling |
| target reliability level | |
| number of CPT soundings | |
| number of fusion samples | |
| cone penetration resistance | |
| equivalent cone penetration resistance in clean sand | |
| sleeve friction | |
| reliability level | |
| sample data | |
| cross-section | |
| cross-section | |
| information gain from fusion sampling | |
| cyclic resistance ratio | |
| cyclic stress ratio | |
| factor of safety | |
| correction factor | |
| normalized cone penetration resistance | |
| soil behavior type index | |
| total vertical stress | |
| effective vertical stress | |
| peak horizontal acceleration at the surface | |
| acceleration of gravity | |
| overburden correction factor | |
| magnitude scaling factor | |
| stress reduction coefficient | |
| soil depth | |
| probability of liquefaction | |
| standard normal cumulative distribution function | |
| liquefaction-induced surface settlement | |
| volume strain | |
| maximum of interest z | |
| maximum cyclic shear strain | |
| relative density of soil | |
| limiting shear strain constraint | |
| matrix represents the 2D data to be characterized | |
| an CPT soundings | |
| ) 2D basis function | |
| -th 2D basis function | |
| an matrix represents a 1D orthonormal basis matrix | |
| an matrix represents a 1D orthonormal basis matrix | |
| measurement matrix specific to this study | |
| common hyperparameter | |
| data to be characterized | |
| data to be characterized | |
| shear wave velocity data obtained by MASW | |
| , respectively | |
| approximation of | |
| a vector represents elements of in a vector format, | |
| likelihood function | |
| prior PDF | |
| approximation of | |
| Kronecker product in linear algebra | |
| an matrix with diagonal elements | |
| reciprocal of unknown variance of the residuals | |
| estimated covariance | |
| a modified Bessel function of the second type with parameter | |
| union of the non-trivial 2D basis functions | |
| estimated covariance | |
| estimated covariance | |
References
- Wang, Y.; Fu, C.; Huang, K. Probabilistic Assessment of Liquefiable Soil Thickness Considering Spatial Variability and Model and Parameter Uncertainties. Géotechnique 2017, 67, 228–241. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, C.; Juang, C.H. Probabilistic and Spatial Assessment of Liquefaction-Induced Settlements through Multiscale Random Field Models. Eng. Geol. 2016, 211, 135–149. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M. Simplified Procedure for Evaluating Soil Liquefaction Potential. J. Soil Mech. Found. Div. 1971, 97, 1249–1273. [Google Scholar] [CrossRef]
- Schmidt, J.; Moss, R. Bayesian Hierarchical and Measurement Uncertainty Model Building for Liquefaction Triggering Assessment. Comput. Geotech. 2021, 132, 103963. [Google Scholar] [CrossRef]
- Boulanger, R.W.; Idriss, I.M. CPT-Based Liquefaction Triggering Procedure. J. Geotech. Geoenviron. Eng. 2016, 142, 04015065. [Google Scholar] [CrossRef]
- Juang, C.H.; Ching, J.; Wang, L.; Khoshnevisan, S.; Ku, C.-S. Simplified Procedure for Estimation of Liquefaction-Induced Settlement and Site-Specific Probabilistic Settlement Exceedance Curve Using Cone Penetration Test (CPT). Can. Geotech. J. 2013, 50, 1055–1066. [Google Scholar] [CrossRef]
- Wang, Y.; Au, S.-K.; Cao, Z. Bayesian Approach for Probabilistic Characterization of Sand Friction Angles. Eng. Geol. 2010, 114, 354–363. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, Y. Bayesian Model Comparison and Selection of Spatial Correlation Functions for Soil Parameters. Struct. Saf. 2014, 49, 10–17. [Google Scholar] [CrossRef]
- Juang, C.H.; Zhang, J.; Shen, M.; Hu, J. Probabilistic Methods for Unified Treatment of Geotechnical and Geological Uncertainties in a Geotechnical Analysis. Eng. Geol. 2019, 249, 148–161. [Google Scholar] [CrossRef]
- Yang, H.; Liu, Z.; Li, Y.; Wei, H.; Huang, N. CatBoost–Bayesian Hybrid Model Adaptively Coupled with Modified Theoretical Equations for Estimating the Undrained Shear Strength of Clay. Appl. Sci. 2023, 13, 5418. [Google Scholar] [CrossRef]
- Zhao, Z.; Duan, W.; Cai, G.; Wu, M.; Liu, S. CPT-Based Fully Probabilistic Seismic Liquefaction Potential Assessment to Reduce Uncertainty: Integrating XGBoost Algorithm with Bayesian Theorem. Comput. Geotech. 2022, 149, 104868. [Google Scholar] [CrossRef]
- Guan, Z.; Wang, Y.; Stuedlein, A.W. Efficient Three-Dimensional Soil Liquefaction Potential and Reconsolidation Settlement Assessment from Limited CPTs Considering Spatial Variability. Soil Dyn. Earthq. Eng. 2022, 163, 107518. [Google Scholar] [CrossRef]
- Tian, H.; Wang, Y. Data-Driven and Physics-Informed Bayesian Learning of Spatiotemporally Varying Consolidation Settlement from Sparse Site Investigation and Settlement Monitoring Data. Comput. Geotech. 2023, 157, 105328. [Google Scholar] [CrossRef]
- Ji, S.; Xue, Y.; Carin, L. Bayesian Compressive Sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Guan, Z.; Wang, Y. CPT-Based Probabilistic Liquefaction Assessment Considering Soil Spatial Variability, Interpolation Uncertainty and Model Uncertainty. Comput. Geotech. 2022, 141, 104504. [Google Scholar] [CrossRef]
- Guan, Z.; Wang, Y. SPT-Based Probabilistic Evaluation of Soil Liquefaction Potential Considering Design Life of Civil Infrastructures. Comput. Geotech. 2022, 148, 104807. [Google Scholar] [CrossRef]
- Guan, Z.; Wang, Y.; Zhao, T. Delineating the Spatial Distribution of Soil Liquefaction Potential in a Cross-Section from Limited Cone Penetration Tests. Soil Dyn. Earthq. Eng. 2021, 145, 106710. [Google Scholar] [CrossRef]
- Guan, Z.; Wang, Y. Assessment of Liquefaction-Induced Differential Ground Settlement and Lateral Displacement Using Standard Penetration Tests with Consideration of Soil Spatial Variability. J. Geotech. Geoenviron. Eng. 2022, 148, 04022018. [Google Scholar] [CrossRef]
- Zhao, T.; Wang, Y.; Xu, L. Efficient CPT Locations for Characterizing Spatial Variability of Soil Properties within a Multilayer Vertical Cross-Section Using Information Entropy and Bayesian Compressive Sensing. Comput. Geotech. 2021, 137, 104260. [Google Scholar] [CrossRef]
- Guan, Z.; Wang, Y.; Zhao, T. Adaptive Sampling Strategy for Characterizing Spatial Distribution of Soil Liquefaction Potential Using Cone Penetration Test. J. Rock Mech. Geotech. Eng. 2022, 14, 1221–1231. [Google Scholar] [CrossRef]
- Montgomery, J.; Boulanger, R.W. Effects of Spatial Variability on Liquefaction-Induced Settlement and Lateral Spreading. J. Geotech. Geoenviron. Eng. 2017, 143, 04016086. [Google Scholar] [CrossRef]
- Huang, J.; Zheng, D.; Li, D.-Q.; Kelly, R.; Sloan, S.W. Probabilistic Characterization of Two-Dimensional Soil Profile by Integrating Cone Penetration Test (CPT) with Multi-Channel Analysis of Surface Wave (MASW) Data. Can. Geotech. J. 2018, 55, 1168–1181. [Google Scholar] [CrossRef]
- Adewoyin, O.; Joshua, E.; Akinwumi, I.; Maxwell, O.; Joel, E. Evaluation of Geotechnical Parameters Using Geophysical Data. J. Eng. Technol. Sci. 2017, 49, 95–113. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Y.; Zhang, L. Fusion of Geotechnical and Geophysical Data for 2D Subsurface Site Characterization Using Multi-Source Bayesian Compressive Sampling. Can. Geotech. J. 2022, 59, 1756–1773. [Google Scholar] [CrossRef]
- Ku, C.-S.; Juang, C.H.; Chang, C.-W.; Ching, J. Probabilistic Version of the Robertson and Wride Method for Liquefaction Evaluation: Development and Application. Can. Geotech. J. 2012, 49, 27–44. [Google Scholar] [CrossRef]
- Robertson, P.K.; Wride, C. (Fear) Evaluating Cyclic Liquefaction Potential Using the Cone Penetration Test. Can. Geotech. J. 1998, 35, 442–459. [Google Scholar] [CrossRef]
- Robertson, P. Performance Based Earthquake Design Using the CPT. In Proceedings of the International Conference on Performance-Based Design in Earthquake, Tokyo, Japan, 25 May 2009; pp. 3–20. [Google Scholar]
- Youd, T.L.; Idriss, I.M. Liquefaction Resistance of Soils: Summary Report from the 1996 NCEER and 1998 NCEER/NSF Workshops on Evaluation of Liquefaction Resistance of Soils. J. Geotech. Geoenviron. Eng. 2001, 127, 297–313. [Google Scholar] [CrossRef]
- Duan, W.; Zhao, Z.; Cai, G.; Pu, S.; Liu, S.; Dong, X. Evaluating Model Uncertainty of an in Situ State Parameter-Based Simplified Method for Reliability Analysis of Liquefaction Potential. Comput. Geotech. 2022, 151, 104957. [Google Scholar] [CrossRef]
- Zhang, G.; Robertson, P.K.; Brachman, R.W.I. Estimating Liquefaction-Induced Lateral Displacements Using the Standard Penetration Test or Cone Penetration Test. J. Geotech. Geoenviron. Eng. 2004, 130, 861–871. [Google Scholar] [CrossRef]
- Ishihara, K.; Yoshimine, M. Evaluation of Settlements in Sand Deposits Following Liquefaction During Earthquakes. Soils Found. 1992, 32, 173–188. [Google Scholar] [CrossRef]
- Idriss, I.M.; Boulanger, R.W. Soil Liquefaction during Earthquakes; Earthquake Engineering Research Institute: Oakland, CA, USA, 2008; p. 136. [Google Scholar]
- Zhao, T.; Hu, Y.; Wang, Y. Statistical Interpretation of Spatially Varying 2D Geo-Data from Sparse Measurements Using Bayesian Compressive Sampling. Eng. Geol. 2018, 246, 162–175. [Google Scholar] [CrossRef]
- Wang, Y.; Li, P. Data-Driven Determination of Sample Number and Efficient Sampling Locations for Geotechnical Site Investigation of a Cross-Section Using Voronoi Diagram and Bayesian Compressive Sampling. Comput. Geotech. 2021, 130, 103898. [Google Scholar] [CrossRef]
- Zhao, T.; Xu, L.; Wang, Y. Fast Non-Parametric Simulation of 2D Multi-Layer Cone Penetration Test (CPT) Data without Pre-Stratification Using Markov Chain Monte Carlo Simulation. Eng. Geol. 2020, 273, 105670. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian Learning and the Relevance Vector Machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar] [CrossRef]
- Yang, H.-Q.; Zhang, L.; Xue, J.; Zhang, J.; Li, X. Unsaturated Soil Slope Characterization with Karhunen–Loève and Polynomial Chaos via Bayesian Approach. Eng. Comput. 2019, 35, 337–350. [Google Scholar] [CrossRef]
- Long, M.; Trafford, A.; McGrath, T.; O’Connor, P. Multichannel Analysis of Surface Waves (MASW) for Offshore Geotechnical Investigations. Eng. Geol. 2020, 272, 105649. [Google Scholar] [CrossRef]
- Yang, H.-Q.; Zhang, L.; Pan, Q.; Phoon, K.-K.; Shen, Z. Bayesian Estimation of Spatially Varying Soil Parameters with Spatiotemporal Monitoring Data. Acta Geotech. 2021, 16, 263–278. [Google Scholar] [CrossRef]
- Liu, J.; Wu, Q.; Amin, M.G. Multi-Task Bayesian Compressive Sensing Exploiting Signal Structures. Signal Process. 2021, 178, 107804. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Zhao, T.; Wang, Y. Determination of Efficient Sampling Locations in Geotechnical Site Characterization Using Information Entropy and Bayesian Compressive Sampling. Can. Geotech. J. 2019, 56, 1622–1637. [Google Scholar] [CrossRef]
- NZGD. New Zealand Geotechnical Database. Available online: https://www.nzgd.org.nz/ (accessed on 26 June 2022).
- Bray, J.; Cubrinovski, M.; Zupan, J.; Taylor, M. Liquefaction Effects on Buildings in the Central Business District of Christchurch. Earthq. Spectra 2014, 30, 85–109. [Google Scholar] [CrossRef]
- Bradley, B.A. Site-Specific and Spatially-Distributed Ground-Motion Intensity Estimation in the 2010–2011 Canterbury Earthquakes. Soil Dyn. Earthq. Eng. 2014, 61–62, 83–91. [Google Scholar] [CrossRef]
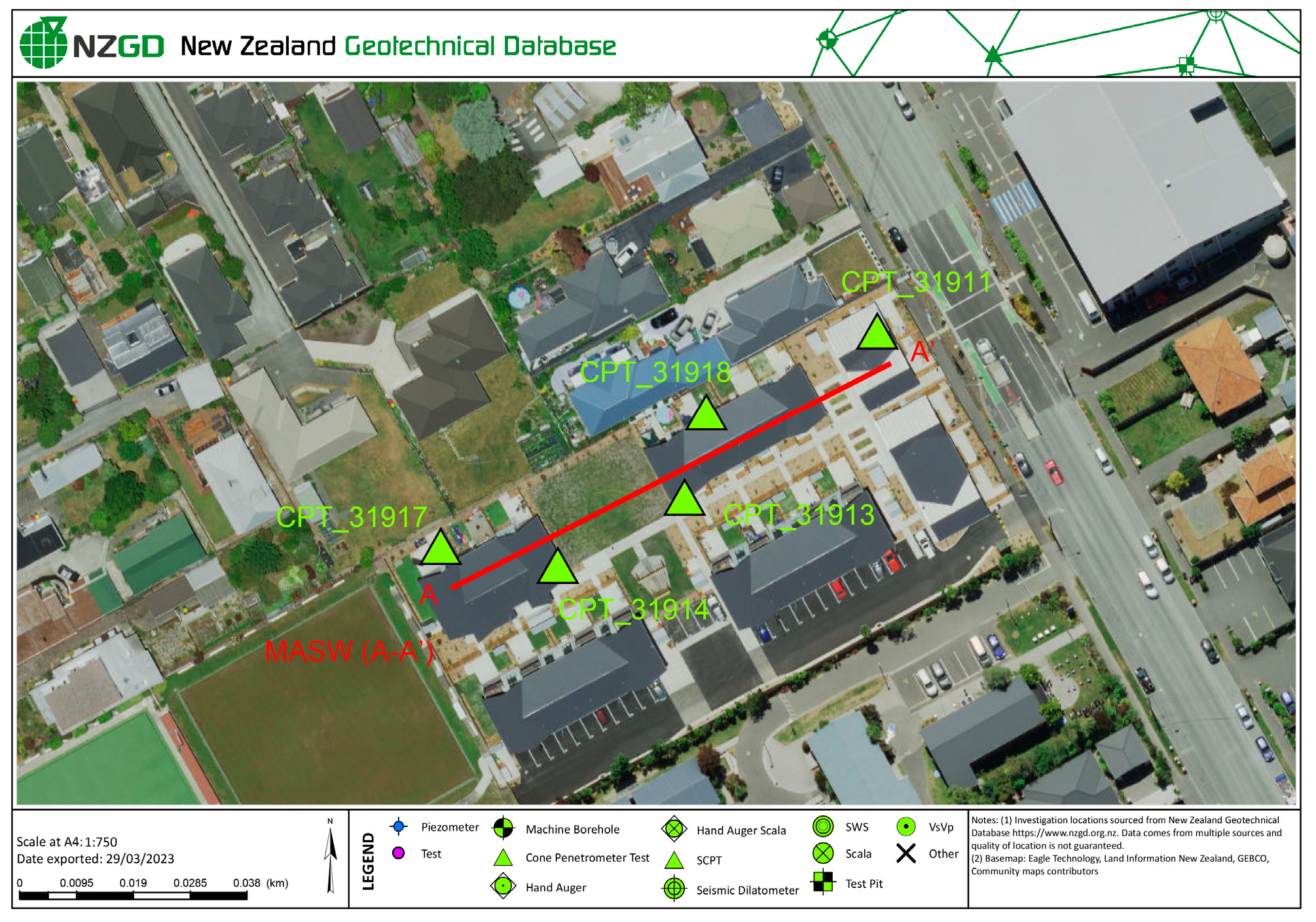



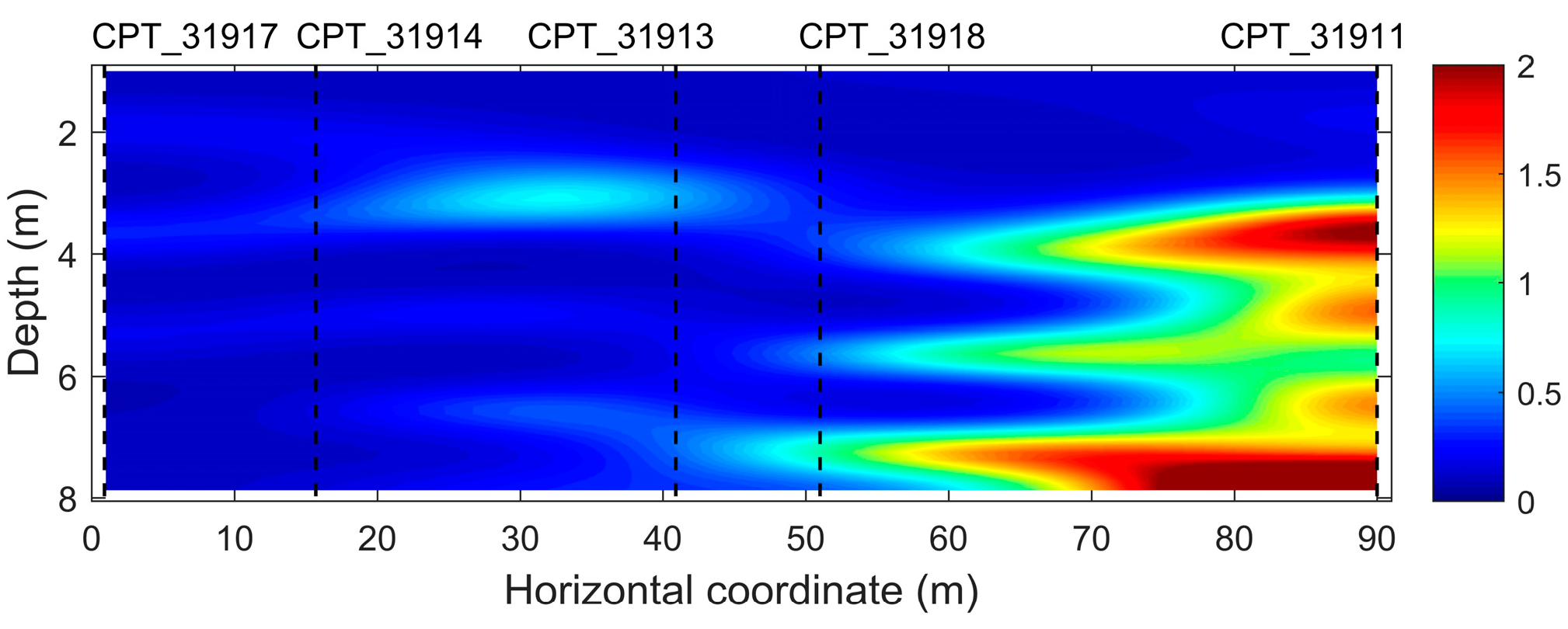
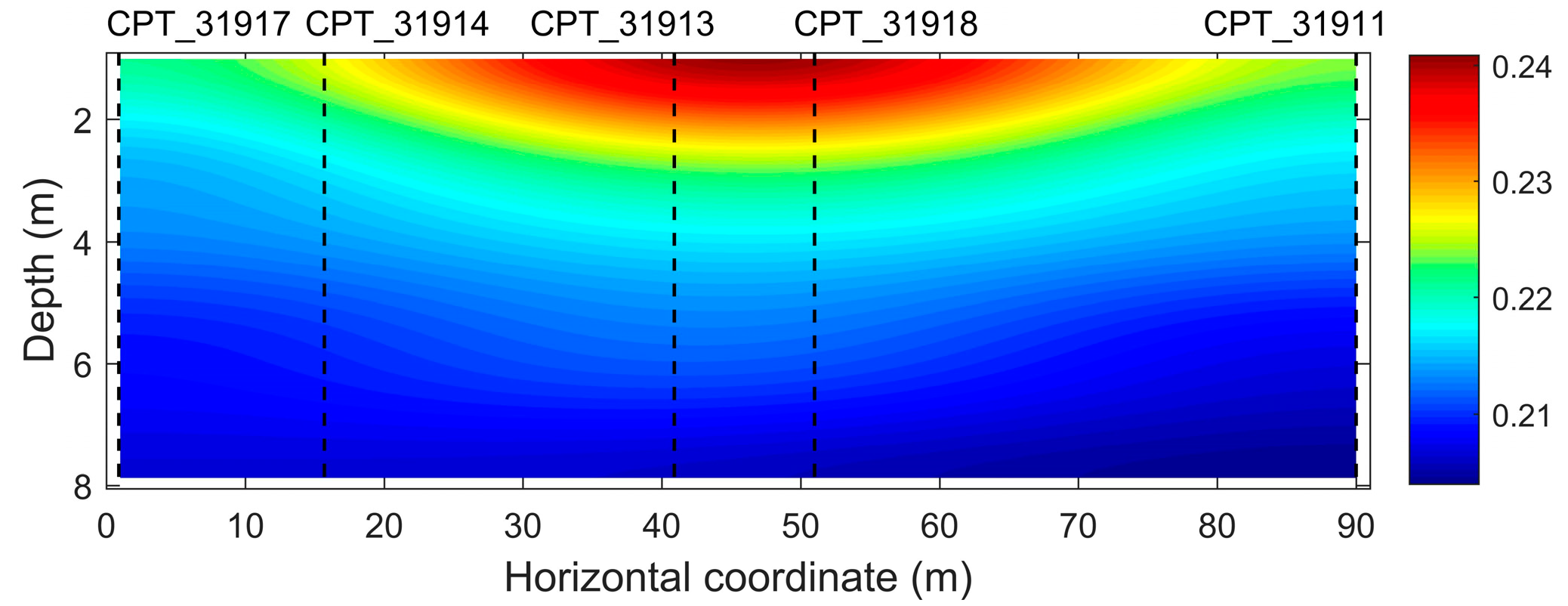

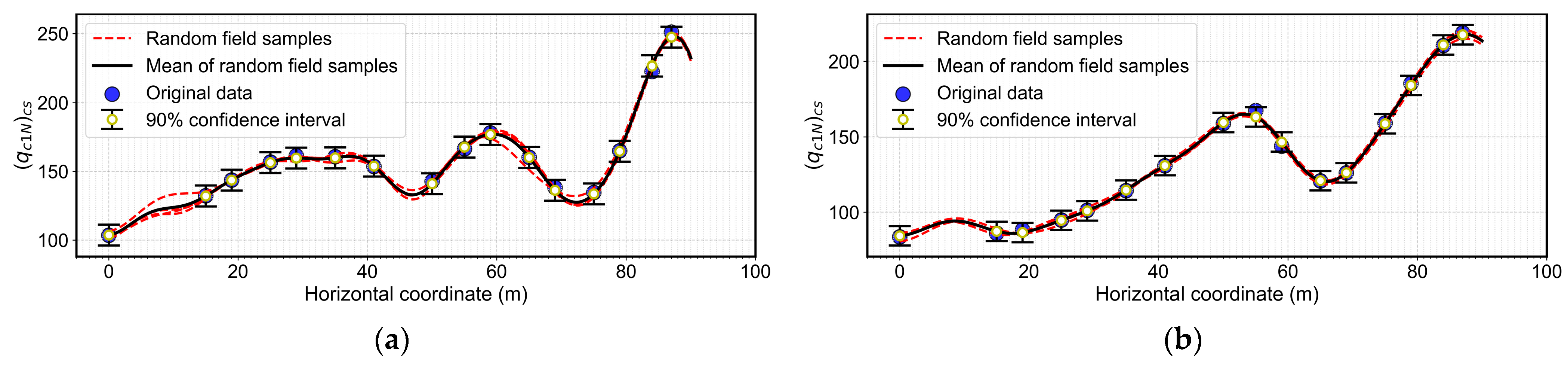
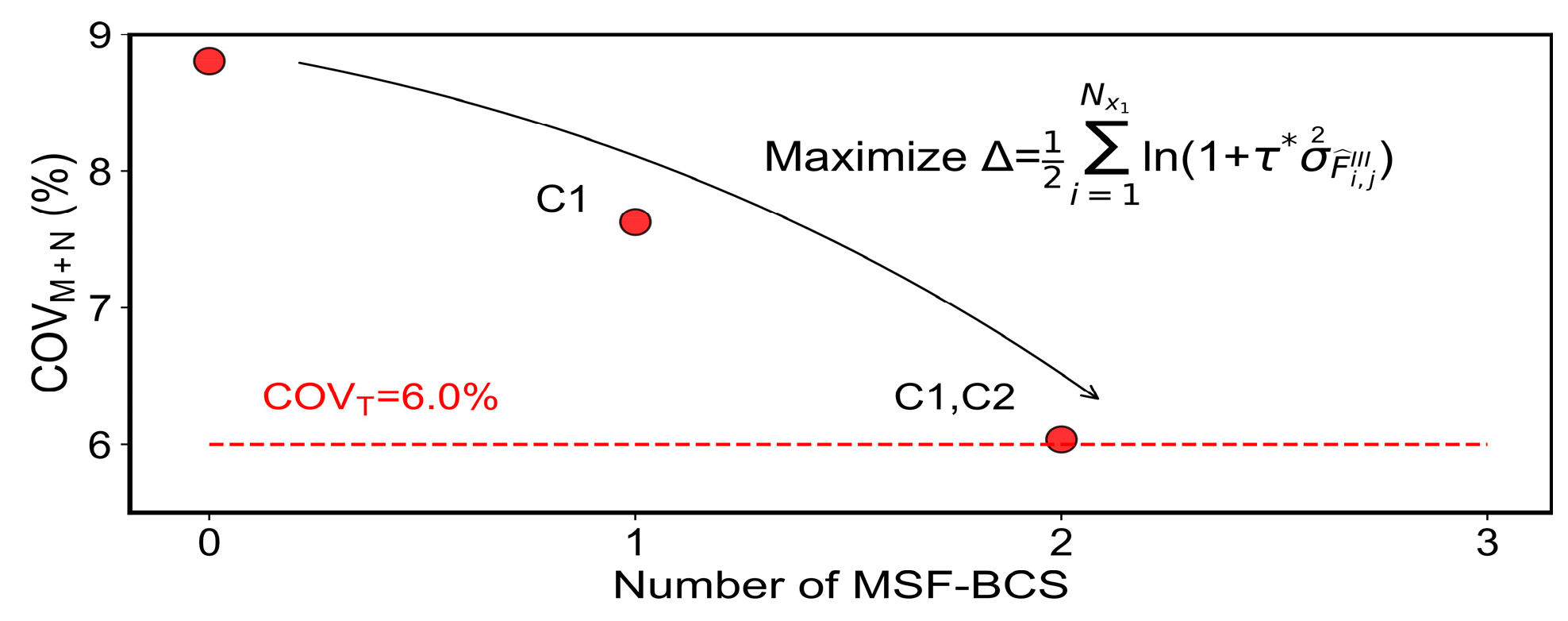
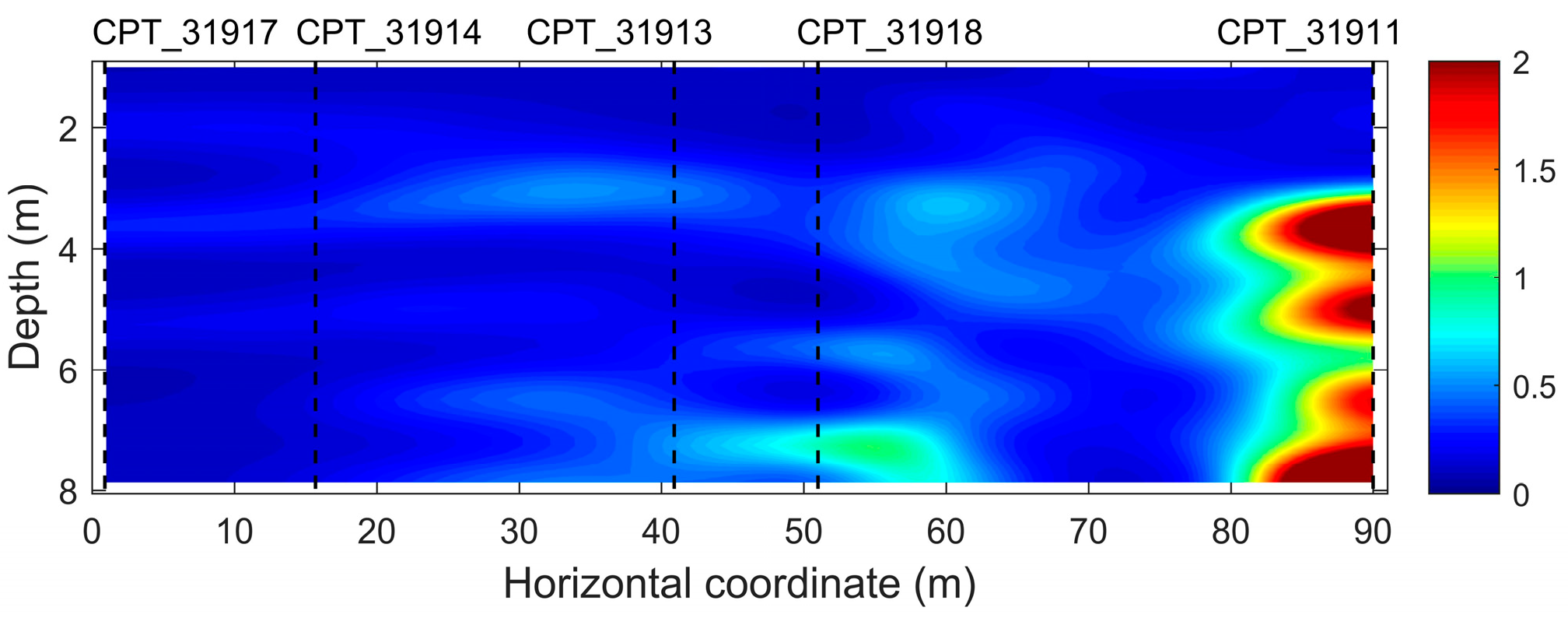

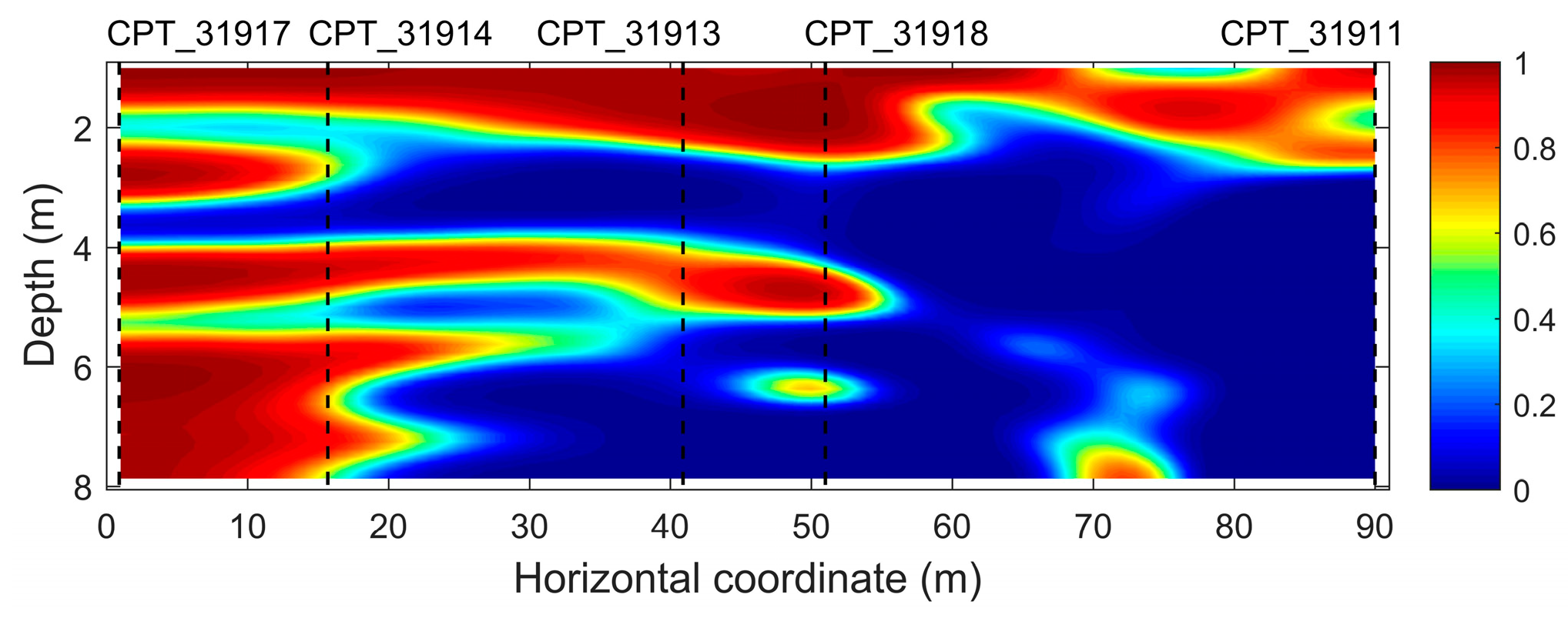

| Parameters | qc (CPT_31917) | qc (CPT_31914) | qc (CPT_31913) | qc (CPT_31918) | qc (CPT_31911) | Vs |
|---|---|---|---|---|---|---|
| Number | 176 | 176 | 176 | 176 | 176 | 128 |
| Range | 0.46–9.78 | 1.22–10.64 | 0.46–13.66 | 0.56–25.90 | 1.41–41.36 | 70.35–241.00 |
| 4.00 | 6.77 | 6.99 | 8.60 | 16.06 | 126.77 | |
| 2.56 | 2.21 | 3.57 | 5.52 | 8.87 | 32.37 |
| Horizontal Coordinate (m) | a1–a2 | a3–a4 | ||||||
|---|---|---|---|---|---|---|---|---|
| Measured Value | Computed Value | CI− | CI+ | Measured Value | Computed Value | CI− | CI+ | |
| 0 | 103.51 | 103.67 | 96.07 | 111.27 | 83.62 | 84.33 | 77.88 | 90.79 |
| 15 | 132.33 | 132.15 | 124.55 | 139.74 | 85.97 | 87.29 | 80.84 | 93.75 |
| 19 | 143.65 | 143.68 | 136.08 | 151.28 | 88.41 | 86.49 | 80.04 | 92.94 |
| 25 | 156.84 | 156.40 | 148.80 | 164.00 | 94.83 | 94.66 | 88.20 | 101.11 |
| 29 | 161.33 | 159.74 | 152.14 | 167.33 | 101.28 | 100.93 | 94.47 | 107.38 |
| 35 | 160.74 | 159.88 | 152.28 | 167.48 | 114.33 | 114.71 | 108.26 | 121.17 |
| 41 | 153.61 | 153.89 | 146.29 | 161.49 | 130.85 | 130.98 | 124.53 | 137.43 |
| 50 | 142.85 | 141.04 | 133.44 | 148.64 | 158.96 | 159.61 | 153.16 | 166.06 |
| 55 | 166.43 | 167.71 | 160.11 | 175.31 | 167.48 | 163.34 | 156.89 | 169.80 |
| 59 | 178.04 | 176.94 | 169.34 | 184.54 | 143.91 | 146.68 | 140.23 | 153.14 |
| 65 | 160.34 | 160.15 | 152.55 | 167.75 | 120.81 | 120.95 | 114.50 | 127.41 |
| 69 | 138.27 | 136.28 | 128.68 | 143.88 | 126.15 | 126.19 | 119.74 | 132.64 |
| 75 | 134.59 | 133.62 | 126.02 | 141.22 | 159.25 | 158.79 | 152.34 | 165.25 |
| 79 | 164.96 | 164.69 | 157.10 | 172.29 | 185.55 | 184.26 | 177.80 | 190.71 |
| 84 | 222.69 | 226.68 | 219.08 | 234.28 | 210.47 | 210.89 | 204.44 | 217.34 |
| 87 | 251.04 | 247.47 | 239.87 | 255.07 | 218.91 | 217.69 | 211.24 | 224.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Liu, Z.; Yan, Y.; Li, Y.; Tao, G. Adaptive Fusion Sampling Strategy Combining Geotechnical and Geophysical Data for Evaluating Two-Dimensional Soil Liquefaction Potential and Reconsolidation Settlement. Appl. Sci. 2023, 13, 5931. https://doi.org/10.3390/app13105931
Yang H, Liu Z, Yan Y, Li Y, Tao G. Adaptive Fusion Sampling Strategy Combining Geotechnical and Geophysical Data for Evaluating Two-Dimensional Soil Liquefaction Potential and Reconsolidation Settlement. Applied Sciences. 2023; 13(10):5931. https://doi.org/10.3390/app13105931
Chicago/Turabian StyleYang, Huajian, Zhikui Liu, Yan Yan, Yuantao Li, and Guozheng Tao. 2023. "Adaptive Fusion Sampling Strategy Combining Geotechnical and Geophysical Data for Evaluating Two-Dimensional Soil Liquefaction Potential and Reconsolidation Settlement" Applied Sciences 13, no. 10: 5931. https://doi.org/10.3390/app13105931
APA StyleYang, H., Liu, Z., Yan, Y., Li, Y., & Tao, G. (2023). Adaptive Fusion Sampling Strategy Combining Geotechnical and Geophysical Data for Evaluating Two-Dimensional Soil Liquefaction Potential and Reconsolidation Settlement. Applied Sciences, 13(10), 5931. https://doi.org/10.3390/app13105931






