Abstract
In this paper, we have constructed a WKB approximation for graphene having a Y-shaped Kekulé lattice distortion and a special folding of the K and valleys, which leads to very specific linear energy dispersions with two non-equivalent pairs of subbands. These obtained semi-classical results, which include the action, electron momentum and wave functions, are utilized to analyze the dynamics of electron tunneling through non-square potential barriers. In particular, we explore resonant scattering of an electron by a potential barrier built on Kekulé-distorted graphene. Mathematically, a group of consecutive equations for a semi-classical action have been solved by following a perturbation approach under the condition of small strain-induced coupling parameter (a good fit to its actual value ∽ 0.1). Specifically, we consider a generalized model for Kek-Y graphene with two arbitrary Fermi velocities. The dependence of the electron transmission amplitude on the potential profile and band parameters of Kekulé-patterned graphene has been explored and analyzed in detail.
1. Introduction
Kekulé-patterned graphene represents an unusual and technologically very promising modification of conventional graphene energy band structure due to coupling of its orbital with spin degrees of freedom. In fact, a periodic Y-shape modification of the bond strengths of graphene, as illustrated in Figure 1, leads to chiral electronic states as well as two nonequivalent coupled Dirac cones with different Fermi velocities [,,]. Practically, such a unique feature can be realized by depositing graphene on a special copper-based substrate []. Here, we focus on Kek-Y graphene, which is further distinguished from Kek-O graphene by a finite bandgap [,,].
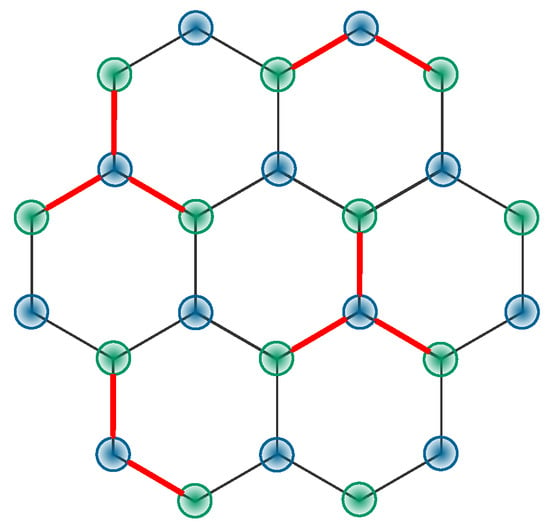
Figure 1.
Atomic structure of Kekulé-distorted graphene: honeycomb lattices of graphene with additional Kek-Y bond texture due to the presence of a substrate.
The most crucial feature of Kek-Y graphene is its valley-momentum locking, i.e., two eigenstate modes of electrons are chiral (helical) and have zero bandgap, while both sublattice pseudospin and isospin are locked to the same group velocity []. Recently, there have been a number of crucial research publications aimed at addressing these unusual electronic, optical and transport properties of Kekulé-distorted graphene [,,,,]. Even though the mismatch between slopes of two Dirac cones appears fixed in Kekul e-patterned graphene, i.e., , we still consider a general case for Kek-Y graphene with two nonequivalent Dirac cones and having two arbitrary Fermi velocities and .
Kekulé-patterned graphene is the newest member in the family of Dirac-cone materials, including graphene [,], silicene [,,] and transition-metal dichalcogenides [,], as well as the most unusual group of - materials [,,]. The most uncommon feature of the - model is the presence of a flat band in its energy dispersions, giving rise to the most unusual electronic and optical properties [,,,,,,,,,,,,,]. On the other hand, the magnetic properties and magnetic-quantization behavior of - materials have also attracted a lot of attention [,,,,], including a phase transition from a diamagnetic to a paramagnetic susceptibility by continuously varying the parameter []. In fact, the low-energy dispersion of the - model looks somewhat similar to that of the generalized Kek-Y graphene model if the Fermi velocity of the lower Dirac cone is greatly reduced compared to the larger one (i.e., ).
Apart from Kek-Y graphing, there is another famous modification of Kekule-patterned graphene, which is referred to as Kek-O. In the latter case, Kekule dimerization takes place in benzene rings of hexagons in graphene.
The energy spectrum of Kek-O graphene demonstrates a large bandgap. Therefore, the case of Kek-O graphene could be considered similar to regular graphene in the presence of circular polarized irradiation discussed above. A substantial bandgap in the energy dispersions of Kek-O graphene evidently results in a tremendous loss of electron transmission over square barrier, as well as significant drop of its optical and Boltzmann conductivity.
The Wentzel–Kramers–Brillouin (WKB), or the semi-classical, theory provides an intuitive but realistic description for dynamical behaviors of electrons in a variety of complex quantum systems under the condition of a high-kinetic energy. In this case, the properties of such electrons are not much different from their classical counterparts and could be effectively described by classical dynamics. However, in contrast to a perturbation theory, the interaction between a particle and an external potential can be very strong, implying that in a number of cases, the WKB description can still be valid even as other types of approximation fail [,,,,,]. Therefore, from this point of view, it is essential and crucial to develop a semi-classical WKB theory for each newly discovered Dirac lattice, such as - or Kekulé-patterned graphene. Mathematically, the WKB approximation is regarded as a solution technique for a differential equation with the highest-order derivative term multiplied by a small parameter. In quantum physics, this small parameter is just Planck’s constant ℏ, so that the solution for a WKB wave function can be sought as a power series of ℏ. However, the WKB for Dirac electrons in graphene is found drastically different from that in the case of a regular Schrödinger electron, and therefore, we expect that the WKB solution for each novel Dirac material will be quite unique compared with all other known solutions. Moreover, the sought wave function for a new material will usually appear as a quickly oscillating function, which is further modulated by a much slower variation from an external potential .
Among multiple applications of the WKB theory, we would also like to calculate electron transmission, or tunneling probability, and investigate the various bound states of an electronic system [,,]. In contrast to previous studies on tunneling and transport of electrons in Kek-Y graphene [,] through complicated numerical computations, WKB methods, on the other hand, provide reliable estimates based on closed-form analytical expressions, which can be easily used to interpret experimental measurements on electron transport.
Studying electron tunneling, often associated with calculating a transmission amplitude, becomes one of the most important issues for each of the newly discovered Dirac materials, mostly because of the so-called Klein paradox, i.e., a full tunneling of chiral Dirac electrons through a square potential barrier, independent of its width and height if the incoming electron moves in the direction perpendicular to the barrier boundary [,,,]. For a finite-angle collision, however, a complete transmission also appears for an oblique (not a normal) incidence due to presence of Fabry–Perot resonances. Such a Klein-tunneling behavior was investigated for all Dirac-cone materials and nano-ribbons [,,], including transport in Kekulé-distorted graphene nanoribbons []. Specifically, a magic transmission was demonstrated for - materials and dice lattice [,,,], in addition to the unusual tunneling behavior of anisotropic Dirac electrons [,,].
The unique properties of electron tunneling and the existence of the Klein paradox will depend on a few factors, and the most crucial one is the energy bandgap between the valence and conduction bands [,,,,]. The two-dimensional materials with a gap do not show Klein tunneling. Such a bandgap in graphene and other Dirac lattices could be created by applying an off-resonance circularly-polarized dressing field, which also turns these material into Haldane-like Chern insulators [,]. However, linearly polarized irradiation normally does not affect the gap, although it can induce or modify the existing anisotropy [,]. Interestingly, the effects of these external fields with different polarizations could further mix with anisotropic and tilted energy dispersions of lattices, such as 1T′MoS2 [,,].
One of the most crucial applications of WKB equations is investigating the electron tunneling for non-trivial potential barriers, such as trapezoidal barriers [] or linearly increasing potentials without a sharp boundary. It was demonstrated for all previously known Dirac materials that the Klein paradox persists in such potential profiles. Verification of this property for Kekulé-patterned graphene is one of the goals of the present paper. Since Dirac electrons moving under a linearly increasing potential can acquire a very large kinetic energy, applying WKB approximation to such a case seems to be the most adequate and efficient approach.
The remaining part of our paper is organized as follows. We begin with a brief review of electronic states and their energy dispersions of Kek-Y graphene in Section 2. In Section 3, we formulate a full WKB approximation for a general case of Kek-Y graphene, which includes finding the semi-classical action, longitudinal electron momentum and WKB wave functions. Section 4 focuses on addressing the electron tunneling and Klein paradox in Kekulé-patterned graphene by utilizing our derived Wentzel–Kramers–Brillouin equations. Moreover, we also consider different methods for calculating electron transmissions through different types of potential barriers, and demonstrate how these methods could be applied to Kekulé-patterned graphene. Finally, we discuss and compare the obtained results and present concluding remarks in Section 5.
2. Energy Band Structure and Electronic States in Kek-Y Graphene
First, we briefly review the electronic band structure and eigenfunctions in Kek-Y graphene. For the type of distortion displayed in Figure 1, the Dirac cones will fold on each other, as seen in Figure 2, which results in two states with no bandgap, but with different Fermi velocities.
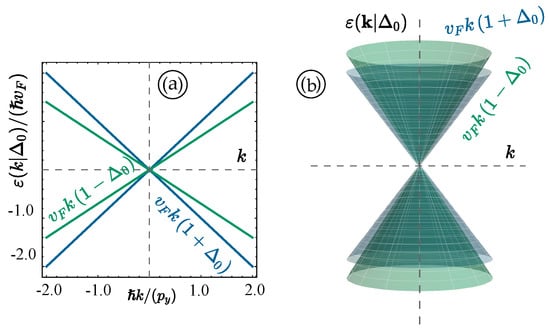
Figure 2.
(a,b) Energy dispersions for Kek-Y graphene represented by two nonequivalent Dirac cones with different Fermi velocities and corresponding to . Here, is a band index, while corresponds to two different Fermi velocities due to strain coupling .
The low-energy Hamiltonian for Kek-Y graphene can be approximately written as [,]:
where is a wave vector of electrons, is the Fermi velocity in regular non-strained graphene and is a dimensionless strain-induced coupling parameter. As , we recover the regular graphene Hamiltonian for unfolded K and valleys, i.e., keeping only the first term on the right hand side of Equation (1). We indicate that Equation (1) holds only for a small strain-coupling parameter , and it may be modified as the stain strength increases. In most cases, however, is always assumed small in order to retain graphene signature of the system. Here, we choose ∽0.1 in our calculations below but derive a generalized model by assuming a substantial difference between two Fermi velocities .
Additionally:
which act in the spin- and pseudo-spin subspaces, respectively. Correspondingly, and in Equation (1) are two unit matrices in the spin- and pseudo-spin subspaces, written as:
Equation (1) is presented by using a Kronecker product of two matrices, defined as:
More specifically, for the case of Pauli matrices, we have:
Therefore, any block-diagonal (b–d) matrix can be built by following this procedure, namely:
The energy dispersions of Kekulé-Y graphene are simply obtained as eigenvalues of the matrix defined in Equation (10), yielding:
which represent two Dirac cones with different Fermi velocities , as displayed in Figure 2, where is a band index while corresponds to two different Fermi velocities due to strain coupling. These two types of subbands are often referred to as “fast” () and “slow” () Dirac cones, and importantly, photo-induced electronic transitions are allowed between these two.
In correspondence with energy dispersions in Equation (11), the normalized wave functions are calculated as:
where is the angle associated with the electron wave vector k with respect to the x axis. The wave function in Equation (12) consists of two subspinors corresponding to standard graphene eigenstates, namely:
Quantum-mechanically, the velocity operators for an electron can be determined by the Heisenberg equation, that is:
which relates to an intraband probability current density , where is presented in Equation (9). Semi-classically, on the other hand, we define another particle velocity , determined by:
which relates to an intraband transport current density , where is the areal density of electrons in our system, while denotes a quantum-mechanical average with respect to the wave function presented in Equation (13).
Generally, from the Schrödinger equation, we know that the intraband probability-current density can be calculated by:
where we treat a Kekulé particle as a free one. The definition in Equation (15) can be employed for calculating the semi-classical transport current density, yielding:
An expression similar to Equation (17) should also be obtained for transport current .
For a Kekule particle, besides the intraband probability current density , there exists another interband probability current density due to (strain) coupling between two Dirac-cones []. By including this interband probability current, the total particle current should be continuous and satisfies the following particle-number conversation law:
Since there are no external sources for the current and each observable quantity is time-independent, every term in Equation (19) equals to zero, leading to:
This implies that even under a non-uniform potential , such as a potential barrier, the total current across the barrier must be conserved. This unique feature plays a crucial role in electron tunneling and transmission calculation. For our considered system, we always assume a translational symmetry along the y-direction, and then a constant.
3. Wentzel–Kramers–Brillouin Approximation
In this section, we aim to derive the semi-classical Wentzel–Kramers–Brillouin (WKB) approximation applied to Kek-Y graphene. We begin with the Hamiltonian formula in Equation (1) and generalize it for the case with a spatially non-uniform potential , including the special case with a square barrier , where is the width of a square barrier.
By taking into account the fact that our system is no longer translationally invariant in the x-direction, we take and obtain from Equation (1) that:
which is independent of y, where remains conserved.
The key idea of the WKB approximation originates from a series expansion in powers of a small parameter ℏ. Since we will consider a semi-classical particle with a large kinetic energy , it is necessary to estimate the order of magnitude for each of the considered quantities. By following Refs. [,], it is reasonable to rewrite the Hamiltonian formula in Equation (21), as well as the corresponding eigenvalue equation, in a form with only dimensionless quantities, namely:
where represents the strength of a potential, e.g., the height of a square-barrier potential. Correspondingly, we also introduce other dimensionless quantities, such as:
In this way, the spatial derivative now becomes:
Such a scheme allows us to modify the Planck constant ℏ, which is our chosen small parameter for a series expansion, leading to:
Consequently, the new energy scale of an incoming particle is large and will not be limited by the Fermi energy of electrons in graphene.
In this study, we follow an established WKB solution for a Dirac equation and expand our sought-after wave function as a series, given by:
where stands for a semi-classical action in the WKB approximation. Here, our goal is finding a differential equation with respect to x, which connects consecutive terms in the expansion introduced in Equation (26). Explicitly, we would seek the form:
where
is proportional to the probability-current operator in Equation (17), , and . Furthermore, the transport operator introduced in Equation (27), which connects each two consecutive terms of expansion in Equation (26), is as follows:
where .
Specifically, for , we obtain:
For the linear homogeneous equation in Equation (30), a non-trivial solution becomes possible only if its determinant is zero, namely:
As a quartic equation, Equation (31) could be solved analytically, but in general, its solutions are too tedious to write down. Instead, we use the fact that . Therefore, as , Equation (31) turns into:
with a set of doubly degenerate solutions for incident energy of an electron, given by:
which results in:
For a finite but small , we are able to solve Equation (31) by using a perturbation method. Assuming:
where derived from the zeroth-order equation in Equation (32), we obtain the first-order correction (on the order of ) from the following equation:
given by:
Equations (35)–(37) define the solution for the x-dependent momentum , while the semi-classical action for a given momentum can be determined by Equation (34). This is one of the most crucial results in semi-classical theory for Kekulé-patterned graphene.
Now, the WKB wave function could be obtained from Equation (27). If we look for an eigenstate formally in the following form:
the relations between its components become:
where is determined from Equations (35)–(37). It is important to point out that the equations in Equation (39) includes strain-induced coupling between two sets of wave functions and , giving rise to a similar interband probability current [] within the semi-classical frame.
In general, the solution for a WKB wave function is quite complicated, but we can model a reliable solution by using the fact that the wave functions in Kek-Y graphene is a combination of two graphene wave function and does not depend on . For this purpose, we first introduce a notation:
where is the angle between wave vector and the x-axis. Making use of this notation, the wave function now takes a simple form:
Finally, in analogy with graphene study, we obtain the following expression:z
and now the wave function in Equation (12) is fully determined.
4. Electron Tunneling in Kekulé-Patterned Graphene
The primary application of the obtained WKB approximation is a good numerical estimate of the electron transmission amplitude for a fast-moving electron. This method is easily applicable to the cases of non-square potential barriers and a wide class of potential profiles as long as this profile is smooth and there is no abrupt change in the particle’s momentum . At the same time, WKB calculations were used to predict or verify the existence of the Klein paradox for a normal incident particle on a square barrier in graphene and other Dirac cone materials, i.e., they could be formally applied to a square barrier as well.
The transmission amplitude is defined as the ratio of the electron current passing through the barrier to the incoming current. Since the total current in the direction perpendicular to a potential barrier is conserved, the reflect current could also be easily calculated as the difference between them. The biggest loss of a transmitted current occurs in the classically forbidden regions (CFR), in which the longitudinal momentum becomes purely imaginary and the moving particle is represented by an evanescent wave, whose amplitude is exponentially decreasing along the x-axis. The transmission amplitude in the WKB theory is estimated by the integral of the purely imaginary momentum over each of the classically forbidden regions along the x-direction. This results in the following equation:
as long as the condition is satisfied. Based on Equation (31), squared longitudinal momentum is determined from:
The calculated locations of CFRs are presented in Figure 3 for and in Figure 4 for . We see that the former case is pretty much equivalent to graphene and the boundaries of the CFR’s are linear and symmetric with respect to . The width of the classically inaccessible region along the x-axis obviously depends on the slope of the potential profile, i.e., a higher slope a corresponds to reduced width of a CFR.
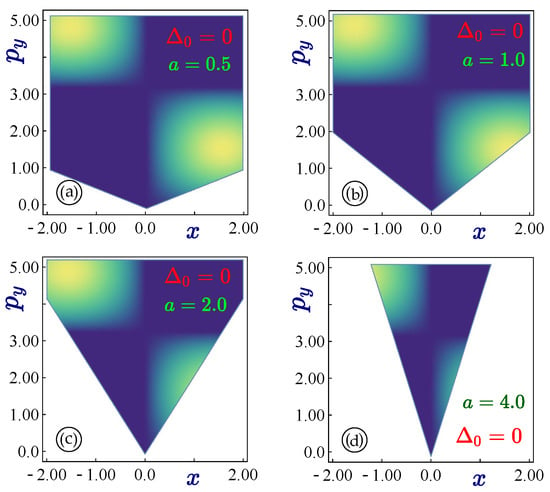
Figure 3.
Regions for the classically forbidden (or classically inaccessible regions) with for an incoming electron with a linear potential . Here, we select a crossing point, corresponding to the electron-to-hole (and back) state transition at . All panels (a–d) are calculated for but different values of a.
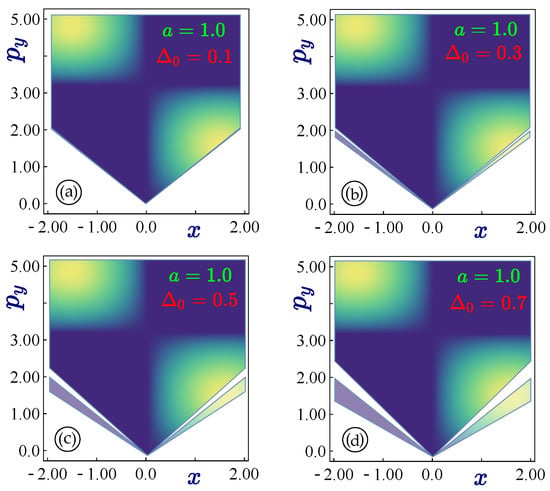
Figure 4.
Regions for the classically forbidden (or classically inaccessible regions) with for an incoming electron with a linear potential . Here, we select a crossing point, corresponding to the electron-to-hole (and back) state transition at . Panels (a–d) are calculated with and various finite values of .
When , the equation with classically forbidden regions is much more complicated and the region itself is extended in a non-trivial way, as seen from Figure 4. However, the boundaries of CFR are still linear and symmetric with respect to . This is in stark contrast with gapped - materials in which the classically inaccessible regions are very complicated, asymmetric and even involve curved boundaries.
Our results for the transmission are presented in Figure 5. First, we find that the expansion of the classical and accessible region leads to lower transmission so that it is more suppressed for a smaller slope a in the potential profile , as found in Figure 5a. Similarly, the suppression of transmission increases for a finite due to the appearance of extended CFRs, However, its dependence on is much smaller compared to that on the potential profile slope a, as can be verified by Figure 5a.
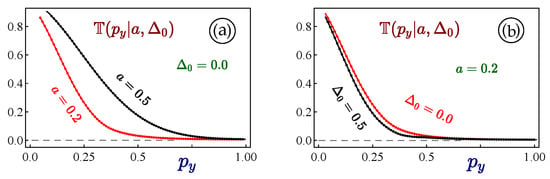
Figure 5.
Transmissions amplitudes calculated by using Equation (43). Panel (a) presents as a function of transverse momentum for and different slopes and . Panel (b) displays calculated as a function of for and different energy gaps and .
It is important to mention that the WKB approximation provides a fairly satisfactory estimate for the electron transmission in the cases as standard techniques are either not applicable or would lead to tremendously complicated equations. This is exactly the case for Kek-Y graphene in which similarly to tunneling of Rashba electrons, there are two non-equivalent solutions for wave vector k at a given energy []. However, in the case of Kek-Y graphene, we would need to solve a quartic equation so as to obtain the k value for a given energy , and then use these expressions to find the transmission, which seems hardly possible.
As mentioned above, the main application of the WKB theory in any existing material is investigating electron tunneling over various potential barriers or regions in which the potential of the incoming particle is larger than its kinetic energy so that a classical particle could not even be present in such regions. These locations are also referred to as classically forbidden or classically inaccessible regions. Another possible application of WKB is investigating electronic bound states with quantized momentum, which are rarely considered for the Dirac lattices.
A general condition for applicability of WKB theory for graphene or another Dirac cone material is given in terms of the momentum as:
which is evidently equivalent to a slow change of the amplitude of a de Broglie wavelength of a particle:
The change of the electron momenta is directly related to the slope of the potential energy profile, such as:
for a regular Schrodinger electron or
for graphene, with Fermi velocity , which implies two important limitations of any WKB approximation: a sharp, sudden change of the potential and the regions in the vicinity of the turning points, where . At the same time, all the results for Klein tunneling over a square barrier with sharp edges and , where is constant, are faithfully reproduced by WKB theory, which appears to be valid much beyond its known range of applicability. At the time, WKB methods provide a straightforward and reliable estimate of the electron transmission amplitudes for the cases when traditional techniques are impossible or extremely complicated, such as for our case of Kek-Y-patterned graphene.
The validity of the WKB method is determined not by the size or height of the potential barrier. However, we should require the potential profile to be smooth and apply the approximation far from the turning points where the momentum of our particle becomes equal or close to zero.
5. Concluding Remarks
In conclusion, we have built a complete semi-classical WKB theory for recently discovered Kek-Y-patterned graphene with two coupled gapless Dirac cones with different Fermi velocities . This includes finding the semi-classical action, x-dependent longitudinal momentum and leading-order WKB wave function. Meanwhile, we have also derived and solved the transport equation, which connects every two successive orders of a sought wave function.
Our obtained WKB equations are further applied to calculate the electron transmission amplitudes based on classically inaccessible regions. We have demonstrated that the slope a of a linear potential can strongly affect electron transmission, while the coupling parameter has a very limited effect on transmission, because it only slightly modifies the location and size of a classically forbidden region for a specified incoming electron.
Our obtained results have numerous applications to constructing and operating a new generation of electronic devices, since the electron transmission amplitude is directly related to the quantum transport in our material. Most of the known models for the electron conductivity, such as Kubo formalism, require the exact knowledge of electron transmission. Applied irradiation could induce or modify the existing bandgap and greatly affect the electron transmission, which is crucial for optoelectronic applications. We are strongly convinced that this work reveals a crucial step in advancing our knowledge on the electronic properties of newly discovered Dirac materials. Our obtained WKB theory provides a powerful tool for systematically investigating crucial electronic and transport properties of novel Dirac materials, which have numerous applications in modern electronic and opto-electronic devices, and especially in valleytronics.
Author Contributions
Methodology, A.I., G.G. and L.Z.; Supervision, A.I. and G.G.; Writing—original draft, A.I., L.Z., G.G. and D.H.; Writing—review & editing, G.G. and D.H. All authors have read and agreed to the published version of the manuscript.
Funding
A.I. would like to acknowledge the funding received from TRADA-53-130 PSC-CUNY Award 65094-00 53. D.H. was supported by the Air Force Office of Scientific Research (AFOSR). G.G. would like to acknowledge Grant No. FA9453-21-1-0046 from the Air Force Research Laboratory (AFRL).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gamayun, O.; Ostroukh, V.; Gnezdilov, N.; Adagideli, İ.; Beenakker, C. Valley-momentum locking in a graphene superlattice with Y-shaped Kekulé bond texture. New J. Phys. 2018, 20, 023016. [Google Scholar] [CrossRef]
- Mohammadi, Y. Electronic spectrum and optical properties of Y-shaped Kekulé-patterned graphene: Band nesting resonance as an optical signature. ECS J. Solid State Sci. Technol. 2022, 11, 121004. [Google Scholar] [CrossRef]
- Herrera, S.A.; Naumis, G.G. Electronic and optical conductivity of Kekulé-patterned graphene: Intravalley and intervalley transport. Phys. Rev. B 2020, 101, 205413. [Google Scholar] [CrossRef]
- Gutiérrez, C.; Kim, C.J.; Brown, L.; Schiros, T.; Nordlund, D.; Lochocki, E.B.; Shen, K.M.; Park, J.; Pasupathy, A.N. Imaging chiral symmetry breaking from Kekulé bond order in graphene. Nat. Phys. 2016, 12, 950–958. [Google Scholar] [CrossRef]
- Coissard, A.; Wander, D.; Vignaud, H.; Grushin, A.G.; Repellin, C.; Watanabe, K.; Taniguchi, T.; Gay, F.; Winkelmann, C.B.; Courtois, H.; et al. Imaging tunable quantum Hall broken-symmetry orders in graphene. Nature 2022, 605, 51–56. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.Y.; Law, K.T.; Lee, P.A. Kekulé valence bond order in an extended Hubbard model on the honeycomb lattice with possible applications to twisted bilayer graphene. Phys. Rev. B 2018, 98, 121406. [Google Scholar] [CrossRef]
- Andrade, E.; Carrillo-Bastos, R.; Naumis, G.G. Valley engineering by strain in Kekulé-distorted graphene. Phys. Rev. B 2019, 99, 035411. [Google Scholar] [CrossRef]
- Andrade, E.; Carrillo-Bastos, R.; Asmar, M.M.; Naumis, G.G. Kekulé-induced valley birefringence and skew scattering in graphene. Phys. Rev. B 2022, 106, 195413. [Google Scholar] [CrossRef]
- Andrade, E.; Naumis, G.G.; Carrillo-Bastos, R. Electronic spectrum of Kekulé patterned graphene considering second neighbor-interactions. J. Phys. Condens. Matter 2021, 33, 225301. [Google Scholar] [CrossRef]
- Mojarro, M.; Ibarra-Sierra, V.; Sandoval-Santana, J.; Carrillo-Bastos, R.; Naumis, G.G. Dynamical Floquet spectrum of Kekulé-distorted graphene under normal incidence of electromagnetic radiation. Phys. Rev. B 2020, 102, 165301. [Google Scholar] [CrossRef]
- Geim, A.K. Graphene: Status and prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [PubMed]
- Neto, A.C.; Guinea, F.; Peres, N.M.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Houssa, M.; Dimoulas, A.; Molle, A. Silicene: A review of recent experimental and theoretical investigations. J. Phys. Condens. Matter 2015, 27, 253002. [Google Scholar] [CrossRef] [PubMed]
- Kara, A.; Enriquez, H.; Seitsonen, A.P.; Voon, L.L.Y.; Vizzini, S.; Aufray, B.; Oughaddou, H. A review on silicene—New candidate for electronics. Surf. Sci. Rep. 2012, 67, 1–18. [Google Scholar] [CrossRef]
- Ezawa, M. A topological insulator and helical zero mode in silicene under an inhomogeneous electric field. New J. Phys. 2012, 14, 033003. [Google Scholar] [CrossRef]
- Choi, W.; Choudhary, N.; Han, G.H.; Park, J.; Akinwande, D.; Lee, Y.H. Recent development of two-dimensional transition metal dichalcogenides and their applications. Mater. Today 2017, 20, 116–130. [Google Scholar] [CrossRef]
- Manzeli, S.; Ovchinnikov, D.; Pasquier, D.; Yazyev, O.V.; Kis, A. 2D transition metal dichalcogenides. Nat. Rev. Mater. 2017, 2, 17033. [Google Scholar] [CrossRef]
- Tabert, C. Electronic Phenomena in 2D Dirac-like Systems: Silicene and Topological Insulator Surface States. Ph.D. Thesis, University of Guelph, Guelph, ON, Canada, 2015. [Google Scholar]
- Illes, E. Properties of the α-T3 Model. Ph.D. Thesis, University of Guelph, Guelph, ON, Canada, 2017. [Google Scholar]
- Bercioux, D.; Urban, D.; Grabert, H.; Häusler, W. Massless Dirac-Weyl fermions in a T 3 optical lattice. Phys. Rev. A 2009, 80, 063603. [Google Scholar] [CrossRef]
- Iurov, A.; Gumbs, G.; Huang, D. Many-body effects and optical properties of single and double layer α-lattices. J. Phys. Condens. Matter 2020, 32, 415303. [Google Scholar] [CrossRef]
- Malcolm, J.; Nicol, E. Frequency-dependent polarizability, plasmons, and screening in the two-dimensional pseudospin-1 dice lattice. Phys. Rev. B 2016, 93, 165433. [Google Scholar] [CrossRef]
- Iurov, A.; Zhemchuzhna, L.; Dahal, D.; Gumbs, G.; Huang, D. Quantum-statistical theory for laser-tuned transport and optical conductivities of dressed electrons in α-T3 materials. Phys. Rev. B 2020, 101, 035129. [Google Scholar] [CrossRef]
- Filusch, A.; Fehske, H. Tunable valley filtering in dynamically strained α-T3 lattices. Phys. Rev. B 2022, 106, 245106. [Google Scholar] [CrossRef]
- Zeng, W.; Shen, R. Pure crossed Andreev reflection assisted transverse valley currents in α-T3 lattices. arXiv 2022, arXiv:2205.14930. [Google Scholar] [CrossRef]
- Li, F.; Zhang, Q.; Chan, K.S. Novel Transport Properties of the α-T3 Lattice with Uniform Electric and Magnetic Fields: The Effects of Flat Bands. Sci. Rep. 2022, 12, 12987. [Google Scholar] [CrossRef] [PubMed]
- Iurov, A.; Gumbs, G.; Huang, D. Temperature-and frequency-dependent optical and transport conductivities in doped buckled honeycomb lattices. Phys. Rev. B 2018, 98, 075414. [Google Scholar] [CrossRef]
- Tamang, L.; Biswas, T. Probing topological signatures in an optically driven α-T3 lattice. Phys. Rev. B 2023, 107, 085408. [Google Scholar] [CrossRef]
- Iurov, A.; Zhemchuzhna, L.; Gumbs, G.; Huang, D.; Dahal, D.; Abranyos, Y. Finite-temperature plasmons, damping, and collective behavior in the α-T3 model. Phys. Rev. B 2022, 105, 245414. [Google Scholar] [CrossRef]
- Biswas, T.; Ghosh, T.K. Dynamics of a quasiparticle in the α-T3 model: Role of pseudospin polarization and transverse magnetic field on zitterbewegung. J. Phys. Condens. Matter 2018, 30, 075301. [Google Scholar] [CrossRef]
- Gorbar, E.; Gusynin, V.; Oriekhov, D. Electron states for gapped pseudospin-1 fermions in the field of a charged impurity. Phys. Rev. B 2019, 99, 155124. [Google Scholar] [CrossRef]
- Oriekhov, D.; Gusynin, V. Optical conductivity of semi-Dirac and pseudospin-1 models: Zitterbewegung approach. Phys. Rev. B 2022, 106, 115143. [Google Scholar] [CrossRef]
- Sukhachov, P.; Oriekhov, D.; Gorbar, E. Optical conductivity of bilayer dice lattices. arXiv 2023, arXiv:2303.08258. [Google Scholar]
- Oriekhov, D.; Gusynin, V. RKKY interaction in a doped pseudospin-1 fermion system at finite temperature. Phys. Rev. B 2020, 101, 235162. [Google Scholar] [CrossRef]
- Balassis, A.; Dahal, D.; Gumbs, G.; Iurov, A.; Huang, D.; Roslyak, O. Magnetoplasmons for the α-T3 model with filled Landau levels. J. Phys. Condens. Matter 2020, 32, 485301. [Google Scholar] [CrossRef] [PubMed]
- Tabert, C.J.; Nicol, E.J. Valley-spin polarization in the magneto-optical response of silicene and other similar 2D crystals. Phys. Rev. Lett. 2013, 110, 197402. [Google Scholar] [CrossRef] [PubMed]
- Tabert, C.J.; Nicol, E.J. Magneto-optical conductivity of silicene and other buckled honeycomb lattices. Phys. Rev. B 2013, 88, 085434. [Google Scholar] [CrossRef]
- Gumbs, G.; Iurov, A.; Huang, D.; Zhemchuzhna, L. Revealing Hofstadter spectrum for graphene in a periodic potential. Phys. Rev. B 2014, 89, 241407. [Google Scholar] [CrossRef]
- Kovács, Á.D.; Dávid, G.; Dóra, B.; Cserti, J. Frequency-dependent magneto-optical conductivity in the generalized α-T3 model. Phys. Rev. B 2017, 95, 035414. [Google Scholar] [CrossRef]
- Raoux, A.; Morigi, M.; Fuchs, J.N.; Piéchon, F.; Montambaux, G. From dia-to paramagnetic orbital susceptibility of massless fermions. Phys. Rev. Lett. 2014, 112, 026402. [Google Scholar] [CrossRef]
- Vogl, M.; Pankratov, O.; Shallcross, S. Semiclassics for matrix hamiltonians: The gutzwiller trace formula with applications to graphene-type systems. Phys. Rev. B 2017, 96, 035442. [Google Scholar] [CrossRef]
- Zhang, Y.; Barlas, Y.; Yang, K. Coulomb impurity under magnetic field in graphene: A semiclassical approach. Phys. Rev. B 2012, 85, 165423. [Google Scholar] [CrossRef]
- Weekes, N.; Iurov, A.; Zhemchuzhna, L.; Gumbs, G.; Huang, D. Generalized WKB theory for electron tunneling in gapped α-T3 lattices. Phys. Rev. B 2021, 103, 165429. [Google Scholar] [CrossRef]
- Zalipaev, V.; Maksimov, D.; Linton, C.; Kusmartsev, F. Spectrum of localized states in graphene quantum dots and wires. Phys. Lett. A 2013, 377, 216–221. [Google Scholar] [CrossRef]
- Zalipaev, V.; Linton, C.; Croitoru, M.; Vagov, A. Resonant tunneling and localized states in a graphene monolayer with a mass gap. Phys. Rev. B 2015, 91, 085405. [Google Scholar] [CrossRef]
- Blaise, K.; Ejiogu, C.; Iurov, A.; Zhemchuzhna, L.; Gumbs, G.; Huang, D. Developing semiclassical Wentzel-Kramers-Brillouin theory for α-T3 model. Phys. Rev. B 2023, 107, 045128. [Google Scholar] [CrossRef]
- Zalipaev, V. Complex WKB approximations in graphene electron-hole waveguides in magnetic field. In Graphene–Synthesis, Characterization, Properties and Applications; BoD—Books on Demand: Norderstedt, Germany, 2011; p. 81. [Google Scholar]
- Wang, J.J.; Liu, S.; Wang, J.; Liu, J.F. Valley-coupled transport in graphene with Y-shaped Kekulé structure. Phys. Rev. B 2018, 98, 195436. [Google Scholar] [CrossRef]
- Andrade, E.; Carrillo-Bastos, R.; Pantaleon, P.A.; Mireles, F. Resonant transport in Kekule-distorted graphene nanoribbons. J. Appl. Phys. 2020, 127, 054304. [Google Scholar] [CrossRef]
- Katsnelson, M.; Novoselov, K.; Geim, A. Chiral tunnelling and the Klein paradox in graphene. Nat. Phys. 2006, 2, 620–625. [Google Scholar] [CrossRef]
- Allain, P.E.; Fuchs, J.N. Klein tunneling in graphene: Optics with massless electrons. Eur. Phys. J. B 2011, 83, 301–317. [Google Scholar] [CrossRef]
- Gumbs, G.; Balassis, A.; Iurov, A.; Fekete, P. Strongly localized image states of spherical graphitic particles. Sci. World J. 2014, 2014, 726303. [Google Scholar] [CrossRef]
- Roslyak, O.; Iurov, A.; Gumbs, G.; Huang, D. Unimpeded tunneling in graphene nanoribbons. J. Phys. Condens. Matter 2010, 22, 165301. [Google Scholar] [CrossRef]
- Iurov, A.; Zhemchuzhna, L.; Gumbs, G.; Huang, D.; Fekete, P.; Anwar, F.; Dahal, D.; Weekes, N. Tailoring plasmon excitations in α-T3 armchair nanoribbons. Sci. Rep. 2021, 11, 20577. [Google Scholar] [CrossRef] [PubMed]
- Illes, E.; Nicol, E. Klein tunneling in the α-T3 model. Phys. Rev. B 2017, 95, 235432. [Google Scholar] [CrossRef]
- Ye, X.; Ke, S.S.; Du, X.W.; Guo, Y.; Lü, H.F. Quantum tunneling in the α-T3 model with an effective mass term. J. Low Temp. Phys. 2020, 199, 1332–1343. [Google Scholar] [CrossRef]
- Cunha, S.; da Costa, D.; Pereira, J.M., Jr.; Costa Filho, R.; Van Duppen, B.; Peeters, F. Tunneling properties in α-T3 lattices: Effects of symmetry-breaking terms. Phys. Rev. B 2022, 105, 165402. [Google Scholar] [CrossRef]
- Mandhour, L.; Bouhadida, F. Klein tunneling in deformed α-T3 lattice. arXiv 2020, arXiv:2004.10144. [Google Scholar]
- Iurov, A.; Zhemchuzhna, L.; Fekete, P.; Gumbs, G.; Huang, D. Klein tunneling of optically tunable Dirac particles with elliptical dispersions. Phys. Rev. Res. 2020, 2, 043245. [Google Scholar] [CrossRef]
- Li, Z.; Cao, T.; Wu, M.; Louie, S.G. Generation of anisotropic massless Dirac fermions and asymmetric Klein tunneling in few-layer black phosphorus superlattices. Nano Lett. 2017, 17, 2280–2286. [Google Scholar] [CrossRef]
- Iurov, A.; Zhemchuzhna, L.; Gumbs, G.; Huang, D.; Fekete, P. Optically modulated tunneling current of dressed electrons in graphene and a dice lattice. Phys. Rev. B 2022, 105, 115309. [Google Scholar] [CrossRef]
- Barbier, M.; Vasilopoulos, P.; Peeters, F. Extra Dirac points in the energy spectrum for superlattices on single-layer graphene. Phys. Rev. B 2010, 81, 075438. [Google Scholar] [CrossRef]
- Iurov, A.; Gumbs, G.; Huang, D. Peculiar electronic states, symmetries, and berry phases in irradiated α-T3 materials. Phys. Rev. B 2019, 99, 205135. [Google Scholar] [CrossRef]
- Kibis, O. Metal-insulator transition in graphene induced by circularly polarized photons. Phys. Rev. B 2010, 81, 165433. [Google Scholar] [CrossRef]
- Barbier, M.; Vasilopoulos, P.; Peeters, F.M. Single-layer and bilayer graphene superlattices: Collimation, additional Dirac points and Dirac lines. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 5499–5524. [Google Scholar] [CrossRef] [PubMed]
- Pereira, J.M.; Peeters, F.; Chaves, A.; Farias, G. Klein tunneling in single and multiple barriers in graphene. Semicond. Sci. Technol. 2010, 25, 033002. [Google Scholar] [CrossRef]
- Dey, B.; Ghosh, T.K. Floquet topological phase transition in the α-T3 lattice. Phys. Rev. B 2019, 99, 205429. [Google Scholar] [CrossRef]
- Iurov, A.; Gumbs, G.; Huang, D. Exchange and correlation energies in silicene illuminated by circularly polarized light. J. Mod. Opt. 2017, 64, 913–920. [Google Scholar] [CrossRef]
- Iurov, A.; Zhemchuzhna, L.; Gumbs, G.; Huang, D. Exploring interacting Floquet states in black phosphorus: Anisotropy and bandgap laser tuning. J. Appl. Phys. 2017, 122, 124301. [Google Scholar] [CrossRef]
- Iorsh, I.; Zezyulin, D.; Kolodny, S.; Sinitskiy, R.; Kibis, O. Floquet engineering of excitons in semiconductor quantum dots. Phys. Rev. B 2022, 105, 165414. [Google Scholar] [CrossRef]
- Kristinsson, K.; Kibis, O.V.; Morina, S.; Shelykh, I.A. Control of electronic transport in graphene by electromagnetic dressing. Sci. Rep. 2016, 6, 20082. [Google Scholar] [CrossRef]
- Tamang, L.; Nag, T.; Biswas, T. Floquet engineering of low-energy dispersions and dynamical localization in a periodically kicked three-band system. Phys. Rev. B 2021, 104, 174308. [Google Scholar] [CrossRef]
- Iurov, A.; Zhemchuzhna, L.; Gumbs, G.; Huang, D.; Tse, W.K.; Blaise, K.; Ejiogu, C. Floquet engineering of tilted and gapped Dirac bandstructure in 1T′-MoS2. Sci. Rep. 2022, 12, 21348. [Google Scholar] [CrossRef]
- Anwar, F.; Iurov, A.; Huang, D.; Gumbs, G.; Sharma, A. Interplay between effects of barrier tilting and scatterers within a barrier on tunneling transport of Dirac electrons in graphene. Phys. Rev. B 2020, 101, 115424. [Google Scholar] [CrossRef]
- Shih, P.H.; Gumbs, G.; Huang, D.; Iurov, A.; Abranyos, Y. Blocked electron transmission/reflection by coupled Rashba–Zeeman effects for forward and backward spin filtering. J. Appl. Phys. 2022, 132, 154302. [Google Scholar] [CrossRef]
- Ang, Y.S.; Ma, Z.; Zhang, C. Chiral-like tunneling of electrons in two-dimensional semiconductors with Rashba spin–orbit coupling. Sci. Rep. 2014, 4, 3780. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).