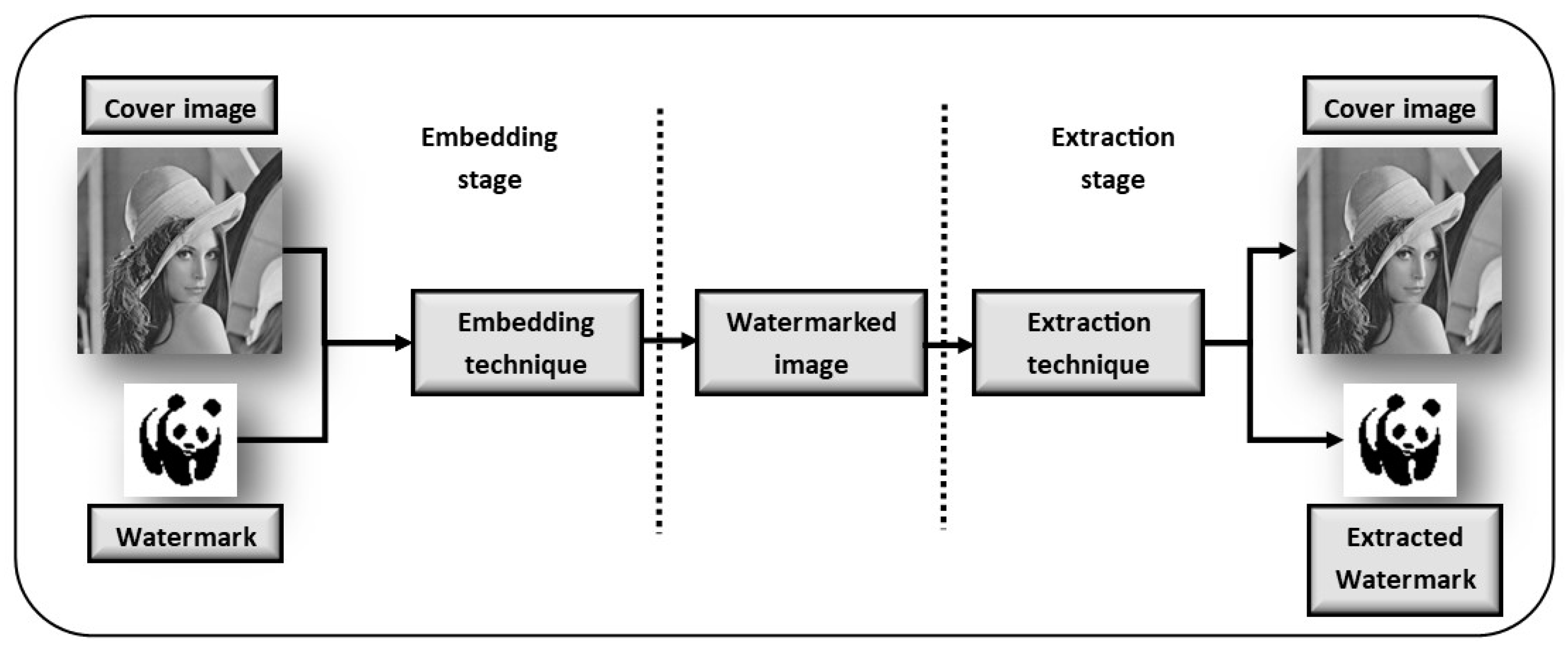
Robust Image Watermarking in Spatial Domain Utilizing Features Equivalent to SVD Transform
Abstract
:1. Introduction
- 1.
- Replication of the redistributed invariant wavelet transform concept to the spatial domain;
- 2.
- Application of the matrix 2-norm instead of SVD to obtain singular values;
- 3.
- Development of a new image watermarking scheme in the spatial domain;
- 4.
- Evaluation of the performance of the proposed scheme for grayscale images using a number of metrics and attacks.
2. Review of the Algorithmic Concepts
2.1. Singular Value Decomposition
2.2. Matrix Norm
2.3. SVD-Based Watermarking Scheme
3. Proposed Watermarking Scheme
3.1. Block-Wise Invariant Maximum Singular Value in the Spatial Domain
3.2. Watermark Embedding Process
- Step 1: Encrypt the watermark image W using the piecewise linear chaotic map (PWLCM) [54] prior to embedding it into the cover image using a secret key (k) to increase the security of the watermarking approach by adding an additional layer. This is one of the chaotic maps that has recently gained popularity due to its dynamic nature, simple form, and effective implementation. Without the correct security key, an impostor or unauthorized user cannot detect the watermark in the watermarked image.
- Step 2: Image B is created by rearranging the pixels of cover image ‘A’ in order to obtain the invariant features described in Section 3.1, and this image is split into 4 × 4 non-overlapping blocks Bi,j (i = 1, 2,…, m/4; j = 1, 2,…, m/4). Because a watermark is introduced one bit at a time into each block, the number of non-overlapping blocks must be greater than or equal to the number of watermark bits. Using the matrix 2-norm (Equation (4)), the invariant largest singular value σmax of each image block of redistributed image B is calculated in the spatial domain instead of applying the SVD transform. In the proposed scheme, the number of blocks is more than the watermark’s size, so these singular values are arranged in descending order, and the largest of these are selected according to the watermark’s capacity. The selection of these singular values is motivated by their good imperceptibility relative to other singular values.
- Step 3: Modification magnitudes T1 and T2, which are decided based on the watermark information, are given by Equation (17):
- Step 4: The potential quantization results Q1 and Q2, utilizing these magnitudes T1 and T2, are now calculated as follows:
- Step 5: Based on Q1 and Q2, the modified singular value corresponding to the singular value is obtained as follows:
- Step 6: Singular value difference ∆σ between modified singular value and its corresponding singular value, , is calculated using Equation (20).
- Step 7: Difference matrix ∆A can be achieved with the help of the difference in singular value ∆σ using Equation (12) as . With the help of this difference matrix and using Equation (9), watermark bits are directly inserted into image block Bi,j by altering the image pixels. The procedure is repeated until all watermark bits are embedded, and then the reverse process is applied to put back the pixels in their original places to create watermarked image Aw.
3.3. Watermark Extraction Process
- Step 1: The pixels of the distorted watermarked image ‘Aw’ are redistributed, as described in Section 3.1. The image is divided into 4 × 4 blocks, and the blocks with the watermark information are selected to directly compute the invariant maximum singular value in the spatial domain instead of the SVD transform by Equation (4).
- Step 2: With the help of the singular values obtained in Step 1 and quantization parameter ‘Q’, the encrypted watermark can be extracted by the following Equation (21).
- Step 3: The decryption process is applied with the proper key to obtain the embedded watermark W’ that was extracted in Step 2.
4. Experimental Results Discussion
4.1. Sensitivity Analysis of Quantization Factor Q
4.2. Imperceptibility Analysis
4.3. Robustness Analysis against Attacks
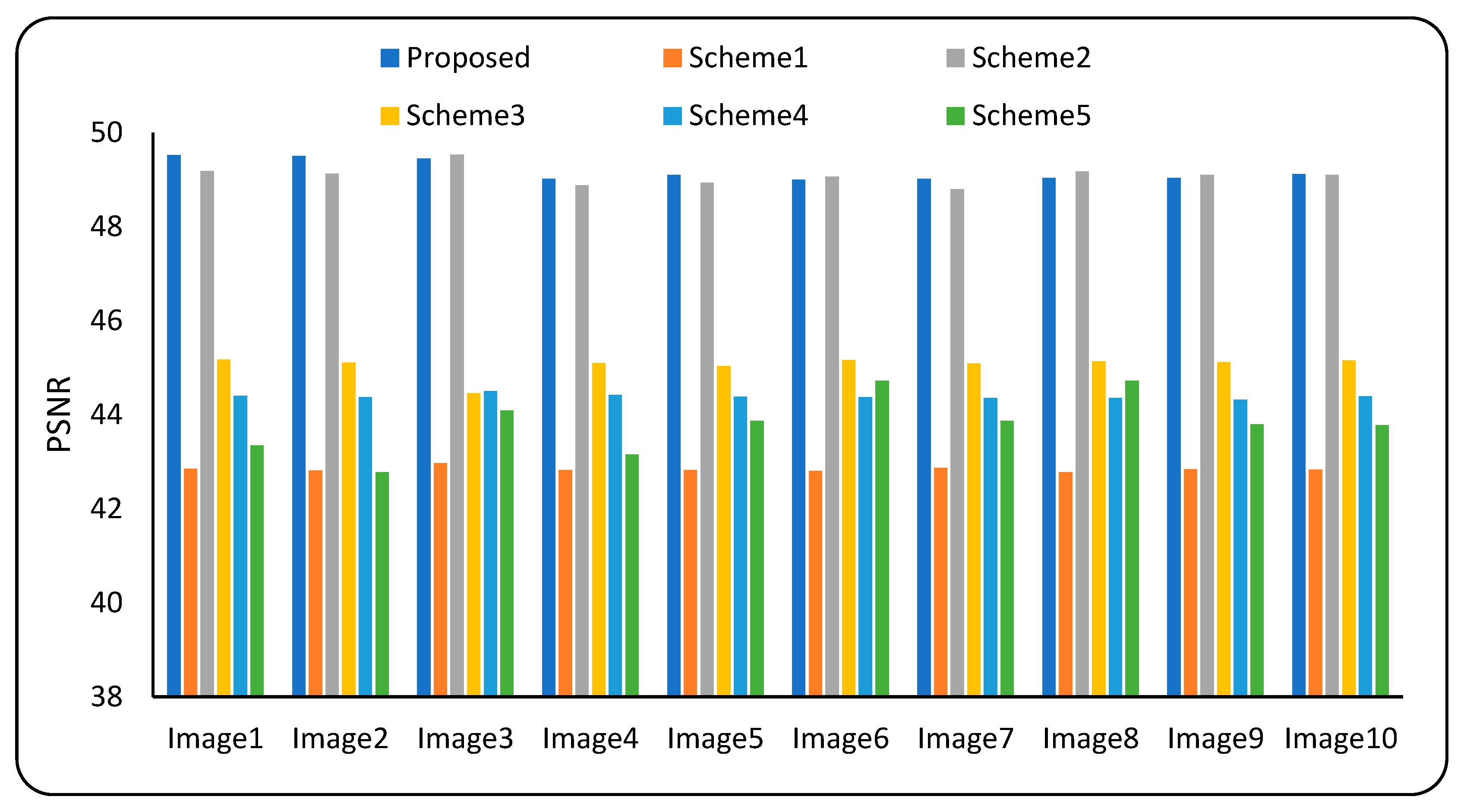
4.4. Comparison with Similar Schemes
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dhawan, S.; Gupta, R. Analysis of Various Data Security Techniques of Steganography: A Survey. Inf. Secur. J. A Glob. Perspect. 2020, 30, 63–87. [Google Scholar] [CrossRef]
- Huh, J.H.; Seo, Y.S. Understanding Edge Computing: Engineering Evolution with Artificial Intelligence. IEEE Access 2019, 7, 164229–164245. [Google Scholar] [CrossRef]
- Tran, D.T.; Huh, J.H. Forecast of Seasonal Consumption Behavior of Consumers and Privacy-Preserving Data Mining with New S-Apriori Algorithm. J. Supercomput. 2023, 1–46. [Google Scholar] [CrossRef]
- Cox, I.; Miller, M.L.; Bloom, J.A. Digital Watermarking; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 2001; ISBN 1-55860-714-5. [Google Scholar]
- Gupta, S.; Saluja, K.; Solanki, V.; Kaur, K.; Singla, P.; Shahid, M. Efficient Methods for Digital Image Watermarking and Information Embedding. Meas. Sens. 2022, 24, 100520. [Google Scholar] [CrossRef]
- Sanivarapu, P.V.; Rajesh, K.N.V.P.S.; Hosny, K.M.; Fouda, M.M. Digital Watermarking System for Copyright Protection and Authentication of Images Using Cryptographic Techniques. Appl. Sci. 2022, 12, 8724. [Google Scholar] [CrossRef]
- El-Kenawy, E.S.M.; Khodadadi, N.; Khoshnaw, A.; Mirjalili, S.; Alhussan, A.A.; Khafaga, D.S.; Ibrahim, A.; Abdelhamid, A.A. Advanced Dipper-Throated Meta-Heuristic Optimization Algorithm for Digital Image Watermarking. Appl. Sci. 2022, 12, 10642. [Google Scholar] [CrossRef]
- Wan, W.; Wang, J.; Zhang, Y.; Li, J.; Yu, H.; Sun, J. A Comprehensive Survey on Robust Image Watermarking. Neurocomputing 2022, 488, 226–247. [Google Scholar] [CrossRef]
- Giri, K.J.; Quadri, S.M.K.; Bashir, R.; Bhat, J.I. DWT Based Color Image Watermarking: A Review. Multimed. Tools Appl. 2020, 79, 32881–32895. [Google Scholar] [CrossRef]
- Alshoura, W.H.; Zainol, Z.; Teh, J.S.; Alawida, M.; Alabdulatif, A. Hybrid SVD-Based Image Watermarking Schemes: A Review. IEEE Access 2021, 9, 32931–32968. [Google Scholar] [CrossRef]
- Abdulloh, F.F.; Rahardi, M.; Putra, W.S.; Amikom, Y.; Sleman, I. A Blind Robust Image Watermarking on Selected DCT Coefficients for Copyright Protection. Artic. Int. J. Adv. Comput. Sci. Appl. 2022, 13, 2022. [Google Scholar] [CrossRef]
- Ray, A.; Roy, S. Recent Trends in Image Watermarking Techniques for Copyright Protection: A Survey. Int. J. Multimed. Inf. Retr. 2020, 9, 249–270. [Google Scholar] [CrossRef]
- Boujerfaoui, S.; Riad, R.; Douzi, H.; Ros, F.; Harba, R. Image Watermarking between Conventional and Learning-Based Techniques: A Literature Review. Electronics 2022, 12, 74. [Google Scholar] [CrossRef]
- Khan, A.; Siddiqa, A.; Munib, S.; Malik, S.A. A Recent Survey of Reversible Watermarking Techniques. Inf. Sci. 2014, 279, 251–272. [Google Scholar] [CrossRef]
- Ahmadi, S.B.B.; Zhang, G.; Wei, S. Robust and Hybrid SVD-Based Image Watermarking Schemes: A Survey. Multimed. Tools Appl. 2020, 79, 1075–1117. [Google Scholar] [CrossRef]
- Mehraj, S.; Mushtaq, S.; Parah, S.A.; Giri, K.J.; Sheikh, J.A.; Gandomi, A.H.; Hijji, M.; Muhammad, K. Spatial Domain-Based Robust Watermarking Framework for Cultural Images. IEEE Access 2022, 10, 117248–117260. [Google Scholar] [CrossRef]
- Ali, M.; Ahn, C.W.; Pant, M.; Kumar, S.; Singh, M.K.; Saini, D. An Optimized Digital Watermarking Scheme Based on Invariant DC Coefficients in Spatial Domain. Electronics 2020, 9, 1428. [Google Scholar] [CrossRef]
- Su, Q.; Yuan, Z.; Liu, D. An Approximate Schur Decomposition-Based Spatial Domain Color Image Watermarking Method. IEEE Access 2019, 7, 4358–4370. [Google Scholar] [CrossRef]
- Bin Faheem, Z.; Ishaq, A.; Rustam, F.; Díez, I.D.L.T.; Gavilanes, D.; Vergara, M.M.; Ashraf, I. Image Watermarking Using Least Significant Bit and Canny Edge Detection. Sensors 2023, 23, 1210. [Google Scholar] [CrossRef]
- Bin Faheem, Z.; Ali, M.; Raza, M.A.; Arslan, F.; Ali, J.; Masud, M.; Shorfuzzaman, M. Image Watermarking Scheme Using LSB and Image Gradient. Appl. Sci. 2022, 12, 4202. [Google Scholar] [CrossRef]
- Sakthivel, S.M.; Sankar, A.R. Computation-Efficient Image Watermarking Architecture with Improved Performance. Comput. Electr. Eng. 2020, 84, 106649. [Google Scholar] [CrossRef]
- Yuan, Z.; Liu, D.; Zhang, X.; Su, Q. New Image Blind Watermarking Method Based on Two-Dimensional Discrete Cosine Transform. Optik 2020, 204, 164152. [Google Scholar] [CrossRef]
- Ariatmanto, D.; Ernawan, F. Adaptive Scaling Factors Based on the Impact of Selected DCT Coefficients for Image Watermarking. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 605–614. [Google Scholar] [CrossRef]
- Pei, L. Research on Digital Image Watermarking Algorithm Based on Scrambling and Singular Value Decomposition. J. Math. 2022, 2022, 4656010. [Google Scholar] [CrossRef]
- Singh, R.; Izhar, L.I.; Elamvazuthi, I.; Ashok, A.; Aole, S.; Sharma, N. Efficient Watermarking Method Based on Maximum Entropy Blocks Selection in Frequency Domain for Color Images. IEEE Access 2022, 10, 52712–52723. [Google Scholar] [CrossRef]
- Elbasi, E.; Mostafa, N.; Cina, E. Robust, Secure and Semi-Blind Watermarking Technique Using Flexible Scaling Factor in Block-Based Wavelet Algorithm. Electronics 2022, 11, 3680. [Google Scholar] [CrossRef]
- Li, L.; Xu, H.H.; Chang, C.C.; Ma, Y.Y. A Novel Image Watermarking in Redistributed Invariant Wavelet Domain. J. Syst. Softw. 2011, 84, 923–929. [Google Scholar] [CrossRef]
- Liu, D.; Yuan, Z.; Su, Q. A Blind Color Image Watermarking Scheme with Variable Steps Based on Schur Decomposition. Multimed. Tools Appl. 2020, 79, 7491–7513. [Google Scholar] [CrossRef]
- Prabha, K.; Shatheesh Sam, I. An Effective Robust and Imperceptible Blind Color Image Watermarking Using WHT. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 2982–2992. [Google Scholar] [CrossRef]
- Garg, P.; Jain, A. A Robust Technique for Biometric Image Authentication Using Invisible Watermarking. Multimed. Tools Appl. 2023, 82, 2237–2253. [Google Scholar] [CrossRef]
- Zermi, N.; Khaldi, A.; Kafi, M.R.; Kahlessenane, F.; Euschi, S. Robust SVD-Based Schemes for Medical Image Watermarking. Microprocess. Microsyst. 2021, 84, 104134. [Google Scholar] [CrossRef]
- Shoron, S.H.; Islam, M.; Uddin, J.; Shon, D.; Im, K.; Park, J.H.; Lim, D.S.; Jang, B.; Kim, J.M. A Watermarking Technique for Biomedical Images Using Smqt, Otsu, and Fuzzy c-Means. Electronics 2019, 8, 975. [Google Scholar] [CrossRef]
- Maity, S.P.; Maity, S.; Sil, J.; Delpha, C. Collusion Resilient Spread Spectrum Watermarking in M-Band Wavelets Using GA-Fuzzy Hybridization. J. Syst. Softw. 2013, 86, 47–59. [Google Scholar] [CrossRef]
- Yang, H.-Y.; Wang, X.-Y.; Zhang, Y.; E-nuo, M. Robust Digital Watermarking in PDTDFB Domain Based on Least Squares Support Vector Machine. Eng. Appl. Artif. Intell. 2013, 26, 2058–2072. [Google Scholar] [CrossRef]
- Takore, T.T.; Rajesh Kumar, P.; Lavanya Devi, G. A New Robust and Imperceptible Image Watermarking Scheme Based on Hybrid Transform and PSO. Int. J. Intell. Syst. Appl. 2018, 10, 50–63. [Google Scholar] [CrossRef]
- Devi, K.J.; Singh, P.; Dash, J.K.; Thakkar, H.K.; Santamaría, J.; Krishna, M.V.J.; Romero-Manchado, A. A New Robust and Secure 3-Level Digital Image Watermarking Method Based on G-BAT Hybrid Optimization. Mathematics 2022, 10, 3015. [Google Scholar] [CrossRef]
- Pallaw, V.K.; Singh, K.U.; Kumar, A.; Singh, T.; Swarup, C.; Goswami, A. A Robust Medical Image Watermarking Scheme Based on Nature-Inspired Optimization for Telemedicine Applications. Electronics 2023, 12, 334. [Google Scholar] [CrossRef]
- Garg, P.; Kishore, R.R. An Efficient and Secured Blind Image Watermarking Using ABC Optimization in DWT and DCT Domain. Multimed. Tools Appl. 2022, 81, 36947–36964. [Google Scholar] [CrossRef]
- Wang, L.; Ji, H.A.; Wang, L.; Ji, H. A Watermarking Optimization Method Based on Matrix Decomposition and DWT for Multi-Size Images. Electronics 2022, 11, 2027. [Google Scholar] [CrossRef]
- Ali, M.; Ahn, C.W.; Pant, M.; Siarry, P. An Image Watermarking Scheme in Wavelet Domain with Optimized Compensation of Singular Value Decomposition via Artificial Bee Colony. Inf. Sci. 2015, 301, 44–60. [Google Scholar] [CrossRef]
- Maity, S.P.; Maity, S.; Sil, J.; Delpha, C. Perceptually Adaptive MC-SS Image Watermarking Using GA-NN Hybridization in Fading Gain. Eng. Appl. Artif. Intell. 2014, 31, 3–14. [Google Scholar] [CrossRef]
- Goyal, A.; Malik, M.; Sharma, S.; Choudhary, S.; Sharma, V.K.; Goyal, A. Image Watermarking in Frequency Domain Using Hu’s Invariant Moments and Firefly Algorithm. nt. J. Image Graph. Signal Process. 2022, 2, 1–15. [Google Scholar] [CrossRef]
- Yazdan Bakhsh, F.; Moghaddam, M.E. A Robust HDR Images Watermarking Method Using Artificial Bee Colony Algorithm. J. Inf. Secur. Appl. 2018, 41, 12–27. [Google Scholar] [CrossRef]
- Cedillo-Hernandez, M.; Cedillo-Hernandez, A.; Garcia-Ugalde, F.J. Improving DFT-Based Image Watermarking Using Particle Swarm Optimization Algorithm. Mathematics 2021, 9, 1795. [Google Scholar] [CrossRef]
- Moosazadeh, M.; Ekbatanifard, G. A New DCT-Based Robust Image Watermarking Method Using Teaching-Learning-Based Optimization. J. Inf. Secur. Appl. 2019, 47, 28–38. [Google Scholar] [CrossRef]
- Hatami, E.; Rashidy Kanan, H.; Layeghi, K.; Harounabadi, A. An Optimized Robust and Invisible Digital Image Watermarking Scheme in Contourlet Domain for Protecting Rightful Ownership. Multimed. Tools Appl. 2023, 82, 2021–2051. [Google Scholar] [CrossRef]
- Su, Q.; Niu, Y.; Wang, Q.; Sheng, G. A Blind Color Image Watermarking Based on DC Component in Thespatial Domain. Optik 2013, 124, 6255–6260. [Google Scholar] [CrossRef]
- Parah, S.A.; Loan, N.A.; Shah, A.A.; Sheikh, J.A.; Bhat, G.M. A New Secure and Robust Watermarking Technique Based on Logistic Map and Modification of DC Coefficient. Nonlinear Dyn. 2018, 93, 1933–1951. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, C.; Zhou, X. A Robust Image Watermarking Scheme Based on SVD in the Spatial Domain. Future Internet 2017, 9, 45. [Google Scholar] [CrossRef]
- Zeng, G.; Qiu, Z. Image Watermarking Based on DC Component in DCT. In Proceedings of the 2nd 2008 International Symposium on Intelligent Information Technology Application Workshop, IITA 2008 Workshop, Shanghai, China, 21–22 December 2008; pp. 573–576. [Google Scholar] [CrossRef]
- Zhang, M.; Ding, W.; Li, Y.; Sun, J.; Liu, Z. Color Image Watermarking Based on a Fast Structure-Preserving Algorithm of Quaternion Singular Value Decomposition. Signal Process. 2023, 208, 108971. [Google Scholar] [CrossRef]
- Zhao, J.; Xu, W.; Zhang, S.; Fan, S.; Zhang, W. A Strong Robust Zero-Watermarking Scheme Based on Shearlets’ High Ability for Capturing Directional Features. Math. Probl. Eng. 2016, 2016, 2643263. [Google Scholar] [CrossRef]
- Ali, M.; Ahn, C.W.; Pant, M.; Siarry, P. A Reliable Image Watermarking Scheme Based on Redistributed Image Normalization and SVD. Discret. Dyn. Nat. Soc. 2016, 2016, 3263587. [Google Scholar] [CrossRef]
- Bakhshandeh, A.; Eslami, Z. An Authenticated Image Encryption Scheme Based on Chaotic Maps and Memory Cellular Automata. Opt. Lasers Eng. 2013, 51, 665–673. [Google Scholar] [CrossRef]












| Attack Index | Description |
|---|---|
| Index0 | No change in watermarked image |
| Index1 | Average filter taking a 3 × 3 window size |
| Index2 | 90° anticlockwise rotation |
| Index3 | 25% central region cropping |
| Index4 | Addition of Gaussian noise with mean 0 and variance 0.005. |
| Index5 | JPEG compression taking a quality factor of 75 |
| Index6 | Rescaling 512 → 256 → 512 |
| Index7 | Median filter taking a 3 × 3 window size |
| Index8 | Salt and pepper noise addition with density of 0.005 |
| Index9 | 10 rows and 10 columns from arbitrary locations are deleted |
| Index10 | Low-pass Gaussian filter with a 3 × 3 window |
| Index11 | Rows flip |
| Index12 | Columns flip |
| Index13 | Motion blur with a 3 × 3 window |
| Index14 | Pixelation with a 2 × 2 window |
| Index15 | Speckle noise with mean of zero and variance of 0.005 |
| IMAGE | PSNR | SSIM | ||||||
|---|---|---|---|---|---|---|---|---|
| W1 | W2 | W3 | W4 | W1 | W2 | W3 | W4 | |
| Image1 | 49.6187 | 49.1559 | 49.5421 | 49.7881 | 0.9957 | 0.9952 | 0.9965 | 0.9966 |
| Image2 | 49.2557 | 49.1345 | 49.8637 | 49.7539 | 0.9950 | 0.9938 | 0.9977 | 0.9969 |
| Image3 | 49.0906 | 49.6372 | 49.5223 | 49.5529 | 0.9955 | 0.9967 | 0.9958 | 0.9962 |
| Image4 | 48.8722 | 49.1299 | 49.2188 | 48.8660 | 0.9972 | 0.9963 | 0.9971 | 0.9973 |
| Image5 | 49.0075 | 48.7838 | 49.3393 | 49.2890 | 0.9964 | 0.9956 | 0.9974 | 0.9965 |
| Image6 | 48.6690 | 49.0954 | 49.2958 | 48.9566 | 0.9946 | 0.9956 | 0.9949 | 0.9951 |
| Image7 | 48.8956 | 49.2559 | 48.8997 | 49.0164 | 0.9957 | 0.9973 | 0.9954 | 0.9964 |
| Image8 | 49.2894 | 49.1746 | 48.8634 | 48.8375 | 0.9841 | 0.9845 | 0.9846 | 0.9857 |
| Image9 | 48.8736 | 49.1341 | 49.2494 | 48.8962 | 0.9940 | 0.9923 | 0.9942 | 0.9934 |
| Image10 | 49.1469 | 49.0825 | 49.3130 | 48.9508 | 0.9954 | 0.9949 | 0.9963 | 0.9939 |
| IMAGE | NCC | BER | ||||||
|---|---|---|---|---|---|---|---|---|
| W1 | W2 | W3 | W4 | W1 | W2 | W3 | W4 | |
| Image1 | 0.9664 | 0.9329 | 0.9501 | 0.9401 | 0.0464 | 0.0376 | 0.0422 | 0.0407 |
| Image2 | 0.9655 | 0.9334 | 0.9480 | 0.9430 | 0.0478 | 0.0377 | 0.0442 | 0.0390 |
| Image3 | 0.9390 | 0.8797 | 0.9145 | 0.8935 | 0.0851 | 0.0740 | 0.0767 | 0.0777 |
| Image4 | 0.9733 | 0.9430 | 0.9585 | 0.9527 | 0.0376 | 0.0321 | 0.0357 | 0.0324 |
| Image5 | 0.9451 | 0.8993 | 0.9187 | 0.9076 | 0.0747 | 0.0597 | 0.0693 | 0.0641 |
| Image6 | 0.9672 | 0.9410 | 0.9546 | 0.9456 | 0.0460 | 0.0328 | 0.0387 | 0.0368 |
| Image7 | 0.9424 | 0.8969 | 0.9213 | 0.9107 | 0.0754 | 0.0581 | 0.0647 | 0.0599 |
| Image8 | 0.9632 | 0.9332 | 0.9513 | 0.9425 | 0.0505 | 0.0373 | 0.0413 | 0.0389 |
| Image9 | 0.9486 | 0.9079 | 0.9287 | 0.9184 | 0.0694 | 0.0524 | 0.0598 | 0.0558 |
| Image10 | 0.9503 | 0.9056 | 0.9320 | 0.9217 | 0.0676 | 0.0546 | 0.0580 | 0.0545 |
| Image/ Attack | Image1 | Image2 | Image3 | Image4 | Image5 | Image6 | Image7 | Image8 | Image9 | Image10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Index0 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Index1 | 0.7691 | 0.7511 | 0.7390 | 0.7906 | 0.6424 | 0.7861 | 0.7187 | 0.7851 | 0.7024 | 0.6909 |
| Index2 | 1.0000 | 1.0000 | 0.9714 | 1.0000 | 1.0000 | 1.0000 | 0.9998 | 1.0000 | 1.0000 | 1.0000 |
| Index3 | 0.8209 | 0.9039 | 0.7628 | 0.9495 | 0.8348 | 0.8619 | 0.6213 | 0.7844 | 0.7515 | 0.7896 |
| Index4 | 0.9994 | 0.9991 | 0.9528 | 0.9997 | 0.9984 | 0.9996 | 0.9949 | 0.9995 | 1.0000 | 0.9962 |
| Index5 | 0.9998 | 0.9996 | 0.9553 | 0.9996 | 0.9987 | 0.9992 | 0.9943 | 0.9990 | 0.9997 | 0.9961 |
| Index6 | 0.9179 | 0.8910 | 0.8473 | 0.9394 | 0.8051 | 0.9301 | 0.8525 | 0.9150 | 0.8620 | 0.8397 |
| Index7 | 0.8406 | 0.8313 | 0.7901 | 0.8651 | 0.7572 | 0.8686 | 0.8085 | 0.8768 | 0.7925 | 0.8385 |
| Index8 | 0.9212 | 0.9270 | 0.9057 | 0.9377 | 0.9348 | 0.9345 | 0.9414 | 0.9245 | 0.9208 | 0.9381 |
| Index9 | 0.9490 | 0.9675 | 0.9045 | 0.8866 | 0.9274 | 0.9139 | 0.8976 | 0.9290 | 0.9061 | 0.9239 |
| Index10 | 0.9996 | 0.9878 | 0.9372 | 0.9827 | 0.9577 | 0.9971 | 0.9857 | 0.9937 | 0.9832 | 0.9636 |
| Index11 | 1.0000 | 1.0000 | 0.9714 | 1.0000 | 1.0000 | 1.0000 | 0.9998 | 1.0000 | 1.0000 | 1.0000 |
| Index12 | 1.0000 | 1.0000 | 0.9714 | 1.0000 | 1.0000 | 1.0000 | 0.9998 | 1.0000 | 1.0000 | 1.0000 |
| Index13 | 0.9405 | 0.9014 | 0.8771 | 0.9594 | 0.8274 | 0.9421 | 0.8755 | 0.9539 | 0.8961 | 0.8662 |
| Index14 | 1.0000 | 1.0000 | 0.9685 | 1.0000 | 0.9997 | 1.0000 | 0.9994 | 1.0000 | 1.0000 | 0.9984 |
| Index15 | 1.0000 | 1.0000 | 0.9522 | 1.0000 | 0.9991 | 1.0000 | 0.9962 | 1.0000 | 1.0000 | 0.9974 |
| Image/ Attack | Image1 | Image2 | Image3 | Image4 | Image5 | Image6 | Image7 | Image8 | Image9 | Image10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Index0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Index1 | 0.1826 | 0.1984 | 0.2444 | 0.1650 | 0.2952 | 0.1710 | 0.2338 | 0.1744 | 0.2432 | 0.2564 |
| Index2 | 0.0000 | 0.0000 | 0.0231 | 0.0000 | 0.0000 | 0.0000 | 0.0002 | 0.0000 | 0.0000 | 0.0000 |
| Index3 | 0.1448 | 0.0799 | 0.1848 | 0.0440 | 0.1331 | 0.1130 | 0.2713 | 0.1708 | 0.1915 | 0.1667 |
| Index4 | 0.0004 | 0.0007 | 0.0378 | 0.0002 | 0.0013 | 0.0003 | 0.0040 | 0.0004 | 0.0001 | 0.0031 |
| Index5 | 0.0001 | 0.0003 | 0.0356 | 0.0003 | 0.0011 | 0.0005 | 0.0046 | 0.0009 | 0.0003 | 0.0033 |
| Index6 | 0.0647 | 0.0884 | 0.1284 | 0.0494 | 0.1586 | 0.0574 | 0.1201 | 0.0681 | 0.1120 | 0.1309 |
| Index7 | 0.1230 | 0.1328 | 0.1866 | 0.1035 | 0.1945 | 0.1028 | 0.1514 | 0.0973 | 0.1655 | 0.1266 |
| Index8 | 0.0636 | 0.0585 | 0.0754 | 0.0500 | 0.0521 | 0.0524 | 0.0468 | 0.0606 | 0.0636 | 0.0495 |
| Index9 | 0.0408 | 0.0258 | 0.0770 | 0.0921 | 0.0590 | 0.0696 | 0.0828 | 0.0576 | 0.0763 | 0.0616 |
| Index10 | 0.0003 | 0.0098 | 0.0502 | 0.0136 | 0.0338 | 0.0022 | 0.0115 | 0.0048 | 0.0132 | 0.0289 |
| Index11 | 0.0000 | 0.0000 | 0.0231 | 0.0000 | 0.0000 | 0.0000 | 0.0002 | 0.0000 | 0.0000 | 0.0000 |
| Index12 | 0.0000 | 0.0000 | 0.0231 | 0.0000 | 0.0000 | 0.0000 | 0.0002 | 0.0000 | 0.0000 | 0.0000 |
| Index13 | 0.0473 | 0.0805 | 0.1004 | 0.0333 | 0.1414 | 0.0477 | 0.1017 | 0.0370 | 0.0840 | 0.1087 |
| Index14 | 0.0000 | 0.0000 | 0.0255 | 0.0000 | 0.0002 | 0.0000 | 0.0005 | 0.0000 | 0.0000 | 0.0013 |
| Index15 | 0.0000 | 0.0000 | 0.0383 | 0.0000 | 0.0007 | 0.0000 | 0.0031 | 0.0000 | 0.0000 | 0.0021 |
| Time | Proposed | Parah et al. [48] | Zhang et al. [49] | Zeng et al. [50] | Su et al. [47] | Elbasi et al. [26] |
|---|---|---|---|---|---|---|
| Embedding time | 0.3086 | 0.0246 | 0.3041 | 0.0279 | 0.0288 | 1.3742 |
| Extraction time | 0.2895 | 0.0092 | 0.2837 | 0.0090 | 0.0144 | 0.9874 |
| Total | 0.5982 | 0.0339 | 0.5878 | 0.0369 | 0.0432 | 2.3616 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, M. Robust Image Watermarking in Spatial Domain Utilizing Features Equivalent to SVD Transform. Appl. Sci. 2023, 13, 6105. https://doi.org/10.3390/app13106105
Ali M. Robust Image Watermarking in Spatial Domain Utilizing Features Equivalent to SVD Transform. Applied Sciences. 2023; 13(10):6105. https://doi.org/10.3390/app13106105
Chicago/Turabian StyleAli, Musrrat. 2023. "Robust Image Watermarking in Spatial Domain Utilizing Features Equivalent to SVD Transform" Applied Sciences 13, no. 10: 6105. https://doi.org/10.3390/app13106105
APA StyleAli, M. (2023). Robust Image Watermarking in Spatial Domain Utilizing Features Equivalent to SVD Transform. Applied Sciences, 13(10), 6105. https://doi.org/10.3390/app13106105






