A Novel Fractional Sine Chaotic Map and Its Application to Image Encryption and Watermarking

Abstract

This article addresses the telecommunications industry’s priority of ensuring information security during the transition to next-generation networks. It proposes an image encryption system that combines watermarking techniques and a discrete fractional sine chaotic map. The authors also incorporate the principles of blockchain to enhance the security of transmitted and received image data. The proposed system utilizes a newly developed sine chaotic map with a fractional difference operator, exhibiting long-term chaotic dynamics. The complexity of this map is demonstrated by comparing it with three other fractional chaotic maps from existing literature, using bifurcation diagrams and the largest Lyapunov exponent. The authors also show the map’s sensitivity to changes in initial conditions through time-series diagrams. To encrypt images, the authors suggest a method involving watermarking of two secret images and encryption based on blockchain technology. The cover image is watermarked with the two hidden images using discrete wavelet transformations. Then, the image pixels undergo diffusion using a chaotic matrix generated from the discrete fractional sine chaotic map. This encryption process aims to protect the image data and make it resistant to unauthorized access. To evaluate the algorithm, the authors perform statistical analysis and critical sensitivity analysis to examine its characteristics. They also analyse different attacks to assess the algorithm’s ability to resist such threats and maintain image quality after decryption. The results demonstrate that the proposed algorithm effectively defends against attacks and ensures image security.

1. Introduction

Ensuring the confidentiality of sensitive information in the digital era is a critical concern. Various research fields, such as cryptography and cyber forensics, aim to protect information from unauthorized access. Information security revolves around preventing unauthorized disclosure, maintaining data integrity, and ensuring accessibility when needed. Image encryption plays a crucial role in securely transmitting information through images, with applications ranging from medical imaging to military operations. With the advancement of technology, the need for robust image encryption algorithms has grown. Multimedia data, including images, are susceptible to attacks and alterations. In military operations, even a slight information leak can pose a significant risk to national security. Therefore, algorithms need to provide strong security measures against various attacks and prevent information detection. One technology that offers advanced data security is blockchain. Industries are exploring blockchain for secure record-keeping, as it replaces centralized systems with decentralized ones involving only the relevant parties in a transaction. Blockchain technology is not limited to financial transactions; it is used for energy transfers between neighbours, copyright verifications in the media industry, and supply chain management. Many industries are embracing blockchain technology due to its advantages.

The working process of blockchain can be explained in simple terms. Transaction data, including details of the parties, conditions, and assets exchanged, are recorded. Consensus is reached among the participants, and the information is securely stored as a block, forming a chain. A final ledger copy is shared with all participants.

Emerging technologies have encouraged industries to explore new methods for enhancing security and overcoming limitations. Blockchain technology offers high security, making it difficult for unauthorized changes to be made to transaction records. It also improves efficiency, transparency, and allows for quick data auditing. Researchers have explored the application of blockchain in secure image sharing [1] and its integration with the Internet of Things (IoT) [2].

Image encryption is a vast field with contributions from researchers across various disciplines. In simple terms, image encryption involves converting an image into an encrypted form using a secret key. The encrypted image is then decrypted by the receiver using the same secret key, but in reverse order. The key used in encryption is of utmost importance. Typically, there are two types of keys: private and public. A private key is a unique key used for both encryption and decryption processes, while public keys consist of separate keys for encryption and decryption. The literature on image encryption encompasses a wide range of algorithms developed to address security requirements. These algorithms aim to protect the confidentiality and integrity of images during transmission and storage. Some methods include the techniques of watermarking [3], steganography [4] and scrambling of images [5]. Over the past few decades, there has been a growing interest in utilizing chaotic systems for cryptography. Chaotic systems have gained popularity due to their unique characteristics such as sensitivity to initial conditions, unpredictability, and randomness. Their implementation in cryptography offers advantages such as cost-effectiveness, computational efficiency, and complexity.

The study of chaos is not a recent development; it was first introduced by Poincare in the 1880s while investigating the three-body problem. However, at that time, there was no formal theory to support the observation of non-periodic oscillations, which hindered the progress of the field. It was in the later part of the twentieth century that Edward Lorenz discovered the sensitivity of chaotic systems to initial conditions, where even a small change can lead to a significantly different outcome. The advent of digital computers played a crucial role in advancing the field. The computational complexity of manually calculating repeated iterations for chaos theory was simplified by electronic computers. As a result, the field of chaos theory experienced significant growth, leading to the development of numerous chaotic systems with strange attractors and hidden attractors. The inherent randomness of chaotic systems makes them well-suited for image encryption processes. When it comes to encrypting images using chaotic maps, the selection of the system used to construct the algorithm becomes a critical task. During the initial phase of the study, logistic map [6] and tent map [7] are used for encryption. The limitations in implementing the system are that the key space is so small that a breach of security is possible. Later, to increase the level of security, higher-dimensional systems, such as the Henon map [8], Tinkerbell map [9], 5D hyperchaotic map [10], are introduced for better key space. An image encryption scheme with a combined 1D map was discussed in [11] and a coupled sine–logistic map was illustrated in [12].

The generalisation of integer-order chaotic systems with arbitrary real or complex orders provides enhanced complexity and non-linearity that highly suit the process of image encryption. Fractional-order derivatives, which are non-local, have the ability to bring the factor of memory into effect. The fractional Lorenz system was considered for the encryption scheme by Radwan et al. in [13]. Application of the fractional-order neural network model was presented in [13] and the authors analysed the characteristics of the complex chaotic system with fractional-order in the image encryption process in [14]. A chaotic system with improper fractional-order is considered for image encryption in [15] and the investigation with improper fractional laser systems was carried out by Yang et al. in [16]. Encryption based on the coexisting attractors of the memristive fractional system was discussed in [17] and the fractional system together with the Fisher–Yates algorithm was employed in [18]. Consequently, during the last decade, discrete time fractional-order systems have gained importance due to their diverse applications. The development of the theory for the field of discrete fractional calculus was due to the pioneering works of Atici and Eloe in [19], Igor Podlubny in [20], and Anastassiou in [21]. Application of discrete fractional calculus to tumour immune systems was discussed in [22], and heat transfer fins and pantograph equations were investigated in [23,24]. Dynamic analysis of the fractional difference chemical reaction model was performed in [25]. The implementation of fractional order in the discrete maps enhances the chaotic nature of the maps. Some recent research contributions based on fractional difference chaotic systems include image encryption with compression based on Bayesian sensing and the 2D fractional discrete time chaotic map in [26]. The application of discrete fractional neural networks to encryption was presented in [27]. The elliptic curve cryptosystem and the 2D fractional-order discrete map are employed for the process of encryption in [28]. Wu et al. presented the technique of encryption of images with chaotic fractional discrete time series in [29] and a novel technique was introduced in [30]. Tempered-type fractional derivatives in discrete time were proposed, and the encryption was discussed in [31]. Motivated by the investigations performed in the recent literature towards the field of image encryption [32,33,34,35,36,37,38], this article aims to contribute the following.

• Construction of a novel fractional difference sine chaotic map with long-term chaotic response illustrated with bifurcation diagrams, Lyapunov exponents, and approximate entropy.
• The application of the proposed discrete fractional sine chaotic map to image encryption of greyscale images is presented by generating a chaotic matrix.
• The watermarking of the secret images at different levels is performed using transform methods.
• For secure transmission of information stored in images, a genesis block is generated to diffuse the pixels of the images that can only be recovered by the recipient with the same genesis block (blockchain concept).

The manuscriptis planned with mathematical prerequisites in Section 2, and novel discrete fractional sine chaotic map construction and comparison are illustrated in Section 3. The scheme of encryption is presented in Section 4, and the analysis of results with supporting figures is provided in Section 5, with a conclusion in Section 6.

2. Prerequisites

This section presents definitions and theorems used in this article. Let ${\mathbb{N}}_{\rho }=\{\rho ,\rho +1,$$\rho +2,\cdots \}$ such that $\rho \in \mathbb{R}.$

Definition 1 

([39]). Consider a real-valued function $\mathsf{\Phi }:{\mathbb{N}}_{\rho }\to \mathbb{R}$. The fractional sum of order β is

$${\mathsf{\Delta }}_{\rho }^{-\beta }\mathsf{\Phi }\left(\omega \right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\beta \right)}}\sum _{\kappa =\rho }^{\omega -\beta }{(\omega -\kappa -1)}^{(\beta -1)}\mathsf{\Phi }\left(\kappa \right),$$

(1)

for $\omega \in {\mathbb{N}}_{\rho +\beta },\beta >0.$

Definition 2 

([39]). For the real-valued $\mathsf{\Phi }:{\mathbb{N}}_{\rho }\to \mathbb{R}$, the Caputo difference of arbitrary order β is

$$\begin{array}{cc}\hfill {}^C{\mathsf{\Delta }}_{\rho }^{\beta }\mathsf{\Phi }\left(\omega \right)=& {\mathsf{\Delta }}_{\rho }^{-(\varpi -\beta )}{\mathsf{\Delta }}^{\varpi }\mathsf{\Phi }\left(\omega \right)\hfill \\ \hfill =& {\displaystyle \frac{1}{\mathsf{\Gamma }(\varpi -\beta )}}\sum _{\kappa =\rho }^{\omega -(\varpi -\beta )}{(\omega -\kappa -1)}^{(\varpi -\beta -1)}\hfill \\ & {\mathsf{\Delta }}^{\varpi }\mathsf{\Phi }\left(\kappa \right),\hfill \end{array}$$

(2)

where $\varpi =\left[\beta \right]+1$, $\beta >0,\omega \in {\mathbb{N}}_{\rho +\varpi -\beta }.$

Theorem 1 

([40]). Consider a β-th-order discrete time system given by

$$\begin{array}{cc}\hfill {}^C{\mathsf{\Delta }}_{\rho }^{\beta }\mathsf{\Phi }\left(\omega \right)=& \mathcal{G}(\omega +\beta -1,\mathsf{\Phi }(\omega +\beta -1\left)\right),\hfill \\ \hfill {\mathsf{\Delta }}^{\varpi }\mathsf{\Phi }\left(\rho \right)=& {\mathsf{\Phi }}_{\varpi },r=⌈\beta ⌉+1,\varpi =0,1,2,\dots ,r-1,\hfill \end{array}$$

(3)

then we obtain the numerical form as follows

$$\mathsf{\Phi }\left(\omega \right)={\mathsf{\Phi }}_0\left(\omega \right)+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\beta \right)}}\sum _{\kappa =\rho +\sigma -\beta }^{\omega -\beta }{(\omega -\kappa +1)}^{(\beta -1)}\mathcal{G}(\kappa +\beta -1,\mathsf{\Phi }(\kappa +\beta -1)),\omega \in {\mathbb{N}}_{\beta +\sigma },$$

(4)

with

$${\mathsf{\Phi }}_0\left(\omega \right)=\sum _{\varpi =0}^{\sigma -1}{\displaystyle \frac{{(\omega -\rho )}^{\left(\varpi \right)}}{\mathsf{\Gamma }(\varpi +1)}}{\mathsf{\Delta }}^{\varpi }\mathsf{\Phi }\left(\rho \right).$$

(5)

Remark 1. 

Choosing the discrete kernel function

$$\sum _{\kappa =\rho +\sigma -\beta }^{\omega -\beta }{(\omega -\kappa +1)}^{(\beta -1)}$$

as ${\displaystyle \frac{\mathsf{\Gamma }(\omega -\kappa )}{\mathsf{\Gamma }\left(\beta \right)\mathsf{\Gamma }(\omega -\kappa -\beta +1)}}$ with assumption $\rho =0$ and $\kappa +\beta =\rho ,$ the numerical formula when $\beta \in (0,1)$ is obtained as

$$\mathsf{\Phi }\left(\omega \right)=\mathsf{\Phi }\left(0\right)+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\beta \right)}}\sum _{\rho =1}^{\omega }{\displaystyle \frac{\mathsf{\Gamma }(\omega -\rho +\beta )}{\mathsf{\Gamma }(\omega -\rho +1)}}\mathcal{G}(\rho -1,\mathsf{\Phi }(\rho -1)).$$

(6)

3. Discrete Time Fractional-Order Sine Chaotic Map (DFSCM)

Many existing discrete fractional maps and their modified versions do not exhibit long-term chaotic behaviour, which is a desirable characteristic for implementing chaotic maps in cryptographic applications. Chaotic maps used in cryptosystems should possess features such as maximum randomness, high non-linearity, and long-range chaotic behaviour. However, several discrete fractional-order maps employed in cryptographic applications have limitations such as limited chaotic range, a small key space, and weak complexity. To address these issues, researchers have developed modified versions of chaotic maps specifically designed for encryption applications. One drawback of maps with short-term chaos is that the probability of selecting secret keys beyond this region that will result in a chaotic regime becomes very low. This limitation compromises the security of the cryptosystem. To overcome these challenges associated with short-term chaotic behaviour and minimal non-linearity, this article presents the construction of a new discrete time fractional map capable of exhibiting long-term chaotic responses.

$$\begin{array}{cc}\hfill x(n+1)=& sin\left(y\left(n\right)(1+bx(n\left)\right)\right)+x_n,\hfill \\ \hfill y(n+1)=& sin\left(x\left(n\right)+c{y}^2\left(n\right)\right)+y_n.\hfill \end{array}$$

(7)

The block diagram for the proposed discrete (7) is given in Figure 1, where D represents one delay in discrete time, ⊗ and ⊕ represents the multiplier and addition, respectively. A discrete time fractional-order sine chaotic map (DFSCM) obtained from (7) is

$$\begin{array}{cc}\hfill {\mathsf{\Delta }}_{\kappa }^{\varpi }x\left(n\right)=& sin\left(y(\varpi +n-1)(1+bx(\varpi +n-1\left)\right)\right),\hfill \\ \hfill {\mathsf{\Delta }}_{\kappa }^{\varpi }y\left(n\right)=& sin\left(x(\varpi +n-1)+c{y}^2(\varpi +n-1)\right),\hfill \end{array}$$

(8)

where ${\mathsf{\Delta }}^{\varpi }$ is the Caputo fractional difference operator with $0<\varpi \le 1$, $n\in {\mathbb{N}}_{\kappa +1-\varpi }$, $b,c$ are real parameters. The system is now converted to a numerically feasible form employing Theorem 1 with $\kappa =0$ as follows

$$\begin{array}{cc}\hfill x\left(n\right)=& x\left(0\right)+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\varpi \right)}}\sum _{\theta =1}^n{\displaystyle \frac{\mathsf{\Gamma }(n-\theta +\varpi )}{\mathsf{\Gamma }(n-\theta +1)}}\left(sin\left(y(\theta -1)(1+bx(\theta -1\left)\right)\right)\right),\hfill \\ \hfill y\left(n\right)=& y\left(0\right)+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\varpi \right)}}\sum _{\theta =1}^n{\displaystyle \frac{\mathsf{\Gamma }(n-\theta +\varpi )}{\mathsf{\Gamma }(n-\theta +1)}}\left(sin\left(x(\theta -1)+c{y}^2(\theta -1)\right)\right).\hfill \end{array}$$

(9)

The behaviour analysis is performed with DFSCM (8) by fixing $\varpi =0.5,$ $b=12$ and initial condition $(0.01,0.01)$ for various $c\in (0,75)$.

Some discrete fractional chaotic maps in the literature are considered for comparing their complexity with newly constructed discrete time fractional map by simulation of bifurcation diagrams and maximum Lyapunov exponents based on the Jacobian matrix method proposed in [41].

Fractional Tinkerbell map: 

Let us consider the fractional discrete time Tinkerbell map [42] of the form

$$\begin{array}{cc}\hfill {\mathsf{\Delta }}_{\kappa }^{\varpi }x\left(n\right)=& x^2(\varpi +n-1)-y^2(\varpi +n-1)+({\zeta }_1-1)x(\varpi +n-1)+{\zeta }_{2}x(\varpi +n-1),\hfill \\ \hfill {\mathsf{\Delta }}_{\kappa }^{\varpi }y\left(n\right)=& 2x(\varpi +n-1)y(\varpi +n-1)+{\zeta }_{3}x(\varpi +n-1)+({\zeta }_4-1)y(\varpi +n-1),\hfill \end{array}$$

(10)

2D Lorentz map: 

The chaotic behaviour of the 2D Lorentz map [43] of the form

$$\begin{array}{cc}\hfill {\mathsf{\Delta }}_{\kappa }^{\varpi }x\left(n\right)=& (1+{\zeta }_1{\zeta }_2)x(\varpi +n-1)-{\zeta }_{2}x(\varpi +n-1)-x(\varpi +n-1)\left[{\zeta }_{2}y(\varpi +n-1)+1\right],\hfill \\ \hfill {\mathsf{\Delta }}_{\kappa }^{\varpi }y\left(n\right)=& (1-{\zeta }_2)y(\varpi +n-1)+{\zeta }_2{x}^2(\varpi +n-1)-y(\varpi +n-1),\hfill \end{array}$$

(11)

2D fractional discrete time chaotic map: 

The discrete time fractional-order chaotic map investigated in [44] is given by

$$\begin{array}{cc}\hfill {\mathsf{\Delta }}_{\kappa }^{\varpi }x\left(n\right)=& {\zeta }_{1}sin\left(y(\varpi +n-1)\right)-x(\varpi +n-1),\hfill \\ \hfill {\mathsf{\Delta }}_{\kappa }^{\varpi }y\left(n\right)=& {\zeta }_{2}sin\left(x(\varpi +n-1)\right)-y(\varpi +n-1),\hfill \end{array}$$

(12)

3.1. Discussion

Based on the observations from the three different fractional chaotic maps obtained from the literature, this section depicts the chaotic response of the novel discrete fractional map proposed in (8). The proposed DFSCM exhibits highly non-linear behaviour, and the chaotic response of the map (8) is visualised in the comparison with the three other discrete fractional maps from the literature in Figure 2. The long-term behaviour of the system ensures the suitability of the system to be employed for cryptosystems, and the randomness of the state variables is exhibited in the form of the phase portrait plane in Figure 3. The phase portrait plane also visualises the trajectories distributed at a highly random level. The main advantages of the proposed DFSCM are the long-term chaotic behaviour, which ensures complexity, and the improved chances of generating a highly secure secret key based on the DFSCM (8).

3.1.1. Sensitivity Analysis

An important aspect of the chaos theory is the sensitiveness to the change in initial conditions of the map. This section investigates the sensitivity of the chaotic map (8) with initial conditions $X_0=(0.01,0.01)$ and $X_1=(0.0101,0.0101)$ for the parameters $b=12$, $c=50$ and $\varpi =0.5$, respectively. Numerical simulation is presented in Figure 4.

3.1.2. Complexity of the Proposed DFSCM

The complexity of the proposed DFSCM is determined based on the results of approximate entropy. The approximate entropy method employed here is adapted from the work of Pincus in [45]. The approximate entropy is a valuable tool to measure the persistence, correlation, and regularity of the time series obtained for chaotic dynamic systems. The evolution of the complexity of the proposed DFSCM (8) is investigated under different circumstances, such as varying the fractional order and the value of parameter b. The approximate entropy is estimated using the following

$$ApEn(d,r,M)\left(\nu \right)={\mathsf{\Phi }}_d\left(r\right)-{\mathsf{\Phi }}_{d+1}\left(r\right),d\ge 1,$$

where ${\mathsf{\Phi }}_d\left(r\right)={\displaystyle \frac{1}{M-d+1}}{\displaystyle \sum _{i=1}^{M-d+1}}log{W}_i^d\left(r\right),$ r is the tolerance factor or filtering noise, d represents the length of data comparison, and the value $W_i^d\left(r\right)$ calculated from ${\displaystyle \frac{\left|\xi \right(i)-\xi (j\left)\right|}{M-d+1}},$ $\xi \left(i\right)$ is the i-th block of a sequence of numbers. Here, the analysis of the randomness of the data series obtained from the DFSCM (8) for $b=12,16$$c=50$ and $\varpi =0.5,0.65,0.8$ is performed for different tolerance values r between $(0,1)$ for a fixed value of $d=2$. The calculated values of approximate entropy are plotted as 2D plots in Figure 5 with values tabulated in

Table 1. Approximate entropy of (8).

b	Tolerance (r)	$\mathit{\varpi }=0.5$		$\mathit{\varpi }=0.65$		$\mathit{\varpi }=0.8$
		$\mathit{M}=\mathbf{1500}$	$\mathit{M}=\mathbf{4500}$	$\mathit{M}=\mathbf{1500}$	$\mathit{M}=\mathbf{4500}$	$\mathit{M}=\mathbf{1500}$	$\mathit{M}=\mathbf{4500}$
12	$r=0.2$	$0.3720$	$0.3303$	$0.7683$	$0.6081$	$1.2507$	$0.9844$
	$r=0.3$	$0.7107$	$0.6485$	$1.1946$	$1.0224$	$1.4293$	$1.3437$
	$r=0.5$	$1.2702$	$1.2302$	$1.5761$	$1.5362$	$1.2964$	$1.4599$
	$r=0.7$	$1.6311$	$1.6054$	$1.5980$	$1.6885$	$1.0919$	$1.3150$
	$r=0.9$	$1.8136$	$1.8045$	$1.5009$	$1.6473$	$0.9106$	$1.1575$
16	$r=0.2$	$0.3492$	$0.3529$	$0.6176$	$0.5384$	$0.9864$	$0.8880$
	$r=0.3$	$0.6694$	$0.6804$	$1.0379$	$0.9209$	$1.3353$	$1.2855$
	$r=0.5$	$1.2414$	$1.2545$	$1.5230$	$1.4719$	$1.4534$	$1.5390$
	$r=0.7$	$1.6152$	$1.6117$	$1.6474$	$1.6830$	$1.3228$	$1.4595$
	$r=0.9$	$1.8104$	$1.8104$	$1.6017$	$1.7159$	$1.1599$	$1.3328$

. The observations from the simulations imply that the higher the value of entropy, the greater the randomness of the data series, and lower values explain the predictive nature of the time series considered for study. In order to gain a detailed insight into the approximate entropy results, we presented the results for different lengths of data, such as $M=1500,4500.$ The variation in the values explains the choice of the tolerance factor for a better illustration of the complexity of the proposed DFSCM.

4. Image Encryption and Decryption

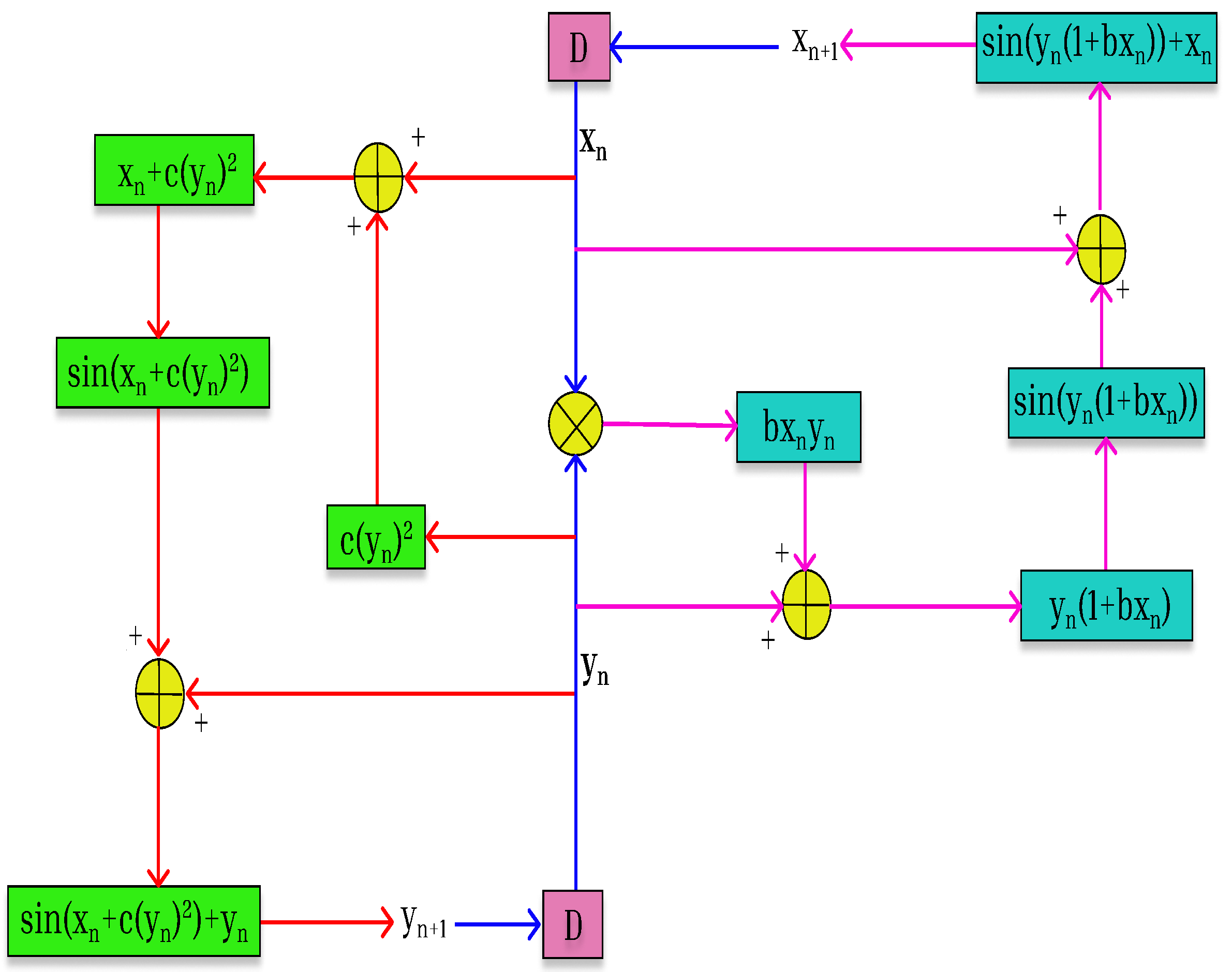
Based on the above results on the chaotic responses and non-linearity exhibited by the discrete fractional map, we employ the DFSCM (8) to generate a chaotic sequence to perform image encryption. This section presents the application of the proposed encryption of images with a discrete time fractional sine map. To ensure the high level of security of the information transmission through images, the concept behind blockchain technology is adapted to ensure the decryption of the image by the authentic receiver. A schematic representation of the image encryption algorithm is presented in Figure 6.

4.1. Scheme of Encryption

The entire process of image encryption is discussed in this section. Our encryption process can be split into three parts

• Embedding secret images: Watermarking using discrete wavelet transforms.
• Partial encryption and diffusion: Generating a chaotic matrix from the discrete fractional sine chaotic map for diffusion of pixels.
• Encryption: Image is integrated into 256 bits and is bit-XORed with genesis block using SHA-256.

A step-by-step procedure of the encryption process is as follows.

Embedding secret images:

• The objective image $\left(P\right)$ of size $K\times L$ is selected and subjected to level 2 or 3 decomposition employing discrete wavelet transformation after converting the image to greyscale [46]. In case of an image of size $256\times 256$, level 1 contains four sub-bands of size $128\times 128$ containing approximation (LL), horizontal (HL), vertical (LH) and diagonal (HH) as shown in Figure 7.

Figure 7. Different levels of decomposition by discrete wavelet transforms.

Figure 7. Different levels of decomposition by discrete wavelet transforms.

2.

Consider the LL sub-band for level 2 decomposition and similarly, the procedure can be followed for level 3 decomposition. The size of the sub-bands is halved at each decomposition.

3.

In our algorithm, we are interested in embedding watermarked images in different levels.

Case (i): Level 2 decomposition with secret images embedded in the LH sub-band of level 1 and the HL sub-band in level 2.

Case (ii): Level 3 decomposition with secret images embedded in the LH sub-band of level 2 and the HL sub-band in level 3.

Case (ii): Level 3 decomposition with secret images embedded in the LH sub-band of level 3 and the HL sub-band in level 3.

4.

Size of the level in which the secret images to be watermarked are selected and the secret images are processed to this size. Singular vector decomposition (SVD) and inverse discrete wavelet transform are employed to obtain watermarked image.

Partial encryption and diffusion:

1.

After the watermarked image is obtained, it is subjected to encryption of the selected portion of the image using the sum of the edge intensity values and respective inverse of the value for recovering the image.

2.

After partial encryption, we employ Fourier transform for inter-block shifting in the image. Let us denote the shifted image by $J_2.$

3.

The discrete fractional chaotic map (8) with parameters $b=12,$ $c=40$ and fractional order $\varpi =0.55$ with initial states $(0.01,0.01)$ is considered to obtain the chaotic matrix. Chaotic sequences are generated from the map (8) and the chaotic matrix is obtained by

for m = 1:K

for n = 1:L

$W(m,n)=floor\left(mod((x\left(m\right)+y\left(n\right))\times 2^{30},256)\right);$

end

end

4.

The chaotic matrix $W(m,n)$ thus obtained from the previous step is employed for the process of diffusion with the shifted image $\left(J_2\right)$ obtained in Step 2. Let the diffused image be denoted by $J_3.$

Encryption:

The encryption process is based on the following concept: In a blockchain, the genesis block serves as the initial block upon which subsequent blocks are built. Each block in the blockchain depends on the hash values of the previous block, with the genesis block having a hash value of 0. A notable feature of the blockchain is that every block contains the complete transaction history from the previous block. Therefore, any slight modification in the transactions would lead to corruption of the entire data.

Applying this concept, the partially encrypted and block-shuffled image obtained in the previous step is divided into 256 blocks. A unique base block, known as the genesis block, is introduced. This genesis block is XORed with the image disintegrated into bits, resulting in blocks shuffled across different regions of the image. The procedure can be summarized as follows:

• The image $J_3$ is divided into 256 small blocks and a genesis block required for construction of blockchain is considered.
• The image blocks are then converted to strings by
  c = 1
  while $p\le K$
  while $q\le L$
  $J_4$(p,q:q + 31)= B(c,:) $\oplus J_3$(p,q:q + 31);
  B(c + 1, :) = uint8(sha256hasher.ComputeHash $\left(J_4(p,q:q+31)\right))$;
  c = c + 1;
  end
  end
• The encrypted image $J_4$ to be sent to the recipient is obtained.

4.2. Decryption Scheme

The procedure of obtaining the plain image from the encrypted image is a simple reverse process, starting with the extraction of the image with the same genesis block and then diffusion with the chaotic matrix $W(m,n)$. An inverse Fourier transform is applied to reshuffle the blocks, and the inverse value of the edge intensity can be used to retain our watermarked image. Once the watermarked image is obtained by applying a discrete wavelet transform to the sub-bands with secret images, the secret image can be obtained.

4.3. Significance of the Proposed Algorithm

Our proposed algorithm presents a two-layer defence mechanism against non-recipient decryption. The first layer of defence is the genesis block, a unique set of SHA-256 code accessible only to the receiver and sender. The diffusion of the encrypted image with a different genesis block than the original one results in a corrupted image, which, on further processing, will not yield any information about the image. The second layer of defence is the chaotic key of the DFSCM which is sensitive to high precision of ${10}^{-16}$, thus making it difficult to break into the algorithm. Thus, our algorithm developed with DFSCM and the concept of blockchain for encryption of images provides a high level of security for the transmission of information. The experimental evaluation of the results also supports our claim in comparison with some recent literature based on chaotic systems.

5. Analysis of Image Encryption and Decryption

The analysis of the proposed encryption algorithm is carried out with the help of several important indicators that ensures the sensitivity of the key, image quality, randomness of the encrypted image and similarity of the decrypted image with that of the input plain image.

There are several test images that are commonly employed; this article, for the analysis of the algorithm, considers a standard peppers image with a size of $256\times 256\times 3$ as an objective image. The main focus of our study involves understanding the influence of watermarking on secret images at different levels after decomposition. The results based on the algorithm for different levels of watermarking are presented in this section in the form of simulations of the numerical values. The numerical values are then compared with different algorithms proposed in the literature. An investigation is then performed with statistical analysis comprising histogram analysis, pixel correlation, ${\chi }^2$ test and robustness analysis supported by noise attacks. Finally, key sensitivity analysis under different key variations is performed. The embedded secret images, results of image encryption and decryption and and recovered secrete images in binary form are presented in Figure 8, Figure 9 and Figure 10, respectively.

5.1. Statistical Analysis

The statistical analysis of the algorithm is presented in this section to understand the random distribution of the pixels in the encrypted image and the correlation between the pixels.

5.1.1. ${\chi }^2$ Test

The uniformity of the histogram obtained for the encrypted images is justified with a ${\chi }^2$ test. If ${\nu }_{\ell }$ denotes the frequency of the observed occurrence and the expected frequency of occurrence is ${\omega }_{\ell }$ then the ${\chi }^2$ value can be obtained from

$${\chi }^2=\sum _{\ell =1}^{256}{\displaystyle \frac{{\nu }_{\ell }-{\omega }_{\ell }}{{\omega }_{\ell }}},$$

(13)

where ℓ is the count of grey levels (256). For a significant level of $0.05,$ the value of ${\chi }^2$ is 293. From

Table 2. ${\chi }^2$ test of encrypted peppers image with level 2 decomposition.

Image	Watermarking Level	${\mathit{\chi }}^2$ Test
Peppers	Level 1—Lena	$269.1328$
$256\times 256$	Level 2—Fingerprint

and

Table 3. ${\chi }^2$ test of encrypted peppers image with level 3 decomposition.

Image	Watermarking Level	${\mathit{\chi }}^2$ Test
Peppers	Level 2—Lena	$245.4453$
$256\times 256$	Level 3—Fingerprint
Peppers	Level 3—Lena	$206.2031$
$256\times 256$	Level 3—Fingerprint

, the ${\chi }^2$ value for all the images is clearly less than 293 and ensures the uniform distribution of the histogram.

Analysis of ${\chi }^2$ test results illustrates the impact of watermarking images at different levels. From Table 2 and Table 3, it is clear that the higher the image watermarking level (Level-3) the smaller the ${\chi }^2$ value, while watermarking images at a smaller level (Level-2) results in a ${\chi }^2$ value close to the ideal value. Histogram uniformity is supported with images watermarked deep into the objective image.

5.1.2. Histogram Analysis

Investigating the image histograms provides information about pixel distribution, and in the cryptosystem, this provides insight into understanding the system’s security against statistical attacks. Images with uniformly distributed pixels are known to withstand such attacks. A comparison is carried out between the input and encrypted image histograms. From Figure 11, it can be observed that the input plain image histogram contains a random distribution, while the pixels in the encrypted image are uniformly distributed between $[0,255]$. Thus, our scheme is clearly secure against statistical attacks.

5.1.3. Correlation Coefficients

Correlation in general is used to study the strength of relationships between any two variables. The higher the correlation, the greater their change in the same direction. The correlation lies between [−1,1] with negative values representing changes in the variables occurring in opposite directions. In the case of image encryption, if the correlation between any two pixels is high, it is simple to track them down with simple probability. Therefore, for safe and secure information transmission it is necessary to have as little correlation between pixels as possible. The correlation coefficients are calculated for both the plain and encrypted image using

$${\rho }_{uw}={\displaystyle \frac{\mathrm{Covariance}\mathrm{of}u\mathrm{and}w}{\sqrt{P\left(u\right)}\sqrt{P\left(w\right)}}},$$

(14)

where the covariance of the pixels u and w is obtained from $\frac{1}{K}{\displaystyle \sum _{\delta =1}^K}(u_{\delta }-E\left(u\right))-(w_{\delta }-E\left(w\right)),$$P\left(u\right)$ represents the variance of u given by $\frac{1}{K}{\displaystyle \sum _{\delta =1}^K}{(u_{\delta }-E\left(u\right))}^2$, $E\left(u\right)=\frac{1}{K}{\displaystyle \sum _{\delta =1}^K}{u}_{\delta }$ is the expectation of u and K is the number of pixels. The correlation coefficients calculated along the diagonal, vertical, and horizontal directions are presented in

Table 4. Correlation Coefficient of peppers image with 2-Level decomposition.

Image	Watermarking Level	Input Image			Encrypted Image
		Horizontal	Vertical	Diagonal	Horizontal	Vertical	Diagonal
Peppers	Level 1—Lena	$0.8516$	$0.9492$	$0.8208$	$0.0264$	$0.0016$	$0.0073$
$256\times 256$	Level 2—Fingerprint

and

Table 5. Correlation coefficient of the peppers image with level 3 decomposition.

Image	Watermarking Level	Input Image			Encrypted Image
		Horizontal	Vertical	Diagonal	Horizontal	Vertical	Diagonal
Peppers	Level 2—Lena	$0.9298$	$0.9517$	$0.9017$	$-0.0101$	$-0.0098$	$-0.0130$
$256\times 256$	Level 3—Fingerprint
Peppers	Level 3—Lena	$0.9447$	$0.9561$	$0.9208$	$0.0043$	$-0.0103$	$-0.0004$
$256\times 256$	Level 3—Fingerprint

. The concentration of pixels for the input and encrypted images is presented in Figure 12. For the plain input image, the concentrations of pixels are very high at certain regions, whereas the pixels are randomly spread for the encrypted image. With visual and numerical support from the tabulated values, it is evident that our algorithm ensures an increase in the confusion of the encrypted images.

5.1.4. Information Entropy

The uncertainty of an image or information transmission is described with information entropy. The entropy of an image is calculated using the distribution of pixels in the histogram. The value can be evaluated by

$$Entropy=-\sum _{\mu }{F}_{\mu }{log}_2\left(F_{\mu }\right),$$

(15)

where the number of pixels is denoted by $\mu$ and the probability of a pixel is $F_{mu}$. An ideal image entropy value is 8 and images with entropy values close to 8 are considered to be random and better encrypted. The values in

Table 6. Entropy analysis of the peppers image with level 2 decomposition.

Image	Watermarking Level	Entropy
		Encrypted Image
Peppers	Level 1—Lena	7.997024
256 × 256	Level 2—Fingerprint

and

Table 7. Entropy Analysis of peppers image with 3-Level decomposition.

Image	Watermarking Level	Entropy
		Encrypted Image
Peppers	Level 2—Lena	$7.997292$
$256\times 256$	Level 3—Fingerprint
Peppers	Level 3—Lena	$7.997724$
$256\times 256$	Level 3—Fingerprint

illustrate the entropy of the different input images and their respective encrypted image. Entropy values of different encrypted images are very close to 8. Our results of the encrypted image entropy reveal higher levels of ambiguity and an uncertain pixel distribution.

5.2. Security Attacks

5.2.1. Differential Attacks

Common indicators for the analysis of these types of attacks are employed by calculating the changing pixel rate (NPCR) between the original input image and the encrypted image and the unified averaged changed intensity (UACI). The calculations for these values are performed in the following way. Let ${\mathsf{\Phi }}^1$ and ${\mathsf{\Phi }}^2$ represent two encrypted images obtained before and after changing one pixel of the input image. Let the bipolar array be denoted $G({\ell }_1,{\ell }_2)$ and defined by

$$G({\ell }_1,{\ell }_2)=\left\{\begin{array}{c}0,if {\mathsf{\Phi }}^1({\ell }_1,{\ell }_2)={\mathsf{\Phi }}^2({\ell }_1,{\ell }_2)\hfill \\ 1,if {\mathsf{\Phi }}^1({\ell }_1,{\ell }_2)\ne {\mathsf{\Phi }}^2({\ell }_1,{\ell }_2)\hfill \end{array}\right.$$

(16)

where ${\mathsf{\Phi }}^1({\ell }_1,{\ell }_2)$ and ${\mathsf{\Phi }}^2({\ell }_1,{\ell }_2)$ are the value of pixels at $grid({\ell }_1,{\ell }_2)$ for ${\mathsf{\Phi }}^1$ and ${\mathsf{\Phi }}^2$. Then

$$NPCR=\sum _{{\ell }_1,{\ell }_2}{\displaystyle \frac{D({\ell }_1,{\ell }_2)}{K}}\times 100\%,$$

(17)

where K is the pixel number.

$$UACI=\sum _{{\ell }_1,{\ell }_2}{\displaystyle \frac{|{\mathsf{\Phi }}^1({\ell }_1,{\ell }_2),{\mathsf{\Phi }}^2({\ell }_1,{\ell }_2)|}{M·K}}\times 100\%,$$

(18)

where M is the largest pixel value based on the encrypted image. For a highly secure image the maximum NPCR is 100$\%,$ the closer the NPCR is to 100 the higher the security level of the encrypted images. Numerical values of the calculated NPCR and UACI for encrypted images of different input images are listed in

Table 8. NPCR and UACI of the peppers image (256 × 256) with level 3 watermarking.

Pixel Change Position	NPCR (%)	UACI (%)
$(210,136)$	$99.601746$	$33.495807$
$(245,114)$	$99.626160$	$33.402231$
$(118,245)$	$99.690247$	$33.592948$
$(243,134)$	$99.633789$	$33.450850$

. The resistance of the algorithm towards differential attacks is evident from the NPCR values close to 100.

5.2.2. Cryptanalysis

The primary objective of cryptanalysis is to obtain partial or complete keys for an encryption algorithm to gain unauthorized access to transmitted information. According to the Kerckhoff principle [47], the security of a cryptographic system relies on the secrecy of the keys, even if all other details are known to the public. In the proposed algorithm, the security primarily depends on two keys: Key 1, which determines the scrambling of the original image using the proposed DFSCM; and Key 2, the genesis block used in the final encryption stage to convert the image into a string of characters. Now, let us consider different attack scenarios on the system. In an attack focused on secret images, suppose the attacker has a collection of watermarked images and performs statistical analyses on the watermarked positions. However, determining the exact region of the secret image becomes challenging due to the images being embedded in different layers using wavelet transforms and the random distribution of pixels resulting from chaotic matrix scrambling. Moreover, Key 2, used to decrypt the image into bits, further reduces the accessibility to the secret image. The probability of the attacker discovering Key 1 is extremely low, estimated at approximately ${\displaystyle \frac{1}{{10}^{70}}}.$ In the case of a chosen plaintext attack, the attacker has access to the encryption algorithm and can obtain encrypted images for any input image. By encrypting a certain number of related watermarked images, the attackers may attempt to discern the pattern between the input and encrypted images. However, our algorithm provides an effective defence against this type of attack due to two main reasons: (1) The complex non-linear behaviour of the proposed DFSCM, which generates a chaotic matrix with high randomness; and (2) the final encryption step that employs the SHA256 hash function, producing vastly different outputs for even minor changes in the input. Based on the above analysis, our encryption algorithm demonstrates a high level of security and proves to be resilient against differential attacks.

5.2.3. Salt-and-Pepper Noise (Spn) Attacks

A secure image encryption algorithm must be able to resist the attack of distortion on the encrypted image. The quality of the image that is able to be restored after noise attacks are studied with the peak signal to noise ratio (PSNR) estimated in decibels (dBs) by

$$PSNR=10log\left({\displaystyle \frac{{255}^2}{MSE\left(\mathrm{\Theta }\right(u,w),\mathrm{\Psi }(u,w\left)\right)}}\right),$$

(19)

where $\mathrm{\Theta }$ and $\mathrm{\Psi }$ represent the original and decrypted image, respectively. MSE denotes the mean squared error. The similarity of the images restored after the attack with the input image is presented with the MSSIM (multi-scale structural similarity index method). The MSSIM actually provides information on the deformity of the decrypted image due to the attack. Noise affects the quality of the image, reducing the quality of the decrypted image obtained after the Spn attack under different intensities on the encrypted image for different images, and is calculated in the form of PSNR and MSSIM, as shown in

Table 9. PSNR and MSSIM of peppers image at different noise levels.

Images	0.0005		0.001		0.01
	PSNR (dB)	MSSIM	PSNR (dB)	MSSIM	PSNR (dB)	MSSIM
Peppers	$47.611569$	$0.949297$	$43.122702$	$0.882821$	$32.571786$	$0.280779$

. Spn at intensities $0.0005,$ $0.001$ and $0.01$ are employed, and the changes in the decrypted images are visualised in Figure 13. Typical PSNR values for an image with good quality are around 30–50 dB. The tabulated PSNR values for the different images clearly lie within the range, and thus, it is evident that our algorithm is capable of withstanding the Spn noise attack and recovering the image with good quality.

The impact of the Spn attack is validated for secret images watermarked at the noise levels 0.005, 0.001 and 0.01, and the simulations are presented in Figure 14. The PSNR and similarity of the extracted watermarked images with and without noise are tabulated in

Table 10. The PSNR and MSSIM of secret images at different noise levels.

Images	0.0005		0.001		0.01
	PSNR (dB)	MSSIM	PSNR (dB)	MSSIM	PSNR (dB)	MSSIM
Lena	$36.267275$	$0.994674$	$31.577759$	$0.984377$	$29.896230$	$0.873192$
Fingerprint	$37.017159$	$0.996788$	$32.713040$	$0.986345$	$29.571403$	$0.875736$

. It can be observed that the Spn attack has a considerably greater effect on the objective image than the watermarked secret images. This change can be observed from the PSNR values of the objective image at a noise level of 0.01, where the similarity between the original and decrypted images is $0.28(28\%)$. In the case of secret images, the similarity between the noiseless extracted image and the noisy image is around $87\%$ for a noise level of 0.01, meaning the information loss is very low and a higher level of information can be recovered.

5.3. Key Security Analysis

5.3.1. Key Space

Our encryption scheme comprises seven keys $x_0,y_0,b,c,\varpi$ for the chaotic maps and so for the keys with precision ${10}^{-14},$ the key space is obtained as ${10}^{70}$. For any safe encryption system a key space of $2^{100}$ is sufficient [48]. Therefore, it is evident that our algorithm has a large enough key space to withstand any attacks.

5.3.2. Sensitivity of the Key

The level of security provided by the encryption algorithm can be understood from the sensitivity of the key. A change in a single bit of the key can result in significant changes to the encrypted image. In order to investigate the sensitivity of the secret keys, we calculate the UACI and NPCR for the encrypted images obtained for the original chaotic keys $x_0$ and $y_0$, and the modified keys obtained by adding $1\times {10}^{-16}$ to the original chaotic keys. For our analysis, we consider the modification of key $x_0$ to $x_0+{10}^{-16}$ and $y_0$ to $y_0+{10}^{-16}$. The tabulated values are presented in

Table 11. NPCR, UACI, PSNR, SSIM values for the sensitivity of the keys with precision $x_0+{10}^{-16}$ and $y_0+{10}^{-16}$.

	${\mathit{x}}_0+{10}^{-16}$	${\mathit{y}}_0+{10}^{-16}$
$NPCR (\%)$	$99.620056$	$99.632263$
$UACI$	$33.482385$	$33.582177$
$PSNR \left(dB\right)$	$27.074867$	$27.085761$
$SSIM$	$0.009156$	$0.011158$

. In order to visualize the impact of a very small change in a key on the decryption process, we present images encrypted with different keys in Figure 15. In the encryption phase, the change in one bit of key NPCR $(\%)$ of the two encrypted images is high, indicating the dissimilarity of the encrypted image, and similarly, in the decryption process, the change of the key results in a completely different image rather than obtaining the input image. Thus, it is clear that the algorithm proposed for encryption is highly sensitive to slight changes in the key.

5.4. Comparison of the Cryptographic Analysis of the Proposed Algorithms with Results from Recent Literature

The analysis of the algorithm is compared to recent literature, and the results are tabulated in

Table 12. Comparisonresults based on the peppers image.

Encrypted Image				Correlation Coefficient
	Entropy	NPCR (%)	UACI (%)	Horizontal	Vertical	Diagonal
$Proposed$	$7.9977$	$99.6902$	$33.5929$	$-0.0043$	$-0.0103$	$-0.0004$
[49]	$7.9972$	$99.6050$	$33.5062$	$0.0025$	$0.0040$	$-0.0015$
[48]	$7.9970$	$99.6048$	$33.4539$	$-0.0011$	$0.0014$	$-0.004$
[50]	$7.9969$	$99.6196$	$33.4150$	$-0.0103$	$-0.0127$	$0.0084$
[51]	$7.9976$	$99.6024$	$33.4975$	$0.0045$	$0.0028$	$0.0010$

. The encrypted image generated by our algorithm exhibits a high level of randomness, as evidenced by its information entropy value of $7.9977$. Furthermore, the NPCR achieves a value of $99.6902$, indicating a significant change between the input and encrypted images. Additionally, the UACI value of $33.5929$ surpasses the values reported in the compared articles, highlighting the effectiveness of our algorithm. The random distribution of pixels in both the input and encrypted images is demonstrated in the latter part of the image. The correlation coefficients obtained are close to zero, further indicating the lack of correlation between the pixel values. These results provide clear evidence that our proposed algorithm possesses the ability to encrypt images effectively and withstand various attacks.

6. Conclusions

A novel discrete fractional sine chaotic map was developed and compared with existing chaotic maps, such as the Tent map, Tinkerbell map, and other fractional chaotic maps proposed in the literature. The comparison of dynamic characteristics confirms that the proposed map exhibits high non-linearity and complex behaviour, making it suitable for image encryption applications. The bifurcation diagrams demonstrate chaotic behaviour over a wide range of parameters, while the positive Lyapunov exponents further support the chaotic nature of the proposed algorithm. To assess the randomness of the chaotic time series generated by the map, approximate entropy results were calculated and tabulated for different tolerance values. These results highlight the randomness and unpredictability of the chaotic sequences. An image encryption algorithm based on the principles of blockchain logic was proposed to enhance the security of information transmission. This scheme ensures a higher level of security for authorized communication between senders and receivers. The incorporation of the transform methods for embedding secret images as watermarks at various levels enhances the transmission of secret messages.

For objective images of size $256\times 256$, the proposed encryption scheme significantly increases the randomness of pixel distribution, as evidenced by the entropy results presented in Table 6 and Table 7. The impact of the chaotic sequences generated by the fractional chaotic map is evident from the high entropy values and the NPCR exceeding $99.69\%$ for a single bit change in the input image. This demonstrates the effectiveness of the proposed encryption scheme for secure information communication through images. Additionally, the incorporation of watermarking techniques extends its applicability to areas such as copyright protection, e-voting, and securing medical and military data. In future research, the concept of genesis block-based encryption can be extended to RGB images, and the inclusion of multi-block image storage can be explored to further enhance the encryption scheme’s capabilities.