Optimal Load Frequency Control of a Hybrid Electric Shipboard Microgrid Using Jellyfish Search Optimization Algorithm
Abstract
1. Introduction
- Recently, the marine industry has adopted renewable energy sources, which makes it crucial to optimize SMGs.
- An emerging area of research concerns the problem of the LFC of ship microgrids, which becomes particularly challenging due to the high fluctuating propulsion loads and low inertia that characterize the SMGs.
- The previous research on LFC in shipboard microgrids overlooked the time delay in communication lines. This gap highlights the need for the further development of improved frequency control techniques.
- Studies carried out in this field investigate and utilize metaheuristic algorithms to determine optimal controller design parameters for microgrids on ships.
- A recently proposed shipboard microgrid system was further examined and analyzed for frequency regulation studies. This extends the scope of previous research in the field of LFC in SMGs, because the study considered the time delay between the sensor and the controller;
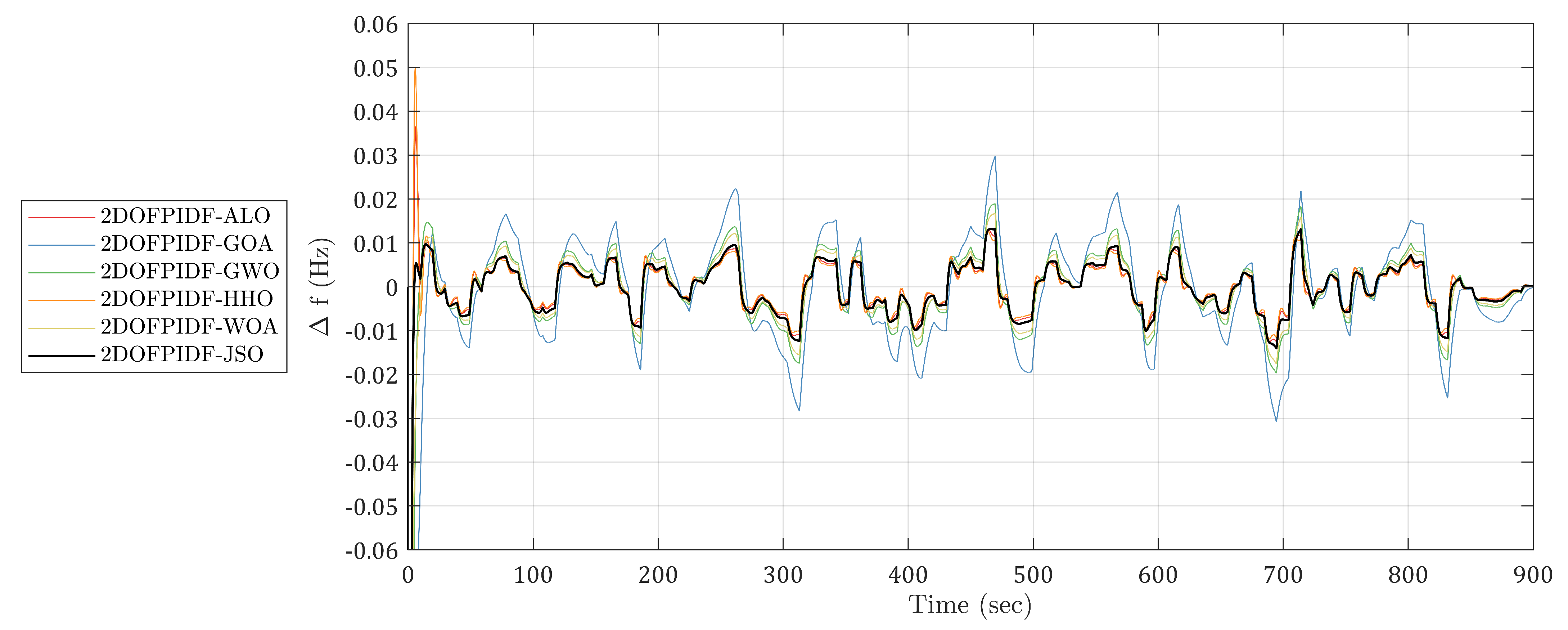
- The performance of different metaheuristics optimization algorithms, including ALO, the GWO, the GOA, HHO, the WOA, and the proposed JSO, was assessed. The evaluation offers insights into which algorithm is most suitable for this application;
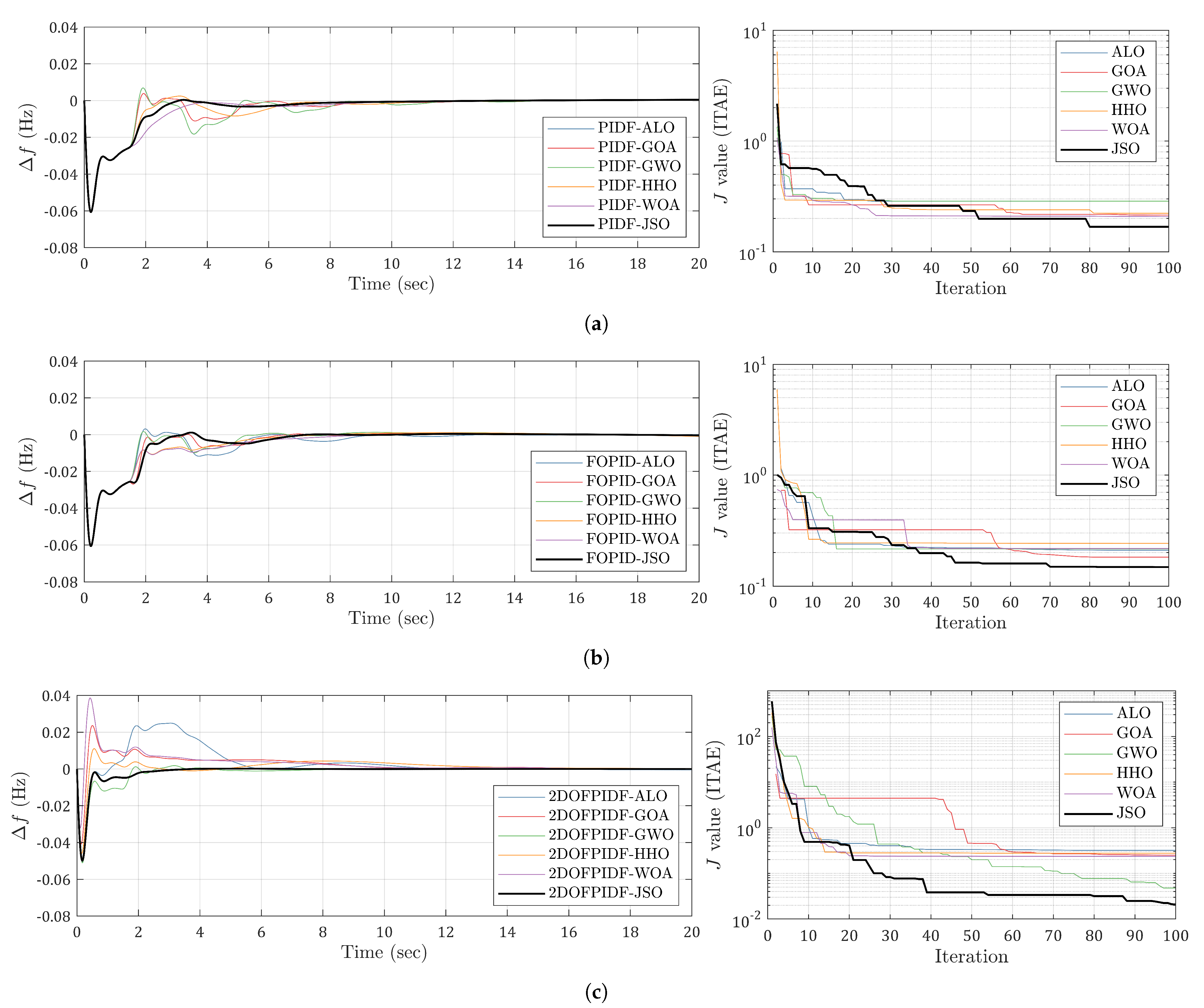
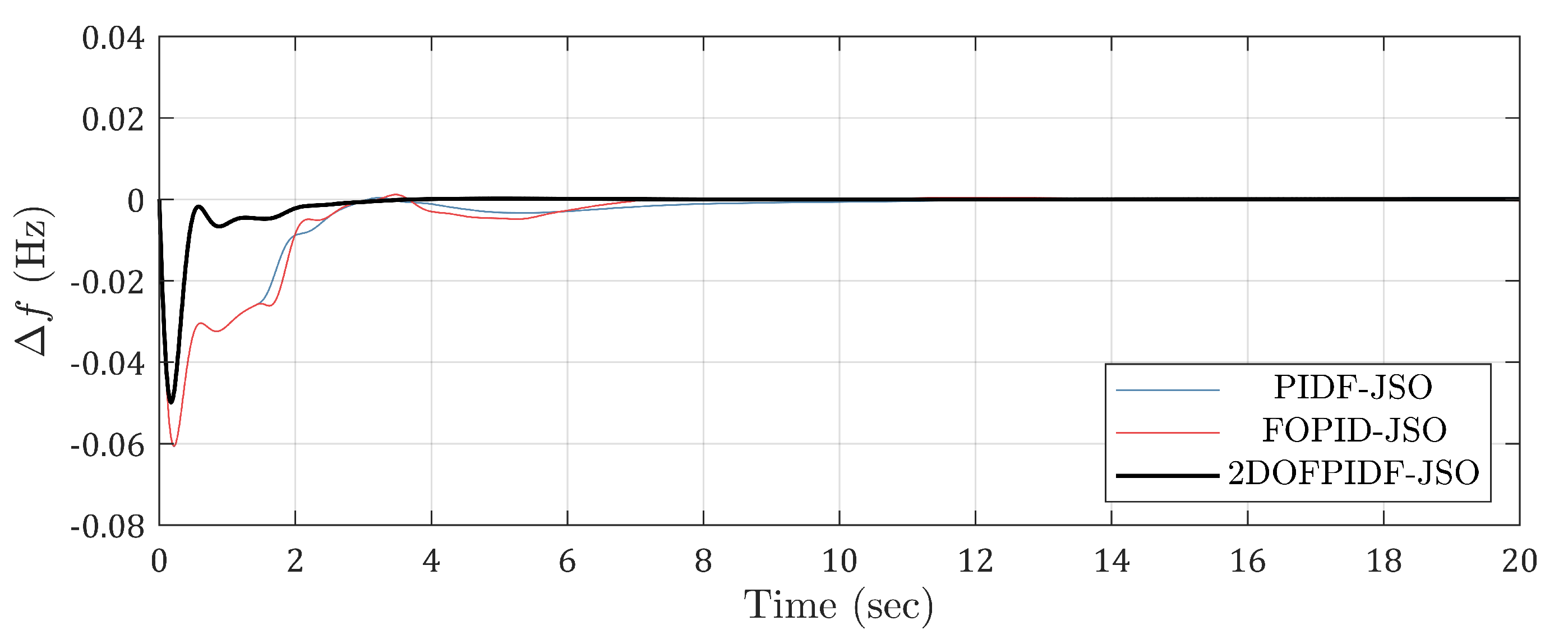
- The performance of various controllers, including PIDF, FOPID, and 2DOF-PIDF, was evaluated. The system dynamics were analyzed under changing solar, wave, and load conditions in the shipboard microgrid. This analysis provides a comprehensive understanding of the system dynamics and highlights the effectiveness of the controllers in regulating frequency;
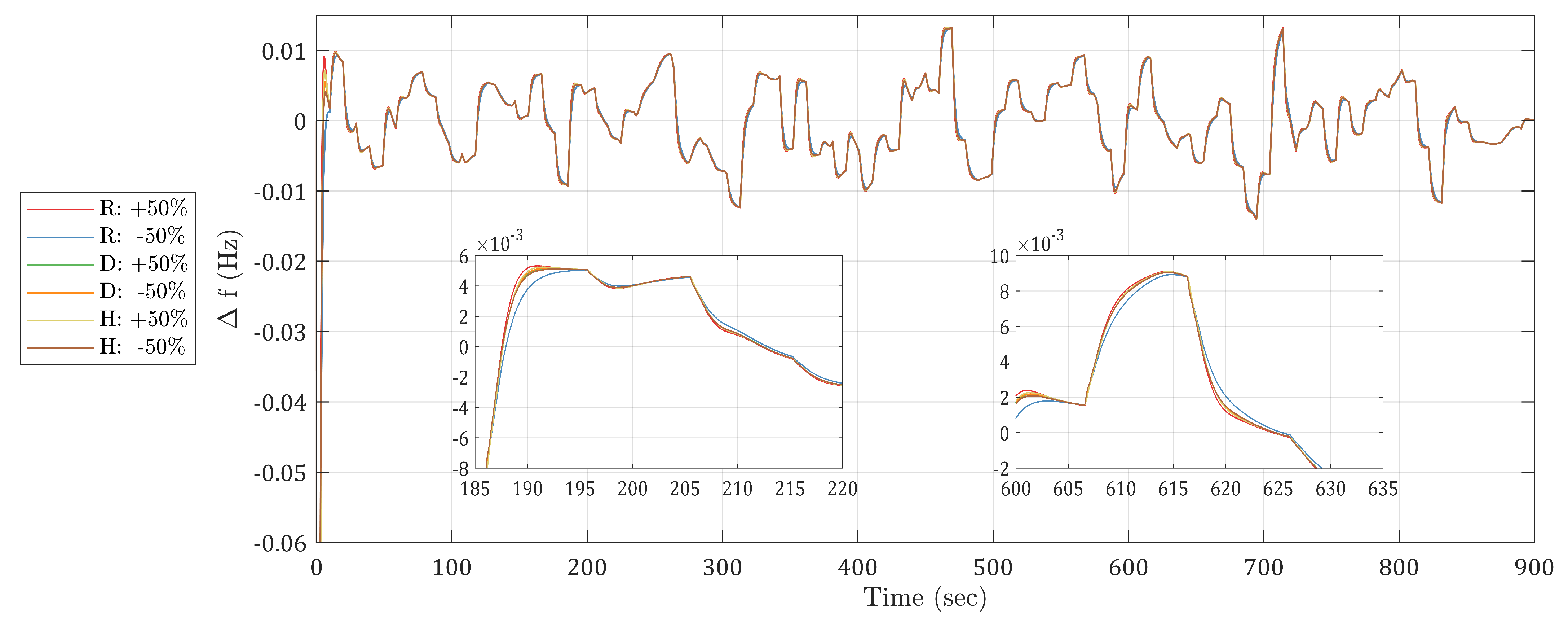
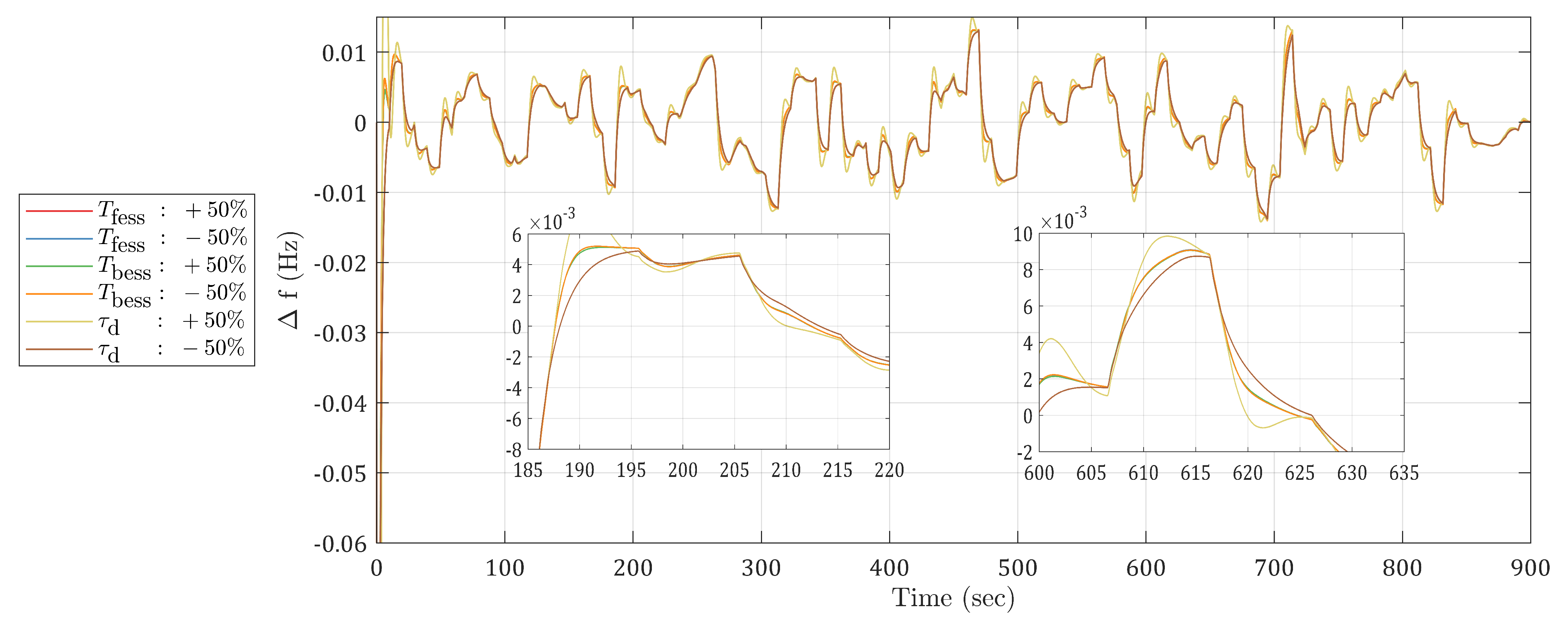
- The sensitivity of the proposed JSO-tuned controller to variations in system parameters was examined. By analyzing the sensitivity, the research provides information on the controller’s resilience and identified how certain parameters influence its effectiveness.
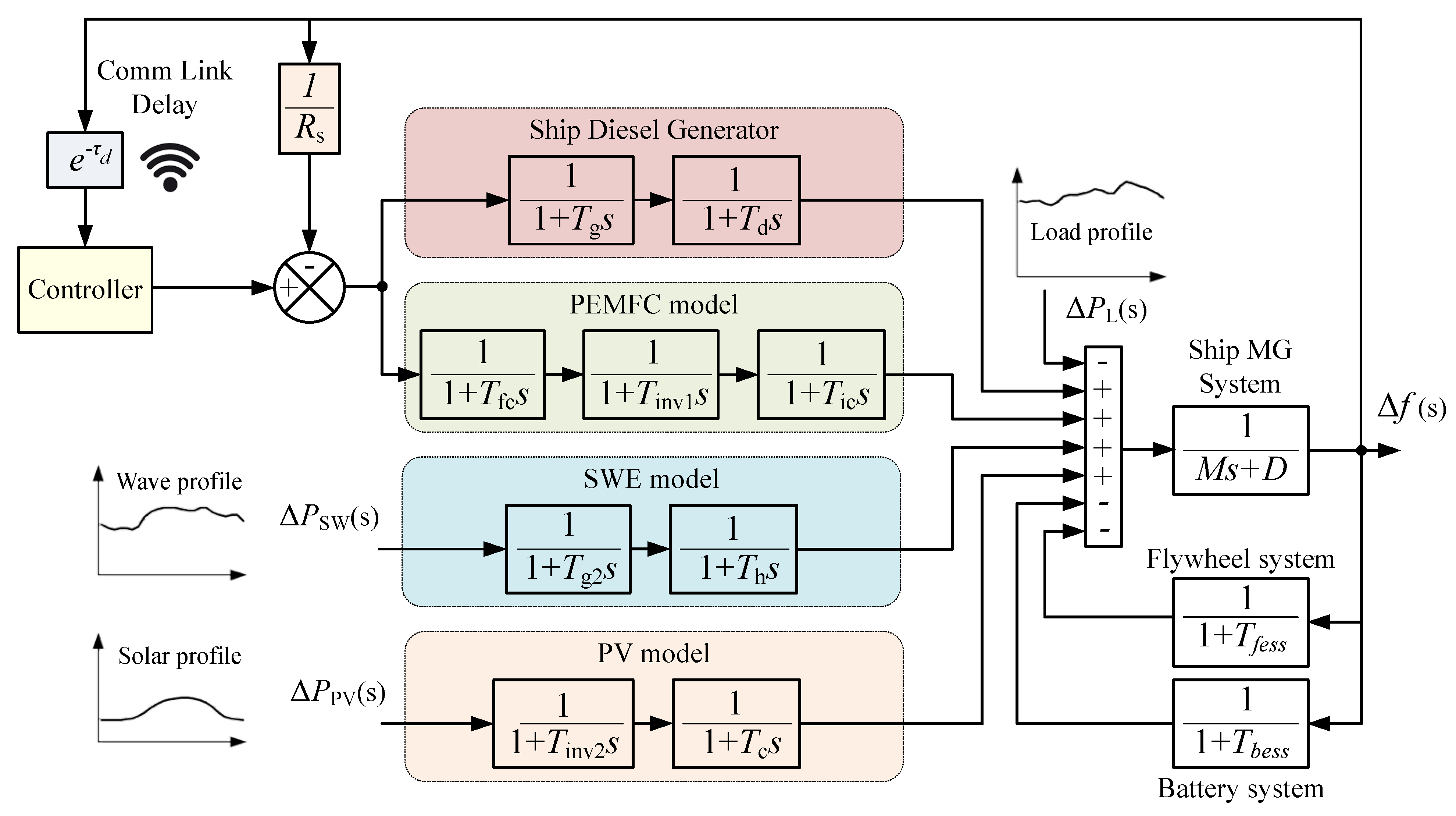
2. Description of the Shipboard Microgrid under Study
2.1. Diesel Generators
2.2. Proton Exchange Membrane Fuel Cell
2.3. Renewable Energy Sources
2.3.1. Sea Wave Energy Source
2.3.2. Photovoltaic Source
2.4. Energy Storage System
3. Control Strategy and Optimization Function
3.1. Optimization Function Justification
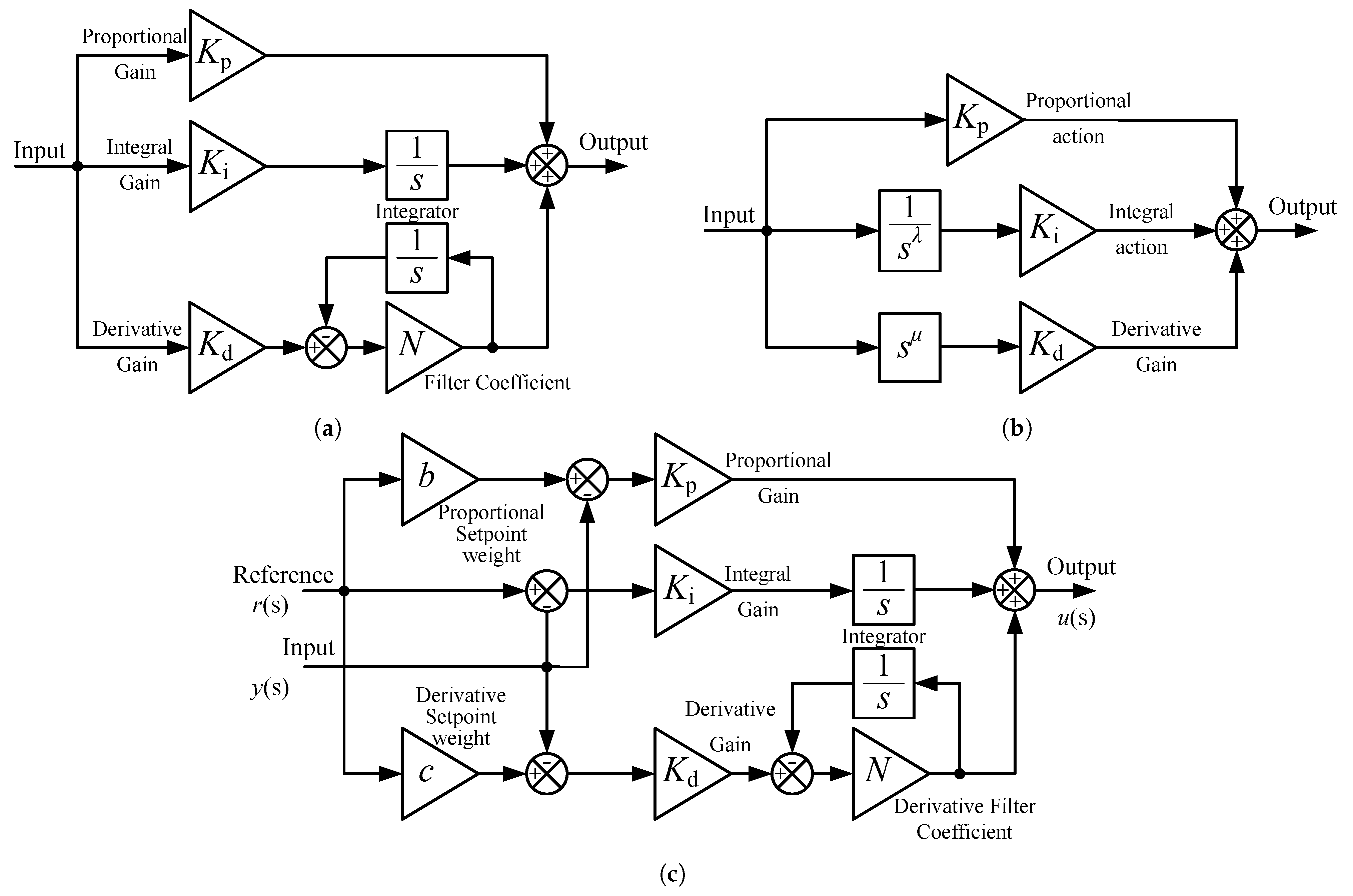
3.2. PIDF Controller
3.3. FOPID Controller
3.4. 2DOF-PIDF Controller
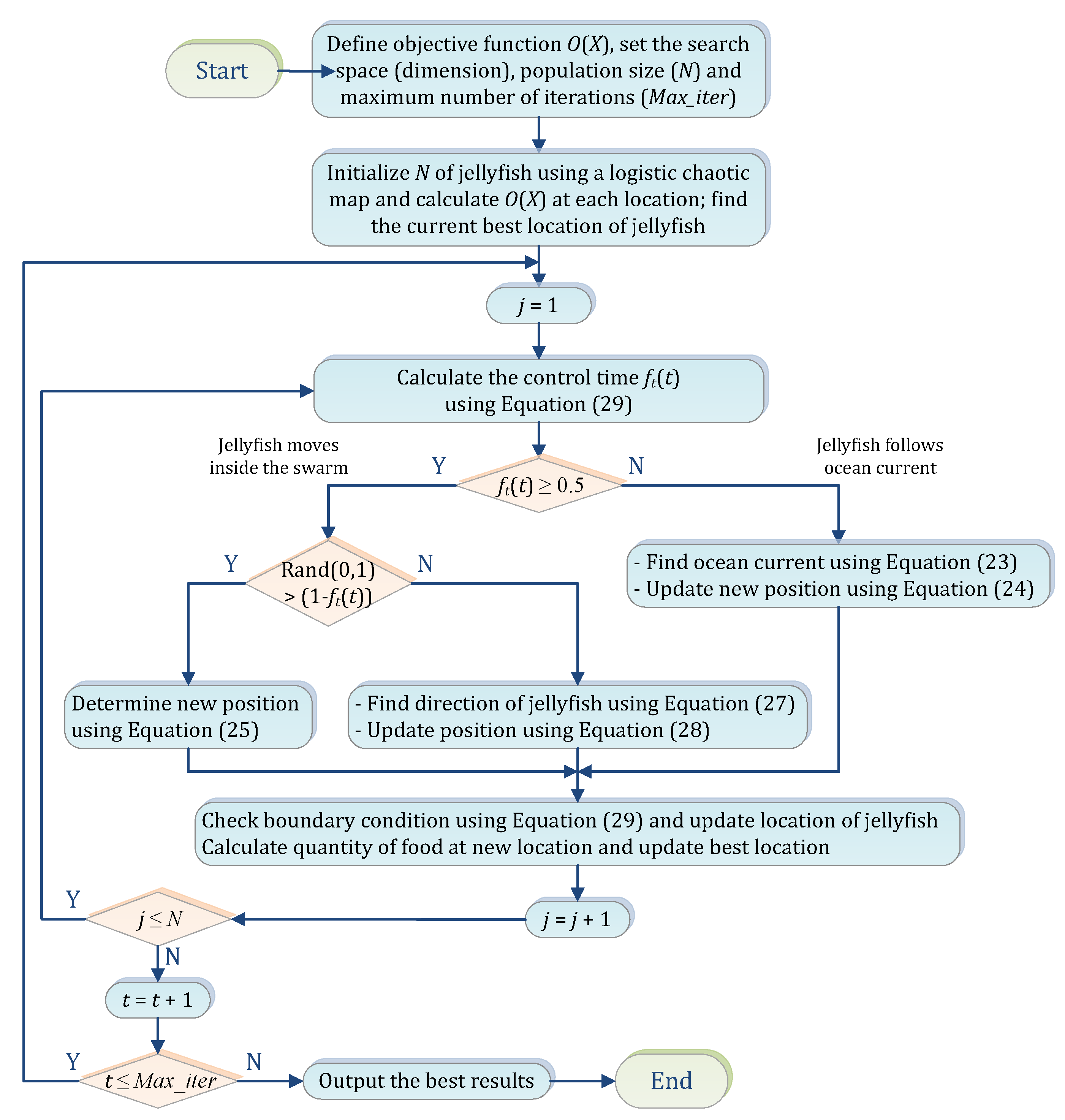
4. Overview of the Jellyfish Search Optimizer
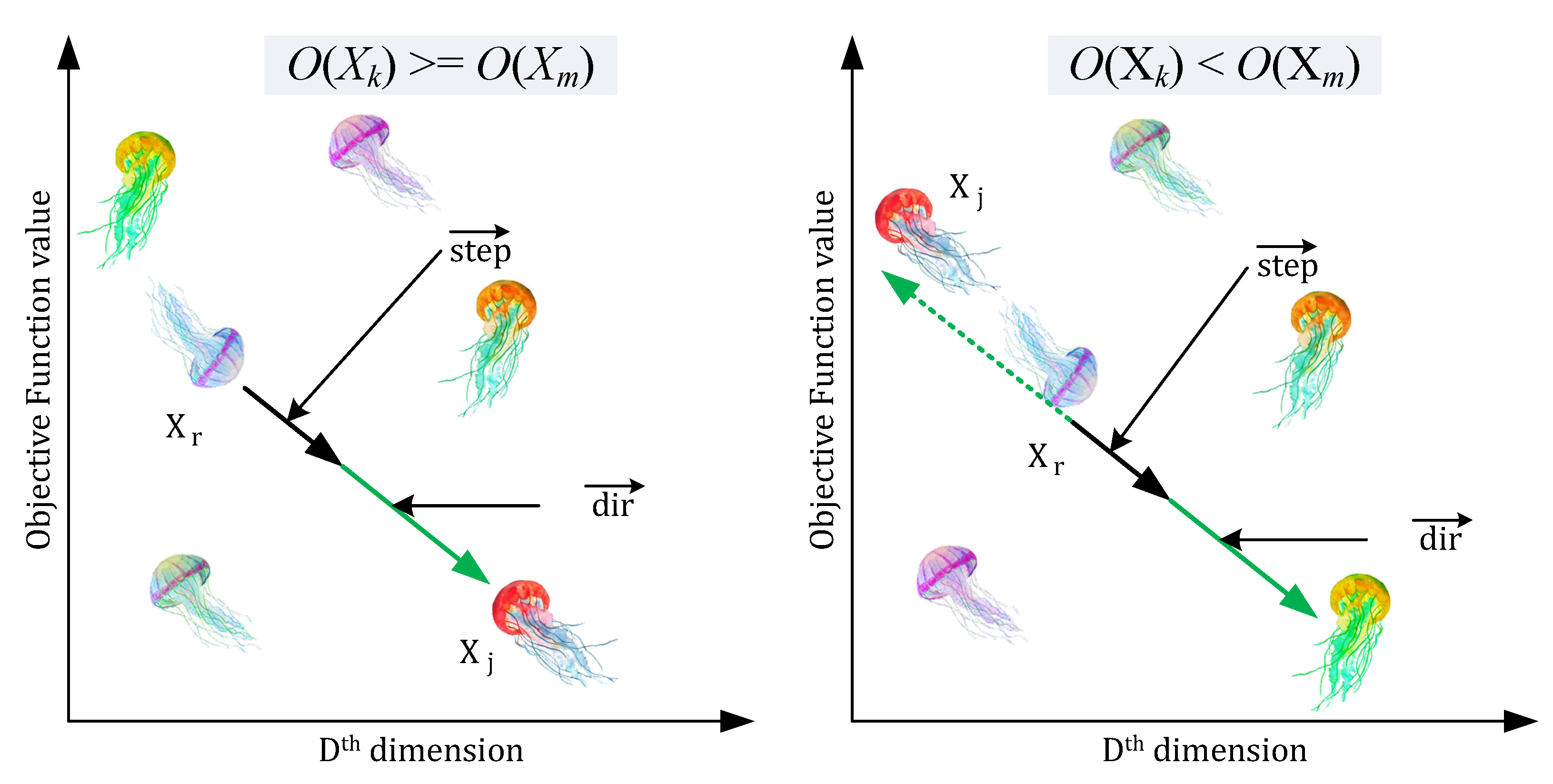
4.1. Mathematical Model
- 1.
- A “time control system” regulates the switching behavior of jellyfish between movement within the swarm and tracking the ocean current.
- 2.
- In their migration through the ocean, jellyfish are attracted to areas where food is more abundant and actively seek out such regions.
- 3.
- The quantity of food present at a given location, as well as the associated objective function dictate the degree of its attractiveness.
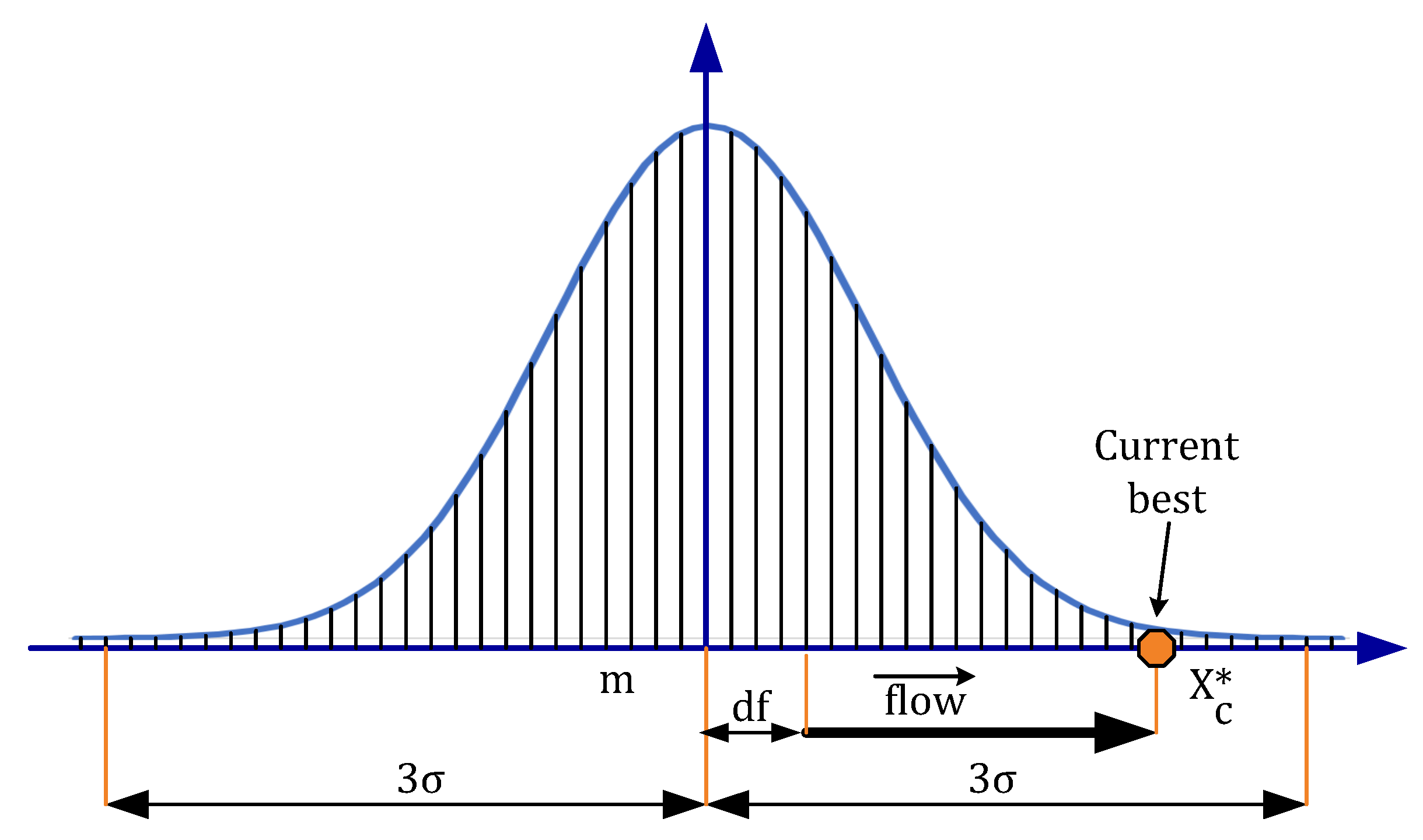
4.1.1. Ocean Current
4.1.2. Jellyfish Swarm
4.1.3. Time Control Mechanism
4.1.4. Population Initialization and Boundary Conditions
5. Controller Optimization Procedure
6. Further Analysis of Designed Controller Robustness
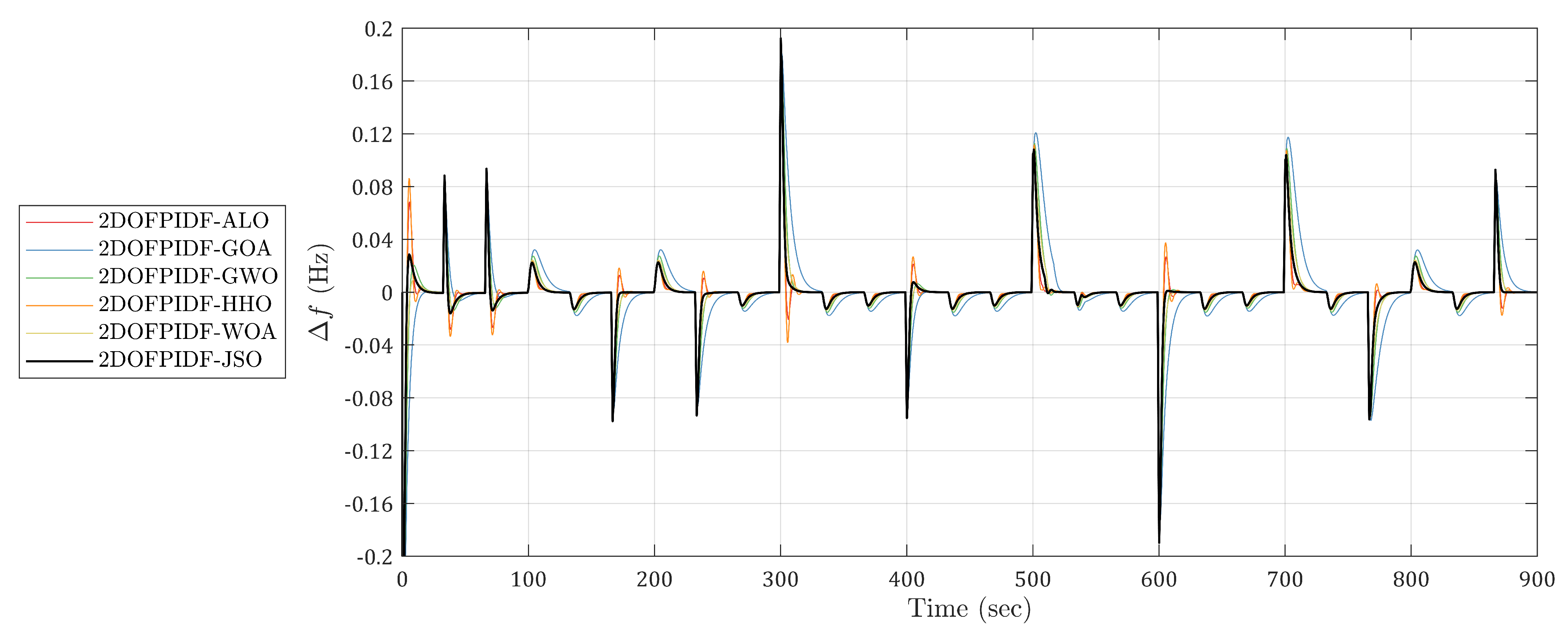
6.1. Case 1: Random Multi-Step Energy–Load Variation
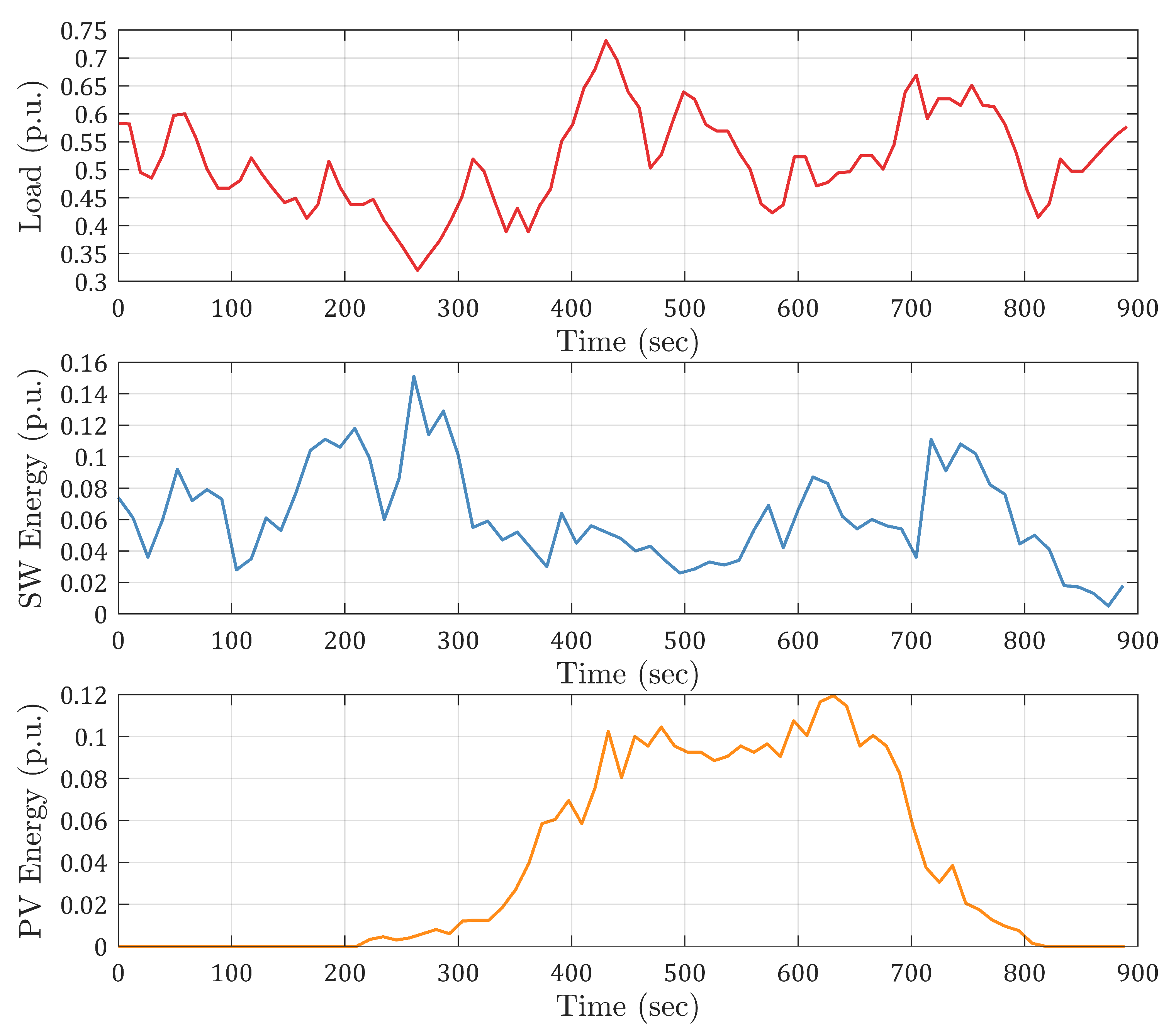
6.2. Case 2: Stochastic Power Fluctuations—Real Data
6.3. Case 3: Sensitivity Analysis—System’s Parameter Variation
7. Conclusions
- -
- The possibility of integrating other green energy sources, such as the combination of wind, PV, and wave energy, into these systems. The orientation of the PV panel and the likelihood of unplanned power generation system shutdowns could both be taken into account in this context;
- -
- Investigations into different hybrid energy storage solutions to solve the issue of LFC. Such a system might combine a superconducting magnetic energy storage (SMES) system with battery storage as an example. This strategy could have distinct advantages over current hybrid storage systems and offer insightful information for enhancing frequency load control for SMGs;
- -
- The SMG considered in this study can be tested in the future with different optimization methods and different controllers, while the corresponding obtained results can then be compared with the findings of the current paper.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 2DOF-PIDF | 2-degree-of-freedom PID with filter | BESS | battery energy storage system |
| ALO | ant-lion optimizer | DG | diesel generator |
| BOA | butterfly optimization algorithm | FC | fuel cell |
| ESS | energy storage system | FESS | flywheel energy storage system |
| FFOPI(D) | fuzzy fractional-order PI(D) | GA | genetic algorithm |
| FOPID | fractional-order PID | GWO | grey wolf optimizer |
| GOA | grasshopper optimization algorithm | ITAE | integral time absolute error |
| HHO | Harris hawks optimization | LFC | load-frequency control |
| JSO | jellyfish search optimizer | NFLOPID | non-linear fractional-order PID |
| MG | microgrid | PIDF | proportional-integral-derivative with filter |
| PEMFC | proton exchange membrane fuel cell | PV | photovoltaics |
| PSO | particle swarm optimization | SDG | ship diesel generator |
| RES | renewable energy source | SPS | shipboard power system |
| SMG | ship microgrid | SSA | salp swarm algorithm |
| SoC | state of charge | TLBO | teaching–learning-based optimization |
| SWE | sea wave energy | WEC | wave energy conversion |
| UC | ultra-capacitors | WOA | whale optimization Algorithm |
Appendix A. System Parameters
| Parameter | Value (Unit) | Parameter | Value (Unit) |
|---|---|---|---|
| Diesel source | PV source | ||
| time constant | 0.08 (s) | time constant () | 4.0 (s) |
| time constant | 0.40 (s) | time constant () | 0.5 (s) |
| ramp rate limit | 0.05 (p.u. MW/s) | flywheel | |
| PEMFC source | time constant () | 0.1 (s) | |
| time constant () | 0.26 (s) | battery | |
| time constant () | 0.04 (s) | time constant () | 0.1 (s) |
| time constant () | 0.004 (s) | system | |
| SWE source | inertia constant (M) | 0.2 (p.u.·s) | |
| time constant () | 0.5 (s) | damping coefficient (D) | 0.012 (p.u./Hz) |
| time constant () | 4.0 (s) | droop regulation (R) | 3.0 (p.u. MW/s) |
References
- Mutarraf, M.; Terriche, Y.; Niazi, K.; Vasquez, J.; Guerrero, J. Energy Storage Systems for Shipboard Microgrids—A Review. Energies 2018, 11, 3492. [Google Scholar] [CrossRef]
- Issa, M.; Ilinca, A.; Martini, F. Ship Energy Efficiency and Maritime Sector Initiatives to Reduce Carbon Emissions. Energies 2022, 15, 7910. [Google Scholar] [CrossRef]
- Latif, A.; Hussain, S.M.S.; Das, D.C.; Ustun, T.S. Double stage controller optimization for load frequency stabilization in hybrid wind-ocean wave energy based maritime microgrid system. Appl. Energy 2021, 282, 116171. [Google Scholar] [CrossRef]
- Inal, O.B.; Charpentier, J.F.; Deniz, C. Hybrid power and propulsion systems for ships: Current status and future challenges. Renew. Sustain. Energy Rev. 2022, 156, 111965. [Google Scholar] [CrossRef]
- Nguyen, H.P.; Hoang, A.T.; Nizetic, S.; Nguyen, X.P.; Le, A.T.; Luong, C.N.; Chu, V.D.; Pham, V.V. The electric propulsion system as a green solution for management strategy of CO2 emission in ocean shipping: A comprehensive review. Int. Trans. Electr. Energy Syst. 2021, 31, e12580. [Google Scholar] [CrossRef]
- Hein, K.; Yan, X.; Wilson, G. Multi-Objective Optimal Scheduling of a Hybrid Ferry with Shore-to-Ship Power Supply Considering Energy Storage Degradation. Electronics 2020, 9, 849. [Google Scholar] [CrossRef]
- Wu, X.; Liu, J.; Men, Y.; Chen, B.; Lu, X. Optimal Energy Storage System and Smart Switch Placement in Dynamic Microgrids with Applications to Marine Energy Integration. IEEE Trans. Sustain. Energy 2022, 14, 1205–1216. [Google Scholar] [CrossRef]
- Bertinelli Salucci, C.; Bakdi, A.; Glad, I.K.; Vanem, E.; De Bin, R. A novel semi-supervised learning approach for State of Health monitoring of maritime lithium-ion batteries. J. Power Sour. 2023, 556, 232429. [Google Scholar] [CrossRef]
- Yang, T.; Wu, L.; Li, X.; Zhu, M.; Brennan, M.J.; Liu, Z. Active Vibration Isolation of a Diesel Generator in a Small Marine Vessel: An Experimental Study. Appl. Sci. 2020, 10, 3025. [Google Scholar] [CrossRef]
- Letafat, A.; Rafiei, M.; Sheikh, M.; Afshari-Igder, M.; Banaei, M.; Boudjadar, J.; Khooban, M.H. Simultaneous energy management and optimal components sizing of a zero-emission ferry boat. J. Energy Storage 2020, 28, 101215. [Google Scholar] [CrossRef]
- Huang, M.; He, W.; Incecik, A.; Cichon, A.; Królczyk, G.; Li, Z. Renewable energy storage and sustainable design of hybrid energy powered ships: A case study. J. Energy Storage 2021, 43, 103266. [Google Scholar] [CrossRef]
- Nasiri, S.; Peyghami, S.; Parniani, M.; Blaabjerg, F. A comprehensive theoretical approach for analysing manoeuvring effects on ships by integrating hydrodynamics and power system. IET Electr. Syst. Transp. 2022, 12, 89–101. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Sultan, H.M.; Mohamed, I.S.; Kuznetsov, O.N.; Do, T.D. Application of Different Optimization Algorithms for Optimal Sizing of PV/Wind/Diesel/Battery Storage Stand-Alone Hybrid Microgrid. IEEE Access 2019, 7, 119223–119245. [Google Scholar] [CrossRef]
- Roy, A.; Auger, F.; Olivier, J.C.; Schaeffer, E.; Auvity, B. Design, Sizing, and Energy Management of Microgrids in Harbor Areas: A Review. Energies 2020, 13, 5314. [Google Scholar] [CrossRef]
- Bao, X.; Xu, X.; Zhang, Y.; Xiong, Y.; Shang, C. Optimal Sizing of Battery Energy Storage System in a Shipboard Power System with considering Energy Management Optimization. Discrete Dyn. Nat. Soc. 2021, 2021, 9032206. [Google Scholar] [CrossRef]
- Mutarraf, M.; Terriche, Y.; Niazi; Khan, F.; Vasquez, J.; Guerrero, J. Control of Hybrid Diesel/PV/Battery/Ultra-Capacitor Systems for Future Shipboard Microgrids. Energies 2019, 12, 3460. [Google Scholar] [CrossRef]
- Xiao, Z.X.; Li, H.M.; Fang, H.W.; Guan, Y.Z.; Liu, T.; Hou, L.; Guerrero, J.M. Operation Control for Improving Energy Efficiency of Shipboard Microgrid Including Bow Thrusters and Hybrid Energy Storages. IEEE Trans. Transp. Electrif. 2020, 6, 856–868. [Google Scholar] [CrossRef]
- Zhaoxia, X.; Tianli, Z.; Huaimin, L.; Guerrero, J.M.; Su, C.L.; Vasquez, J.C. Coordinated Control of a Hybrid-Electric-Ferry Shipboard Microgrid. IEEE Trans. Transp. Electrif. 2019, 5, 828–839. [Google Scholar] [CrossRef]
- Kumar, D.; Mathur, H.D.; Bhanot, S.; Bansal, R.C. Forecasting of solar and wind power using LSTM RNN for load frequency control in isolated microgrid. Int. J. Model. Simul. 2021, 41, 311–323. [Google Scholar] [CrossRef]
- Alayi, R.; Zishan, F.; Seyednouri, S.R.; Kumar, R.; Ahmadi, M.H.; Sharifpur, M. Optimal Load Frequency Control of Island Microgrids via a PID Controller in the Presence of Wind Turbine and PV. Sustainability 2021, 13, 10728. [Google Scholar] [CrossRef]
- Wang, H.; Zeng, G.; Dai, Y.; Bi, D.; Sun, J.; Xie, X. Design of a Fractional Order Frequency PID Controller for an Islanded Microgrid: A Multi-Objective Extremal Optimization Method. Energies 2017, 10, 1502. [Google Scholar] [CrossRef]
- Fayek, H.H. Load Frequency Control of a Power System with 100% Renewables. In Proceedings of the 2019 54th International Universities Power Engineering Conference (UPEC), Bucharest, Romania, 3–6 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Yildirim, B.; Gheisarnejad, M.; Khooban, M.H. A New Parameter Tuning Technique for Noninteger Controllers in Low-Inertia Modern Power Grids. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 279–288. [Google Scholar] [CrossRef]
- Koley, I.; Datta, A.; Panda, G.K.; Debbarma, S. TLBO Optimised PIDD Controller for Coordinated Control in a Hybrid AC/DC Microgrid. In Proceedings of the 2022 4th International Conference on Energy, Power and Environment (ICEPE), Shillong, India, 29 April–1 May 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Lal, D.K.; Barisal, A.K.; Tripathy, M. Load Frequency Control of Multi Area Interconnected Microgrid Power System using Grasshopper Optimization Algorithm Optimized Fuzzy PID Controller. In Proceedings of the 2018 Recent Advances on Engineering, Technology and Computational Sciences (RAETCS), Allahabad, India, 6–8 February 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Askarzadeh, A. A Memory-Based Genetic Algorithm for Optimization of Power Generation in a Microgrid. IEEE Trans. Sustain. Energy 2018, 9, 1081–1089. [Google Scholar] [CrossRef]
- Sharma, P.; Prakash, A.; Shankar, R.; Parida, S.K. A Novel Hybrid Salp Swarm Differential Evolution Algorithm Based 2DOF Tilted-Integral-Derivative Controller for Restructured AGC. Electr. Power Compon. Syst. 2019, 47, 1775–1790. [Google Scholar] [CrossRef]
- Chung, I.Y.; Liu, W.; Cartes, D.A.; Schoder, K. Control parameter optimization for a microgrid system using particle swarm optimization. In Proceedings of the 2008 IEEE International Conference on Sustainable Energy Technologies, Singapore, 24–27 November 2008; pp. 837–842. [Google Scholar] [CrossRef]
- Malik, S.; Suhag, S. A coordinated control strategy for frequency regulation in hybrid shipboard power system using novel salp swarm algorithm tuned fractional controller. Int. J. Ambient Energy 2022, 43, 5638–5653. [Google Scholar] [CrossRef]
- Choudhary, A.K.; Prakash, S.; Sharma, M.; Dhundhara, S. Grasshopper optimisation based robust power/frequency regulator for shipboard micro-grid. IET Renew. Power Gener. 2020, 14, 3568–3577. [Google Scholar] [CrossRef]
- Mondal, A.; Latif, A.; Das, D.C.; Hussain, S.M.S.; Al-Durra, A. Frequency regulation of hybrid shipboard microgrid system using butterfly optimization algorithm synthesis fractional-order controller. Int. J. Numer. Modell. Electron. Netw. Devices Fields 2022, e3058. [Google Scholar] [CrossRef]
- Chou, J.S.; Molla, A. Recent advances in use of bio-inspired jellyfish search algorithm for solving optimization problems. Sci. Rep. 2022, 12, 19157. [Google Scholar] [CrossRef]
- Shubham; Roy, S.P.; Mehta, R.K.; Singh, A.K.; Roy, O.P. A novel application of jellyfish search optimisation tuned dual-stage (1 + PI)TID controller for microgrid employing electric vehicle. Int. J. Ambient Energy 2022, 43, 8408–8427. [Google Scholar] [CrossRef]
- Fathy, A.; Kassem, A.M. Antlion optimizer-ANFIS load frequency control for multi-interconnected plants comprising photovoltaic and wind turbine. ISA Trans. 2019, 87, 282–296. [Google Scholar] [CrossRef]
- Srinivasarathnam, C.; Yammani, C.; Maheswarapu, S. Load Frequency Control of Multi-microgrid System considering Renewable Energy Sources Using Grey Wolf Optimization. Smart Sci. 2019, 7, 198–217. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. Grasshopper optimization algorithm scaled fractional order PI-D controller applied to reduced order model of load frequency control system. Int. J. Modell. Simul. 2020, 40, 217–242. [Google Scholar] [CrossRef]
- Karnavas, Y.L.; Nivolianiti, E. Load Frequency Control in Multi-Source Power Generation Systems using Harris Hawks Optimization Algorithm. In Proceedings of the 2022 International Conference on Communications, Information, Electronic and Energy Systems (CIEES), Veliko Tarnovo, Bulgaria, 24–26 November 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. Whale optimization algorithm applied to load frequency control of a mixed power system considering non-linearities and PLL dynamics. Energy Syst. 2020, 11, 699–728. [Google Scholar] [CrossRef]
- Yildirim, B.; Gheisarnejad, M.; Khooban, M.H. A Robust Non-Integer Controller Design for Load Frequency Control in Modern Marine Power Grids. IEEE Trans. Emerg. Top. Comput. Intell. 2022, 6, 852–866. [Google Scholar] [CrossRef]
- Esfahani, Z.; Roohi, M.; Gheisarnejad, M.; Dragičević, T.; Khooban, M.H. Optimal Non-Integer Sliding Mode Control for Frequency Regulation in Stand-Alone Modern Power Grids. Appl. Sci. 2019, 9, 3411. [Google Scholar] [CrossRef]
- Bhuyan, S.; Hota, P.; Panda, B. Power Quality Analysis of a Grid-connected Solar/Wind/Hydrogen Energy Hybrid Generation System. Int. J. Power Electron. Drive Syst. 2018, 9, 377–389. [Google Scholar] [CrossRef]
- Methekar, R.; Prasad, V.; Gudi, R. Dynamic analysis and linear control strategies for proton exchange membrane fuel cell using a distributed parameter model. J. Power Sour. 2007, 165, 152–170. [Google Scholar] [CrossRef]
- Obara, S. Analysis of a fuel cell micro-grid with a small-scale wind turbine generator. Int. J. Hydrogen Energy 2007, 32, 323–336. [Google Scholar] [CrossRef]
- Nolte, J.D.; Ertekin, R.C. Wave power calculations for a wave energy conversion device connected to a drogue. J. Renew. Sustain. Energy 2014, 6, 013117. [Google Scholar] [CrossRef]
- Hasanien, H.M. Whale optimisation algorithm for automatic generation control of interconnected modern power systems including renewable energy sources. IET Gener. Transm. Distrib. 2018, 12, 607–614. [Google Scholar] [CrossRef]
- Lee, D.J.; Wang, L. Small-Signal Stability Analysis of an Autonomous Hybrid Renewable Energy Power Generation/Energy Storage System Part I: Time-Domain Simulations. IEEE Trans. Energy Convers. 2008, 23, 311–320. [Google Scholar] [CrossRef]
- Sahu, R.K.; Chandra Sekhar, G.; Panda, S. DE optimized fuzzy PID controller with derivative filter for LFC of multi source power system in deregulated environment. Ain Shams Eng. J. 2015, 6, 511–530. [Google Scholar] [CrossRef]
- Sharma, M.; Bansal, R.K.; Prakash, S.; Dhundhara, S. Frequency Regulation in PV integrated Power System using MFO tuned PIDF controller. In Proceedings of the 2018 IEEE 8th Power India International Conference (PIICON), Kurukshetra, India, 10–12 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Zhao, C.; Jiang, M.; Huang, Y. Formal Verification of Fractional-Order PID Control Systems Using Higher-Order Logic. Fractal Fract. 2022, 6, 485. [Google Scholar] [CrossRef]
- Soni, V.; Parmar, G.; Kumar, M.; Panda, S. Hybrid Grey Wolf Optimization-Pattern Search (hGWO-PS) Optimized 2DOF-PID Controllers for Load Frequency Control (LFC) in Interconnected Thermal Power Plants. Int. J. Soft Comput. 2016, 6, 1244–1256. [Google Scholar] [CrossRef]
- Sahu, R.K.; Panda, S.; Rout, U.K.; Sahoo, D.K. Teaching learning based optimization algorithm for automatic generation control of power system using 2-DOF PID controller. Int. J. Electr. Power Energy Syst. 2016, 77, 287–301. [Google Scholar] [CrossRef]
- Chou, J.S.; Truong, D.N. A novel metaheuristic optimizer inspired by behavior of jellyfish in ocean. Appl. Math. Comput. 2021, 389, 125535. [Google Scholar] [CrossRef]
- Alam, A.; Verma, P.; Tariq, M.; Sarwar, A.; Alamri, B.; Zahra, N.; Urooj, S. Jellyfish Search Optimization Algorithm for MPP Tracking of PV System. Sustainability 2021, 13, 11736. [Google Scholar] [CrossRef]


| Parameter | Lower Limit | Upper Limit | Parameter | Lower Limit | Upper Limit |
|---|---|---|---|---|---|
| −3.0 | 3.0 | 0.0 | 2.0 | ||
| −3.0 | 3.0 | 0.0 | 2.0 | ||
| −3.0 | 3.0 | b | 0.0 | 5.0 | |
| N | 0.0 | 5.0 | c | 0.0 | 5.0 |
| Controller | Algorithm | ITAE | N | (mHz) | (mHz) | (s) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ALO | 0.2867 | −0.8400 | 0.1743 | −1.8700 | 0.0010 | −59.761 | 6.6323 | 14.5059 | |||
| GOA | 0.2146 | −1.2721 | 0.2020 | 1.1019 | 0.5233 | −59.761 | 3.8077 | 12.3677 | |||
| PIDF | GWO | 0.2867 | −0.8372 | 0.1741 | −0.0677 | 0.0390 | −59.761 | 6.8512 | 14.5088 | ||
| HHO | 0.2228 | −1.2141 | 0.1981 | 0.9253 | 1.0212 | −59.761 | 2.4283 | 13.8521 | |||
| JSO | 0.1683 | −1.5236 | 0.2116 | 2.6151 | 0.4902 | −59.761 | 0.0000 | 12.4524 | |||
| WOA | 0.2081 | −1.0997 | 0.1849 | 1.8759 | 0.5992 | −59.761 | 0.0000 | 13.1046 | |||
| Controller | Algorithm | ITAE | (mHz) | (mHz) | (s) | ||||||
| ALO | 0.2095 | −1.6244 | 0.1564 | 0.8213 | 1.0842 | 0.1311 | −60.171 | 3.1125 | 12.1313 | ||
| GOA | 0.1818 | −0.6785 | 0.0437 | 0.1998 | 1.5684 | 0.6036 | −60.171 | 0.0000 | 17.3533 | ||
| FOPID | GWO | 0.2157 | −0.7583 | 0.0280 | 0.0980 | 1.7795 | 0.0645 | −60.171 | 1.5037 | 18.1233 | |
| HHO | 0.2418 | −0.9179 | 0.0295 | 0.5486 | 1.6904 | 0.0001 | −60.171 | 0.0000 | 18.2348 | ||
| JSO | 0.1479 | −2.1209 | 0.0817 | 1.6633 | 1.3457 | 0.1281 | −60.171 | 0.0000 | 14.3062 | ||
| WOA | 0.2156 | −3.0000 | 0.0540 | 2.6208 | 1.4169 | 0.0001 | −60.171 | 0.0000 | 16.1266 | ||
| Controller | Algorithm | ITAE | (mHz) | (mHz) | (s) | ||||||
| ALO | 0.3194 | −0.0004 | 0.3316 | −0.0173 | 0.2535 | 2.1355 | 0.6743 | −50.361 | 0.0000 | 15.0948 | |
| GOA | 0.2509 | 0.0250 | 0.9357 | 0.0694 | 1.4305 | 1.0224 | 1.0163 | −40.875 | 22.854 | 15.6126 | |
| 2DOF-PIDF | GWO | 0.0476 | 0.3158 | 0.6525 | 0.0746 | 0.2651 | 0.9977 | 1.0763 | −51.074 | 0.0000 | 7.6739 |
| HHO | 0.2748 | 0.0002 | 0.5862 | 0.1683 | 0.5233 | 0.6058 | 1.0170 | −45.477 | 10.853 | 14.5107 | |
| JSO | 0.0208 | 0.3920 | 0.8355 | −0.2296 | 0.0074 | 0.9978 | 0.0067 | −49.863 | 0.0000 | 3.1547 | |
| WOA | 0.2370 | 0.0151 | 1.0074 | 0.0005 | 3.5649 | 1.0543 | 2.8871 | −32.122 | 38.175 | 15.2957 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karnavas, Y.L.; Nivolianiti, E. Optimal Load Frequency Control of a Hybrid Electric Shipboard Microgrid Using Jellyfish Search Optimization Algorithm. Appl. Sci. 2023, 13, 6128. https://doi.org/10.3390/app13106128
Karnavas YL, Nivolianiti E. Optimal Load Frequency Control of a Hybrid Electric Shipboard Microgrid Using Jellyfish Search Optimization Algorithm. Applied Sciences. 2023; 13(10):6128. https://doi.org/10.3390/app13106128
Chicago/Turabian StyleKarnavas, Yannis L., and Evaggelia Nivolianiti. 2023. "Optimal Load Frequency Control of a Hybrid Electric Shipboard Microgrid Using Jellyfish Search Optimization Algorithm" Applied Sciences 13, no. 10: 6128. https://doi.org/10.3390/app13106128
APA StyleKarnavas, Y. L., & Nivolianiti, E. (2023). Optimal Load Frequency Control of a Hybrid Electric Shipboard Microgrid Using Jellyfish Search Optimization Algorithm. Applied Sciences, 13(10), 6128. https://doi.org/10.3390/app13106128







