Electromagnetic Radiation Space Field Construction Collected along the Road Based on Layered Radial Basis Function
Abstract
:1. Introduction
2. Construction Method of EMR-SF along the Road Collection Data
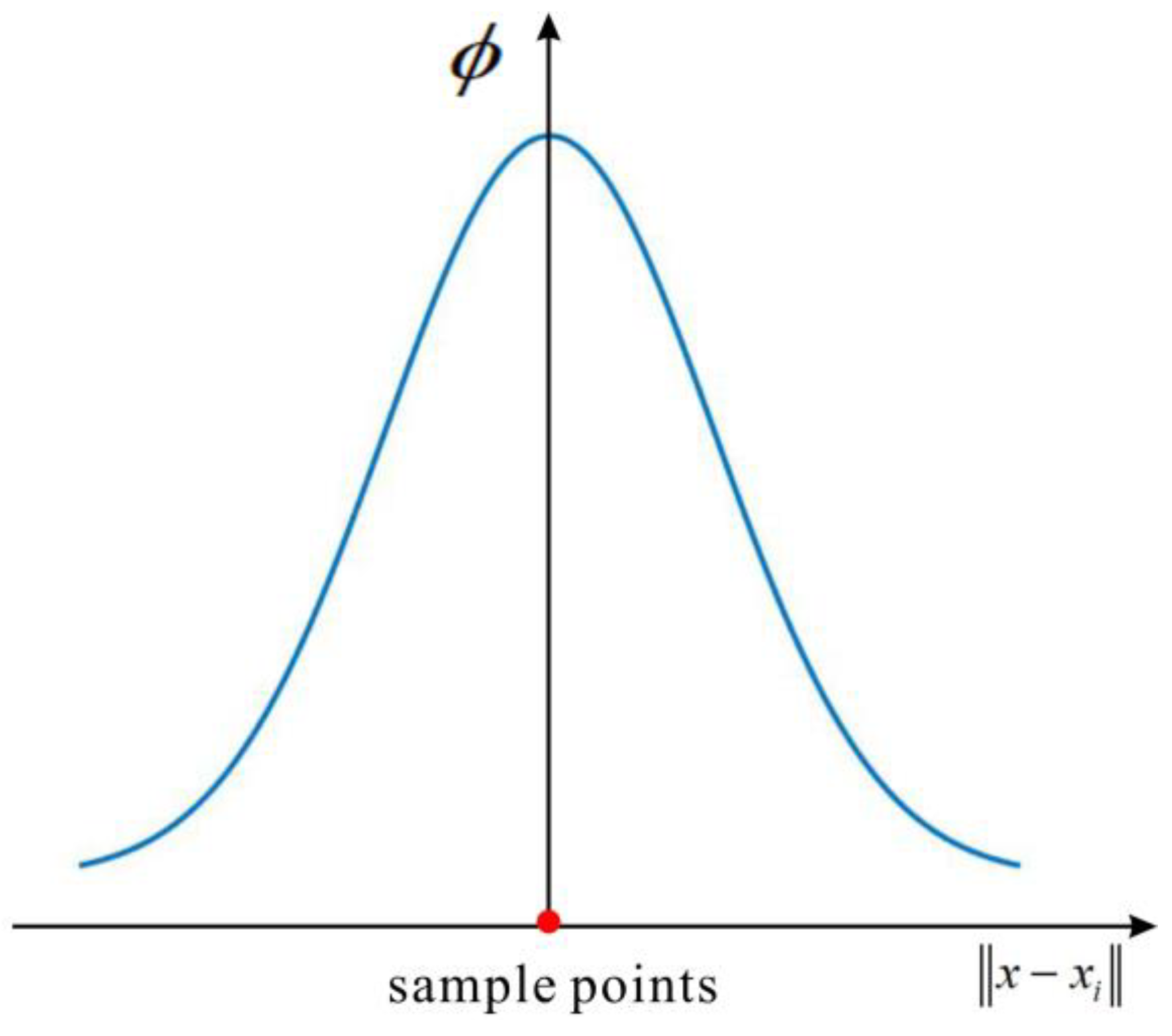
2.1. LRBF Interpolation Method
- Grid point density: the density of the grid points depends on the spacing distance between the grid points. If the spacing distance is large, the grid point density is small; otherwise, the density is large. The increase in the number of sample points xi is affected by the density of the grid points in the LRBF interpolation process. Too few grid points will cause the loss of data in the center of the sampling range, while too many grid points will cause data redundancy, both of which are not conducive to the construction of a space field by the LRBF. After determining the density of the grid point, it is necessary to determine the number of layers m of the grid point, which is affected by the interval distance between layers.
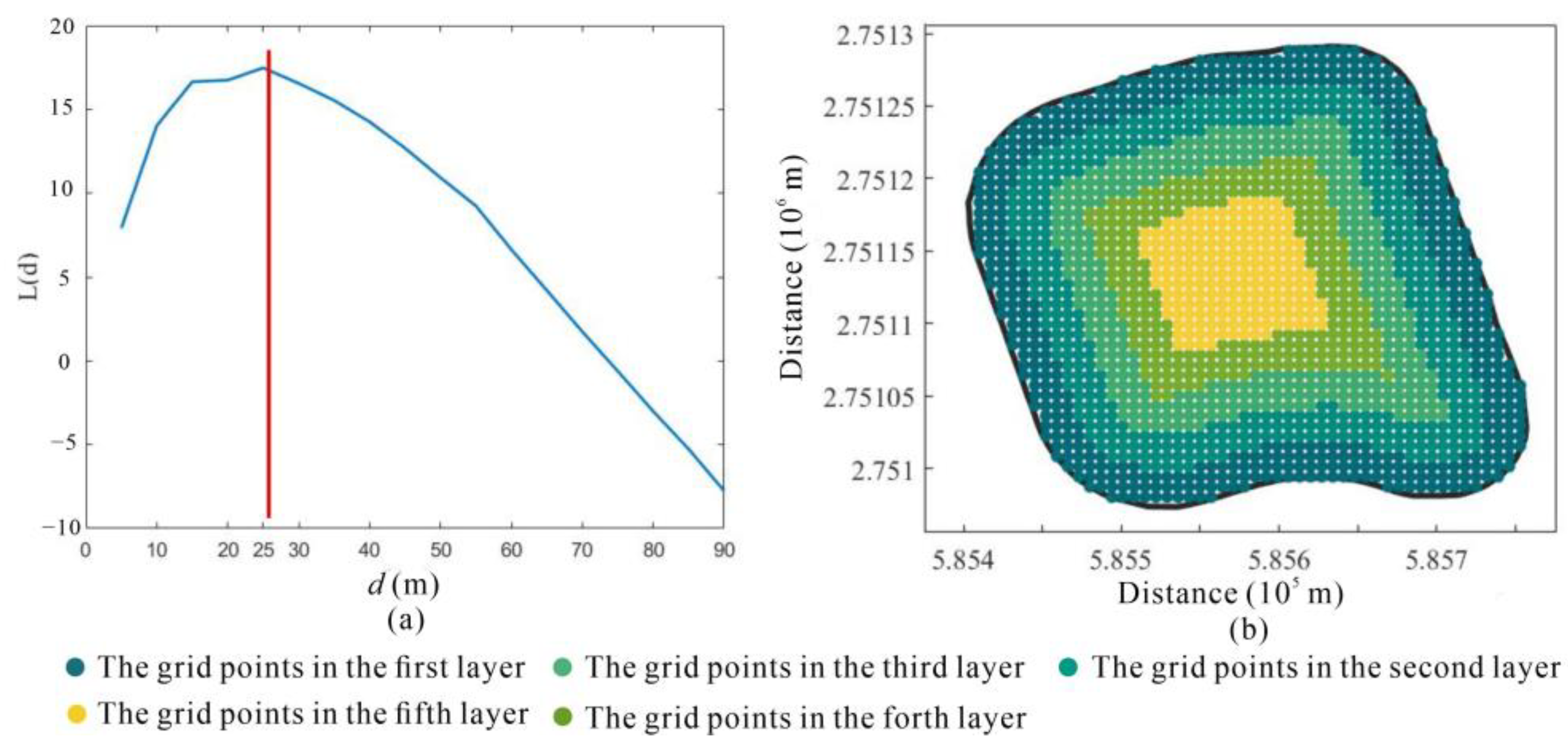
- Layered interval distance: the distance between the adjacent two layers represents the layered interval distance. The layered interval distance of the grid points affects the number of layers m, which determines the number of grid points in each layer. If the layering interval is too large and the number of layers is too small, it is not conducive to the inward expansion of the sampling data. However, if the layering interval is too small and the number of layers is too large, it will lead to more error propagation times, which will affect the interpolation results. Therefore, a suitable interval distance is found to improve the interpolation accuracy of LRBF.
2.2. Construction of the Grid Points in the LRBF
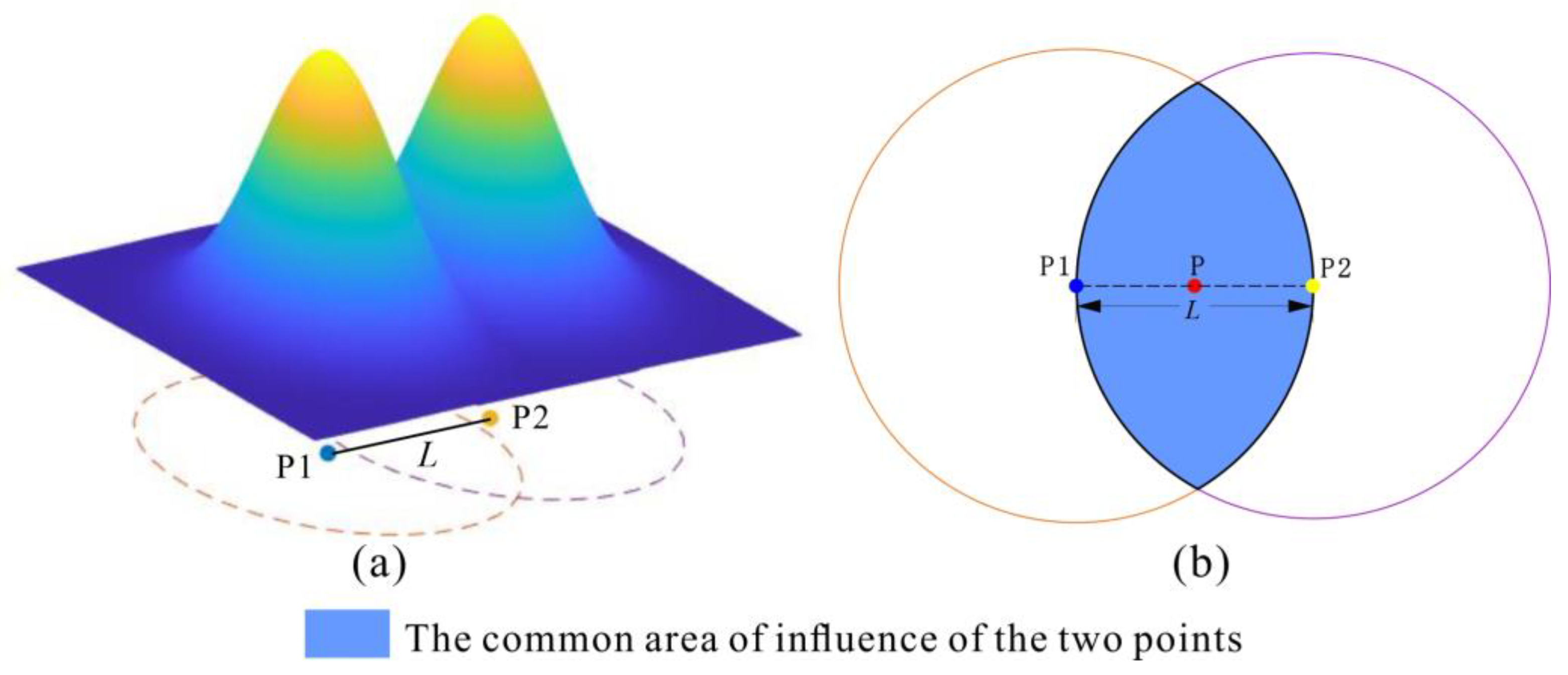
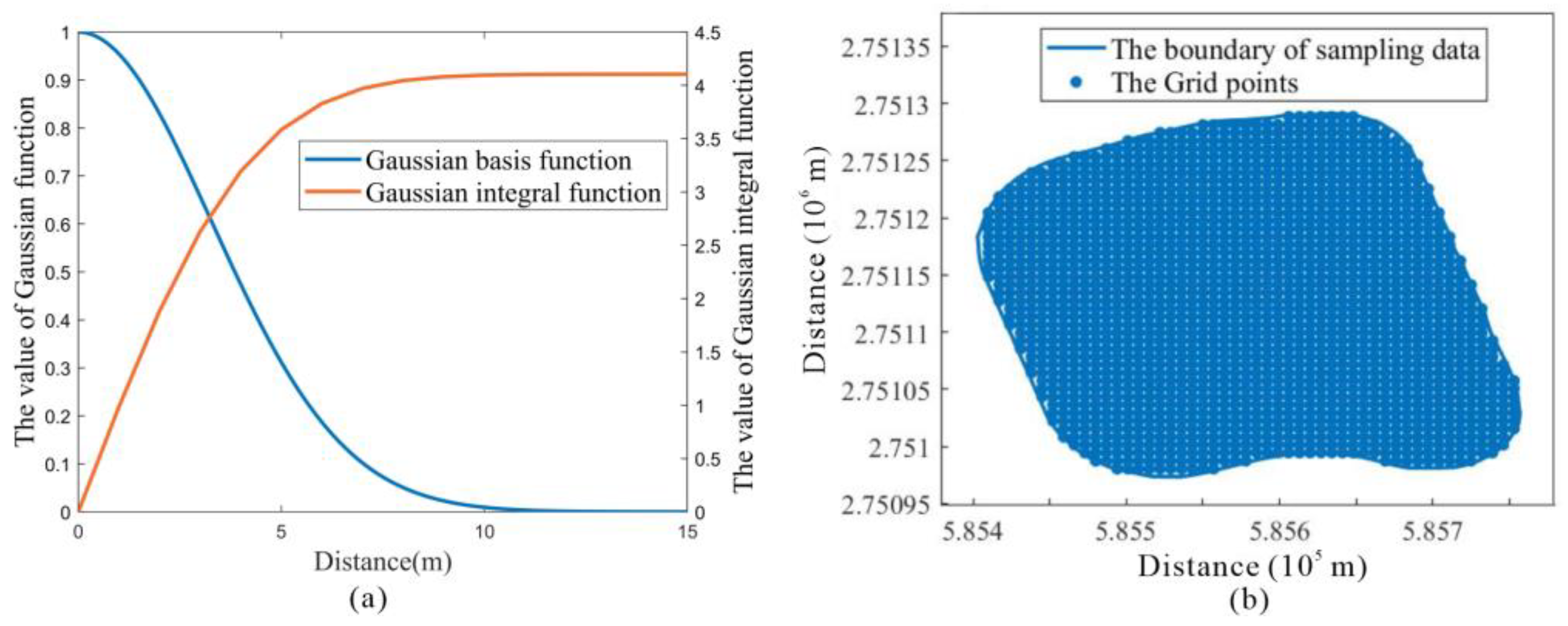
2.2.1. Maximum Influence Distance of the Sample Points
2.2.2. Grid Points Density
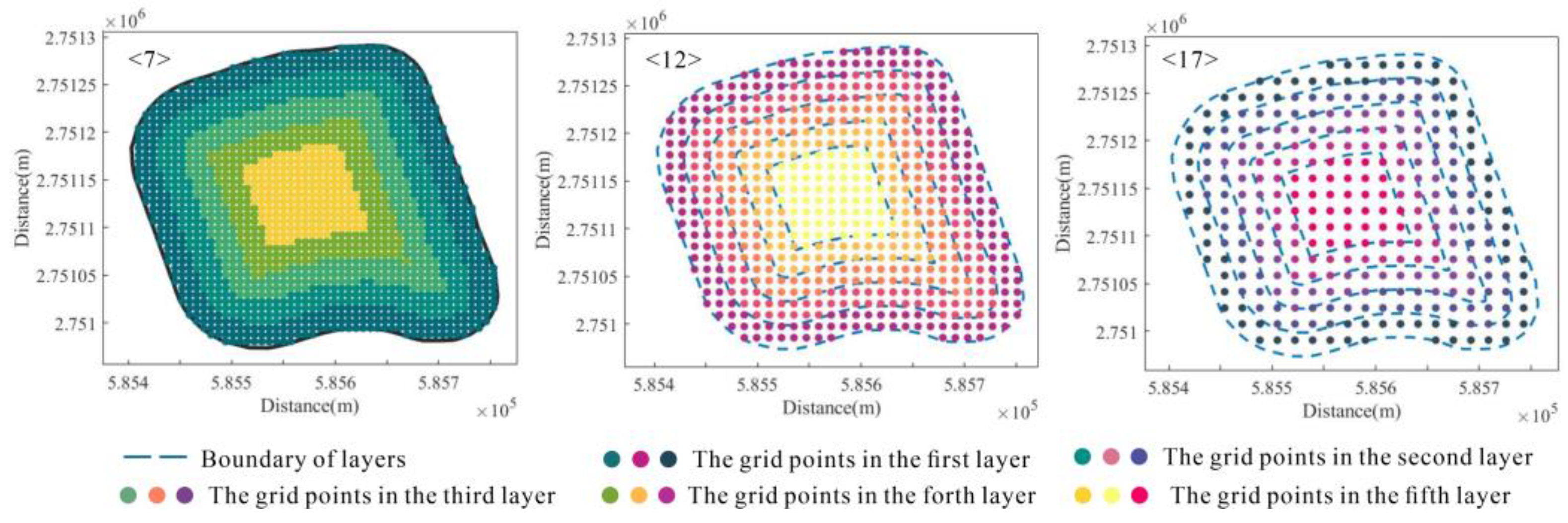
2.3. The Layered Grid Points in the LRBF
2.4. Construction of EMR-SF by the LRBF
- (1)
- The interpolation sample point set S = S0 is initialized, and the index number l = 1 is set.
- (2)
- Point set Gl is taken from the grid point set.
- (3)
- The EMR value of each point in point set Gl is generated by sample point set S according to Equation (1).
- (4)
- Point set Gl is added to the interpolation sample point set S to form a new interpolation sample point set S = S ∪ Gl.
- (5)
- l = l + 1.
- (6)
- Steps (2)–(5) are repeated until the EMR value of each grid point is calculated.
- (7)
- Finally, the EMR-SF is constructed according to the updated interpolation dataset S = {S0, G1, G2,..., Gl}.
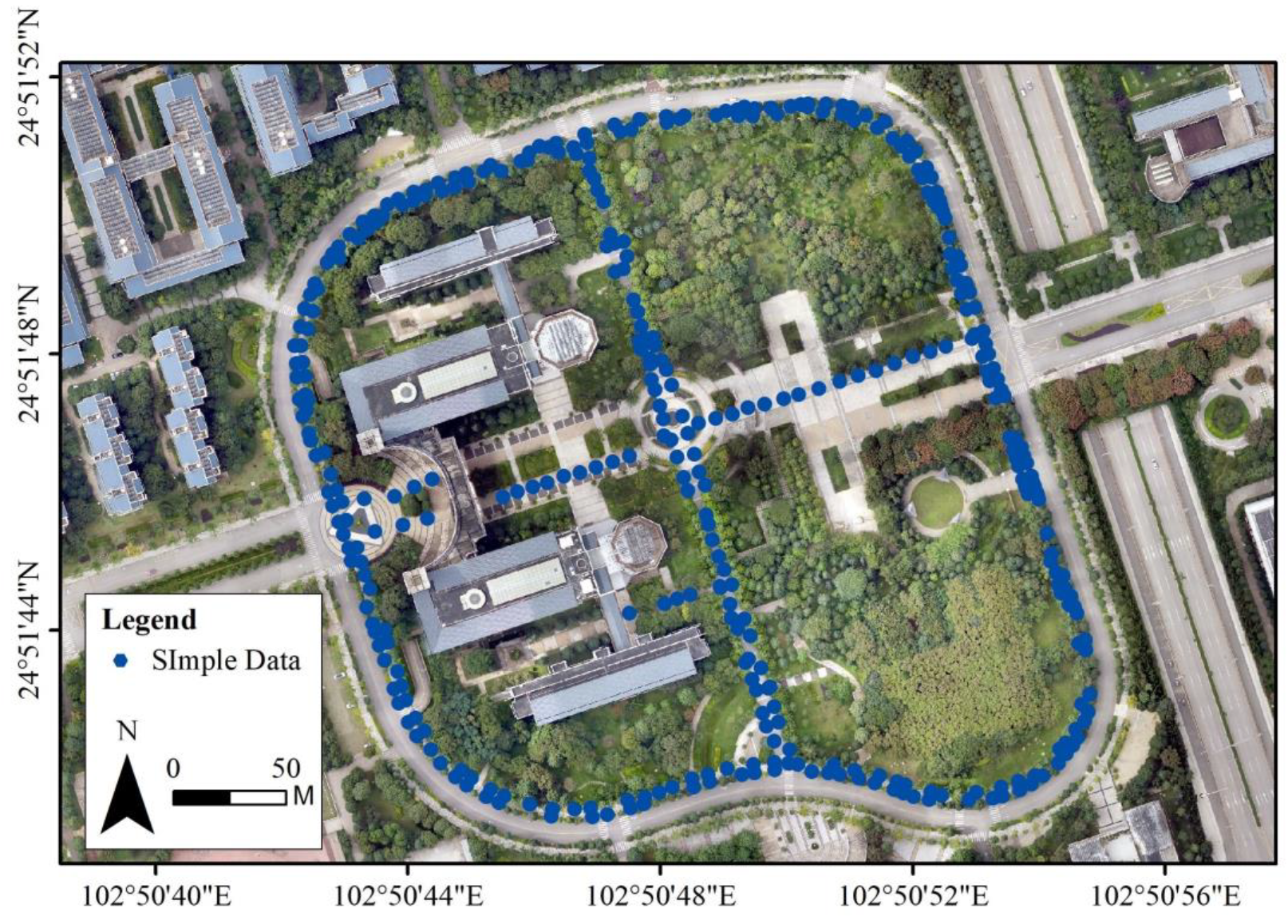
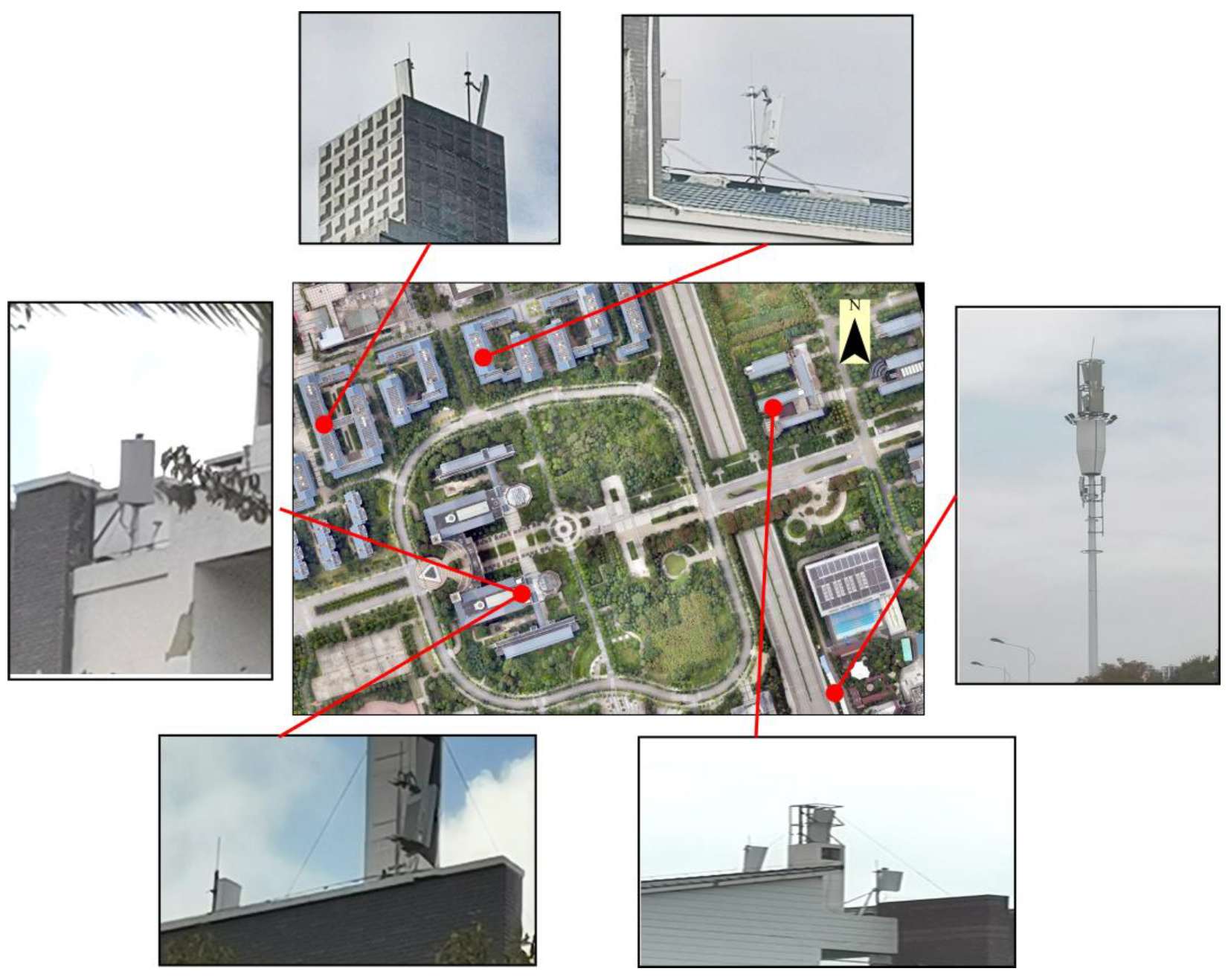
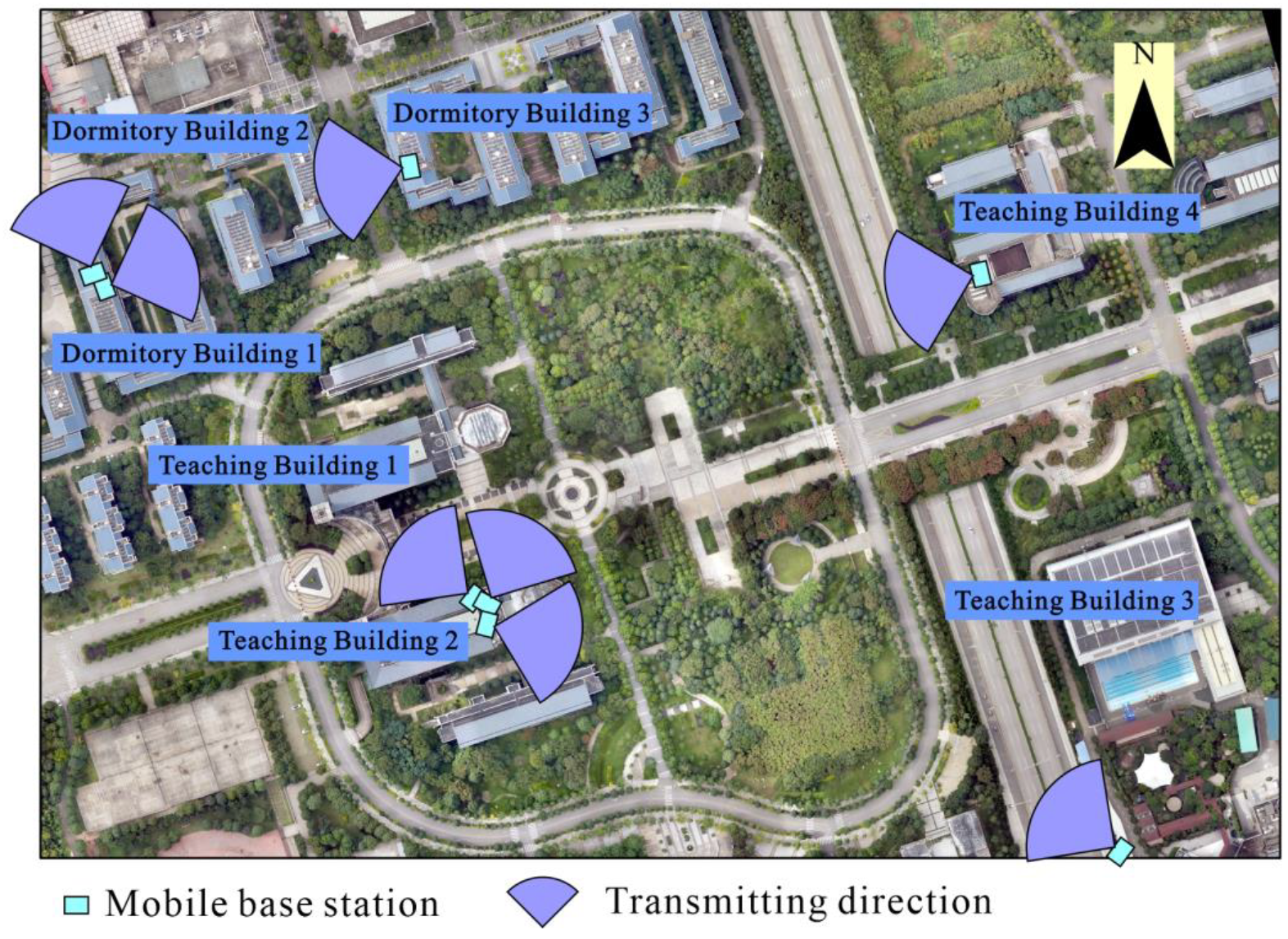
3. Study Area and Data Collection
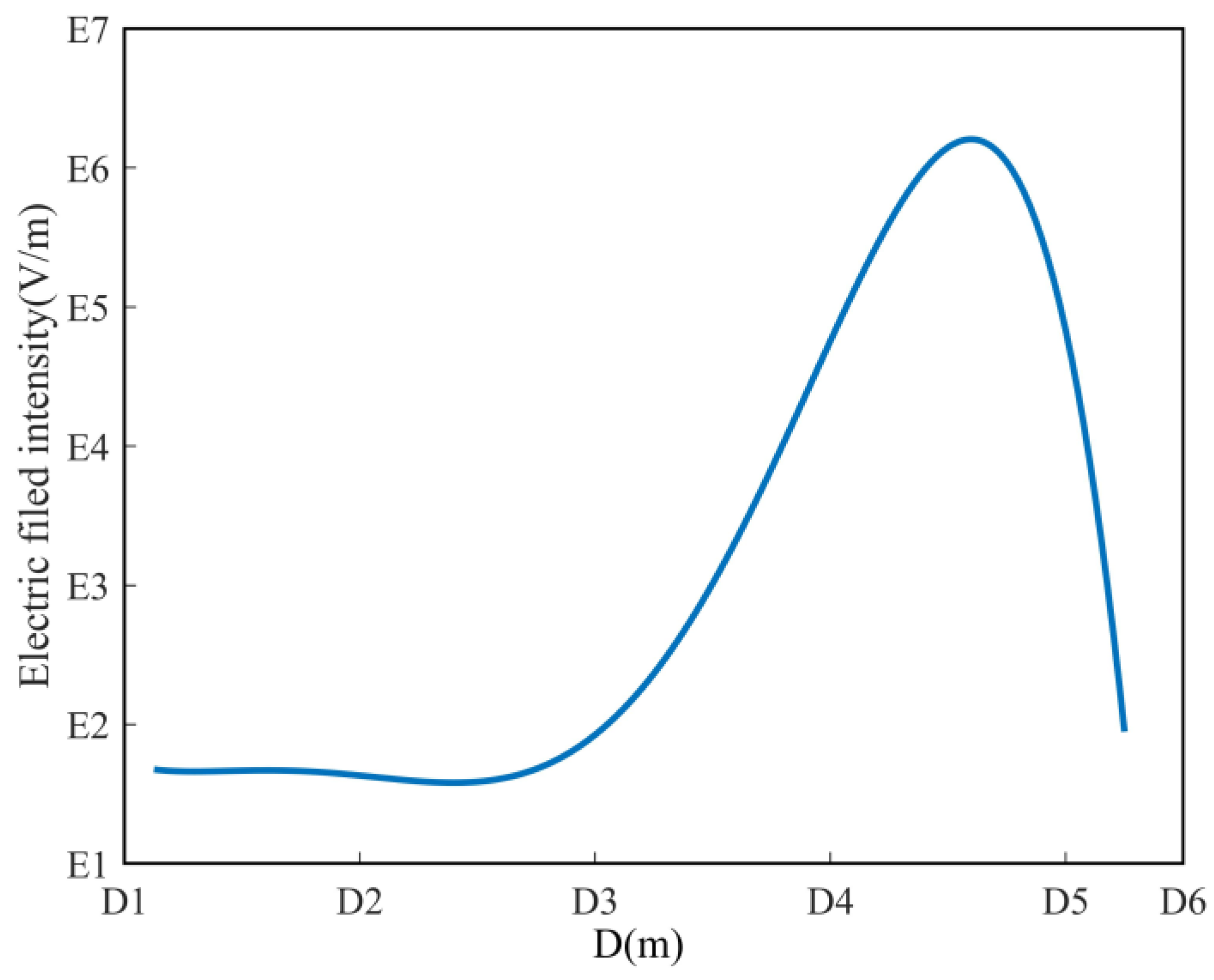
4. Experimental Results
4.1. The Grid Point Construction Results in LRBF
4.2. The Grid Points Layered Results in LRBF
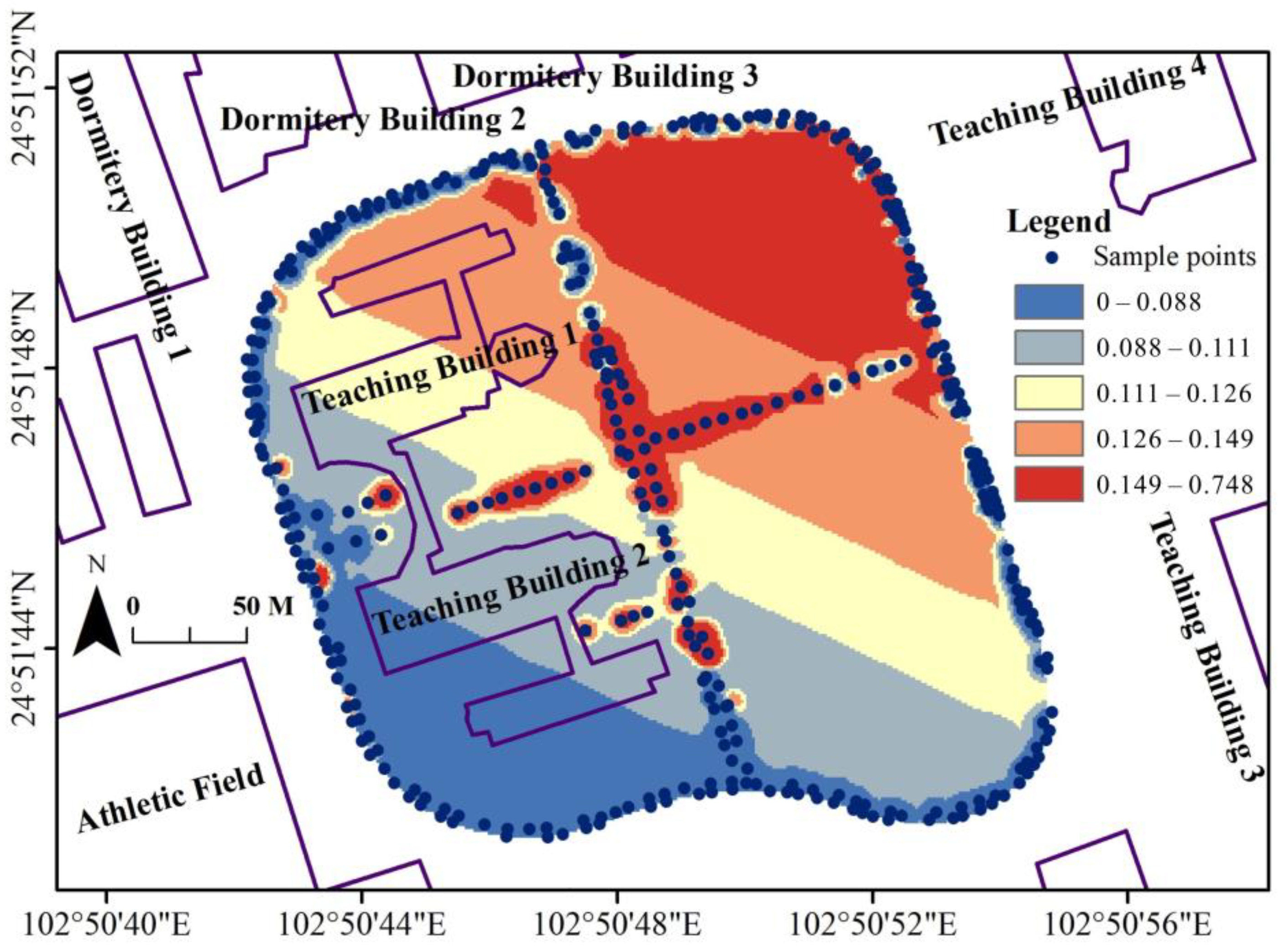
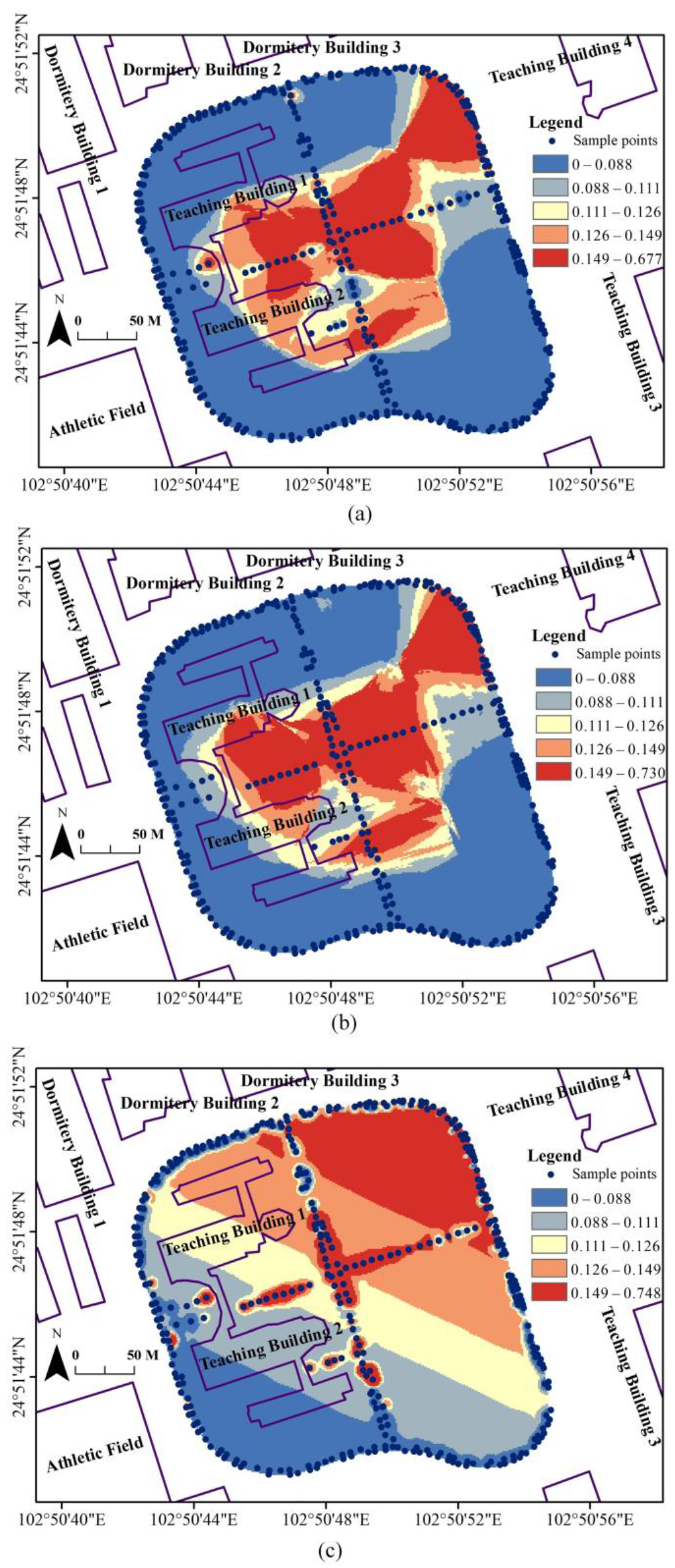
4.3. The EMR-SF Construction Results by LRBF
4.3.1. Experimental Results
4.3.2. Accuracy Comparison
5. Discussion
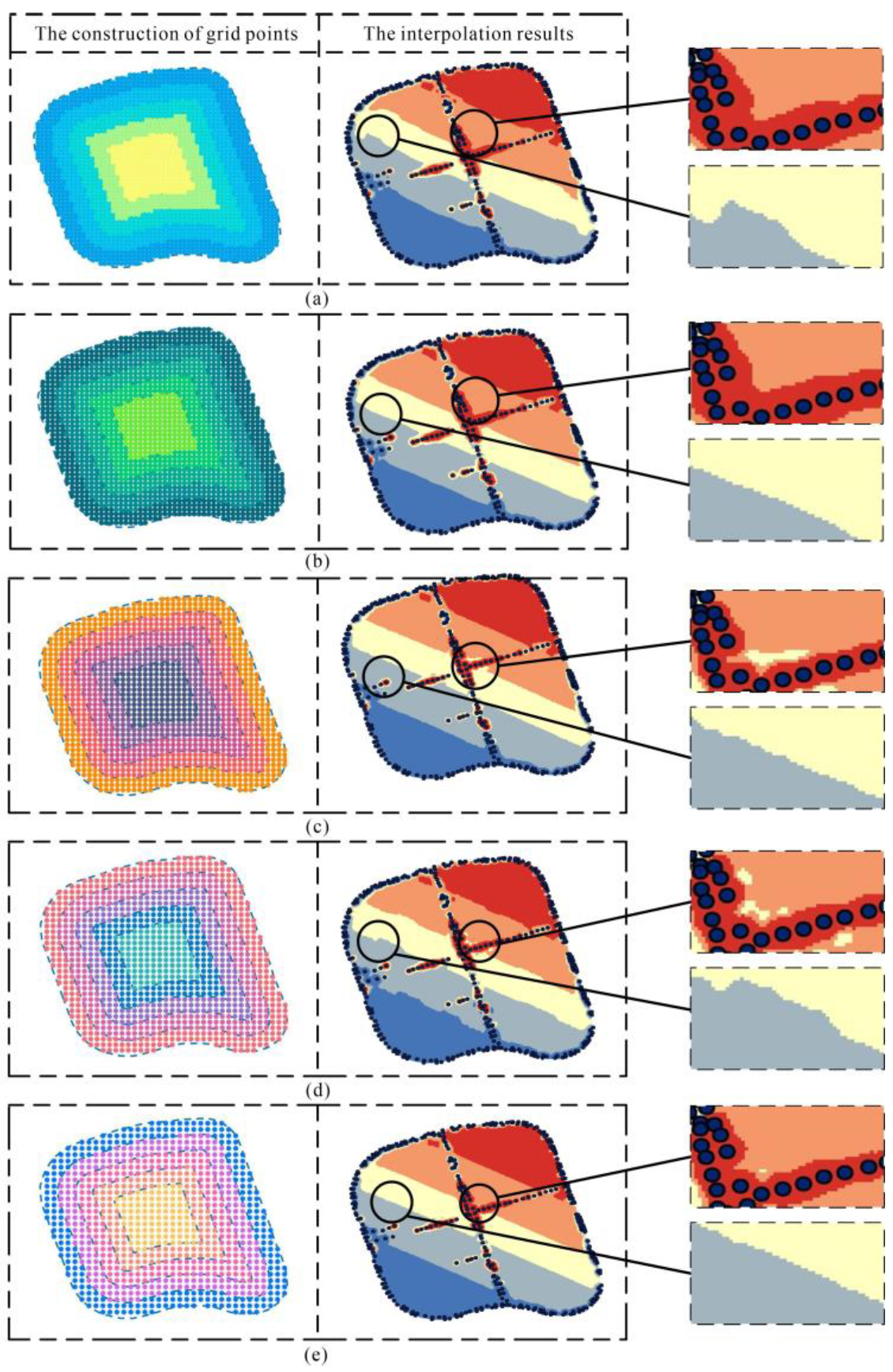
5.1. Grid Point Constructed and Layered Interpolation
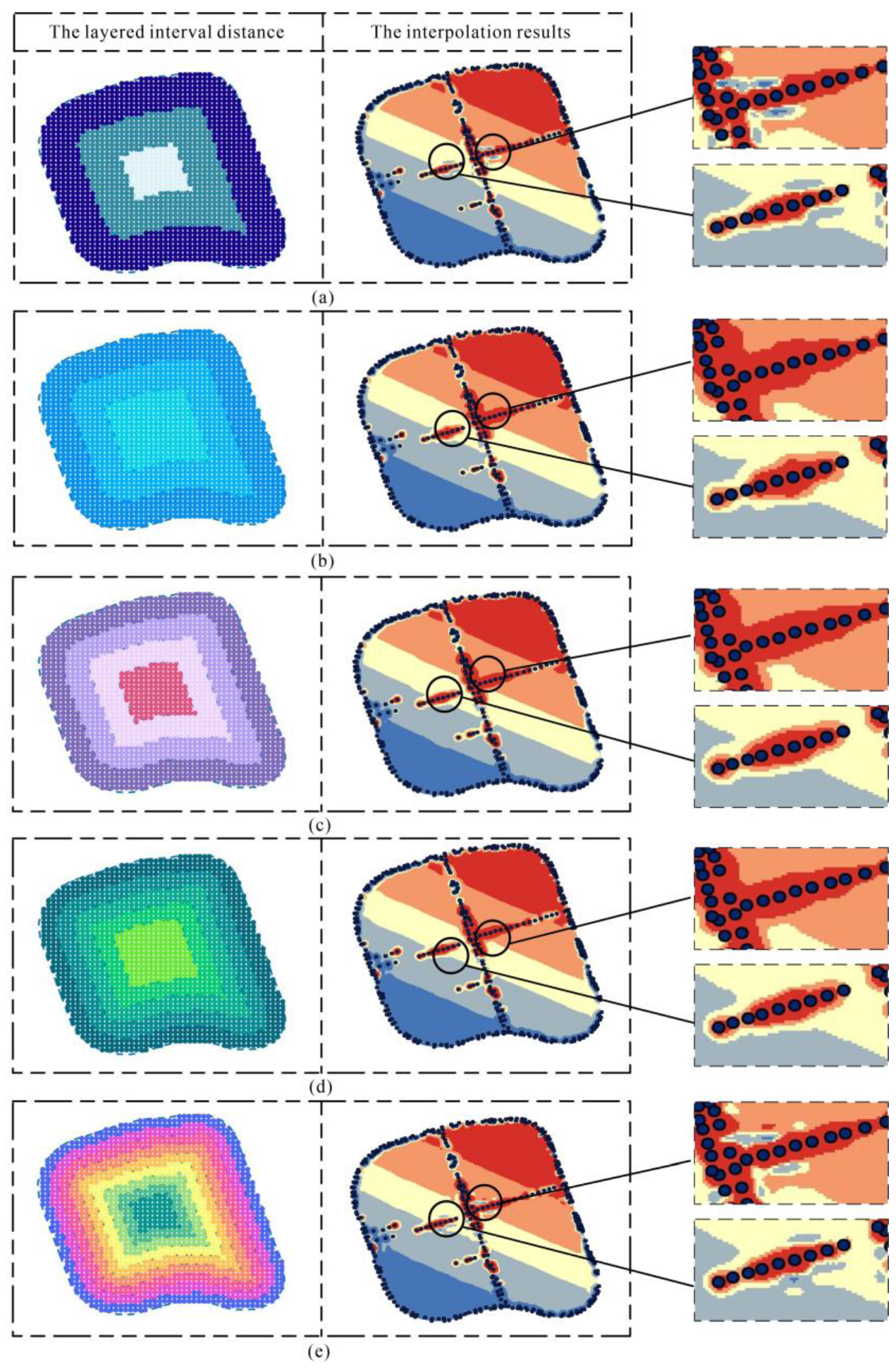
5.2. Comparison of the Result of EMR-SF between Different Interval Distances of the Grid Point by LRBF
5.3. Comparison of the Result of EMR-SF between Different Layered Interval Distances by LRBF
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sagnard, F. Educational Graphical Interfaces to Learn about Radiation and Propagation of Electromagnetic Waves. IEEE Trans. Educ. 2004, 47, 389–396. [Google Scholar] [CrossRef]
- Redlarski, G.; Lewczuk, B.; Żak, A.; Koncicki, A.; Krawczuk, M.; Piechocki, J.; Jakubiuk, K.; Tojza, P.; Jaworski, J.; Ambroziak, D. The Influence of Electromagnetic Pollution on Living Organisms: Historical Trends and Forecasting Changes. BioMed Res. Int. 2015, 2015, 234098. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sarkar, T.K.; Abdallah, M.N.; Salazar-Palma, M. Survey of Available Experimental Data of Radio Wave Propagation for Wireless Transmission. IEEE Trans. Antennas Propag. 2018, 66, 6665–6672. [Google Scholar] [CrossRef]
- Mollel, M.S.; Michael, K. Comparison of Empirical Propagation Path Loss Models for Mobile Communication. 2014. Available online: https://dspace.nm-aist.ac.tz/handle/20.500.12479/1167 (accessed on 4 May 2021).
- Yilmaz, H.B.; Tugcu, T. Location estimation-based radio environment map construction in fading channels. Wirel. Commun. Mob. Comput. 2015, 15, 561–570. [Google Scholar] [CrossRef]
- Oudira, H.; Diouane, L.; Garah, M. Empirical Path Loss Models Optimization for Mobile Communication. In Proceedings of the 2018 IEEE 5th International Congress on Information Science and Technology (CiSt), Marrakech, Morocco, 21–27 October 2018; pp. 443–448. [Google Scholar]
- Faruk, N.; Popoola, S.I.; Surajudeen-Bakinde, N.T.; Oloyede, A.A.; Abdulkarim, A.; Olawoyin, L.A.; Ali, M.; Calafate, C.T.; Atayero, A.A. Path Loss Predictions in the VHF and UHF Bands within Urban Environments: Experimental Investigation of Empirical, Heuristics and Geospatial Models. IEEE Access 2019, 7, 77293–77307. [Google Scholar] [CrossRef]
- Maiti, P.; Mitra, D. Complexity reduction of ordinary kriging algorithm for 3D REM design. Phys. Commun. 2022, 55, 101912. [Google Scholar] [CrossRef]
- Navarro-Camba, E.A.; Segura-García, J.; Gomez-Perretta, C. Exposure to 50 Hz Magnetic Fields in Homes and Areas Surrounding Urban Transformer Stations in Silla (Spain): Environmental Impact Assessment. Sustainability 2018, 10, 2641. [Google Scholar] [CrossRef] [Green Version]
- Céspedes, V.H.; Cadavid, L.F.D.; Gómez, Y.A.G. Electromagnetic pollution maps as a resource for assessing the risk of emissions from mobile communications antennas. Int. J. Electr. Comput. Eng. 2020, 10, 4244–4251. [Google Scholar] [CrossRef]
- Tuysuz, B.; Mahmutoglu, Y. Measurement and mapping of the GSM-based electromagnetic pollution in the Black Sea region of Turkey. Electromagn. Biol. Med. 2017, 36, 132–140. [Google Scholar] [CrossRef]
- Li, Z. An enhanced dual IDW method for high-quality geospatial interpolation. Sci. Rep. 2021, 11, 9903–9917. [Google Scholar] [CrossRef]
- Zhao, W.; Cao, T.; Li, Z.; Sheng, J. Comparison of IDW, cokriging and ARMA for predicting spatiotemporal variability of soil salinity in a gravel–sand mulched jujube orchard. Environ. Monit. Assess. 2019, 191, 376. [Google Scholar] [CrossRef]
- Gu, K.; Zhou, Y.; Sun, H.; Dong, F.; Zhao, L. Spatial distribution and determinants of PM2. 5 in China’s cities: Fresh evidence from IDW and GWR. Environ. Monit. Assess. 2021, 193, 15. [Google Scholar] [CrossRef]
- Han, Z.; Liao, J.; Qi, Q.; Sun, H.; Wang, J. Radio Environment Map Construction by Kriging Algorithm Based on Mobile Crowd Sensing. Wirel. Commun. Mob. Comput. 2019, 2019, 4064201. [Google Scholar] [CrossRef] [Green Version]
- Uddin, M. On the selection of a good value of shape parameter in solving time-dependent partial differential equations using RBF approximation method. Appl. Math. Model. 2014, 38, 135–144. [Google Scholar] [CrossRef]
- Casciola, G.; Lazzaro, D.; Montefusco, L.B.; Morigi, S. Shape preserving surface reconstruction using locally anisotropic radial basis function interpolants. Comput. Math. Appl. 2006, 51, 1185–1198. [Google Scholar] [CrossRef] [Green Version]
- Casciola, G.; Montefusco, L.B.; Morigi, S. Edge-driven Image Interpolation using Adaptive Anisotropic Radial Basis Functions. J. Math. Imaging Vis. 2010, 36, 125–139. [Google Scholar] [CrossRef]
- Casciola, G.; Lazzaro, D.; Montefusco, L.B.; Morigi, S. Fast surface reconstruction and hole filling using positive definite radial basis functions. Numer. Algorithms 2005, 39, 289–305. [Google Scholar] [CrossRef]
- Buhmann, M.D. Radial Basis Functions: Theory and Implementations; Cambridge University Press: Cambridge, UK, 2003; Volume 12. [Google Scholar]
- Fornberg, B.; Zuev, J. The Runge phenomenon and spatially variable shape parameters in RBF interpolation. Comput. Math. Appl. 2007, 54, 379–398. [Google Scholar] [CrossRef] [Green Version]
- Fasshauer, G.E.; Zhang, J.G. On choosing “optimal” shape parameters for RBF approximation. Numer. Algorithms 2007, 45, 345–368. [Google Scholar] [CrossRef]
- Bayona, V.; Moscoso, M.; Kindelan, M. Optimal constant shape parameter for multiquadric based RBF-FD method. J. Comput. Phys. 2011, 230, 7384–7399. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 11–23. [Google Scholar] [CrossRef]
- Abualigah, L.M.; Khader, A.T.; Hanandeh, E.S. A new feature selection method to improve the document clustering using particle swarm optimization algorithm. J. Comput. Sci. 2018, 25, 456–466. [Google Scholar] [CrossRef]
- Hohl, A.; Zheng, M.; Tang, W.; Delmelle, E.; Casas, I. Spatiotemporal point pattern analysis using Ripley’s K function. In Geospatial Data Science Techniques and Applications; CRC Press: Boca Raton, FL, USA, 2017; pp. 155–176. [Google Scholar]
- Coco, S.; Laudani, A.; Mazzurco, L. A novel 2-D ray tracing procedure for the localization of EM field sources in urban environment. IEEE Trans. Magn. 2004, 40, 1132–1135. [Google Scholar] [CrossRef]
- Zvezdina, M.Y.; Shokova, Y.A.; Krivtsova, M.; Saldaev, D.; Shashkin, O. Electromagnetic environment estimation near communications system reflector antennae. In Proceedings of the 2017 Radiation and Scattering of Electromagnetic Waves (RSEMW), Divnomorskoe, Russia, 26–30 June 2017; pp. 69–72. [Google Scholar]
- Zvezdina, M.Y.; Shokova, Y.A.; Kundryukova, N.; Kutukova, V.; Pozdnyakova, A. Visualization of electromagnetic environment near GSM antennae. IOP Conf. Ser. Earth Environ. Sci. 2017, 50, 012029. [Google Scholar] [CrossRef] [Green Version]






| Interpolation Method | Ordinary Kriging | IDW | LRBF |
|---|---|---|---|
| RMSE | 0.0582 | 0.0482 | 0.0378 |
| MAE | 0.0295 | 0.0323 | 0.0179 |
| MAXE | 0.50 | 0.47 | 0.45 |
| MINE | 0.8 × 10−5 | 0.2 × 10−4 | 0.3 × 10−4 |
| Interval Distance of Grid Point (m) | RBFGP | LRBF |
|---|---|---|
| 17 | 0.0741 | 0.0713 |
| 12 | 0.0697 | 0.0645 |
| 7 | 0.0425 | 0.0378 |
| Interval Distance of Grid Points (m) | RMSE | MAE | MAXE | MINE |
|---|---|---|---|---|
| 10 | 0.0618 | 0.0322 | 0.508 | 0.2 × 10−5 |
| 9 | 0.0568 | 0.0292 | 0.512 | 0.1 × 10−7 |
| 8 | 0.0568 | 0.0289 | 0.524 | 0.1 × 10−4 |
| 7 (maximum influence distance) | 0.0378 | 0.0179 | 0.45 | 0.3 × 10−4 |
| 6 | 0.0356 | 0.0211 | 0.32 | 0.8 × 10−7 |
| Layered Interval Distance (m) | RMSE | MAE | MAXE | MINE |
|---|---|---|---|---|
| 55 | 0.0453 | 0.0231 | 0.47 | 0.9 × 10−7 |
| 45 | 0.0398 | 0.0231 | 0.51 | 0.5 × 10−4 |
| 35 | 0.0373 | 0.0176 | 0.45 | 0.3 × 10−5 |
| 25 (maximum aggregation distance) | 0.0378 | 0.0179 | 0.45 | 0.2 × 10−4 |
| 15 | 0.0418 | 0.0195 | 0.43 | 0.3 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Duan, P.; Li, J.; Liu, J. Electromagnetic Radiation Space Field Construction Collected along the Road Based on Layered Radial Basis Function. Appl. Sci. 2023, 13, 6153. https://doi.org/10.3390/app13106153
Zhang J, Duan P, Li J, Liu J. Electromagnetic Radiation Space Field Construction Collected along the Road Based on Layered Radial Basis Function. Applied Sciences. 2023; 13(10):6153. https://doi.org/10.3390/app13106153
Chicago/Turabian StyleZhang, Jie, Ping Duan, Jia Li, and Jiajia Liu. 2023. "Electromagnetic Radiation Space Field Construction Collected along the Road Based on Layered Radial Basis Function" Applied Sciences 13, no. 10: 6153. https://doi.org/10.3390/app13106153
APA StyleZhang, J., Duan, P., Li, J., & Liu, J. (2023). Electromagnetic Radiation Space Field Construction Collected along the Road Based on Layered Radial Basis Function. Applied Sciences, 13(10), 6153. https://doi.org/10.3390/app13106153





