Abstract
Differential evolution (DE) is one of the best evolutionary algorithms (EAs). In recent decades, many techniques have been developed to enhance the performance of this algorithm, such as the Improve Self-Adaptive Differential Evolution (ISADE) algorithm. Based on the analysis of the aspects that may improve the performance of ISADE, we proposed a modified ISADE version with applying the Gauss distribution for mutation procedure. In ISADE, to determine the scaling factor (F), the population is ranked, then, based on the rank number, population size, and current generation, the formula of the Sigmoid function is used. In the proposed algorithm, F is amplified by a factor which is generated based on Gaussian distribution. It has the potential to enhance the variety of population. In comparison with several reference algorithms regarding converging speed and the consistency of optimal solutions, the simulation results reveal the performance of the suggested algorithm is exceptional.
1. Introduction
A few recent decades witness a class of many powerful evolutionary algorithms and their applications. Like many other evolutionary algorithms, differential evolution is a population-based technique. This algorithm is developed by Rainer Storn and Kenneth V. Price [1]. It is inspired by the evolution phenomenon in nature and is a strong tool to solve engineering problems. There are three mechanisms (mutation, crossover, and selection) operating in DE in which three control parameters (population size, scaling factor, and crossover rate) have significant effect on exploration and exploitation of this algorithm.
Parallel to the development of computer and industry 4.0, evolutionary algorithms gradually demonstrate its pros in comparison with a traditionally mathematical method, such as the gradient descent method [2] and the Newton–Raphson method [3]. It results that more and more researchers focus on improvement of evolutionary algorithms and differential evolution has not been laying out this trend.
A literature review on the advance of the differential evolution algorithm, we cannot ignore some state of art developments, such as self-adaptive differential evolution algorithm (SaDE) [4], self-adaptive jDE algorithm (JDE) [5], and adaptive differential evolution with optional external archive (JADE) [6]. Recently, Yong Wang et al. incorporated the covariance matrix learning and by adjusting the bimodal distribution parameter to generate the control parameters of mutation and crossover operators, the effectiveness of DE is improved in solving problems that have a high correlation among variables [7]. Ali Wagdyy Mohamed and Ali Khater Mohamed randomly selected two factors from the best and worst individuals in each current generation, and the third vector was chosen from the middle individuals. This mechanism effectively keeps the balance between the global exploration and local exploitation abilities for searching process [8]. Tam bui et al. described an improved different evolution algorithm with opposition-based learning mechanism [9]. Each of the above-mentioned algorithms may work best for one or some specific problems. Thus, study in this field is still on-going and this paper introduces an improved version of DE which solved all four groups of benchmark functions with outstanding convergence speed.
Gaussian distribution, also called normal distribution, is a continuous function which is popularly used in optimization. It provides an excellent possibility to produce a new candidate for crossover operation based on a current position. Simultaneously, adaptive strategy of standard deviation parameter keeps good balance between exploitation and exploration process. This paper adopts a scaling factor generated by Gaussian distribution to improve mutation operation in a self-adaptive differential evolution algorithm (also named ISADE) proposed by Tam bui et al. [10]. This factor will be applied to three types of mutation operation (DE/best/1, DE/best/2, and DE/rand to best/1) with equally random selection probability. In addition, standard deviation parameter of Gaussian distribution is updated by comparing the global best fitness value between the current and previous generations. The proposed algorithm is tested in 19 benchmark functions and 4 conventional engineering problems. Numerical simulation results confirm that the proposed algorithm express significant improvement in comparison to the original DE and some recent related works.
The remain of this paper is composed of five sections. Section 2 describes the method of original DE. Section 3 reviews some recent related works on the applications of Gaussian distribution to DE. A modified Differential Evolution is introduced in Section 4. Section 5 describes comparisons of the proposed DE algorithm with the others and its application in real problem. Finally, Section 6 comprises some brief conclusions.
2. Review of Differential Evolution
The DE algorithm is firstly introduced by Rainer Storn and Kenneth V. Price [1]. It mainly consists of the four operations, such as initialization, crossover, mutation, and selection, as described in Algorithm 1.
| Algorithm 1: DE algorithm | |
| Initialization: Generate initial population within boundary. | |
| While termination condition is not reached. | |
| Mutation: Calculate mutation vector . | |
| Crossover: Perform crossover to create vector. | |
| Selection: Select the candidates for the next generation based on fitness value. | |
| End. | |
| Return the best solution. | |
2.1. Initialization Operation
The DE is a population-based algorithm, thus, an initial population need to be generated randomly by uniform probability. This procedure increases a diversity of population and scatters individuals in the entire domain. Assume that are dimension of problem and population size, respectively. The search space is constrained within lower boundary LB = [] and upper boundary UB = []. NP individuals are randomized by Equation (1).
where is the j-th component of the i-th individual.
2.2. Mutation Operation
In this stage, DE deploys mutation schemes to produce an i-th new vector for each i-th vector . Equations (2)–(6) are the five most commonly applied mutation schemes in different kinds of DE algorithms.
where is best vector in current population at generation; , and are exclusively randomized from []. As can be seen that the effectiveness of mutation operation much depends on scaling factor F. Thus, many previous studies concentrated on this point to improve the performance of DE algorithm [1]. Likewise, the author of this paper introduced an adaptive scaling factor [10] which is formulated as follows:
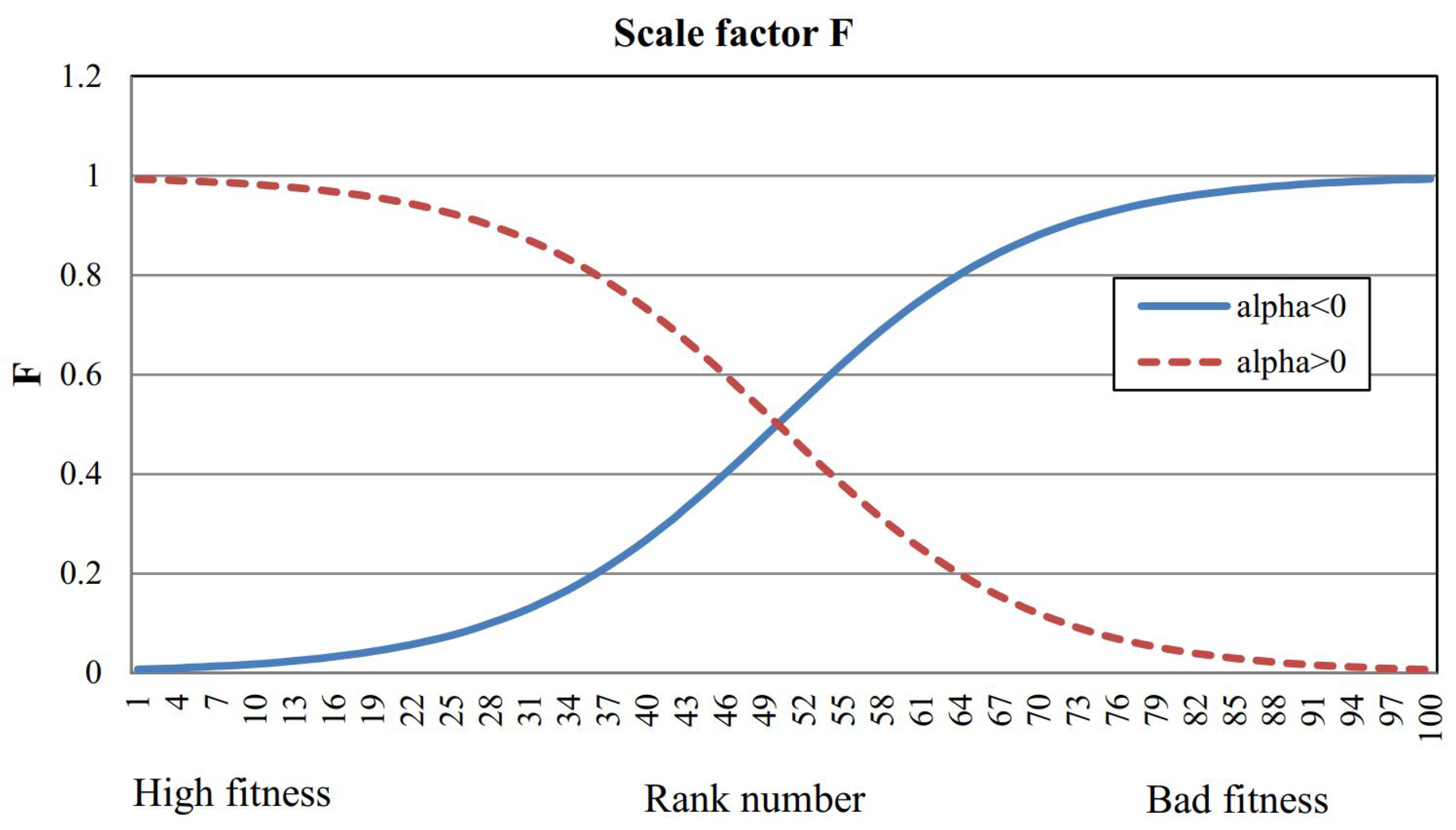
Adaptive scaling factor : in the beginning iterations, initial scaling factor of the i-th individual is set to be high and it will gradually decrease after certain iteration for proper exploitation. The value is produced by a Sigmoid function as in Equation (7).
In which is the control parameter that decides the trend value of scaling factor , as illustrated in Figure 1.
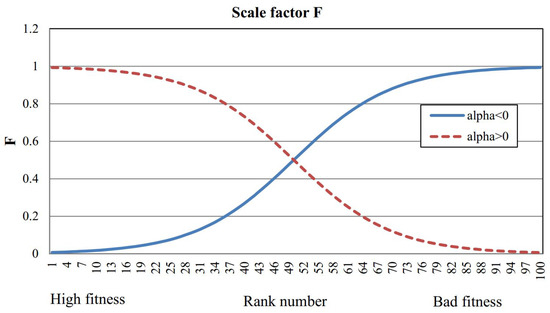
Figure 1.
Value of initial scaling factor depends on rank number i, population size , and .
ISADE gives an addition scaling as in Equation (8).
where and are the maximum and minimum value of F, of which the recommended values are 0.8 and 0.15, respectively. and are the maximum iteration, and the non-linear modulation index. is determined as in Equation (9).
where and are selected in the [0, 15] range. and are 6.0 and 0.2, respectively. Lastly, scaling factor is determined for each individual in each iteration, as in Equation (10). In mutation operation, each individual within a population will be assigned a unique scaling factor. This approach is designed to ensure a balance between exploration and exploitation by the algorithm.
2.3. Crossover Operation
Once the mutation has been carried out on the selected individuals, DE then utilizes a crossover operation as Equation (11).
In which , and x are, respectively, trial vector, mutation vector, and current vector. is a crossover limitation within the range of (0, 1). is a randomly chosen number from set {1, 2, …, D}.
2.4. Selection Operation
In this stage, trial vector u and target vector x will be compared with each other in order to pick out the better fitness for the next generation. This operation is carried out as in Equation (12).
To improve the exploration ability of ISADE, Tam Bui et al. applied the opposition-based learning scheme [11] and named EOBL-DE [9]. In the first opposition-based learning scheme, EOBL-DE generate 2NP population consisting of NP initial candidates and their corresponding opposition. Equation (13) determines the opposition of particle . After that, all 2NP candidates will be evaluated and ranked by their fitness value. NP best candidates are selected for the next generation.
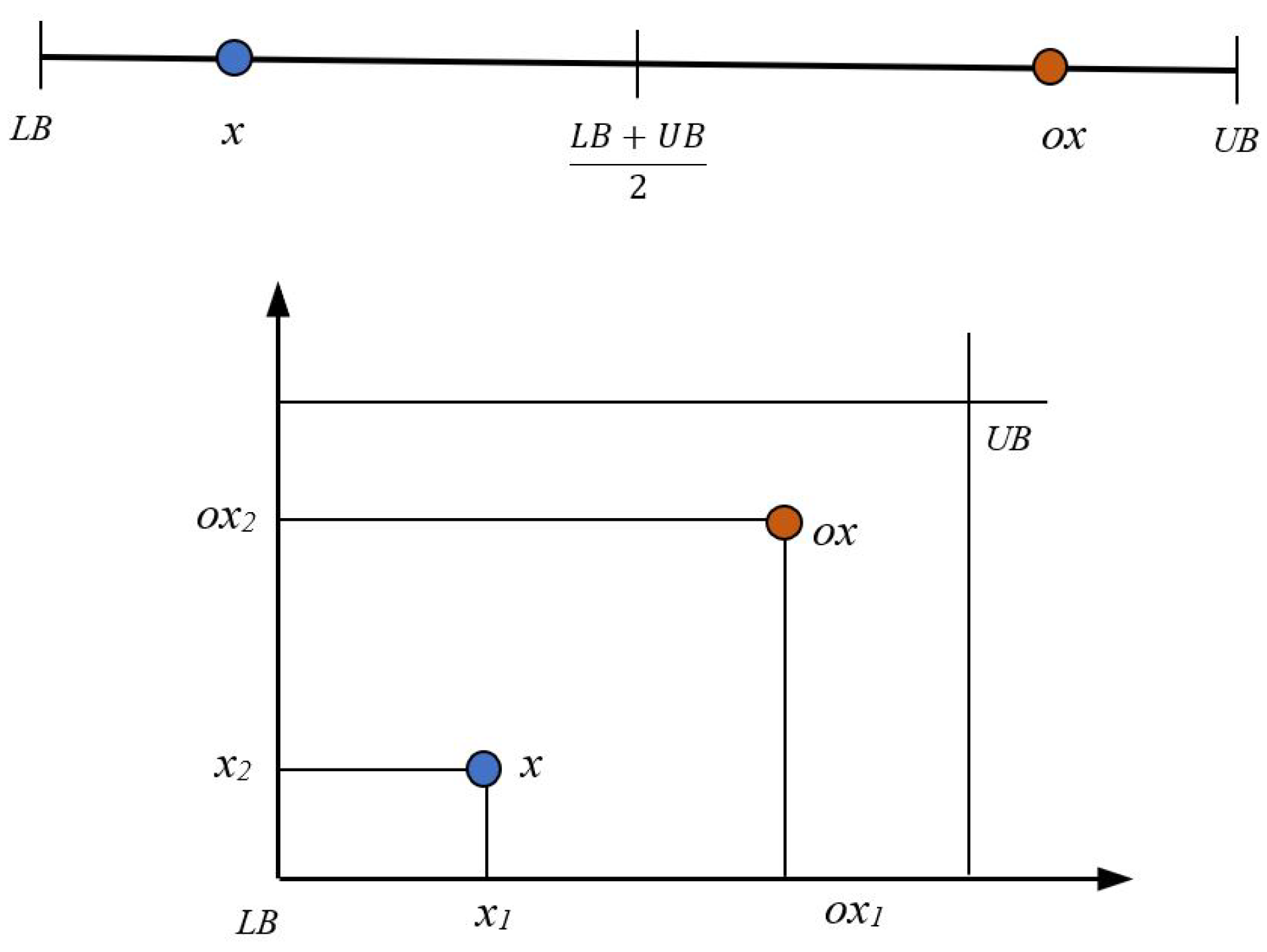
In which and designate the lowest and highest possible values for . Figure 2 illustrates the position of a candidate and its corresponding opposite in both one- and two-dimensional graphs, where blue point is a current candidate and orange points is its corresponding opposition particle.
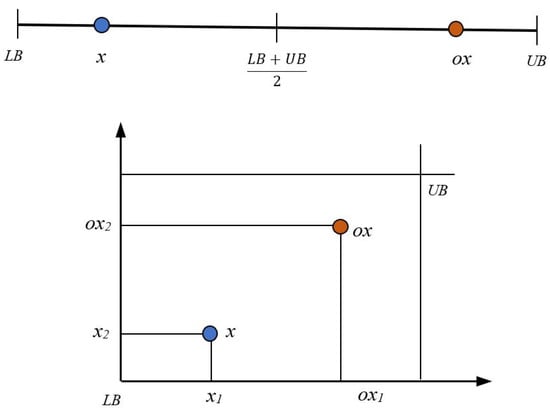
Figure 2.
Definition of opposition particle.
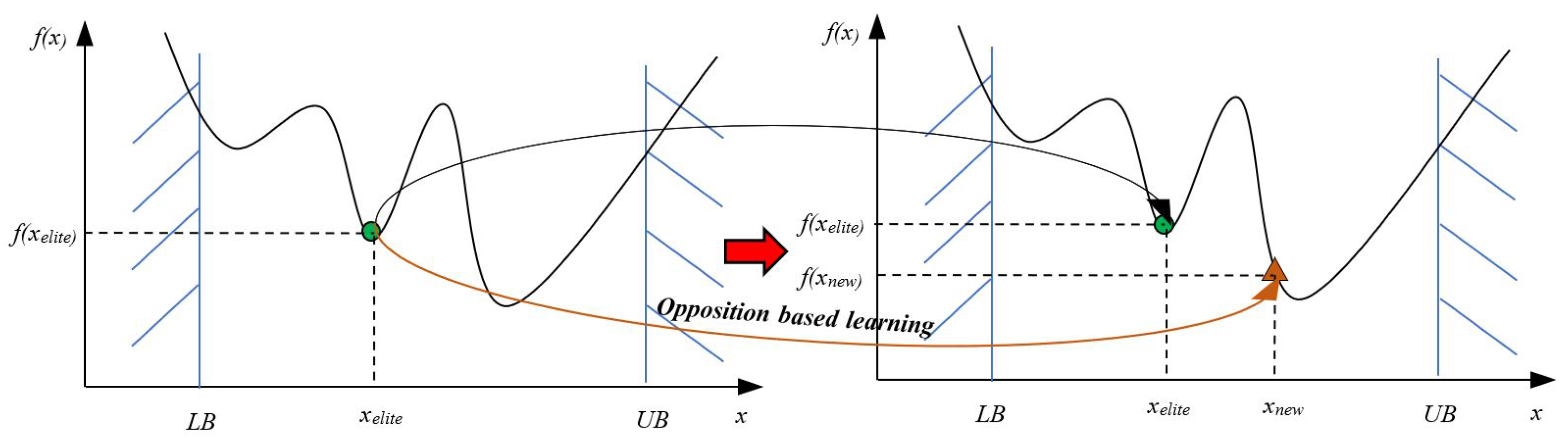
The second scheme applied the opposition-based learning strategy to the elite candidates in a selection operation. After ranking all candidates by their fitness value, only a certain number of the top best particles are selected to calculate their opposition. The candidate and its corresponding opposition will then be assessed and compared to each other based on their fitness value in order to find out the most suitable ones for the next generation. Figure 3 described the elite-based opposition strategy of EOBL-DE. The elite particle is marked in green, while its corresponding opposition is marked in orange. It was confirmed that applying OBL to elite particles enhanced the local search ability of ISADE.
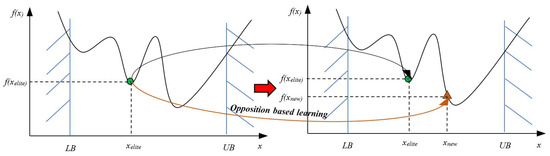
Figure 3.
Searching strategy of elite-based opposition particle.
3. Related Works
In the process of the EAs, Gaussian distribution is applied by the different approaches as the follows.
H. Zheng et al. [12] proposed a modification of Cuckoo search algorithm (GCS), which applied a Gaussian random step instead of Lévy flight when producing a new solution. GCS was validated to be better than standard Cuckoo search algorithm when comparing the best solution and convergence rate.
X.-S. He et al. [13] used a Gaussian random vector to generate the new offspring vector based on current position. This procedure is considered as an additional mutation operation after updating process of original bat algorithm.
Z. Lin and Q. Zhang [14] integrated a Gauss mutation into particle swarm optimization. New candidate is generated by adding Gaussian distribution-based random number to current solution. Adoption Gaussian distribution will give a high probability in producing a number around the mean and low probability of a large number; thus, a new population will contain two inevitably important abilities of evolutionary process, exploration and exploitation.
Focusing on DE, Jena et al. [15] added a Gaussian random variable to the parent vector to produce a new solution, in which the standard deviation is formulated as Equation (14).
where is fitness value of evaluating candidate, , is global fitness value. This define controls the adding amount of perturbation and guarantees the distribution of a suitable random value to each parent vector in population.
Sun et al. [16] combined Gauss distribution and crossover operator to deploy mutation operation where the mean and the standard deviation are dynamically adjusted at each iteration. This mechanism was expected to improve the diversity of population and performed the effectiveness on benchmark functions and real-world engineering problem.
Li and Jin [17] randomized scale factor through two Gauss distributions to increase the chance to escape from local optima. However, all the above-mentioned studies show that there is no free lunch in search and optimization. Each optimization algorithm is significantly affected on a specific benchmark function; this paper proposed a novel algorithm using a mutation mechanism with Gauss distribution which solved all representations in four groups of benchmark function. In addition, the proposed algorithm has an outstanding performance on convergence speed in comparison with the original DE and its recent improvement.
4. Modified Differential Evolution
Gaussian distribution is widely used in probability and statistics, and is often applied to create real-valued random variables. Gaussian distribution gives a good chance to exploit a new potential candidate in the optimization of many complex functions. In this paper, we the improved exploration ability of EOBL-DE by using Gauss distribution. Our introduced strategy will generate a new trial vectors in mutation operation by Gaussian perturbation mechanism which multiples Gaussian random variable to a vector difference () in Equation (15), () and () in Equation (16), and () in Equation (17).
The equation for mutation operation schemes has been modified as the following Equations (15)–(17).
where , and are randomized from []; N(,) is a Gaussian random variable with mean and standard deviation . Recommended value for is 1, whereas is defined in Equation (18). is calculated to be suitable for each i-th individual based on the fitness value.
where T = *, recommended value for is 1.5, is current number of iteration. The G-ISADE algorithm is described as in Algorithm 2.
| Algorithm 2: G-ISADE algorithm. | ||
| Initialization: Generate initial population of NP candidates and their corresponding opposition within boundary. | ||
| Generate initial Gauss variables. | ||
| Evaluation and rank: Ranking all 2NP population based on comparing fitness value. After that, NP particles will be selected for the next generation. | ||
| While termination condition is not reached. | ||
| Adaptive scaling factor: Calculating mutation adaptive scaling factor F by Equation (10). | ||
| Mutation: Calculate mutation vector by Equations (15)–(17). | ||
| Crossover: Perform crossover to create vector. | ||
| Selection: Calculate oppositon of a certain top best number of particles. Select the NP candidates for the next generation based on fitness value. | ||
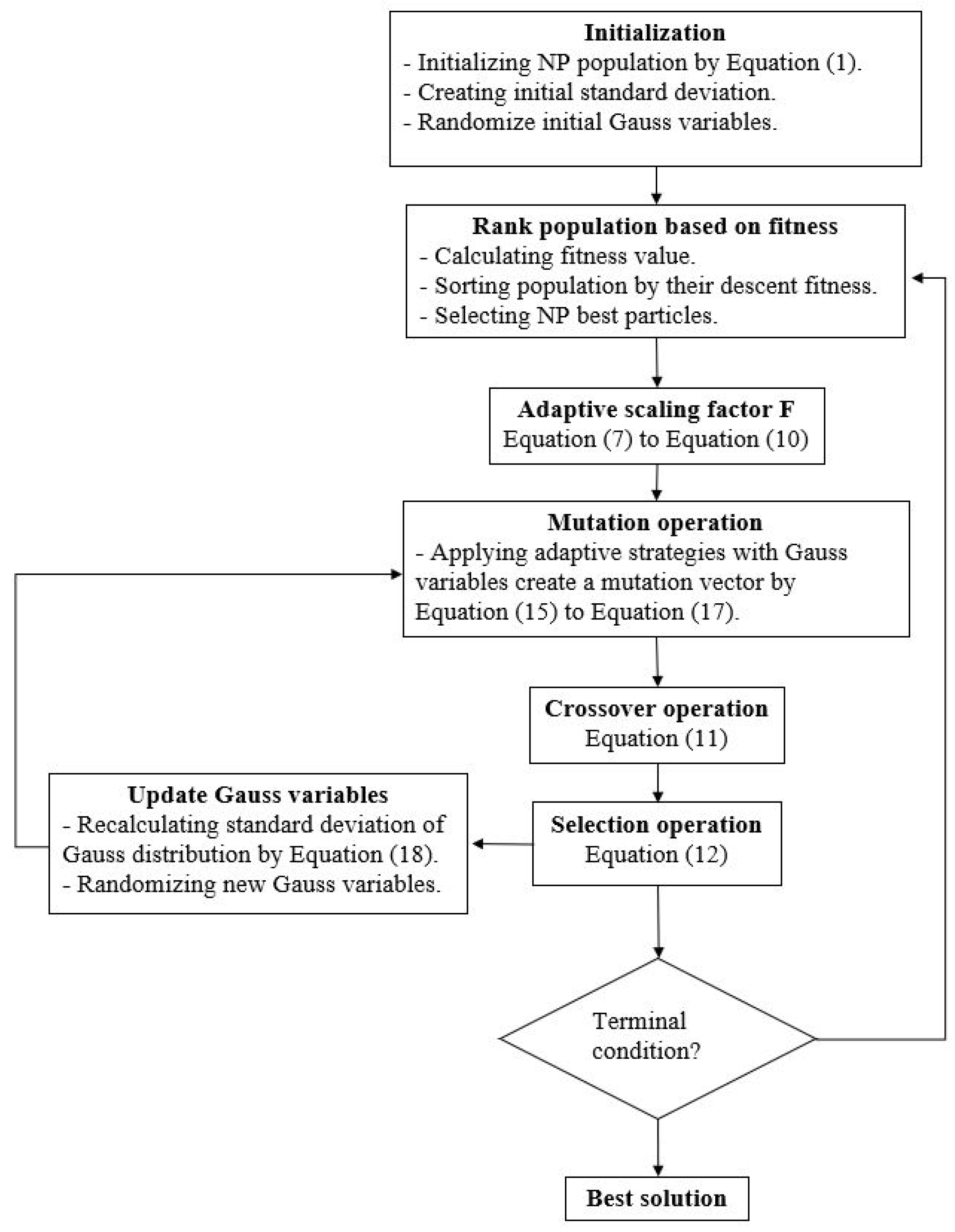
| Update Gauss variables: Recalculate standard deviation of Gauss distribution and generate new Gauss variable. The details of this step can be seen in the procedure of G-ISADE in Figure 4. | ||
| End. | ||
| Return the best solution. | ||
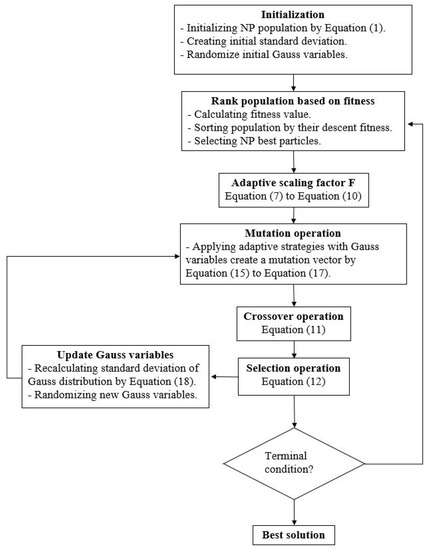
Figure 4.
Procedure of G-ISADE.
Recently, L. Tang et al. [18] presented an individual-dependent mechanism for DE, namely IDE. This approach deployed a similar scale factor () to mutation operation, this parameter is randomized from a normal distribution (), where is original scale factor, associated with individual and determined by Equation (19).
where is an index of the fitness value of individual after raking; is number of population. Standard derivation is set to . This is different from G-ISADE, which used a strategy to calculate standard deviation at each iteration. The comparison of two these algorithms is implemented in Section 5.
5. Numerical Simulation
This section is to compare the performance of the presented method with the previous methods, consisting of the original DE and its developed version on the following issues, convergence speed, stability, and accuracy.
5.1. Benchmark Function
The novel algorithm is tested with 19 benchmark-test functions which are multidimensional problems [19] that contain multidimensional unimodal and multimodal functions.
All tested functions are continuous and divided into four groups as the following:
- Function group 1 is separable and unimodal: Sphere (f1), weighted sphere (f12), Sum of Different Power (f13), Bent Cigar (f17).
- Function group 2 is non-separable and unimodal: Schwefel’s Problem 1.2 (f6), Schawefel or Schwefel function 2.22 (f8), Rosenbrock (f2).
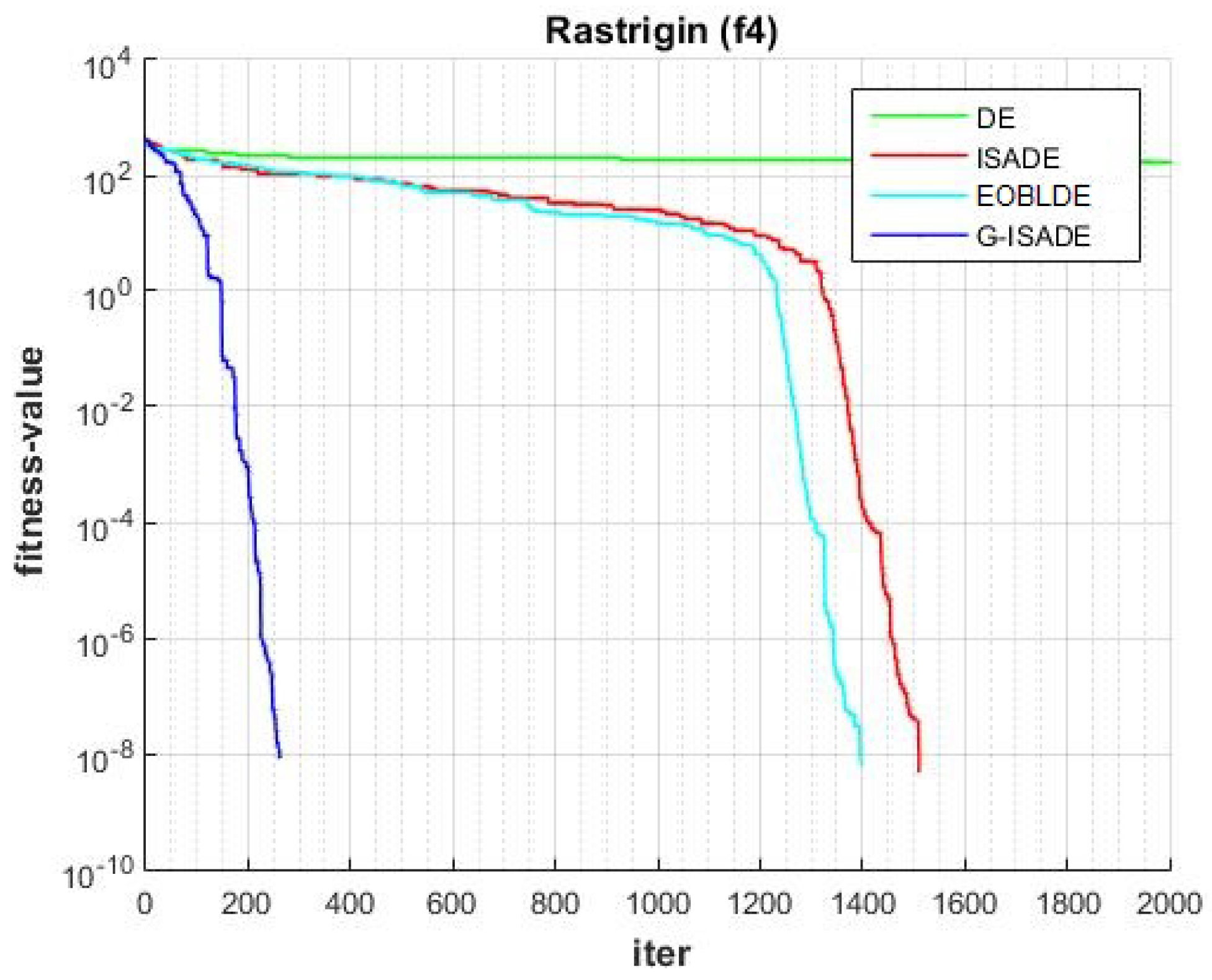
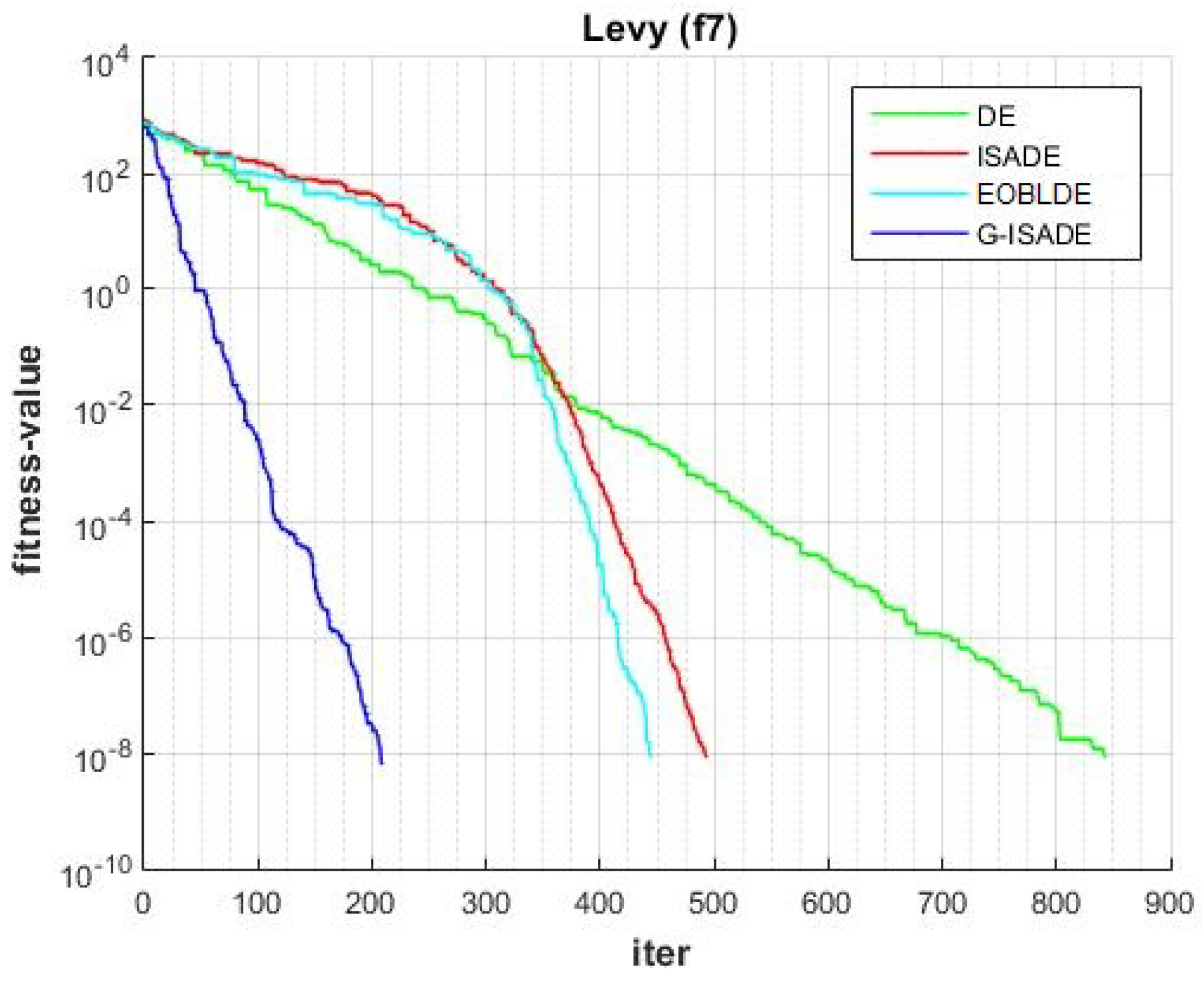
- Function group 3 is separable and multimodal: Rastrigin (f4), Levy (f7), Alpine (f10), Schwefel’s Problem 2.26 (f19).
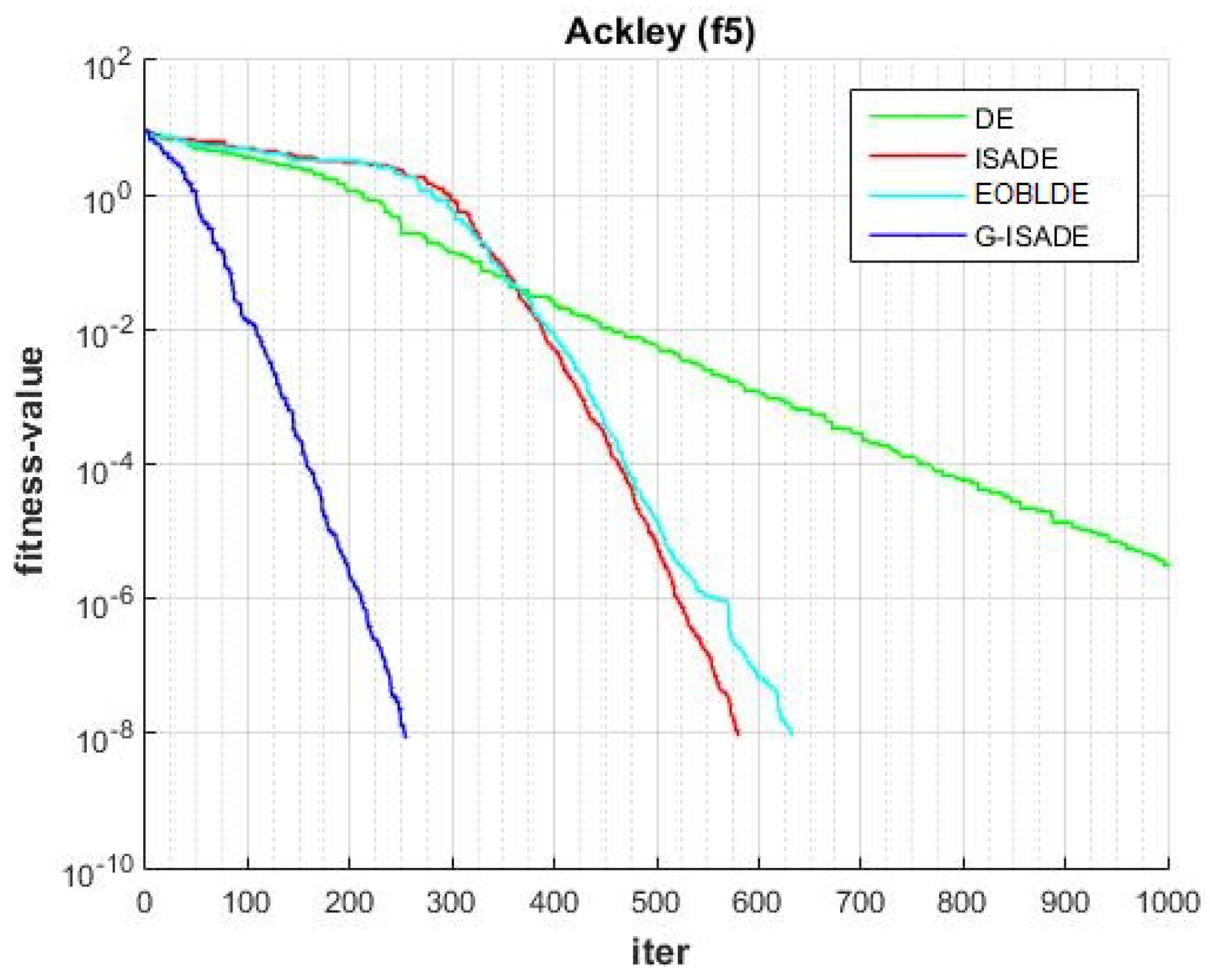
- Function group 4 is non-separable and multimodal: Ackley (f5), Griewank (f3), Zakharov (f14), Exponential Problem (f15), Salomon Problem (f16); Schaffer function (f9), Pathological (f11), Expanded Schaffer’s F6 (f18).
The formulae of all tested benchmarks are expressed in Appendix A. All benchmark functions are rendered hereafter as problems of minimization, however, they do not lack generality as they can also be used for problems of maximization by simply converting the sign of the objective function.
5.2. Performance Comparison of Proposed Algorithm with IDE
This section is to compare search ability of G-ISADE with IDE. To have a fair comparison, we also set up the same searching condition with their original paper, such as the dimensionality of the test functions are 30; the number of populations, ; and the searching process will stop at iteration of . The benchmark functions, such as , and , were tested with 51 independent runs, these test functions are representative functions of four considered groups and are also considered in the original paper of IDE. We define an error value () which is the difference between the obtained optimal fitness value with the known one and this value is taken to zero if it is less than . The mean value of the 51 runs with standard derivation is shown in Table 1. The comparison results show that the proposed approach is better than IDE while solving the considered functions. With the test functions, , and , the error value of the fitness is less than and is taken to zero, the new approach expresses significant robustness. These results proved the more powerful searching ability of the proposed method in comparison with IDE.

Table 1.
Average of fitness value (Mean) and the standard deviation (Std) of 51 runs.
5.3. Performance Comparison of G-ISADE with Its Previous Improvements
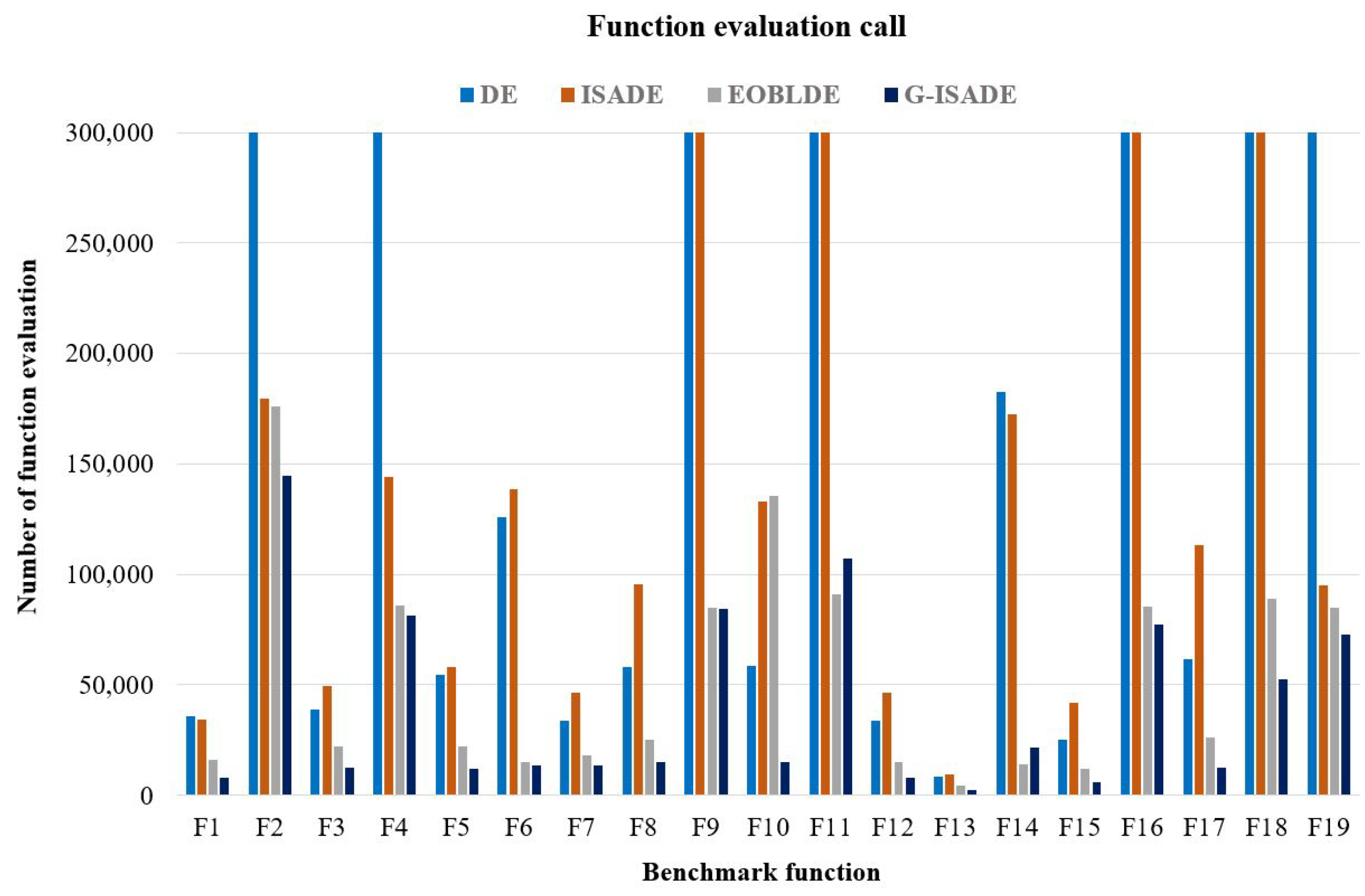
In this part, we will assess and compare the effectiveness of the suggested algorithms (G-ISADE) with the original DE [1] and some previous improvements of DE, such as ISADE [10], JOBLDE, and EOBLDE [9]. The comparing criterion are the success rate (SR) and the total count of function evaluations (FE) where SR is calculated by the ratio of the number of the successful findings in total number of samples, NS = 30, one numerical simulation can accomplish if the ending condition is reached (error value, ); FE is the most popular parameter for calculating the convergence speed of an optimization algorithm, measured by the number of the function calls to compute the fitness value. In addition, an improvement rate (IR) is defined by improvement percentage ratio on FE of the proposed algorithm in comparison with original DE, this factor is to confirm the effectiveness of the proposed algorithm on the convergence speed while solving the benchmark functions.
In the experiment, the parameter was set as follows. The number of dimensions, and the number of populations, . From original DE algorithm proposed by Storn and Price [1], we chose and . All of the benchmarks were independently tested with 30 random initial samples. This was carried out using a random number generator in MATLAB software, version R2015a with a fixed seed. The simulation results are described in Table 2 and Figure 5. As can be seen, G-ISADE and EOBLDE could obtain the optimal solutions for all considered benchmark functions. ISADE was not able to reach the optimal solution for the test function , and while DE demonstrated instability in reaching the termination condition of the error value (); it was unable to succeed in solving the test function , and . In terms of comparing the number of function evaluation calls, G-ISADE achieved the optimal solution using fewer function evaluation calls, except for test functions and . With the 11 test functions , and , the proposed method demonstrated a significant improvement in terms of the convergence speed.

Table 2.
Performance comparison of proposed algorithm with the others.
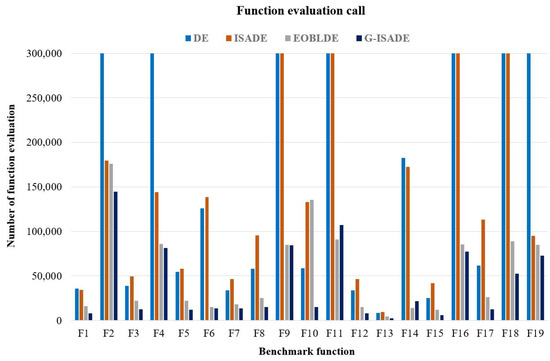
Figure 5.
Comparison of function evaluation calls.
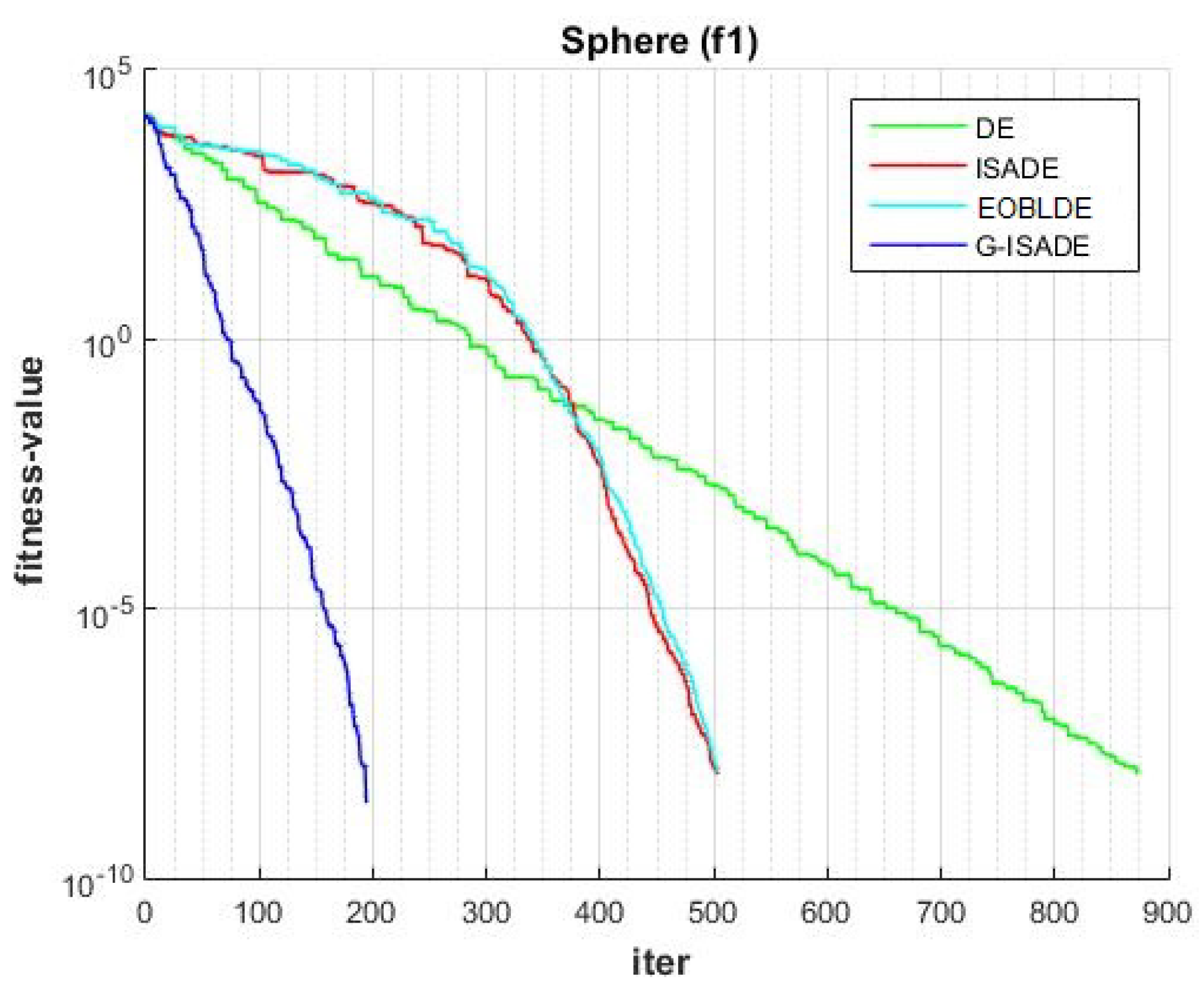
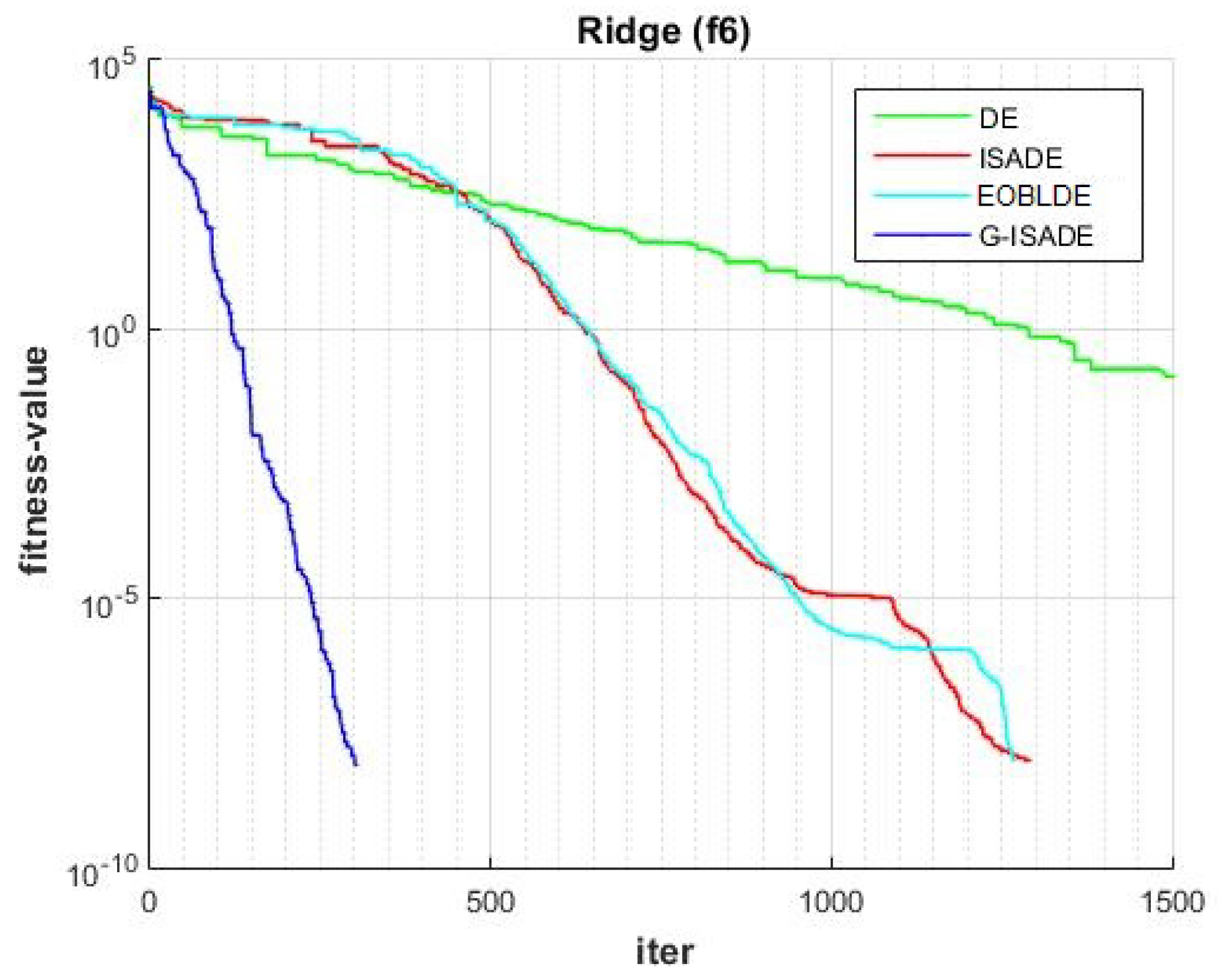
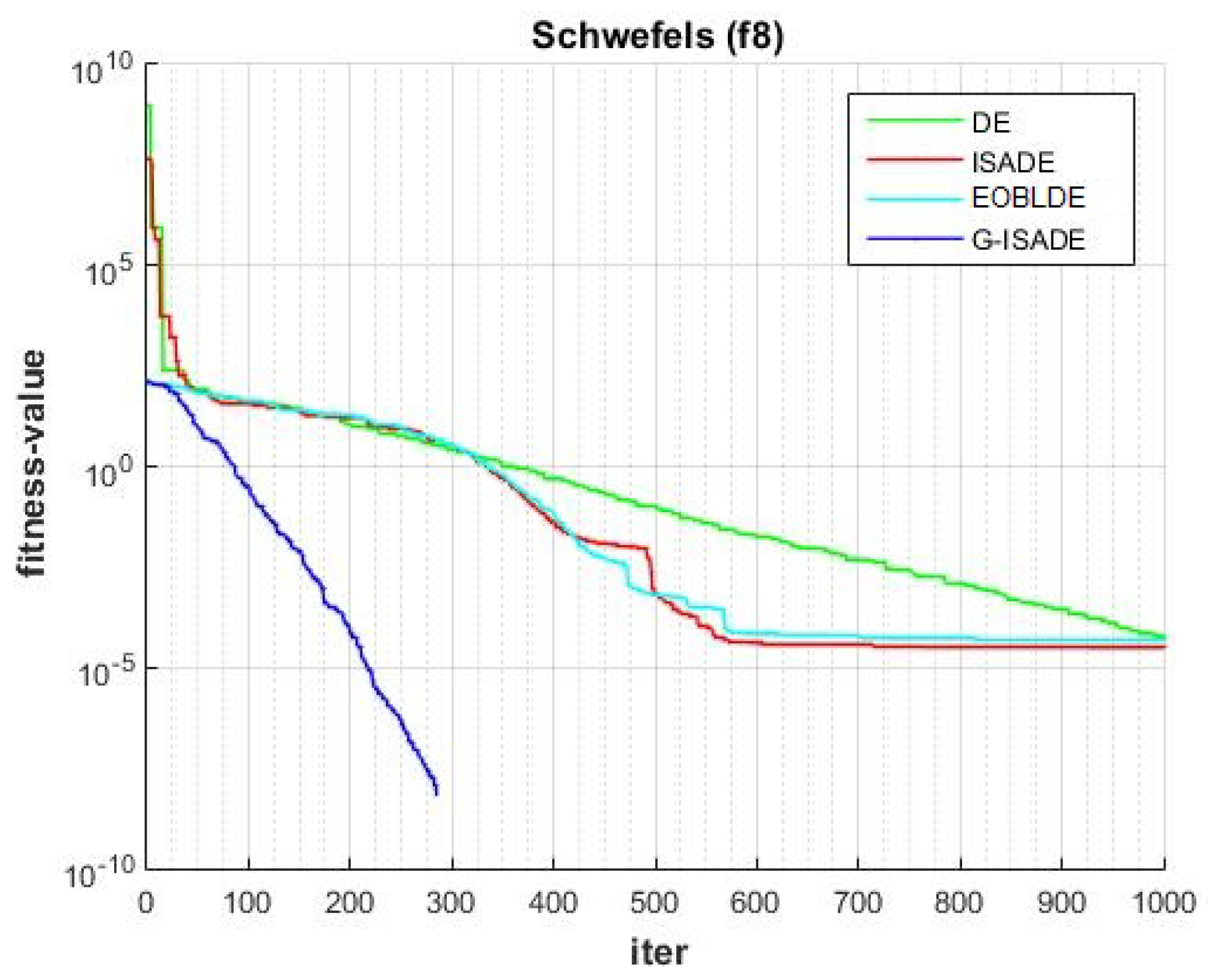
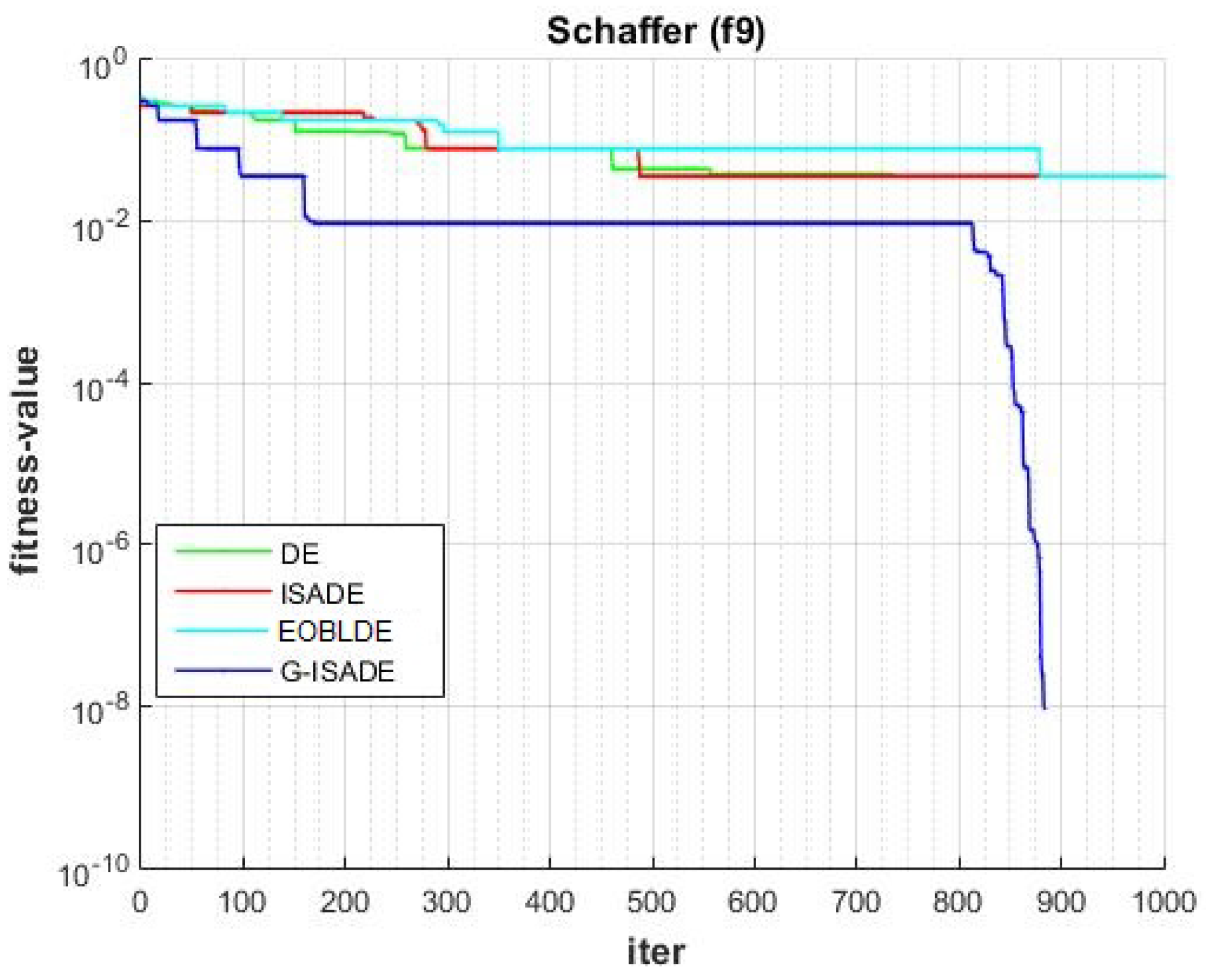
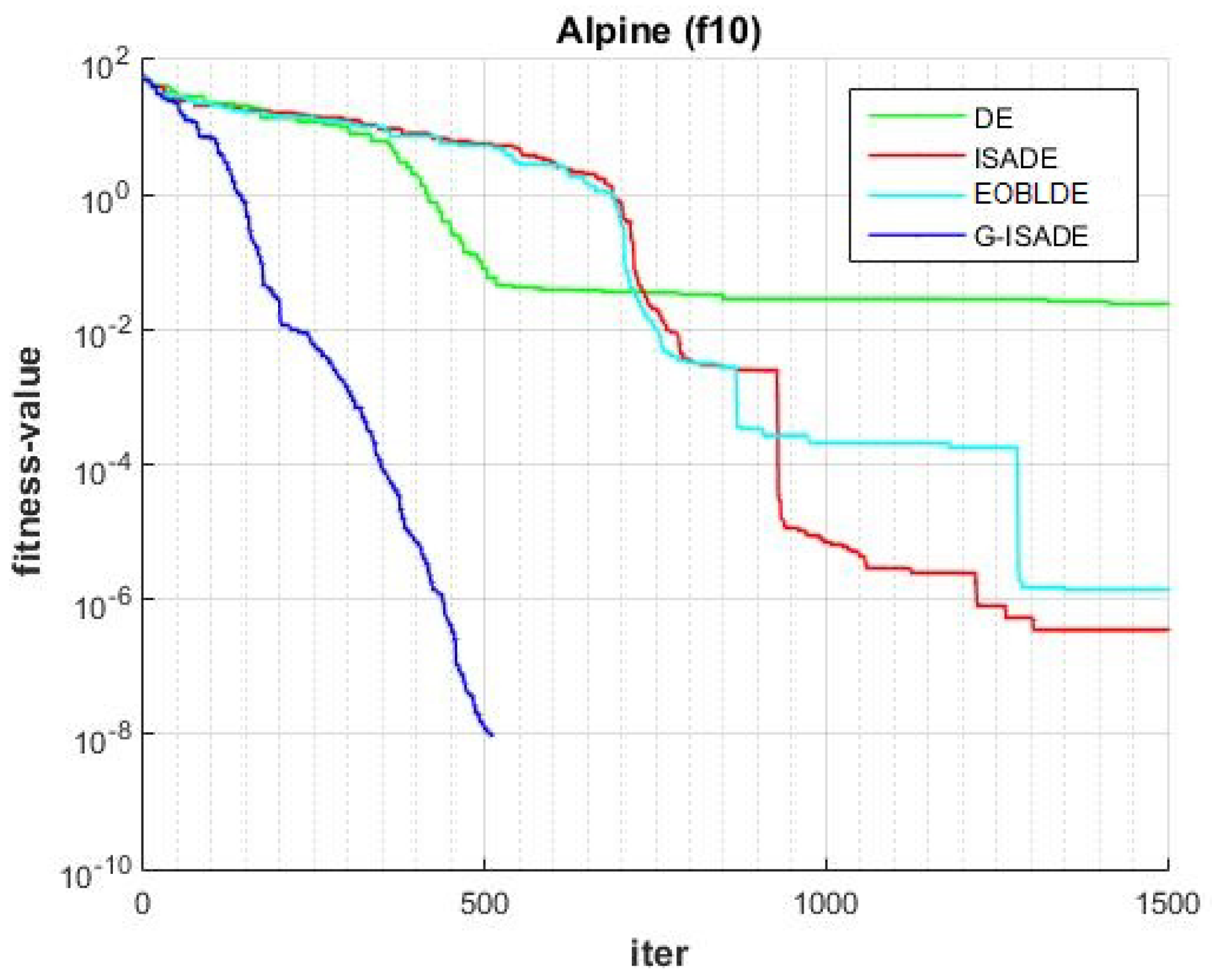
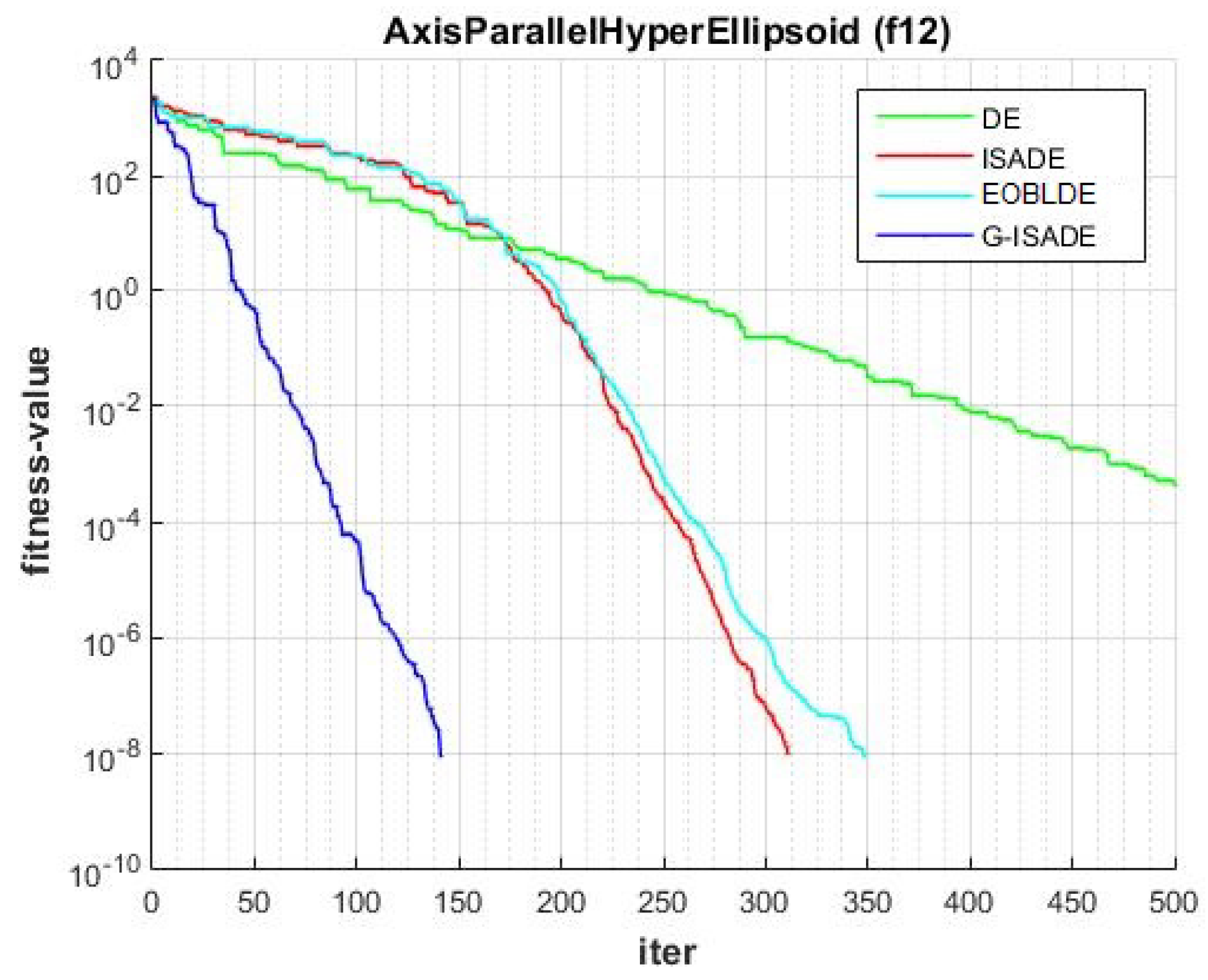
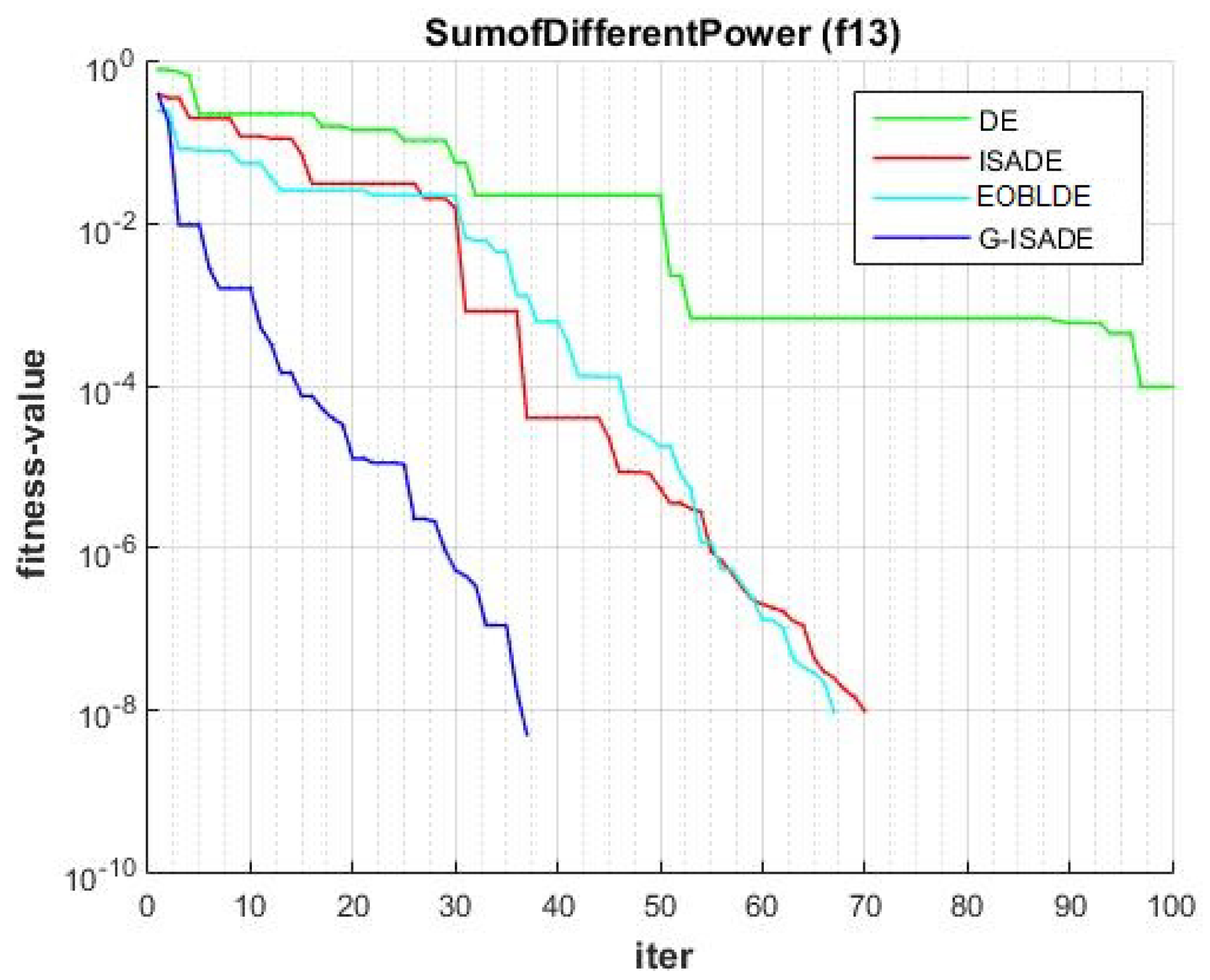
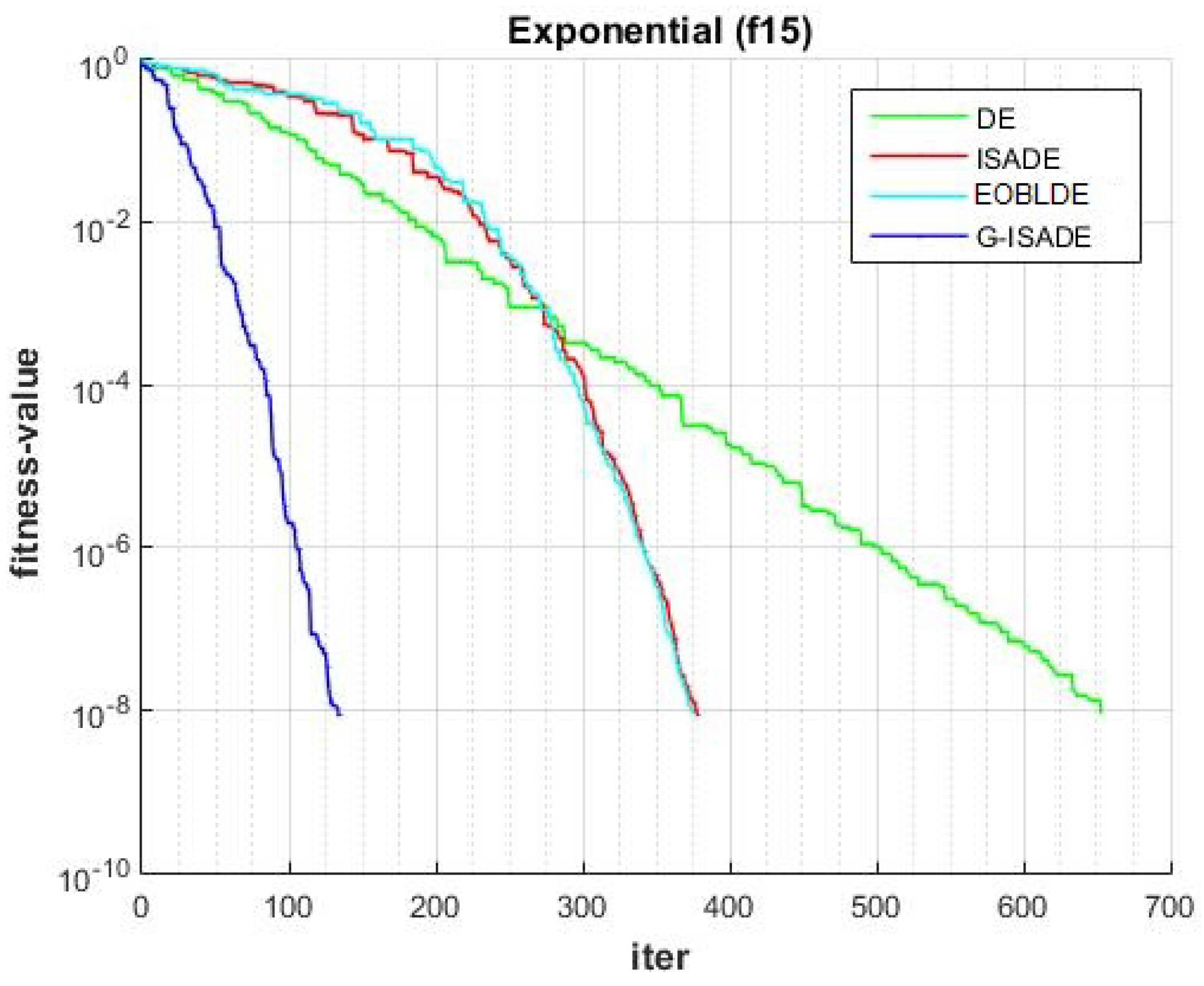
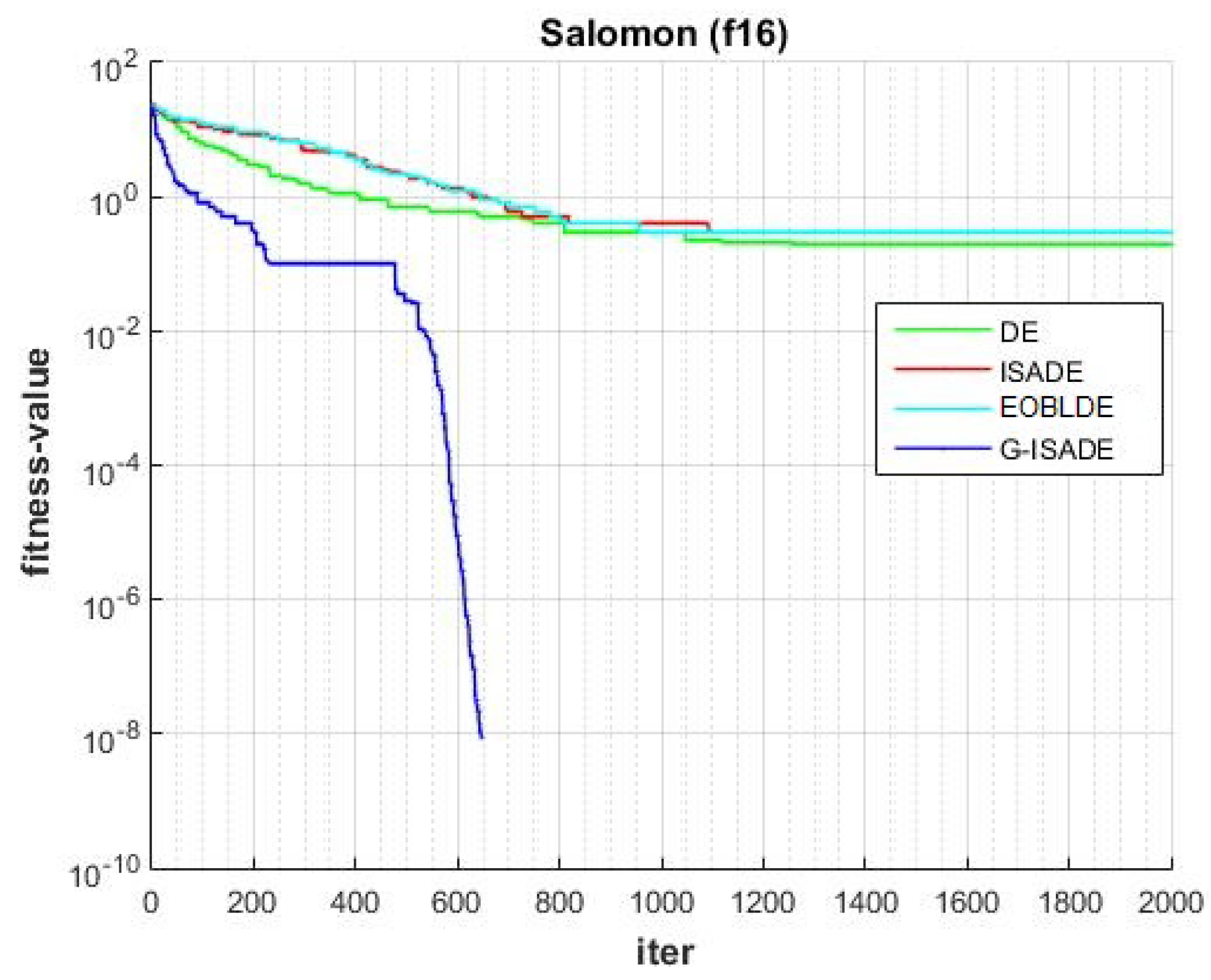
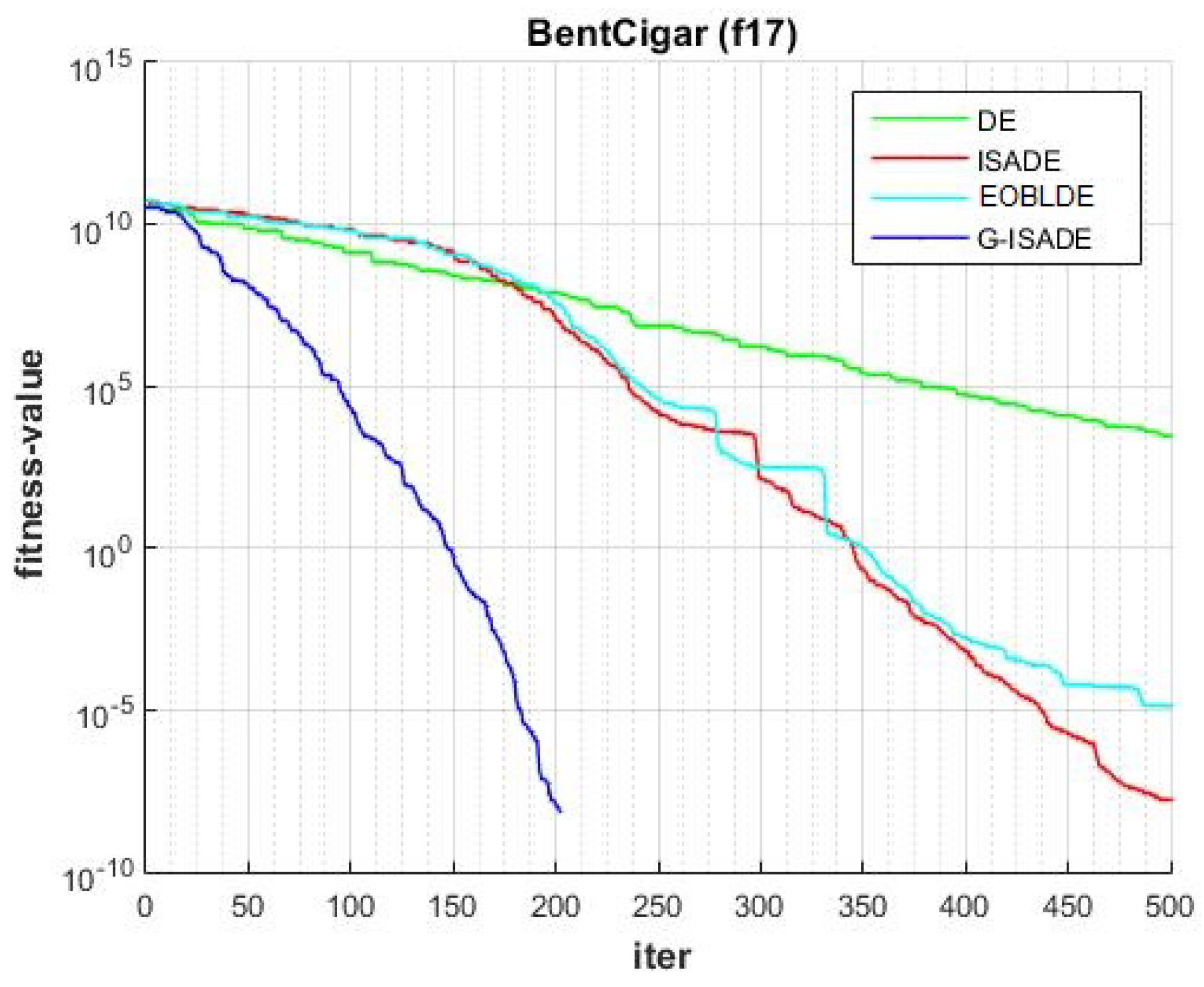
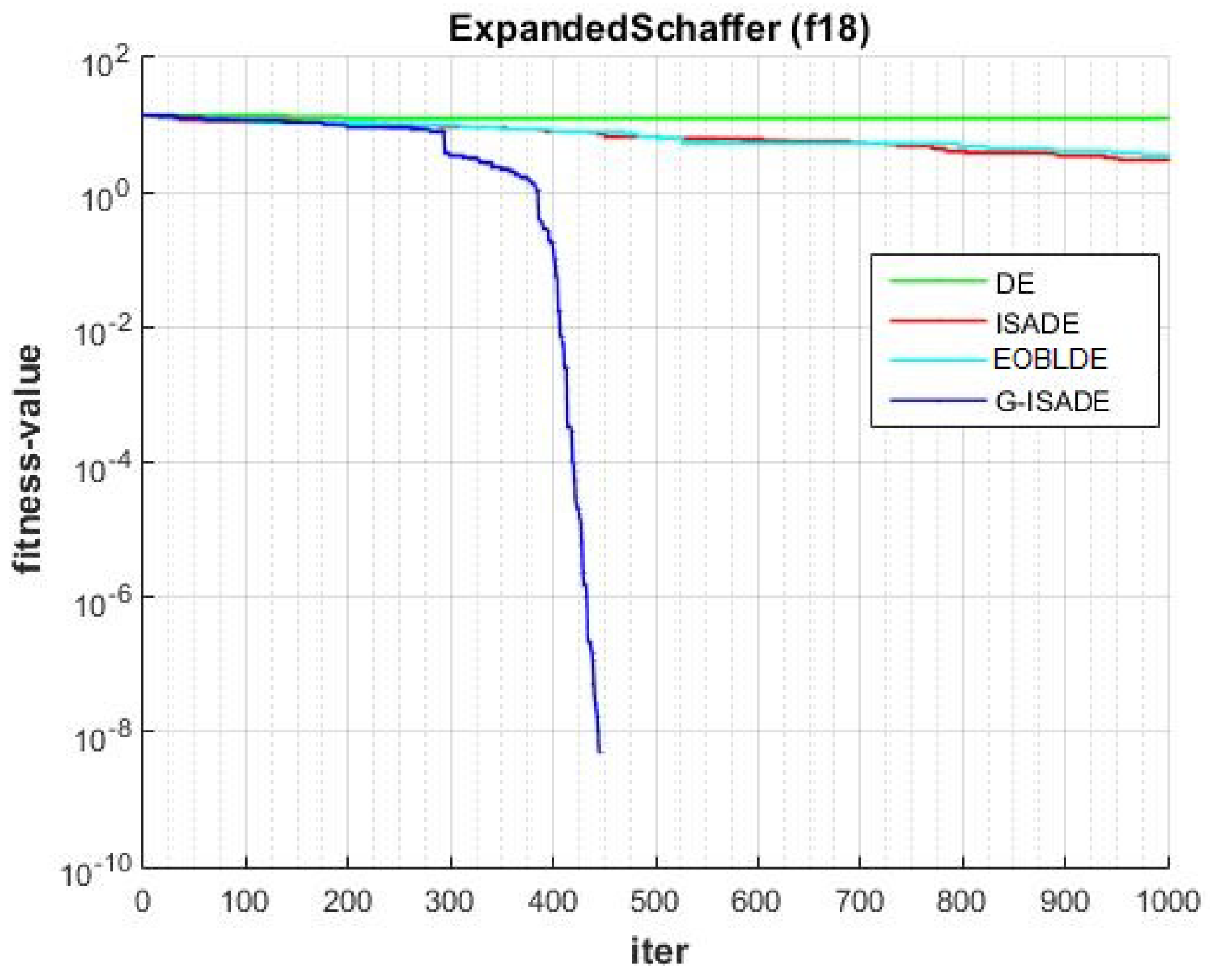
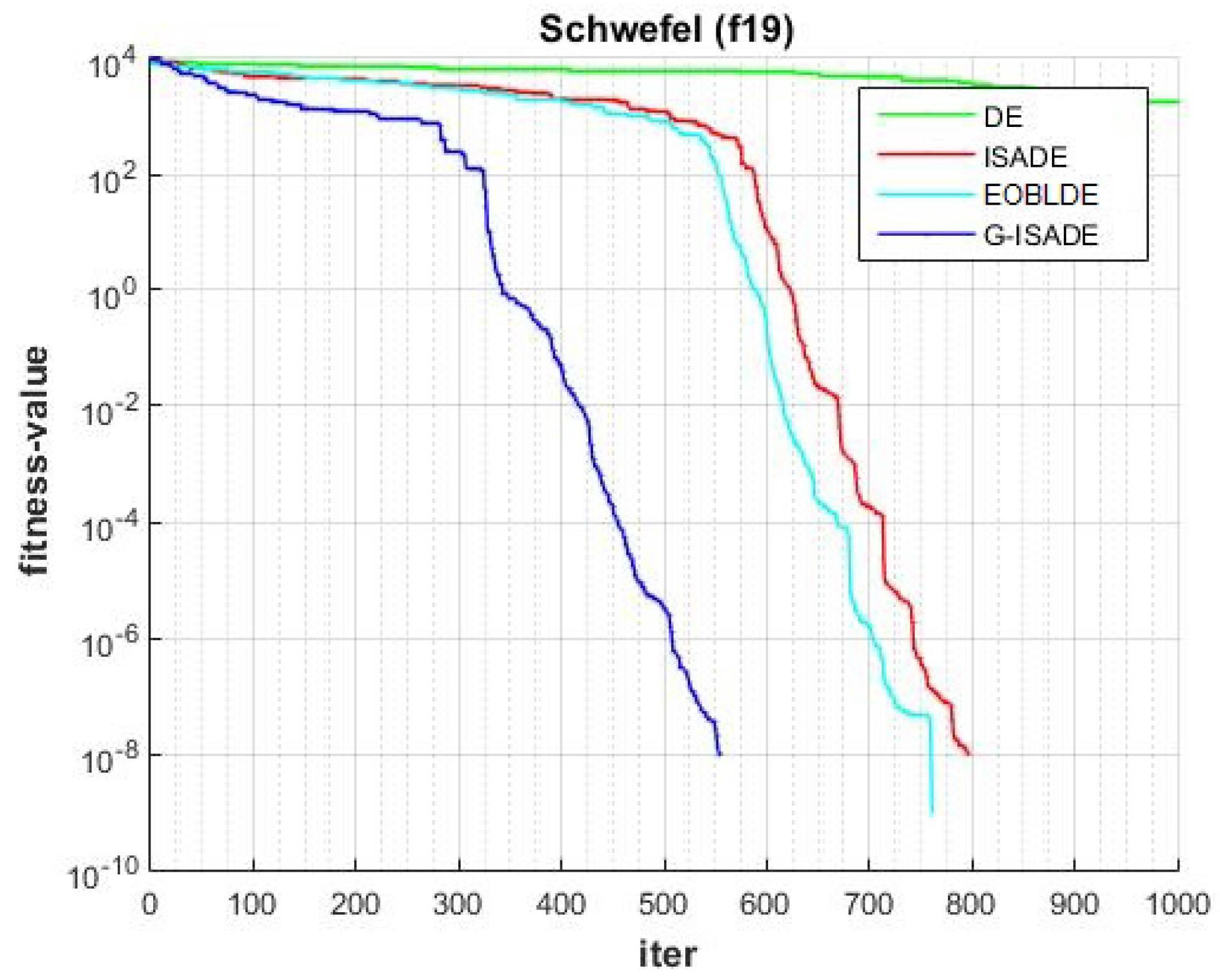
Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21 and Figure 22 express the behavior of the convergence of all algorithms for 17 benchmark-test problems except for and because the performance of the proposed algorithm was not as good as EOBLDE for these test functions. On the graph, the number of iterations is shown on the horizontal axis, while the function value is shown on the vertical axis. These graphs show that the proposed algorithm achieved convergence to the global optimum minimum value with in fewer iterations when compared to the remaining reference algorithms.
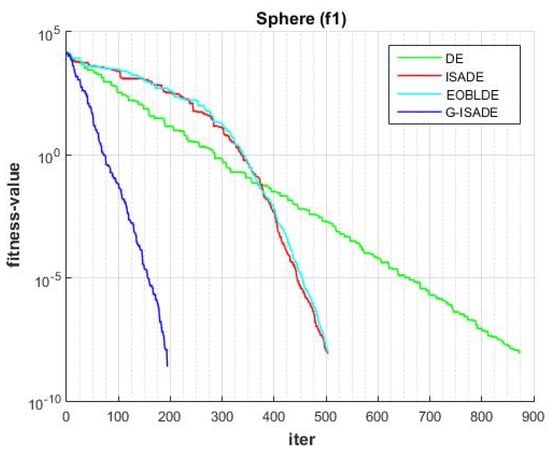
Figure 6.
Convergence comparison for f1.
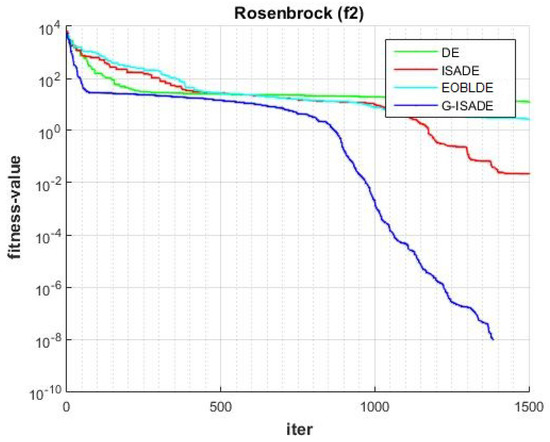
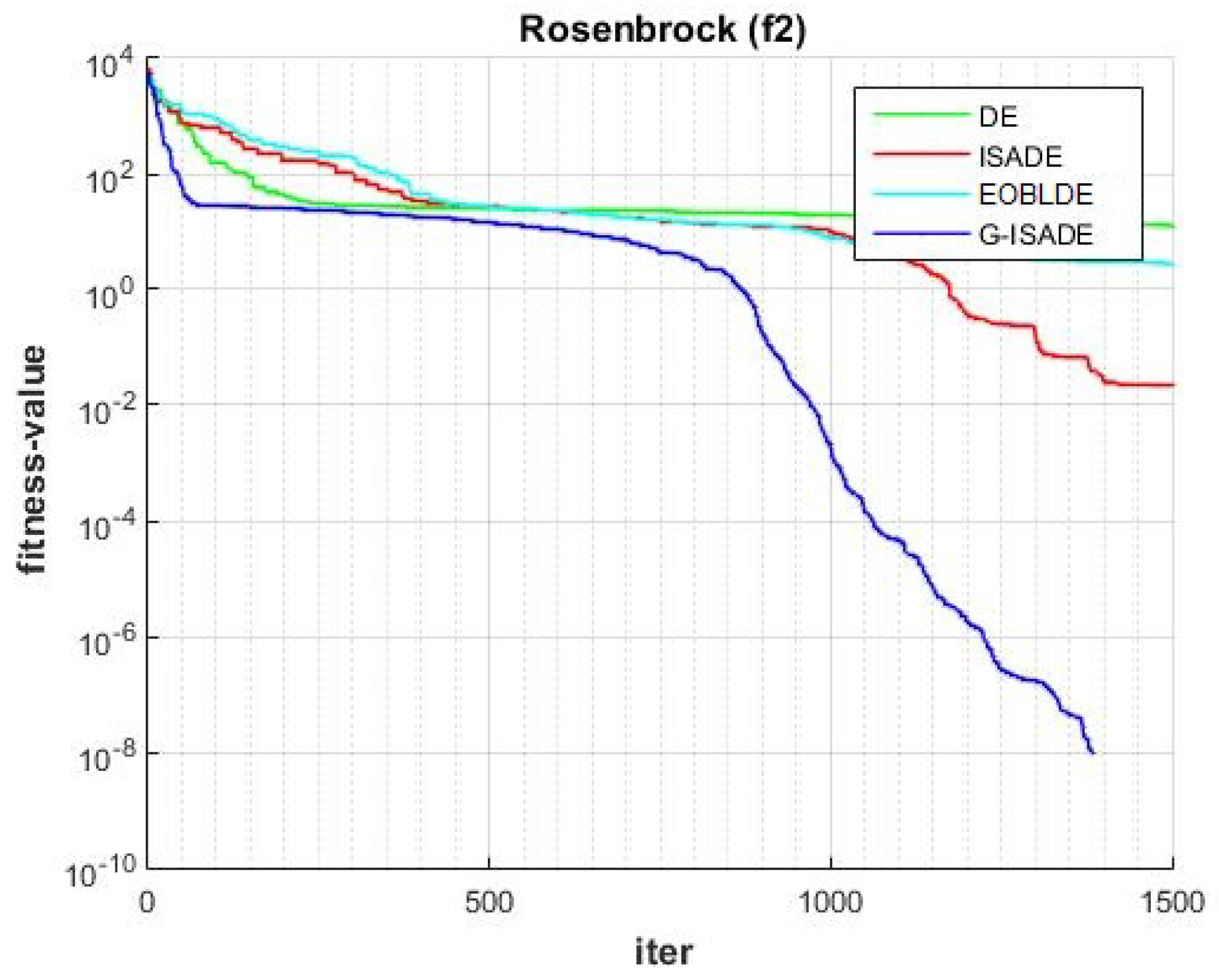
Figure 7.
Convergence comparison for f2.
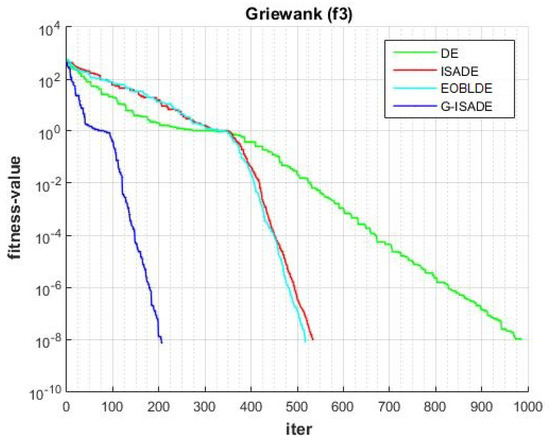
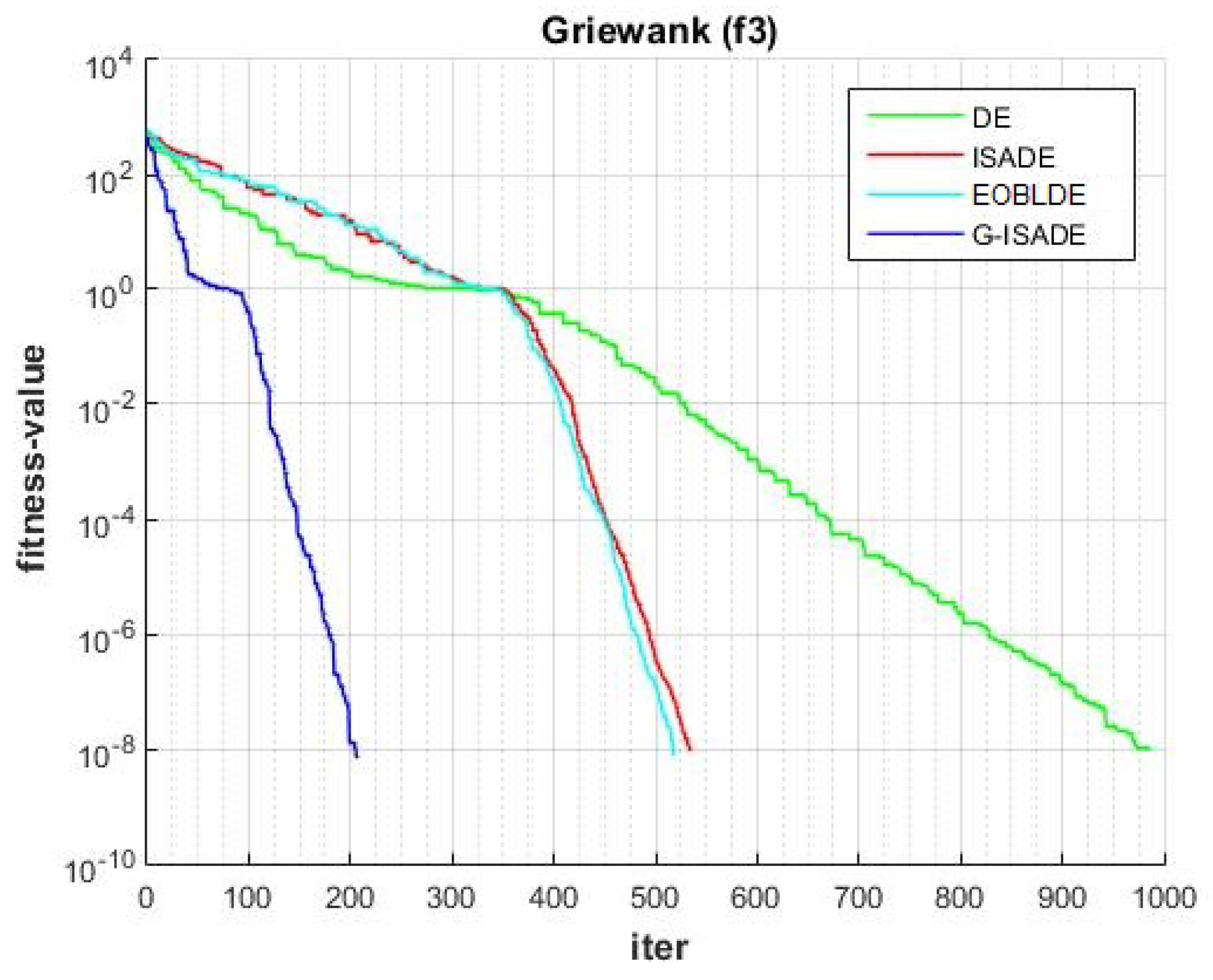
Figure 8.
Convergence comparison for f3.
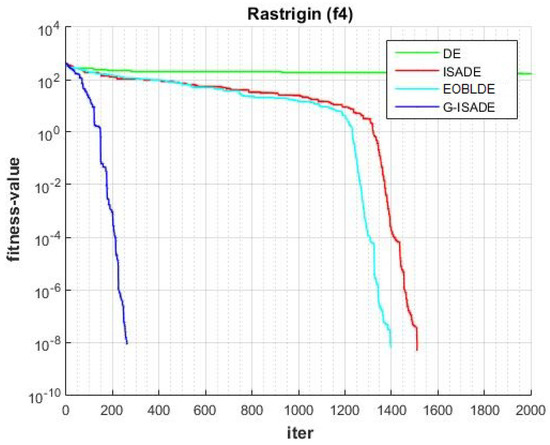
Figure 9.
Convergence comparison for f4.
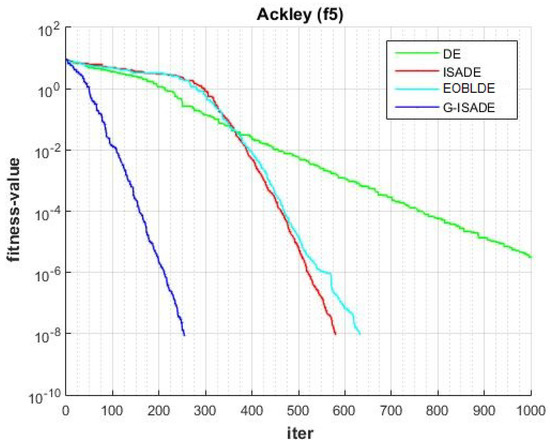
Figure 10.
Convergence comparison for f5.
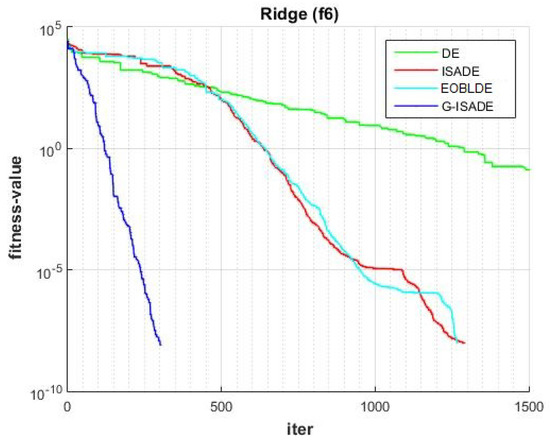
Figure 11.
Convergence comparison for f6.
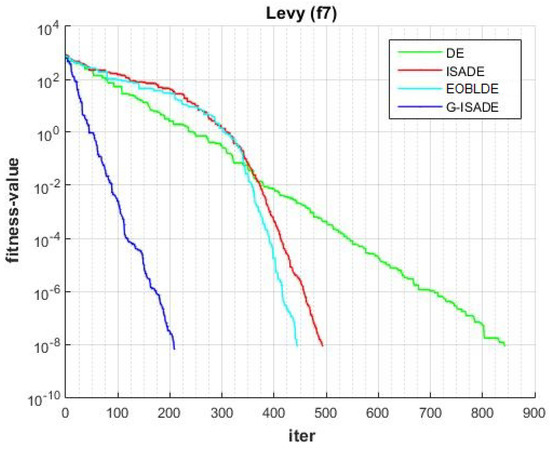
Figure 12.
Convergence comparison for f7.
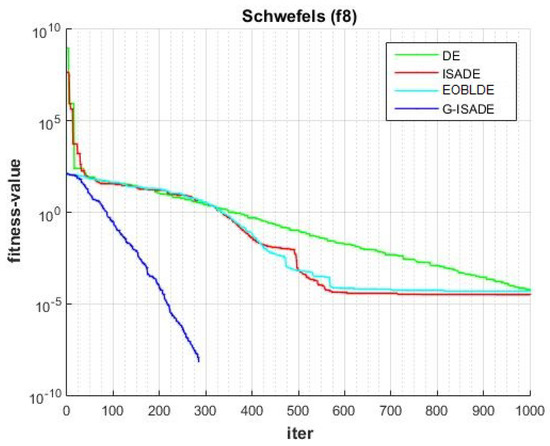
Figure 13.
Convergence comparison for f8.
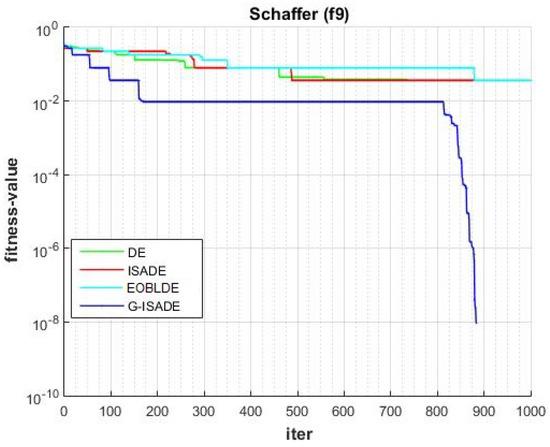
Figure 14.
Convergence comparison for f9.
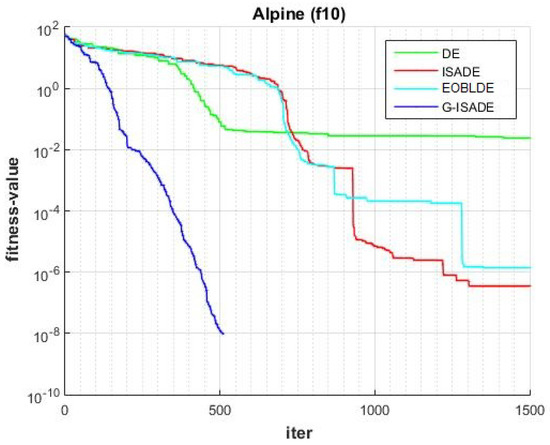
Figure 15.
Convergence comparison for f10.
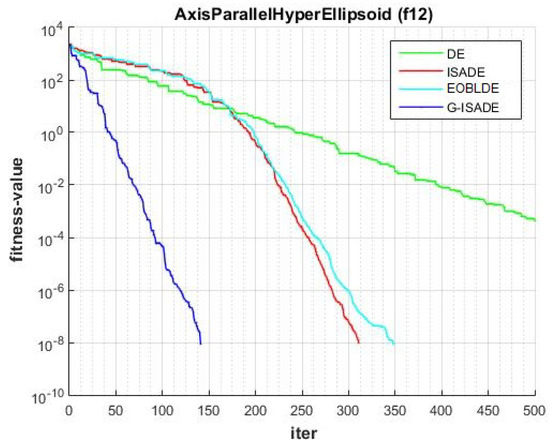
Figure 16.
Convergence comparison for f12.
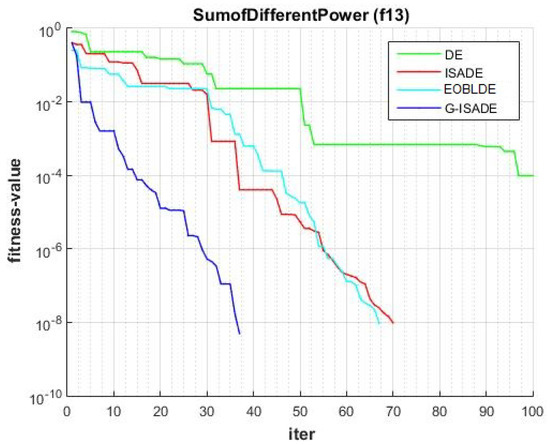
Figure 17.
Convergence comparison for f13.
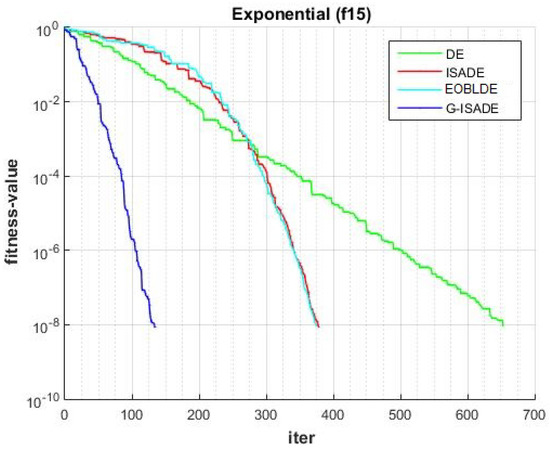
Figure 18.
Convergence comparison for f15.
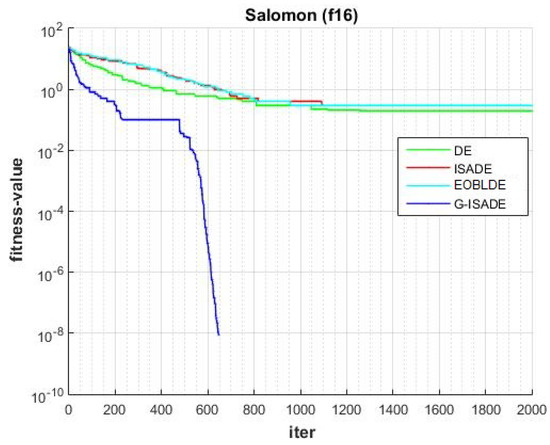
Figure 19.
Convergence comparison for f16.
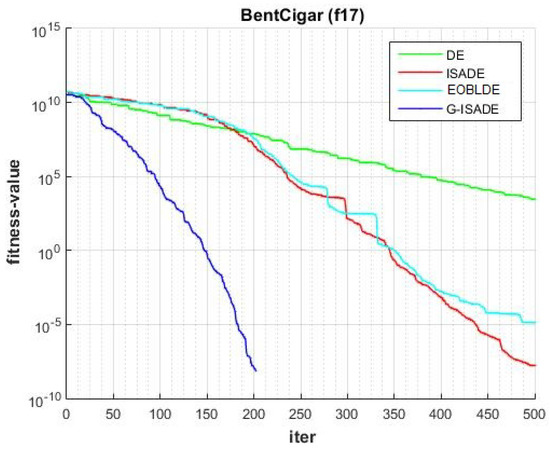
Figure 20.
Convergence comparison for f17.
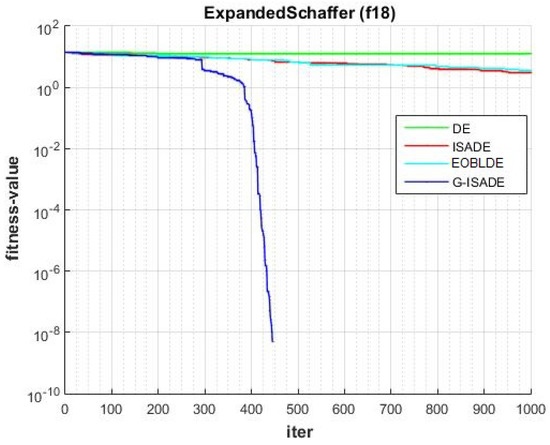
Figure 21.
Convergence comparison for f18.
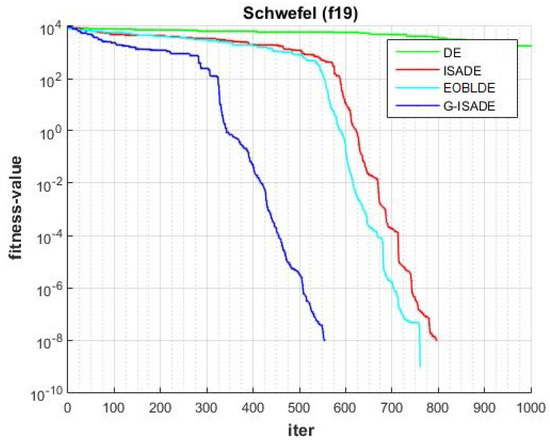
Figure 22.
Convergence comparison for f19.
5.4. Modified Differential Evolution for Real-World Problem
To prove the ability of the introduced methods, the four popular real-world problems are considered and solved in this section. The parameters of the experiments are set as follows, the number of population , the terminal condition is that the iteration or the function evaluation reach the maximum value. All numerical simulations are independently implemented 30 runs for each test problem.
5.4.1. Welded-Beam Design Problem
The objective of this problem is to minimize the manufacturing cost by optimizing a welded beam under some constraint conditions [20]. Figure 23 shows the structure of a welded-beam. The target is to determine the four optimal design variables, such as , and subjected to shear stress , bending stress , and end deflection on beam in the condition of bending force at the end of bar F. The optimization problem is modeled by Equation (20).
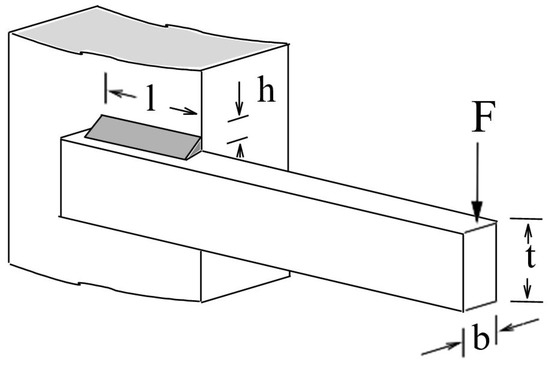
Figure 23.
Welded-beam design problem.
Minimize:
Subject to
With ; ; ;
; ;
With
With
With where , and .
Our optimal solution is compared with several approaches, including the coevolutionary differential evolution method (CDE) [21], coevolutionary particle-swarm optimization (CPSO) [22], GA-based coevolution model (CGA) [23], and elite opposition-based learning differential evolution (EOBLDE) [9] as expressed in Table 3 and Table 4. As can be seen, our optimal solution is better than the remaining methods; in particular, the standard deviation value is “0” that proved the exceptional convergence ability of our method while solving the welded-beam design problem.

Table 3.
Best solution for welded beam problem.

Table 4.
Statistical results for welded beam problem.
5.4.2. Design Problem of Air-Storage Tank
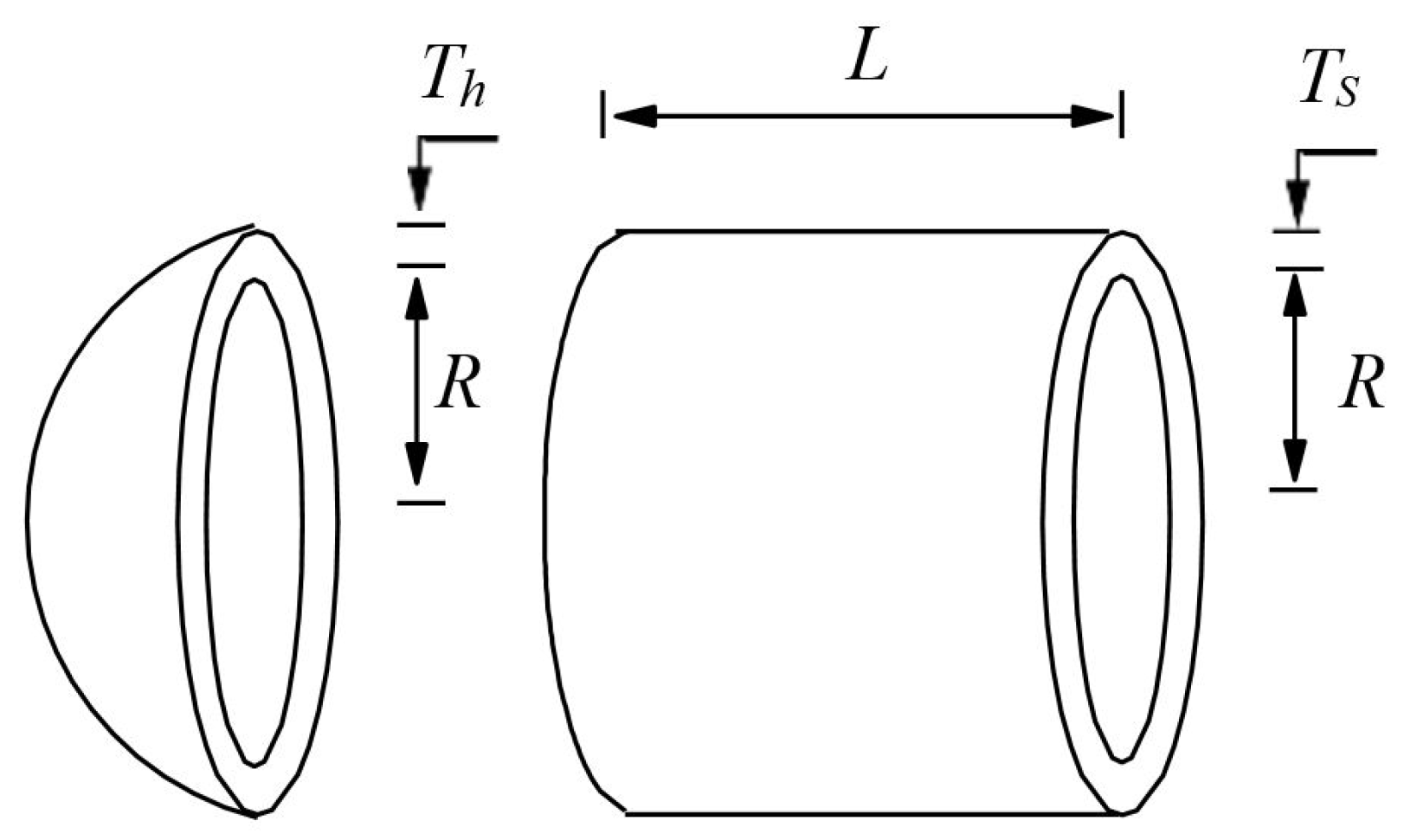
In this section, the dimension of the air-storage tank is optimized, high-compression pressure of 3000 psi is applied to the structure [24]. The design domain is a cylindrical structure with half of a sphere at both heads as Figure 24. The target is to minimize the manufacturing cost by evaluating design variables, including end thickness , head thickness , inner radius , and cylindrical length . This optimization problem is described by Equations (28)–(32) as below.
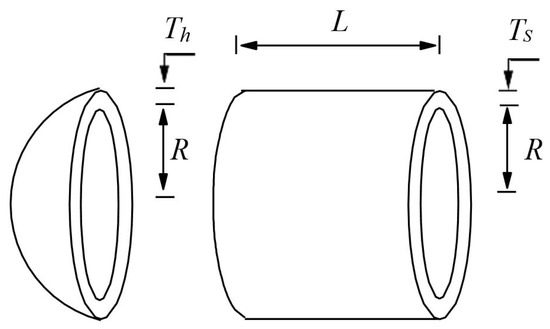
Figure 24.
Design problem of air-storage tank.
Minimize:
Subject to
where , , and .
The four methods, such as CDE, CPSO, CGA, and EOBLDE, were continued compared with our solution for this problem. The comparison results were given in Table 5 and Table 6. The best solution of G-ISADE is better than that of the other algorithms. As can be seen in Table 6, the search ability of G-ISADE is also better than the remains since the worst solution found by G-ISADE is better than those of the others.

Table 5.
Best solution for air-storage tank problem.

Table 6.
Statistical results for air-storage tank problem.
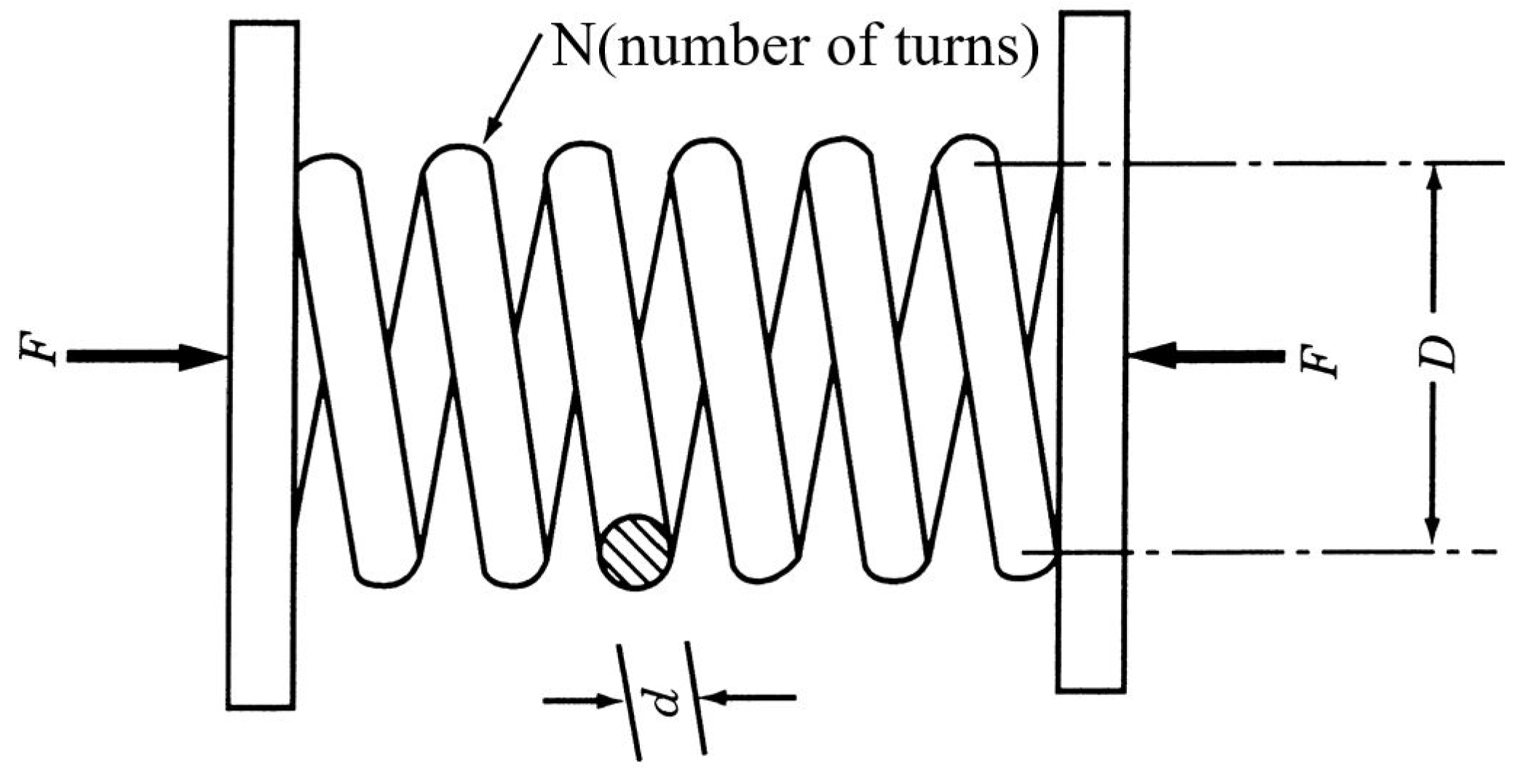
5.4.3. Design Problem of Compression Spring
A compression spring will be considered in this part [25]. The target is to minimize weight of spring, while constraint functions are limitation of deflection, shear stress, surge frequency, moreover, outside diameter and design variables are limited in certain range. The optimized parameters were wire diameter , outer diameter , and number of turns , as seen in Figure 25. This optimization problem is described by Equations (33)–(37).
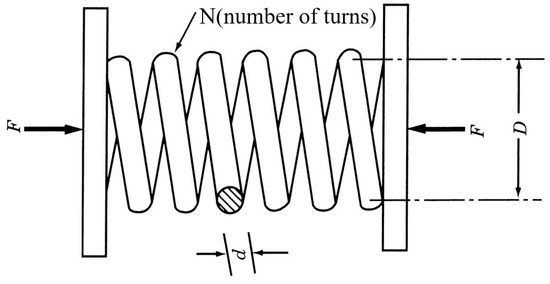
Figure 25.
Tension/compression-spring design problem.
Minimize:
Subject to
where , , and .
Our optimal solution for this problem was evaluated with the four methods, namely CDE, CPSO, CGA, and EOBLDE. The best solution for all approaches is shown in Table 7, while their statistics are expressed in Table 8. The optimal solution obtained by G-ISADE is better than those of the other approaches.

Table 7.
Best solution for the compression spring problem.

Table 8.
Statistical results for compression spring problem.
5.4.4. Optimization Problem of Gear Reducer
Gear reducer is widely applied in machinery, it is used to reduce the speed and increase the torque taken by the motor. This research applied the modified differential evolution to two optimization problems, single stage and two-stage planetary spur gear reducer.
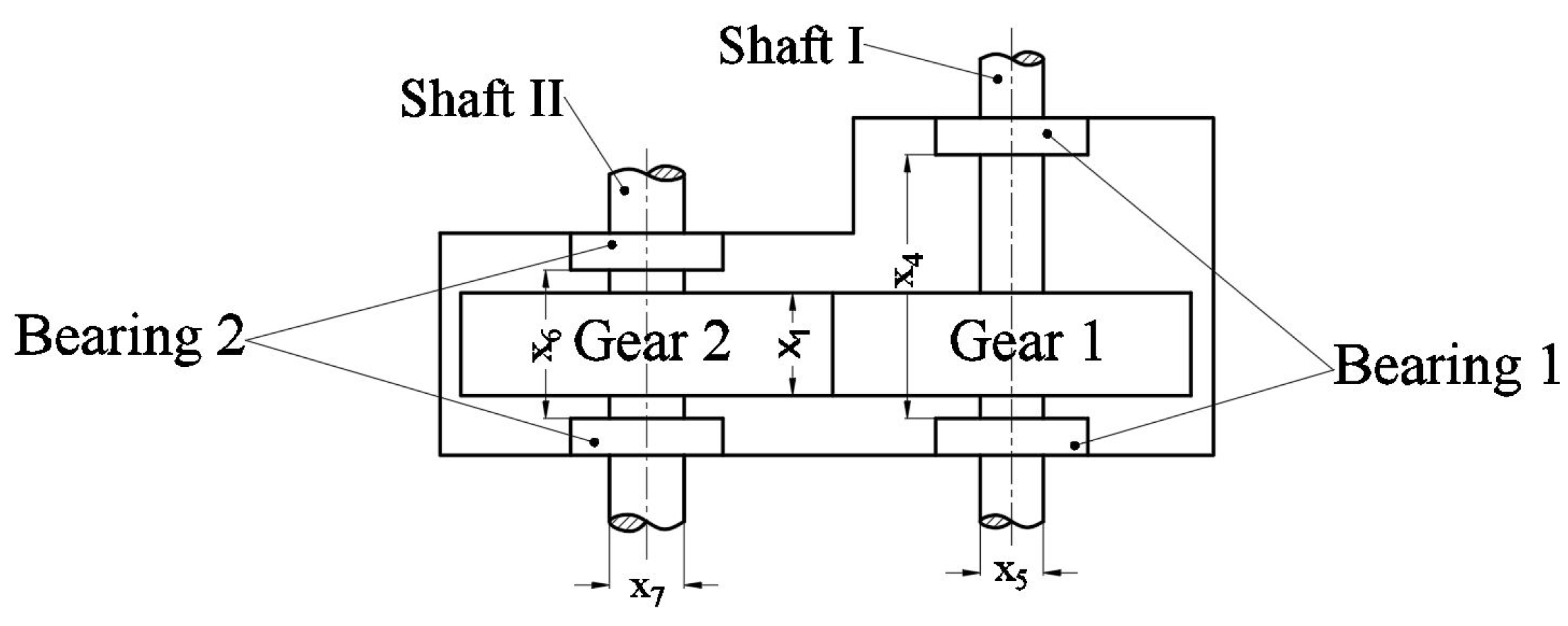
Problem 1: Single stage spur gear reducer
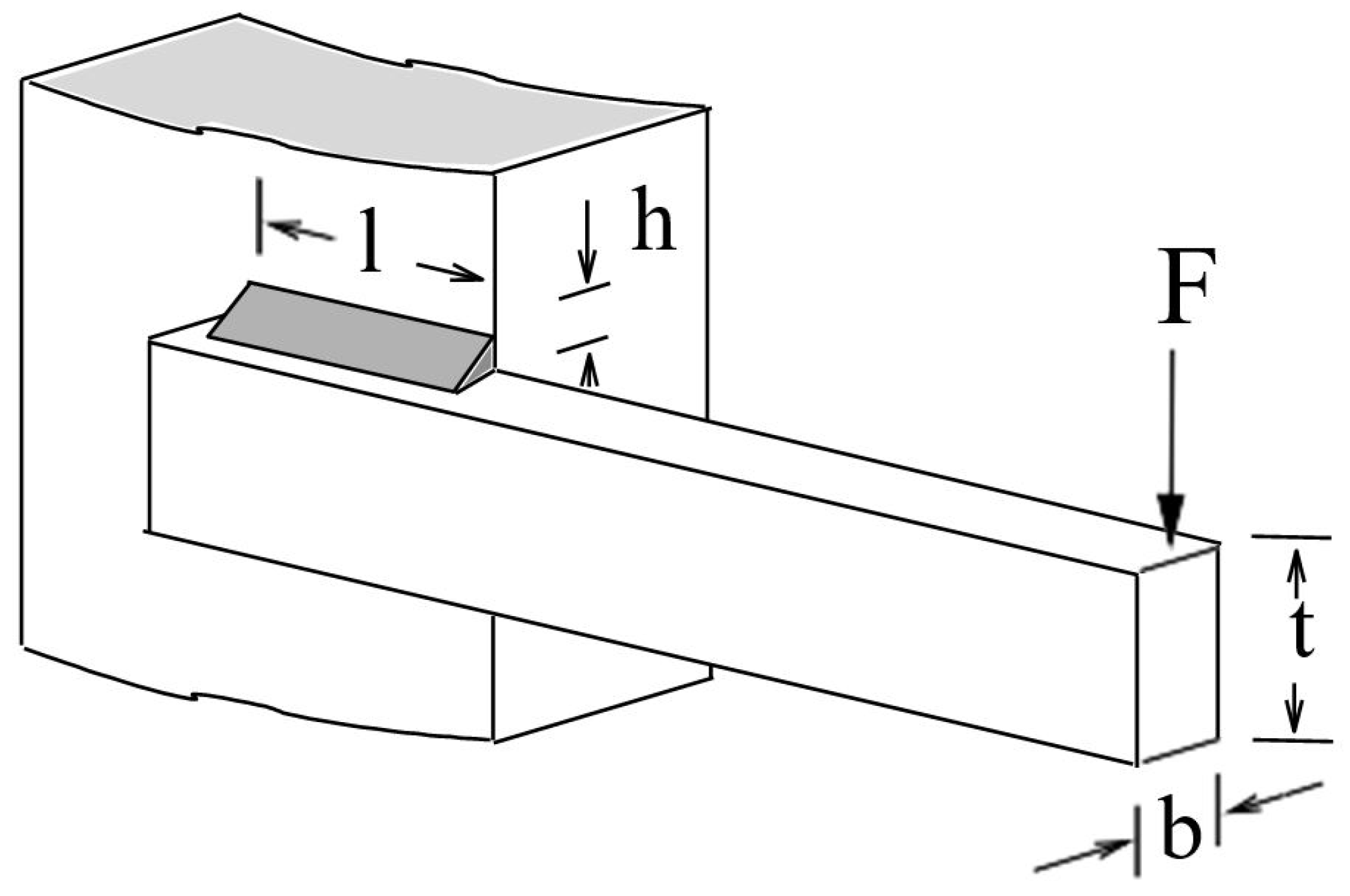
This problem is described in [26] and shown in Figure 26, it contains seven design variables, including the face width, ; the gear module, ; the teeth number on pinion gear, ; the length and diameter of the shaft I, and , respectively; and the length and diameter of the shaft II, and , respectively. The target is the minimal weight of speed reducer box expressed in Equation (38). This problem is bounded by 11 constraint functions as Equations (39)–(49).
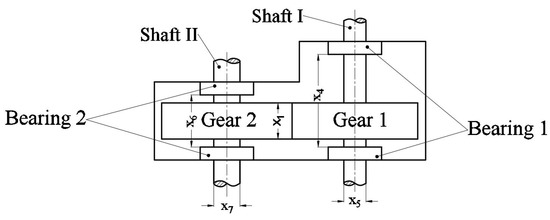
Figure 26.
Single stage spur gear reducer.
Design variable: = [2.6, 3.6]; = [0.7, 0.8]; = [17, 28], is an integer; = [7.3, 8.3]; = [7.3, 8.3]; = [2.9, 3.9]; = [5, 5.5].
Minimize:
Subject to
Table 9 and Table 10 show the comparison of the our optimal solution with previous research which consists of the artificial immune system genetic algorithm (AIS-GA) [27], real-coded steady-state genetic algorithm (APM) [28], and EOBLDE. From Table 9, the best solution of G-ISADE is better than those of the remain algorithms. In addition, the standard deviation in statistical results of G-ISADE is “0”, that verified the ability of convergence of the proposed method in solving minimal weight problem of single stage spur gear reducer box.

Table 9.
Best solution for single stage spur gear reducer problem.

Table 10.
Statistical results for single stage spur gear reducer problem.
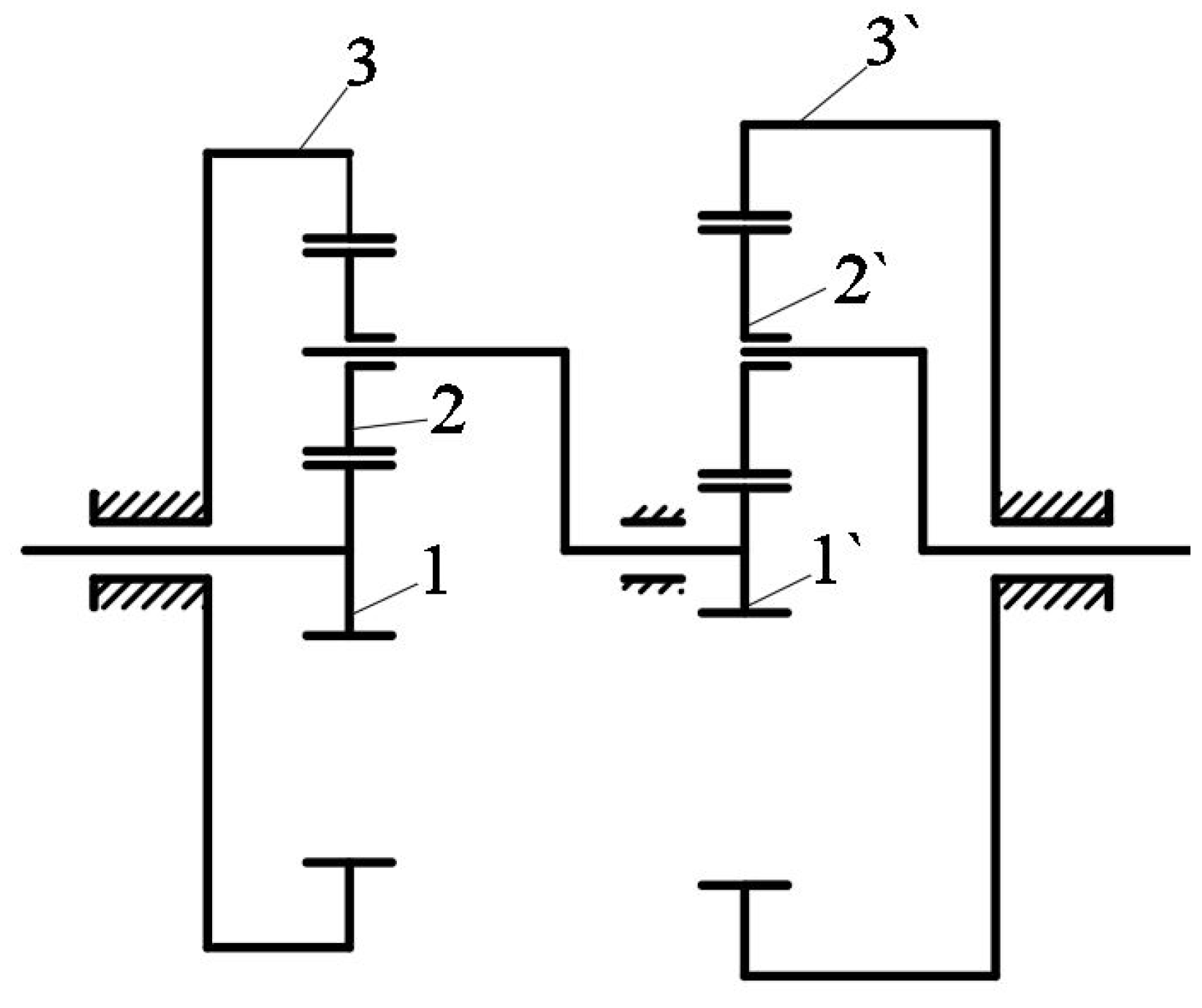
Problem 2: Two-stage planetary gear reducer
Planetary gear reducer plays an important role in transmission systems and are commonly applied in industry. It has many pros in comparison with normal transmission systems, such as weight reduction, compact dimensions, wide range of speed ratios, and high efficiency.
This section considers a two-stage planetary gear reducer, as described in Figure 27. This problem involves nine design variables, including the number of teeth on the primary sun gear (1) and the secondary sun gear (1), which are and , respectively; the gear module, ; the face width, ; the sun gear`s modification coefficient, ; and the first-stage transmission ratio, . To minimize the weight of the planetary gear reducer, the total volume of all sun gears and planetary gears is set as the objective function and displayed in Equation (50) with 10 constraint functions, which include stress limitations, and the adjacent condition is expressed in Equations (51)–(60). The details of the problem can be found in [29].
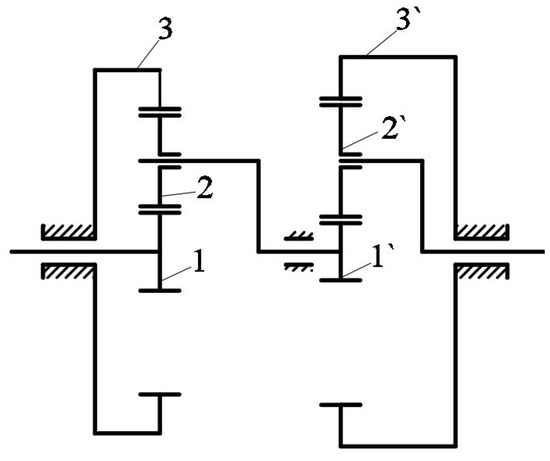
Figure 27.
Two-stage planetary gear reducer.
Design variable: = [17, 30]; = [2, 5]; = [55, 61]; = [0.2, 0.5]; = [5, 30]; = [17, 30]; = [2, 5]; = [140, 200]; = [0.2, 0.5]
Minimum:
where u is the total transmission ratio of the planetary gear system, u = 30.
Subject to
The obtained solution is compared with the original DE, as shown in Table 11. Our optimal solution is better than the candidate generated by the original DE.

Table 11.
Best solution for two-stage planetary gear reducer problem.
6. Conclusions
This paper addressed the application of a new approach for solving optimization problem of mechanical engineering. The proposed algorithm is an improve version of ISADE, it adopts a Gaussian random variable to mutation operation.
Firstly, the proposed method is verified through numerical simulation with 19 benchmark functions. The new approaches proved to be highly effective across all the testing criteria. The updated strategies significantly improved the convergence speed and accuracy in comparison with the previous approaches.
In addition, the new method is also a powerful tool to solve real-world engineering problems. By introducing this method, our research contributes one more option to engineers when solving the real problems in their work.
Author Contributions
Conceptualization, V.-T.N.; methodology, V.-T.N.; numerical simulation and validation, V.-T.N.; formal analysis, writing—original draft preparation, V.-T.N.; writing—review and editing, V.-M.T.; supervision, N.-T.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Hanoi University of Science and Technology (HUST) under project number T2022-PC-036.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
This work was also supported by the Centennial SIT Action for the 100th anniversary of Shibaura Institute of Technology to enter the top ten Asian Institute of Technology.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DE | Differential evolution |
| EAs | Evolutionary algorithms |
| ISADE | Improve Self-Adaptive Differential Evolution |
| SaDE | Self-adaptive differential evolution algorithm |
| SR | Success rate |
| FE | Function evaluations |
Appendix A
Shere function:
Rosenbrock function:
Griewank function:
Rastrigin function:
Ackley function:
Ridge function:
Levy function:
Schawefel function:
Schaffer function:
Alpine function:
Pathological function:
Weighted sphere function:
Sum of Different Power function:
Zakharov function:
Exponential Problem:
Salomon Problem:
Bent Cigar Function:
Expanded Schaffer’s F6 Function:
Schwefel Function:
References
- Storn, R.; Price, K. Differential Evolution-A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Lemarechal, C. Cauchy and the Gradient Method. Doc. Math. Extra 2012, ISMP, 251–254. [Google Scholar]
- Wallis, J. A Treatise of Algebra, Both Historical and Practical; Richard Davis: Oxford, UK, 1685. [Google Scholar]
- Qin, A.K.; Suganthan, P.N. Self-Adaptive Differential Evolution Algorithm for Numerical Optimization. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005; pp. 1785–1791. [Google Scholar]
- Brest, J.; Greiner, S.; Boskovic, B.; Mernik, M.; Zumer, V. Self-Adapting Control Parameters in Differential Evolution: A Comparative Study on Numerical Benchmark Problems. IEEE Trans. Evol. Comput. 2006, 10, 646–657. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive Differential Evolution with Optional External Archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Wang, Y.; Li, H.-X.; Huang, T.; Li, L. Differential evolution based on covariance matrix learning and bimodal distribution parameter setting. Appl. Soft Comput. 2014, 18, 232–247. [Google Scholar] [CrossRef]
- Ali W., M.; Ali K., M. Adaptive guided differential evolution algorithm with novel mutation for numerical optimization. Int. J. Mach. Learn. Cybern. 2019, 10, 253–277. [Google Scholar]
- Tam, B.; Trung, N.; Hiroshi, H. Opposition-based learning for self-adaptive control parameters in differential evolution for optimal mechanism design. J. Adv. Mech. Des. Syst. Manuf. 2019, 13, 4. [Google Scholar]
- Tam, B.; Pham, H.; Hiroshi, H. Improve Self-Adaptive Control Parameters in Differential Evolution for Solving Constrained Engineering Optimization Problems. J. Comput. Sci. Technol. 2013, 7, 59–74. [Google Scholar]
- Tizhoosh H., R. Opposition-Based Learning: A New Scheme for Machine Intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation, Vienna, Austria, 28–30 November 2005; pp. 695–701. [Google Scholar]
- Zheng, H.; Zhou, Y. A Novel Cuckoo Search Optimization Algorithm Base on Gauss Distribution. J. Comput. Inf. Syst. 2012, 8, 4193–4200. [Google Scholar]
- He, X.-S.; Ding, W.J.; Yang, X.S. Bat algorithm based on simulated annealing and Gaussian perturbations. Neural Comput. Appl. 2014, 25, 459–468. [Google Scholar] [CrossRef]
- Lin, Z.; Zhang, Q. An effective hybrid particle swarm optimization with Gaussian mutation. J. Algorithms Comput. Technol. 2017, 11, 271–280. [Google Scholar] [CrossRef]
- Jena, C.; Basu, M.; Panigrahi, C.K. Differential evolution with Gaussian mutation for combined heat and power economic dispatch. Soft Comput. 2016, 20, 681–688. [Google Scholar] [CrossRef]
- Sun, G.; Lan, Y.; Zhao, R. Differential evolution with Gaussian mutation and dynamic parameter adjustment. Soft Comput. 2019, 23, 1615–1642. [Google Scholar] [CrossRef]
- Li, X.; Yin, M. Modified differential evolution with self-adaptive parameters method. J. Comb. Optim. 2016, 31, 546–576. [Google Scholar] [CrossRef]
- Tang, L.; Dong, Y.; Liu, J. Differential Evolution with an Individual-Dependent Mechanism. IEEE Trans. Evol. Comput. 2015, 19, 560–574. [Google Scholar] [CrossRef]
- Suganthan, P.N.; Hansen, N.; Liang, J.J.; Deb, K.; Chen, Y.-P.; Auger, A.; Tiwari, S. Problem Definitions and Evaluation Criteria for the CEC 2005 Special Session on Real-Parameter Optimization; Technical Report Number 2005005; Nanyang Technological University: Singapore; KanGAL: Kanpur, India, 2005. [Google Scholar]
- Ragsdell, K.; Phillips, D. Optimal Design of a Class of Welded Structures using Geometric Programming. ASME J. Manuf. Sci. Eng. 1976, 98, 1021–1025. [Google Scholar] [CrossRef]
- Huang, F.; Wang, L.; He, Q. An effective co-evolutionary differential evolution for constrained optimization. Appl. Math. Comput. 2007, 186, 340–356. [Google Scholar] [CrossRef]
- He, Q.; Wang, L. An effective co-evolutionary particle swarm optimization for constrained engineering design problems. Eng. Appl. Artif. Intell. 2007, 20, 89–99. [Google Scholar] [CrossRef]
- Coello, C.A.C. Use of a self-adaptive penalty approach for engineering optimization problems. Comput. Ind. 2000, 41, 113–127. [Google Scholar] [CrossRef]
- Sandgren, E. Nonlinear Integer and Discrete Pro-gramming in Mechanical Design Optimization. ASME J. Mech. Des. 1990, 112, 223–229. [Google Scholar] [CrossRef]
- Belegundu, A. A Study of Mathematical Programming Methods for Structural Optimization. Ph.D. Thesis, University of Iowa, Iowa City, IA, USA, 1982. [Google Scholar]
- Golinski, J. Optimal synthesis problems solved by means of nonlinear programming and random methods. J. Mech. 1970, 3, 287–309. [Google Scholar] [CrossRef]
- Bernardino, H.; Barbosa, H.; Lemonge, A.; Fonseca, L. A new hybrid AIS-GA for constrained optimization problems inmechanical engineering. In Proceedings of the IEEE Congress on Evolutionary Computation, Hong Kong, China, 1–6 June 2008; pp. 1455–1462. [Google Scholar]
- Lemonge, A.C.C.; Barbosa, H.J.C.; Borgesc, C.C.H.; Silvad, F.B.S. Constrained optimization problems in mechanical engineering design using a real-coded steady-state genetic algorithm. Mecánica Comput. 2010, 29, 9287–9303. [Google Scholar]
- Chen, T.; Zhang, Z.; Chen, D.; Li, Y. The Optimization of Two-Stage Planetary Gear Train Based on Mathmatica. In Pervasive Computing and the Networked World: Joint International Conference, ICPCA/SWS 2012, Istanbul, Turkey, 28–30 November 2012; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7719, pp. 122–136. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).