Effects of Abrupt Cross-Section Area Change on theMultiparameter Propagation Characteristics of Premixed Methane–Air Explosion in Pipes
Abstract
:1. Introduction
2. Experimental Research on Gas Explosion Shock Wave along Pipes with Abrupt Cross-Section Area Change
2.1. Experimental System
2.2. Experimental Scheme
2.3. Experimental Results and Analysis
3. Numerical Simulations of Gas Explosion along Pipelines with Abrupt Cross-Section Area Changes
3.1. Numerical Calculation Methods
3.2. Analysis of Pressure Wave Transmission Process in the Pipes
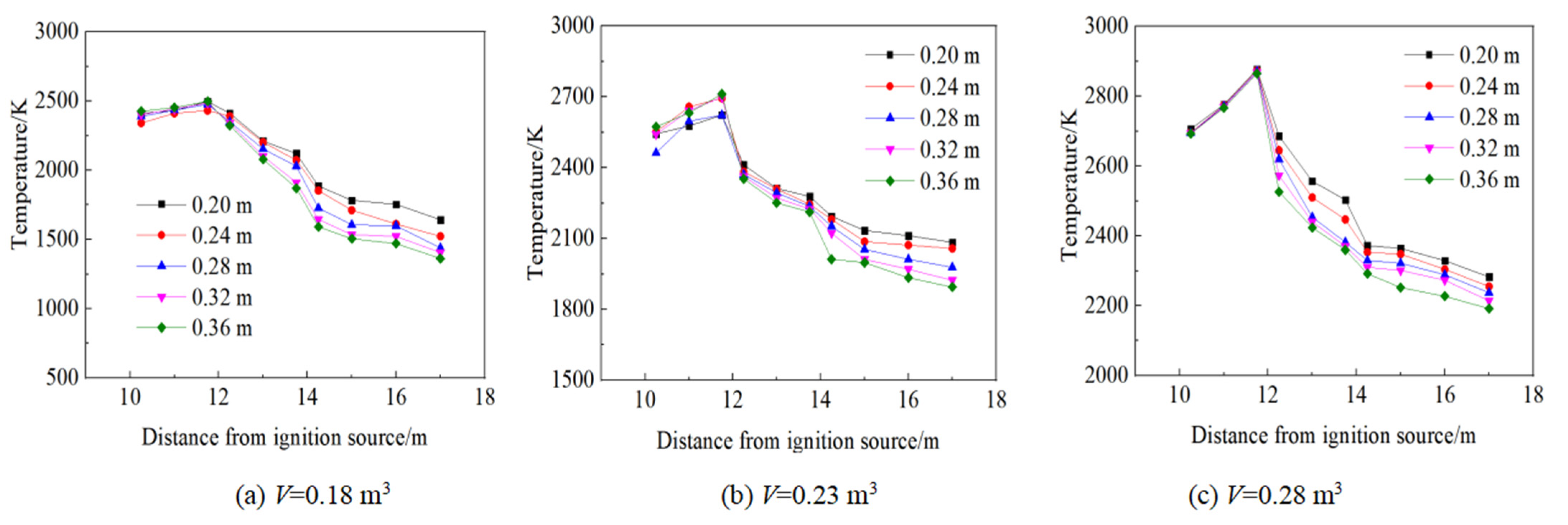
3.3. Change Laws of Explosion Temperature in the Pipe
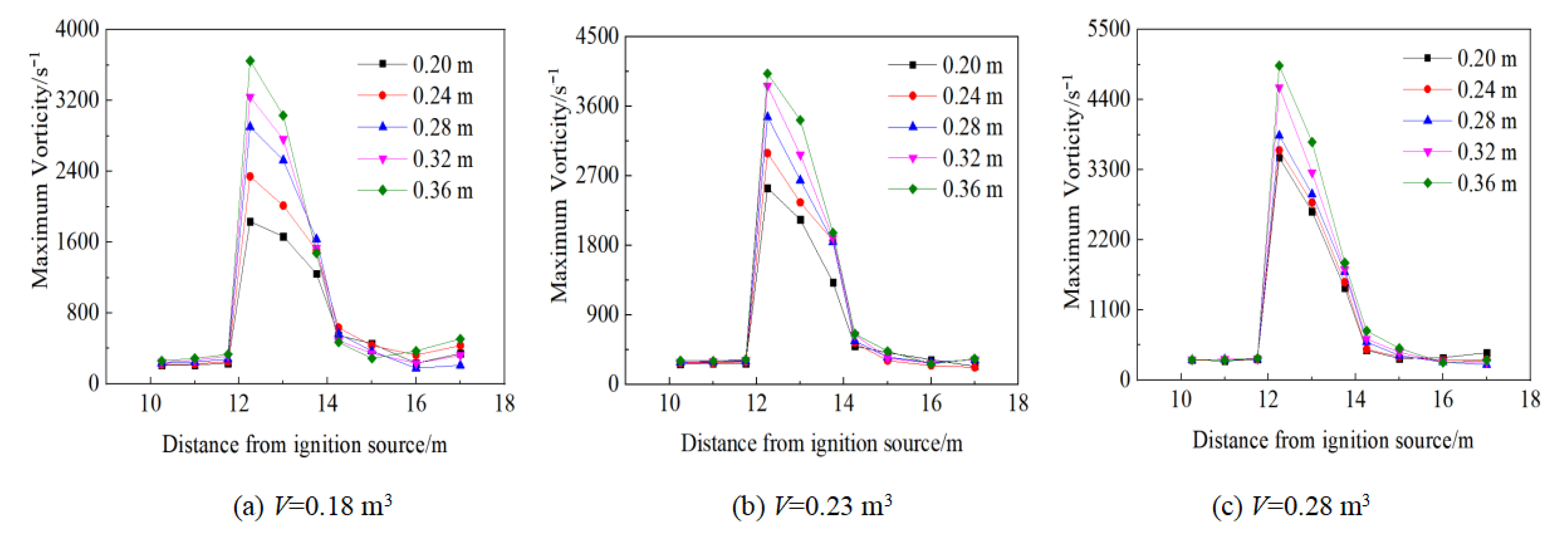
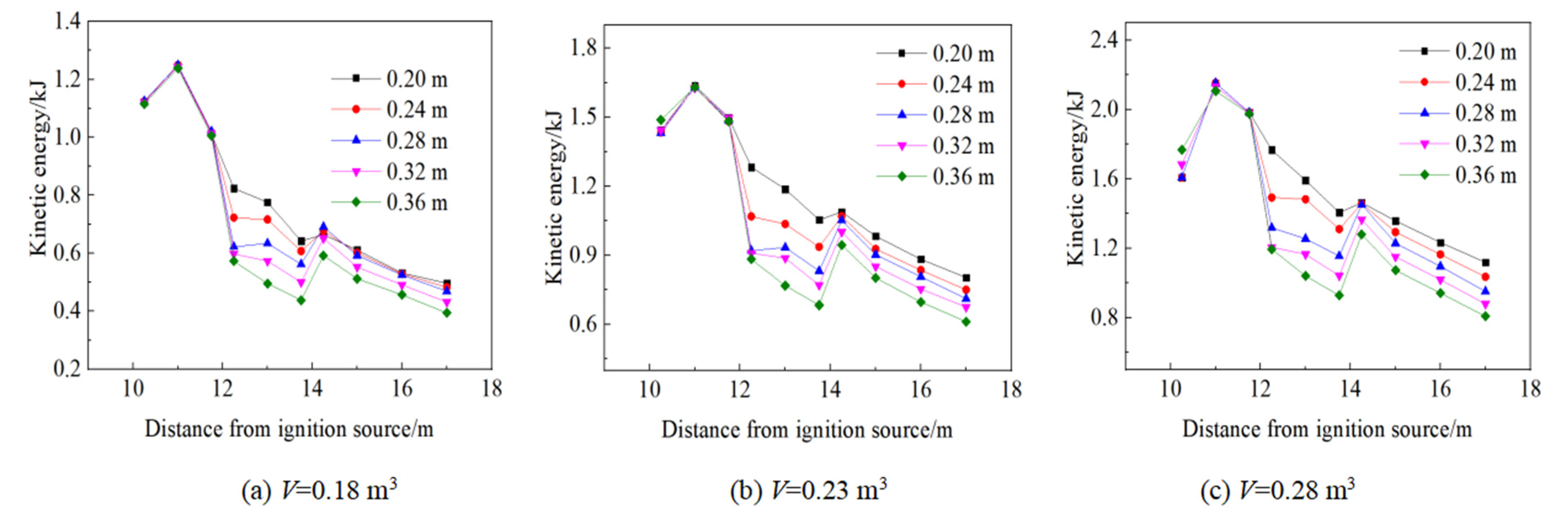
3.4. Change Laws of Vorticity and Kinetic Energy
4. Conclusions
- (1)
- When the cross-section area of the pipe changes abruptly from small to large, the shock wave overpressure decreases. In contrast, the shock wave overpressure increases when the cross-section of the pipe changes abruptly from large to small. When the diameter of the larger section of pipe is less than 0.24 m, the peak overpressure decreases, then sharply increases, and finally decreases. However, when the diameter is greater than 0.24 m, the peak overpressure exhibits a more complex sequence of decreasing, increasing, decreasing, increasing, and finally decreasing;
- (2)
- The overpressure changes in pipes along abrupt cross-section changes can be characterized by the attenuation coefficient, increase coefficient, and reflection coefficient. For a fixed ratio of cross-section areas, the attenuation coefficient increases with an increase in initial peak overpressure before the abrupt cross-section change, whereas the increasing coefficient and reflection coefficient both exhibit a decreasing trend. The coupling relationships between attenuation coefficients, increasing coefficients, reflection coefficients, and initial peak pressure and the ratio of cross-section areas were obtained;
- (3)
- The peak temperature decreases as the cross-section area changes. Moreover, a larger fuel volume creates a greater decrease in peak temperature. This demonstrates that the counter-current effect of the gas explosion pressure wave and reflected wave can inhibit the propagation of the explosion flame under the influence of an abrupt change in cross-section structure;
- (4)
- The vorticity in pipes with abrupt cross-section area changes presents a clear peak, which indicates that gas explosion propagation is affected by the action of turbulence induced by an abrupt cross-section change. Moreover, a larger fuel volume or ratio of cross-section areas has a more obvious effect on turbulence action. In the propagation process of a gas explosion, when the cross-section area changes abruptly, kinetic energy is converted to static pressure energy and vice versa. This indicates that the large eddy motion formed by strong restraint enhances kinetic energy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ding, C.; He, X.; Nie, B. Numerical simulation of airflow distribution in mine tunnels. Int. J. Min. Sci. Technol. 2017, 27, 663–667. [Google Scholar] [CrossRef]
- Lolon, S.A.; Brune, J.F.; Bogin, G.E.; Grubb, J.W.; Saki, S.A.; Juganda, A. Computational fluid dynamics simulation on the longwall gob breathing. Int. J. Min. Sci. Technol. 2017, 27, 185–189. [Google Scholar] [CrossRef]
- Yueze, L.; Akhtar, S.; Sasmito, A.P.; Kurnia, J.C. Prediction of air flow, methane, and coal dust dispersion in a room and pillar mining face. Int. J. Min. Sci. Technol. 2017, 27, 657–662. [Google Scholar] [CrossRef]
- Jeffery, L.K. Looking ahead to significant improvements in mining safety and health through innovative research and effective diffusion into the industry. Int. J. Min. Sci. Technol. 2015, 25, 325–332. [Google Scholar]
- Jia, Z.W.; Jing, G.X.; Cheng, L.; Li, M.J. Study on propagation rules about gas explosion shock wave in the laneway with abrupt change of section area. China Saf. Sci. J. 2007, 17, 92–94. [Google Scholar]
- Yang, S.Z.; Jing, G.X.; Jia, Z.W. Injury study on impact current of gas explosion in coal mine. J. China Coal Soc. 2009, 34, 1354–1358. [Google Scholar]
- Liu, J.B.; Yao, L.M.; Zhang, Y.; Chen, J. The calculation method of local pressure drop on variable cross-section circular tube structure. Mach. Des. Manuf. 2016, 5, 83–87. [Google Scholar]
- Gao, K.; Qi, Z.; Jia, J.; Li, S.; Liu, Z.; Liu, Z. Investigation of coupled control of gas accumulation and spontaneous combustion in the goaf of coal mine. AIP Adv. 2020, 10, 045314. [Google Scholar] [CrossRef]
- Rong, G.Y.; Cheng, M.; Sheng, Z.H.; Liu, X.; Zhang, Y.; Wang, J. The behavior of the propagating velocity of rotating detonation waves and counter-rotating shock waves in a hollow combustor. Acta Astronaut. 2022, 200, 371–387. [Google Scholar] [CrossRef]
- Niu, Y.; Shi, B.; Jiang, B. Experimental study of overpressure evolution laws and flame propagation characteristics after methane explosion in transversal pipe networks. Appl. Therm. Eng. 2019, 154, 18–23. [Google Scholar] [CrossRef]
- Salzano, E.; Marra, S.F.; Russo, G.; Lee, J.H.S. Numerical simulation of turbulent gas flames in tube. J. Hazard. Mater. 2019, 95, 233–247. [Google Scholar] [CrossRef] [PubMed]
- Lin, B.-Q.; Guo, C.; Sun, Y.-M.; Zhu, C.-J.; Hong, Y.-D.; Yao, H. Effect of bifurcation on premixed methane-air explosion overpressure in pipes. J. Loss Prev. Process Ind. 2016, 43, 464–470. [Google Scholar] [CrossRef]
- Wang, M.-M.; Wu, Z.-N. Reflection of rightward moving shocks of the first and second families over a steady oblique shock wave. J. Fluid Mech. 2022, 936, A18. [Google Scholar] [CrossRef]
- Jing, G.X.; Guo, S.S.; Wu, Y.L. Investigation on the characteristics of single-phase gas explosion and gas-coal dust coupling explosion in bifurcated tubes. Therm. Sci. 2021, 25, 3595–3605. [Google Scholar] [CrossRef]
- Fang, H.; Xue, H.; Tang, W. Blast wave propagation characteristics in FPSO: Effect of cylindrical obstacles. Ocean Eng. 2023, 274, 114066. [Google Scholar] [CrossRef]
- Qin, J.; Tan, Y.X.; Wang, Z.Q. Experimental the influence of the shape of obstacles in pipelines on gas explosion. Coal Sci. Technol. 2012, 40, 60–62. [Google Scholar]
- Gao, K.; Jia, J.Z.; Liu, Y.H. Study on the characteristics of gas secondary explosion caused by explosion shock wave and high temperature coupling. J. Saf. Sci. Technol. 2016, 12, 35–38. [Google Scholar]
- Lin, Z.D.; Li, R.J.; Liu, E.L. Impact of obstacles on shock wave of gas explosion. J. Saf. Sci. Technol. 2014, 10, 28–32. [Google Scholar]
- Sun, L.; Jiang, B.; Gu, F. Effects of changes in pipe cross-section on the explosion-proof distance and the propagation characteristics of gas explosions. J. Nat. Gas Sci. Eng. 2015, 25, 236–241. [Google Scholar] [CrossRef]
- Zheng, Y.S.; Wang, C. Numerical simulation for the influence of variable cross-section tube on explosion characteristics of methane. Trans. Beijing Inst. Technol. 2009, 29, 947–949. [Google Scholar]
- Yin, H.R.; Weng, C.S. Propagation characteristic of detonation wave in variable cross-section sudden expansion pipe. Aero Weapon. 2016, 6, 66–72. [Google Scholar]
- Jia, Z.-W.; Li, B.; Xu, S.-M. Research on Gas Exploration Shock Wave Spread Law via One-Way Bifurcation Pipeline. Adv. Civ. Eng. 2018, 2018, 5012393. [Google Scholar] [CrossRef]
- Xue, F.; Sun, B.; Jiao, R.; Chen, J. Numerical studies on the acoustic characteristics of the U-shaped corrugated pipes and application investigations. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 233, 1136–1149. [Google Scholar] [CrossRef]
- Frolov, S.; Aksenov, V.; Shamshin, I. Shock wave and detonation propagation through U-bend tubes. Proc. Combust. Inst. 2007, 31, 2421–2428. [Google Scholar] [CrossRef]
- Zhu, C.-J.; Gao, Z.-S.; Lu, X.-M.; Lin, B.-Q.; Guo, C.; Sun, Y.-M. Experimental study on the effect of bifurcations on the flame speed of premixed methane/air explosions in ducts. J. Loss Prev. Process Ind. 2017, 49, 545–550. [Google Scholar] [CrossRef]
- Zhu, C.-J.; Gao, Z.-S.; Lin, B.-Q.; Tan, Z.; Sun, Y.-M.; Ye, Q.; Hong, Y.-D.; Guo, C. Flame acceleration in pipes containing bends of different angles. J. Loss Prev. Process Ind. 2016, 43, 273–279. [Google Scholar] [CrossRef]
- Zhou, A.; Wang, K.; Wang, L.; Du, F.; Li, Z. Numerical simulation for propagation characteristics of shock wave and gas flow induced by outburst intensity. Int. J. Min. Sci. Technol. 2015, 25, 107–112. [Google Scholar] [CrossRef]
- Nicholas, G.; Nicholas, Z. Quantifying model form uncertainty in Reynolds-averaged turbulence models with Bayesian deep neural networks. J. Comput. Phys. 2019, 383, 125–147. [Google Scholar]
- Dastbelaraki, A.; Yaghoubi, M.; Tavakol, M.M.; Rahmatmand, A. Numerical analysis of convection heat transfer from an array of perforated fins using the Reynolds averaged Navier–Stokes equations and large-eddy simulation method. Appl. Math. Model. 2018, 63, 660–687. [Google Scholar] [CrossRef]
- Ciccarelli, G.; Dorofeev, S. Flame acceleration and transition to detonation in ducts. Prog. Energy Combust. Sci. 2008, 34, 499–550. [Google Scholar] [CrossRef]
- Jiang, L.; Liu, H.; Wu, D.; Wang, J.; Xie, M.-Z.; Bai, M. Pore-Scale Simulation of Hydrogen–Air Premixed Combustion Process in Randomly Packed Beds. Energy Fuels 2017, 31, 12791–12803. [Google Scholar] [CrossRef]
- Xiao, H.; Wang, J.; Liu, Z.; Liu, W. A consistent SIMPLE algorithm with extra explicit prediction—SIMPLEPC. Int. J. Heat Mass Transf. 2018, 120, 1255–1265. [Google Scholar] [CrossRef]
- Yang, W.M. A finite volume method for ferrohydrodynamic problems coupled with microscopic magnetization dynamics. Appl. Math. Comput. 2023, 441, 127704. [Google Scholar] [CrossRef]
- Chen, G.F.; Lv, J.L.; Zhang, X.Y. Finite volume element method for nonlinear elliptic equations on quadrilateral meshes. Comput. Math. Appl. 2023, 140, 154–168. [Google Scholar] [CrossRef]
- Chen, X.F.; Chen, M.; Zhang, Q.M.; Yi, C. Experimental investigation of gas explosion microstructure and dynamic characteristics in a semi-vented pipe. J. China Coal Soc. 2010, 35, 246–249. [Google Scholar]
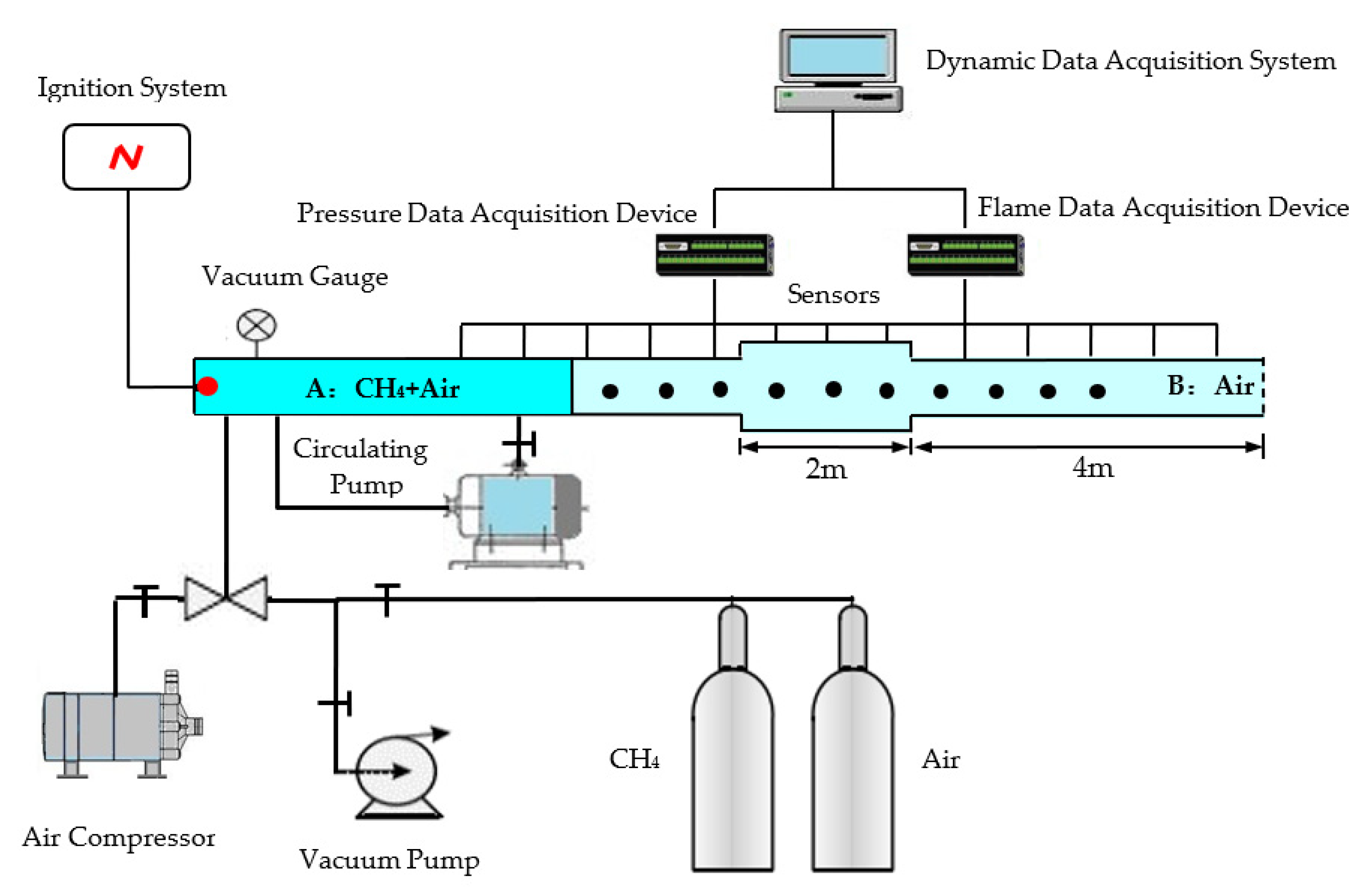

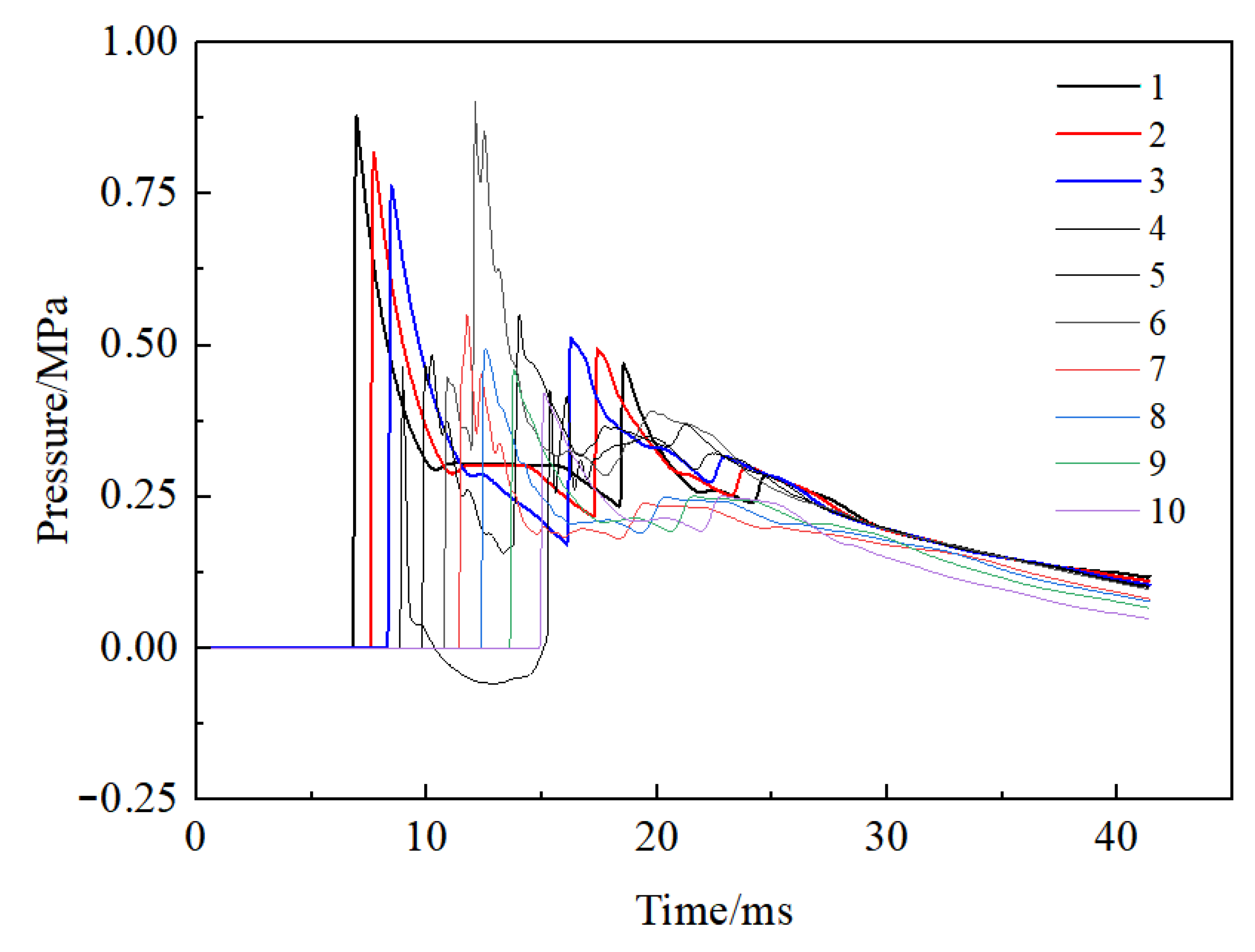
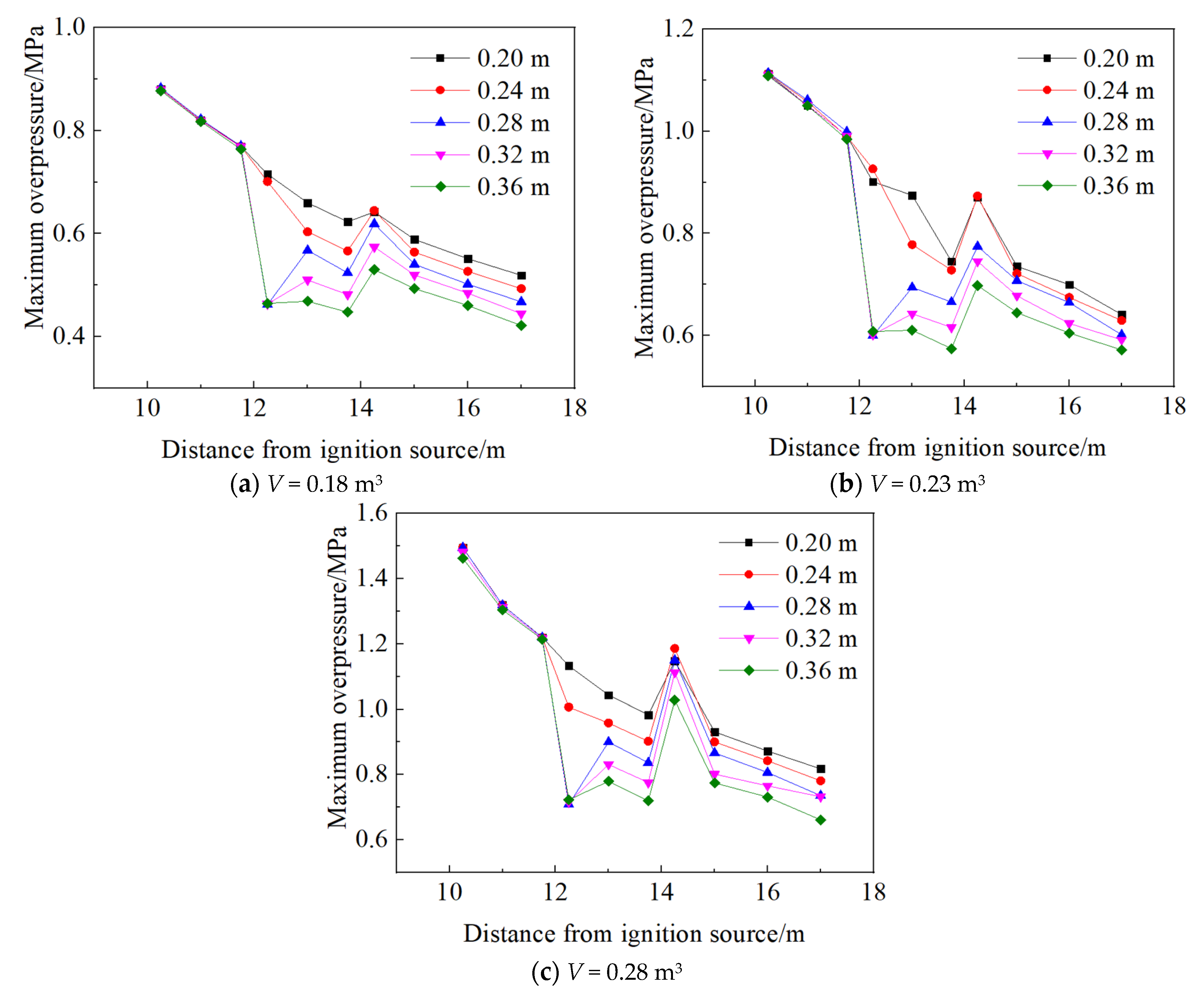
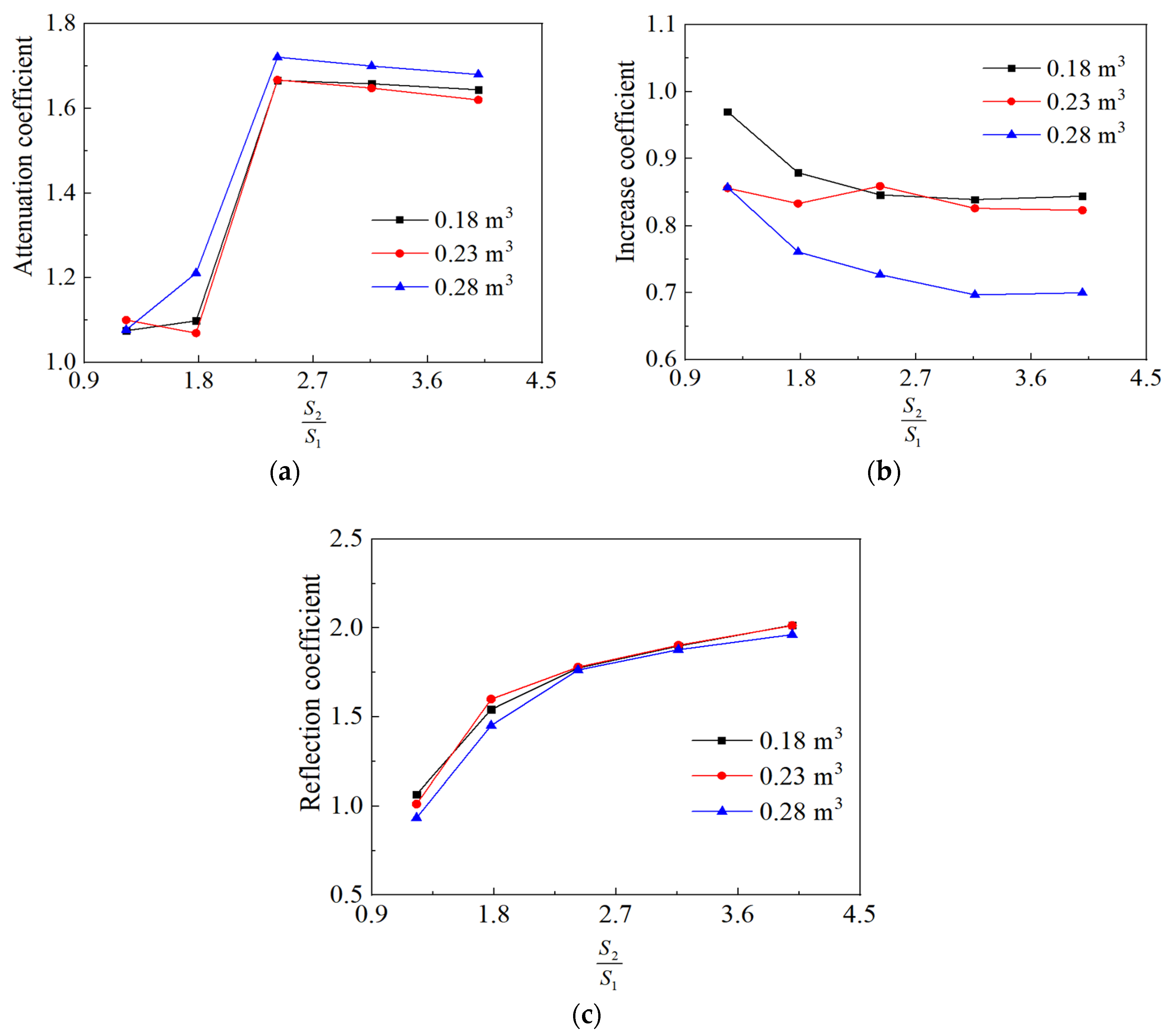


| Measurement Point | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Distance | 10.25 | 11 | 11.75 | 12.25 | 13 | 13.75 | 14.25 | 15 | 16 | 17 |
| Fuel Volume/m3 | Cross-Section Change from Small to Large | Cross-Section Change from Large to Small | |||||||
|---|---|---|---|---|---|---|---|---|---|
| k | Ω | Ψ | |||||||
| 0.18 | 1.23 | 0.7695 | 0.7155 | 1.075 | 0.6230 | 0.6422 | 0.6642 | 0.970 | 1.066 |
| 1.78 | 0.7695 | 0.7011 | 1.098 | 0.5663 | 0.6446 | 0.8735 | 0.879 | 1.542 | |
| 2.42 | 0.7701 | 0.4622 | 1.666 | 0.5239 | 0.6192 | 0.9297 | 0.846 | 1.775 | |
| 3.16 | 0.7685 | 0.4635 | 1.658 | 0.4815 | 0.5741 | 0.9145 | 0.839 | 1.899 | |
| 4.00 | 0.7638 | 0.4646 | 1.644 | 0.4475 | 0.5299 | 0.9020 | 0.844 | 2.016 | |
| 0.23 | 1.23 | 0.9915 | 0.9013 | 1.100 | 0.7452 | 0.8710 | 0.7542 | 0.856 | 1.012 |
| 1.78 | 0.9903 | 0.9263 | 1.069 | 0.7279 | 0.8734 | 1.1648 | 0.833 | 1.600 | |
| 2.42 | 0.9995 | 0.5995 | 1.667 | 0.6655 | 0.7745 | 1.1846 | 0.859 | 1.780 | |
| 3.16 | 0.9910 | 0.6014 | 1.648 | 0.6156 | 0.7451 | 1.1716 | 0.826 | 1.903 | |
| 4.00 | 0.9845 | 0.6078 | 1.620 | 0.5742 | 0.6978 | 1.1565 | 0.823 | 2.014 | |
| 0.28 | 1.23 | 1.2197 | 1.1328 | 1.077 | 0.9831 | 1.1473 | 0.9177 | 0.857 | 0.934 |
| 1.78 | 1.2196 | 1.0067 | 1.211 | 0.9022 | 1.1859 | 1.3102 | 0.761 | 1.452 | |
| 2.42 | 1.2194 | 0.7085 | 1.721 | 0.8361 | 1.1501 | 1.4748 | 0.727 | 1.764 | |
| 3.16 | 1.2166 | 0.7156 | 1.700 | 0.7755 | 1.1123 | 1.4566 | 0.697 | 1.878 | |
| 4.00 | 1.2140 | 0.7226 | 1.680 | 0.7197 | 1.0275 | 1.4125 | 0.700 | 1.963 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, J.; Jiang, B.; Tang, M.; Zhou, L.; Yang, Y. Effects of Abrupt Cross-Section Area Change on theMultiparameter Propagation Characteristics of Premixed Methane–Air Explosion in Pipes. Appl. Sci. 2023, 13, 6372. https://doi.org/10.3390/app13116372
Qiu J, Jiang B, Tang M, Zhou L, Yang Y. Effects of Abrupt Cross-Section Area Change on theMultiparameter Propagation Characteristics of Premixed Methane–Air Explosion in Pipes. Applied Sciences. 2023; 13(11):6372. https://doi.org/10.3390/app13116372
Chicago/Turabian StyleQiu, Jinwei, Bingyou Jiang, Mingyun Tang, Liang Zhou, and Yingdi Yang. 2023. "Effects of Abrupt Cross-Section Area Change on theMultiparameter Propagation Characteristics of Premixed Methane–Air Explosion in Pipes" Applied Sciences 13, no. 11: 6372. https://doi.org/10.3390/app13116372
APA StyleQiu, J., Jiang, B., Tang, M., Zhou, L., & Yang, Y. (2023). Effects of Abrupt Cross-Section Area Change on theMultiparameter Propagation Characteristics of Premixed Methane–Air Explosion in Pipes. Applied Sciences, 13(11), 6372. https://doi.org/10.3390/app13116372





