A Special Structural Based Weighted Network Approach for the Analysis of Protein Complexes
Abstract
:1. Introduction
2. Preliminaries
3. Methods
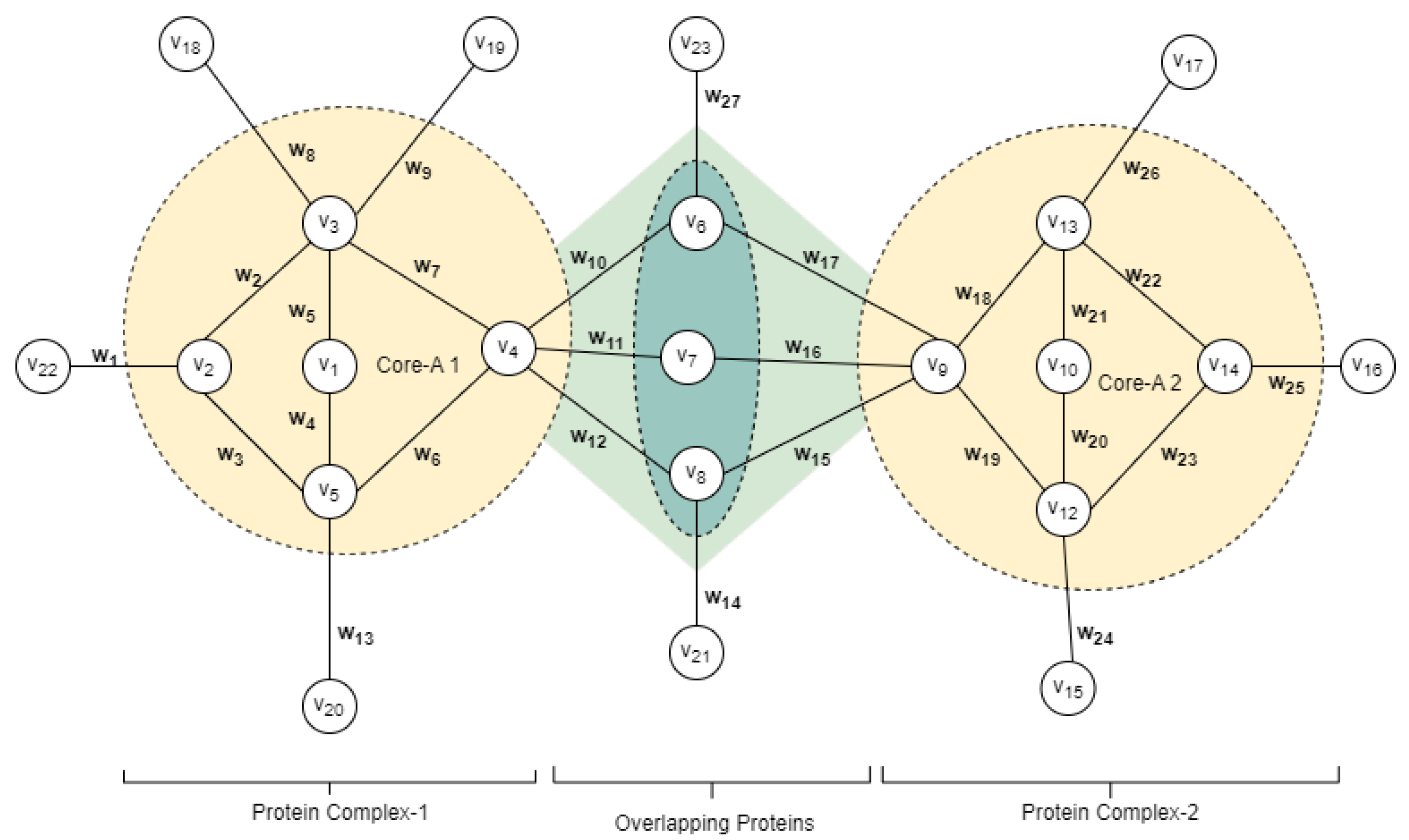
3.1. Building Weighted PPI Network
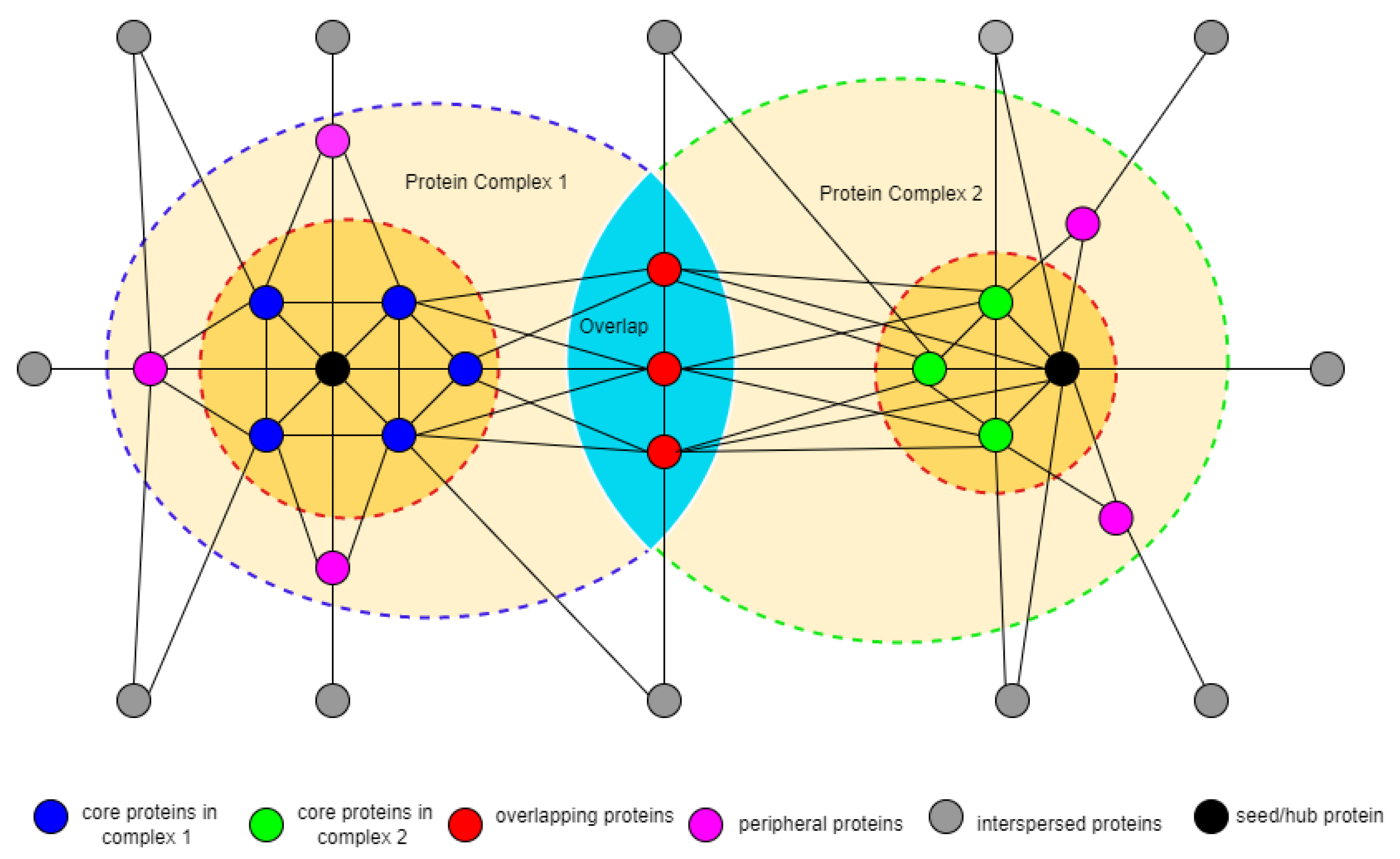
3.2. Identifying Overlapping Structures
3.3. Identifying Seed Proteins
3.4. Identifying Local Modularity Structures
3.5. Identifying Complex Core Structure
3.6. Detection of Attachment Proteins to Complex Core
3.6.1. Overlapping Attachment Proteins
3.6.2. Peripheral Attachment Protein
3.7. Protein Core Attachment and Protein Complex Formation
4. Datasets and Evaluation Criteria
4.1. Experimental PPI Datasets
4.2. Evaluation Criteria
4.2.1. Computation of Recall, Precision and F-Measure
4.2.2. Coverage Rate
4.2.3. Maximum Matching Ratio
4.2.4. Separation and ACC
4.2.5. Functional Enrichment Analysis
5. Results and Discussion
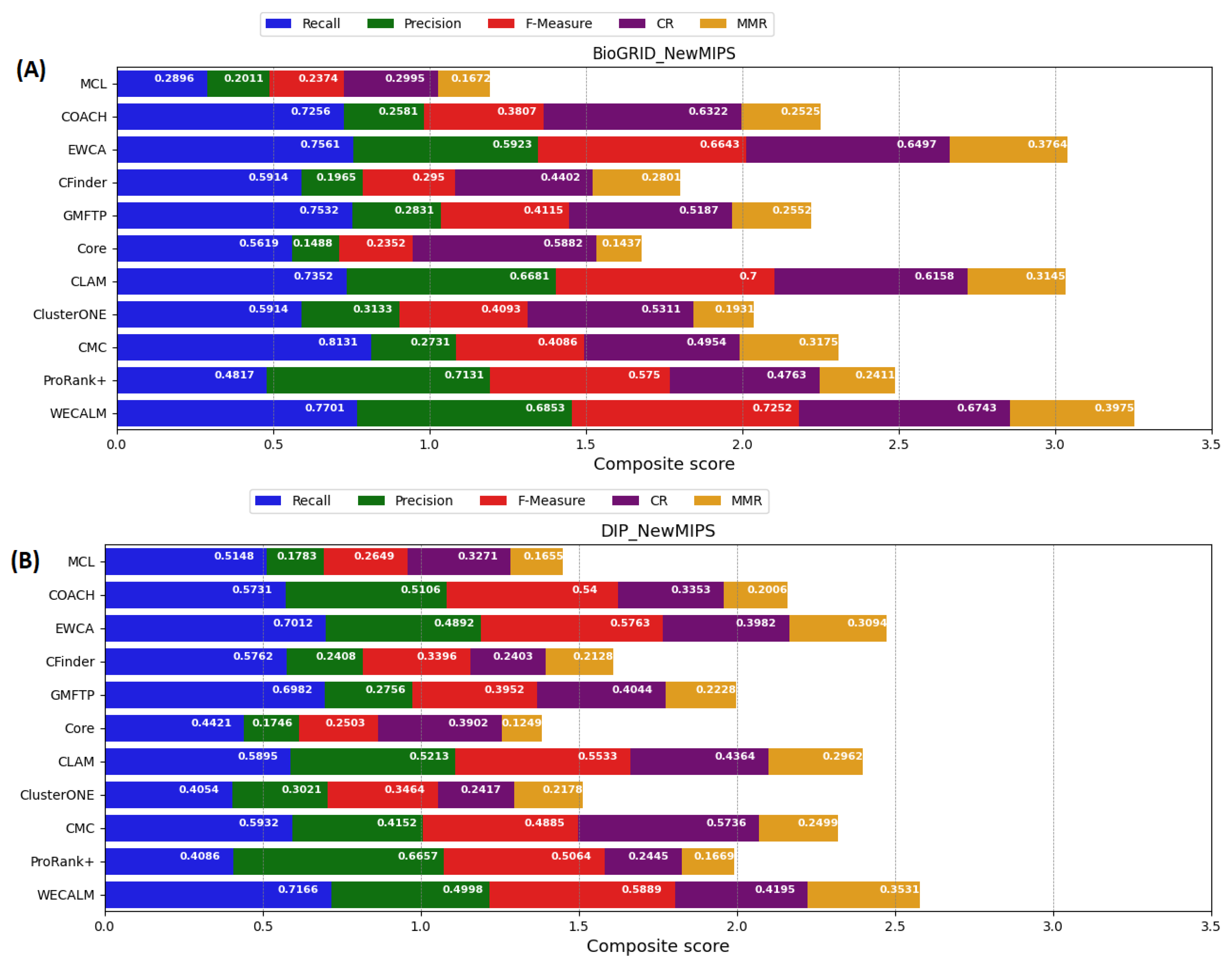
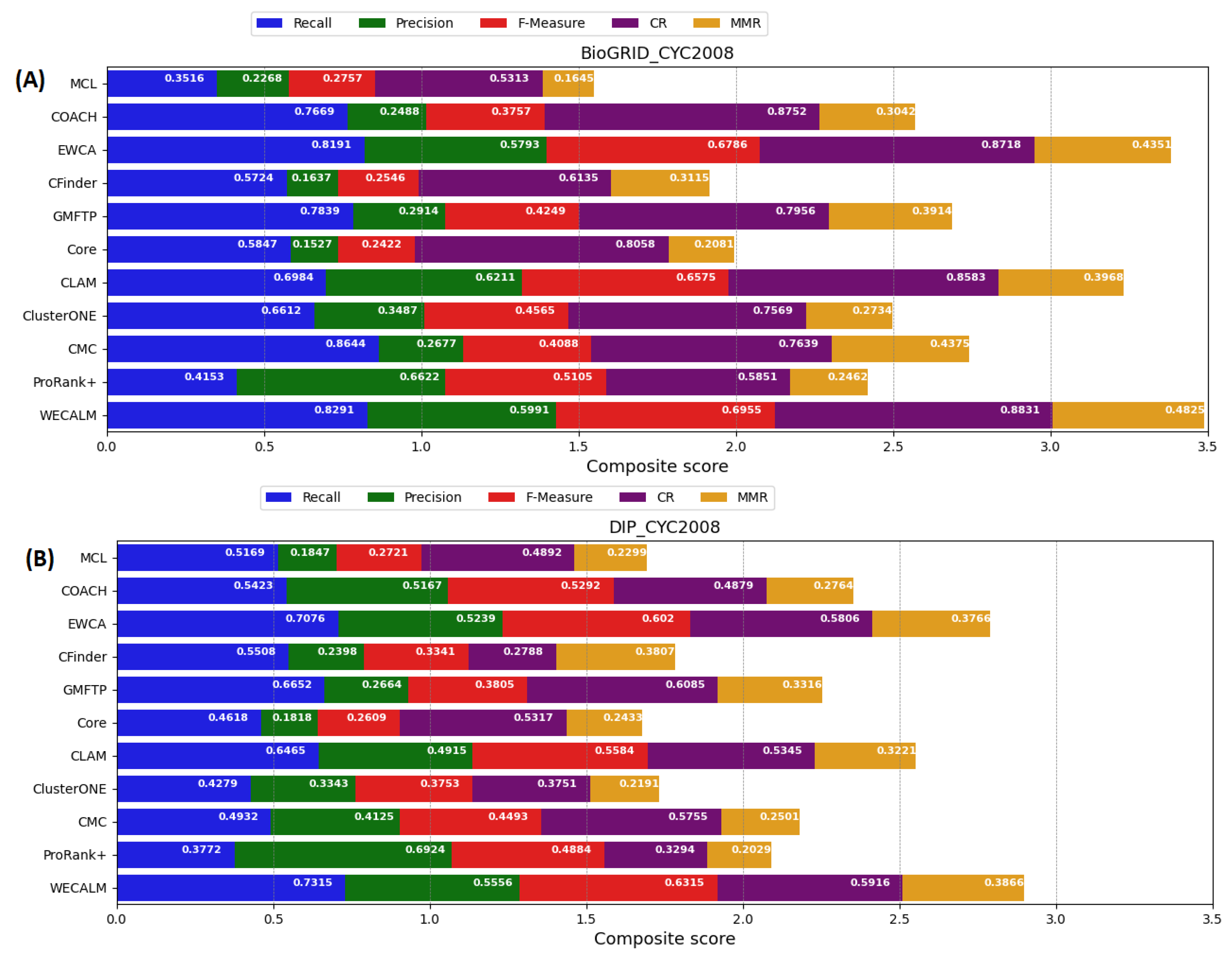
5.1. Performance Comparison of WECALM with Other Algorithm
5.1.1. Performance on NewMIPS Complexes
5.1.2. Performance on CYC2008 Complexes
5.2. Parametric Selection
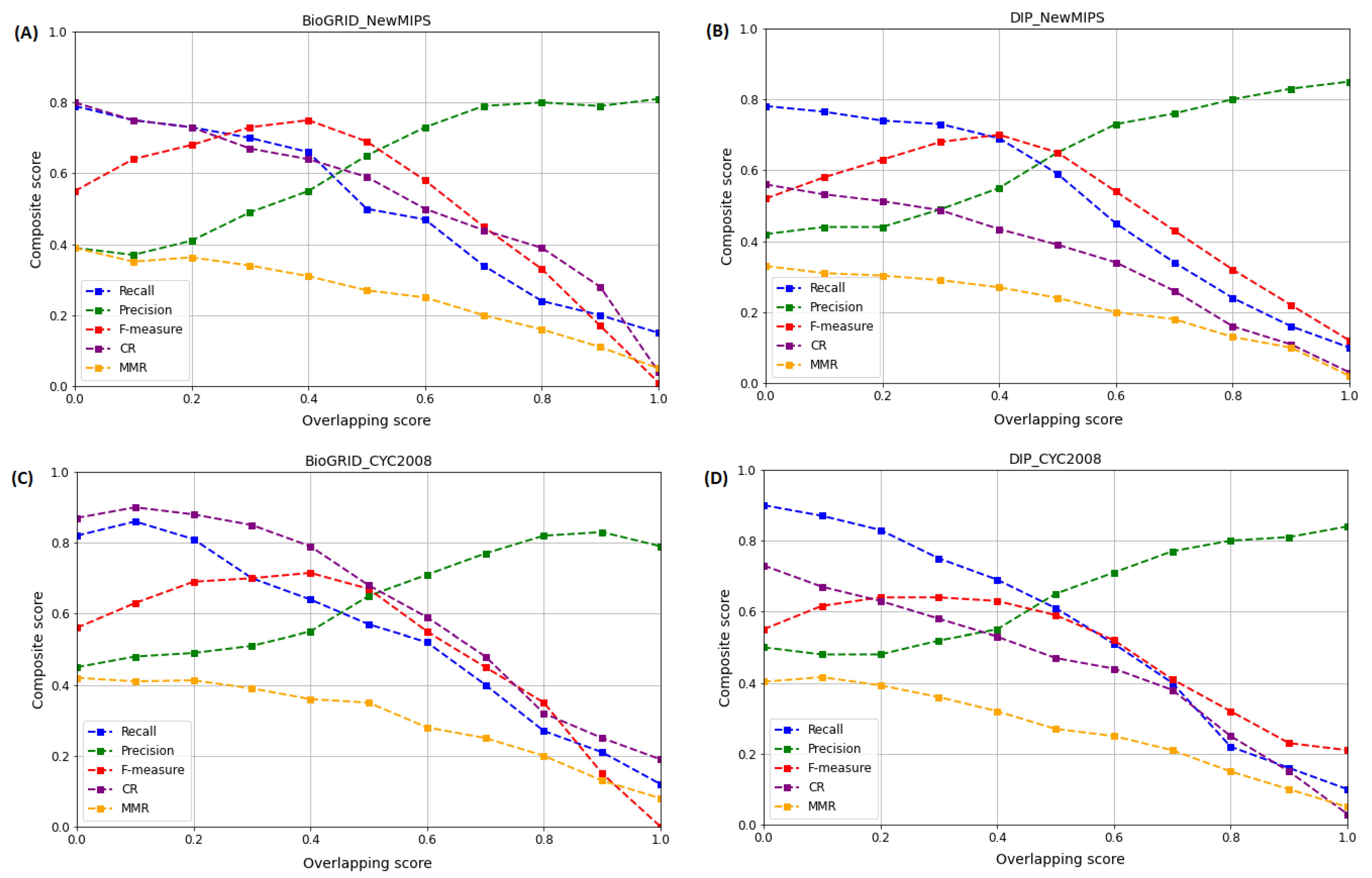
5.2.1. Effect of Varying on the Performance of WECALM
5.2.2. Effect of Varying on the Performance of WECALM
5.2.3. Effect of Varying on the Performance of WECALM
5.3. Computational Complexity Analysis
5.4. Function Enrichment Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Performance Comparison of WECALM with the Other Algorithms
Performance Comparison
| Dataset | Algorithm | Recall | Precision | F-Measure | CR | MMR | Sep | ACC |
|---|---|---|---|---|---|---|---|---|
| BioGRID | MCL | 0.2896 | 0.2011 | 0.2374 | 0.2995 | 0.1672 | 0.2679 | 0.2167 |
| COACH | 0.7256 | 0.2581 | 0.3808 | 0.6322 | 0.2525 | 0.5532 | 0.2777 | |
| EWCA | 0.7561 | 0.5923 | 0.6643 | 0.6497 | 0.3764 | 0.6149 | 0.5221 | |
| CFinder | 0.5914 | 0.1965 | 0.2950 | 0.4402 | 0.2801 | 0.3912 | 0.2131 | |
| GMFTP | 0.7532 | 0.2831 | 0.4115 | 0.5187 | 0.2552 | 0.5174 | 0.4522 | |
| Core | 0.5619 | 0.1488 | 0.2352 | 0.5882 | 0.1437 | 0.4575 | 0.3456 | |
| CLAM | 0.7352 | 0.6681 | 0.7001 | 0.6158 | 0.3145 | 0.6478 | 0.5576 | |
| ClusterONE | 0.5914 | 0.3133 | 0.4096 | 0.5311 | 0.1931 | 0.4851 | 0.2951 | |
| CMC | 0.5131 | 0.2731 | 0.3565 | 0.4954 | 0.3175 | 0.3976 | 0.5313 | |
| ProRank+ | 0.4817 | 0.7131 | 0.5750 | 0.4763 | 0.2411 | 0.6276 | 0.5119 | |
| WECALM | 0.7701 | 0.6853 | 0.7252 | 0.6743 | 0.3975 | 0.7765 | 0.6015 | |
| DIP | MCL | 0.5148 | 0.1783 | 0.2649 | 0.3271 | 0.1655 | 0.2927 | 0.1655 |
| COACH | 0.5731 | 0.5106 | 0.5400 | 0.3353 | 0.2006 | 0.3833 | 0.2917 | |
| EWCA | 0.7012 | 0.4892 | 0.5763 | 0.3982 | 0.3094 | 0.6198 | 0.5994 | |
| CFinder | 0.5762 | 0.2408 | 0.3397 | 0.2403 | 0.2128 | 0.3543 | 0.3613 | |
| GMFTP | 0.6982 | 0.2756 | 0.3952 | 0.4044 | 0.2228 | 0.5548 | 0.4229 | |
| Core | 0.4421 | 0.1746 | 0.2503 | 0.3902 | 0.1249 | 0.5439 | 0.4374 | |
| CLAM | 0.5895 | 0.5213 | 0.5533 | 0.4364 | 0.2962 | 0.6625 | 0.5456 | |
| ClusterONE | 0.4054 | 0.3021 | 0.3462 | 0.2417 | 0.2178 | 0.3041 | 0.3185 | |
| CMC | 0.5932 | 0.4152 | 0.4885 | 0.5736 | 0.2499 | 0.3793 | 0.3151 | |
| ProRank+ | 0.4086 | 0.6657 | 0.5064 | 0.2445 | 0.1669 | 0.6451 | 0.5567 | |
| WECALM | 0.7166 | 0.4998 | 0.5889 | 0.4195 | 0.3531 | 0.8195 | 0.6317 |
| Dataset | Algorithm | Recall | Precision | F-Measure | CR | MMR | Sep | ACC |
|---|---|---|---|---|---|---|---|---|
| BioGRID | MCL | 0.3516 | 0.2268 | 0.2757 | 0.5313 | 0.1645 | 0.3831 | 0.2549 |
| COACH | 0.7669 | 0.2488 | 0.3757 | 0.8752 | 0.3042 | 0.5375 | 0.4117 | |
| EWCA | 0.8191 | 0.5793 | 0.6786 | 0.8718 | 0.4351 | 0.6578 | 0.6035 | |
| CFinder | 0.5724 | 0.1637 | 0.2546 | 0.6135 | 0.3115 | 0.5634 | 0.4215 | |
| GMFTP | 0.7839 | 0.2914 | 0.4249 | 0.7956 | 0.3914 | 0.6192 | 0.4591 | |
| Core | 0.5847 | 0.1527 | 0.2422 | 0.8058 | 0.2081 | 0.4126 | 0.2742 | |
| CLAM | 0.6984 | 0.6211 | 0.6575 | 0.8583 | 0.3968 | 0.7293 | 0.7153 | |
| ClusterONE | 0.6612 | 0.3487 | 0.4566 | 0.7569 | 0.2734 | 0.5162 | 0.3574 | |
| CMC | 0.4644 | 0.2677 | 0.3396 | 0.7639 | 0.3375 | 0.4611 | 0.4375 | |
| ProRank+ | 0.4153 | 0.6622 | 0.5105 | 0.5851 | 0.2462 | 0.6105 | 0.5979 | |
| WECALM | 0.8291 | 0.5991 | 0.6956 | 0.8831 | 0.4825 | 0.7825 | 0.6983 | |
| DIP | MCL | 0.5169 | 0.1847 | 0.2722 | 0.4892 | 0.2299 | 0.3519 | 0.3125 |
| COACH | 0.5423 | 0.5167 | 0.5292 | 0.4879 | 0.2764 | 0.4272 | 0.3967 | |
| EWCA | 0.7076 | 0.5239 | 0.6020 | 0.5806 | 0.3766 | 0.6436 | 0.5527 | |
| CFinder | 0.5508 | 0.2398 | 0.3341 | 0.2788 | 0.3807 | 0.3758 | 0.4187 | |
| GMFTP | 0.6652 | 0.2664 | 0.3804 | 0.6085 | 0.3316 | 0.6235 | 0.4136 | |
| Core | 0.4618 | 0.1818 | 0.2609 | 0.5317 | 0.2433 | 0.3351 | 0.3519 | |
| CLAM | 0.6465 | 0.4915 | 0.5584 | 0.5345 | 0.3221 | 0.6833 | 0.6721 | |
| ClusterONE | 0.4279 | 0.3343 | 0.3754 | 0.3751 | 0.2191 | 0.3957 | 0.3519 | |
| CMC | 0.4932 | 0.4125 | 0.4493 | 0.5755 | 0.2501 | 0.4576 | 0.3251 | |
| ProRank+ | 0.3772 | 0.6924 | 0.4884 | 0.3294 | 0.2029 | 0.5929 | 0.5817 | |
| WECALM | 0.7315 | 0.5556 | 0.6315 | 0.5916 | 0.3866 | 0.7596 | 0.6569 |
Appendix B. A Function Enrichment Analysis
Appendix B.1. A Function Enrichment Analysis on BioGRID Complex
| Complex ID | Cluster Frequency | Genome Frequency | p-Value (BP) | FDR | FALSE Positive | Gene Ontology Term |
|---|---|---|---|---|---|---|
| 1 | 9 of 12 genes,75.0% | 44 of 7166 genes, 0.6% | 0.0000 | 0.0000 | positive regulation of transcription elongation by RNA polymerase II | |
| 9 of 12 genes, 75.0% | 47 of 7166 genes, 0.7% | 0.0000 | 0.0000 | regulation of transcription elongation by RNA polymerase II | ||
| 9 of 12 genes,75.0% | 52 of 7166 genes, 0.7% | 0.0000 | 0.0000 | positive regulation of DNA-templated transcription, elongation | ||
| 9 of 12 genes,75.0% | 55 of 7166 genes, 0.8% | 0.0000 | 0.0000 | regulation of DNA-templated transcription elongation | ||
| 9 of 12 genes, 75.0% | 96 of 7166 genes, 1.3% | 0.0000 | 0.0000 | transcription elongation by RNA polymerase II | ||
| 2 | 12 of 13 genes, 92.3% | 936 of 7166 genes, 13.1% | 0.0000 | 0.0000 | amide metabolic process | |
| 12 of 13 genes,92.3% | 1348 of 7166 genes,18.8% | 0.0000 | 0.0000 | organonitrogen compound biosynthetic process | ||
| 12 of 13 genes, 92.3% | 1816 of 7166 genes, 25.3% | 0.0000 | 0.0000 | cellular nitrogen compound biosynthetic process | ||
| 12 of 13 genes, 92.3% | 2109 of 7166 genes, 29.4% | 0.0000 | 0.0000 | cellular biosynthetic process | ||
| 12 of 13 genes, 92.3% | 2725 of 7166 genes, 38.0% | 0.0000 | 0.0000 | cellular nitrogen compound metabolic process | ||
| 3 | 11 of 12 genes, 91.7% | 367 of 7166 genes, 5.1% | 0.0000 | 0.0000 | rRNA processing | |
| 11 of 12 genes, 91.7% | 423 of 7166 genes, 5.9% | 0.0000 | 0.0000 | rRNA metabolic process | ||
| 11 of 12 genes, 91.7% | 482 of 7166 genes, 6.7% | 0.0000 | 0.0000 | ribosome biogenesis | ||
| 11 of 12 genes, 91.7% | 492 of 7166 genes, 6.9% | 0.0000 | 0.0000 | ncRNA processing | ||
| 11 of 12 genes, 91.7% | 2159 of 7166 genes, 30.1% | 0.0000 | 0.0000 | gene expression | ||
| 4 | 13 of 14 genes, 92.9% | 204 of 7166 genes, 2.8% | 0.0000 | 0.0000 | cytoplasmic translation | |
| 13 of 14 genes, 92.9% | 820 of 7166 genes, 11.4% | 0.0000 | 0.0000 | translation | ||
| 13 of 14 genes, 92.9% | 824 of 7166 genes, 11.5% | 0.0000 | 0.0000 | peptide biosynthetic process | ||
| 13 of 14 genes, 92.9% | 841 of 7166 genes, 11.7% | 0.0000 | 0.0000 | peptide metabolic process | ||
| 13 of 14 genes, 92.9% | 879 of 7166 genes, 12.3% | 0.0000 | 0.0000 | amide biosynthetic process | ||
| 5 | 12 of 13 genes, 92.3% | 204 of 7166 genes, 2.8% | 0.0000 | 0.0000 | ribosomal large subunit biogenesis | |
| 12 of 13 genes, 92.3% | 820 of 7166 genes, 11.4% | 0.0000 | 0.0000 | biosynthetic process | ||
| 12 of 13 genes, 92.3% | 824 of 7166 genes, 11.5% | 0.0000 | 0.0000 | peptide biosynthetic process | ||
| 12 of 13 genes, 92.3% | 841 of 7166 genes, 11.7% | 0.0000 | 0.0000 | ribonucleoprotein complex biogenesis | ||
| 12 of 13 genes, 92.3% | 879 of 7166 genes, 12.3% | 0.0000 | 0.0000 | cellular biosynthetic process |
Appendix B.2. A Function Enrichment Analysis on DIP Complex
| Complex ID | Cluster Frequency | Genome Frequency | p-Value | FDR | FALSE Positive | Gene Ontology Term |
|---|---|---|---|---|---|---|
| 1 | 11 of 12 genes, 91.7% | 125 of 7166 genes, 1.7% | 0.0000 | 0.0000 | ribosomal large subunit biogenesis | |
| 11 of 12 genes, 91.7% | 482 of 7166 genes, 6.7% | 0.0000 | 0.0000 | ribosome biogenesis | ||
| 11 of 12 genes, 91.7% | 576 of 7166 genes, 8.0% | 0.0000 | 0.0000 | ribonucleoprotein complex biogenesis | ||
| 11 of 12 genes, 91.7% | 1272 of 7166 genes, 17.8% | 0.0000 | 0.0000 | cellular component biogenesis | ||
| 11 of 12 genes, 91.7% | 2424 of 7166 genes, 33.8% | 0.0008 | 0.0000 | cellular component organization or biogenesis | ||
| 2 | 3 of 4 genes, 75.0% | 56 of 7166 genes, 0.8% | 0.0000 | 0.0000 | purine ribonucleoside triphosphate metabolic process | |
| 3 of 4 genes, 75.0% | 58 of 7166 genes, 0.8% | 0.0000 | 0.0000 | purine nucleoside triphosphate metabolic process | ||
| 3 of 4 genes, 75.0% | 119 of 7166 genes, 1.7% | 0.0000 | 0.0000 | nucleotide biosynthetic process | ||
| 3 of 4 genes, 75.0% | 121 of 7166 genes, 1.7% | 0.0000 | 0.0000 | nucleoside phosphate biosynthetic process | ||
| 3 of 4 genes, 75.0% | 125 of 7166 genes, 1.7% | 0.0000 | 0.0000 | ribonucleotide metabolic process | ||
| 3 | 9 of 10 genes, 90.0% | 20 of 7166 genes, 0.3% | 0.0000 | 0.0000 | ATP biosynthetic process | |
| 9 of 10 genes, 90.0% | 20 of 7166 genes, 0.3% | 0.0000 | 0.0000 | proton motive force-driven ATP synthesis | ||
| 9 of 10 genes, 90.0% | 24 of 7166 genes, 0.3% | 0.0000 | 0.0000 | purine nucleoside triphosphate biosynthetic process | ||
| 9 of 10 genes, 90.0% | 24 of 7166 genes, 0.3% | 0.0000 | 0.0000 | purine ribonucleoside triphosphate biosynthetic process | ||
| 9 of 10 genes, 90.0% | 30 of 7166 genes, 0.4% | 0.0000 | 0.0000 | ribonucleoside triphosphate biosynthetic process | ||
| 4 | 10 of 11 genes, 90.9% | 20 of 7166 genes, 0.3% | 0.0000 | 0.0000 | proton transmembrane transport | |
| 10 of 11 genes, 90.9% | 20 of 7166 genes, 0.3% | 0.0000 | 0.0000 | purine ribonucleotide metabolic process | ||
| 10 of 11 genes, 90.9% | 24 of 7166 genes, 0.3% | 0.0000 | 0.0000 | nucleotide biosynthetic process | ||
| 10 of 11 genes, 90.9% | 24 of 7166 genes, 0.3% | 0.0000 | 0.0000 | nucleoside phosphate biosynthetic process | ||
| 10 of 11 genes, 90.9% | 30 of 7166 genes, 0.4% | 0.0000 | 0.0000 | ribonucleotide metabolic process | ||
| 5 | 9 of 10 genes, 90.0% | 444 of 7166 genes, 6.2% | 0.0000 | 0.0000 | intracellular protein transport | |
| 9 of 10 genes, 90.0% | 449 of 7166 genes, 6.3% | 0.0000 | 0.0000 | vesicle-mediated transport | ||
| 9 of 10 genes, 90.0% | 630 of 7166 genes, 8.8% | 0.0000 | 0.0000 | protein transport | ||
| 9 of 10 genes, 90.0% | 651 of 7166 genes, 9.1% | 0.0000 | 0.0000 | establishment of protein localization | ||
| 9 of 10 genes, 90.0% | 742 of 7166 genes, 10.4% | 0.0000 | 0.0000 | intracellular transport |
Appendix B.3. Detected Protein Complexes with 100% Cluster Frequency
| Dataset | Complex ID | Cluster Frequency | Genome Frequency | p-Value (BP) | FDR | FALSE Positive | Gene Ontology Term |
|---|---|---|---|---|---|---|---|
| BioGRID | 1 | 12 of 12 genes, 100.0% | 122 of 7166 genes, 1.7% | 0.0000 | 0.0000 | mRNA splicing, via spliceosome | |
| 2 | 42 of 42 genes, 100.0% | 123 of 7166 genes, 1.7% | 0.0000 | 0.0000 | RNA splicing, | ||
| 3 | 10 of 10 genes, 100.0% | 10 of 7166 genes, 0.1% | 0.0000 | 0.0000 | spliceosomal tri-snRNP complex assembly | ||
| 4 | 19 of 19 genes, 100.0% | 132 of 7166 genes, 1.8% | 0.0000 | 0.0000 | RNA splicing, via transesterification reactions | ||
| 5 | 36 of 36 genes, 100.0% | 157 of 7166 genes, 2.2% | 0.0000 | 0.0000 | RNA splicing | ||
| 6 | 11 of 11 genes, 100.0% | 20 of 7166 genes, 0.3% | 0.0000 | 0.0000 | spliceosomal snRNP assembly | ||
| 7 | 10 of 10 genes, 100.0% | 229 of 7166 genes, 3.2% | 0.0000 | 0.0000 | mRNA processing | ||
| 8 | 17 of 17 genes, 100.0% | 350 of 7166 genes, 4.9% | 0.0000 | 0.0200 | mRNA metabolic process | ||
| 9 | 42 of 42 genes, 100.0% | 347 of 7166 genes, 4.8% | 0.0000 | 0.0000 | DNA-directed 5’-3’ RNA polymerase activity | ||
| 10 | 23 of 23 genes, 100.0% | 34 of 7166 genes, 0.5% | 0.0000 | 0.0000 | 5’-3’ RNA polymerase activity | ||
| DIP | 1 | 19 of 19 genes, 100.0% | 62 of 7166 genes, 0.9% | 0.0000 | 0.0000 | nucleotide-excision repair | |
| 2 | 39 of 39 genes, 100.0% | 234 of 7166 genes, 3.3% | 0.0000 | 0.0000 | ubiquitin-dependent protein catabolic process | ||
| 3 | 36 of 36 genes, 100.0% | 240 of 7166 genes, 3.3% | 0.0000 | 0.0000 | modification-dependent protein catabolic process | ||
| 4 | 10 of 10 genes, 100.0% | 262 of 7166 genes, 3.7% | 0.0000 | 0.0000 | modification-dependent macromolecule catabolic process | ||
| 5 | 14 of 14 genes, 100.0% | 264 of 7166 genes, 3.7% | 0.0000 | 0.0000 | proteolysis involved in protein catabolic process | ||
| 6 | 13 of 13 genes, 100.0% | 293 of 7166 genes, 4.1% | 0.0000 | 0.0000 | protein catabolic process | ||
| 7 | 15 of 15 genes, 100.0% | 309 of 7166 genes, 4.3% | 0.0000 | 0.0000 | DNA repair | ||
| 8 | 12 of 12 genes, 100.0% | 350 of 7166 genes, 4.9% | 0.0000 | 0.0000 | cellular response to DNA damage stimulus | ||
| 9 | 31 of 31 genes, 100.0% | 407 of 7166 genes, 5.7% | 0.0000 | 0.0000 | organonitrogen compound catabolic process | ||
| 10 | 17 of 17 genes, 100.0% | 416 of 7166 genes, 5.8% | 0.0000 | 0.0000 | proteolysis |
References
- Almeida, R.M.; Dell’Acqua, S.; Krippahl, L.; Moura, J.J.; Pauleta, S.R. Predicting Protein–Protein interactions using bigger: Case studies. Molecules 2016, 21, 1037. [Google Scholar] [CrossRef] [PubMed]
- Bustamam, A.; Siswantining, T.; Kaloka, T.P.; Swasti, O. Application of bimax, pols, and lcm-mbc to find bicluster on interactions protein between hiv-1 and human. Austrian J. Stat. 2020, 49, 1–18. [Google Scholar] [CrossRef]
- Tripathi, S.; Moutari, S.; Dehmer, M.; Emmert-Streib, F. Comparison of module detection algorithms in protein networks and investigation of the biological meaning of predicted modules. BMC Bioinform. 2016, 17, 129. [Google Scholar] [CrossRef] [PubMed]
- Li, X.L.; Ng, S.K. Biological Data Mining in Protein Interaction Networks; IGI Global: Hershey, PA, USA, 2009. [Google Scholar]
- Wu, D.; Hu, X. Topological analysis and sub-network mining of Protein–Protein interactions. In Research and Trends in Data Mining Technologies and Applications; IGI Global: Hershey, PA, USA, 2007; pp. 209–240. [Google Scholar]
- Larsen, P.E.; Collart, F.; Dai, Y. Incorporating network topology improves prediction of protein interaction networks from transcriptomic data. Int. J. Knowl. Discov. Bioinform. (IJKDB) 2010, 1, 1–19. [Google Scholar] [CrossRef]
- Ahnert, S.E.; Marsh, J.A.; Hernández, H.; Robinson, C.V.; Teichmann, S.A. Principles of assembly reveal a periodic table of protein complexes. Science 2015, 350, aaa2245. [Google Scholar] [CrossRef]
- Tong, A.H.Y.; Drees, B.; Nardelli, G.; Bader, G.D.; Brannetti, B.; Castagnoli, L.; Evangelista, M.; Ferracuti, S.; Nelson, B.; Paoluzi, S.; et al. A combined experimental and computational strategy to define protein interaction networks for peptide recognition modules. Science 2002, 295, 321–324. [Google Scholar] [CrossRef]
- Shen, X.; Yi, L.; Jiang, X.; Zhao, Y.; Hu, X.; He, T.; Yang, J. Neighbor affinity based algorithm for discovering temporal protein complex from dynamic PPI network. Methods 2016, 110, 90–96. [Google Scholar] [CrossRef]
- Zhang, X.F.; Dai, D.Q.; Ou-Yang, L.; Yan, H. Detecting overlapping protein complexes based on a generative model with functional and topological properties. BMC Bioinform. 2014, 15, 186. [Google Scholar] [CrossRef]
- Shen, X.; Zhou, J.; Yi, L.; Hu, X.; He, T.; Yang, J. Identifying protein complexes based on brainstorming strategy. Methods 2016, 110, 44–53. [Google Scholar] [CrossRef]
- Liu, G.; Wong, L.; Chua, H.N. Complex discovery from weighted PPI networks. Bioinformatics 2009, 25, 1891–1897. [Google Scholar] [CrossRef]
- Adamcsek, B.; Palla, G.; Farkas, I.J.; Derényi, I.; Vicsek, T. CFinder: Locating cliques and overlapping modules in biological networks. Bioinformatics 2006, 22, 1021–1023. [Google Scholar] [CrossRef]
- Van Dongen, S.M. Graph clustering by Flow Simulation. Ph.D. Thesis, University of Utrecht, Utrecht, The Netherlands, 2000. [Google Scholar]
- Vlasblom, J.; Wodak, S.J. Markov clustering versus affinity propagation for the partitioning of protein interaction graphs. BMC Bioinform. 2009, 10, 99. [Google Scholar] [CrossRef]
- Ochieng, P.J.; Kusuma, W.; Haryanto, T. Detection of protein complex from Protein–Protein interaction network using Markov clustering. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2017; Volume 835, p. 012001. [Google Scholar]
- Wang, R.; Liu, G.; Wang, C. Identifying protein complexes based on an edge weight algorithm and core-attachment structure. BMC Bioinform. 2019, 20, 471. [Google Scholar] [CrossRef]
- Xie, D.; Yi, Y.; Zhou, J.; Li, X.; Wu, H. A novel temporal protein complexes identification framework based on density–Distance and heuristic algorithm. Neural Comput. Appl. 2019, 31, 4693–4701. [Google Scholar] [CrossRef]
- Jiang, P.; Singh, M. SPICi: A fast clustering algorithm for large biological networks. Bioinformatics 2010, 26, 1105–1111. [Google Scholar] [CrossRef]
- Nepusz, T.; Yu, H.; Paccanaro, A. Detecting overlapping protein complexes in Protein–Protein interaction networks. Nat. Methods 2012, 9, 471–472. [Google Scholar] [CrossRef]
- Wang, R.; Liu, G.; Wang, C.; Su, L.; Sun, L. Predicting overlapping protein complexes based on core-attachment and a local modularity structure. BMC Bioinform. 2018, 19, 305. [Google Scholar] [CrossRef]
- Wu, M.; Li, X.; Kwoh, C.K.; Ng, S.K. A core-attachment based method to detect protein complexes in PPI networks. BMC Bioinform. 2009, 10, 169. [Google Scholar] [CrossRef]
- Leung, H.C.; Xiang, Q.; Yiu, S.M.; Chin, F.Y. Predicting protein complexes from PPI data: A core-attachment approach. J. Comput. Biol. 2009, 16, 133–144. [Google Scholar] [CrossRef]
- Hanna, E.M.; Zaki, N. Detecting protein complexes in protein interaction networks using a ranking algorithm with a refined merging procedure. BMC Bioinform. 2014, 15, 204. [Google Scholar] [CrossRef]
- Palla, G.; Derényi, I.; Farkas, I.; Vicsek, T. Uncovering the overlapping community structure of complex networks in nature and society. Nature 2005, 435, 814–818. [Google Scholar] [CrossRef] [PubMed]
- Karp, R.M. Reducibility among combinatorial problems. In Proceedings of the Complexity of Computer Computations: Proceedings of a symposium on the Complexity of Computer Computations, New York, NY, USA, 20–22 March 1972; Springer: Berlin/Heidelberg, Germany, 1972; pp. 85–103. [Google Scholar]
- Gens, G.V.; Levner, E.V. Computational complexity of approximation algorithms for combinatorial problems. In Proceedings of the Mathematical Foundations of Computer Science 1979: Proceedings, 8th Symposium, Olomouc, Czechoslovakia, 3–7 September 1979; Springer: Berlin/Heidelberg, Germany, 1979; pp. 292–300. [Google Scholar]
- Spirin, V.; Mirny, L.A. Protein complexes and functional modules in molecular networks. Proc. Natl. Acad. Sci. USA 2003, 100, 12123–12128. [Google Scholar] [CrossRef] [PubMed]
- Bader, S.; Kühner, S.; Gavin, A.C. Interaction networks for systems biology. FEBS Lett. 2008, 582, 1220–1224. [Google Scholar] [CrossRef] [PubMed]
- Zaki, N.; Efimov, D.; Berengueres, J. Protein complex detection using interaction reliability assessment and weighted clustering coefficient. BMC Bioinform. 2013, 14, 163. [Google Scholar] [CrossRef]
- Cao, B.; Luo, J.; Liang, C.; Wang, S.; Ding, P. Pce-fr: A novel method for identifying overlapping protein complexes in weighted Protein–Protein interaction networks using pseudo-clique extension based on fuzzy relation. IEEE Trans. Nanobiosci. 2016, 15, 728–738. [Google Scholar] [CrossRef]
- Wang, J.; Chen, G.; Liu, B.; Li, M.; Pan, Y. Identifying protein complexes from interactome based on essential proteins and local fitness method. IEEE Trans. Nanobiosci. 2012, 11, 324–335. [Google Scholar] [CrossRef]
- Kreimer, A.; Borenstein, E.; Gophna, U.; Ruppin, E. The evolution of modularity in bacterial metabolic networks. Proc. Natl. Acad. Sci. USA 2008, 105, 6976–6981. [Google Scholar] [CrossRef]
- Luo, F.; Yang, Y.; Chen, C.F.; Chang, R.; Zhou, J.; Scheuermann, R.H. Modular organization of protein interaction networks. Bioinformatics 2007, 23, 207–214. [Google Scholar] [CrossRef]
- Poyatos, J.F.; Hurst, L.D. How biologically relevant are interaction-based modules in protein networks? Genome Biol. 2004, 5, R93. [Google Scholar] [CrossRef]
- Ren, J.; Wang, J.; Li, M.; Wang, L. Identifying protein complexes based on density and modularity in Protein–Protein interaction network. BMC Syst. Biol. 2013, 7, S12. [Google Scholar] [CrossRef]
- Bóta, A.; Csizmadia, L.; Pluhár, A. Community detection and its use in Real Graphs. In Proceedings of the 2010 Mini-Conference on Applied Theoretical Computer Science , Koper, Slovenia, 13–14 October 2010. [Google Scholar]
- Gera, I.; London, A.; Pluhár, A. Greedy algorithm for edge-based nested community detection. In Proceedings of the 2022 IEEE 2nd Conference on Information Technology and Data Science (CITDS), Debrecen, Hungary, 16–18 May 2022; pp. 86–91. [Google Scholar]
- Dezso, Z.; Oltvai, Z.N.; Barabási, A.L. Bioinformatics analysis of experimentally determined protein complexes in the yeast Saccharomyces cerevisiae. Genome Res. 2003, 13, 2450–2454. [Google Scholar] [CrossRef]
- Pu, S.; Vlasblom, J.; Emili, A.; Greenblatt, J.; Wodak, S.J. Identifying functional modules in the physical interactome of Saccharomyces cerevisiae. Proteomics 2007, 7, 944–960. [Google Scholar] [CrossRef]
- Gavin, A.C.; Aloy, P.; Grandi, P.; Krause, R.; Boesche, M.; Marzioch, M.; Rau, C.; Jensen, L.J.; Bastuck, S.; Dümpelfeld, B.; et al. Proteome survey reveals modularity of the yeast cell machinery. Nature 2006, 440, 631–636. [Google Scholar] [CrossRef]
- Bruckner, S.; Hüffner, F.; Komusiewicz, C. A graph modification approach for finding core–periphery structures in protein interaction networks. Algorithms Mol. Biol. 2015, 10, 16. [Google Scholar] [CrossRef]
- Meng, X.; Li, W.; Peng, X.; Li, Y.; Li, M. Protein interaction networks: Centrality, modularity, dynamics, and applications. Front. Comput. Sci. 2021, 15, 156902. [Google Scholar] [CrossRef]
- Ma, X.; Gao, L. Predicting protein complexes in protein interaction networks using a core-attachment algorithm based on graph communicability. Inf. Sci. 2012, 189, 233–254. [Google Scholar] [CrossRef]
- Mete, M.; Tang, F.; Xu, X.; Yuruk, N. A structural approach for finding functional modules from large biological networks. BMC Bioinform. 2008, 9, S19. [Google Scholar] [CrossRef]
- Yang, J.; Leskovec, J. Overlapping communities explain core–Periphery organization of networks. Proc. IEEE 2014, 102, 1892–1902. [Google Scholar] [CrossRef]
- Vieira, V.d.F.; Xavier, C.R.; Evsukoff, A.G. A comparative study of overlapping community detection methods from the perspective of the structural properties. Appl. Netw. Sci. 2020, 5, 51. [Google Scholar] [CrossRef]
- Gu, L.; Han, Y.; Wang, C.; Chen, W.; Jiao, J.; Yuan, X. Module overlapping structure detection in PPI using an improved link similarity-based Markov clustering algorithm. Neural Comput. Appl. 2019, 31, 1481–1490. [Google Scholar] [CrossRef]
- Wang, Y.; Qian, X. Functional module identification in protein interaction networks by interaction patterns. Bioinformatics 2014, 30, 81–93. [Google Scholar] [CrossRef] [PubMed]
- Aloy, P.; Bottcher, B.; Ceulemans, H.; Leutwein, C.; Mellwig, C.; Fischer, S.; Gavin, A.C.; Bork, P.; Superti-Furga, G.; Serrano, L.; et al. Structure-based assembly of protein complexes in yeast. Science 2004, 303, 2026–2029. [Google Scholar] [CrossRef] [PubMed]
- Luo, F.; Li, B.; Wan, X.F.; Scheuermann, R.H. Core and periphery structures in protein interaction networks. BMC Bioinform. 2009, 10, S8. [Google Scholar] [CrossRef] [PubMed]
- Bader, G.D.; Hogue, C.W. Analyzing yeast protein–protein interaction data obtained from different sources. Nat. Biotechnol. 2002, 20, 991–997. [Google Scholar] [CrossRef]
- Bader, G.D.; Hogue, C.W. An automated method for finding molecular complexes in large protein interaction networks. BMC Bioinform. 2003, 4, 2. [Google Scholar] [CrossRef]
- Kourtellis, N.; Alahakoon, T.; Simha, R.; Iamnitchi, A.; Tripathi, R. Identifying high betweenness centrality nodes in large social networks. Soc. Netw. Anal. Min. 2013, 3, 899–914. [Google Scholar] [CrossRef]
- Barabasi, A.L.; Oltvai, Z.N. Network biology: Understanding the cell’s functional organization. Nat. Rev. Genet. 2004, 5, 101–113. [Google Scholar] [CrossRef]
- Gosak, M.; Markovič, R.; Dolenšek, J.; Rupnik, M.S.; Marhl, M.; Stožer, A.; Perc, M. Network science of biological systems at different scales: A review. Phys. Life Rev. 2018, 24, 118–135. [Google Scholar] [CrossRef]
- Han, J.D.J. Understanding biological functions through molecular networks. Cell Res. 2008, 18, 224–237. [Google Scholar] [CrossRef]
- Del Sol, A.; O’Meara, P. Small-world network approach to identify key residues in protein–protein interaction. Proteins Struct. Funct. Bioinform. 2005, 58, 672–682. [Google Scholar] [CrossRef]
- Del Sol, A.; Fujihashi, H.; O’Meara, P. Topology of small-world networks of protein–protein complex structures. Bioinformatics 2005, 21, 1311–1315. [Google Scholar] [CrossRef]
- Wang, X.; Li, L.; Cheng, Y. An overlapping module identification method in Protein–Protein interaction networks. BMC Bioinform. 2012, 13, S4. [Google Scholar] [CrossRef]
- Liu, C.; Li, J.; Zhao, Y. Exploring hierarchical and overlapping modular structure in the yeast protein interaction network. BMC Genom. 2010, 11, S17. [Google Scholar] [CrossRef]
- Jaccard, P. The distribution of the flora in the alpine zone. 1. New Phytol. 1912, 11, 37–50. [Google Scholar] [CrossRef]
- Goodrich, M.T.; Ozel, E. Modeling the small-world phenomenon with road networks. In Proceedings of the 30th International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 1–4 November 2022; pp. 1–10. [Google Scholar]
- Menezes, M.B.; Kim, S.; Huang, R. Constructing a Watts-Strogatz network from a small-world network with symmetric degree distribution. PLoS ONE 2017, 12, e0179120. [Google Scholar] [CrossRef]
- Zahiri, J.; Emamjomeh, A.; Bagheri, S.; Ivazeh, A.; Mahdevar, G.; Tehrani, H.S.; Mirzaie, M.; Fakheri, B.A.; Mohammad-Noori, M. Protein complex prediction: A survey. Genomics 2020, 112, 174–183. [Google Scholar] [CrossRef]
- Lensink, M.F.; Velankar, S.; Wodak, S.J. Modeling protein–protein and protein–peptide complexes: CAPRI 6th edition. Proteins Struct. Funct. Bioinform. 2017, 85, 359–377. [Google Scholar] [CrossRef]
- Xenarios, I.; Salwinski, L.; Duan, X.J.; Higney, P.; Kim, S.M.; Eisenberg, D. DIP, the Database of Interacting Proteins: A research tool for studying cellular networks of protein interactions. Nucleic Acids Res. 2002, 30, 303–305. [Google Scholar] [CrossRef] [PubMed]
- Stark, C.; Breitkreutz, B.J.; Reguly, T.; Boucher, L.; Breitkreutz, A.; Tyers, M. BioGRID: A general repository for interaction datasets. Nucleic Acids Res. 2006, 34, D535–D539. [Google Scholar] [CrossRef]
- Ma, C.Y.; Chen, Y.P.P.; Berger, B.; Liao, C.S. Identification of protein complexes by integrating multiple alignment of protein interaction networks. Bioinformatics 2017, 33, 1681–1688. [Google Scholar] [CrossRef]
- Pu, S.; Wong, J.; Turner, B.; Cho, E.; Wodak, S.J. Up-to-date catalogues of yeast protein complexes. Nucleic Acids Res. 2009, 37, 825–831. [Google Scholar] [CrossRef]
- Mewes, H.W.; Frishman, D.; Mayer, K.F.; Münsterkötter, M.; Noubibou, O.; Pagel, P.; Rattei, T.; Oesterheld, M.; Ruepp, A.; Stümpflen, V. MIPS: Analysis and annotation of proteins from whole genomes in 2005. Nucleic Acids Res. 2006, 34, D169–D172. [Google Scholar] [CrossRef] [PubMed]
- Luc, P.V.; Tempst, P. PINdb: A database of nuclear protein complexes from human and yeast. Bioinformatics 2004, 20, 1413–1415. [Google Scholar] [CrossRef] [PubMed]
- Kanehisa, M.; Goto, S.; Sato, Y.; Furumichi, M.; Tanabe, M. KEGG for integration and interpretation of large-scale molecular data sets. Nucleic Acids Res. 2012, 40, D109–D114. [Google Scholar] [CrossRef]
- Dwight, S.S.; Harris, M.A.; Dolinski, K.; Ball, C.A.; Binkley, G.; Christie, K.R.; Fisk, D.G.; Issel-Tarver, L.; Schroeder, M.; Sherlock, G.; et al. Saccharomyces Genome Database (SGD) provides secondary gene annotation using the Gene Ontology (GO). Nucleic Acids Res. 2002, 30, 69–72. [Google Scholar] [CrossRef]
- Li, X.; Wu, M.; Kwoh, C.K.; Ng, S.K. Computational approaches for detecting protein complexes from protein interaction networks: A survey. BMC Genom. 2010, 11, S3. [Google Scholar] [CrossRef]
- Li, M.; Chen, J.e.; Wang, J.x.; Hu, B.; Chen, G. Modifying the DPClus algorithm for identifying protein complexes based on new topological structures. BMC Bioinform. 2008, 9, 398. [Google Scholar] [CrossRef]
- Brohee, S.; Van Helden, J. Evaluation of clustering algorithms for Protein–Protein interaction networks. BMC Bioinform. 2006, 7, 488. [Google Scholar] [CrossRef]
- Li, X.L.; Foo, C.S.; Ng, S.K. Discovering protein complexes in dense reliable neighborhoods of protein interaction networks. In Computational Systems Bioinformatics: (Volume 6); World Scientific: Singapore, 2007; pp. 157–168. [Google Scholar]
- Friedel, C.C.; Krumsiek, J.; Zimmer, R. Bootstrapping the interactome: Unsupervised identification of protein complexes in yeast. J. Comput. Biol. 2009, 16, 971–987. [Google Scholar] [CrossRef]
- Maulik, U.; Mukhopadhyay, A.; Bhattacharyya, M.; Kaderali, L.; Brors, B.; Bandyopadhyay, S.; Eils, R. Mining quasi-bicliques from HIV-1-human protein interaction network: A multiobjective biclustering approach. IEEE/ACM Trans. Comput. Biol. Bioinform. 2012, 10, 423–435. [Google Scholar] [CrossRef]
- Cao, B.; Luo, J.; Liang, C.; Wang, S. Identifying protein complexes by combining network topology and biological characteristics. J. Comput. Theor. Nanosci. 2016, 13, 7666–7675. [Google Scholar] [CrossRef]
- Wu, Z.; Liao, Q.; Liu, B. idenPC-MIIP: Identify protein complexes from weighted PPI networks using mutual important interacting partner relation. Briefings Bioinform. 2021, 22, 1972–1983. [Google Scholar] [CrossRef]
- Cherry, J.M.; Adler, C.; Ball, C.; Chervitz, S.A.; Dwight, S.S.; Hester, E.T.; Jia, Y.; Juvik, G.; Roe, T.; Schroeder, M.; et al. SGD: Saccharomyces genome database. Nucleic Acids Res. 1998, 26, 73–79. [Google Scholar] [CrossRef]
- Li, B.; Liao, B. Protein complexes prediction method based on core—Attachment structure and functional annotations. Int. J. Mol. Sci. 2017, 18, 1910. [Google Scholar] [CrossRef]
- Xiao, Q.; Luo, P.; Li, M.; Wang, J.; Wu, F.X. A Novel Core-Attachment–Based Method to Identify Dynamic Protein Complexes Based on Gene Expression Profiles and PPI Networks. Proteomics 2019, 19, 1800129. [Google Scholar] [CrossRef]


| Datasets | Number of Protein | Number of Edges | Network Density |
|---|---|---|---|
| BioGRID | 5640 | 59,748 | |
| DIP | 4930 | 17,202 | |
| Human | 15,459 | 144,687 | |
| Yeast | 6194 | 74,826 |
| Complex Datasets | Number of Protein Complexes | Overlapping Complexes | Non-Overlapping Complexes | Protein Coverage | Average Size |
|---|---|---|---|---|---|
| NewMIPS | 328 | 283 | 45 | 1171 | 14.93 |
| CYC2008 | 236 | 108 | 128 | 1628 | 4.71 |
| Human complexes | 2289 | - | - | 6206 | 8.57 |
| Yeast complexes | 1045 | - | - | 2773 | 8.92 |
| Dataset | Algorithm | F-Measure | CR | MMR | Sep | ACC | CPU Run Time (s) | |
|---|---|---|---|---|---|---|---|---|
| Human | MCL | 315 | 0.1001 | 0.1759 | 0.0105 | 0.1753 | 0.2167 | 5906.34 |
| COACH | 4484 | o.2455 | 0.5408 | 0.0677 | 0.5216 | 0.2777 | 2851.05 | |
| EWCA | 1979 | 0.4048 | 0.5221 | 0.0964 | 0.6081 | 0.5221 | 29.37 | |
| CFinder | 449 | 0.1256 | 0.2834 | 0.0116 | 0.3912 | 0.2511 | 3896.35 | |
| GMFTP | 773 | 0.2651 | 0.4193 | 0.0419 | 0.4917 | 0.3852 | 254.67 | |
| Core | 576 | 0.1621 | 0.3267 | 0.1267 | 0.3573 | 0.2778 | 2853.14 | |
| CALM | 1108 | 0.5127 | 0.5182 | 0.1394 | 0.6894 | 0.5289 | 198.39 | |
| ClusterONE | 375 | 0.1026 | 0.3071 | 0.0207 | 0.3773 | 0.2975 | 4895.78 | |
| CMC | 672 | 0.1251 | 0.2503 | 0.0183 | 0.2975 | 0.3313 | 3904.83 | |
| ProRank+ | 838 | 0.3651 | 0.2856 | 0.0687 | 0.5526 | 0.5613 | 282.66 | |
| WECALM | 2367 | 0.4255 | 0.5155 | 0.0981 | 0.6155 | 0.6219 | 28.45 | |
| Yeast | MCL | 298 | 0.1104 | 0.2761 | 0.0117 | 0.1625 | 0.1395 | 4967.47 |
| COACH | 1551 | 0.2083 | 0.5521 | 0.0466 | 0.3583 | 0.3117 | 3603.31 | |
| EWCA | 936 | 0.4199 | 0.6182 | 0.0982 | 0.5904 | 0.5879 | 18.54 | |
| CFinder | 351 | 0.1429 | 0.2749 | 0.0281 | 0.3453 | 0.4163 | 3432.07 | |
| GMFTP | 675 | 0.2763 | 0.3129 | 0.0309 | 0.5145 | 0.4092 | 229.89 | |
| Core | 402 | 0.2124 | 0.2968 | 0.3285 | 0.1517 | 0.3218 | 2543.34 | |
| CALM | 732 | 0.4015 | 0.6787 | 0.1433 | 0.6261 | 0.6532 | 154.89 | |
| ClusterONE | 317 | 0.2012 | 0.2767 | 0.0285 | 0.3371 | 0.3255 | 3989.92 | |
| CMC | 589 | 0.2115 | 0.1975 | 0.0198 | 0.2934 | 0.3553 | 2987.63 | |
| ProRank+ | 516 | 0.2712 | 0.2816 | 0.0487 | 0.5471 | 0.5602 | 251.54 | |
| WECALM | 1891 | 0.4216 | 0.6394 | 0.0487 | 0.64131 | 0.6534 | 17.65 |
| Dataset | Algorithm | Significant Detected | |||||
|---|---|---|---|---|---|---|---|
| BioGRID | MCL | 121 | 41 (33.88%) | 28 (23.14%) | 26 (21.49%) | 12 (9.92%) | 107 (88.43%) |
| COACH | 166 | 76 (45.78%) | 32 (19.28%) | 37 (22.29%) | 16 (9.64%) | 161 (96.98%) | |
| EWCA | 1388 | 658 (47.41%) | 211 (15.20%) | 299 (21.54%) | 173 (12.46%) | 1341 (96.61%) | |
| CFinder | 352 | 103 (29.26%) | 53 (15.10%) | 78 (22.16%) | 35 (9.94%) | 269 (76.42%) | |
| GMFTP | 597 | 73 (12.23%) | 59 (9.88%) | 156 (26.13%) | 161 (26.97%) | 449 (75.21%) | |
| Core | 576 | 255 (44.27%) | 105 (18.23%) | 68 (11.81%) | 35 (6.08%) | 463 (80.38%) | |
| CALM | 1108 | 587 (52.98%) | 236 (21.29%) | 116 (10.47%) | 96 (8.66%) | 1035 (93.41%) | |
| ClusterONE | 294 | 107 (36.40%) | 35 (11.91%) | 43 (14.62%) | 25 (8.50%) | 210 (71.43%) | |
| CMC | 1113 | 125 (11.23%) | 89 (7.99%) | 258 (23.18%) | 360 (32.34%) | 832 (74.75%) | |
| ProRank+ | 746 | 479 (64.21%) | 105 (14.08%) | 97 (13.00%) | 47 (6.30%) | 728 (97.59%) | |
| WECALM | 1412 | 687 (48.65%) | 217 (15.37%) | 312 (22.09%) | 172 (12.18%) | 1388 (98.30%) | |
| DIP | MCL | 142 | 41 (28.87%) | 29 (20.42%) | 17 (11.97%) | 26 (18.31%) | 113 (79.58%) |
| COACH | 329 | 21 (6.38%) | 25 (7.59%) | 66 (20.06%) | 32 (9.73%) | 144 (43.77%) | |
| EWCA | 964 | 188 (19.50%) | 126 (13.07%) | 319 (33.09%) | 236 (24.48%) | 869 (90.15%) | |
| CFinder | 352 | 157 (44.60%) | 39 (11.08%) | 31 (8.81%) | 45 (12.78%) | 272 (77.27%) | |
| GMFTP | 548 | 43 (7.85%) | 36 (6.57%) | 105 (19.16%) | 166 (30.29%) | 350 (63.87%) | |
| Core | 412 | 131 (31.79%) | 87 (21.12%) | 52 (12.62%) | 45 (10.922%) | 315 (76.46%) | |
| CALM | 755 | 256 (33.91%) | 127 (16.82%) | 112 (14.83%) | 108 (14.31%) | 603 (80.53%) | |
| ClusterONE | 315 | 119 (37.78%) | 49 (15.56%) | 38 (12.06%) | 29 (9.21%) | 235 (74.60%) | |
| CMC | 303 | 3 (0.99%) | 8 (2.64%) | 58 (19.14%) | 77 (25.41%) | 146 (48.18%) | |
| ProRank+ | 338 | 74 (21.89%) | 77 (22.78%) | 125 (36.98%) | 41 (12.13%) | 319 (93.79%) | |
| WECALM | 1018 | 269 (26.42%) | 187 (18.37%) | 358 (35.17%) | 165 (16.21%) | 979 (96.17%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ochieng, P.J.; Dombi, J.; Kalmár, T.; Krész, M. A Special Structural Based Weighted Network Approach for the Analysis of Protein Complexes. Appl. Sci. 2023, 13, 6388. https://doi.org/10.3390/app13116388
Ochieng PJ, Dombi J, Kalmár T, Krész M. A Special Structural Based Weighted Network Approach for the Analysis of Protein Complexes. Applied Sciences. 2023; 13(11):6388. https://doi.org/10.3390/app13116388
Chicago/Turabian StyleOchieng, Peter Juma, József Dombi, Tibor Kalmár, and Miklós Krész. 2023. "A Special Structural Based Weighted Network Approach for the Analysis of Protein Complexes" Applied Sciences 13, no. 11: 6388. https://doi.org/10.3390/app13116388
APA StyleOchieng, P. J., Dombi, J., Kalmár, T., & Krész, M. (2023). A Special Structural Based Weighted Network Approach for the Analysis of Protein Complexes. Applied Sciences, 13(11), 6388. https://doi.org/10.3390/app13116388





