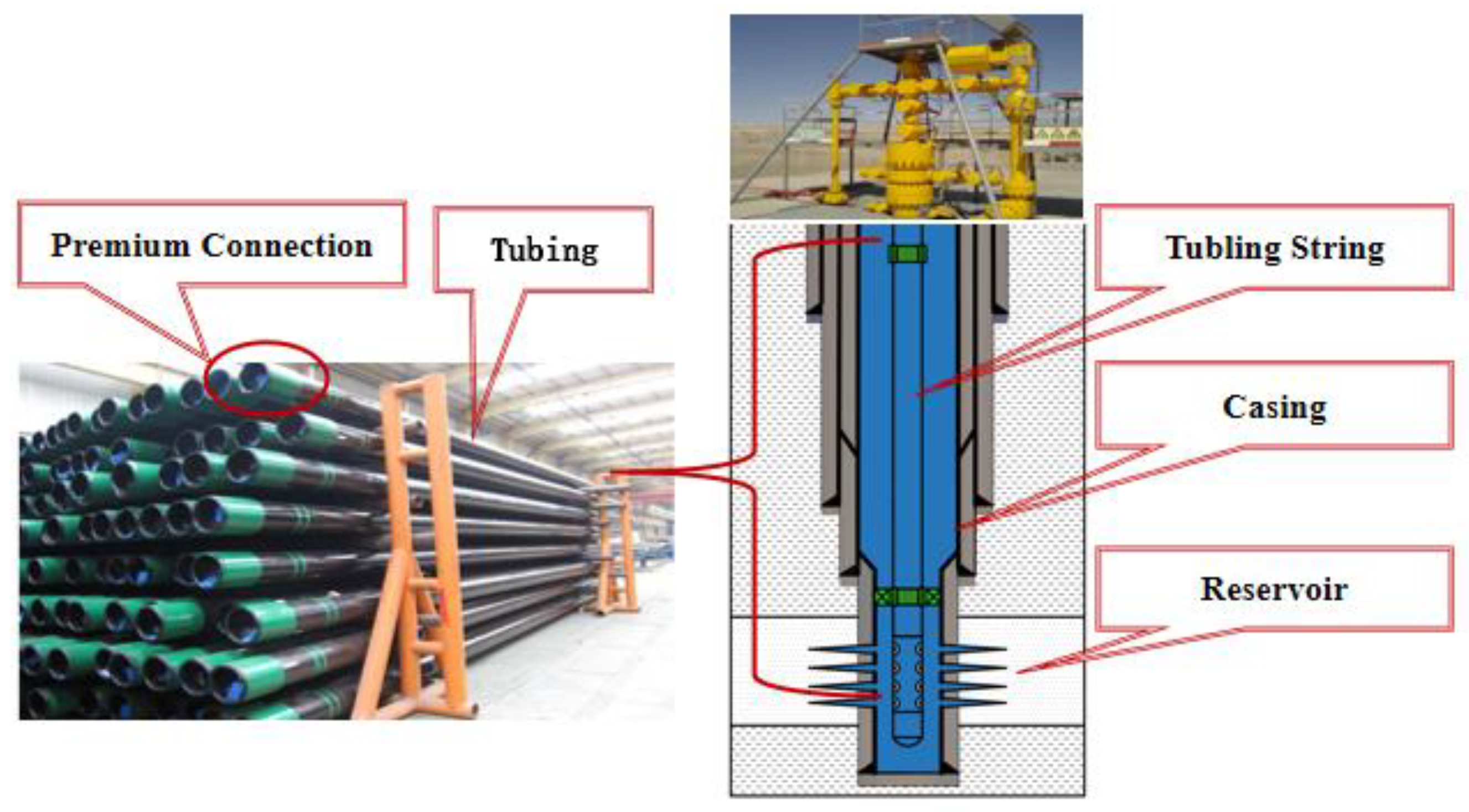
Sealability Analyses of Premium Connections Characterized by a Surface Fractal Function
Abstract
1. Introduction
2. Analysis of Fractal Surface Contact Behavior
2.1. The W-M Fractal Function
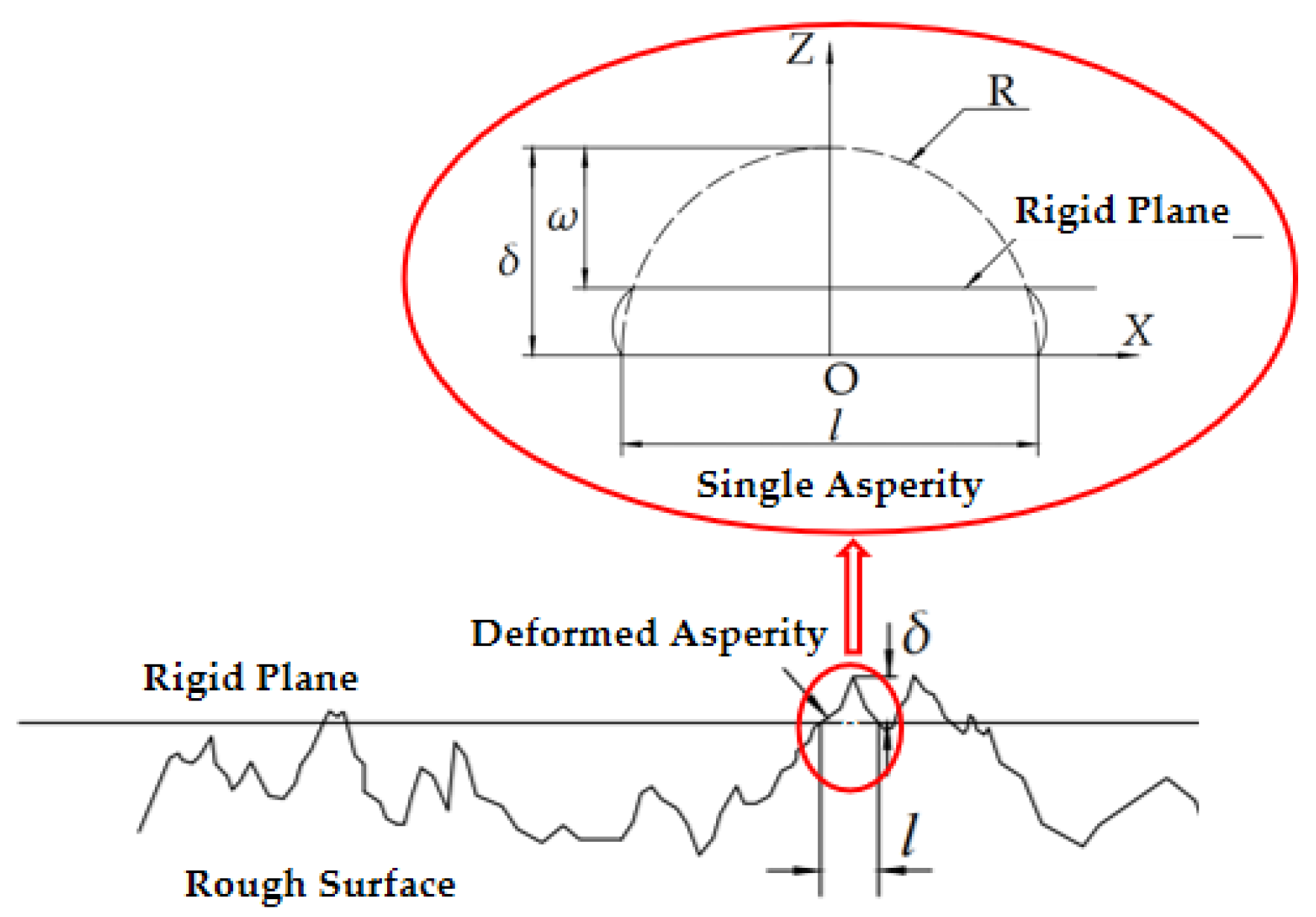
2.2. Contact Behavior Analysis of Single Asperities
2.3. Analysis of the Contact Behavior of the Full-Size Area
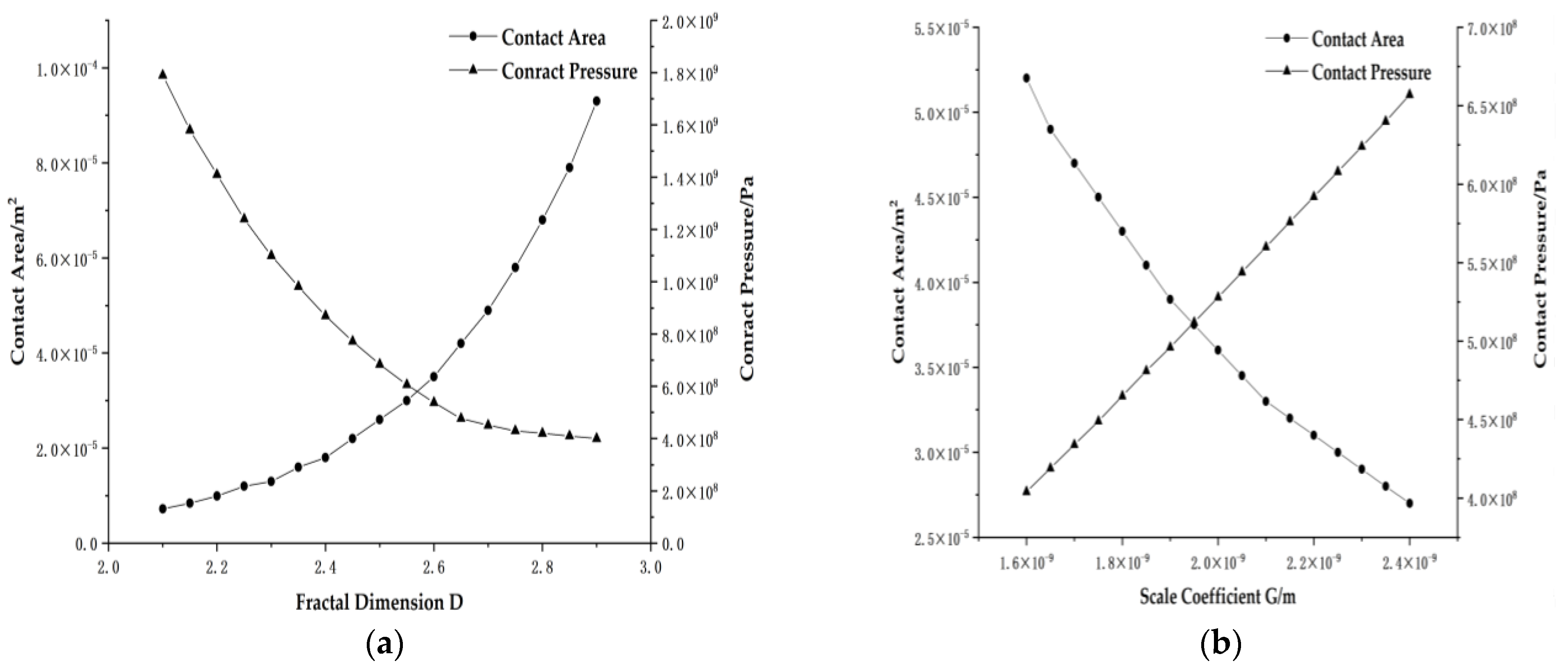
2.4. Influence of Fractal Parameters on Surface Contact Behavior
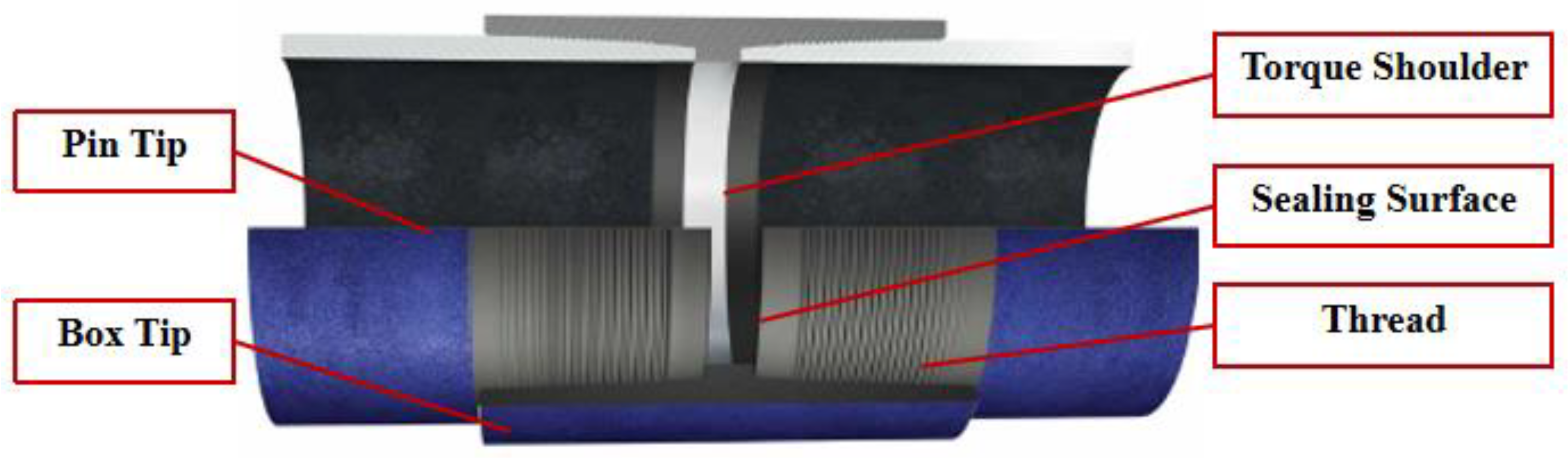
3. Contact Analysis of Premium Connections
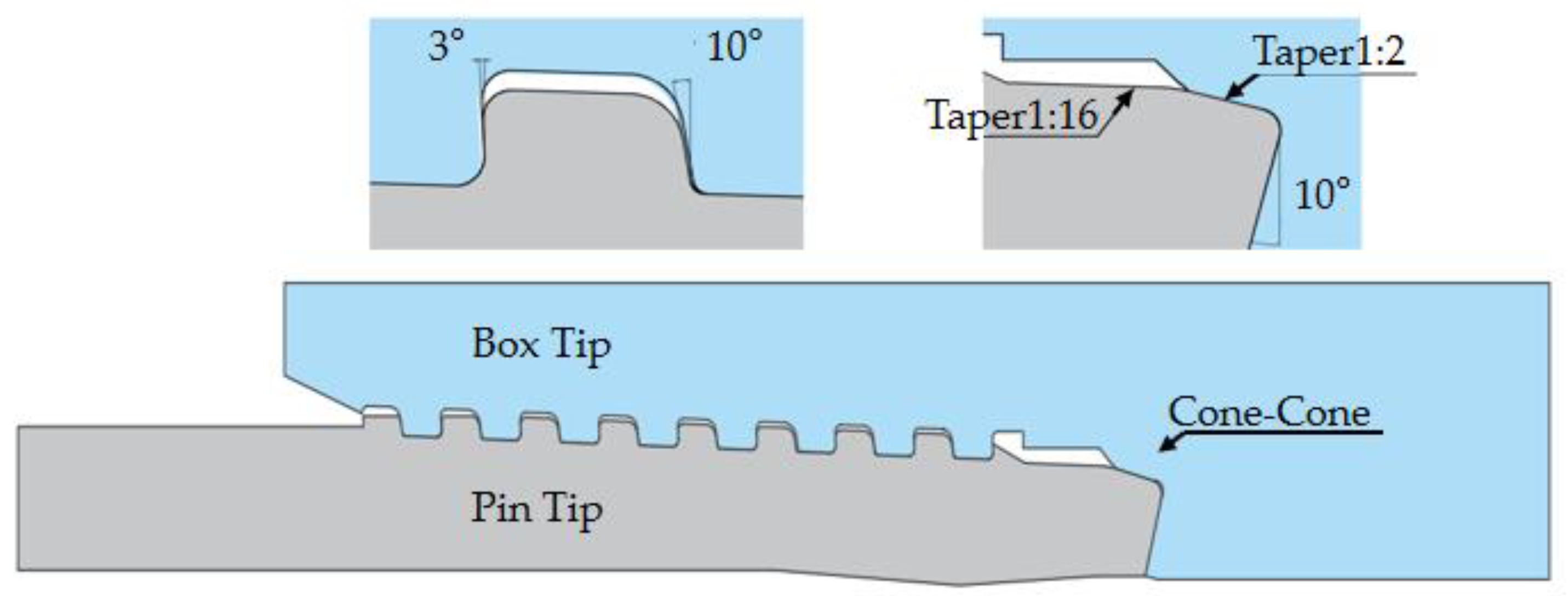
3.1. Establishment of the Fractal Model of a Premium Connection
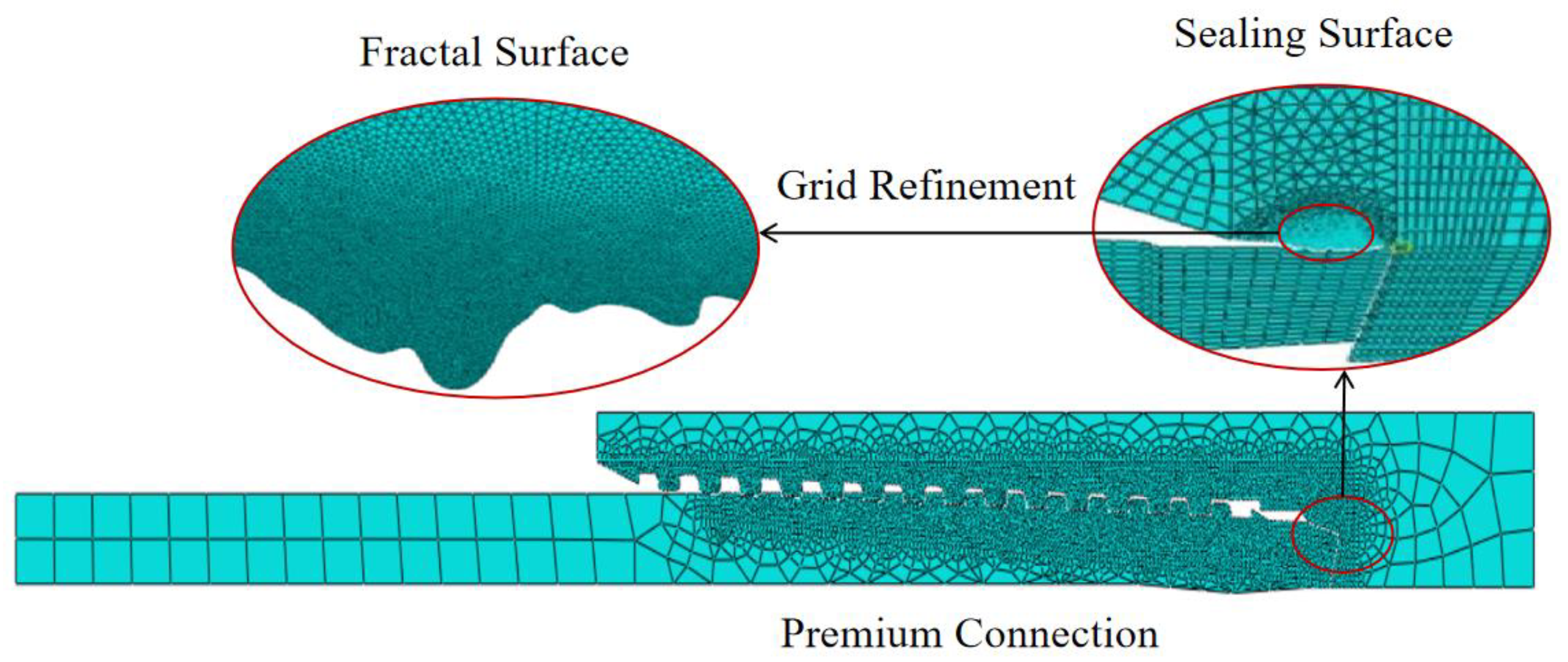
3.2. Mesh Independence Verification
3.3. Analysis of Influencing Factors
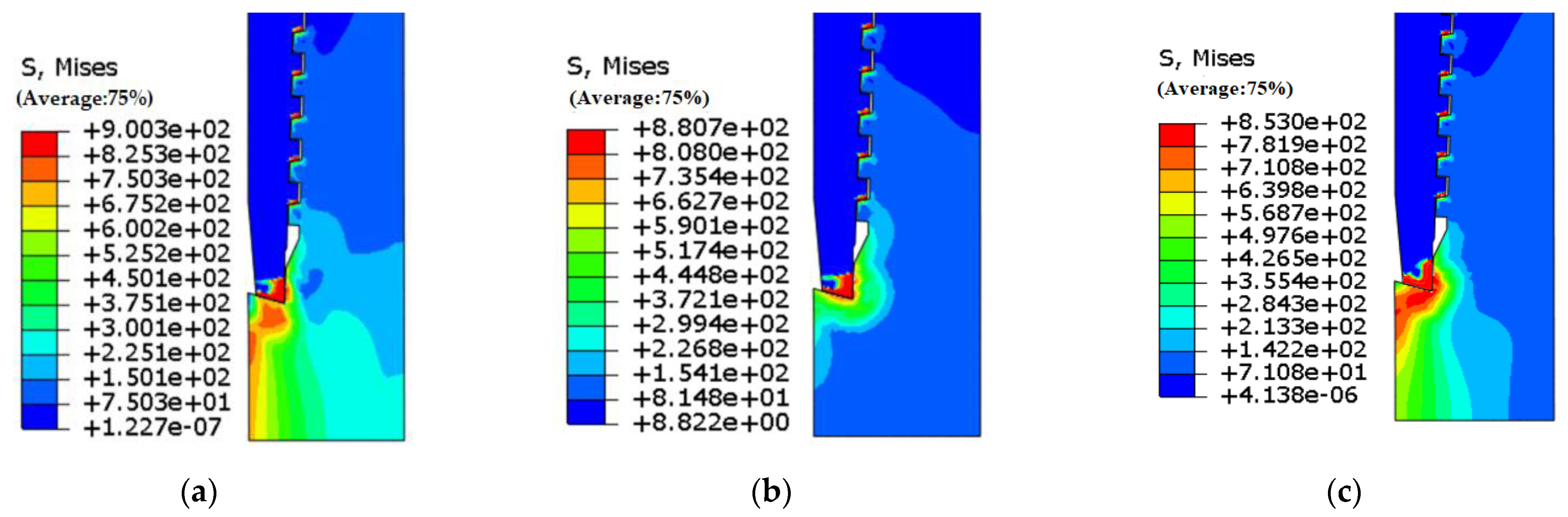
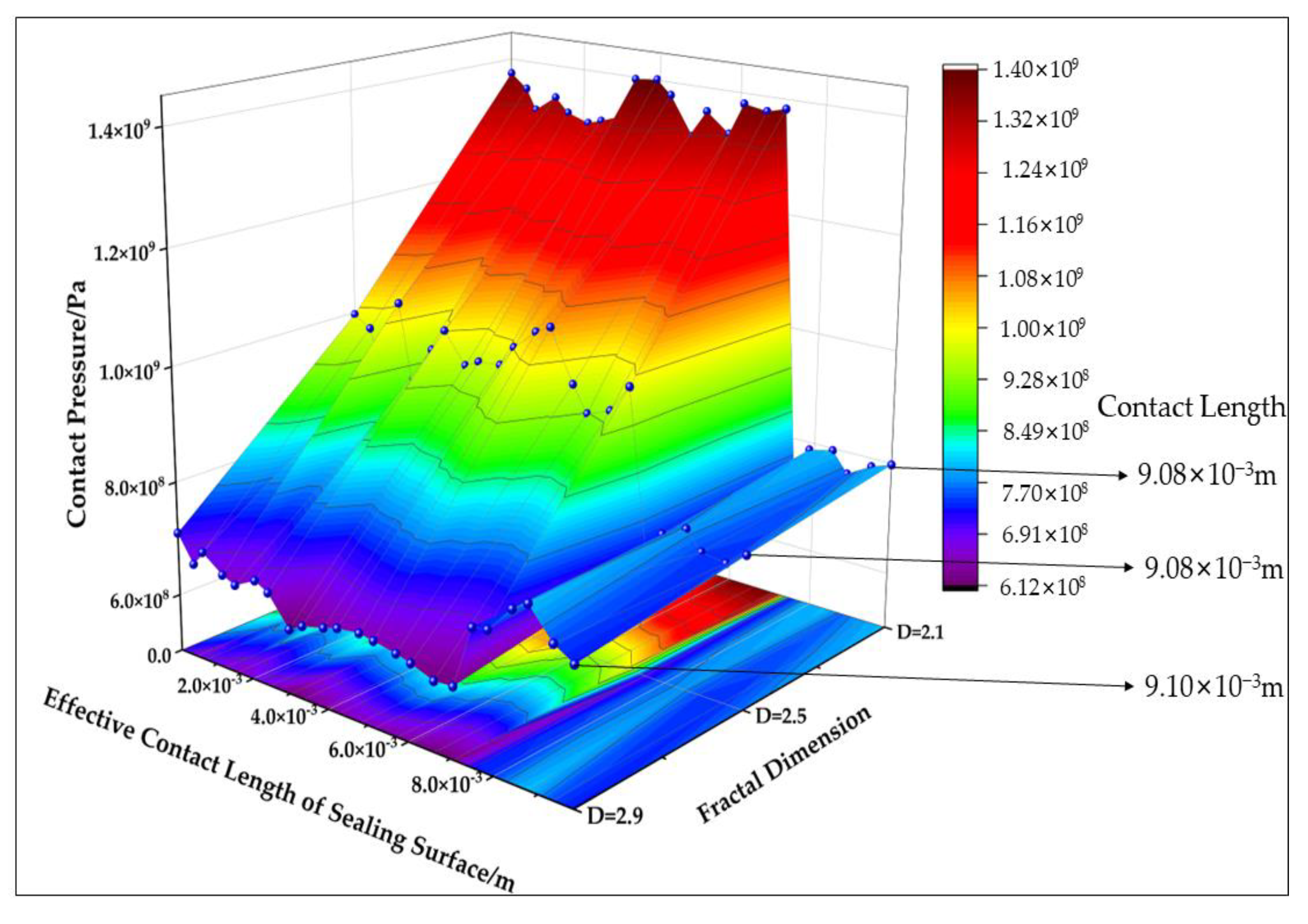
3.3.1. The Fractal Dimension
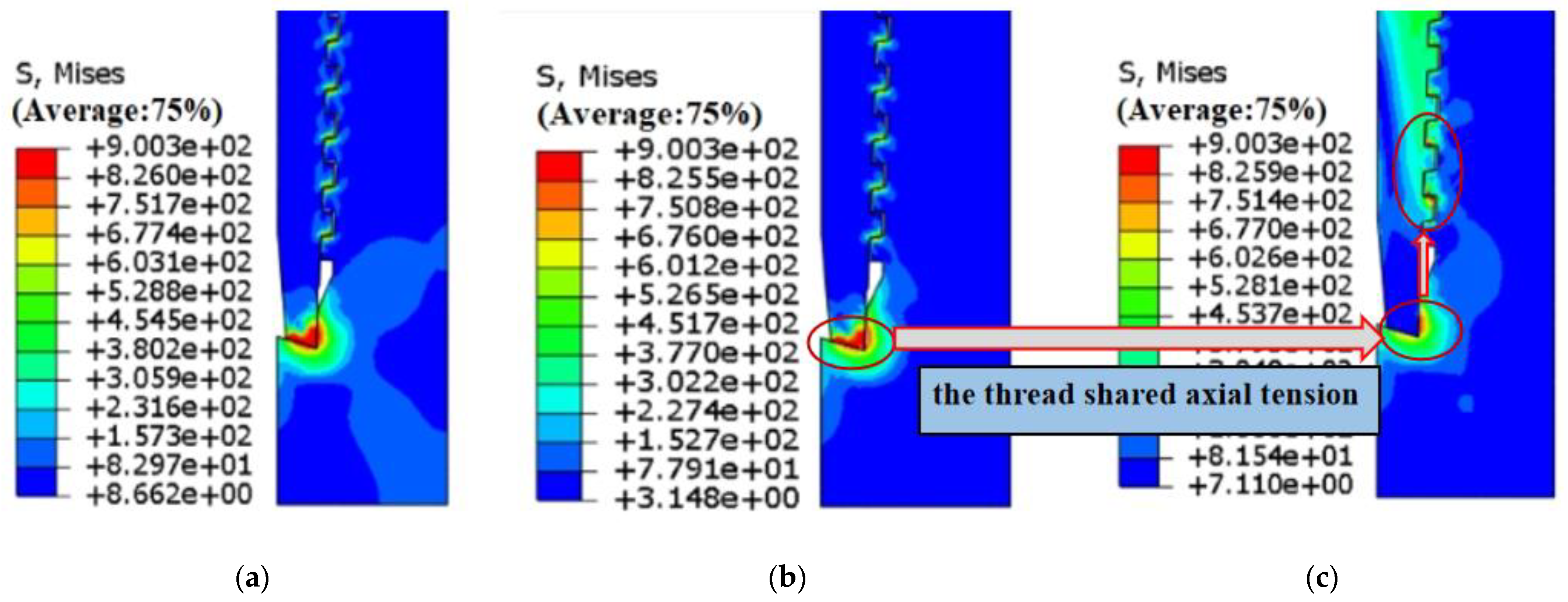
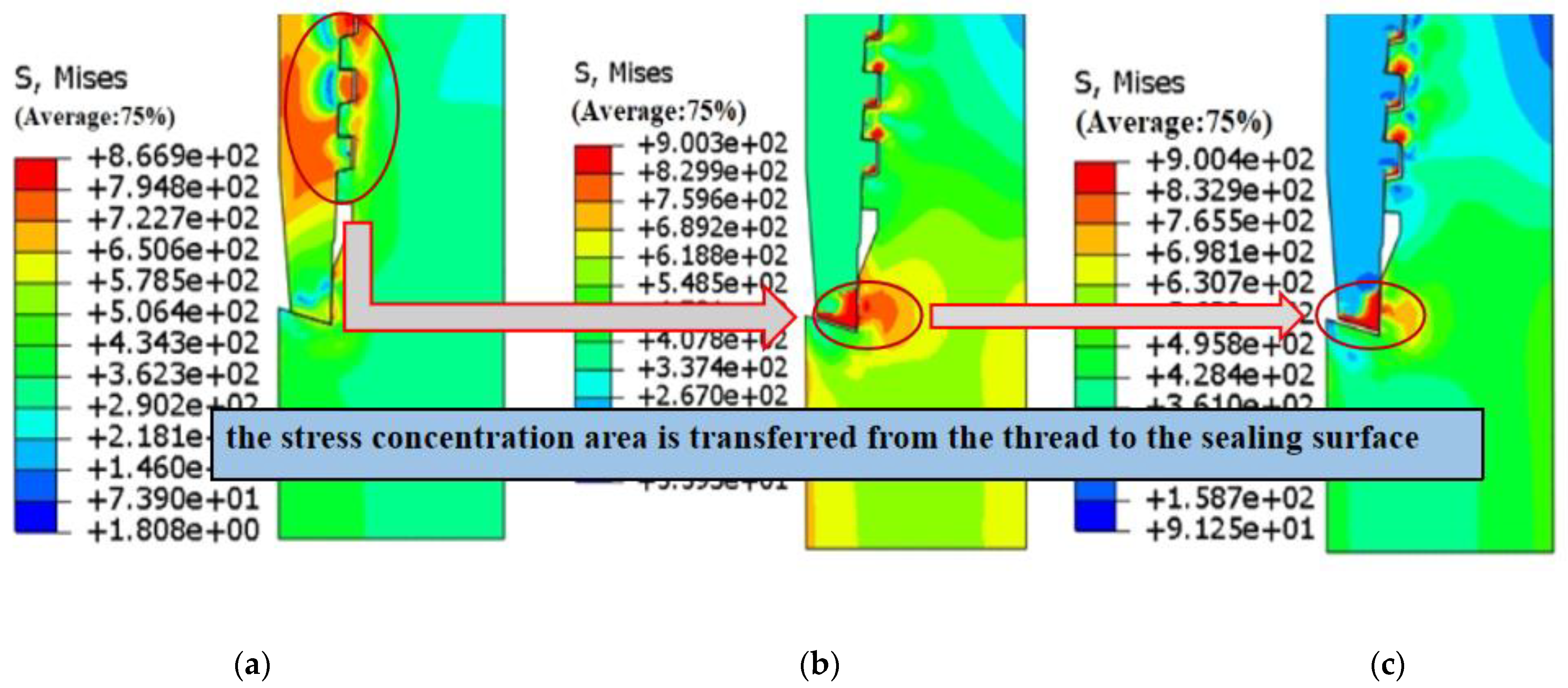
3.3.2. The Influence of Axial Tension
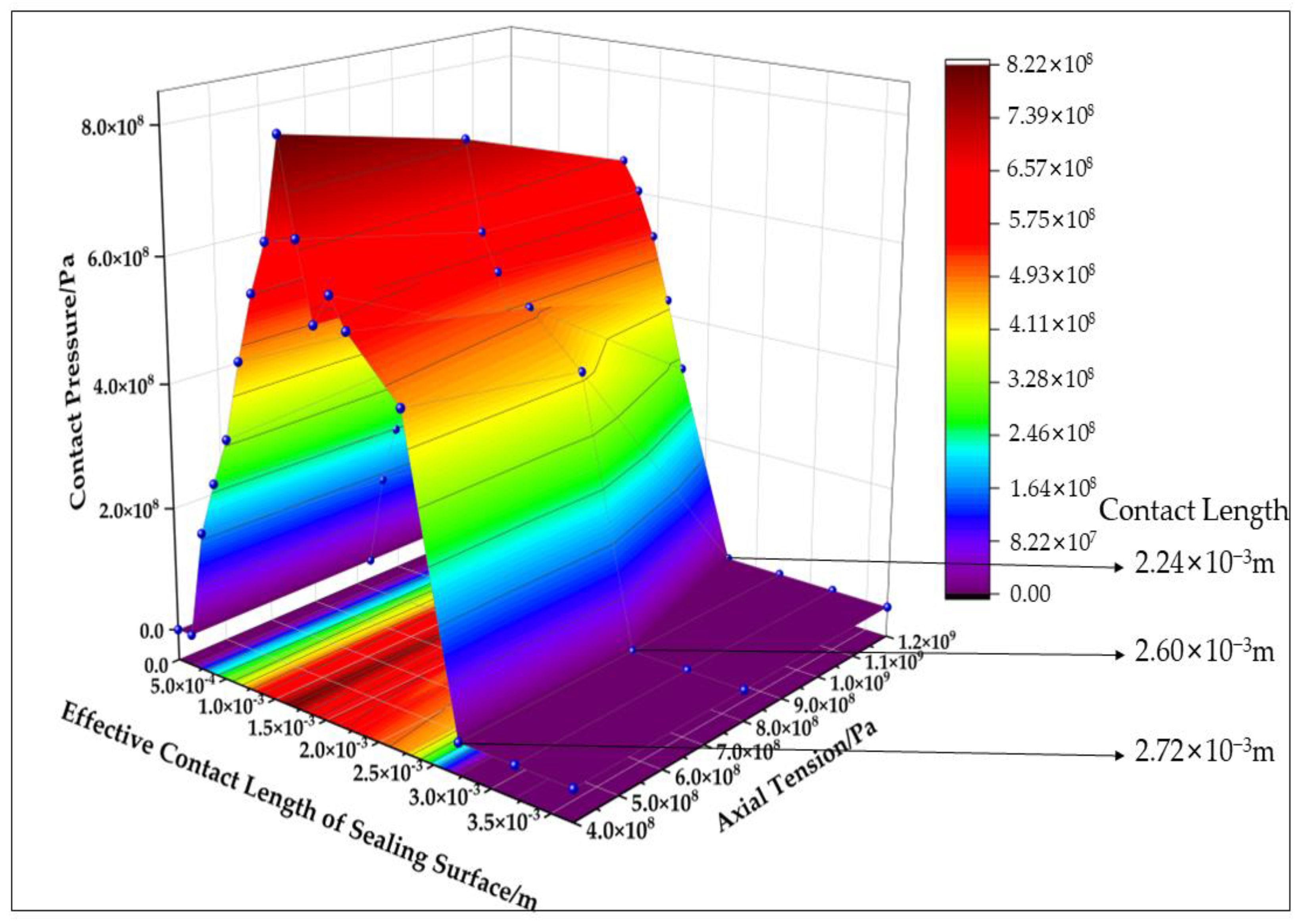
3.3.3. The Influence of Internal Pressure
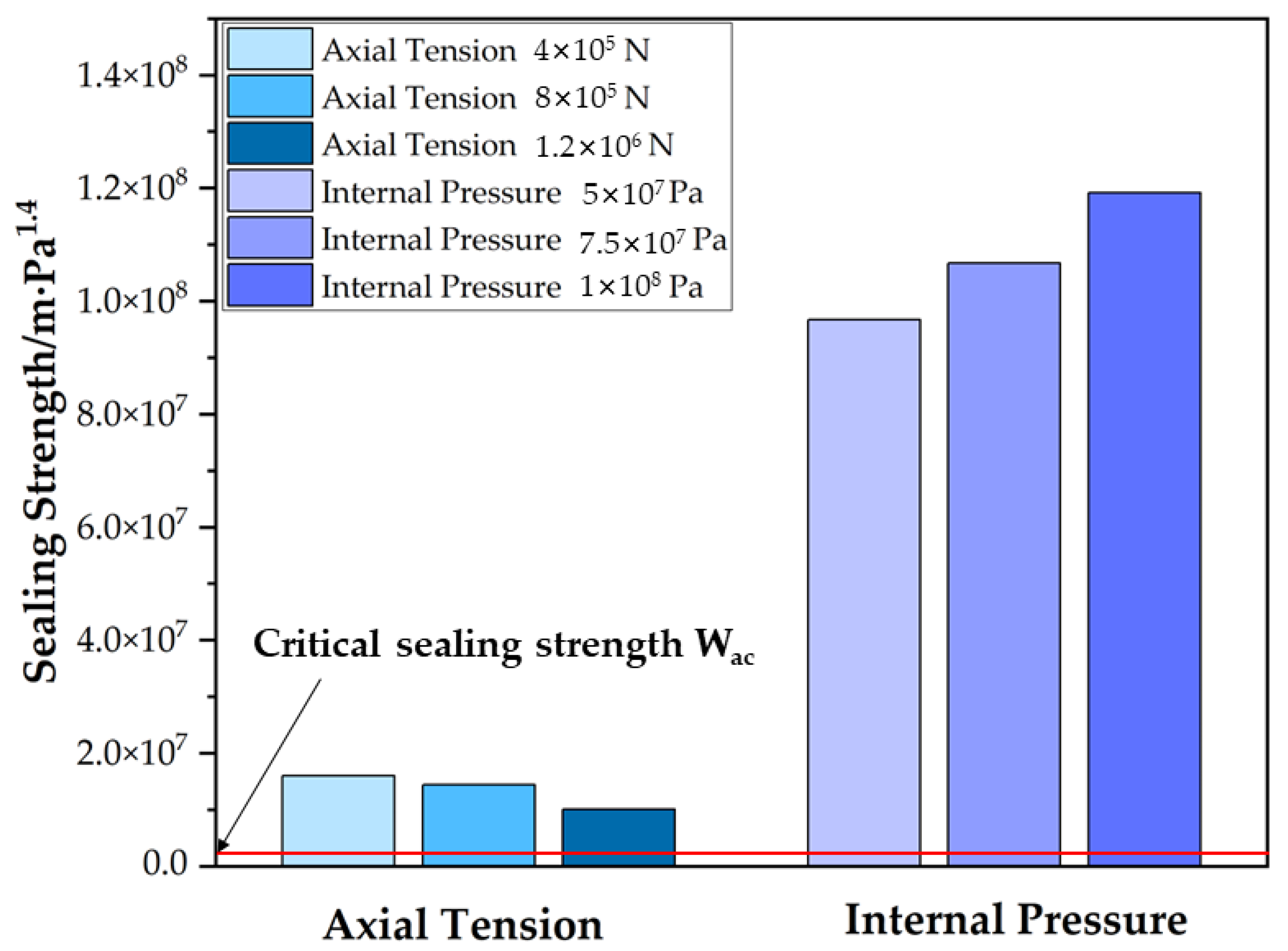
4. Analysis of the Sealability of Premium Connections
5. Conclusions
- (1)
- Compared with the scale coefficient G, the influence of fractal dimension D on contact area and contact pressure is more significant. With the increase in fractal dimension, the number of asperities on the fractal surface increases, and the contact area exhibits exponential growth, while the contact pressure decreases exponentially. When the fractal dimension D is less than 2.5, the maximum Von Mises stress is 8.81 × 108 Pa and the maximum contact pressure on the sealing surface is 1.20 × 109 Pa, making it prone to gluing and ultimately leading to sealing failure. Conversely, when the fractal dimension D is greater than 2.7, the contact pressure distribution on the sealing surface is more uniform, which improves sealability.
- (2)
- As the axial tension increases, stress concentration in the area gradually shifts from the sealing surface to the threaded portion, resulting in a reduction in the contact pressure and the effective contact length of the sealing surface. When the axial tension reaches 1.2 × 106 N, the sealing surface experiences significant displacement along the axial direction, the effective contact length is reduced from 2.72 × 10−3 m to 2.24 × 10−3 m, and the maximum contact pressure is reduced from 8.10 × 108 Pa to 6.39 × 108 Pa, which leads to a 30% decrease in sealing strength and therefore poses a high risk of sealing failure.
- (3)
- As the internal pressure increases, the plastic deformation ratio of the fractal surface asperities significantly increases, leading to a proportional increase in the contact pressure and effective contact length of the sealing surface. When the internal pressure reaches 1 × 108 Pa, the effective contact length is increased from 9.08 × 10−3 m to 1.06 × 10−2 m, the maximum contact pressure is increased from 8.67 × 108 Pa to 1.37 × 109 Pa, and the sealing strength is increased by 23%. At the same time, the maximum Von Mises stress on the sealing surface reached 9 × 108 Pa, resulting in a significant stress concentration on the sealing surface.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FEM | finite element model |
| HPTP | high-pressure and high-temperature |
| 2D | two-dimensional |
| 3D | three-dimensional |
| W-M | Weierstrass–Mandelbrot fractal function |
| W-B | Majumdar–Bhushan function |
| FEA | finite element analysis |
References
- Matthews, C. Assessing tubular connection leakage integrity. World Oil 2002, 223, 82–84. [Google Scholar]
- Zhang, X.; Huang, Y.; Wen, S. Fractal model of contact stiffness of joint surfaces. Trans. Chin. Soc. Agric. Mach. 2000, 31, 89–91. [Google Scholar]
- Zhang, Y.; Lian, Z.; Zhou, M. Research on Micro-Leakage Mechanism of Premium Connection Sealing Surface of Tubing and Casing. Lubr. Eng. 2019, 44, 93–98. [Google Scholar]
- Wang, J.D.; Feng, Y.R.; Lin, K.; Qin, C.Y.; Song, Y.P. Comparison analysis of premium connection’s seal structure. Zhongguo Shi You Daxue Xuebao J. China Univ. Pet. Ed. Nat. Sci. 2010, 34, 126–130. [Google Scholar]
- Shen, Z.; Wang, P.; Li, L.; Feng, C. Simulation calculation analysis of seal reliability of premium thread connection. Oil Field Equip 2012, 41, 10–13. [Google Scholar]
- Hillis, D.J.; Eddy, M.P.; Cassagne, T. Failure Investigation of a C110 Connection from a High Pressure High Temperature Well; CORROSION 2014; OnePetro: Richardson, TX, USA, 2014. [Google Scholar]
- Peiravi, M.M.; Alinejad, J.; Ganji, D.; Maddah, S. 3D optimization of baffle arrangement in a multi-phase nanofluid natural convection based on numerical simulation. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 2583–2605. [Google Scholar] [CrossRef]
- Chen, W.; Di, Q.; Zhang, H.; Chen, F.; Wang, W. The sealing mechanism of tubing and casing premium threaded connections under complex loads. J. Pet. Sci. Eng. 2018, 171, 724–730. [Google Scholar] [CrossRef]
- Murtagian, G.; Fanelli, V.; Villasante, J.; Johnson, D.; Ernst, H. Sealability of stationary metal-to-metal seals. J. Tribol. 2004, 126, 591–596. [Google Scholar] [CrossRef]
- Xie, J.; Rong, F.; Dessein, T. Methodology for Reliability-Based Design and Assessment of Tubular Connection Sealability in HPHT Wells. In Proceedings of the International Conference on Oil Country Tubular Goods and Tubular String, Xi’an, China, 22–23 May 2014. [Google Scholar]
- Toyooka, T.; Itadani, M.; Yorifuji, A. Development of manufacturing process “HISTORY” for producing innovative high frequency welded steel tubes with excellent properties. Kawasaki Steel Tech. Rep. Engl. Ed. 2002, 33, 145–150. [Google Scholar]
- Peiravi, M.M.; Alinejad, J. Hybrid conduction, convection and radiation heat transfer simulation in a channel with rectangular cylinder. J. Therm. Anal. Calorim. 2019, 140, 2733–2747. [Google Scholar] [CrossRef]
- Zeng, W.; Song, H.; Xie, H. Sealing characteristics analysis of VX gasket for a subsea wellhead connector based on sealing contact strength. Lubr. Eng. 2019, 44, 121–126. [Google Scholar]
- Sofuoglu, H.; Ozer, A. Thermomechanical analysis of elastoplastic medium in sliding contact with fractal surface. Tribol. Int. 2008, 41, 783–796. [Google Scholar] [CrossRef]
- Ausloos, M.; Berman, D. A multivariate Weierstrass–Mandelbrot function. Proc. R. Soc. Lond. A Math. Phys. Sci. 1985, 400, 331–350. [Google Scholar]
- Majumdar, A.; Bhushan, B. Fractal model of elastic-plastic contact between rough surfaces. J. Tribol. 1991, 113, 1–11. [Google Scholar] [CrossRef]
- Jourani, A. Effect of 3D fractal dimension on contact area and asperity interactions in elastoplastic contact. AIP Adv. 2016, 6, 055309. [Google Scholar] [CrossRef]
- Yan, W.; Komvopoulos, K. Contact analysis of elastic-plastic fractal surfaces. J. Appl. Phys. 1998, 84, 3617–3624. [Google Scholar] [CrossRef]
- Kumar, P.G.; Vigneswaran, V.; Balaji, K.; Vinothkumar, S.; Prabakaran, R.; Sakthivadivel, D.; Meikandan, M.; Kim, S.C. Augmented v-corrugated absorber plate using shot-blasting for solar air heater–Energy, Exergy, Economic, and Environmental (4E) analysis. Process Saf. Environ. Prot. 2022, 165, 514–531. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Yan, K.; Fang, B. A fractal model for predicting thermal contact conductance considering elasto-plastic deformation and base thermal resistances. J. Mech. Sci. Technol. 2019, 33, 475–484. [Google Scholar] [CrossRef]
- Lin, L.P.; Lin, J.F. An elastoplastic microasperity contact model for metallic materials. J. Tribol. 2005, 127, 666–672. [Google Scholar]
- Feng, X.; Lu, F.; Shen, G.L. Contact Model of Sealing Surfaces for Flange and Metallic Gasket Based on Fractal Theory. In Advanced Materials Research; Trans Tech Publications: Cham, Switzerland, 2011; pp. 1571–1576. [Google Scholar]
- Liu, P.; Zhao, H.; Huang, K.; Chen, Q. Research on normal contact stiffness of rough surface considering friction based on fractal theory. Appl. Surf. Sci. 2015, 349, 43–48. [Google Scholar] [CrossRef]
- Liu, J.; Shen, H.; Yang, Y. Finite element implementation of a varied friction model applied to torsional fretting wear. Wear 2014, 314, 220–227. [Google Scholar] [CrossRef]
- Dou, Y.; Li, Y.; Cao, Y.; Yu, Y.; Zhang, J.; Zhang, L. FE simulation of sealing ability for premium connection based on ISO 13679 CAL IV tests. Int. J. Struct. Integr. 2021, 12, 138–148. [Google Scholar] [CrossRef]
- Xu, H.; Yang, B.; Zhang, Z.; Shi, T. Elastic-plastic contact stress analysis on sphere to cone sealing structure for tubing and casing premium connection. Chin. J. Appl. Mech. 2021, 38, 1258–1263. [Google Scholar]
- Görtan, M.O. Investigation of Cold Extrusion Process Using Coupled Thermo-Mechanical FEM Analysis and Adaptive Friction Modeling. In AIP Conference Proceedings; AIP Publishing LLC: Dublin, UK, 2017; p. 140011. [Google Scholar]
- Nielsen, C.; Bay, N. Review of friction modeling in metal forming processes. J. Mater. Process. Technol. 2018, 255, 234–241. [Google Scholar] [CrossRef]
- Yoshihiro, N.; Seiichi, N.; Tetsuro, K. Leak-proof tests of special joints for oil country tubular goods. Sumitomo Met. 1974, 26, 97–105. [Google Scholar]
- Zhao, L.; Yan, Y.; Yan, X. Uncertainty analysis framework for tubular connection sealability of underground gas storage wells. J. Loss Prev. Process. Ind. 2021, 72, 104590. [Google Scholar] [CrossRef]
- Xie, J.; Matthews, C.; Hamilton, A. A Study of Sealability Evaluation Criteria for Casing Connections in Thermal Wells. In SPE Canada Heavy Oil Technical Conference; OnePetro: Richardson, TX, USA, 2016. [Google Scholar]
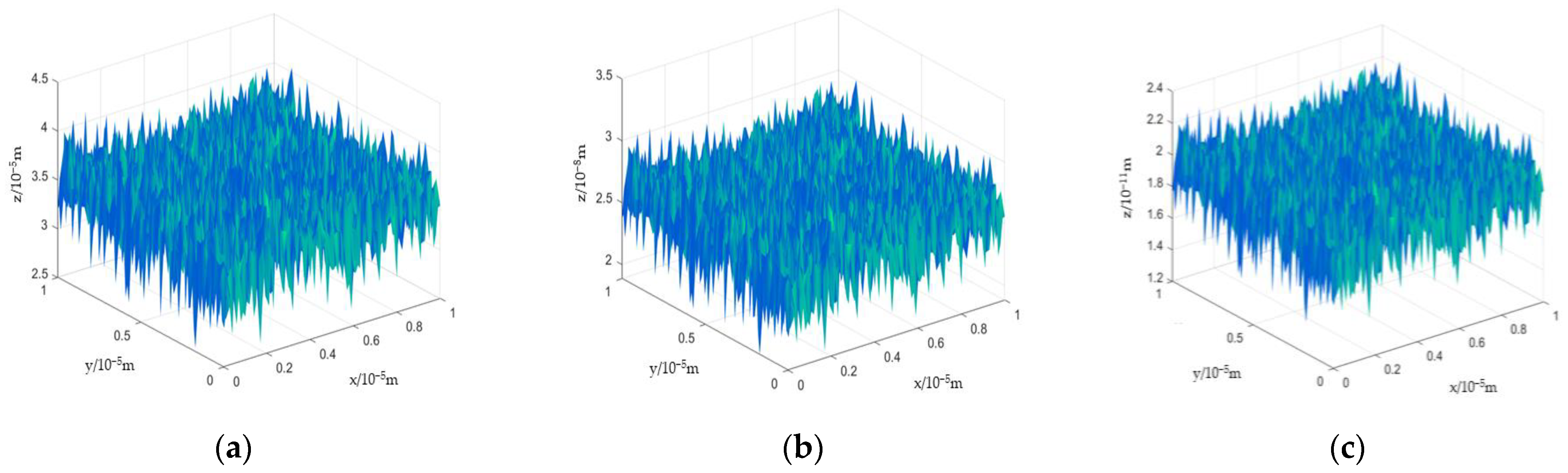


| G (m) | M | γ | L (m) |
|---|---|---|---|
| 1 × 10−13 | 10 | 1.5 | 1 × 10−5 |
| Parameters | D | G (m) | E (Pa) | H (Pa) | γ |
|---|---|---|---|---|---|
| (a) | 2.1–2.9 | 2.0 × 10−9 | 7.58 × 108 | 9.85 × 108 | 1.5 |
| (b) | 2.5 | 1.6–2.4 × 10−9 | 7.58 × 108 | 9.85 × 108 | 1.5 |
| Mesh Size (m) | Number of Element | Maximum Contact Pressure (Pa) | Change Rate of Contact Pressure (%) |
|---|---|---|---|
| 6 × 10−6 | 4319 | 9.75 × 108 | |
| 5 × 10−6 | 5451 | 1.06 × 109 | 8.72 |
| 4 × 10−6 | 6902 | 1.15 × 109 | 8.49 |
| 3 × 10−6 | 10,608 | 1.20 × 109 | 4.35 |
| 2 × 10−6 | 21,584 | 1.14 × 109 | 3.33 |
| 1 × 10−6 | 81,812 | 1.21 × 109 | 4.31 |
| Fractal Dimension D | 2.1 | 2.5 | 2.9 |
|---|---|---|---|
| Maximum Von Mises stress (Pa) | 9.00 × 108 | 8.81 × 108 | 8.53 × 108 |
| Maximum contact pressure (Pa) | 1.39 × 109 | 1.20 × 109 | 7.45 × 108 |
| Axial Tension (N) | Internal Pressure (Pa) | |||||
|---|---|---|---|---|---|---|
| 4 × 105 | 8 × 105 | 1.2 × 106 | 5 × 107 | 7.5 × 107 | 1 × 108 | |
| Average contact pressure (Pa) | 5.13 × 108 | 4.74 × 108 | 4.26 × 108 | 6.75 × 108 | 7.83 × 108 | 8.70 × 108 |
| Effective contact length (m) | 2.57 × 10−3 | 2.57 × 10−3 | 2.09 × 10−3 | 9.08 × 10−3 | 9.48 × 10−3 | 1.05 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Qu, Z.; Cao, Y.; Dou, Y.; Li, J. Sealability Analyses of Premium Connections Characterized by a Surface Fractal Function. Appl. Sci. 2023, 13, 6467. https://doi.org/10.3390/app13116467
Yu Y, Qu Z, Cao Y, Dou Y, Li J. Sealability Analyses of Premium Connections Characterized by a Surface Fractal Function. Applied Sciences. 2023; 13(11):6467. https://doi.org/10.3390/app13116467
Chicago/Turabian StyleYu, Yang, Zhan Qu, Yinping Cao, Yihua Dou, and Juncheng Li. 2023. "Sealability Analyses of Premium Connections Characterized by a Surface Fractal Function" Applied Sciences 13, no. 11: 6467. https://doi.org/10.3390/app13116467
APA StyleYu, Y., Qu, Z., Cao, Y., Dou, Y., & Li, J. (2023). Sealability Analyses of Premium Connections Characterized by a Surface Fractal Function. Applied Sciences, 13(11), 6467. https://doi.org/10.3390/app13116467





