Optimized Design of Flexible Quick-Change System Based on Genetic Algorithm and Monte Carlo Method
Abstract
:1. Introduction
2. Material and Methods
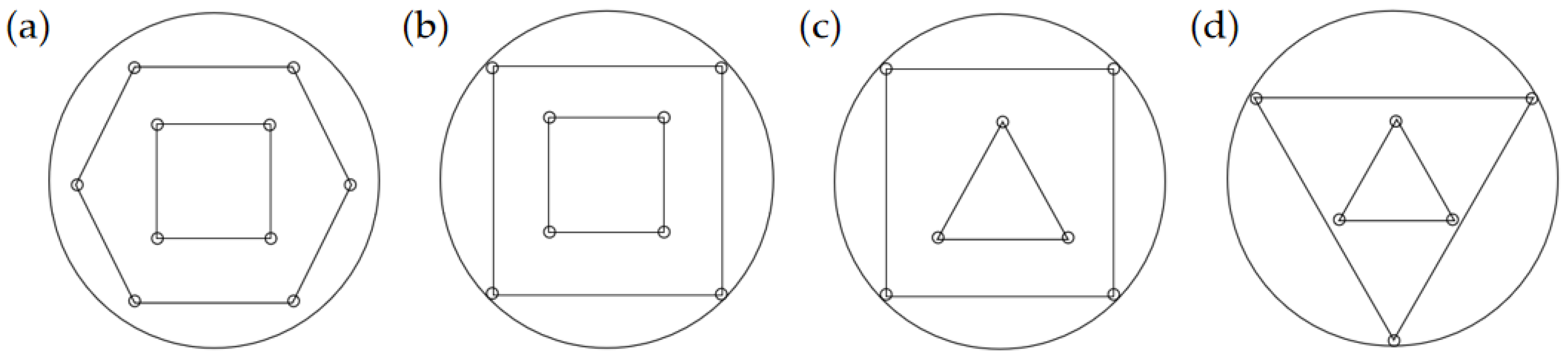
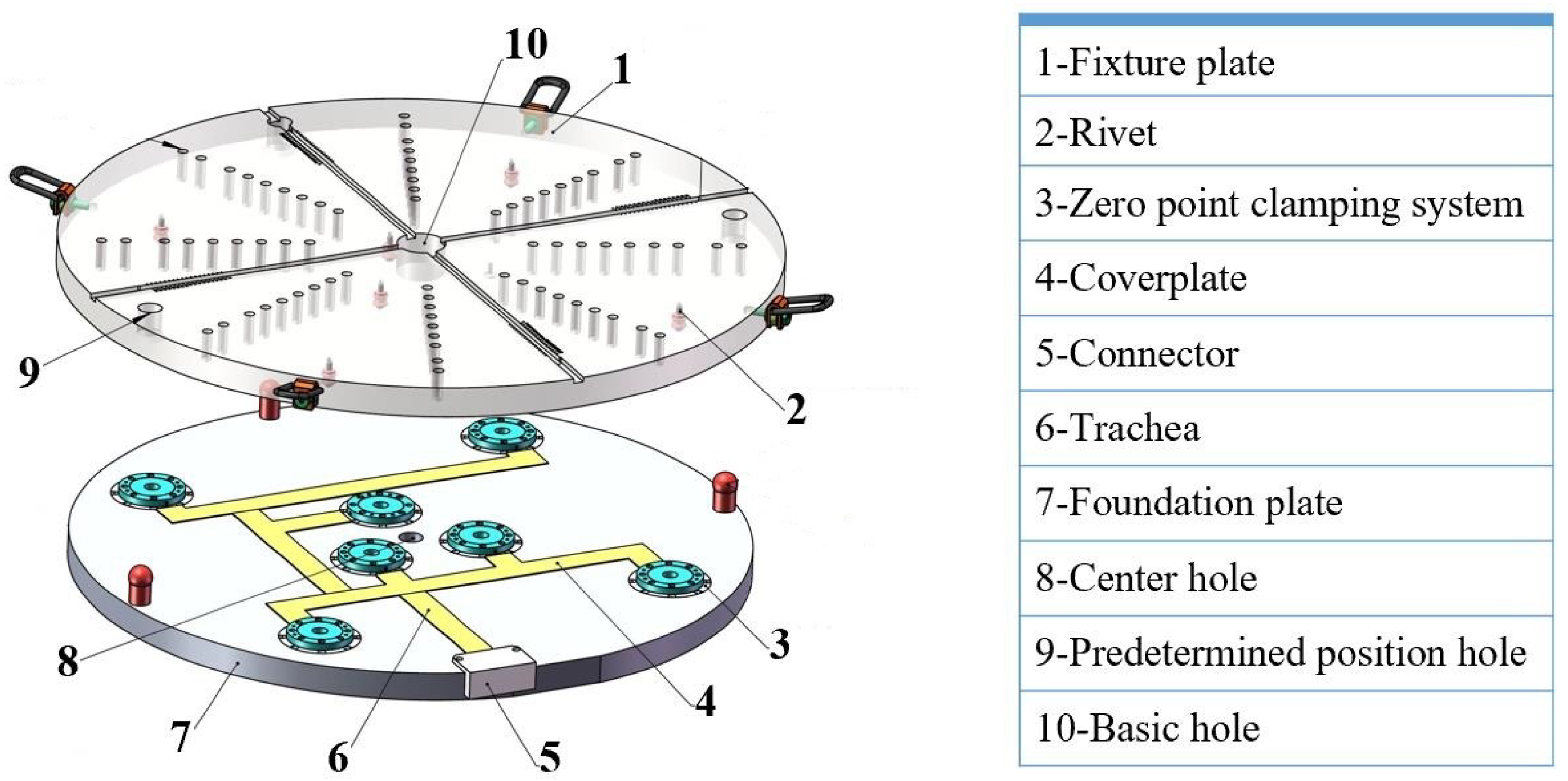
2.1. Layout Structure Design Optimization of a Flexible Quick-Change Process System
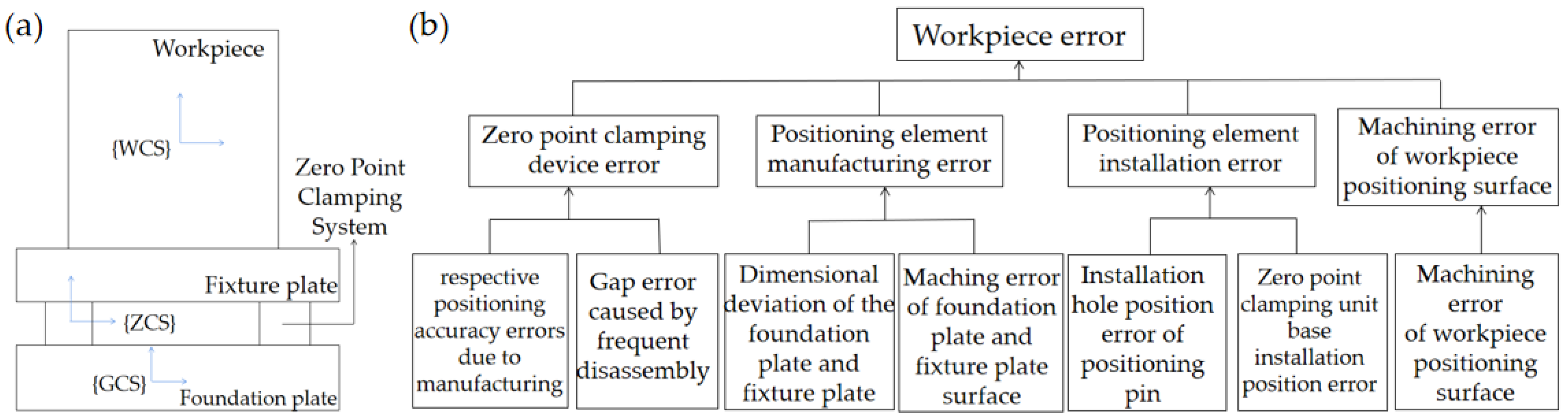
2.2. Error Model and Optimization of a Flexible Quick-Change Process System Based on the Monte Carlo Method
2.2.1. Zero Point Clamping Unit Error Model
2.2.2. Error Model Caused by Components except the Zero Point Clamping Unit
3. Results and Discussion
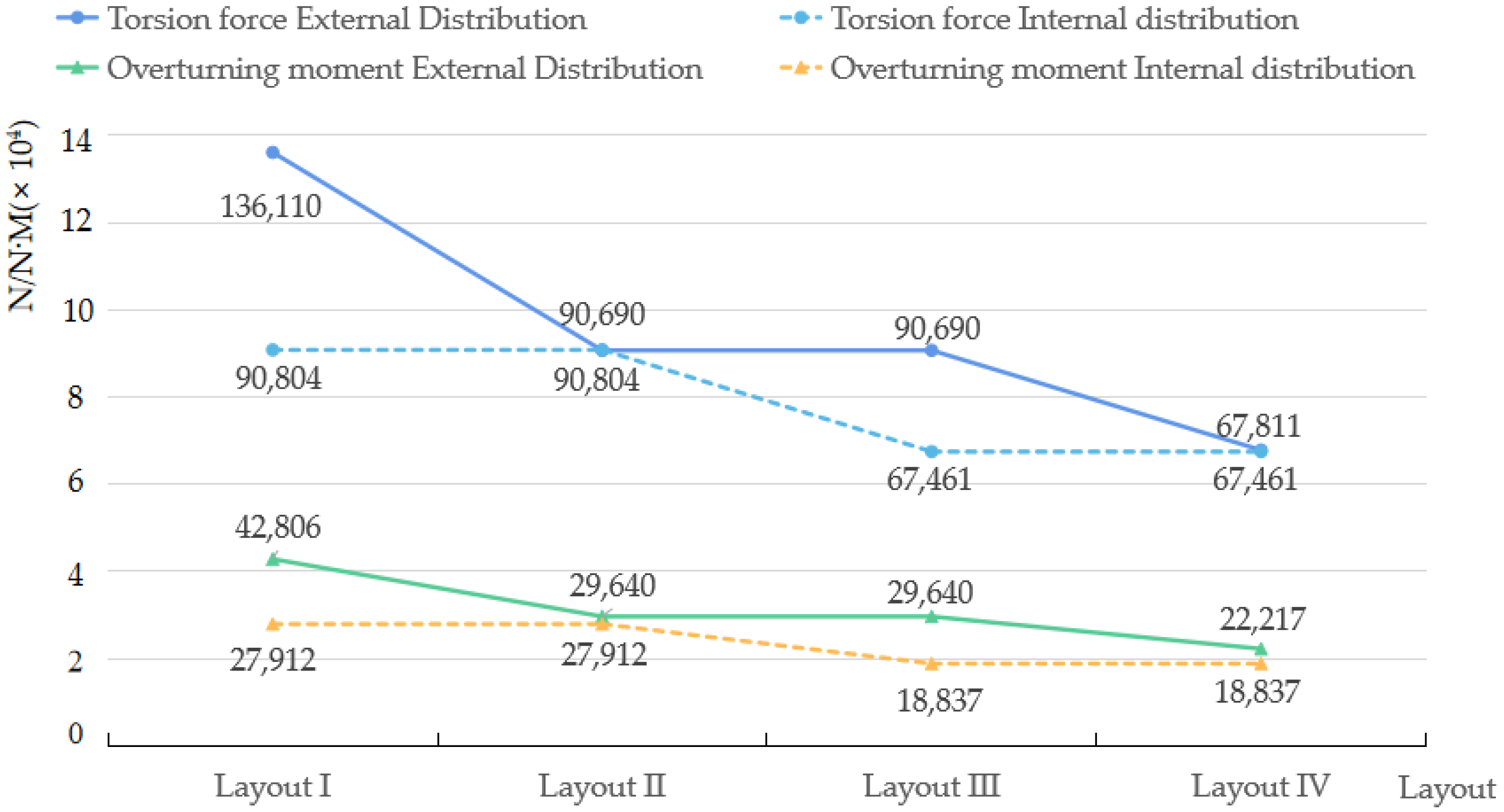
3.1. Mechanical Properties of the Different Zero Point Positioning Unit Layouts
3.2. Optimization of Positioning Error of a Flexible Quick-Change Process System Based on the Monte Carlo Method
3.3. Finite Element Simulation Analysis of a Flexible Quick-Change Process System
3.3.1. Flexible Quick-Change Process System Lifting and Changing Process Error Analysis
3.3.2. Flexible Quick-Change Process System Extreme Working Condition Error Analysis
3.4. Functional Verification Experiment Analysis of the Flexible Quick-Change System
4. Conclusions
- (1)
- The flexible quick-change process system is capable of quickly clamping off-line, moving machined pieces, and aligning them. In contrast to the flexible quick-change process system, which uses zero point clamping technology, each changeover only takes 2 min. This significantly reduces machine downtime by 79% and boosts changeover efficiency by 53%, ultimately increasing machining efficiency. Most importantly, the system provides a high level of repetitive positioning accuracy (0.0041–0.0081 mm);
- (2)
- The maximum shear force, torsion force, and overturning force that the flexible quick-change system can withstand are the vectorial combinations of the forces on each zero point clamping unit, and they all increase with the increase in the distribution number of zero point clamping units. However, with the same number of positioning units, the repeated positioning accuracy will increase with the increase in distance between the two zero point clamping units, and the applied force and the average strain of the system will be slightly changed. The “dot matrix” zero layout structure is determined through genetic algorithm optimization (four positioning units are squarely distributed in the outer circle and located in the position of the radius of the outer circle, which is 537.67 mm, and three positioning units are regular triangles distributed in the inner circle). By using the optimization algorithm, blind design based on experience can be avoided, and the flexible quick-change system can bear a greater load and have high positioning accuracy;
- (3)
- The Monte Carlo method was used to analyze the influence of system load and extreme working conditions on six components of workpiece pose deviation in the process of lifting transposition, and it was concluded that the displacement deviation and rotation angle deviation obeyed normal distribution within a certain range. However, each error source has a different sensitivity to the overall pose error of the workpiece. By optimizing the Z-axis flatness with a greater error sensitivity of 0.01 mm, the repetitive positioning accuracy of the system is controlled within 0.01 mm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bao, Y.; Wang, B.; He, Z.X.; Kang, R.K.; Guo, J. Recent progress in flexible supporting technology for aerospace thin-walled parts: A review. Acad. J. Second. Mil. Med. Univ. 2022, 35, 10–26. [Google Scholar] [CrossRef]
- Yuan, Y.H.; Gu, D.D.; Lin, K.J.; Ge, Q.; Shi, X.Y.; Wang, H.R.; Hu, K.M. Influence of structural features on processability, microstructures, chemical compositions, and hardness of selective laser melted complex thin-walled components. Int. J. Adv. Manuf. Technol. 2020, 109, 1643–1654. [Google Scholar] [CrossRef]
- Hao, Q.L.; Yang, Q. A self-adaptive auxiliary fixture for deformation control in blade machining. Int. J. Adv. Manuf. Technol. 2020, 111, 1415–1423. [Google Scholar] [CrossRef]
- Ding, G.Z.; Wang, Y.F.; Yuan, S.M.; Lin, L.; Zhao, Z.C. Research on Rapid and Accurate Fixture Design for Non-Intervention Machining of Complex Parts. Metals 2022, 12, 1174. [Google Scholar] [CrossRef]
- Li, X.Y.; Yang, Y.F.; Li, L.; Shi, Y.W.; Zhao, G.L.; He, N.; Qian, N.; Mu, Z. An Approach for Optimising the Fixturing Configuration in Flexible Machining Fixtures. Int. J. Prod. Res. 2021, 59, 6223–6240. [Google Scholar] [CrossRef]
- Liu, Y.; Guan, S.X.; Zhao, H.; Liu, W.E.; Duan, L.C.; Sha, Y.D. Evolutionary Design of Machining Fixture Layout for Thin-Walled Structure. Math. Probl. Eng. 2022, 2022, 5216966. [Google Scholar] [CrossRef]
- Rex, F.M.T.; Hariharasakthisudhan, P.; Andrews, A.; Abraham, B.P. Optimization of flexible fixture layout to improve form quality using parametric finite element model and mixed discrete-integer genetic algorithm. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2022, 236, 16–29. [Google Scholar]
- Aderiani, A.R.; Warmefjord, K.; Soderberg, R.; Lindkvist, L.; Lindau, B. Optimal design of fixture layouts for compliant sheet metal assemblies. Int. J. Adv. Manuf. Technol. 2020, 110, 2181–2201. [Google Scholar] [CrossRef]
- Wu, D.B.; Zhao, B.; Wang, H.; Zhang, K.Y.; Yu, J. Investigate on computer-aided fixture design and evaluation algorithm for near-net-shaped jet engine blade. J. Manuf. Process. 2020, 54, 393–412. [Google Scholar] [CrossRef]
- Wu, B.H.; Zheng, Z.Y.; Wang, J.; Zhang, Z.; Zhang, Y. Layout optimization of auxiliary support for deflection errors suppression in end milling of flexible blade. Int. J. Adv. Manuf. Technol. 2021, 115, 1889–1905. [Google Scholar] [CrossRef]
- Du, J.; Liu, C.H.; Liu, J.F.; Zhang, Y.S.; Shi, J.J. Optimal Design Of Fixture Layout For Compliant Part With Application In Ship Curved Panel Assembly. J. Manuf. Sci. Eng. 2021, 143, 061007. [Google Scholar] [CrossRef]
- Vinosh, M.; Raj, T.N.; Prasath, M. Optimization of Sheet Metal Resistance Spot Welding Process Fixture Design. Mater. Today Proc. 2021, 45, 1696–1700. [Google Scholar] [CrossRef]
- Ramesh, M.; Sundararaman, K.A. Development of Hybrid Artificial Neural Network–Particle Swarm Optimization Model and Comparison of Genetic and Particle Swarm Algorithms for Optimization of Machining Fixture Layout. Int. J. Precis. Eng. Manuf. 2022, 23, 1411–1430. [Google Scholar] [CrossRef]
- Qazani, M.R.C.; Parvaz, H.; Pedrammehr, S. Optimization of fixture locating layout design using comprehensive optimized machine learning. Int. J. Adv. Manuf. Technol. 2022, 122, 2701–2717. [Google Scholar] [CrossRef]
- Yu, K.G. Robust fixture design of compliant assembly process based on a support vector regression model. Int. J. Adv. Manuf. Technol. 2019, 103, 111–126. [Google Scholar] [CrossRef]
- Dosdoğru, A.T.; Göçken, M.; Geyik, F. Integration of genetic algorithm and Monte Carlo to analyze the effect of routing flexibility. Int. J. Adv. Manuf. Technol. 2015, 81, 1379–1389. [Google Scholar] [CrossRef]
- Munavalli, J.R.; Rao, S.V.; Srinivasan, A.; Van Merode, F. Dynamic Layout Design Optimization to Improve Patient Flow in Outpatient Clinics Using Genetic Algorithms. Algorithms 2022, 15, 85. [Google Scholar] [CrossRef]
- Liu, Z.; Hong, H.; Gan, Z.; Chen, Y.; Xing, K. Flexible Zoom Telescopic Optical System Design Based on Genetic Algorithm. Photonics 2022, 9, 536. [Google Scholar] [CrossRef]
- Zhao, X.S.; Tan, R.K.; Wang, Z.; Zou, X.C.; Hu, Z.J.; Sun, T. The Design and Implementation of a High-Precision Positioner Fixture. Micromachines 2021, 12, 1227. [Google Scholar] [CrossRef]
- Liu, Y.X.; Liang, Q.H.; Luo, L. Prediction and Analysis of Fixture Positioning Error Based on Monte Carlo Simulation. Mach. Des. Res. 2019, 35, 104–109+113. [Google Scholar]
- Guo, F.Y.; Liu, J.H.; Wang, Z.Q.; Zou, F.; Zhao, X.D. Positioning error guarantee method with two-stage compensation strategy for aircraft flexible assembly tooling. J. Manuf. Syst. 2020, 55, 285–301. [Google Scholar] [CrossRef]
- Butt, S.U.; Arshad, M.; Baqai, A.A.; Saeed, H.A.; Din, N.A.; Khan, R.A. Locator Placement Optimization For Minimum Part Positioning Error During Machining Operation Using Genetic Algorithm. Int. J. Precis. Eng. Manuf. 2021, 22, 1169. [Google Scholar] [CrossRef]
- Yang, F.Y.; Xing, Y.F.; Li, X.X. A comprehensive error compensation strategy for machining process with general fixture layouts. Int. J. Adv. Manuf. Technol. 2020, 107, 2707–2717. [Google Scholar] [CrossRef]
- Peng, D.Q.; Wang, L.M.; Shao, Y.M. Position prediction and error compensation for a large thin-walled box-shaped workpiece in a fixture. Int. J. Adv. Manuf. Technol. 2021, 116, 2633–2649. [Google Scholar] [CrossRef]




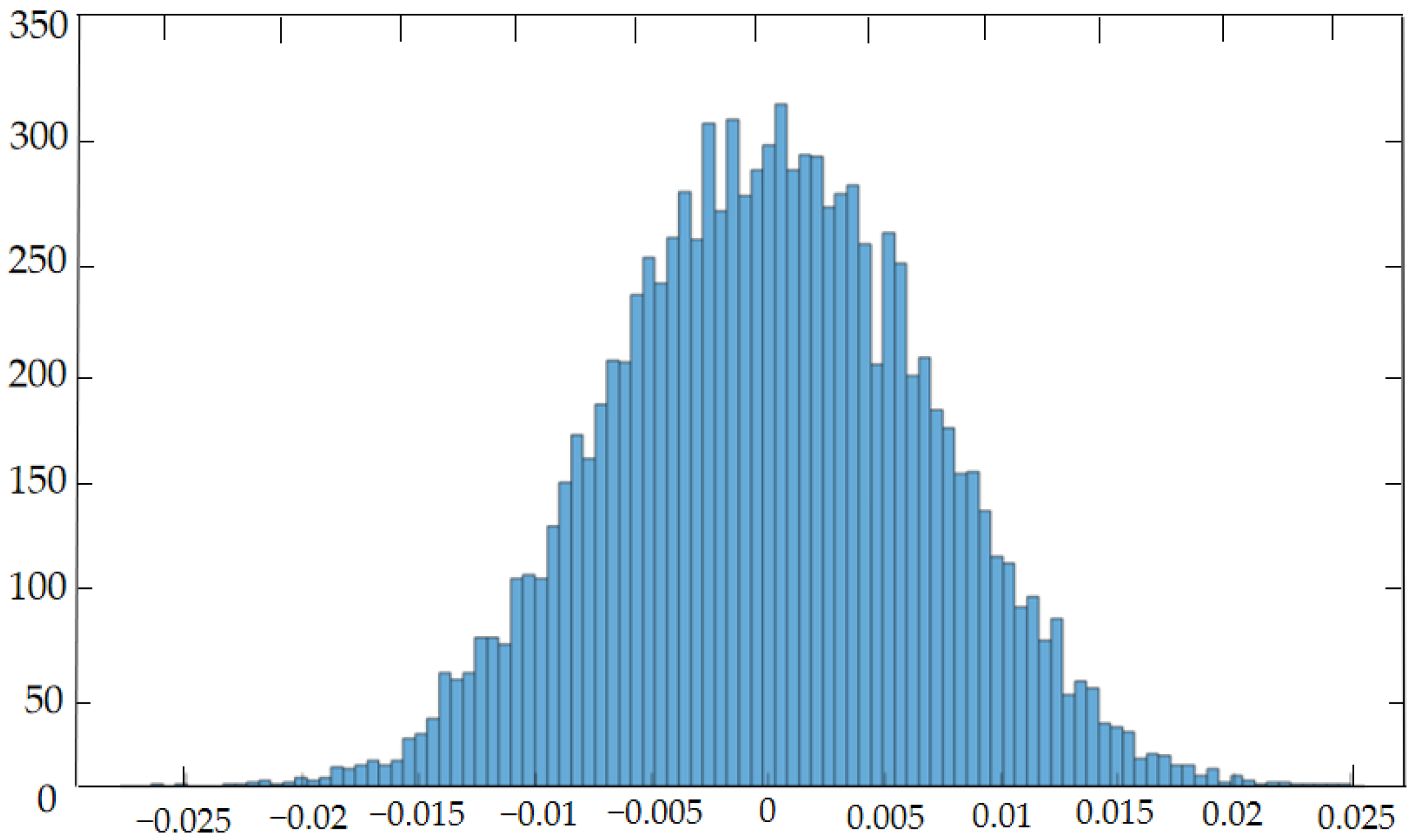
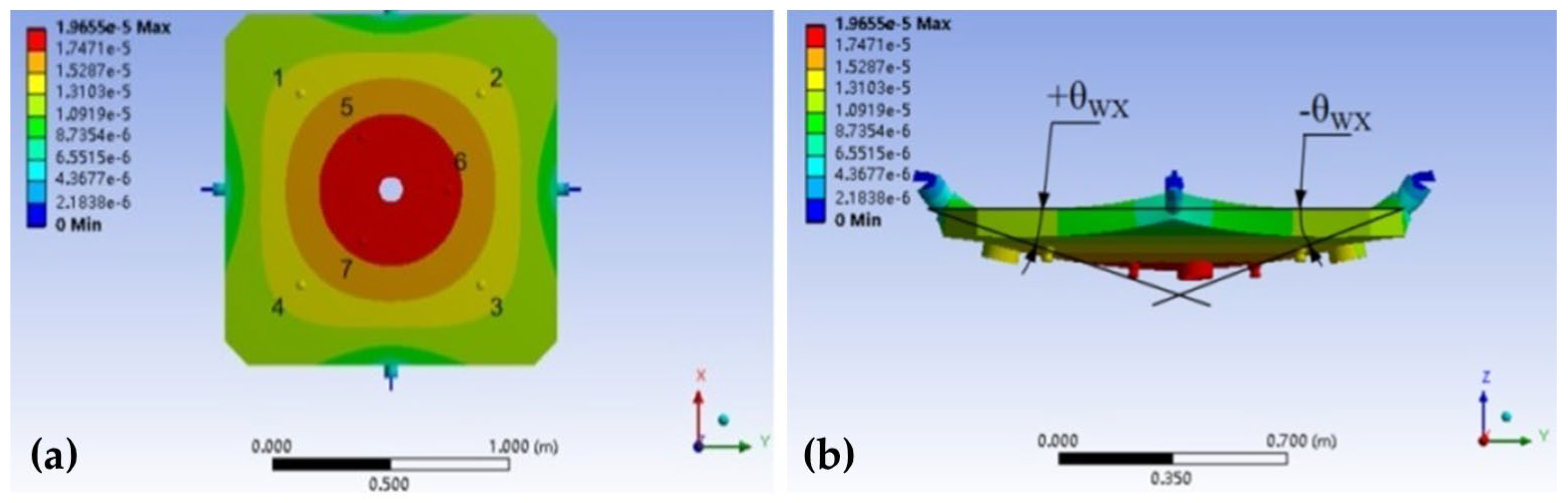
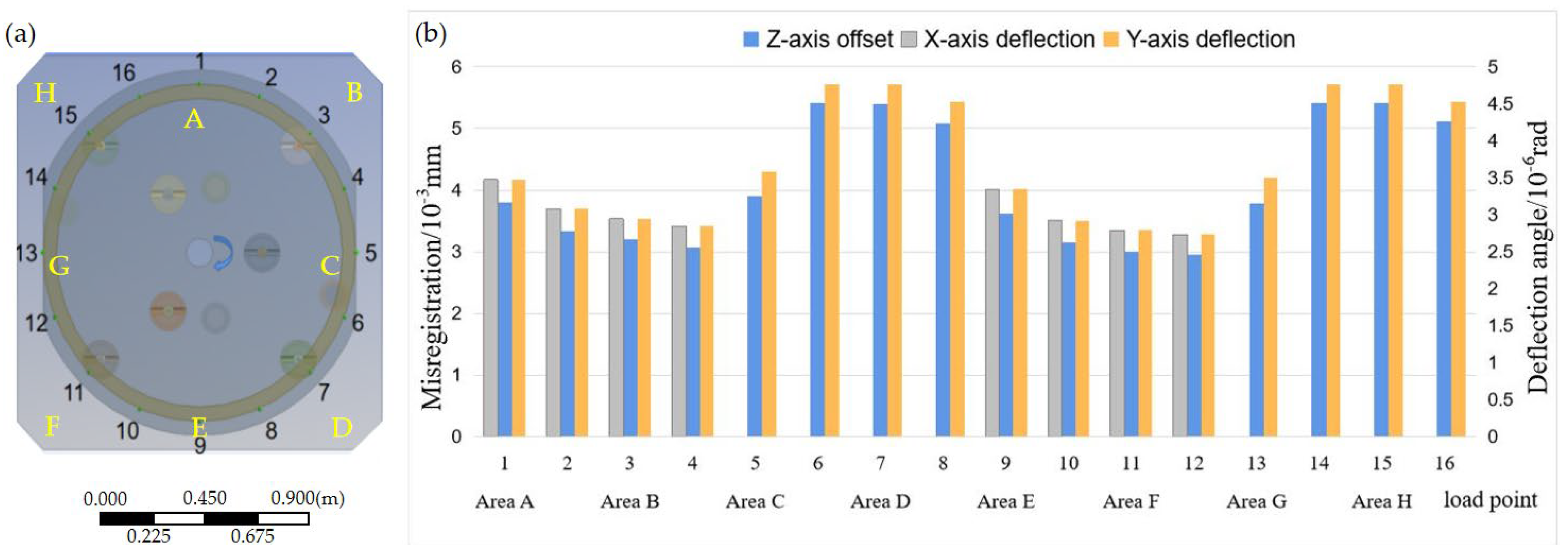

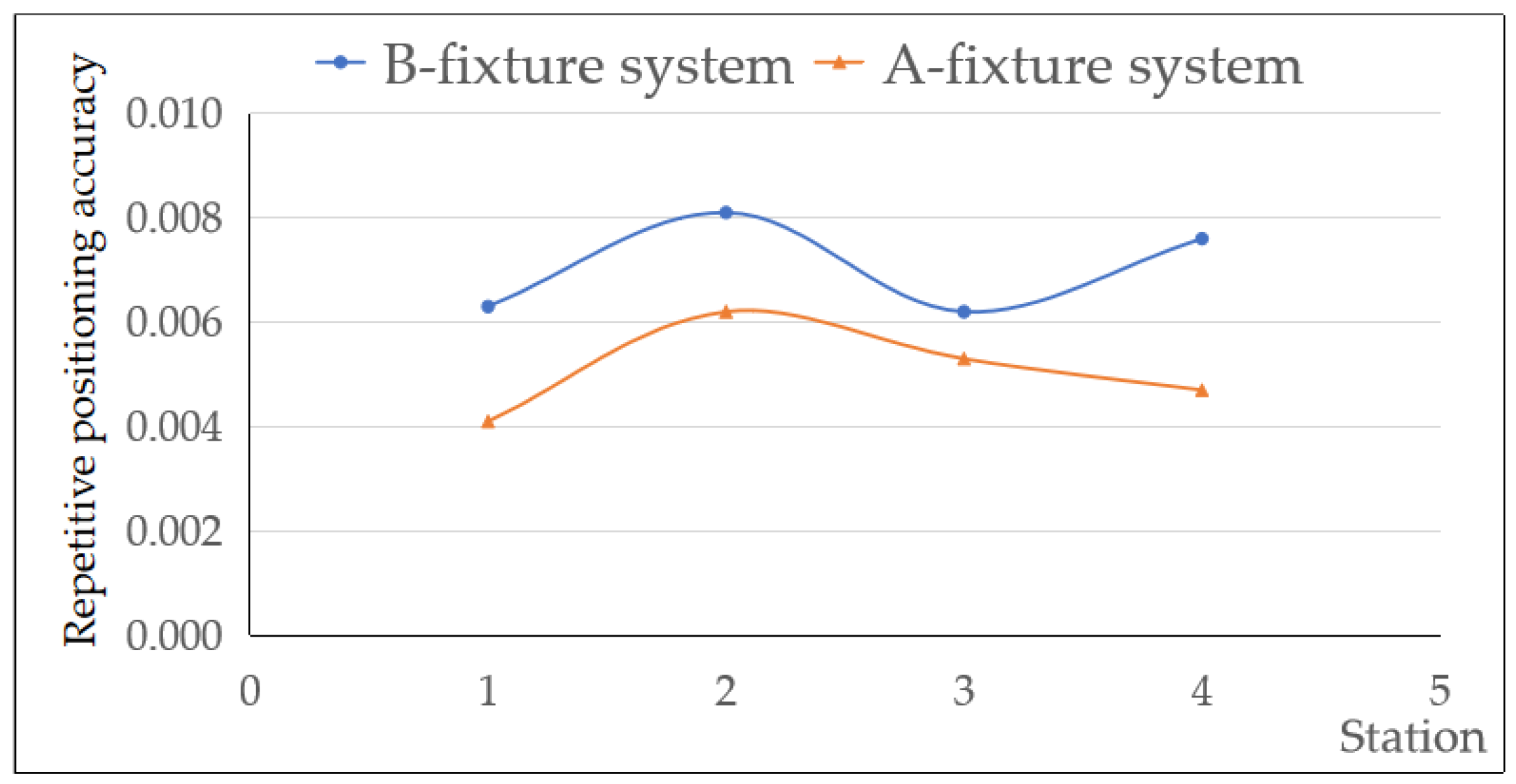
| X-Axis (ΔX) | Y-Axis (ΔY) | Z-Axis (ΔZ) | |
|---|---|---|---|
| Outer ring positioning pin | 3.8 × 10−3 mm | 3.8 × 10−3 mm | 1.52 × 10−5 mm |
| Inner ring positioning pin | 3.2 × 10−3 mm | 2 × 10−3 mm | 1.96 × 10−5 mm |
| Foundation Plate | Fixture Plate A | Fixture Plate B | |
|---|---|---|---|
| Position error (mm) | 0.0026~0.0094 | 0.0012~0.0128 | 0.0023~0.0098 |
| Flatness error (mm) | 0.0114 | 0.0067 | 0.0079 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Zhang, Y.; Wu, J.; Wu, G.; Li, C.; Zhang, Z. Optimized Design of Flexible Quick-Change System Based on Genetic Algorithm and Monte Carlo Method. Appl. Sci. 2023, 13, 6482. https://doi.org/10.3390/app13116482
Zhang H, Zhang Y, Wu J, Wu G, Li C, Zhang Z. Optimized Design of Flexible Quick-Change System Based on Genetic Algorithm and Monte Carlo Method. Applied Sciences. 2023; 13(11):6482. https://doi.org/10.3390/app13116482
Chicago/Turabian StyleZhang, Huang, Yuehong Zhang, Jianan Wu, Guihua Wu, Chunlei Li, and Zhiqi Zhang. 2023. "Optimized Design of Flexible Quick-Change System Based on Genetic Algorithm and Monte Carlo Method" Applied Sciences 13, no. 11: 6482. https://doi.org/10.3390/app13116482
APA StyleZhang, H., Zhang, Y., Wu, J., Wu, G., Li, C., & Zhang, Z. (2023). Optimized Design of Flexible Quick-Change System Based on Genetic Algorithm and Monte Carlo Method. Applied Sciences, 13(11), 6482. https://doi.org/10.3390/app13116482






