A Non-Linear Non-Planar Coupling Mechanism of Suspended Cables in Thermal Conditions
Abstract
:1. Introduction
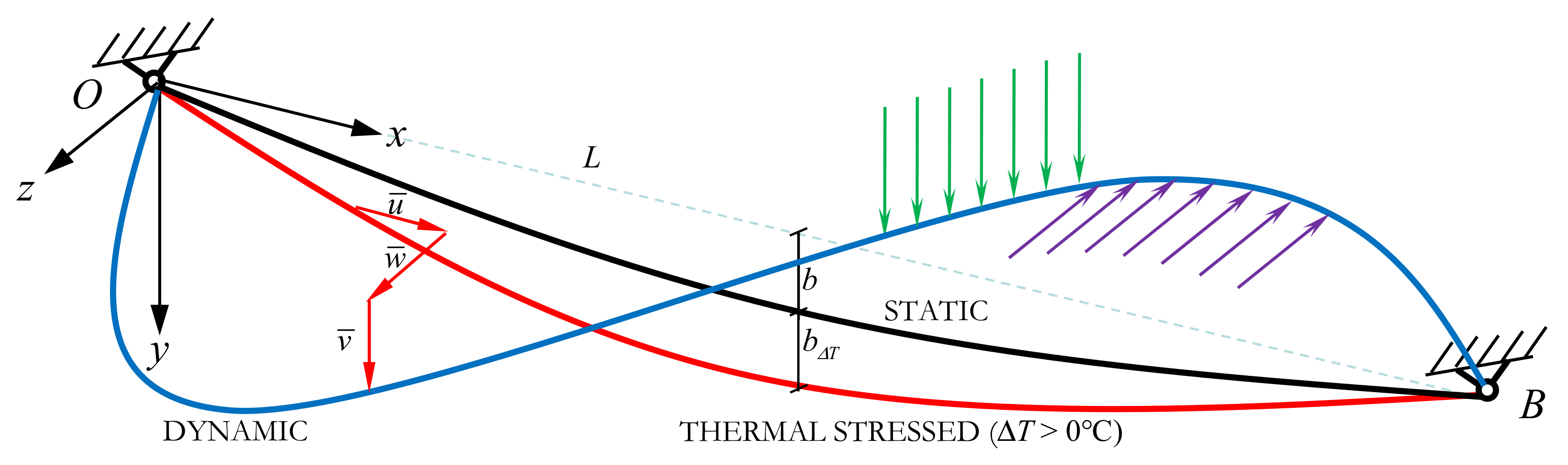
2. Mathematical Modeling and Equations
3. Perturbation Analysis and Modulation Equations
4. Numerical Examples and Illustrations
4.1. Parameters and Coefficients
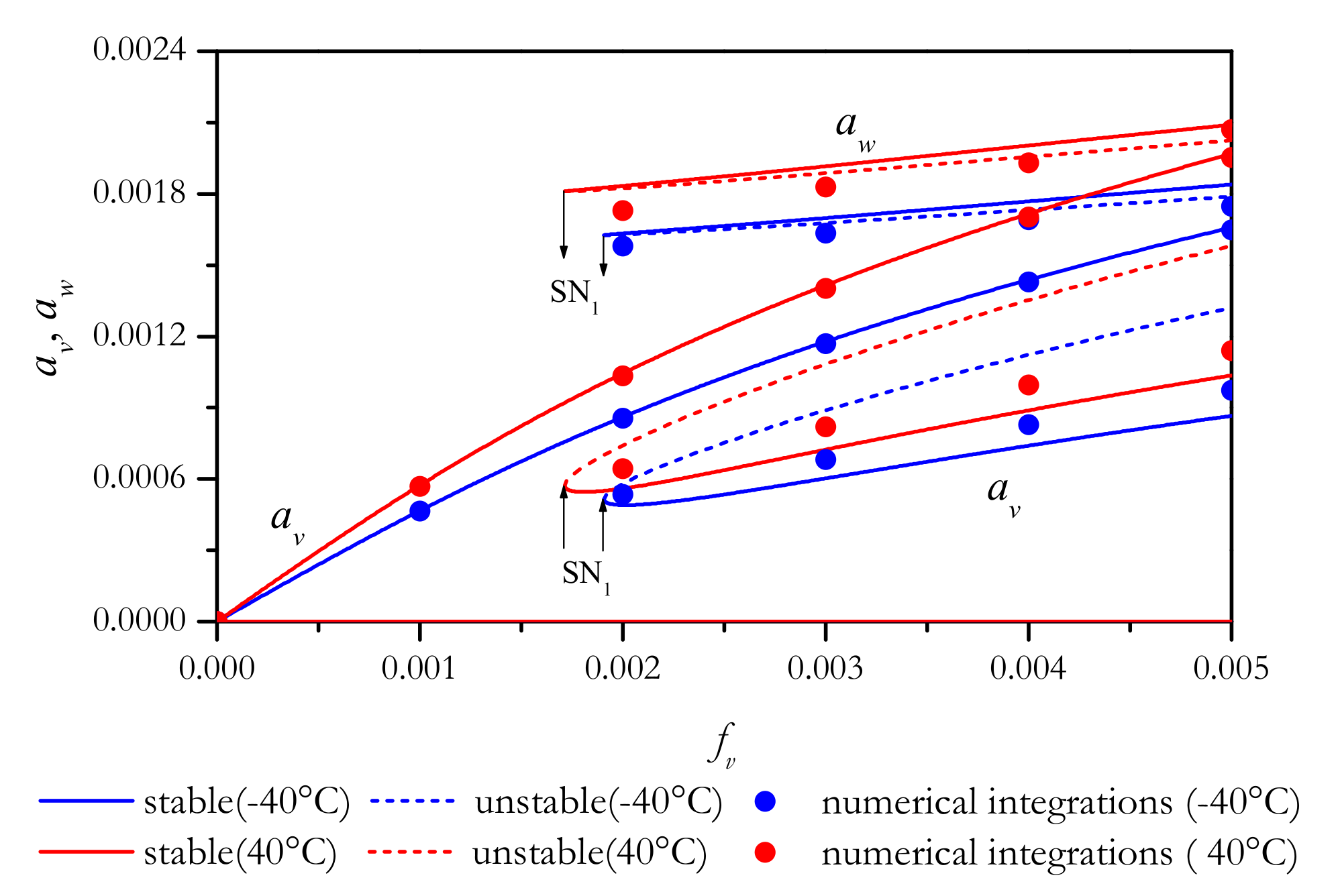
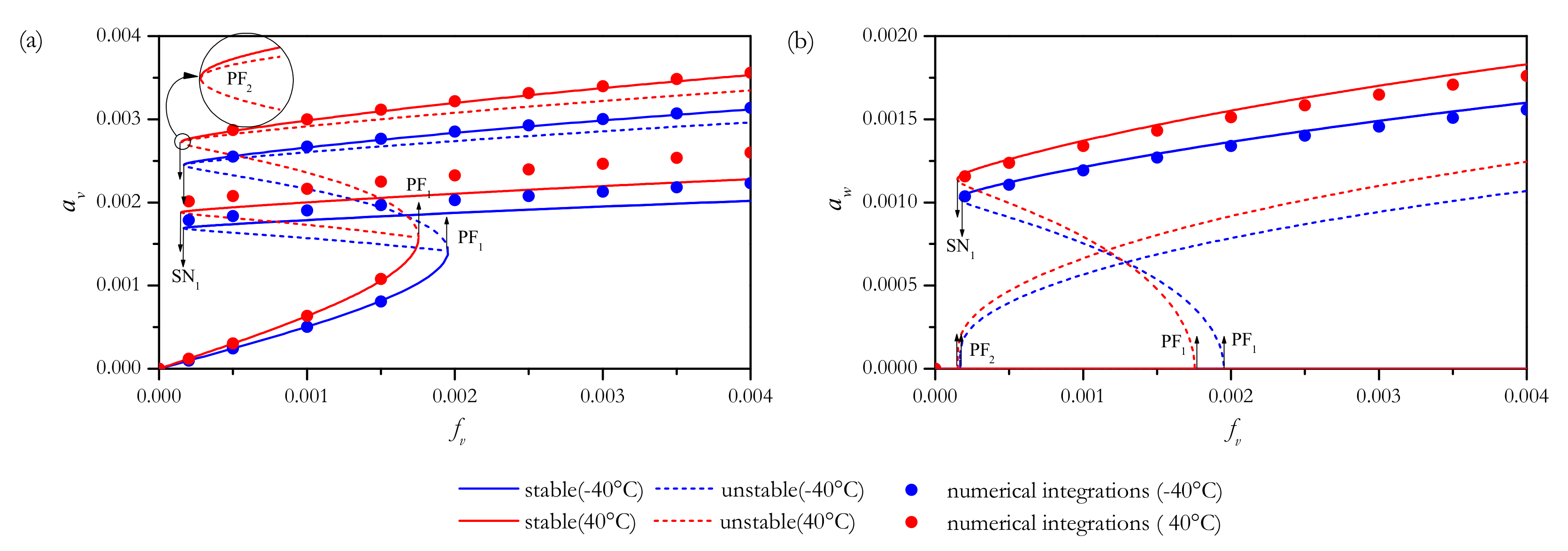
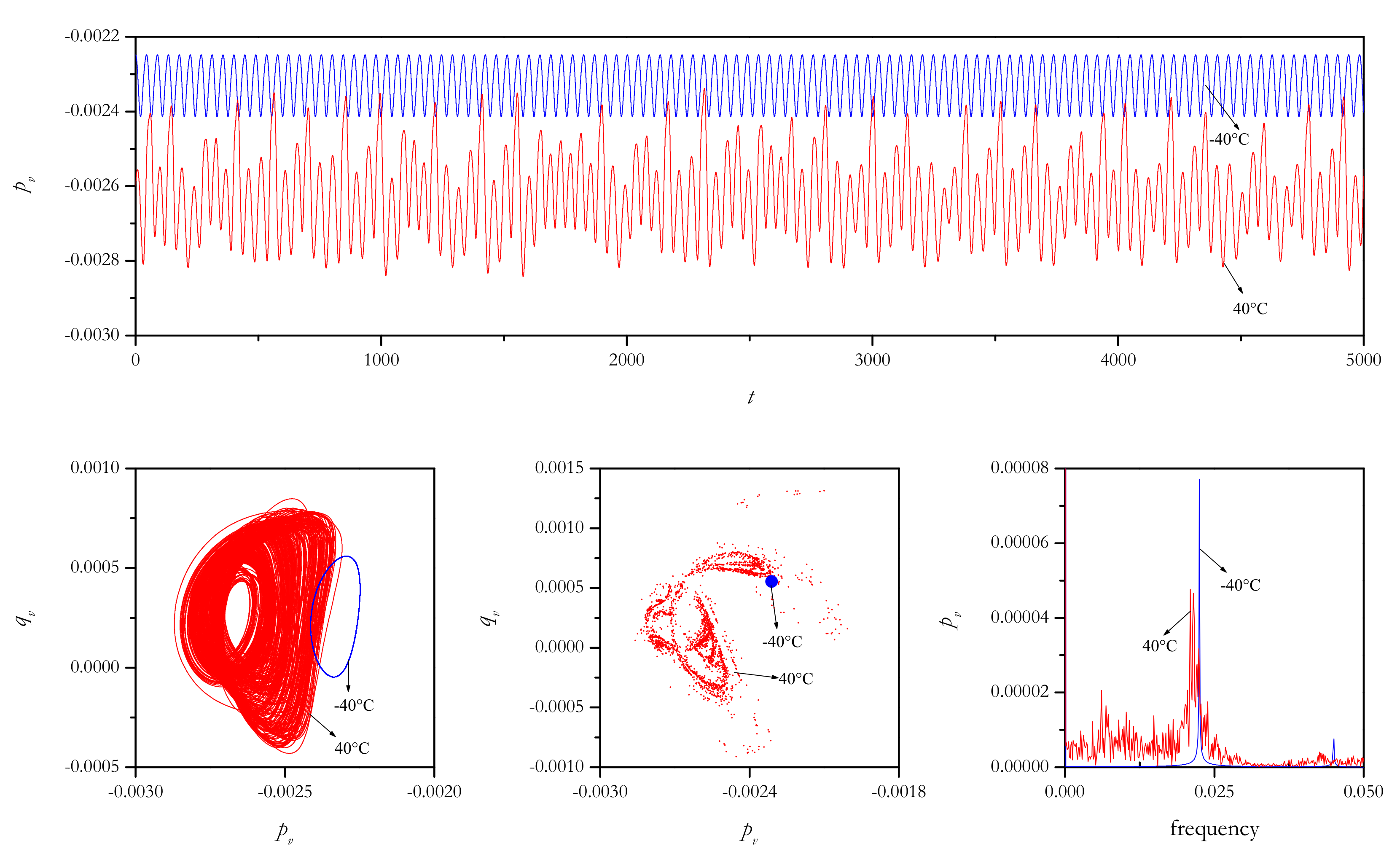
4.2. Bifurcation and Stability Analysis
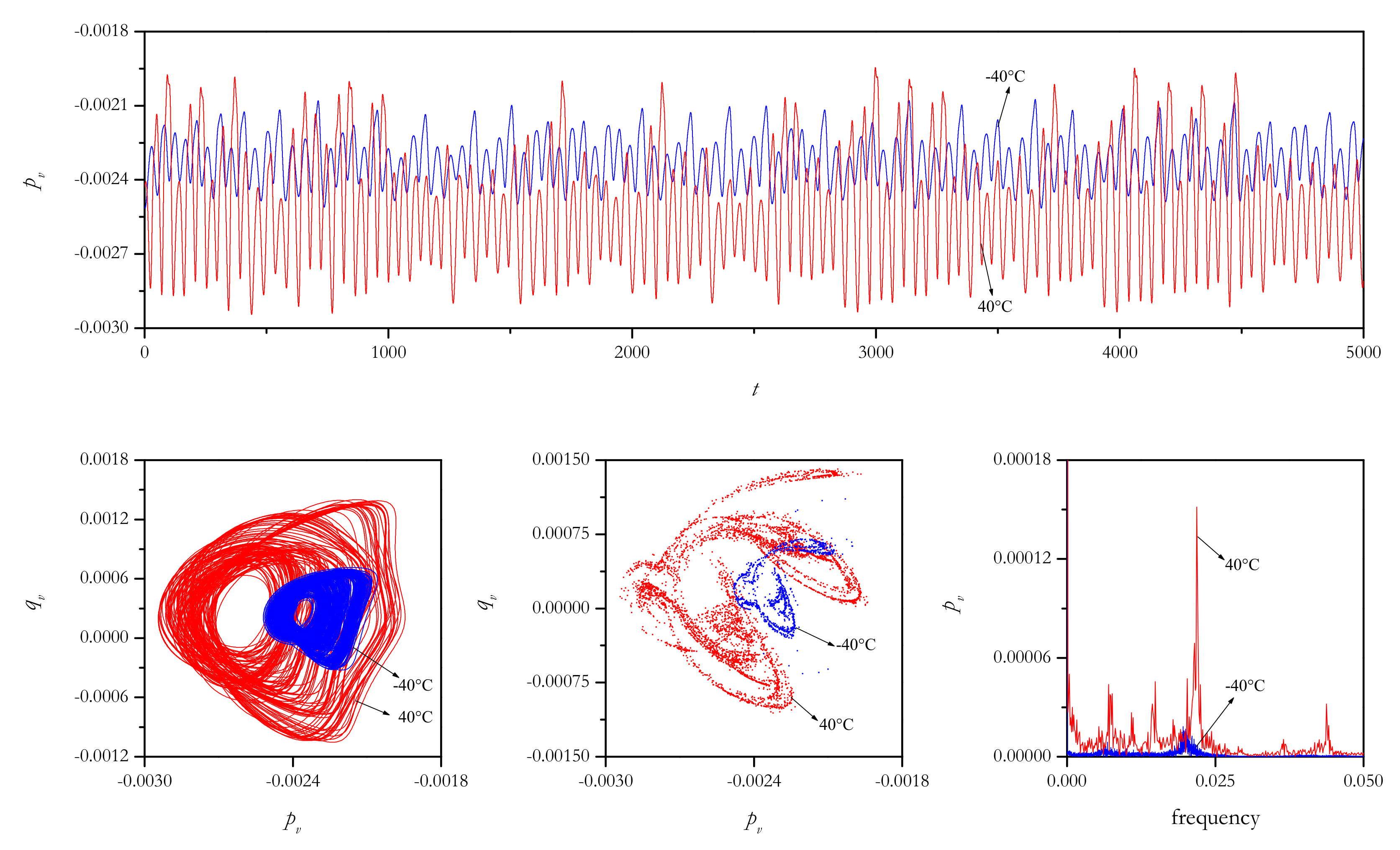
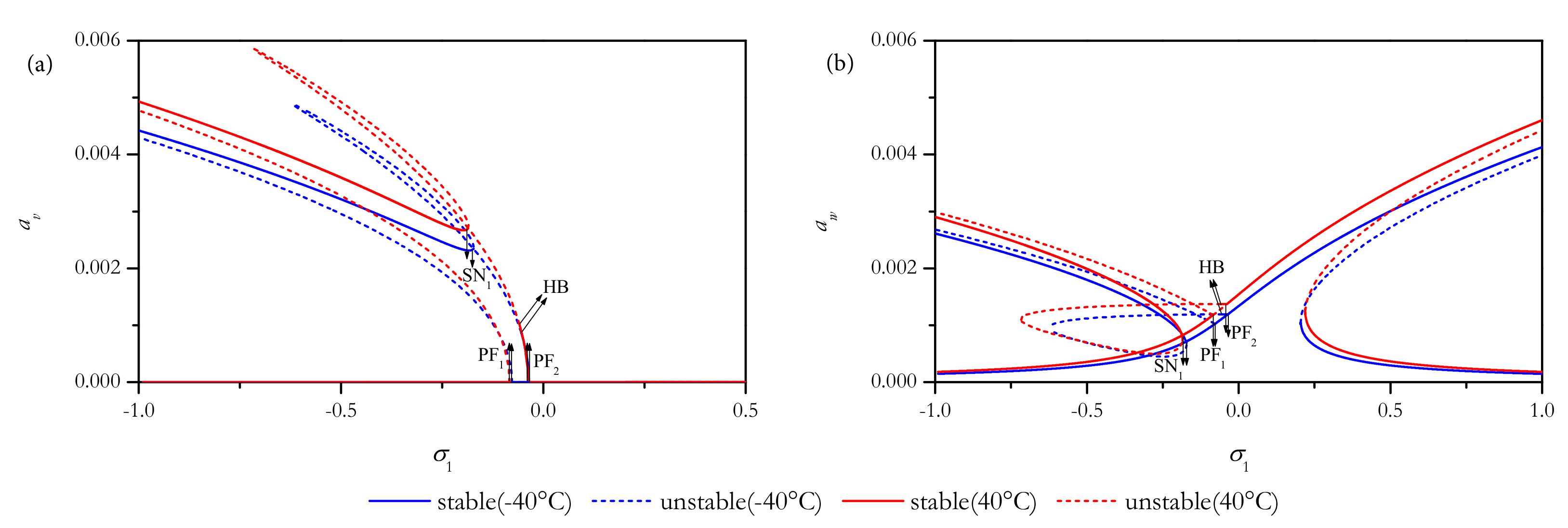
4.2.1. In-Plane Excitations
4.2.2. Out-of-Plane Excitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Warminski, J.; Zulli, D. Revisited modelling and multimodal non-linear oscillations of a sagged cable under support motion. Meccanica 2016, 51, 2541–2575. [Google Scholar] [CrossRef]
- Yi, Z. Stanciulescu I. Non-linear normal modes of a shallow arch with elastic constraints for two-to-one internal resonances. Non-Linear Dyn. 2016, 83, 1577–1600. [Google Scholar] [CrossRef]
- Qiao, W.; Guo, T.; Kang, H.; Zhao, Y. An asymptotic study of non-linear coupled vibration of arch-foundation structural system. Eur. J. Mech. Solid. 2022, 96, 104711. [Google Scholar] [CrossRef]
- Peng, J.; Xiang, M.; Wang, L.; Xie, X.; Sun, H.; Yu, J. Non-linear primary resonance in vibration control of cable-stayed beam with time delay feedback. Mech. Sys. Sig. Proc. 2020, 137, 106488. [Google Scholar] [CrossRef]
- Cong, Y.; Kang, H.; Yan, G.; Guo, T. Modeling, dynamics, and parametric studies of a multi-cable-stayed beam model. Acta Mech. 2020, 231, 4947–4970. [Google Scholar] [CrossRef]
- Gattulli, V.; Lepidi, M.; Potenza, F.; Sabatino, U.D. Modal interactions in the non-linear dynamics of a beam-cable-beam. Non-Linear Dyn. 2019, 96, 2547–2566. [Google Scholar] [CrossRef]
- Sun, C.; Jiao, D.; Lin, J.; Li, C.; Tan, C. Modal characteristics of sagged-cable-crosstie systems. Part 1: Modeling and validation. Appl. Math. Model. 2023, 119, 698–716. [Google Scholar] [CrossRef]
- Sun, C.; Liu, W.; Jiao, D.; Li, C. Modal characteristics of sagged-cable-crosstie systems. Part 2: Parametric analysis. Appl. Math. Model. 2023, 119, 549–565. [Google Scholar] [CrossRef]
- Wang, Z.; Li, T.; Yao, S. Non-linear dynamic analysis of space cable net structures with one to one internal resonances. Non-Linear Dyn. 2014, 78, 1461–1475. [Google Scholar] [CrossRef]
- Rega, G. Non-linear vibrations of suspended cables Part I: Modeling and analysis. Appl. Mech. Rev. 2004, 57, 443–478. [Google Scholar] [CrossRef]
- Srinil, N.; Rega, G.; Chucheepsakul, S. Large amplitude three-dimensional free vibrations of inclined sagged elastic cables. Non-Linear Dyn. 2003, 33, 129–154. [Google Scholar] [CrossRef]
- Rega, G. Non-linear vibrations of suspended cables, Part II: Deterministic phenomena. Appl. Mech. Rev. 2004, 57, 479–514. [Google Scholar] [CrossRef]
- Perkins, N.C. Modal interactions in the non-linear response of elastic cables under parametric/external excitation. Int. J. Non-Linear Mech. 1992, 27, 233–250. [Google Scholar] [CrossRef]
- Benedettini, F.; Rega, G.; Alaggio, R. Non-linear oscillations of a four-degree-of-freedom model of a suspended cable under multiple internal resonance conditions. J. Sound Vib. 1995, 182, 775–798. [Google Scholar] [CrossRef]
- Pakdemirli, M.; Nayfeh, S.A.; Nayfeh, A.H. Analysis of one-to-one autoparametric resonances in cables—Discretization vs. direct treatment. Non-Linear Dyn. 1995, 8, 65–83. [Google Scholar] [CrossRef]
- Lee, C.; Perkins, N.C. Three-dimensional oscillations of suspended cables involving simultaneous internal resonances. Non-Linear Dyn. 1995, 8, 45–63. [Google Scholar] [CrossRef]
- Rega, G.; Lacarbonara, W.; Nayfeh, A.H.; Chin, C.M. Multiple resonances in suspended cables: Direct versus reduced-order models. Int. J. Non-Linear Mech. 1999, 34, 901–924. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Chin, C.M.; Lacarbonara, W. Multimode interactions in suspended cables. J. Vib. Control 2002, 8, 337–387. [Google Scholar] [CrossRef]
- Gattulli, V.; Martinelli, L.; Perotti, F.; Vestroni, F. Non-linear oscillations of cables under harmonic loading using analytical and finite element models. Comput. Methods Appl. Mech. Eng. 2004, 193, 69–85. [Google Scholar] [CrossRef]
- Berlioz, A.; Lamarque, C.-H. A non-linear model for the dynamics of an inclined cable. J. Sound Vib. 2005, 279, 619–639. [Google Scholar] [CrossRef]
- Srinil, N.; Rega, G. The effects of kinematic condensation on internally resonant forced vibrations of shallow horizontal cables. Int. J. Non-Linear Mech. 2007, 42, 180–195. [Google Scholar] [CrossRef]
- Gonzalez-Buelga, A.; Neild, S.A.; Wagg, D.J.; Macdonald, J.H.G. Modal stability of inclined cables subjected to vertical support excitation. J. Sound Vib. 2008, 318, 565–579. [Google Scholar] [CrossRef]
- Abe, A. Validity and accuracy of solutions for non-linear vibration analyses of suspended cables with one-to-one internal resonance. Non-Linear Anal. Real World Appl. 2010, 11, 2594–2602. [Google Scholar] [CrossRef]
- Luongo, A.; Zulli, D. Dynamic instability of inclined cables under combined wind flow and support motion. Non-Linear Dyn. 2012, 67, 71–87. [Google Scholar] [CrossRef]
- Guo, T.; Kang, H.; Wang, L.; Zhao, Y. Cable’s non-planar coupled vibrations under asynchronous out-of-plane support motions: Travelling wave effect. Arch. Appl. Mech. 2016, 86, 1647–1663. [Google Scholar] [CrossRef]
- Macdonald, J.H.G. Multi-modal vibration amplitudes of taut inclined cables due to direct and/or parametric excitation. J. Sound Vib. 2016, 363, 473–494. [Google Scholar] [CrossRef]
- Zulli, D.; Piccardo, G.; Luongo, A. On the non-linear effects of the mean wind force on the galloping onset in shallow cables. Non-Linear Dyn. 2021, 103, 3127–3148. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Non-linear Interactions: Analytical, Computational, and Experimental Method; Wiley Series in Non-linear Science; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Manevich, A.I.; Manevich, L.I. The Mechanics of Non-linear Systems with Internal Resonances; Imperial College Press: London, UK, 2005. [Google Scholar]
- Xia, Y.; Chen, B.; Weng, S.; Ni, Y.Q.; Xu, Y.L. Temperature effect on the vibration properties of civil structures: A literature review and case studies. J. Civ. Struct. Health Monit. 2012, 2, 29–46. [Google Scholar] [CrossRef]
- Treyssède, F. Finite element modeling of temperature load effects on the vibration of local modes in multi-cable structures. J. Sound Vib. 2018, 413, 191–204. [Google Scholar] [CrossRef]
- Zhou, H.; Ni, Y.Q.; Ko, J.M. Eliminating temperature effect in vibration-based structural damage detection. J. Eng. Mech. 2011, 137, 785–796. [Google Scholar] [CrossRef]
- Ma, L.; Xu, H.; Munkhbaatar, T.; Li, S. An accurate frequency-based method for identifying cable tension while considering environmental temperature variation. J. Sound Vib. 2021, 490, 115693. [Google Scholar] [CrossRef]
- Montassar, S.; Mekki, O.B.; Vairo, G. On the effects of uniform temperature variations on stay cables. J. Civ. Struct. Health Monit. 2015, 5, 735–742. [Google Scholar] [CrossRef]
- Lepidi, M.; Gattulli, V. Static and dynamic response of elastic suspended cables with thermal effects. Int. J. Solids Struct. 2012, 49, 1103–1116. [Google Scholar] [CrossRef]
- Bouaanani, N.; Marcuzzi, P. Finite difference thermoelastic analysis of suspended cables including extensibility and large sag effects. J. Therm. Stress. 2011, 34, 18–50. [Google Scholar] [CrossRef]
- Treyssède, F. Free linear vibrations of cables under thermal stress. J. Sound Vib. 2009, 327, 1–8. [Google Scholar] [CrossRef]
- Zhao, Y.; Peng, J.; Zhao, Y.; Chen, L. Effects of temperature variations on non-linear planar free and forced oscillations at primary resonances of suspended cables. Non-Linear Dyn. 2017, 89, 2815–2827. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, C.; Chen, L.; Peng, J. Non-linear vibration behaviors of suspended cables under two-frequency excitation with temperature effects. J. Sound Vib. 2018, 416, 279–294. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, C.; Chen, L. Non-linear planar secondary resonance analyses of suspended cables with thermal effects. J. Therm. Stress. 2019, 42, 1515–1534. [Google Scholar] [CrossRef]
- Zhao, Y.; Zheng, P. Parameter analyses of suspended cables subjected to simultaneous combination, super and sub-harmonic excitations. Steel Compos. Struct. 2021, 40, 203–216. [Google Scholar]
- Zheng, P.; Zhao, Y.; Wu, X.; Chen, L. Revisited modeling and non-linear oscillation behaviors of multi-segment damaged suspended cables in thermal environments. Meccanica 2022, 57, 1831–1851. [Google Scholar] [CrossRef]
- Zhao, Y.; Zheng, P.; Lin, H.; Chen, L. Non-linear coupled dynamics of suspended cables due to crossover points shifting and symmetry breaking. Eur. J. Mech. A-Solid. 2023, 99, 104921. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, H. Non-linear dynamics of suspended cables in thermal environments under periodic excitation: Two-to-one internal resonance. Int. J. Bifurcat. Chaos. 2021, 31, 2150153. [Google Scholar] [CrossRef]
- Lacarbonara, W.; Rega, G.; Nayfeh, A.H. Resonant nonliear normal modes. Part I: Analytical treatment for structural one-dimensional systems. Int. J. Non-Linear Mech. 2003, 38, 851–872. [Google Scholar] [CrossRef]
- Lacarbonara, W.; Rega, G. Resonant nonliear normal modes. Part II: Activation/orthogonality conditions for shallow structural systems. Int. J. Non-Linear Mech. 2003, 38, 873–887. [Google Scholar] [CrossRef]
- Ermentrout, B. Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XPPAUT fro Researchers and Students; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]



| Parameter (Unit) | Value |
|---|---|
| Density (kg/m) | 7800 |
| Area of cross-section A (m) | |
| Young’s modulus E (Pa) | |
| Thermal expansion coefficient (1/C) | |
| Cable span L (m) | 200 |
| Damping ratio / (1) | 0.005/0.006 |
| Temperature variations (C) | ±40 |
| C | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| −40 | −5295 | −196,781 | −590,337 | −10,590 | −590,337 | −1,770,990 | |||
| 0 | −4402 | −4402 | −163,579 | −490,736 | −8803 | −490,736 | −1,472,200 | ||
| 40 | −3452 | −3452 | −128,293 | −384,875 | −6904 | −384,875 | −1,154,610 |
| C | |||||
|---|---|---|---|---|---|
| 0 | |||||
| 40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Lin, H.; Ni, W.; Zhao, Y. A Non-Linear Non-Planar Coupling Mechanism of Suspended Cables in Thermal Conditions. Appl. Sci. 2023, 13, 6646. https://doi.org/10.3390/app13116646
Guo Z, Lin H, Ni W, Zhao Y. A Non-Linear Non-Planar Coupling Mechanism of Suspended Cables in Thermal Conditions. Applied Sciences. 2023; 13(11):6646. https://doi.org/10.3390/app13116646
Chicago/Turabian StyleGuo, Zhirui, Henghui Lin, Weilong Ni, and Yaobing Zhao. 2023. "A Non-Linear Non-Planar Coupling Mechanism of Suspended Cables in Thermal Conditions" Applied Sciences 13, no. 11: 6646. https://doi.org/10.3390/app13116646






