Effects of Drying–Wetting Cycle and Fines Content on Hysteresis and Dynamic Properties of Granite Residual Soil under Cyclic Loading

Abstract

In southern China, granite residual soil (GRS) is widely used as road base material. Thus, it is important to study the effects of hot and rainy climates and cyclic loads generated by trains on the dynamic properties of GRS. In this work, by means of dynamic triaxial tests, the effects of the number of drying and wetting (D–W) cycles, fines content and number of load cycles on the hysteresis curve, dynamic shear modulus G_d and damping ratio λ of GRS are systematically investigated. The experimental results illustrate the changes in the morphology of the hysteresis curve and dynamic parameters with the numbers of load and D–W cycles, as well as the fines content. Namely, the area S, center offset d, and residual strain ε_sp of the hysteresis curve decrease with the increase of load cycle number, increase with the growth of fines content, and first decrease with the increase of D–W cycle number, then slowly increase to stabilized values. However, the major axis gradient k exhibits exactly the opposite relationships. Meanwhile, the dynamic shear modulus G_d increases with the growing load cycles and decreases with the addition of fines content, and the damping ratio λ shows the opposite behavior. It is also shown that G_d and λ vary linearly with respect to logN, where N is the number of D–W cycles. The dynamic properties of GRS are mostly affected by the number of load cycles, which is followed by the fines content and then the number of D–W cycles. The influence of the latter two factors on the dynamic properties of GRS may be primarily due to contact form changes between soil particles.

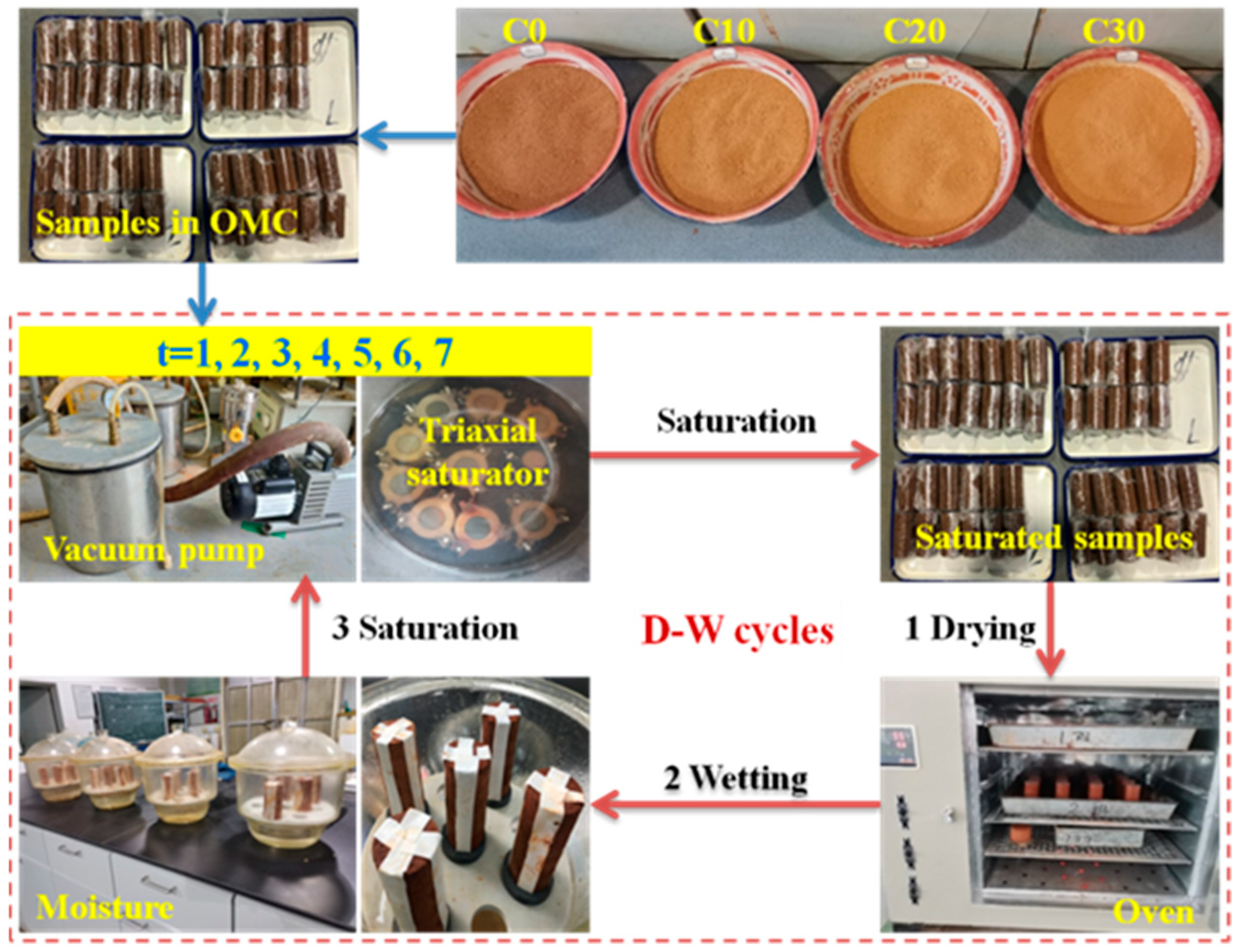
1. Introduction

Granite residual soil (GRS), a product of the in situ weathering of igneous parent rocks, is widely distributed in the humid tropical regions of southern China [1,2], especially in the Fujian province. GRS covers approximately three-fifths of areas in many cities such as Xiamen, Fuzhou, Quanzhou, etc. Since the essential mineral grains of GRS are quartz and kaolinite, while the secondary mineral grains are feldspar, chlorite and other ferric minerals, GRS is characterized by high mica content, loose structure, water sensitivity, and low cohesion [3,4,5]. GRS can satisfy most engineering conditions under dry conditions, but its mechanical and compressive properties change drastically after exposure to water. However, the degradation of the mechanical properties for GRS in the railway subgrade is strongly influenced by the rise of moisture content, which causes an interlayer of coarse and fine particles due to the release of contacts between the soil particles subjected to cyclic loading [6,7]. Owing to the subgrade interlayer, the reduction of the shear strength and compressibility of GRS results in severe damage to the roadbed, such as uneven settlement, track irregularity and mud pumping of the railway subgrade.

The cyclic loads, such as seismic actions, periodic waves, tide forces, and traffic or train loads, have a significant influence on the dynamic properties of soils. During cyclic loading, the pore water and soil particles in saturated soils assigned to the load will vary continuously with time, and different fines contents will change the capability of pore water to bear the load [8]. Several studies reported that the fines contents can significantly affect the dynamic properties of the soil [9,10]. This is due to the fact that fine particles change the contact style and skeleton structure between soil particles [11,12]. When the fines content is low, these fine particles exist with coarse particles on the skeleton nodes to play the role of a ball, making the contact surface between coarse particles reduce the inter-grain friction. When the fines content becomes high, the soil tends to a dense state, and the static friction between particles increases, which then prevents the misaligned slip between particles [13]. Moreover, the GRS subgrades are commonly subjected to seasonal drying and wetting (D–W) cycles in southern China because of the subtropical climate [14,15,16]. After repeated D–W cycles, GRS is prone to cracking due to a series of changes, such as reduced fine particles, coarsened pores, and loose structure, among other characteristics [1,17,18]. The reciprocating migration of the pore water, caused by both cyclic loading of train vibration and D–W cycles, drives a further movement of the internal fine particles and contributes to the development of original cracks [19,20,21]. The occurrence of cracks and changes in pore space affect the soil water characteristic curve (SWCC) and the hysteresis curve of unsaturated GRS [22,23,24,25], and the shear modulus can be predicted by matrix suction with the help of the SWCC curve. All these factors not only accelerate the formation of coarse-fine grain interlayers of GRS but also cause irreversible structural damage and fatigue failure of the subgrade. Therefore, it is important to understand the dynamic properties of GRS under D–W cycles for different fines contents of GRS.

The hysteresis curve describes the dynamic stress–strain relationship curve of soils under cyclic loadings. Its morphology provides a concise visualization of the dynamic soil performance, such as the dynamic deformation, viscous hysteresis, stiffness change, and energy loss. The hysteresis curve and backbone curve together constitute the viscoelastic dynamic constitutive model. It is a well-known fact that dynamic parameters such as the shear modulus G_d, damping ratio λ, and accumulative plastic strain ε_sp are important indexes to evaluate the safety and stability of subgrade constructions. G_d and λ can be easily extracted from the evolution of hysteresis curves. The present study on hysteresis curves mainly focuses on frozen clay, peaty soils, swelling soils, etc. It is noted that a series of works on the hysteresis curves of frozen clay has been completed by Luo et al. [26]. They first considered the effect of stress loading conditions on the hysteresis curve morphology [26] and then investigated the negative temperature after realizing that the melting of ice crystals under negative temperature affects the mechanical properties [27]. Later, they also took into account the confining pressure and loading frequency [28].

In the study on peaty soils, Huang et al. [29] considered the effect of confining pressure and loading frequency on the hysteresis curve. Zhu et al. [30] took into account the stress amplitude on this basis and the factors affecting the hysteresis curve of expansive soils, which mainly include the confining pressure and loading frequency [31,32]. Different test factors can greatly affect the dynamic elastic modulus E_d and damping ratio λ. For example, Xu et al. [33] considered the effects of loading frequency, stress amplitude, initial partial stress and confining pressure on the dynamic elastic modulus E_d of soft clays and showed that E_d increases with the increase of cyclic stress amplitude, initial partial stress, and confining pressure; the lower the vibration frequency, the faster the decay of E_d. Wang et al. [34] analyzed the effect of dynamic stress ratio and confining pressure on E_d of saturated gravel sands and found that E_d increases with increasing confining pressure and dynamic stress ratio. Wu et al. [35] studied the effects of sea sand admixture, loading frequency and dynamic stress on E_d and λ of cured silts, which demonstrated that E_d increases with the growing sand admixture and loading frequency. It first increases and then decreases with the increase of dynamic stress, while λ follows the opposite relationship. Hysteresis curves have strong variability for different types of soils in different regions, and so do the dynamic parameters. Chen et al. [36] investigated the effect of G_d and λ of GRS under different confining pressure and stress amplitude and found that G_d decreases with the increase of stress amplitude and λ inversely. In addition, increasing the surrounding pressure can suppress the decay of G_d with dynamic stress. The results of Yin et al. [37] on the effect of confining pressure and dynamic stress amplitude on G_d showed the same trends as those of Chen et al. [36]. Furthermore, Yin et al. [37] also found that the greater the water content in the soil, the faster G_d decays.

The development of a dynamic constitutive model to quantitatively describe the dynamic deformation characteristics of soil under cyclic loading is a key issue [38]. The common soil models can be divided into three categories. The first type is the Masing model [39], which assumes that the hysteresis curve is obtained by doubling the skeleton curve, and defines the “upper skeleton curve criterion” and the “upper great circle criterion”. The second type is the equivalent linear model, which assumes that the soil is a viscoelastic material, and introduces E_d and λ as dynamic model parameters into the dynamic stress–strain model, for example, the Hardin–Drnevich model [40] and Ramberg–Osgood model [41], etc. The third type is the Iwan model [42], which describes the dynamic stress–strain relationship of the soil by combining different elastoplastic units either in series or in parallel. Except for the above three categories, there are also empirical models of E_d with the number of load cycles, often denoted by N, confining pressure and deviator stress dynamic intrinsic relationship proposed by scholars. Wu et al. [43] and Xu et al. [33] established the empirical models for E_d versus N in the study of soft clay soils, both in the form of E_d = alnN + b. In addition, Xu et al. [33] correlated the fitted parameters a and b with the stress amplitude, confining pressure and loading frequency on this basis. Mu et al. [44] divided the stability zone, damage zone, and critical zone based on the law of accumulated deformation of undisturbed red clays under different confining pressures and stress amplitudes. Based upon this, the concept of equivalent dynamic elastic modulus E_d-equal was proposed, and an empirical model was established. The model is E_d-equal = alnN + b (stability zone a > 0, damage zone a < 0). Although this type of model is not directly associated with strain, it can also better reflect the dynamic property changes and can be associated with the studied factors, which is easy for practical application.

Previous works focused on the effect of confining pressure, loading frequency, or stress amplitude on the hysteresis curve and dynamic parameters for peaty soils, soft soils or GRS. In the meantime, the empirical models of E_d with the number of load cycles are proposed according to the influencing factors for specific soils. It is noted that the D–W cycles and fine particles have a large influence on the dynamic characteristics of GRS, and the process of D–W cycles will affect the change of fines content. However, few studies describe in detail the dynamic properties and explain the dynamic mechanism of GRS under the D–W cycles and fines content.

In view of the phenomenon of pulping and mudging under the train cyclic dynamic load in a hot and rainy climate, this work focuses on the dynamic characteristics of GRS under cyclic loading by D–W cycles and fines content through hysteresis curves and further reveals the mechanism underlying the effect of fine particles and D–W cycles on the dynamic characteristics of GRS. Through the experimental data analysis, the characteristics of the hysteresis curve and the variation of parameters are revealed. It supports the comprehensive understanding of the dynamic properties of GRS. In addition, the dynamic shear modulus and dynamic damping ratio models established based on the dynamic triaxial experimental data can provide the prediction of dynamic parameters of residual soil considering the influence of D–W cycles and fines content. It is helpful to carry out dynamic analysis of railway subgrade stability and provide theoretical support for the construction of the railroad subgrade in the residual soil area.

2. Experimental Setup

2.1. Test Materials

The GRS used in this study was extracted from the edge of a railway subgrade, representing typical soils therein. The GRS was dried for 48 h, pulverized and then sieved through a 5.0 mm sieve to generate the prepared soils.

The specific soil gravity (G_s) is 2.72. The particle size distribution of the soil obtained from sieve analysis exhibits a composition of 37.2% fines (<0.075 mm), 57.3% sand (0.075~4.75 mm), and 5.5% Gravel grain (>4.75 mm). The values of liquid limit (LL), plastic limit (PL) and PI are 46.6%, 23.8% and 22.8%, respectively. The maximum dry density and optimal moisture content (OMC) of the soil are 1.65 g/cm³ and 20.3%. According to the Criteria for classification of soils (GBJ145-90) [45], the soil is classified as residual soil. In order to study the influence of fines content, the soil is divided into seven particle groups (5–2 mm, 2–1 mm, 1–0.5 mm, 0.5–0.25 mm, 0.25–0.1 mm, 0.1–0.075 mm and <0.075 mm) by the sieving method. In order to meet the specification requirements for high-speed railroad bed fillers [46], the fines content varies from 0%, 10%, 20%, to 30% by adding fine particles (particle size < 0.075 mm). The percentages refer to the ratio of the dry mass of fine particles to the dry mass of soil. The Standard Proctor tests were conducted to obtain the optimal moisture content and maximum dry density of the adjusted soils. The particle size distributions and physical properties of soils with different fines contents are illustrated in

Table 1. The physical parameters of the soil used for experiment.

Soil No.	Grain Size Fractions/%					Liquid Limit LL/%	Plastic Limit PL/%	Plasticity Index PI/%	Uniformity Coefficient, Cu	Coefficient Curvature, Cc	Optimal Moisture Content wop/%	Maximum Dry Density ρdmax/g·cm−3
	d < 0.075 mm	d < 0.1 mm	d < 0.25 mm	d < 0.5 mm	d < 2 mm
C0	0	5.50	10.61	26.09	77.18	44.2	28.3	15.9	5.06	1.11	20.3	1.65
C10	10	10.47	15.31	29.98	78.38	52.3	30.1	22.2	15.16	2.94	21.6	1.68
C20	20	20.42	24.73	37.76	80.78	47.4	24.4	23.0	24.08	3.02	22.0	1.67
C30	30	30.37	34.14	45.54	83.19	47.6	23.4	24.2	23.10	0.17	23.3	1.65

.

2.2. Preparation of GRS Samples

The GRS samples were prepared through the standard procedure defined by the Specification of Soil Tests (GB/T50123-1999) [47]. The distilled water was added to the prepared soils to reach the optimal moisture content of each group, and the soil mixtures were kept in the enclosed bags without evaporation for 48 h to ensure the water could be uniformly distributed. Subsequently, the soil triaxial samples were compacted in five equal layers on the bottom platen inside a split mold with a height of 100 mm and a diameter of 50 mm. The weight and height of each layer were measured to obtain a homogeneous dry density of 95% of ρ_dmax. The acceptable error for quality variation within the same set of soil samples is set at less than 1%. If the variation exceeds 1%, the soil samples will be re-prepared. It ensures the consistency and reliability of the soil samples.

2.3. Drying–Wetting Cycle Process

To explore the effect of the D–W cycles on the dynamic properties of GRS in the railway subgrade, the soil samples subjected to D–W cycles were used to conduct the dynamic triaxial tests. According to the environmental parameters, the severe D–W cycles of the railway subgrade of Xiamen in Fujian province caused by the summer monsoon climate conditions were simulated, which included the highest temperature of about 55 °C (that is close to that at the ground surface in summer) and the moisture content of approximately 10% (which is equal to the moisture content of subgrade in-situ). The prepared soil samples in OMC were all wetted to saturation and were then subjected to the D–W cycles. Each D–W cycle includes three phases, namely, drying, wetting and saturation. The first D–W cycle process for soil samples involves three steps: initial moisture content to saturation, drying to a 10% moisture content state, and then saturation again. The subsequent D–W cycles of a soil sample are considered to have undergone a D–W cycle as long as it dries from the saturated state to 10% moisture content and then wets to saturation.

To find an optimum maximum number of D–W cycles, a series of preliminary tests were conducted with respect to 5, 7, 9, and 11 D–W cycles under the same testing conditions. The results indicated that their stress–strain curves of 7, 9, and 11 D–W cycles are very close. Thus, seven D–W cycles were used as the maximum D–W cycles from a time-saving point of view. In the present study, GRS samples with different D–W cycles were prepared via the following procedures (see Figure 1):

(1) Drying process. The soil samples were put into the oven at 55 °C for about 6 h (to simulate real drying field conditions), then taken out and left for 24 h to cool down naturally to room temperature. Finally, the samples were weighed to determine the change in moisture content over time. The trial test results showed that the change of moisture content is less than 0.5%, and the moisture content remains around 10%, indicating that the samples at 10% moisture content are in completely dry conditions.

(2) Wetting process. The samples were first pasted by the wet filter papers, then sprayed uniformly with water every 10 min using an electric sprayer. The wetting process is continuously monitored for soil sample quality and moisture content, and it is terminated when neither changes.

(3) Saturation process. The saturation process includes vacuum saturation and back-pressure saturation. In vacuum saturation, triaxial saturators filled with the soil samples were placed in a barrel for vacuum saturation. The triaxial saturator is shown in Figure 1. Each triaxial saturator had a permeable stone at each end, and the specimen was placed between two permeable stones. During the saturation process, the specimen was saturated by exhaust and water absorption through two permeable stones. The procedure was as follows: First, the soil samples were vacuumed in the saturator with a vacuum pump for 2 h, then the vacuum pump valve was closed, and the water filling valve was opened to add water. When the water level reached 3/4 of the soil sample height, the valve was closed, and the vacuum pump was opened for 2 h. Then the soil samples were kept under a vacuum of one standard atmosphere pressure for 24 h. The back-pressure saturation was used to install the soil samples in a dynamic triaxial instrument by applying back pressure to monitor the pore water pressure coefficient B, and when the value of B reached above 95%, the saturation process finished.

2.4. Dynamic Triaxial Test

The dynamic triaxial test was carried out using the British GDS (Global Digital Systems) standard dynamic triaxial test system. A static load of 15 kPa σ_s was applied to simulate the action of the superstructure. Considering the effect of D–W cycles and the limited depth of the train load, the confining consolidation pressure σ₃ was set to 60 kPa.

Generally, the dynamic loads of high-speed trains are between 30 kPa and 70 kPa [48], and the loading frequency is between 1 Hz and 5 Hz, with actual data measured as 1.39–1.85 Hz [49]. Therefore, the dynamic load’s amplitude σ_d was set to 60 kPa, and the loading frequency was set to 2 Hz. The experiment was over as soon as the axial strain of the soil sample exceeded 10% or the number of vibration cycles reached 10,000 [50].

3. Hysteresis Curve Characteristics of GRS

The hysteresis curve refers to the dynamic stress–strain relationship throughout a load cycle. Its morphological characteristics can be used to describe the dynamic deformation, viscosity, stiffness change, energy loss, and other significant dynamic aspects of soil. The shape of the hysteresis curve can be affected by the confining pressure, load frequency, load amplitude, stress history, and naturally occurring environmental changes in the soil.

3.1. Hysteresis Curve Shape

Figure 2 illustrates the trend of the hysteresis curve variations for different fines contents without D–W cycles after 500 cyclic loadings. The corresponding observations are summarized as follows: (1) The hysteresis curve changes from the initial shuttle-like to a willow shape as the number of load cycles increases. (2) The largest hysteresis loop lies in the first cycle, and it gradually becomes smaller and denser in the following cycles. GRS exhibits an elastoplastic behavior, and the irreversible plastic strain gradually enlarges with increasing cyclic numbers. (3) As the fines content increases, the axial strain increases significantly. Comparing the axial strain of C0 with that of C30, the latter is nearly three times the former. The reasons behind these observations could be that the fine particles play a lubricating role on the surface of the coarse particles when the fines content increases from 0% to 10%. Moreover, when the fines content further increases to 30%, the fine particles may block the internal drainage channel of pores, resulting in the accumulation of excess pore water pressure. As the pore water pressure accumulates to the limit, the fine particles will be pushed out, and the axial strain will increase. Consequently, the axial strain becomes greater and greater with the increase of the fines content.

Figure 3 plots the hysteresis curve changes of soil samples without adding fine particles for the 1st, 3rd, 5th, and 7th D–W cycles under 500 loading cycles. It can be observed that the hysteresis curve changes show a non-monotonic pattern. The axial strain decreases first and then increases significantly when the number of D–W cycles increases. With the results of Dou et al. [51] and Fu et al. [52], it is inferred that such a result in this paper is probably due to the new skeleton formed by fine and coarse particles being denser within three D–W cycles and the axial strain decreases. However, when the number of D–W cycles continuously increases to five, the hydrophilic capacity of clay minerals decreases, and the adhesion between particles weakens. At the same time, the soil structure becomes loose under the combined action of dynamic load and D–W cycles, which eventually leads to significant growth of axial strain.

3.2. Hysteresis Curve Parameters

To a certain extent, the hysteresis curve’s evolution law reveals the soil’s internal structure change rule. By extracting the parameters of the shape change from the hysteresis curve, the influence of external conditions on soil damage can be obtained. This study uses the hysteresis curve area S, the slope of the long axis k, the center offset of hysteresis curve d and residual strain ε_sp to analyze the hysteresis curve characteristics of GRS. The calculation methods of S, k, d and ε_sp and their variations will be introduced separately below.

(1)

Hysteresis curve area S

The variation of S normally indicates the degree of soil compaction. A large S shows that the soil structure is loose and easily compacted and that a large amount of energy is lost during compaction. On the contrary, a small S indicates that the soil structure is dense and difficult to compact, and less energy is lost during compaction.

The area of the arc from the initial point of loading, to the final point of unloading is the area of the hysteresis curve. The hysteresis curve area S is expressed as follows:

$$S={\displaystyle \int {\sigma }_{di}}d{\epsilon }_i$$

(1)

where σ_di and ε_i denote the deviator stress and the axial strain under the ith loading cycle.

(2)

Major axis gradient k

The stiffness and elasticity modulus of the soil can be reflected by the major axis gradient k of the hysteresis curve. When k grows, the soil stiffness and elasticity modulus increase and vice versa. The major axis gradient k is calculated by:

$$k=\frac{{\sigma }_{N,\max }-{\sigma }_{N,\min }}{{\epsilon }_{N,\max }-{\epsilon }_{N,\min }}$$

(2)

where ${\sigma }_{N,\max }$, ${\epsilon }_{N,\max }$, ${\sigma }_{N,\min }$ and ${\epsilon }_{N,\min }$ are the maximum and the minimum stress and strain of the Nth hysteresis curve, respectively.

(3)

Center offset d

The center offset d is the distance between the centers of the previous and subsequent hysteresis curves, which reflects the soil deformation and internal structural damage. The larger the d, the greater the irrecoverable deformation of the soil sample and the greater the damage to the internal structure of the soil, and vice versa. Since the graph enclosed by the hysteresis curve is not a regular shape, it is not trivial to pinpoint the exact location of the center point. This work primarily studies the trend of its center distance with loading and D–W cycles. The difference between the strain maximum of the previous hysteresis curve and the latter hysteresis curve is proportional to the center distance. Therefore, the center offset d is computed as follows:

$$d={\epsilon }_{N,\max }-{\epsilon }_{N-1,\max }$$

(3)

where ${\epsilon }_{N,\max }$ and ${\epsilon }_{N-1,\max }$ represent the maximum strain of the Nth and the (N − 1)th hysteresis curve, respectively.

(4)

Residual strain ε_sp

The residual strain is the strain difference between the end point of loading and the starting point in one cycle, namely, the degree of non-closure or the size of the opening of the hysteresis curve. Thus, the residual strain ε_sp is given as follows:

$${\epsilon }_{sp}={\epsilon }_e-{\epsilon }_s$$

(4)

where ${\epsilon }_s$ and ${\epsilon }_e$ are the strain values corresponding to the starting and ending points of the Nth loading, respectively.

3.3. Effect of Number of Loading Cycles on the Hysteresis Curve Parameters

The morphology of the hysteresis curve of GRS changes dramatically with the increase of loading cycles, resulting in significant changes in its morphological parameters. As shown in Figure 4, it is observed that the higher the number of loads, the smaller the area and the degree of opening, while the larger the degree of tilt.

Figure 5 plots the variation and trends of S, k, d and ε_sp for different fines contents with cyclic loads, respectively, and the following results can be obtained from the analysis: (1) From Figure 5a,c,d, it can be observed that with the increase of the number of loads, the decrease of S, d and ε_sp is significant in the early loading period (N ≤ 20), while the decrease in S, d and ε_sp slows down and stabilizes in the late loading period (N > 20). These observations are consistent with those obtained by Zhuang et al. and Wei et al. [32,53]. The ratio of the decrease under the first 20 loads to the total decrease can be found in

Table 2. The ratio of the reduction of morphological parameters of the first 20 loads to the total reduction.

Hysteresis Curve Morphology Parameters	C0	C10	C20	C30
S	72.9%	79.5%	79.2%	79.7%
d	90.5%	94.5%	92.6%	92.3%
${\epsilon }_{sp}$	94.4%	96.6%	95.0%	93.0%

. The average reduction ratio for S, d and ε_sp are 77.8%, 92.5% and 94.8%, respectively, with a maximum of 96.6% and a minimum of 72.9%. (2) Unlike the other three parameters, as shown in Figure 5b, k increases sharply in the early load stage and then increases slowly, and moreover, k approximately changes linearly with LogN.

The reason for these observations might be that in the early stage of loading (N ≤ 20), the soil is rapidly compacted and the deformation of the soil is predominantly plastic [54]. At this stage, the internal structural damage and residual strain of the soil are most obvious, while in the late stage of loading, the soil compactness is enhanced with filled pores and increasing contact between soil particles, and the soil deformation gradually transitions from plastic to elastic, so the residual strain decreases and the soil stiffness gradually increases.

3.4. Effect of Number of Fines Content on the Hysteresis Curve Parameters

The fines content in the GRS affects the shape of the hysteresis curve. Figure 6 depicts the variation of four hysteresis curve parameters with the fines content. According to the amount of fines content, it is divided into three ranges, i.e., low fines content (C0 to C10, Range I), medium fines content (C10 to C20, Range II) and high fines content (C20 to C30, Range III). When the fines content increases, S, d, and ε_sp of the hysteresis curve increase. They increase quickly in Range I and Range III but slowly in Range II. Additionally, the influence of fines content is greater at low-load cycles than at high-load cycles. Taking S as an example, the values of S under cyclic load are listed in

Table 3. Hysteresis curve area S under cyclic load (T0, for example).

Loading Cycle N	SC0	SC10	SC20	SC30
1	3.97	6.53	7.25	10.70
2	3.03	4.57	5.44	8.39
3	2.61	3.66	4.47	6.91
4	2.35	3.14	3.90	5.94
5	2.16	2.82	3.50	5.24
6	2.03	2.61	3.24	4.79
7	1.93	2.44	3.05	4.42
8	1.85	2.32	2.88	4.10
9	1.78	2.22	2.73	3.84
10	1.72	2.12	2.62	3.63
20	1.43	1.39	2.07	2.69
Average	2.26	3.07	3.74	5.51
1000	0.68	0.70	0.98	1.01
2000	0.61	0.57	0.88	0.85
3000	0.56	0.52	0.82	0.79
4000	0.53	0.49	0.78	0.73
5000	0.52	0.47	0.75	0.70
6000	0.50	0.46	0.73	0.66
7000	0.49	0.45	0.71	0.64
8000	0.48	0.44	0.70	0.62
9000	0.47	0.44	0.68	0.66
Average	0.54	0.50	0.78	0.74

. Under low load cycles (N = 1–20), the average area of S_C30 is 6.04, 2.5 times that of S_C0. However, the average area of S_C30 is only 1.4 times that of S_C0 under high-loading cycles (N = 1000–10,000). The soil group of C0 has the maximum k, and the increase of fines content makes k decrease. k has a noticeable decrease in Range I and Range III, but it has a small change at low load cycles and fluctuates at high loading cycles in Range II.

3.5. Effect of D–W Cycles on the Hysteresis Curve Parameters

The morphological parameters for four groups of soils with different fines contents soil under seven D–W cycles were plotted in Figure 7, Figure 8, Figure 9 and Figure 10 to illustrate in detail the effect of D–W cycles. Since the compaction effect of soil is obvious in the first 20 loading cycles, these parameters change do not fully reflect soil properties. In addition, excessive loading numbers also affect soil properties (see the green and grey areas in Figure 7a,b), and the center offset d and residual strain ε_sp mainly occurs at N < 100, after which they are close to 0. Therefore, N = 20 to 90 (blue area) is the load-interval that best represents the influence of the D–W cycle on soil properties.

Figure 7, Figure 8, Figure 9 and Figure 10 plot S, d and ε_sp versus the numbers of D–W cycles for different fines contents. S, d and ε_sp have a similar variation. With the increase of D–W cycles, they first decrease slightly at T0~3, then increase slowly at T3~5, and finally reach a relatively stable state at T5–7. Smaller values are usually reached at the 2nd or 3rd D–W cycle. Besides, when the fines content is high, the S, d and ε_sp values of the 7th D–W cycle are similar to those without the D–W cycles.

From Figure 7, Figure 8, Figure 9 and Figure 10b, it can be observed that the k fluctuates at T0~3, while there is a significant decrease at T3~5, followed by a gradual stabilization at T5~7. Compared to S, d and ε_sp, k shows an opposite variation as the D–W cycles increase. The major axis gradient k_ave under different D–W cycles are calculated and listed in

Table 4. Variation of major axis gradient k_ave under different D–W cycles.

kave	Times of D–W Cycles																Δk = kmax − kmin
	0		1		2		3		4		5		6		7
	N1	N3	N1	N3	N1	N3	N1	N3	N1	N3	N1	N3	N1	N3	N1	N3	N1	N3
C0	397	652	399	614	429	620	391	580	356	530	267	472	275	436	267	418	162	233
C10	277	456	291	480	276	442	268	431	285	432	229	392	239	380	216	352	75	127
C20	280	535	301	463	230	409	333	491	290	468	237	358	230	390	265	392	102	176
C30	189	457	213	392	220	408	222	377	220	392	209	359	215	386	220	364	33	97

Note: k_ave means the average of k under different numbers of loads. N1 means N = 1, 2, 3, …, 9; N3 means N = 1000, 2000, 3000, …, 9000.

. The value of k_ave first increases and then decreases. Usually, the range of k_ave is larger at the later load stage than that at the early load stage.

The above variation may be explained as follows. As shown by the schematic diagram of the initial state of GRS in Figure 11a, the grain sizes of GRS are mainly between 0.5 mm and 0.075 mm, and the total amounts of coarse and fine particles are close, while the content of medium particles is quite low. Due to the small content of medium particles, the macrospores are larger and are filled by fine particles and pore water. At the beginning of D–W cycles (T2~3, see Figure 11b), the fine particles are dispersed, and the cementitious substances in the fine particles are dissolved in the water and partly lost with the migration of water [1,55]. However, during the drying process, the fine particles re-combine and aggregate to form a denser soil skeleton [56], resulting in a soil energy loss, a reduction of plastic deformation and an increase in stiffness. In the middle of D–W cycles (T3~5, see Figure 11c), the intrusion of water makes fine particles expand and disperse into finer particles, weakening the adhesion among the fine particles in the wetting process. On the other hand, finer particles continue to be lost with the water migration in the drying process [57]. Ultimately, the soil structure gradually loosens, so it shows more +energy loss and plastic strain characteristics. At the later D–W process (T5–7, see Figure 11d), some coarse particles are broken into fine particles after undergoing the previous D–W cycles, and with the further dispersion of fine particles, the fine contents filled in the pores increase. More fine particles wrap the coarse particles, resulting in a more stable skeleton structure. As a result, the variation of parameters is stabilized.

3.6. Summary

Table 5. Range of parameters under different factors.

Range of Parameters under Different Load Levels
	ΔSave (N3−N1)				Δkave (N3−N1)				Δdave (N2−N1)/%				Δεspave (N2−N1)/%
	C0	C10	C20	C30	C0	C10	C20	C30	C0	C10	C20	C30	C0	C10	C20	C30
T0	−1.86	−2.86	−3.26	−5.30	254.3	178.7	254.6	267.9	−1.6	−2.82	−3.89	−8.05	−2.06	−3.83	−4.84	−9.82
T1	−1.92	−2.63	−2.55	−3.56	214.6	189.4	162.2	178.2	−1.38	−2.63	−2.29	−4.32	−1.80	−3.38	−2.92	−5.36
T2	−1.42	−3.03	−3.27	−3.57	191.4	166.3	179	188.2	−0.88	−2.84	−3.82	−4.49	−1.16	−3.68	−4.48	−5.60
T3	−1.39	−2.58	−1.98	−3.47	188.6	162.8	158	155.2	−0.95	−2.79	−1.84	−4.16	−1.24	−3.58	−2.36	−5.17
T4	−1.43	−2.27	−2.16	−3.52	174.0	146.9	178	171.9	−1.01	−2.31	−2.54	−4.56	−1.26	−2.87	−3.18	−5.64
T5	−3.05	−3.02	−2.67	−3.49	205.3	162.3	121.6	150.3	−3.41	−3.42	−3.09	−4.41	−4.27	−4.27	−3.91	−5.42
T6	−2.85	−2.74	−3.00	−3.49	161.5	141.4	159.6	170.9	−2.34	−3.11	−3.19	−4.43	−3.06	−3.9	−4.11	−5.45
T7	−2.67	−3.49	−2.51	−3.11	151.1	136.8	127.7	143.4	−1.78	−3.86	−2.86	−3.79	−2.37	−4.8	−3.55	−4.72
Range of parameters under different fines content
	ΔSave				Δkave				Δdave/%				Δεspave/%
	N1		N3		N1		N3		N1		N2		N1		N2
T0	3.62		0.28		208.7		195.8		7.25		0.81		8.61		0.85
T1	1.98		0.48		186.0		222.5		3.44		0.50		4.01		0.46
T2	3.02		0.87		208.8		221.9		4.18		0.57		5.07		0.63
T3	2.33		0.57		169.6		203.1		3.73		0.52		4.41		0.48
T4	2.73		0.65		135.8		137.9		4.17		0.63		4.95		0.57
T5	0.89		0.45		58.1		113.6		1.65		0.33		1.91		0.40
T6	1.14		0.50		59.4		56.2		2.48		0.39		2.76		0.37
T7	1.21		0.78		51.6		65.9		2.50		0.42		2.91		0.48
Range of parameters under different D–W cycles
	ΔSave				Δkave				Δdave/%				Δεspave/%
	N1		N3		N1		N3		N1		N2		N1		N2
C0	2.22		0.59		161.8		233.3		3.08		0.55		3.71		0.60
C10	1.02		0.73		75.3		127.9		1.88		0.42		2.25		0.44
C20	1.35		0.94		102.4		176.1		2.27		0.31		2.90		0.45
C30	1.85		0.53		33.1		97.6		4.67		0.42		5.54		0.49

Note: ‘−’ means the value of the parameter decreases with the number of load cycles.

tabulates the influence of the number of load cycles, fines content and the number of D–W cycles on each parameter. It can be observed that the number of load cycles has the strongest influence on the four parameters, while the number of D–W cycles has the weakest influence on the parameters. The variation of ΔS_ave by the number of load cycles is greater than 1.39, while the variation of ΔS_ave by fines content and D–W cycles is less than 1.39 in most cases, especially in N3, where the variation is all less than 0.94 (see column ‘ΔS_ave’ in Table 5). The number of D–W cycles has the least influence on the parameters. For example, Δε_spave changes by fines content reach 4% in more than half of the cases, while Δε_spave changes by D–W cycle periods surpass 4% only once.

In addition, there is a coupling between the factors that will change the degree of influence of the parameters. For example, the degree of influence of the loading cycles on four parameters is the greatest at T0-C30 (ΔS_ave = −5.3, Δk_ave = 267.9, Δd_ave = −8.05, Δε_spave = −9.82), the degree of influence of fine particle contents and number of D–W cycles on S, d, ε_sp is the least at N1-T5 (ΔS_ave = 0.89, Δd_ave = 1.65%, Δε_spave = 1.91%) and N1-C10 (ΔS_ave = 1.02, Δd_ave = 1.88%, Δε_spave = 2.25%), respectively. In addition, there is a significant decrease in the degree of influence of the number of loading cycles after one D–W cycle.

4. Characteristics and Models of Dynamic Parameters of GRS

4.1. Dynamic Parameters of GRS

(1)

Dynamic shear modulus G_d

Since the dynamic shear modulus (G_d) can not be directly determined in the dynamic triaxial tests, it is usually calculated indirectly, as follows:

$$G_d=\frac{E_d}{2(1+\mu )}$$

(5)

where E_d is elasticity modulus, μ is Poisson’s ratio. According to [58], the Poisson’s ratio of GRS ranges from 0.3 to 0.33, thus μ is taken as 0.3 in this study.

The dynamic elasticity modulus (E_d) is obtained from the dynamic triaxial test. It can be obtained as:

$$E_d=\frac{{\sigma }_A-{\sigma }_B}{{\epsilon }_A-{\epsilon }_B}$$

(6)

where ${\sigma }_A$, ${\sigma }_B$ and ${\epsilon }_A$, ${\epsilon }_B$ are the stress and strain values corresponding to the intersection points of A and B, respectively.

(2)

Damping ratio λ

The damping ratio is the ratio of the dissipated energy and the elastic strain energy in one load cycle. According to the Standard for geotechnical testing method (GB/T 50123-2019) [59], the formula is given as follows:

$$\lambda =\frac{1}{4\pi }\frac{A_z}{A_s}$$

(7)

where A_z is the area of the hysteresis curve and A_s is the area of the triangle.

4.2. Characteristics of Dynamic Parameters of GRS

By taking soil that has not undergone any D–W cycle as an example, Figure 12 depicts the dynamic shear modulus G_d and damping ratio λ with the number of load cycles for GRS. It is easy to see that the variation of dynamic parameters with the number of loading cycles has two stages, i.e., the initial loading stage (N < 20) and the late loading stage (N ≥ 20). In the initial loading stage (N < 20), with the increases in the number of loads, the dynamic shear modulus G_d grows rapidly while the damping ratio λ decreases rapidly. It exhibits obvious strain-hardening characteristics [60]. This may be due to the significant compaction effect of soil, and the soil deformation is dominated by plastic deformation. Therefore, the change of dynamic parameters at this stage does not reflect the soil characteristics. In the late loading stage (N ≥ 20), both the increasing rate of dynamic shear modulus and the decreasing rate of damping ratio slows down and afterward reach stabilization (N > 1000). The dynamic shear modulus growth and the damping ratio reduction at this stage are mainly attributable to the particle dislocation and pore compression in the soil, resulting in pore water pressure and further compaction of the soil. The soil enters the elastoplastic deformation stage. When the number of load cycles continues to increase (N > 1000), the soil becomes more dense, and the soil deformation is dominated by elastic deformation. At this stage, dynamic parameters tend to be fixed. Therefore, the change of dynamic parameters at 20~1000 loading cycles is analyzed below.

The effect of fines content on the dynamic parameters of GRS is closely related to its water content. When the soil is in the saturated state, the larger the fines contents, the smaller the dynamic shear modulus and the higher the damping ratio [61]. Figure 13 plots the evolution of dynamic parameters with the variation of fines contents of GRS. The dynamic shear modulus shows a trend of decreasing, then increasing, and finally decreasing again with the increase of fines content (see Figure 13a). The damping ratio generally shows an increasing trend with the increase of fines content, and the growth rate slows down as the number of load cycles increases (see Figure 13b).

Figure 14 and Figure 15 illustrate how the dynamic shear modulus and damping ratio of GRS vary with the number of D–W cycles. The variations of dynamic shear modulus affected by the number of D–W cycles are different for GRS with different fines content (see Figure 14). It is observed that the influence of the number of D–W cycles on the dynamic shear modulus is greater when the fine particle content is low (see Figure 14a–d).

Table 6. Range in dynamic shear modulus among seven D–W cycles.

ΔGd/MPa	N = 10	N = 50	N = 100	N = 500	N = 1000	N = 5000	N = 9000
C0	7.31	7.63	8.11	8.76	8.4	10.55	10.23
C10	3.35	3.61	3.59	4.01	3.75	4.83	5.42
C20	4.01	4.61	4.72	5.88	6.59	7.77	5.84
C30	1.37	2.23	2.57	3.14	3.29	4.25	1.76

shows the range of dynamic shear modulus among seven D–W cycles. The range G_d for C0 is nearly three or five times that for C30. Meanwhile, compared with the dynamic shear modulus without D–W cycles, the dynamic shear modulus after several D–W cycles exhibit a decreasing trend (see

Table 7. Dynamic shear modulus (T0 and T7).

Gd/MPa	N = 10		N = 50		N = 100		N = 500		N = 1000		N = 5000		N = 9000
	T0	T7	T0	T7	T0	T7	T0	T7	T0	T7	T0	T7	T0	T7
C0	18.2	11.8	19.6	13.0	20.4	13.6	22.4	14.6	22.9	15.3	25.7	15.9	26.4	16.7
C10	13.3	10.7	14.6	11.6	14.8	12.1	16.0	12.8	16.5	13.4	17.8	13.9	18.2	14.3
C20	14.6	12.7	16.7	13.2	17.1	13.4	18.9	14.1	19.7	14.3	21.6	15.4	22.4	16.0
C30	11.8	10.7	13.2	11.8	14.1	12.0	15.5	12.9	16.2	13.4	18.3	14.3	16.2	14.8

, G_dT7 < G_dT0).

The relationship between the damping ratio of GRS with D–W cycles is depicted in Figure 15. Compared with the influence of the number of cyclic loading on the damping ratio, the influence of D–W cycles on it is negligible.

Table 8. Range in damping ratio among seven D–W cycles.

Δλ	N = 10	N = 50	N = 100	N = 500	N = 1000	N = 5000	N = 9000
C0	0.105	0.065	0.056	0.053	0.058	0.057	0.059
C10	0.034	0.028	0.029	0.041	0.048	0.058	0.061
C20	0.070	0.053	0.045	0.053	0.058	0.068	0.025
C30	0.084	0.044	0.044	0.047	0.047	0.038	0.035

. shows the range of damping ratios among seven D–W cycles. It is observed that the differences are very small. It can be concluded that the damping ratio of GRS is less affected by D–W cycles.

4.3. Dynamic Parameter Models of GRS

Some scholars have proposed formulas for fitting the dynamic elastic modulus E_d and the number of loading cycles N [33,44]. The form of the proposed formulas is the same (see Equation (8)). Mu et al. [44] established the relationship between the dynamic elastic modulus E_d and the confining pressure σ₃. Xu et al. [33] explored the effects of frequency f, dynamic load amplitude σ_d, initial partial stress σ_s, and confining pressure σ₃ on E_d.

$$E=A\ln N+B$$

(8)

where A and B are fitting parameters, and N is the number of load cycles.

The model fitting parameters proposed above are related to the load and not to the soil properties. Therefore, the two models are presented to predict the dynamic shear modulus and damping ratio considering soil properties (D–W cycles and fine particle content).

(1)

Dynamic shear modulus model

From Figure 16, it can be observed that the relationship between the dynamic shear modulus and the number of load cycles (N > 20) can be approximated by a straight line through the transformation of G = $\frac{G_d-G_{d10}}{G_{d1000}-G_{d10}}$. Therefore, all the data in Figure 16 are fitted according to the following formula:

$$\frac{G_d-G_{d20}}{G_{d1000}-G_{d20}}=a_G\log (N)+b_G, 20\le N\le 1000$$

(9)

where $G_{d20}$ and $G_{d1000}$ are the dynamic shear modulus after 1 and 1000 loading cycles under C0 and T0. ‘a_G’ and ‘b_G’ are the fitting parameters and N is number of load cycles. The fitting results are shown in Figure 16 and

Table 9. Fitting results (G_d).

Soil No.	D–W Cycles	aG	bG	R2	Soil No.	D–W Cycles	aG	bG	R2
C0	0	0.529	−0.590	0.9895	C20	0	0.500	−1.205	0.9900
	1	0.602	−1.410	0.9403		1	0.359	−1.325	0.9731
	2	0.408	−0.816	0.9544		2	0.349	−1.431	0.9947
	3	0.494	−0.305	0.9899		3	0.266	−0.938	0.9944
	4	0.433	−0.978	0.9596		4	0.289	−1.204	0.9917
	5	0.445	−1.377	0.9975		5	0.188	−1.606	0.9452
	6	0.273	−1.153	0.9840		6	0.321	−1.778	0.9963
	7	0.361	−1.728	0.9895		7	0.190	−1.388	0.9839
C10	0	0.308	−1.306	0.9832	C30	0	0.480	−1.883	0.9983
	1	0.331	−1.200	0.9891		1	0.334	−1.961	0.9976
	2	0.243	−1.245	0.9959		2	0.347	−1.753	0.9945
	3	0.289	−1.422	0.9608		3	0.282	−1.820	0.9980
	4	0.251	−1.304	0.9947		4	0.318	−1.774	0.9955
	5	0.355	−1.917	0.9958		5	0.288	−2.004	0.9909
	6	0.277	−1.753	0.9834		6	0.325	−1.897	0.9938
	7	0.275	−1.864	0.9849		7	0.272	−1.849	0.9906

.

It is important to highlight that prior to utilizing Equation (9), a preliminary test needs to be conducted to determine the dynamic shear modulus for N = 20 and N = 1000 without the DW cycle of GRS.

(2)

Damping ratio model

As can be observed from Figure 17, the damping ratio and the number of loadings follow an exponential relationship, so the fitted equation is defined as:

$$\lambda =a_{\lambda }\log (N)+b_{\lambda }, 20\le N\le 1000$$

(10)

where a_λ and b_λ are the fitting parameters and N is the number of loading cycles.

The values fitted from equation and the laboratory data are represented in Figure 17.

Table 10. Fitting results (λ).

Soil No.	D–W Cycles	aλ	bλ	R2	Soil No.	D–W Cycles	aλ	bλ	R2
C0	0	−0.034	0.176	0.9791	C20	0	−0.043	0.220	0.9709
	1	−0.032	0.150	0.9819		1	−0.046	0.175	0.9957
	2	−0.030	0.124	0.9960		2	−0.052	0.208	0.9627
	3	−0.025	0.143	0.9821		3	−0.031	0.168	0.9762
	4	−0.025	0.138	0.9904		4	−0.033	0.190	0.9628
	5	−0.042	0.210	0.9604		5	−0.031	0.191	0.9599
	6	−0.046	0.207	0.9788		6	−0.038	0.190	0.9662
	7	−0.052	0.210	0.9877		7	−0.029	0.174	0.9401
C10	0	−0.039	0.175	0.9901	C30	0	−0.059	0.256	0.9557
	1	−0.039	0.196	0.9825		1	−0.043	0.186	0.9537
	2	−0.049	0.198	0.9916		2	−0.043	0.222	0.9631
	3	−0.031	0.191	0.9607		3	−0.045	0.187	0.9648
	4	−0.032	0.189	0.9769		4	−0.040	0.220	0.9542
	5	−0.038	0.200	0.9702		5	−0.038	0.208	0.9418
	6	−0.029	0.182	0.9676		6	−0.039	0.214	0.9491
	7	−0.045	0.211	0.9894		7	−0.034	0.201	0.9546

describes the values for the parameters as well as the determination coefficients R². In general, the experimental data are close to the continuous lines of the models. In this sense, both the dynamic shear modulus and damping ratio models are very accurate, since in all the cases the determination coefficients (R²) yield a result of over 94% (Table 9 and Table 10). However, the coupling effect of fines content and D–W cycles are obvious, it is difficult to determine the relationship between the fitting parameters, D–W cycles, and the fines content, but the laws presented in the model can be applied to engineering.

5. Conclusions

The dynamic behaviors of GRS in Southern China were experimentally studied. The effects of load cycles, fines content, and D–W cycles were investigated through the dynamic triaxial tests, where four fines contents and seven D–W cycles were considered. The main conclusions are as follows:

(1) The morphology of the hysteresis curve changes with the numbers of load and D–W cycles, as well as the fines content. The hysteresis curve area S, center offset d, and residual strain ε_sp of GRS vary similarly with the increase of load cycles. They all decrease sharply in the early stage(N < 20), and the reduction rate slows down in the later load stage (20 ≤ N ≤ 1000) and finally stabilizes in the end(N > 1000). The major axis gradient k increases with the number of load cycles and approximately changes linearly with log N. At the same time, as the fines content increases, S, d and ε_sp increase and k decreases. All of these properties fluctuate with the increase of D–W cycles and tend to be stable after about seven D–W cycles.

(2) The growth of dynamic shear modulus and the reduction of damping ratio with the number of load cycles can be divided into the rapid change stage(N < 20) and the slow change stage (20 ≤ N ≤ 1000). Moreover, the dynamic shear modulus and damping ratio show a good linear relationship with the logarithmic number of load cycles and two prediction equations were obtained by the data fitting. With the increase of fines content, the dynamic shear modulus shows a trend of decreasing while the damping ratio shows an increasing trend. The dynamic shear modulus changes with D–W cycles, and it decreases after several D–W cycles. However, the damping ratio is less affected by D–W cycles.

(3) The dynamic characteristics of GRS are influenced by the number of load cycles, fines content, as well as the number of D–W cycles. Among them, the number of load cycles has the dominant influence and the number of D–W cycles has the least influence. The influence of fines content is more pronounced for the low number of load cycles than for the high number of load cycles. In addition, the effects of fines content and the number of D–W cycles are not independent.

(4) Fitting models are proposed to estimate the dynamic shear modulus and damping ratio based on the number of load cycles. These models can predict dynamic shear modulus and damping ratio considering the effects of fines content and D–W for dynamic stability analysis of railway subgrade.