Arbitrary-Order Sensitivity Analysis of Eigenfrequency Problems with Hypercomplex Automatic Differentiation (HYPAD)
Abstract
:Featured Application
Abstract
1. Introduction
2. Background
2.1. First Order Sensitivities of Eigenvalues and Eigenvectors
2.2. Arbitrary-Order Differentiation Using HYPAD
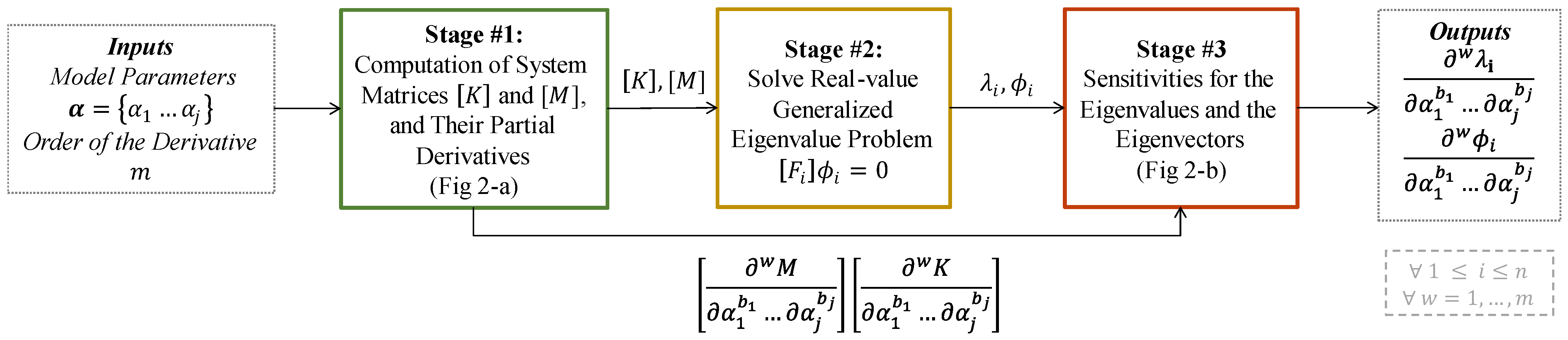
3. Sensitivity Analysis for Eigenfrequency Problems Using HYPAD
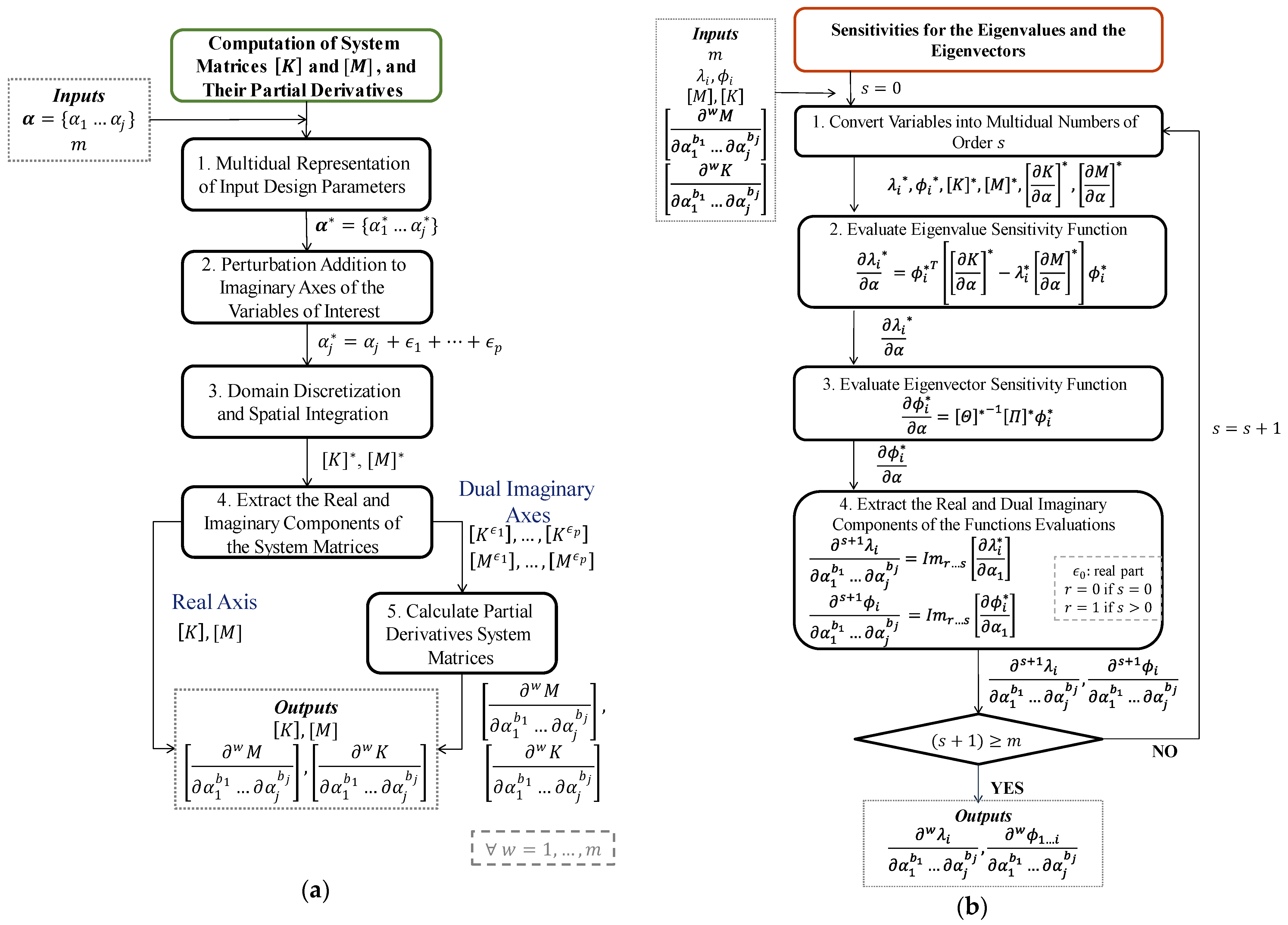
- The first step is to convert all the input parameters of the model into multidual variables of order m.
- Next, unitary perturbations, h, are added to the independent imaginary axes of the multidual axis of the specific variables for which the sensitivities want to be calculated. Here, adding perturbations to the same parameter in two different independent imaginary axes results in having second-order derivatives with respect to the perturbed parameter. Similarly, perturbing two different variables in two different independent imaginary axes results in crossed second-order derivatives. Following this logic, any combination of arbitrary-order sensitivities can be obtained.
- With the design parameters represented as multidual numbers and the appropriate perturbations applied, the structural system is discretized to obtain the global mass and stiffness matrices. Regardless of the discretization and spatial integration method used (e.g., FEM, BEM, SFEM, or others), when any input design parameter is represented as multidual and consequently perturbed, the mass and stiffness matrices will result in two multidual matrices and . This approach is non-intrusive because the discretization and integration algorithms are unchanged; however, as the variables are multidual, algebraic operations are conducted using MultiZ.
- The next step in the methodology is to extract the real and imaginary information of and to form real matrices with dimensions , with being the number of DOF in the system, and is the number of dual imaginary axes. Each matrix corresponds to an axis on and . The matrices obtained with the information from the real axes of and correspond to the global ] and ] matrices for the system and are identical to those obtained from a traditional real-variable analysis; while the matrices formed with the imaginary axes (e.g., ,…, , and ,…, ) contain the information related to the partial derivatives of and with respect to the design input parameters that were perturbed.
- Finally, to complete the first stage, the derivatives of the system matrices are computed following Equation (7).
- The first step in Stage 3 is to convert , , , [, [, and into multidual variables of order s. This procedure will allow the use of HYPAD to calculate the sensitivities. For instance, during the first iteration, when s = 0, the input parameters are converted into zero-order multidual numbers (i.e., multiduals of zero-order are real numbers). In subsequent iterations (e.g., s > 0), each imaginary axis of the multidual number contains the partial derivatives of the variables with respect to the input parameters of the model. In the case of the variables and [ that are already first-order sensitivities, the real part corresponds to the first-order sensitivities (e.g., [ and ), and the imaginary axes contain partial derivatives up to order . In the case of and , the real part corresponds to the eigenvalues and eigenvectors, and the imaginary axes are built from their derivatives with respect to the specific variables of interest. Note that the sensitivities for and up to order are always available because of the iterative nature of the procedure. Moreover, all combinations of partial derivatives of and are available from the first stage. More details on how to construct the multidual arrays are provided in the Supplementary Material, and the analytical demonstration in Section 4.
- With the multidual arrays, Equation (3) is evaluated, which results in a multidual variable that contains the first-order sensitivities in the real axis, and the order sensitivities in the dual imaginary axis. The expression evaluated at the multidual sampling points is:
- Subsequently, using the same multidual arrays, Equation (4) is evaluated to calculate another multidual variable . As for the eigenvalues, this variable contains in the real part, the first-order sensitivities of the eigenvectors, and in the dual imaginary axes, the sensitivities. The expression evaluated at the multidual sampling points is:
- At this point, the order sensitivities of the eigenvalues and the eigenvectors lie in the imaginary axes of and found in step 2 and 3, respectively. Thus, to obtain the sensitivities, such coefficients are extracted by following the next rules. In the first iteration, when , all the variables are multidual numbers of order zero (real numbers); therefore, this corresponds to a traditional first-order sensitivities calculation following the methodologies of Fox and Kapoor [17] and Yang and Peng [33]. In this case, the real part () contains the sensitivity information. In subsequent iterations , the [] is extracted, and the sensitivities are calculated by following Equation (7). To exemplify the specific axes that must be extracted on each pass through the loop, consider for instance the case of fourth-order sensitivities, the last iteration corresponds to ; therefore, the should be extracted, which corresponds to the axis of the multidual number.
4. Sensitivity Analysis for Eigenfrequency Problems Using HYPAD
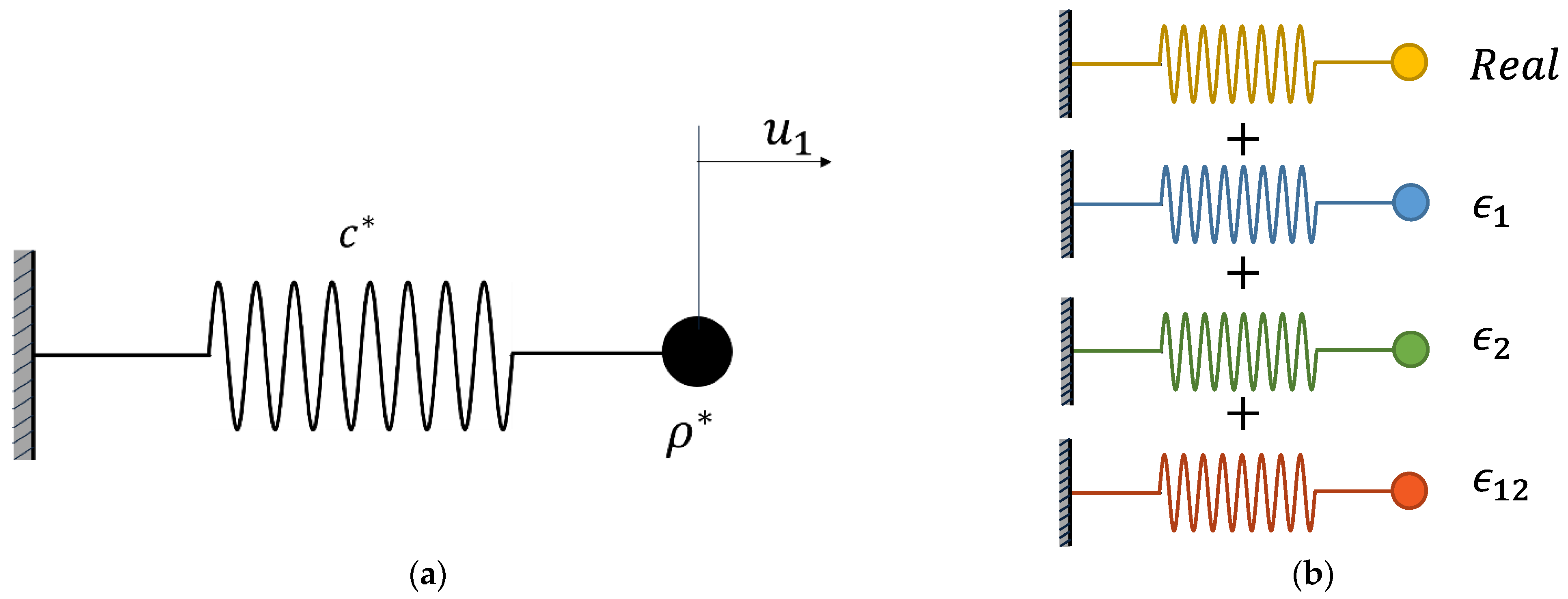
4.1. Simple Harmonic Oscillator
- For the case of mixed second-order sensitivities, both variables and must be converted into multidual arrays. In this case, bi-dual numbers are used with . Therefore, three imaginary axes (e.g., , , and ) are required. A graphical representation of this procedure is shown in Figure 3b.
- Next, to calculate mixed second-order partial derivatives with respect to and , both variables are perturbed by applying a unitary step to the imaginary axes and , respectively:
- As this system corresponds to a one degree of freedom problem, no domain discretization and spatial integrations are necessary. Following the conventions from Figure 2, we have and .
- Consequently, the real components of the multidual variables and are extracted to form the following arrays:
- Similarly, the partial derivatives of and are obtained by evaluating Equation (7) using the information from the dual imaginary components of the multidual variables and as follows:
- In this pass, multidual numbers of order zero (real numbers) were employed; therefore, the input variables and the partial derivatives obtained in Stage 1 were kept as real numbers.
- The first-order sensitivities of the eigenvalues were obtained by evaluating Equation (3):
- Similarly, the first-order sensitivities for the eigenvectors are obtained by evaluating Equation (4):
- This case, which constitutes the first pass through the loop, does not require explicitly extracting the real parts from Equations (20)–(23); this is because, after the evaluation, the multidual number constitutes the first-order sensitivity per se.
- All variables are first converted into multidual numbers of order one:
- Then, the expression in Equation (3) is evaluated with the multidual arrays from Equation (24) as follows:
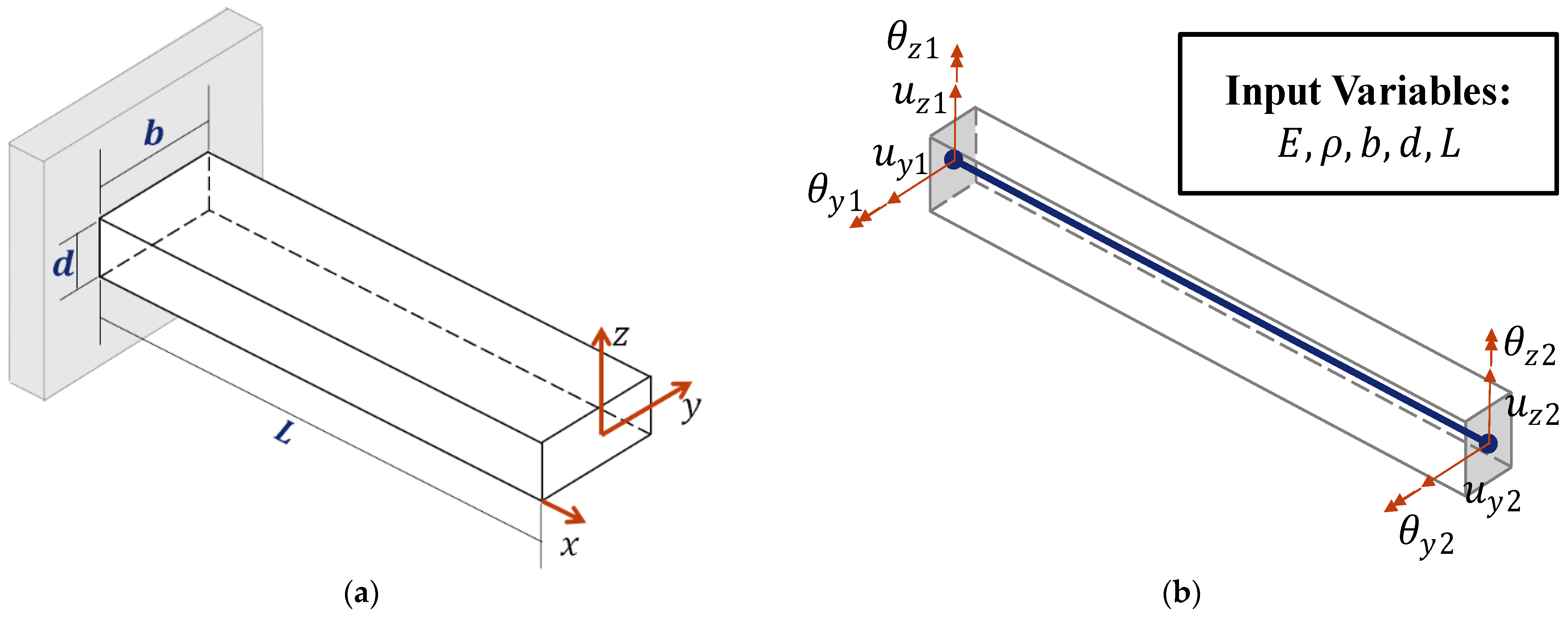
4.2. Free Vibration of a Cantilever Beam
4.2.1. Sensitivity Analysis of a Cantilever Beam with Distinct Eigenvalues
4.2.2. Cantilever Beam with Repeated Eigenvalues
5. Global Design Variable
6. Directional Design Variables (Geometrical)
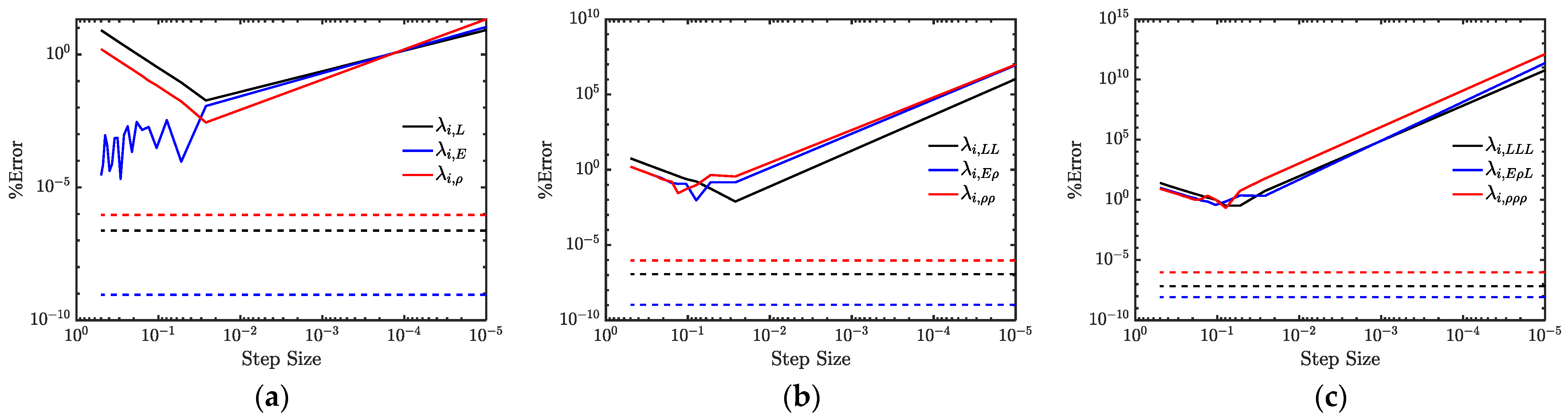
7. Perturbation Step Size Converge Analysis
8. Discussion
9. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Expansion Terms in the Expression from Equation (26a)
Appendix B. Analytical Solution for the Derivatives of the Eigenvalues and Eigenvectors for a Single DOF System
References
- Ruiz, D.; Bellido, J.C.; Donoso, A. Eigenvector sensitivity when tracking modes with repeated eigenvalues. Comput. Methods Appl. Mech. Eng. 2017, 326, 338–357. [Google Scholar] [CrossRef]
- Lin, R.M.; Ng, T.Y. New theoretical developments on eigenvector derivatives with repeated eigenvalues. Mech. Syst. Signal Process. 2019, 129, 677–693. [Google Scholar] [CrossRef]
- Zhong, W.; Cheng, G. Second-Order Sensitivity Analysis of Multimodal Eigenvalues and Related Optimization Techniques. J. Struct. Mech. 1986, 14, 421–436. [Google Scholar] [CrossRef]
- Lin, R.M.; Mottershead, J.E.; Ng, T.Y. A state-of-the-art review on theory and engineering applications of eigenvalue and eigenvector derivatives. Mech. Syst. Signal Process. 2020, 138, 106536. [Google Scholar] [CrossRef]
- Mottershead, J.E.; Link, M.; Friswell, M.I. The sensitivity method in finite element model updating: A tutorial. Mech. Syst. Signal Process. 2011, 25, 2275–2296. [Google Scholar] [CrossRef]
- Yoon, G.H.; Donoso, A.; Carlos Bellido, J.; Ruiz, D. Highly efficient general method for sensitivity analysis of eigenvectors with repeated eigenvalues without passing through adjacent eigenvectors. Int. J. Numer. Methods Eng. 2020, 121, 4473–4492. [Google Scholar] [CrossRef]
- Pryse, S.E.; Kundu, A.; Adhikari, S. Projection methods for stochastic dynamic systems: A frequency domain approach. Comput. Methods Appl. Mech. Eng. 2018, 338, 412–439. [Google Scholar] [CrossRef] [Green Version]
- Francis, J.G.F. The QR Transformation A Unitary Analogue to the LR Transformation—Part 1. Comput. J. 1961, 4, 265–271. [Google Scholar] [CrossRef] [Green Version]
- Francis, J.G.F. The QR Transformation—Part 2. Comput. J. 1962, 4, 332–345. [Google Scholar] [CrossRef] [Green Version]
- Sorensen, D.C. Implicit Application of Polynomial Filters in a k-Step Arnoldi Method. SIAM J. Matrix Anal. Appl. 1992, 13, 357–385. [Google Scholar] [CrossRef] [Green Version]
- Davidson, E.R. The iterative calculation of a few of the lowest eigenvalues and corresponding eigenvectors of large real-symmetric matrices. J. Comput. Phys. 1975, 17, 87–94. [Google Scholar] [CrossRef]
- Andrew, A.L. Iterative Computation of Derivatives of Eigenvalues and Eigenvectors. IMA J. Appl. Math. 1979, 24, 209–218. [Google Scholar] [CrossRef]
- Tan, R.C.E.; Andrew, A.L. Computing Derivatives of Eigenvalues and Elgenvectors by Simultaneous Iteration. IMA J. Numer. Anal. 1989, 9, 111–122. [Google Scholar] [CrossRef]
- Tan, R.C.E. Some acceleration methods for iterative computer of derivatives of eigenvalues and eigenvectors. Int. J. Numer. Methods Eng. 1989, 28, 1505–1519. [Google Scholar] [CrossRef]
- Burchett, B.T.; Costello, M. QR-based algorithm for eigenvalue derivatives. AIAA J. 2002, 40, 2319–2322. [Google Scholar] [CrossRef]
- Wittrick, W.H. Rates of Change of Eigenvalues, With Reference to Buckling and Vibration Problems. J. R. Aeronaut. Soc. 1962, 66, 590–591. [Google Scholar] [CrossRef]
- Fox, R.L.; Kapoor, M.P. Rates of change of eigenvalues and eigenvectors. AIAA J. 1968, 6, 2426–2429. [Google Scholar] [CrossRef]
- Rogers, L.C. Derivatives of eigenvalues and eigenvectors. AIAA J. 1970, 8, 943–944. [Google Scholar] [CrossRef]
- Plaut, R.H.; Huseyin, K. Derivatives of eigenvalues and eigenvectors in non-self-adjoint systems. AIAA J. 1973, 11, 250–251. [Google Scholar] [CrossRef]
- Rudisill, C.S. Derivatives of eigenvalues and eigenvectors for a general matrix. AIAA J. 1974, 12, 721–722. [Google Scholar] [CrossRef]
- Jankovic, M.S. Exact nth derivatives of eigenvalues and eigenvectors. J. Guid. Control. Dyn. 1994, 17, 136–144. [Google Scholar] [CrossRef]
- Garza, J.; Millwater, H.R. Multicomplex Newmark-Beta Time Integration Method for Sensitivity Analysis in Structural Dynamics. AIAA J. 2015, 53, 1188–1198. [Google Scholar] [CrossRef]
- Lim, K.B.; Junkins, J.L.; Wang, B.P. Re-examination of eigenvector derivatives. J. Guid. Control. Dyn. 1987, 10, 581–587. [Google Scholar] [CrossRef]
- Iott, J.; Haftka, R.; Adelman, H.M. Selecting Step Sizes in Sensitivity Analysis by Finite Differences. No. NASA-TM-86382. 1985. Available online: https://ntrs.nasa.gov/citations/19850025225 (accessed on 24 May 2023).
- Wang, B.P.; Apte, A.P. Complex variable method for eigensolution sensitivity analysis. AIAA J. 2006, 44, 2958–2961. [Google Scholar] [CrossRef]
- Navarro, J.D.; Millwater, H.R.; Montoya, A.H.; Restrepo, D. Arbitrary-Order Sensitivity Analysis in Phononic Metamaterials Using the Multicomplex Taylor Series Expansion Method Coupled with Bloch’s Theorem. J. Appl. Mech. 2021, 89, 021007. [Google Scholar] [CrossRef]
- Fujikawa, M.; Tanaka, M.; Mitsume, N.; Imoto, Y. Hyper-dual number-based numerical differentiation of eigensystems. Comput. Methods Appl. Mech. Eng. 2022, 390, 114452. [Google Scholar] [CrossRef]
- Zhang, D.; Wei, F.-S. Computation of eigenvector derivatives with repeated eigenvalues using a complete modal space. AIAA J. 1995, 33, 1749–1753. [Google Scholar] [CrossRef]
- Nelson, R.B. Simplified calculation of eigenvector derivatives. AIAA J. 1976, 14, 1201–1205. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Z.; Chen, S.; Zhang, G. An accurate modal truncation method for eigenvector derivatives. Comput. Struct. 1999, 73, 609–614. [Google Scholar] [CrossRef]
- Balmes, E. Efficient sensitivity analysis based on finite element model reduction. In Proceedings of the International Modal Analysis Conference—IMAC, Santa Barbara, CA, USA, 2–5 February 1998; Volume 2, pp. 1118–1124. [Google Scholar]
- Bernard, M.L.; Bronowicki, A.J. Modal expansion method for eigensensitivity with repeated roots. AIAA J. 1994, 32, 1500–1506. [Google Scholar] [CrossRef]
- Yang, Q.; Peng, X. An exact method for calculating the eigenvector sensitivities. Appl. Sci. 2020, 10, 2577. [Google Scholar] [CrossRef] [Green Version]
- Ojalvo, I.U. Efficient computation of modal sensitivities for systems with repeated frequencies. AIAA J. 1988, 26, 361–366. [Google Scholar] [CrossRef]
- Dailey, R.L. Eigenvector derivatives with repeated eigenvalues. AIAA J. 1989, 27, 486–491. [Google Scholar] [CrossRef]
- Li, Z.; Lai, S.K.; Wu, B. A new method for computation of eigenvector derivatives with distinct and repeated eigenvalues in structural dynamic analysis. Mech. Syst. Signal Process. 2018, 107, 78–92. [Google Scholar] [CrossRef]
- Wu, B.S.; Xu, Z.H.; Li, Z.G. Improved nelson’s method for computing eigenvector derivatives with distinct and repeated eigenvalues. AIAA J. 2007, 45, 950–952. [Google Scholar] [CrossRef]
- Friswell, M.I. The Derivatives of Repeated Eigenvalues and Their Associated Eigenvectors. J. Vib. Acoust. 1996, 118, 390–397. [Google Scholar] [CrossRef]
- Song, D.; Han, W.; Chen, S.; Qiu, Z. Simplified calculation of eigenvector derivatives with repeated eigenvalues. AIAA J. 1996, 34, 859–862. [Google Scholar] [CrossRef]
- Friswell, M.I. Calculation of second and higher order eigenvector derivatives. J. Guid. Control. Dyn. 1995, 18, 919–921. [Google Scholar] [CrossRef]
- Bernard, J.E.; Kwon, S.K.; Wilson, J.A. Differentiation of mass and stiffness matrices for high order sensitivity calculations in finite element-based equilibrium problems. ASME. J. Mech. Des. 1993, 115, 829–832. [Google Scholar] [CrossRef]
- Long, X.Y.; Jiang, C.; Han, X. New method for eigenvector-sensitivity analysis with repeated eigenvalues and eigenvalue derivatives. AIAA J. 2015, 53, 1226–1235. [Google Scholar] [CrossRef]
- Seyranian, A.P.; Lund, E.; Olhoff, N. Multiple eigenvalues in structural optimization problems. Struct. Optim. 1994, 8, 207–227. [Google Scholar] [CrossRef]
- Cheng, G.; Olhoff, N. Rigid body motion test against error in semi-analytical sensitivity analysis. Comput. Struct. 1993, 46, 515–527. [Google Scholar] [CrossRef]
- Olhoff, N.; Rasmussen, J.; Lund, E. A Method of “Exact” Numerical Differentiation for Error Elimination in Finite-Element-Based Semi-Analytical Shape Sensitivity Analyses. Mech. Struct. Mach. 1993, 21, 1–66. [Google Scholar] [CrossRef]
- Olhoff, N.; Lund, E. Finite Element Based Engineering Design Sensitivity Analysis and Optimization. In Advances in Structural Optimization: Solid Mechanics and Its Applications; Herskovits, J., Ed.; Springer: Dordrecht, The Netherlands, 1995; Volume 25. [Google Scholar] [CrossRef]
- Bletzinger, K.U.; Firl, M.; Daoud, F. Approximation of derivatives in semi-analytical structural optimization. Comput. Struct. 2008, 86, 1404–1416. [Google Scholar] [CrossRef]
- Lantoine, G.; Russell, R.P.; Dargent, T. Using Multicomplex Variables for Automatic Computation of High-Order Derivatives. ACM Trans. Math. Softw. 2012, 38, 1–21. [Google Scholar] [CrossRef]
- Fike, J.; Alonso, J. The Development of Hyper-Dual Numbers for Exact Second-Derivative Calculations. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2011. [Google Scholar]
- Voorhees, A.; Millwater, H.; Bagley, R. Complex variable methods for shape sensitivity of finite element models. Finite Elem. Anal. Des. 2011, 47, 1146–1156. [Google Scholar] [CrossRef]
- Voorhees, A.; Millwater, H.; Bagley, R.; Golden, P. Fatigue sensitivity analysis using complex variable methods. Int. J. Fatigue 2012, 40, 61–73. [Google Scholar] [CrossRef]
- Voorhees, A.; Bagley, R.; Millwater, H.; Golden, P. Application of Complex Variable Methods for Fatigue Sensitivity Analysis. In Proceedings of the 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Palm Springs, CA, USA, 4–7 May 2009; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2009. [Google Scholar]
- Montoya, A.; Millwater, H. Sensitivity analysis in thermoelastic problems using the complex finite element method. J. Therm. Stress. 2017, 40, 302–321. [Google Scholar] [CrossRef]
- Balzani, D.; Gandhi, A.; Tanaka, M.; Schröder, J. Numerical calculation of thermo-mechanical problems at large strains based on complex step derivative approximation of tangent stiffness matrices. Comput. Mech. 2015, 55, 861–871. [Google Scholar] [CrossRef]
- Ramirez Tamayo, D.; Montoya, A.; Millwater, H. A virtual crack extension method for thermoelastic fracture using a complex-variable finite element method. Eng. Fract. Mech. 2018, 192, 328–342. [Google Scholar] [CrossRef]
- Wagner, D.; Garcia, M.J.; Montoya, A.; Millwater, H. A finite element-based adaptive energy response function method for 2D curvilinear progressive fracture. Int. J. Fatigue 2019, 127, 229–245. [Google Scholar] [CrossRef]
- Ramirez-Tamayo, D.; Soulami, A.; Gupta, V.; Restrepo, D.; Montoya, A.; Millwater, H. A complex-variable cohesive finite element subroutine to enable efficient determination of interfacial cohesive material parameters. Eng. Fract. Mech. 2021, 247, 107638. [Google Scholar] [CrossRef]
- Montoya, A.; Fielder, R.; Gomez-Farias, A.; Millwater, H. Finite-Element Sensitivity for Plasticity Using Complex Variable Methods. J. Eng. Mech. 2015, 141, 04014118. [Google Scholar] [CrossRef]
- Hürkamp, A.; Tanaka, M.; Kaliske, M. Complex step derivative approximation of consistent tangent operators for viscoelasticity based on fractional calculus. Comput. Mech. 2015, 56, 1055–1071. [Google Scholar] [CrossRef]
- Fielder, R.; Montoya, A.; Millwater, H.; Golden, P. Residual stress sensitivity analysis using a complex variable finite element method. Int. J. Mech. Sci. 2017, 133, 112–120. [Google Scholar] [CrossRef]
- Gomez-Farias, A.; Montoya, A.; Millwater, H. Complex finite element sensitivity method for creep analysis. Int. J. Press. Vessel. Pip. 2015, 132–133, 27–42. [Google Scholar] [CrossRef]
- Monsalvo, J.F.; García, M.J.; Millwater, H.; Feng, Y. Sensitivity analysis for radiofrequency induced thermal therapies using the complex finite element method. Finite Elem. Anal. Des. 2017, 135, 11–21. [Google Scholar] [CrossRef]
- Fielder, R.; Millwater, H.; Montoya, A.; Golden, P. Efficient estimate of residual stress variance using complex variable finite element methods. Int. J. Press. Vessel. Pip. 2019, 173, 101–113. [Google Scholar] [CrossRef]
- Tanaka, M.; Fujikawa, M.; Balzani, D.; Schröder, J. Robust numerical calculation of tangent moduli at finite strains based on complex-step derivative approximation and its application to localization analysis. Comput. Methods Appl. Mech. Eng. 2014, 269, 454–470. [Google Scholar] [CrossRef]
- Chun, J. Sensitivity analysis of system reliability using the complex-step derivative approximation. Reliab. Eng. Syst. Saf. 2021, 215, 107814. [Google Scholar] [CrossRef]
- Smith, D.E.; Siddhi, V. Generalized Approach for Incorporating Normalization Conditions in Design Sensitivity Analysis of Eigenvectors. AIAA J. 2006, 44, 2552–2561. [Google Scholar] [CrossRef]
- Wedderburn, J.H.M. On Hypercomplex Numbers. Proc. Lond. Math. Soc. 1908, s2-6, 77–118. [Google Scholar] [CrossRef]
- Eastham, M.S.P. 2968. On the definition of dual numbers. Math. Gaz. 1961, 45, 232–233. [Google Scholar] [CrossRef]
- Balcer, M.R.; Millwater, H.; Favorite, J.A. Multidual Sensitivity Method in Ray-Tracing Transport Simulations. Nucl. Sci. Eng. 2021, 195, 907–936. [Google Scholar] [CrossRef]
- Kantor, I.L.; Kantor, I.L.; Solodovnikov, A.S. Hypercomplex Numbers: An Elementary Introduction to Algebras; Springer: New York, NY, USA, 1989. [Google Scholar]
- Martins, J.R.R.A.; Sturdza, P.; Alonso, J.J. The connection between the complex-step derivative approximation and algorithmic differentiation. ACM Trans. Math. Softw. 2001, 46, 23. [Google Scholar] [CrossRef] [Green Version]
- Millwater, H.R.; Shirinkam, S. Multicomplex Taylor Series Expansion For Computing High-Order Derivatives. Int. J. Apllied Math. 2014, 27, 311–334. [Google Scholar] [CrossRef] [Green Version]
- Aguirre-Mesa, A.M.; Garcia, M.J.; Millwater, H. MultiZ: A library for computation of high order derivatives using multicomplex or multidual numbers. ACM Trans. Math. Softw. 2020, 46, 1–30. [Google Scholar] [CrossRef]
- Price, G.B. An Introduction to Multicomplex Spaces and Functions; Dekker: New York, NY, USA, 1991. [Google Scholar]
- Aguirre-Mesa, A.M.; Garcia, M.J.; Aristizabal, M.; Wagner, D.; Ramirez-Tamayo, D.; Montoya, A.; Millwater, H. A block forward substitution method for solving the hypercomplex finite element system of equations. Comput. Methods Appl. Mech. Eng. 2021, 387, 114195. [Google Scholar] [CrossRef]
- Bottega, W.J. Engineering Vibrations; Taylor & Francis: Abingdon, UK, 2006. [Google Scholar]
- Anderson, E.; Bai, Z.; Bischof, C.; Blackford, S.; Demmel, J.; Dongarra, J.; Du Croz, J.; Greenbaum, A.; Hammarling, S.; McKenney, A.; et al. {LAPACK} Users’ Guide; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1999. [Google Scholar]

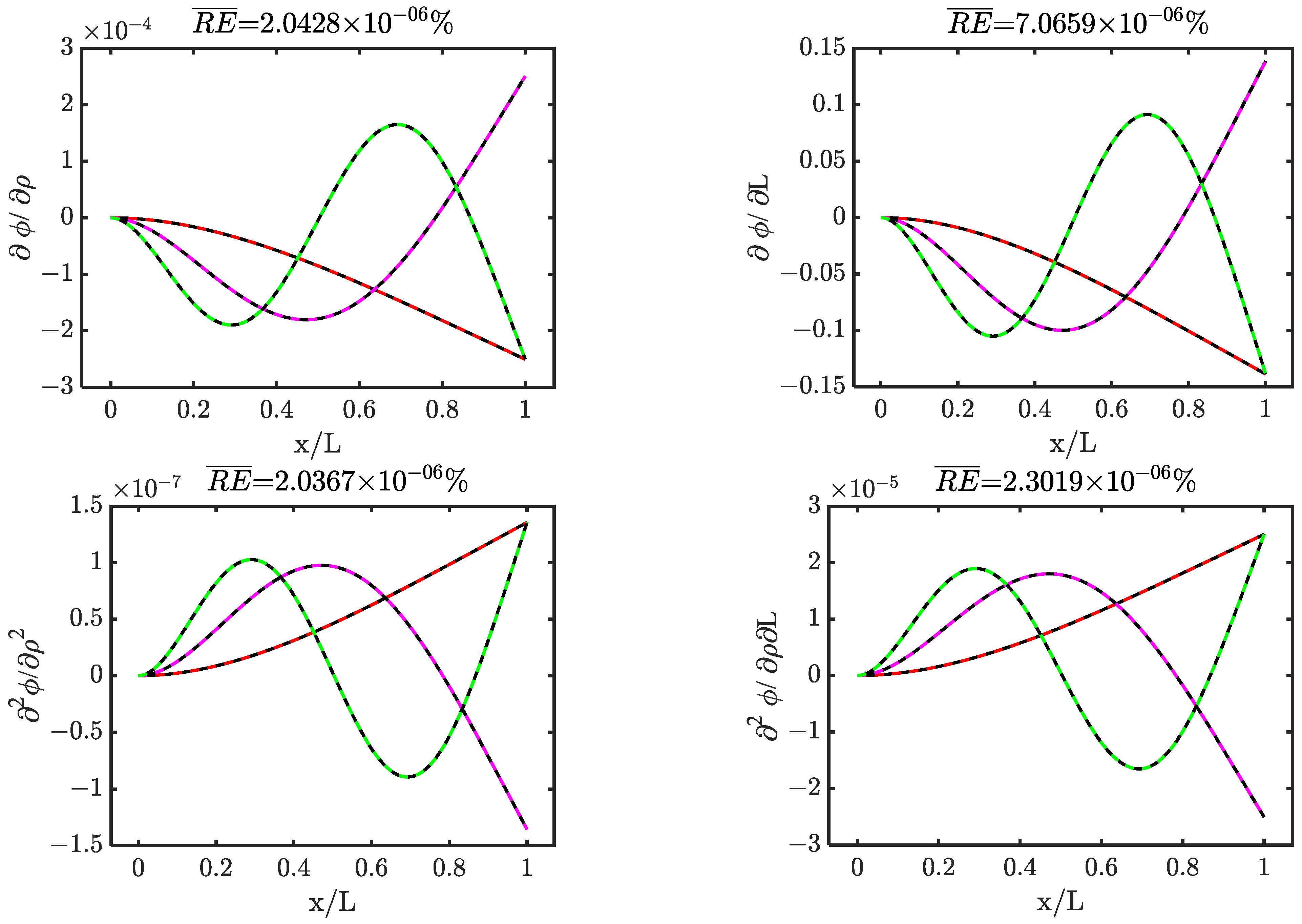
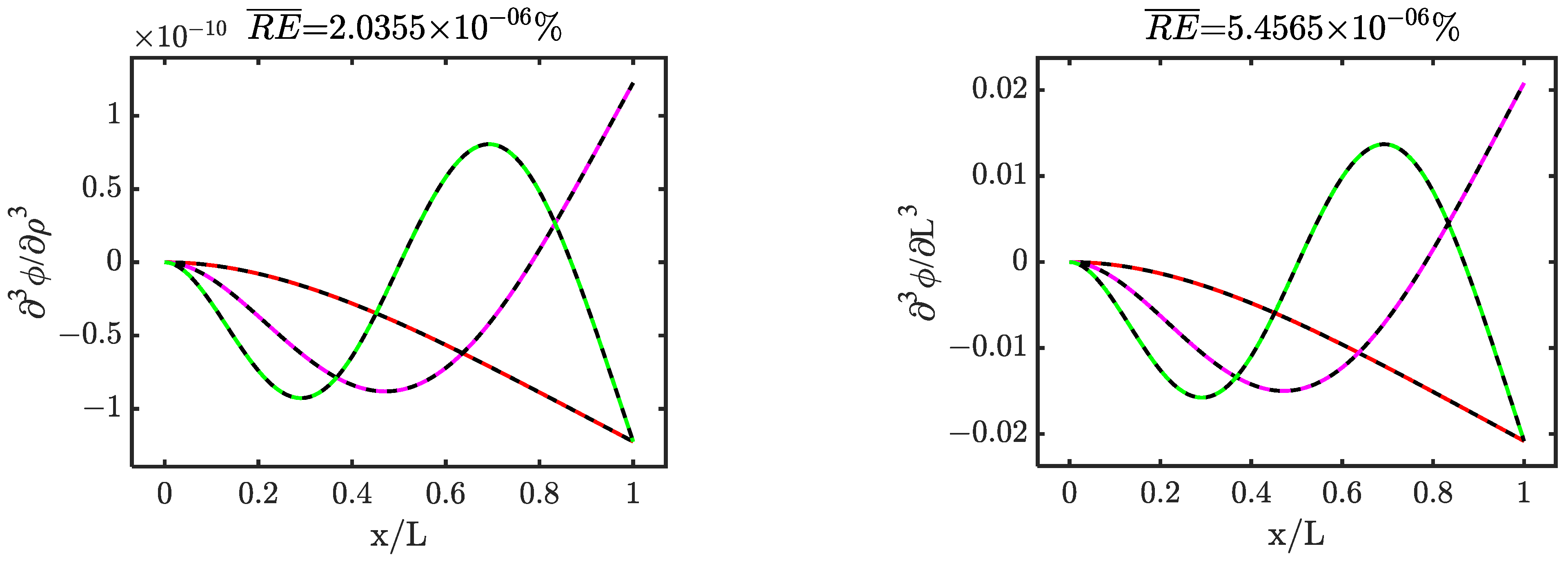
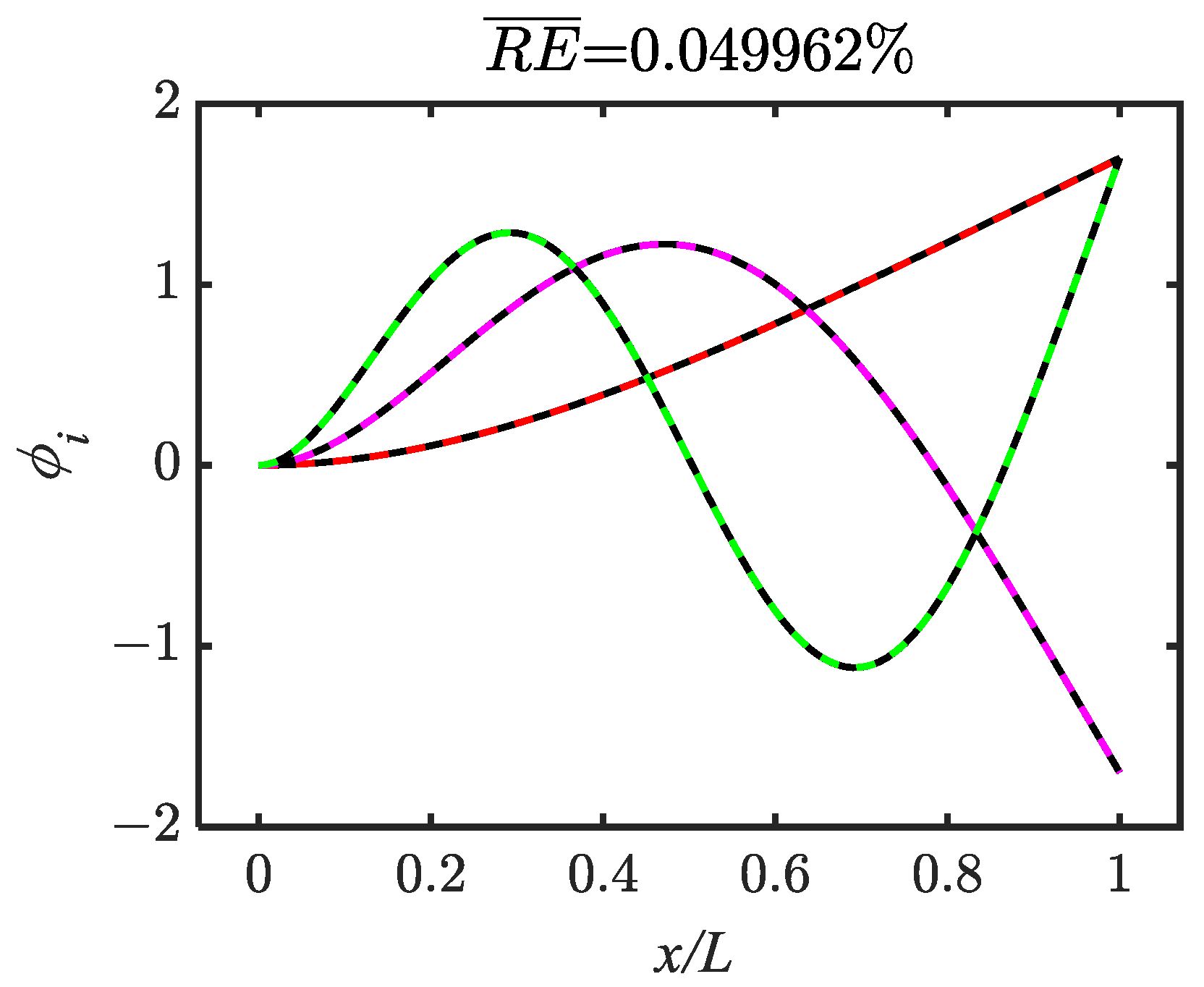

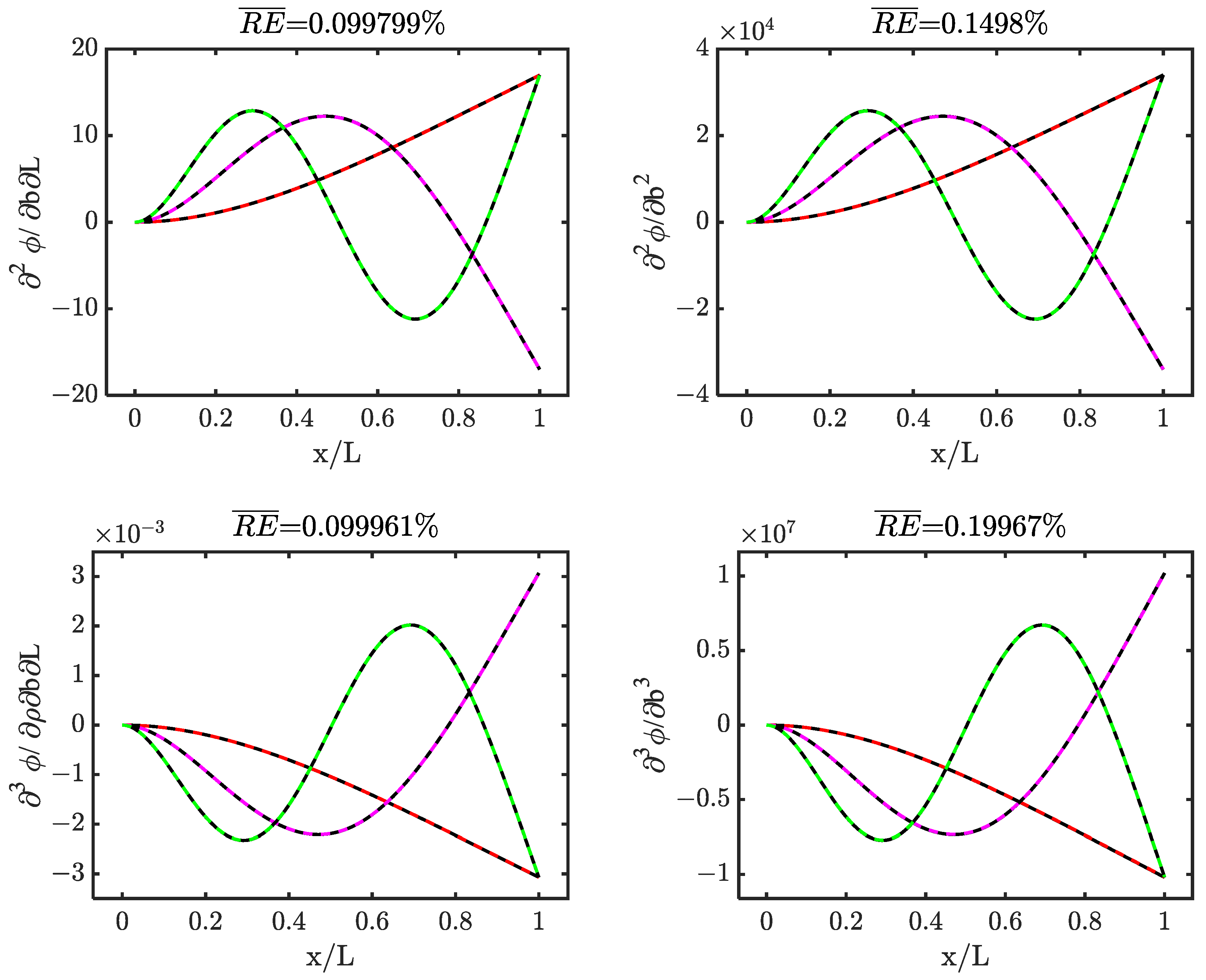
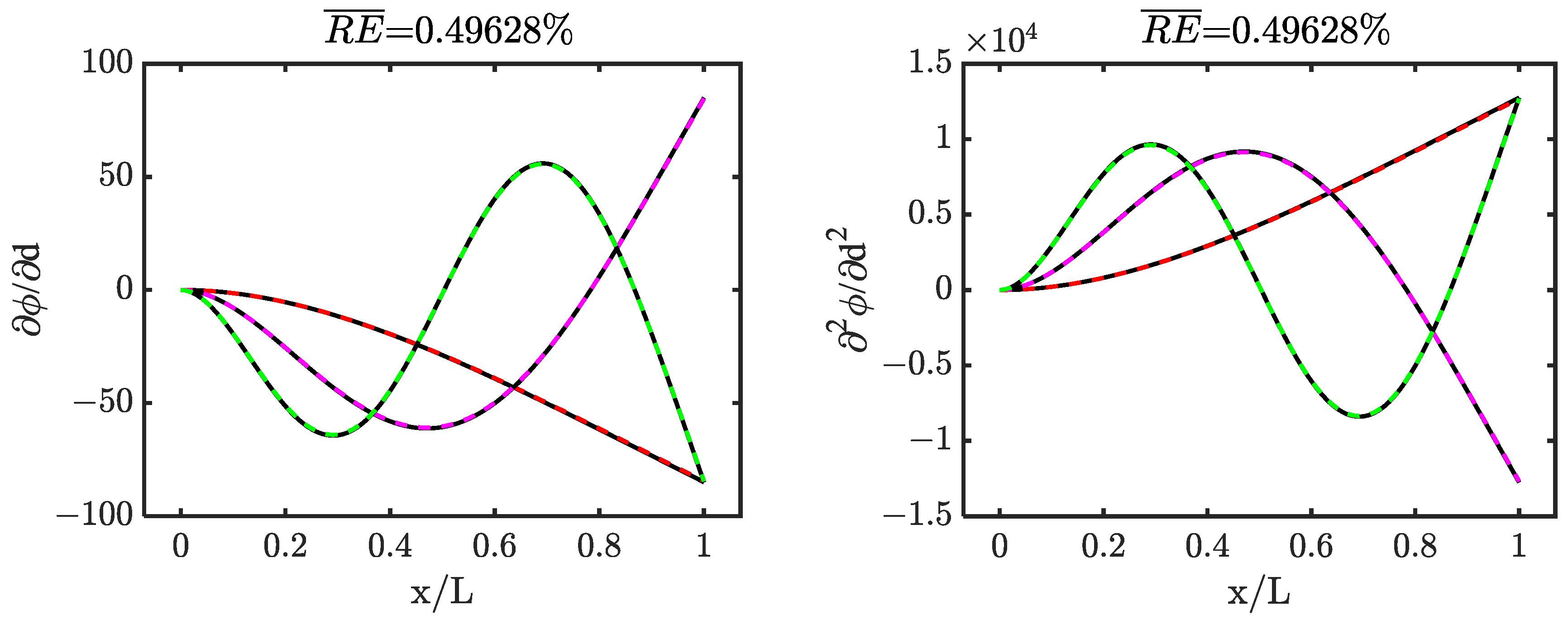
| Mode i | (%Error ) |
|---|---|
| 1 | 4.100 (92.390) |
| 2 | 9.225 (2.775) |
| 3 | (1.616) |
| 4 | 362.299 (0.842) |
| 5 | 1262.435 (5.348) |
| 6 | 2840.480 (5.243) |
| Mode i | () | () | |
|---|---|---|---|
| 1 | (92.390) | (93.180) | (93.716) |
| 2 | (2.775) | (2.806) | (2.826) |
| 3 | (1.616) | (1.620) | (1.623) |
| 4 | (0.842) | (0.842) | (0.843) |
| 5 | (5.348) | (5.348) | (5.348) |
| 6 | (5.243) | (5.243) | (5.243) |
| Mode i | |||
|---|---|---|---|
| 1 | (23.643) | (11.605) | (6.725) |
| 2 | (2.916) | (0.827) | (0.216) |
| 3 | (0.883) | (0.791) | (0.739) |
| 4 | (0.683) | (0.691) | (0.696) |
| 5 | (5.308) | (5.295) | (5.290) |
| 6 | (5.276) | (5.282) | (5.284) |
| Mode i | |||
|---|---|---|---|
| 1 | 0.0595 (0.0911) | −0.215 (0.107) | 0.172 (0.831) |
| 2 | 0.134 (0.137) | −0.483 (0.178) | 0.3866 (0.585) |
| 3 | 2.337 (0.679) | −8.436 (0.679) | 6.750 (0.689) |
| 4 | 5.258 (0.672) | −18.983 (0.671) | 15.187 (0.675) |
| 5 | 18.323 (5.286) | −66.147 (5.286) | 52.918 (5.286) |
| 6 | 2578 (5.285) | −148.830 (5.285) | 119.060 (5.285) |
| Mode i | (%Error |
|---|---|
| 1, 2 | 4.100 (75.618) |
| 3, 4 | 161.020 (1.152) |
| 5, 6 | 1262.400 (5.330) |
| Mode i. | (%Error | (%Error | (%Error |
|---|---|---|---|
| 1, 2 | 0.0819 (67.996) | 0.0819 (213.889) | 0.00 |
| 3, 4 | 3.220 (0.250) | 3.220 (0.207) | 0.00 |
| 5, 6 | 25.249 (5.231) | 25.249 (5.502) | 0.00 |
| Mode i | (%Error | (%Error | (%Error |
|---|---|---|---|
| 1, 2 | −0.296 (68.632) | −0.0655 (19.942) | 0.236 (19.657) |
| 3, 4 | −11.626 (0.247) | −2.576 (0.619) | 9.301 (0.621) |
| 5, 6 | −91.150 (5.231) | −20.189 (5.280) | 72.920 (5.280) |
| Mode i | (%Error | (%Error |
|---|---|---|
| 1 | 0.0819 (11.746) | 0.0819 (23.098) |
| 2 | 0.000 | 0.000 |
| 3 | 3.220 (0.856) | 3.220 (0.383) |
| 4 | 0.000 | 0.000 |
| 5 | 25.249 (5.260) | 25.249 (5.334) |
| 6 | 0.000 | 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velasquez-Gonzalez, J.C.; Navarro, J.D.; Aristizabal, M.; Millwater, H.R.; Montoya, A.; Restrepo, D. Arbitrary-Order Sensitivity Analysis of Eigenfrequency Problems with Hypercomplex Automatic Differentiation (HYPAD). Appl. Sci. 2023, 13, 7125. https://doi.org/10.3390/app13127125
Velasquez-Gonzalez JC, Navarro JD, Aristizabal M, Millwater HR, Montoya A, Restrepo D. Arbitrary-Order Sensitivity Analysis of Eigenfrequency Problems with Hypercomplex Automatic Differentiation (HYPAD). Applied Sciences. 2023; 13(12):7125. https://doi.org/10.3390/app13127125
Chicago/Turabian StyleVelasquez-Gonzalez, Juan C., Juan David Navarro, Mauricio Aristizabal, Harry R. Millwater, Arturo Montoya, and David Restrepo. 2023. "Arbitrary-Order Sensitivity Analysis of Eigenfrequency Problems with Hypercomplex Automatic Differentiation (HYPAD)" Applied Sciences 13, no. 12: 7125. https://doi.org/10.3390/app13127125
APA StyleVelasquez-Gonzalez, J. C., Navarro, J. D., Aristizabal, M., Millwater, H. R., Montoya, A., & Restrepo, D. (2023). Arbitrary-Order Sensitivity Analysis of Eigenfrequency Problems with Hypercomplex Automatic Differentiation (HYPAD). Applied Sciences, 13(12), 7125. https://doi.org/10.3390/app13127125








