Modeling and Performance Analysis of a Pump-Driven Chip-Level Two-Phase Cooling System in Data Centers
Abstract
Featured Application
Abstract
1. Introduction
2. Modeling
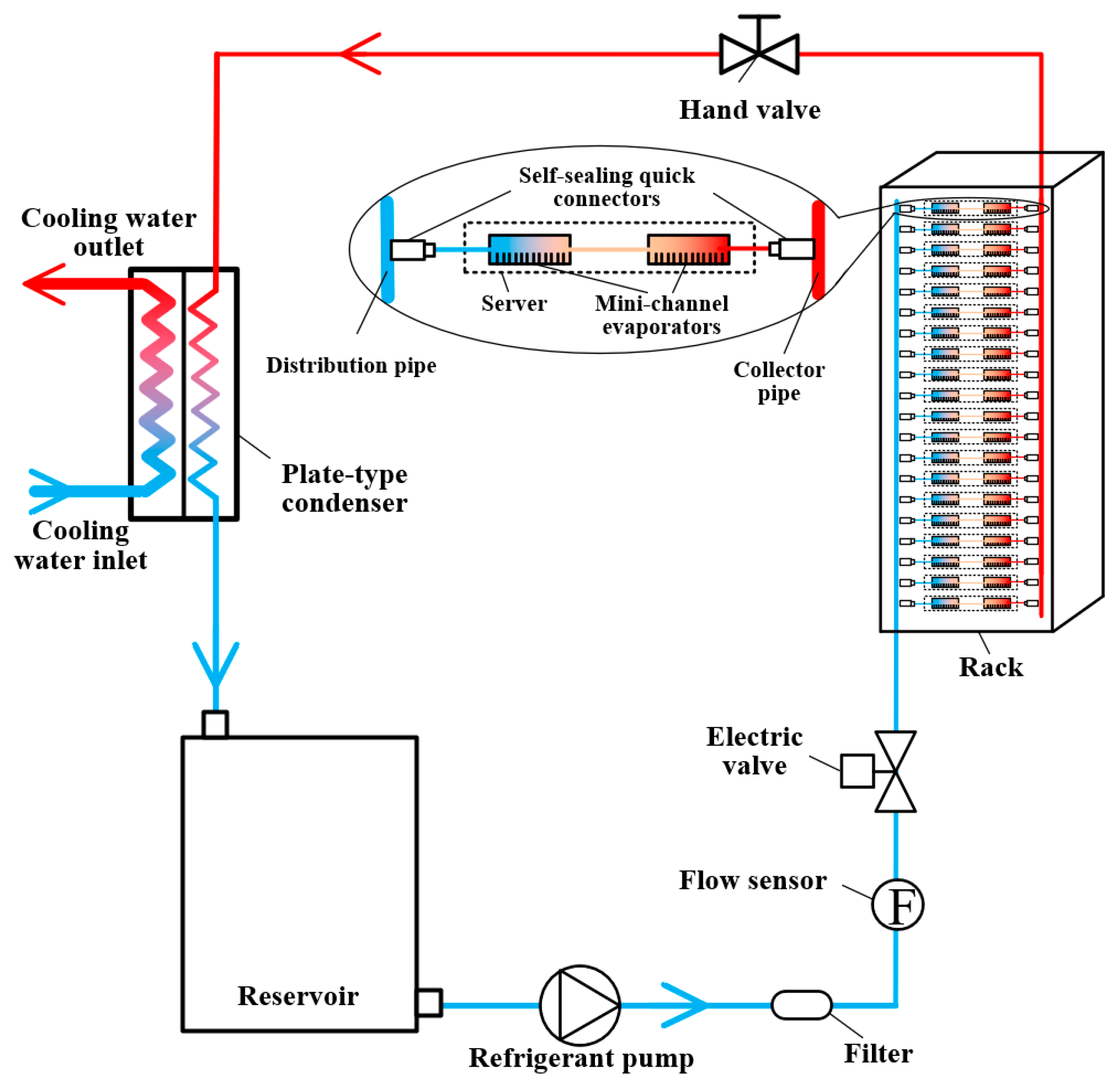
2.1. Introduction of the PCTCS and Assumptions
- The system’s fluid flow and heat transfer are presumed to be steady-state;
- The reservoir’s volume is sizable and not fully liquid-filled. Due to its proximity to the pump, variations in the refrigerant state between the reservoir inlet and pump inlet are negligible;
- All components of the PCTCS, excluding the evaporator and condenser, are assumed to be adiabatic;
- Power disparities among servers, along with any variations in the refrigerant flow and state upon server entry, are ignored. Consequently, the heat transfer and pressure drop across each server are identical, and the refrigerant state on exiting each server is assumed to be uniform;
- The fluid is assumed to be in thermodynamic equilibrium;
- Parameters are averaged across sections, and a one-dimensional model is applied.
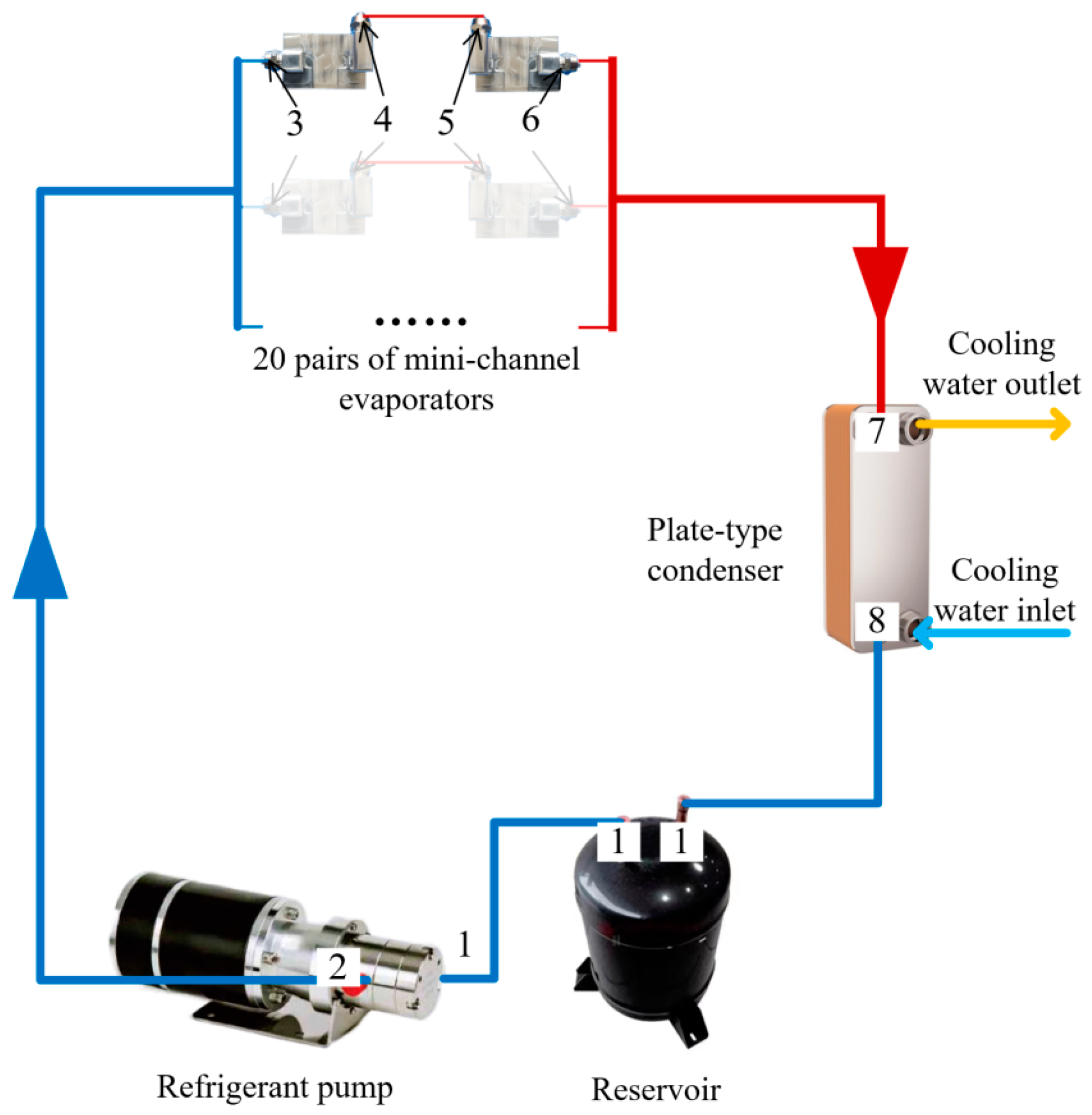
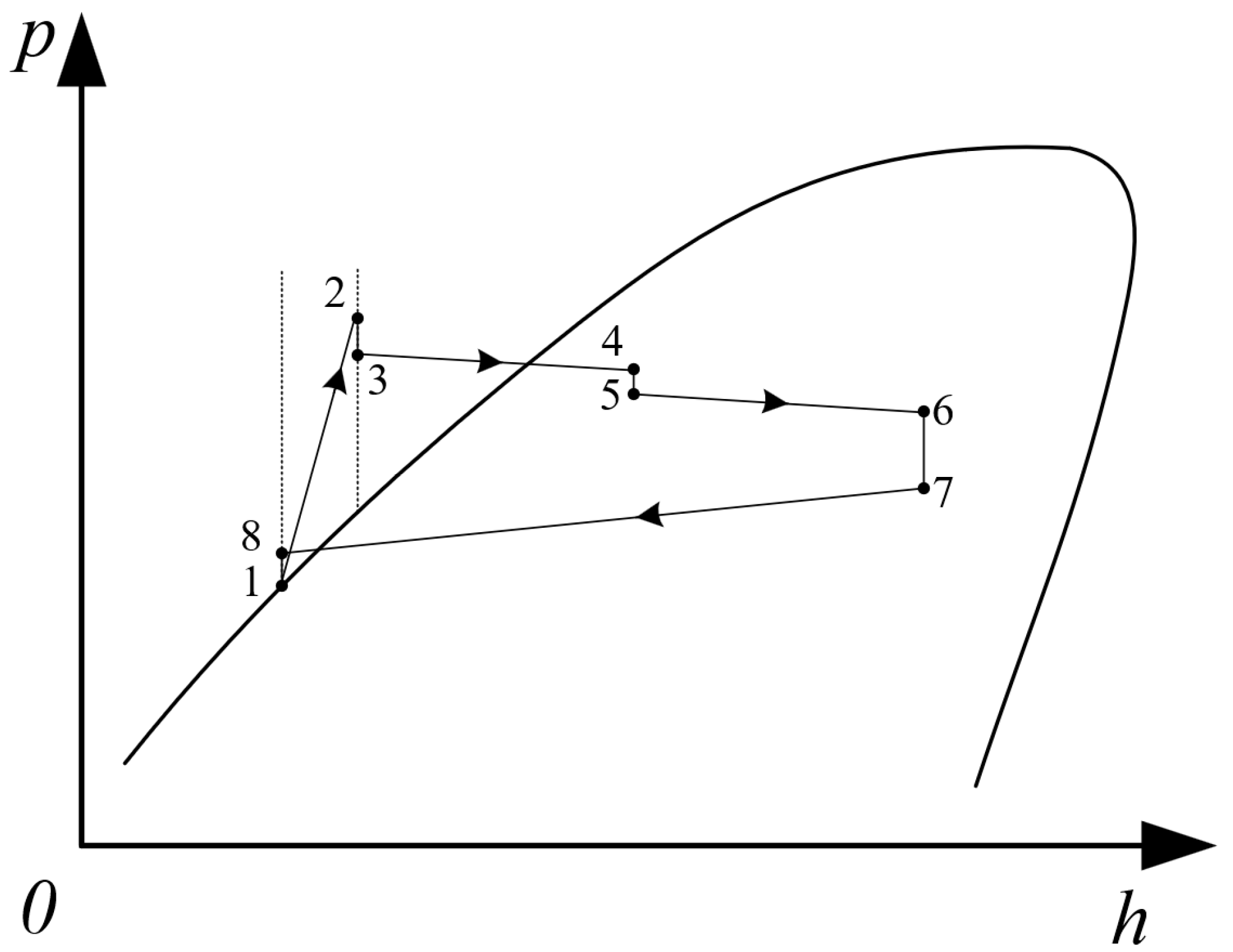
2.2. Mathematical Models and Correlations
2.2.1. Connecting Pipe Model
- Pressure drop for single-phase flow
- Frictional pressure drop (Pdfsp)
- 2.
- Gravitational pressure drop (Pdgsp)
- Pressure drop for two-phase flow
- Frictional pressure drop (Pdfsp)
- Gravitational pressure drop
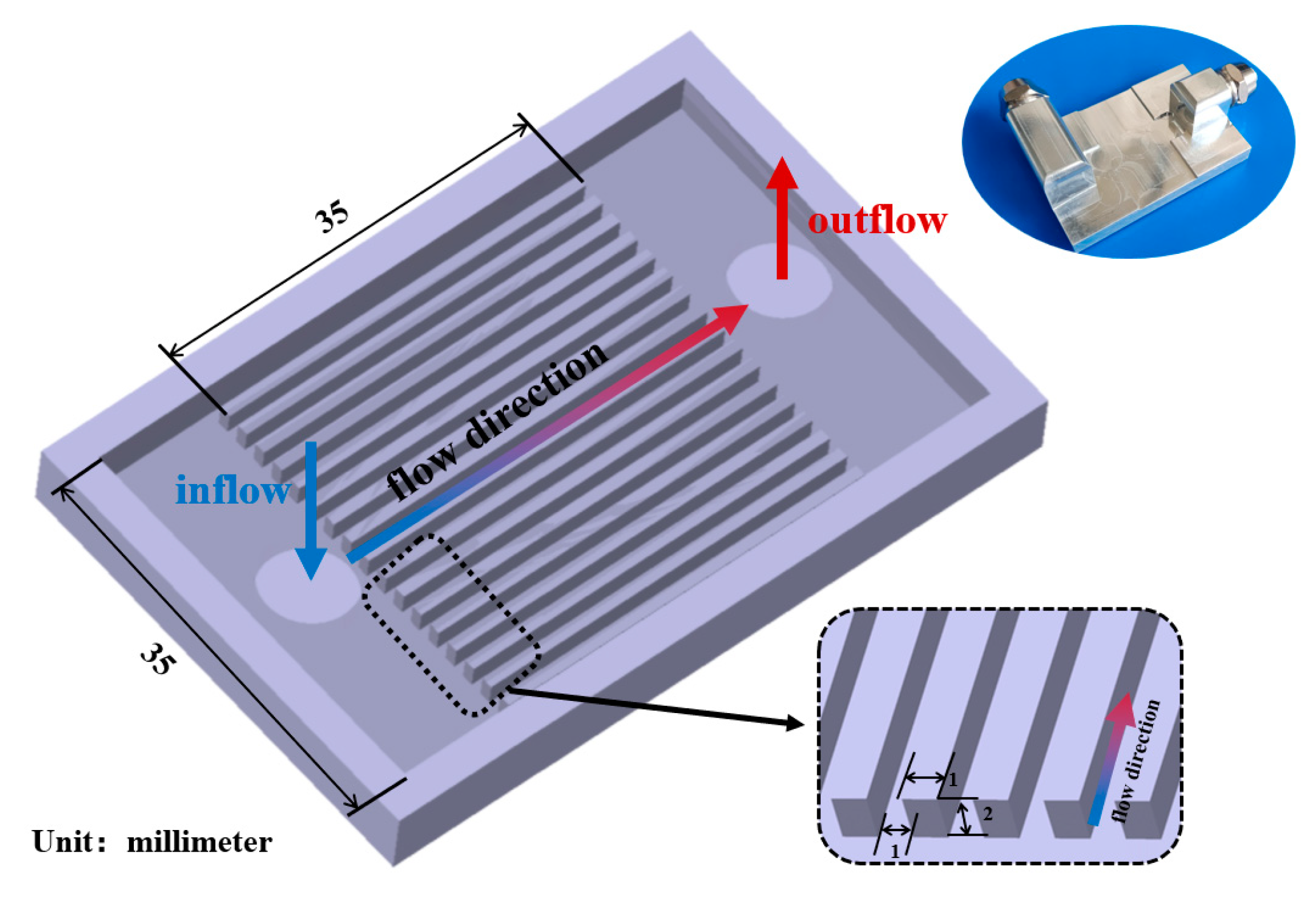
2.2.2. Mini-Channel Evaporator Model
- Pressure drop for single-phase and two-phase flow
- Heat transfer model
- Single-phase convection
- 2.
- Saturated flow boiling correlation
- 3.
- Subcooling flow boiling correlation
2.2.3. Plate-Type Condenser Model
- Pressure drop for single-phase and two-phase refrigerant flow
- Heat transfer model
2.2.4. Pump Model
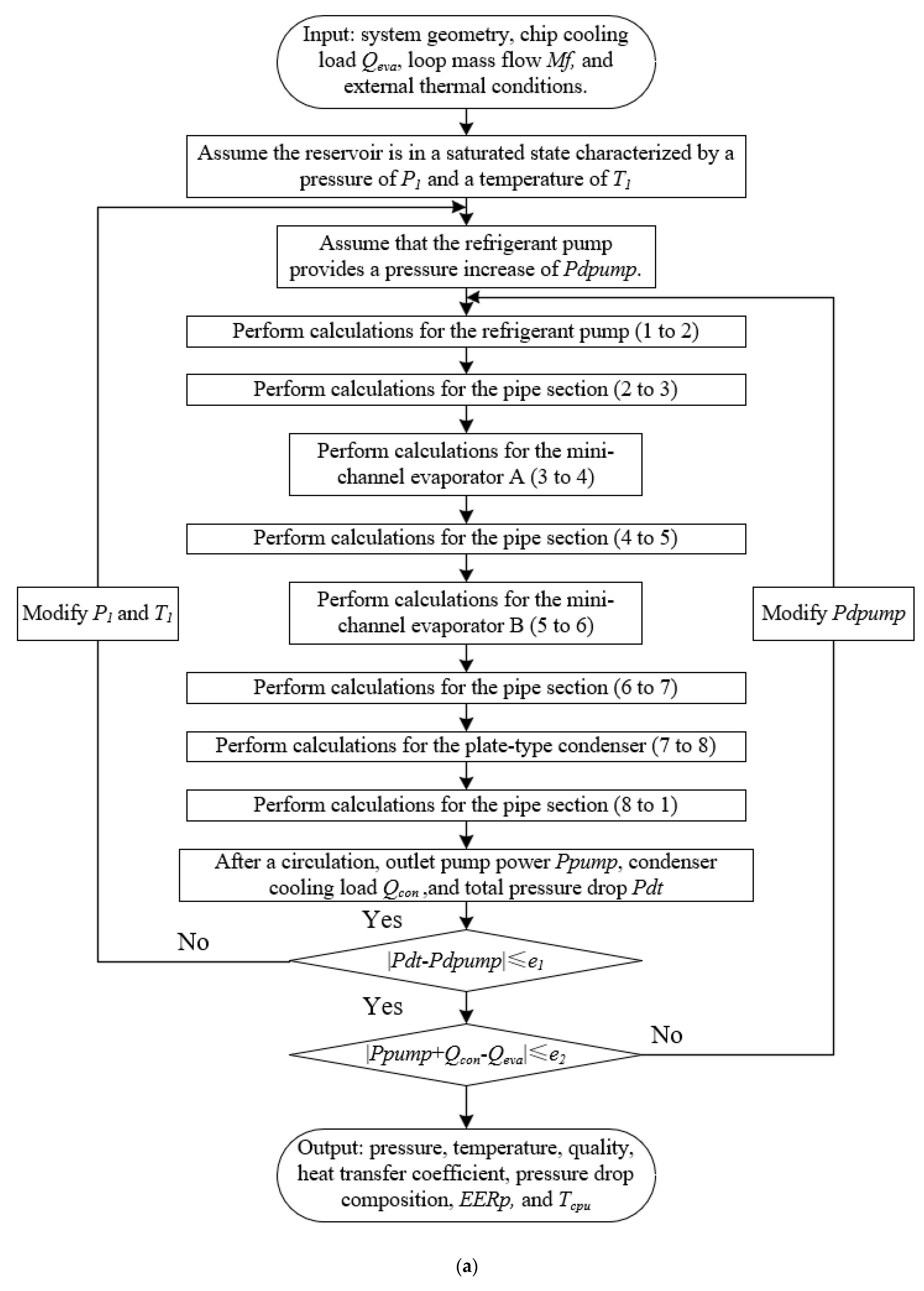
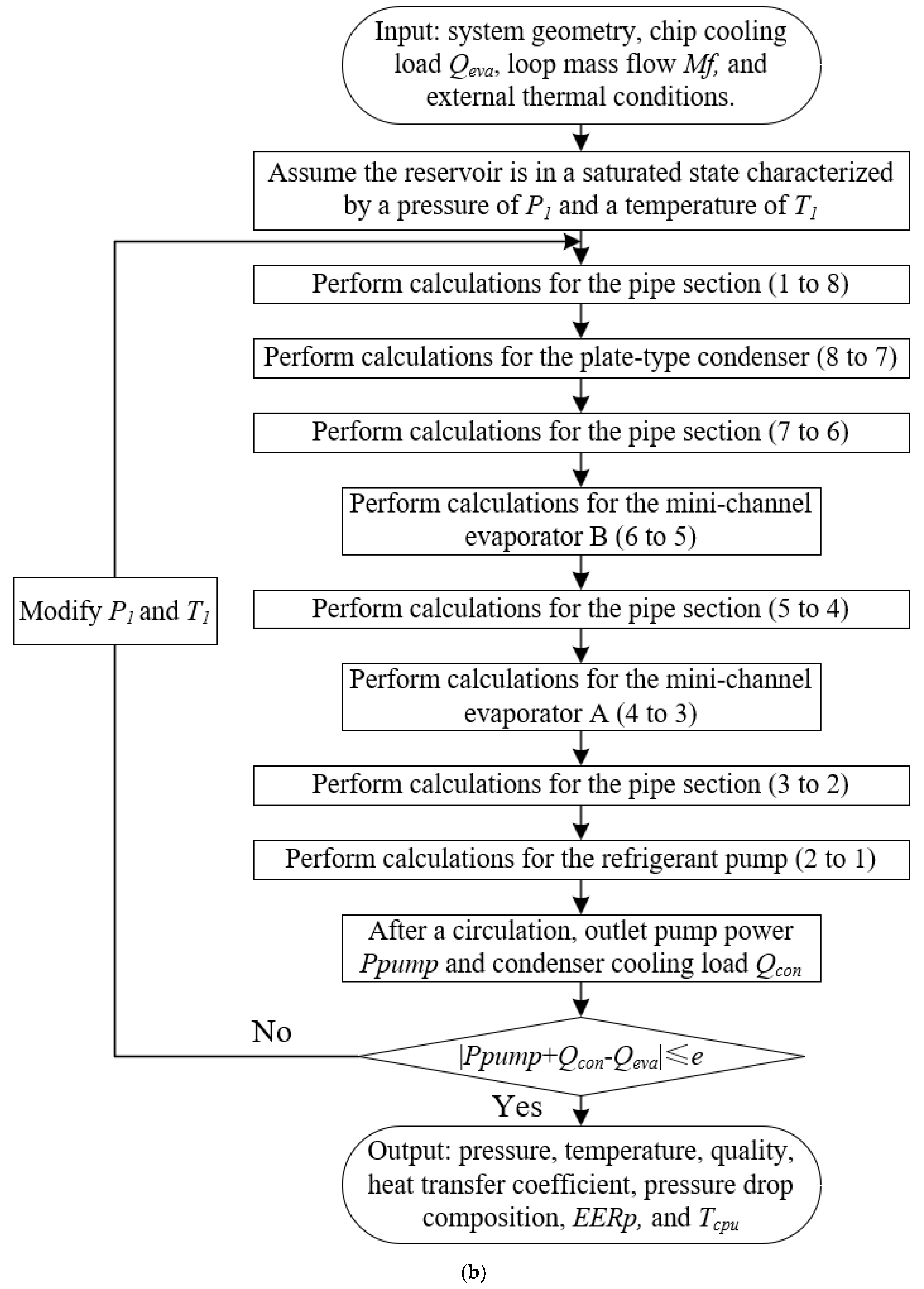
2.3. Solution Procedure
2.4. Model Verification
2.5. Performance Evaluation Method
2.6. Simulation Conditions and Scope of Study
- Default configuration;
- Three different types of refrigerants, namely, R-113, R-134a, and R-32, were selected to facilitate an analysis of their impacts on the performance of the PCTCS. These refrigerants have atmospheric boiling points of 47.6 °C, −26.1 °C, and −51.7 °C, respectively, thus representing low-, medium-, and high-pressure refrigerants. Their widespread use in refrigeration and data center heat dissipation, coupled with their distinctly varying physical properties, make them ideal for evaluating the diverse influences they can exert on the performance of the PCTCS;
- The impact of the condenser height on the PCTCS performance was assessed. The condenser height was altered relative to the reservoir and the evaporator by varying the heights of the connecting pipes in sections 6-7 and 8-1. The configurations included 0 m, 0 m (same height); 1 m, −1 m (condenser is 1 m higher); and −1 m, 1 m (condenser is 1 m lower);
- The cooling water temperature range was established between 15 and 60 °C, with increments of 5 °C.
3. Results and Discussion
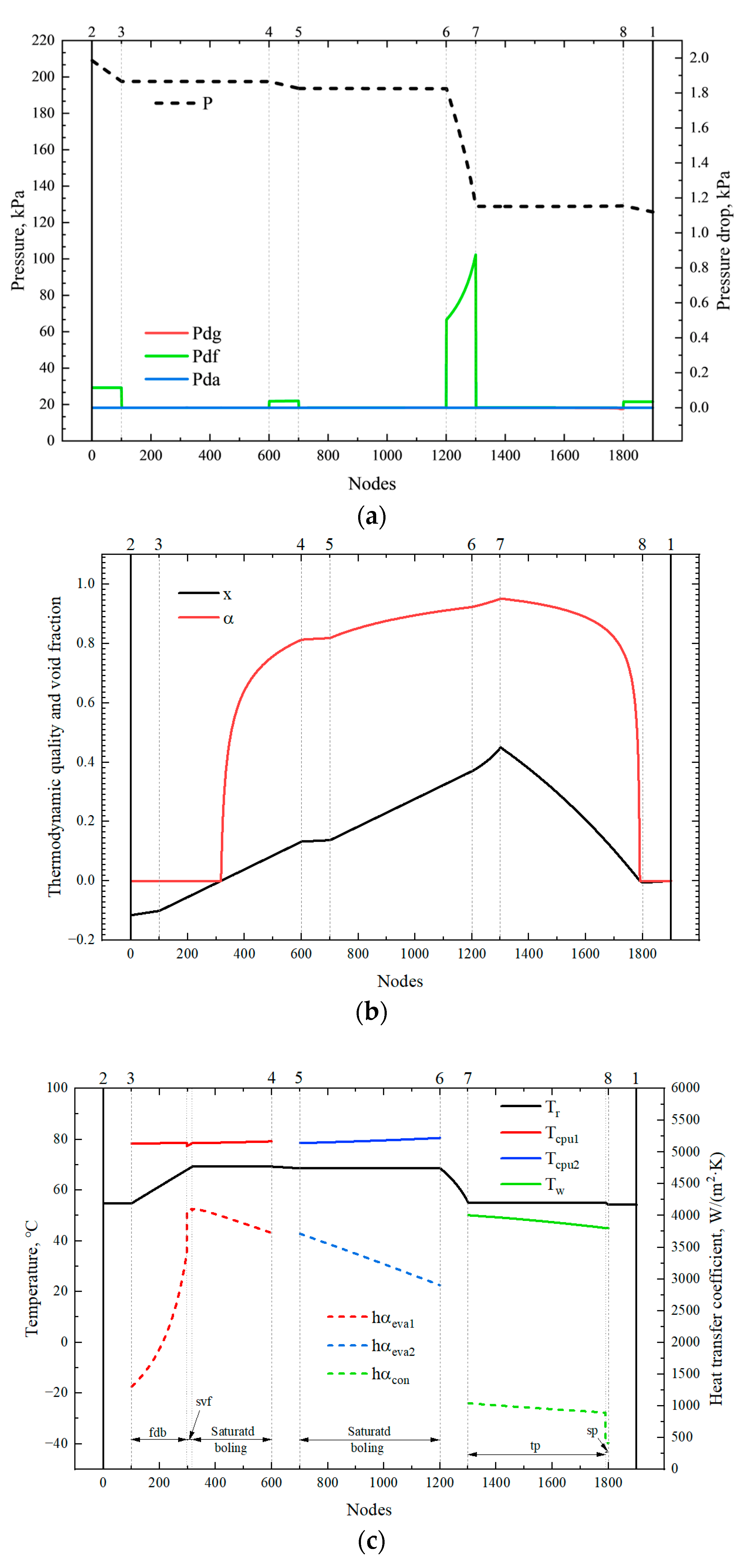
3.1. Simulation Results with the Default Configuration
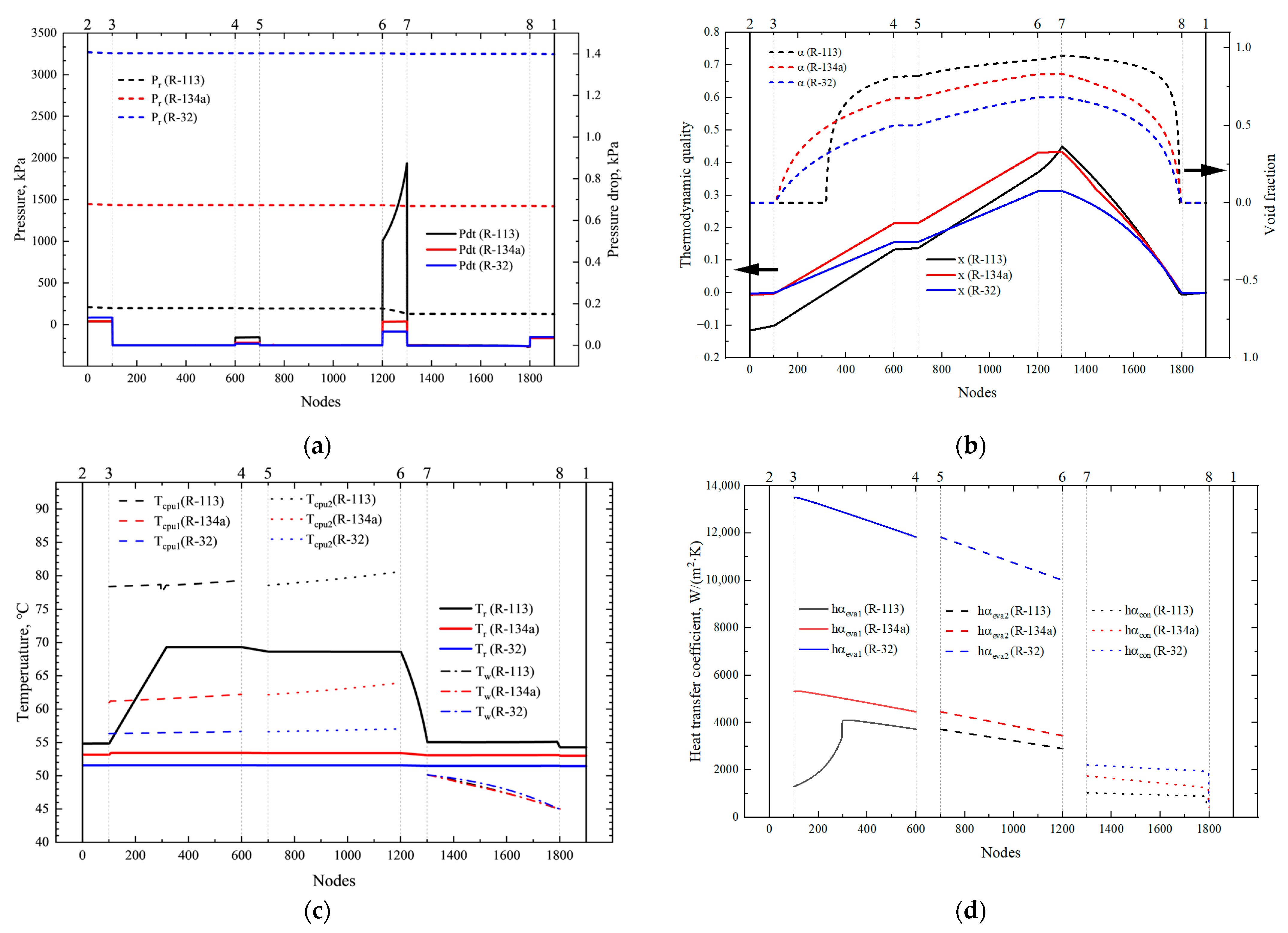
3.2. Influence of the Refrigerant Type
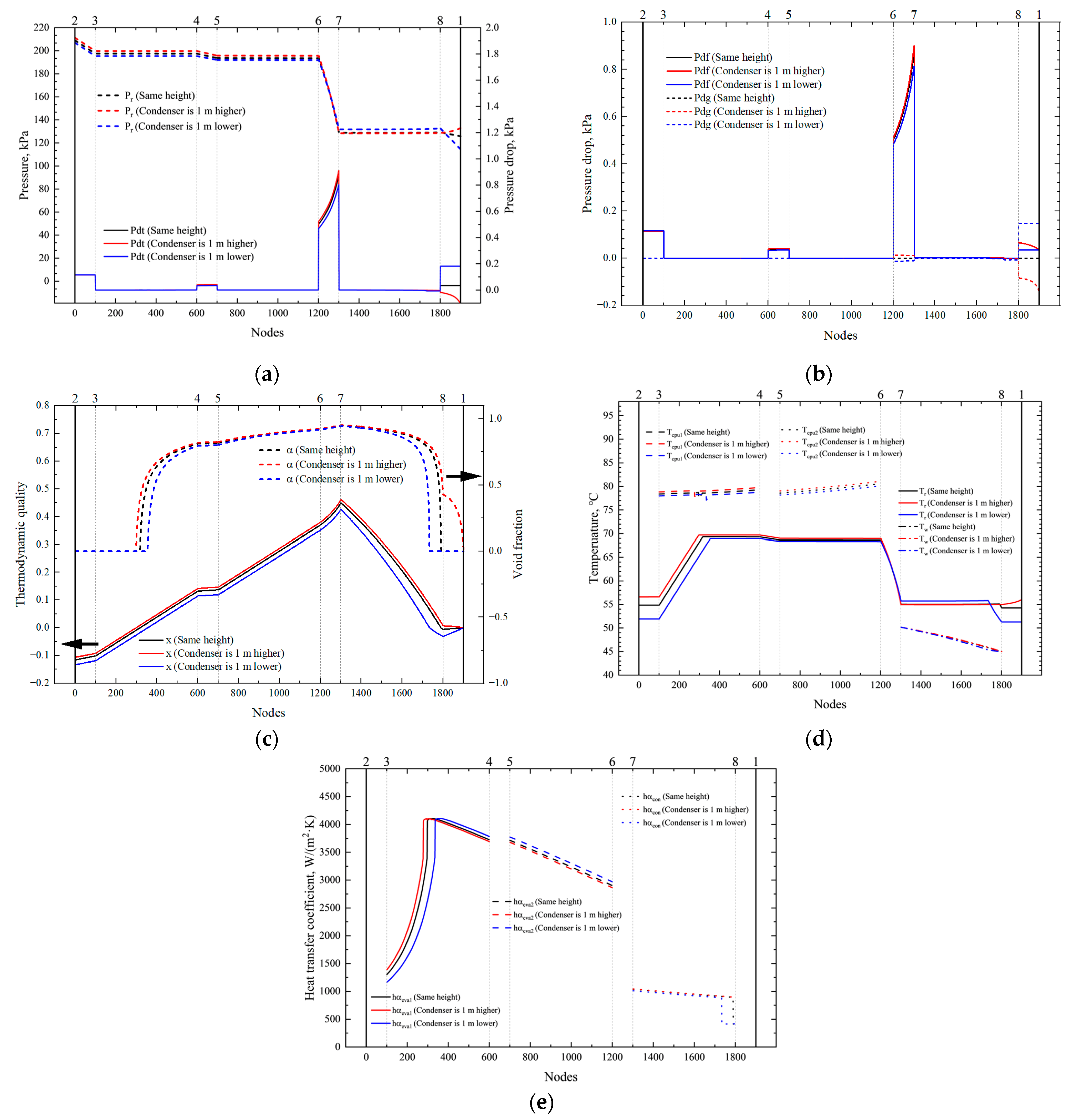
3.3. Impact of the Condenser Height
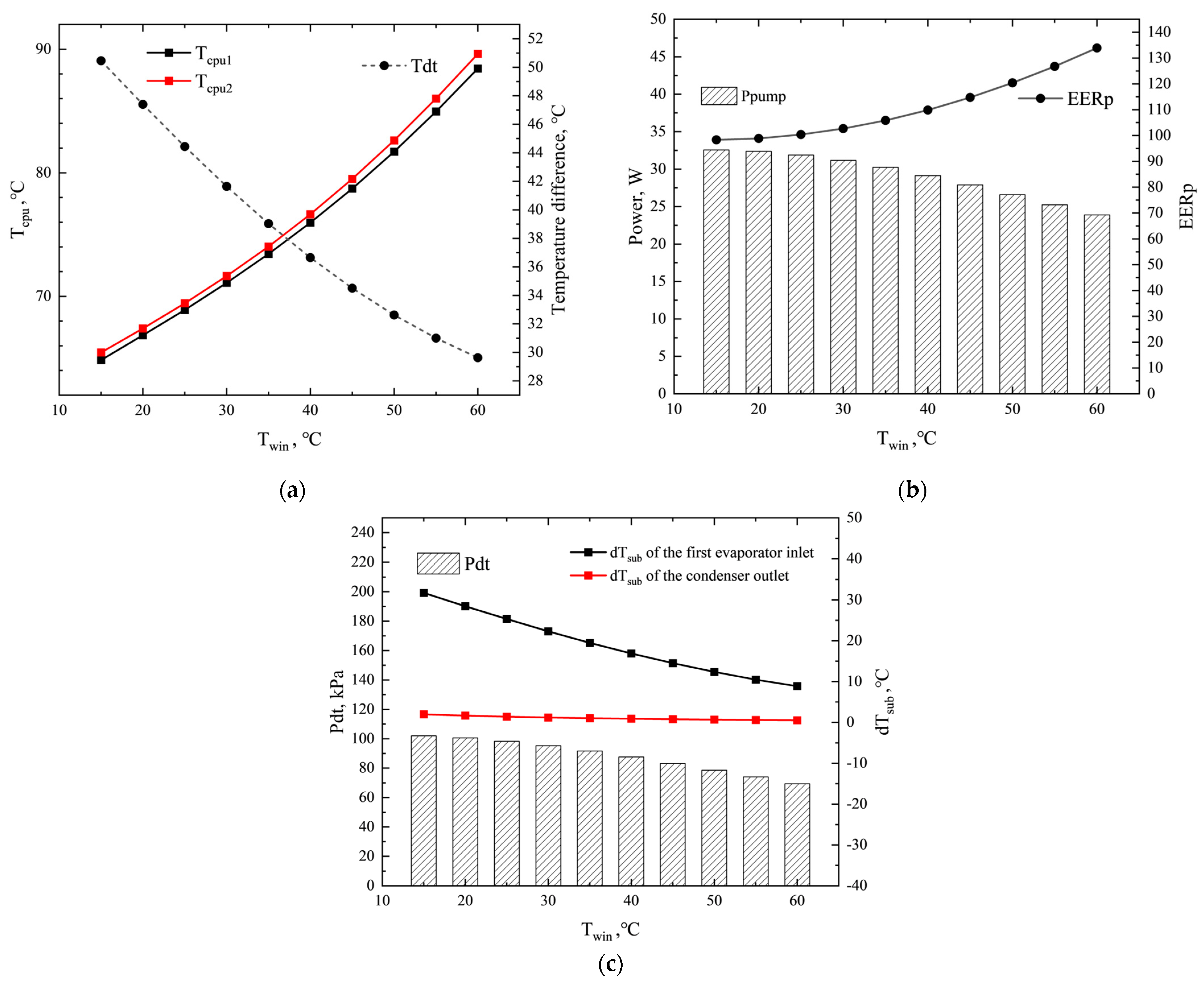
3.4. Influence of the Cooling Water Temperature
4. Conclusions
- The constructed model has been validated in harmony with experimental studies, attesting to its precision in simulating the PCTCS;
- The results from our simulations suggest that the PCTCS can efficiently manage CPU power as high as 80 W, attaining an EERp of up to 115, while ensuring that the temperatures of the two CPUs remain at 78.72 °C and 79.50 °C—within the CPUs’ thermal tolerance limits—when the inlet cooling water temperature is 45 °C;
- The choice of refrigerant significantly affects the PCTCS’s performance. Utilizing R-32 and R-134a as refrigerants results in superior energy efficiency and temperature performance compared to R-113, with R-32 showing the best overall performance. However, the choice of refrigerant necessitates the consideration of factors such as safety, maintenance, and cost in actual applications;
- Increasing the condenser’s height decreases the subcooling in the PCTCS’s evaporators and condenser. While a higher condenser location improves the PCTCS’s energy efficiency, it adversely affects its temperature performance. However, these disparities are marginal, suggesting that the condenser’s height exerts a limited effect on the PCTCS’s comprehensive performance. In practical applications, this effect can generally be ignored;
- The cooling water temperature significantly influences the PCTCS’s performance. A higher cooling water temperature enhances both the temperature performance and energy efficiency of the PCTCS, in addition to facilitating natural cooling and waste heat recovery. Therefore, it is advisable to maximize the cooling water temperature during PCTCS operation, provided the CPU temperature remains within safe limits.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, H.; Zhang, Z.; Yang, L. A review on airflow distribution and management in data center. Energy Build. 2018, 179, 264–277. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, H.; Wang, Z. Thermal Management and Energy Consumption in Air, Liquid, and Free Cooling Systems for Data Centers: A Review. Energies 2023, 16, 1279. [Google Scholar] [CrossRef]
- Petrović, S.; Colangelo, A.; Balyk, O.; Delmastro, C.; Gargiulo, M.; Simonsen, M.B.; Karlsson, K. The role of data centres in the future Danish energy system. Energy 2020, 194, 116928. [Google Scholar] [CrossRef]
- Masanet, E.; Shehabi, A.; Lei, N.; Smith, S.; Koomey, J. Recalibrating global data center energy-use estimates. Science 2020, 367, 984–986. [Google Scholar] [CrossRef]
- Zhang, Y.; Shan, K.; Li, X.; Li, H.; Wang, S. Research and Technologies for next-generation high-temperature data centers—State-of-the-arts and future perspectives. Renew. Sustain. Energy Rev. 2023, 171, 112991. [Google Scholar] [CrossRef]
- Mitchell-Jackson, J.; Koomey, J.G.; Nordman, B.; Blazek, M. Data center power requirements: Measurements from Silicon Valley. Energy 2003, 28, 837–850. [Google Scholar] [CrossRef]
- Moazamigoodarzi, H.; Tsai, P.J.; Pal, S.; Ghosh, S.; Puri, I.K. Influence of cooling architecture on data center power consumption. Energy 2019, 183, 525–535. [Google Scholar] [CrossRef]
- Han, Z.; Wei, H.; Sun, X.; Bai, C.; Xue, D.; Li, X. Study on influence of operating parameters of data center air conditioning system based on the concept of on-demand cooling. Renew. Energy 2020, 160, 99–111. [Google Scholar] [CrossRef]
- Han, Z.; Ji, Q.; Wei, H.; Xue, D.; Sun, X.; Zhang, X.; Li, X. Simulation study on performance of data center air-conditioning system with novel evaporative condenser. Energy 2020, 210, 118521. [Google Scholar] [CrossRef]
- Nadjahi, C.; Louahlia, H.; Lemasson, S. A review of thermal management and innovative cooling strategies for data center. Sustain. Comput. Inform. Syst. 2018, 19, 14–28. [Google Scholar] [CrossRef]
- Daraghmeh, H.M.; Wang, C.-C. A review of current status of free cooling in datacenters. Appl. Therm. Eng. 2017, 114, 1224–1239. [Google Scholar] [CrossRef]
- Güğül, G.N.; Gökçül, F.; Eicker, U. Sustainability analysis of zero energy consumption data centers with free cooling, waste heat reuse and renewable energy systems: A feasibility study. Energy 2023, 262, 125495. [Google Scholar] [CrossRef]
- Nada, S.A.; El-Zoheiry, R.M.; Elsharnoby, M.; Osman, O.S. Experimental investigation of hydrothermal characteristics of data center servers’ liquid cooling system for different flow configurations and geometric conditions. Case Stud. Therm. Eng. 2021, 27, 101276. [Google Scholar] [CrossRef]
- Li, L.; Zheng, W.; Wang, X.; Wang, X. Coordinating liquid and free air cooling with workload allocation for data center power minimization. In Proceedings of the 11th International Conference on Autonomic Computing ({ICAC} 14), Philadelphia, PA, USA, 18–20 June 2014; pp. 249–259. [Google Scholar]
- Joshi, Y.; Kumar, P. Energy Efficient Thermal Management of Data Centers; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kheirabadi, A.C.; Groulx, D. Cooling of server electronics: A design review of existing technology. Appl. Therm. Eng. 2016, 105, 622–638. [Google Scholar] [CrossRef]
- Habibi Khalaj, A.; Halgamuge, S.K. A Review on efficient thermal management of air- and liquid-cooled data centers: From chip to the cooling system. Appl. Energy 2017, 205, 1165–1188. [Google Scholar] [CrossRef]
- Madhour, Y.; Olivier, J.; Costa-Patry, E.; Paredes, S.; Michel, B.; Thome, J.R. Flow Boiling of R134a in a Multi-Microchannel Heat Sink With Hotspot Heaters for Energy-Efficient Microelectronic CPU Cooling Applications. IEEE Trans. Compon. Packag. Manuf. Technol. 2011, 1, 873–883. [Google Scholar] [CrossRef]
- Wu, D.; Marcinichen, J.B.; Thome, J.R. Experimental evaluation of a controlled hybrid two-phase multi-microchannel cooling and heat recovery system driven by liquid pump and vapor compressor. Int. J. Refrig. 2013, 36, 375–389. [Google Scholar] [CrossRef]
- Marcinichen, J.B.; Olivier, J.A.; Oliveira, V.d.; Thome, J.R. A review of on-chip micro-evaporation: Experimental evaluation of liquid pumping and vapor compression driven cooling systems and control. Appl. Energy 2012, 92, 147–161. [Google Scholar] [CrossRef]
- Xue, Z.H.; Ai, B.C.; Qu, W. Data center energy conservation study utilizing loop heat pipes as a chip-level cooling technique and its industrial application. Appl. Therm. Eng. 2023, 220, 119715. [Google Scholar] [CrossRef]
- Mao, Z.; Asai, Y.; Yamanoi, A.; Seki, Y.; Wiranata, A.; Minaminosono, A. Fluidic rolling robot using voltage-driven oscillating liquid. Smart Mater. Struct. 2022, 31, 105006. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, B.; Shi, W.; Han, L.; Li, X. Modeling and performance analysis of a two-phase thermosyphon loop with partially/fully liquid-filled downcomer. Int. J. Refrig. 2015, 58, 172–185. [Google Scholar] [CrossRef]
- Marcinichen, J.B.; Thome, J.R. New novel green computer two-phase cooling cycle: A model for its steady-state simulation. In Proceedings of the Proceedings of the 23rd International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems-ECOS2010, Lausanne, Switzerland, 14–17 June 2010. [Google Scholar]
- Ong, C.L.; Amalfi, R.L.; Marcinichen, J.B.; Lamaison, N.; Thome, J.R. Two-phase mini-thermosyphon for cooling of datacenters: Experiments, modeling and simulations. In Proceedings of the International Electronic Packaging Technical Conference and Exhibition, San Francisco, CA, USA, 29 August–1 September 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017; p. V001T002A003. [Google Scholar]
- Zhang, P.; Wei, X.; Yan, L.; Xu, H.; Yang, T. Review of recent developments on pump-assisted two-phase flow cooling technology. Appl. Therm. Eng. 2019, 150, 811–823. [Google Scholar] [CrossRef]
- Wang, L.; Yang, T.; Yuana, W.; Ren, K. Experimental study of pump-driven chip-level two-phase cooling system for data centres. Indoor Built Environ. 2023. accepted. [Google Scholar]
- Brown, G.O. The history of the Darcy-Weisbach equation for pipe flow resistance. In Environmental and Water Resources History; American Society of Civil Engineers: Washington, DC, USA, 2003; pp. 34–43. [Google Scholar]
- Asadi, M.; Xie, G.; Sunden, B. A review of heat transfer and pressure drop characteristics of single and two-phase microchannels. Int. J. Heat Mass Transf. 2014, 79, 34–53. [Google Scholar] [CrossRef]
- Müller-Steinhagen, H.; Heck, K. A simple friction pressure drop correlation for two-phase flow in pipes. Chem. Eng. Process. Process Intensif. 1986, 20, 297–308. [Google Scholar] [CrossRef]
- Tahery, R.; Ehterami, S. Two-phase Frictional Pressure Drop in Horizontal Channels. In Proceedings of the 7th International Chemical Engineering Congress & Exhibition (IChEC 2011), Kish, Iran, 21–24 November 2011. [Google Scholar]
- Ribatski, G.; Wojtan, L.; Thome, J.R. An analysis of experimental data and prediction methods for two-phase frictional pressure drop and flow boiling heat transfer in micro-scale channels. Exp. Therm. Fluid Sci. 2006, 31, 1–19. [Google Scholar] [CrossRef]
- Smith, S. Void fractions in two-phase flow: A correlation based upon an equal velocity head model. Proc. Inst. Mech. Eng. 1969, 184, 647–664. [Google Scholar] [CrossRef]
- Shah, R.; London, A.L. Laminar Flow Forced Convection in Ducts, Supplement 1 to Advances in Heat Transfer; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Gnielinski, V. New equations for heat and mass transfer in turbulent pipe and channel flow. Int. Chem. Eng. 1976, 16, 359–368. [Google Scholar]
- Subramanian, R.S. Heat Transfer in Flow through Conduits; Department of Chemical and Biomolecular Engineering, Clarkson University Project: Potsdam, NY, USA, 2015. [Google Scholar]
- Kandlikar, S.G.; Balasubramanian, P. An Extension of the Flow Boiling Correlation to Transition, Laminar, and Deep Laminar Flows in Minichannels and Microchannels. Heat Transf. Eng. 2004, 25, 86–93. [Google Scholar] [CrossRef]
- Kandlikar, S.G. A general correlation for saturated two-phase flow boiling heat transfer inside horizontal and vertical tubes. J. Heat Transfer. 1990, 112, 219–228. [Google Scholar] [CrossRef]
- Kandlikar, S. A model for predicting the two-phase flow boiling heat transfer coefficient in augmented tube and compact heat exchanger geometries. ASME J. Heat Transf. 1991, 113, 966–972. [Google Scholar] [CrossRef]
- Kandlikar, S.G. Heat transfer characteristics in partial boiling, fully developed boiling, and significant void flow regions of subcooled flow boiling. J. Heat Transfer. 1998, 120, 395–401. [Google Scholar] [CrossRef]
- Kandlikar, S.G. Development of a flow boiling map for subcooled and saturated flow boiling of different fluids inside circular tubes. J. Heat Transfer. 1991, 113, 190–200. [Google Scholar] [CrossRef]
- Saha, P.; Zuber, N. Point of net vapor generation and vapor void fraction in subcooled boiling. In Proceedings of the International Heat Transfer Conference Digital Library, Tokyo, Japan, 3–7 September 1974. [Google Scholar]
- Longo, G.A.; Righetti, G.; Zilio, C. A new computational procedure for refrigerant condensation inside herringbone-type Brazed Plate Heat Exchangers. Int. J. Heat Mass Transf. 2015, 82, 530–536. [Google Scholar] [CrossRef]
- Eldeeb, R.; Aute, V.; Radermacher, R. A survey of correlations for heat transfer and pressure drop for evaporation and condensation in plate heat exchangers. Int. J. Refrig. 2016, 65, 12–26. [Google Scholar] [CrossRef]
- Lemmon, E.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 8.0; Natl Std. Ref. Data Series (NIST NSRDS); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2007.
- Palm, B.R.; Khodabandeh, R. Choosing working fluid for two-phase thermosyphon systems for cooling of electronics. J. Electron. Packag. 2003, 125, 276–281. [Google Scholar] [CrossRef]
- Yuan, L.; Joshi, Y.; Nakayama, W. Effect of condenser location and imposed circulation on the performance of a compact two-phase thermosyphon. Microscale Thermophys. Eng. 2003, 7, 163–179. [Google Scholar] [CrossRef]
- Ma, Y.; Ma, G.; Zhang, S.; Zhou, F. Cooling performance of a pump-driven two phase cooling system for free cooling in data centers. Appl. Therm. Eng. 2016, 95, 143–149. [Google Scholar] [CrossRef]
- Ong, K.; Haider-E-Alahi, M. Performance of a R-134a-filled thermosyphon. Appl. Therm. Eng. 2003, 23, 2373–2381. [Google Scholar] [CrossRef]

| Refrigerant Flow (m3/h) | Pump Power (W) | Total Pressure Drop (kPa) | Average CPU Temperature (°C) | |||
|---|---|---|---|---|---|---|
| Exp. | Sim. | Exp. | Sim. | Exp. | Sim. | |
| 0.12 | 36 | 33 | 57.8 | 54.7 | 62.3 | 60.3 |
| 0.15 | 42 | 40 | 75.0 | 75.6 | 62.5 | 61.1 |
| 0.18 | 51 | 48 | 101.5 | 99.1 | 62.6 | 62.3 |
| Categories | Connecting Pipes | Mini-Channel Evaporator | Plate-Type Condenser | |||
|---|---|---|---|---|---|---|
| Label | 2-3 | 4-5 | 6-7 | 8-1 | 3-4, 5-6 | 7-8 |
| Length (m) | 10 | 0.5 | 10 | 3 | 0.035 | 0.25 |
| Width/Diameter (m) | 0.008 | 0.003 | 0.012 | 0.008 | 0.035 | 0.111 |
| Height (m) | 0 | 0 | Variable (default 0) | Variable (default 0) | 0.002 | 0.25 |
| Heat transfer area (m2) | - | - | - | - | 0.00303 | 0.48 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Pdt (kPa) | 83.21 | Tdt (°C) | 34.50 |
| Ppump (W) | 27.9 | cpu1 (°C) | 78.72 |
| EERp | 115 | cpu2 (°C) | 79.50 |
| ηcon | 0.513 | Tdcpu (°C) | 0.78 |
| dTsub of the first evaporator inlet (°C) | 14.44 | Scpu12 | 0.08 |
| dTsub of the condenser outlet (°C) | 0.78 | Scpu22 | 0.34 |
| Parameter | Refrigerant Type | Parameter | Refrigerant Type | ||||
|---|---|---|---|---|---|---|---|
| R-113 | R-134a | R-32 | R-113 | R-134a | R-32 | ||
| Pdt (kPa) | 83.21 | 26.80 | 23.68 | Tdt (°C) | 34.50 | 17.97 | 11.82 |
| Ppump (W) | 27.9 | 12.3 | 14.3 | cpu1 (°C) | 78.72 | 61.66 | 56.48 |
| EERp | 115 | 260 | 224 | cpu2 (°C) | 79.50 | 62.97 | 56.82 |
| ηcon | 0.513 | 0.634 | 0.792 | Tdcpu (°C) | 0.78 | 1.31 | 0.34 |
| dTsub of the first evaporator inlet (°C) | 14.51 | 0.30 | 0.02 | Scpu12 | 0.08 | 0.34 | 0.02 |
| dTsub of the condenser outlet (°C) | 0.78 | 0.06 | 0.02 | Scpu22 | 0.34 | 0.26 | 0.01 |
| Parameter | Condenser Position | Parameter | Condenser Position | ||||
|---|---|---|---|---|---|---|---|
| Same Height | 1 m Higher | 1 m Lower | Same Height | 1 m Higher | 1 m Lower | ||
| Pdt (kPa) | 83.21 | 78.14 | 92.53 | Tdt (°C) | 34.50 | 34.97 | 34.05 |
| Ppump (W) | 27.9 | 26.27 | 30.86 | cpu1 (°C) | 78.72 | 79.16 | 78.28 |
| EERp | 115 | 122 | 104 | cpu2 (°C) | 79.50 | 79.97 | 79.05 |
| ηcon | 0.513 | 0.518 | 0.479 | Tdcpu (°C) | 0.78 | 0.81 | 0.77 |
| dTsub of the first evaporator inlet (°C) | 14.51 | 13.17 | 17.06 | Scpu12 | 0.08 | 0.09 | 0.07 |
| dTsub of the condenser outlet (°C) | 0.78 | - | 4.59 | Scpu22 | 0.34 | 0.37 | 0.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Cheng, H.; Yang, T.; Yuan, W.; Ren, K. Modeling and Performance Analysis of a Pump-Driven Chip-Level Two-Phase Cooling System in Data Centers. Appl. Sci. 2023, 13, 7472. https://doi.org/10.3390/app13137472
Wang L, Cheng H, Yang T, Yuan W, Ren K. Modeling and Performance Analysis of a Pump-Driven Chip-Level Two-Phase Cooling System in Data Centers. Applied Sciences. 2023; 13(13):7472. https://doi.org/10.3390/app13137472
Chicago/Turabian StyleWang, Leixin, Hao Cheng, Tongzhi Yang, Weixing Yuan, and Kexian Ren. 2023. "Modeling and Performance Analysis of a Pump-Driven Chip-Level Two-Phase Cooling System in Data Centers" Applied Sciences 13, no. 13: 7472. https://doi.org/10.3390/app13137472
APA StyleWang, L., Cheng, H., Yang, T., Yuan, W., & Ren, K. (2023). Modeling and Performance Analysis of a Pump-Driven Chip-Level Two-Phase Cooling System in Data Centers. Applied Sciences, 13(13), 7472. https://doi.org/10.3390/app13137472






