Numerical Investigation of the Cavitation Characteristics in Venturi Tubes: The Role of Converging and Diverging Sections
Abstract
:1. Introduction
2. Materials and Methods
2.1. Governing Equation and Turbulence Model
2.2. Cavitation Model
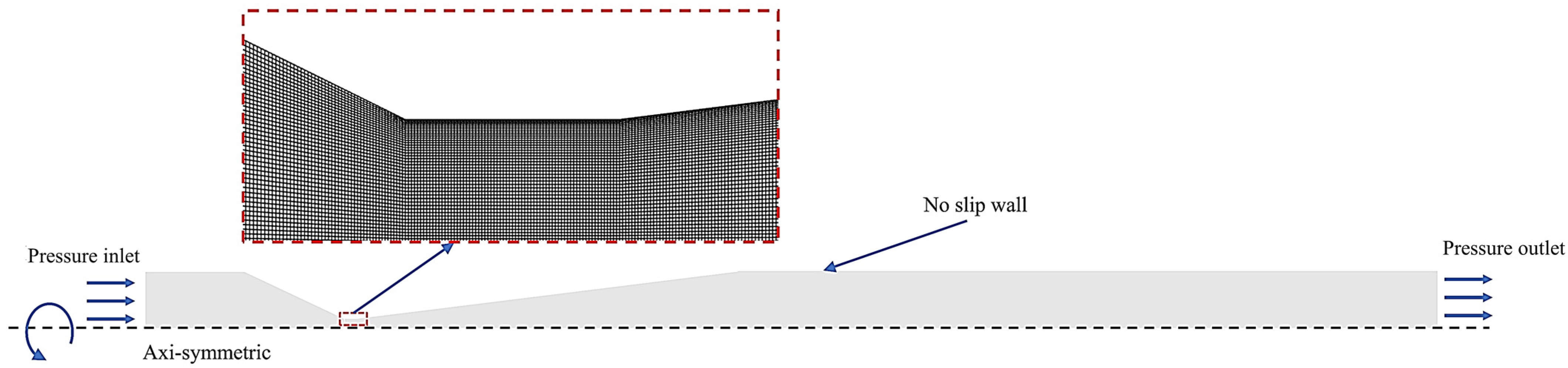
2.3. Geometric Model
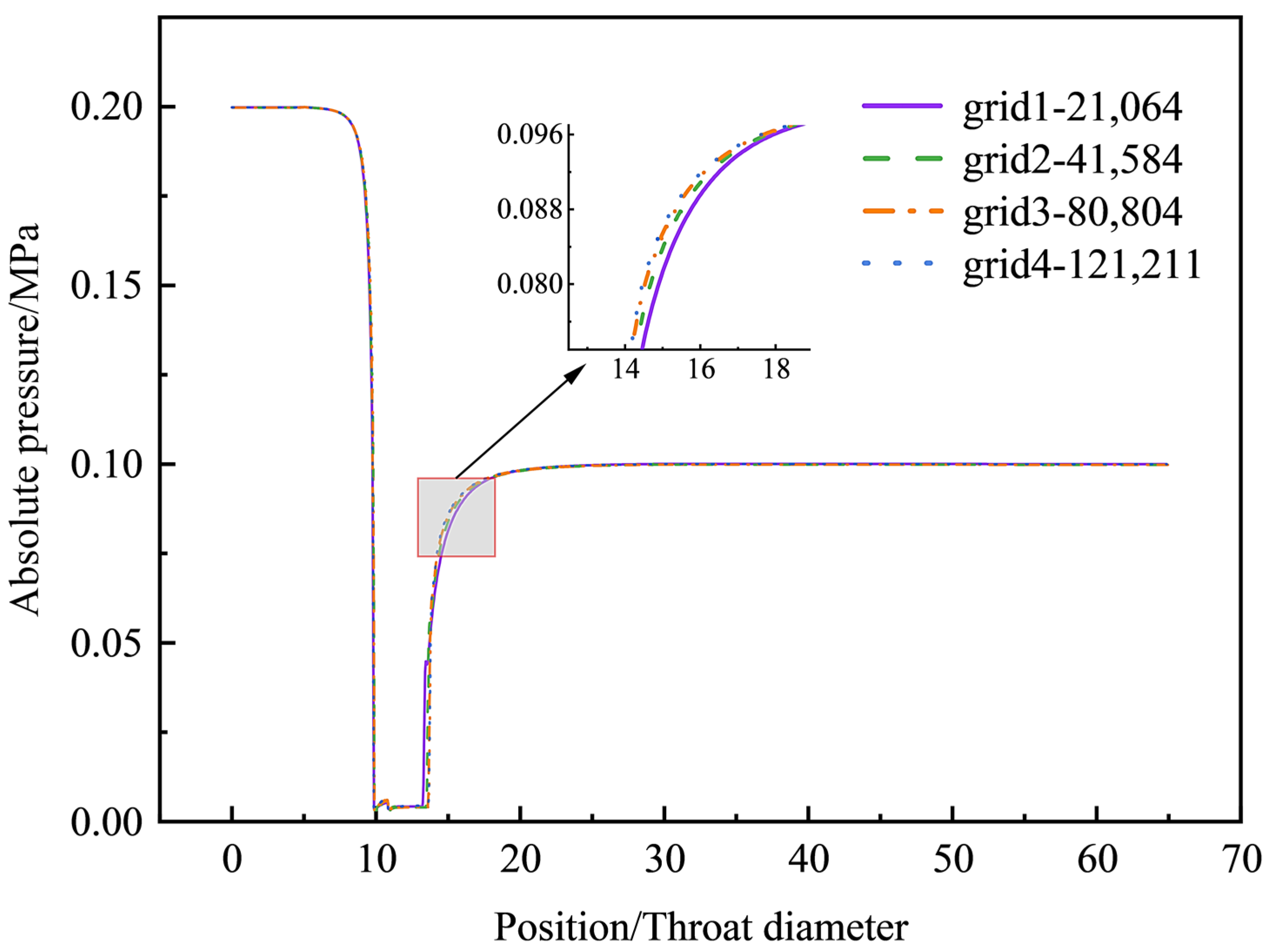
2.4. Solution Strategy and Grid Independence
3. Results and Discussion
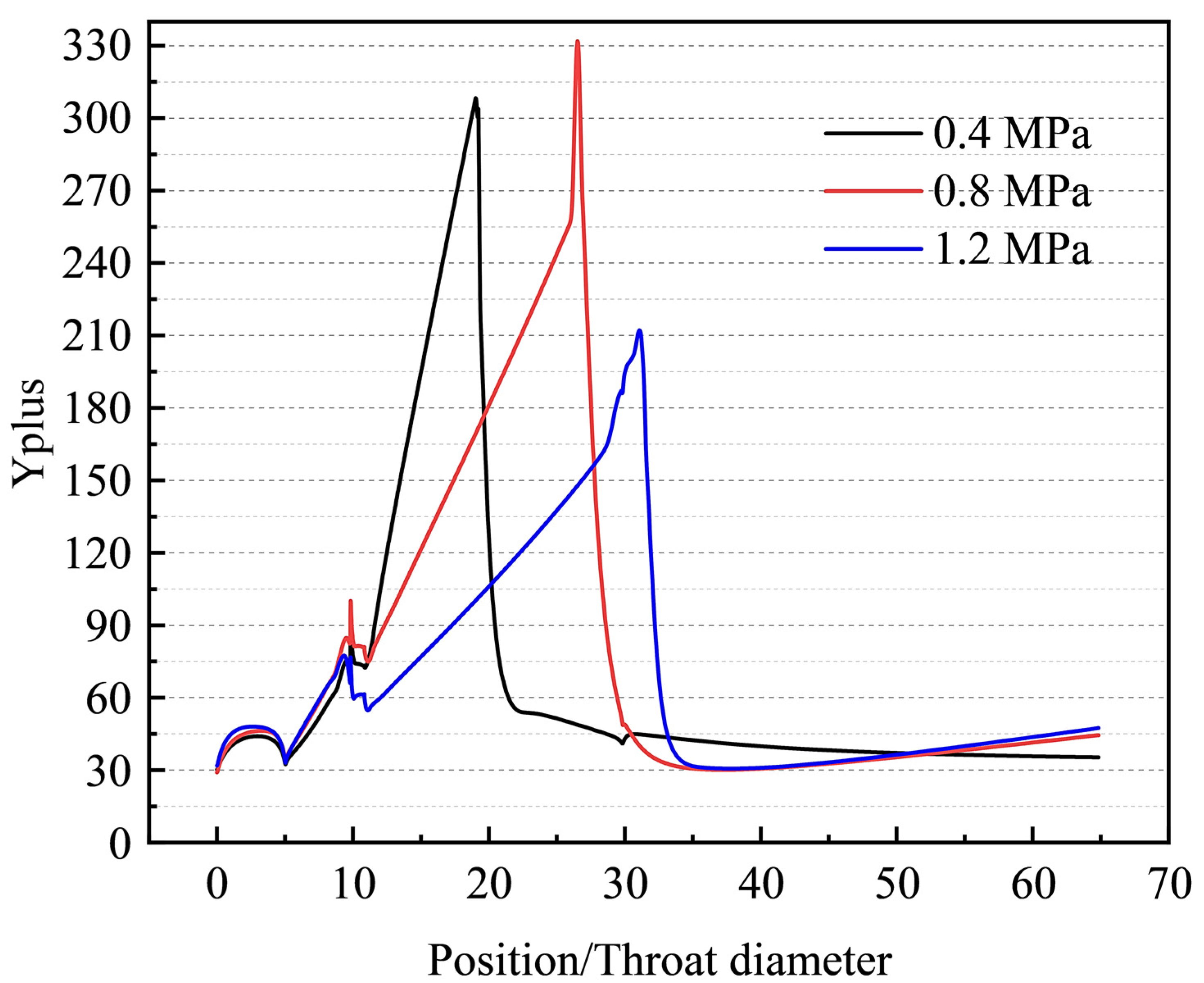
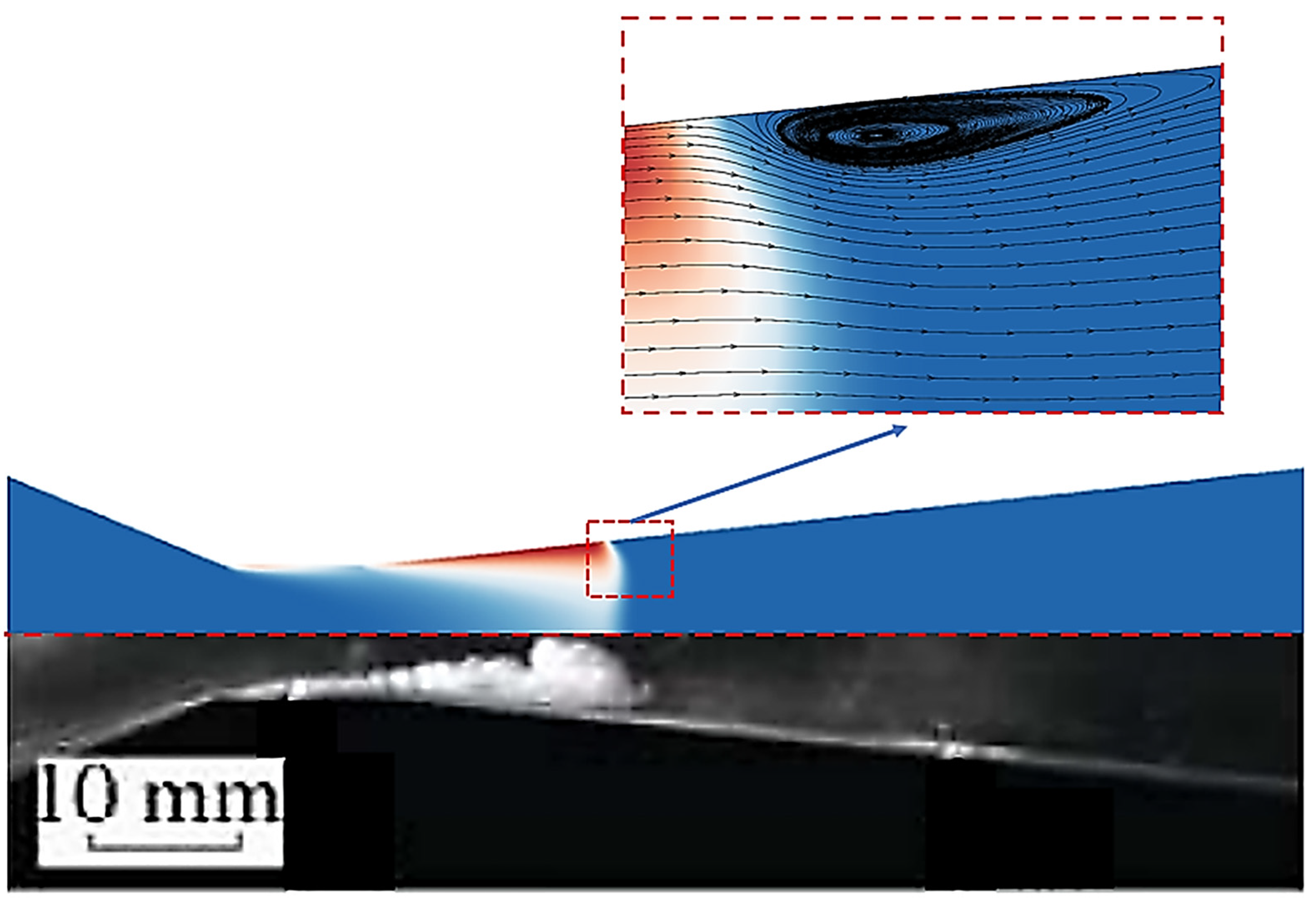
3.1. Verification of the Simulation Method
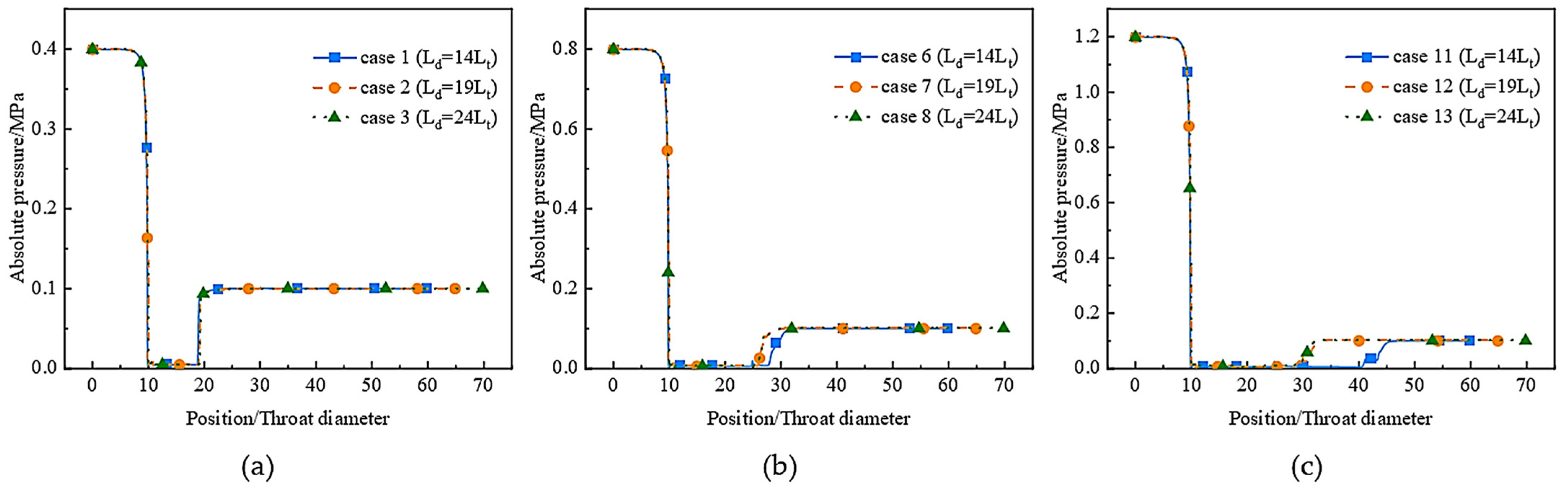
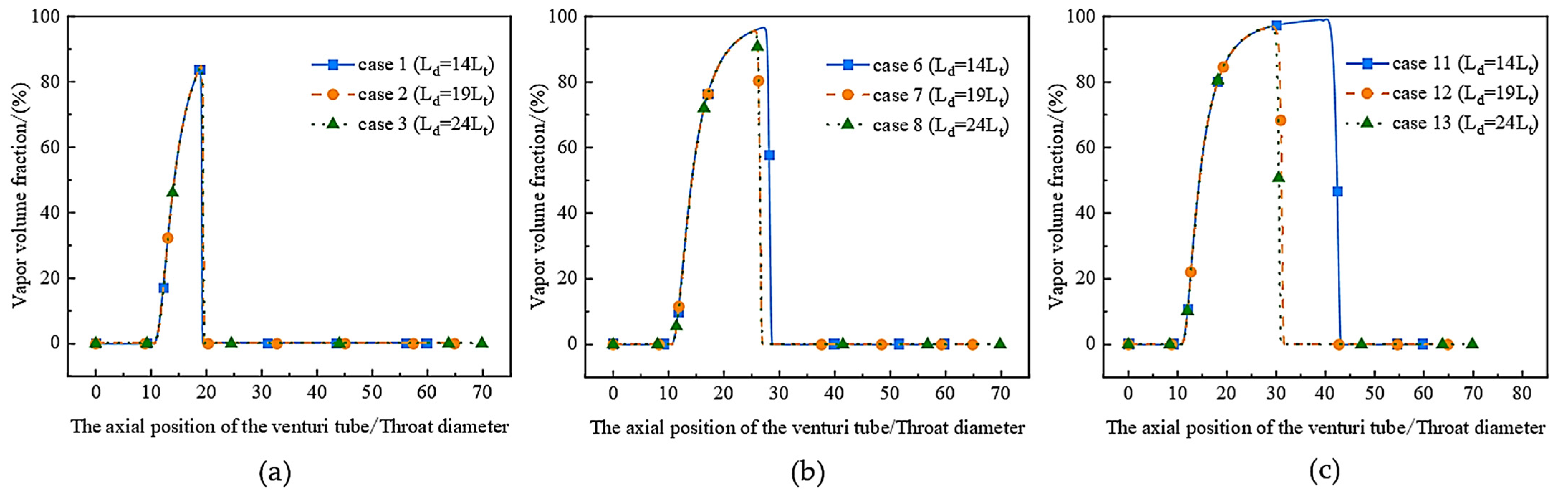
3.2. Effects of Divergent Length on Cavitation Characteristics
3.2.1. Analysis of Pressure and Vapor Volume Fraction
3.2.2. Analysis of Cavitation Collapse Strength
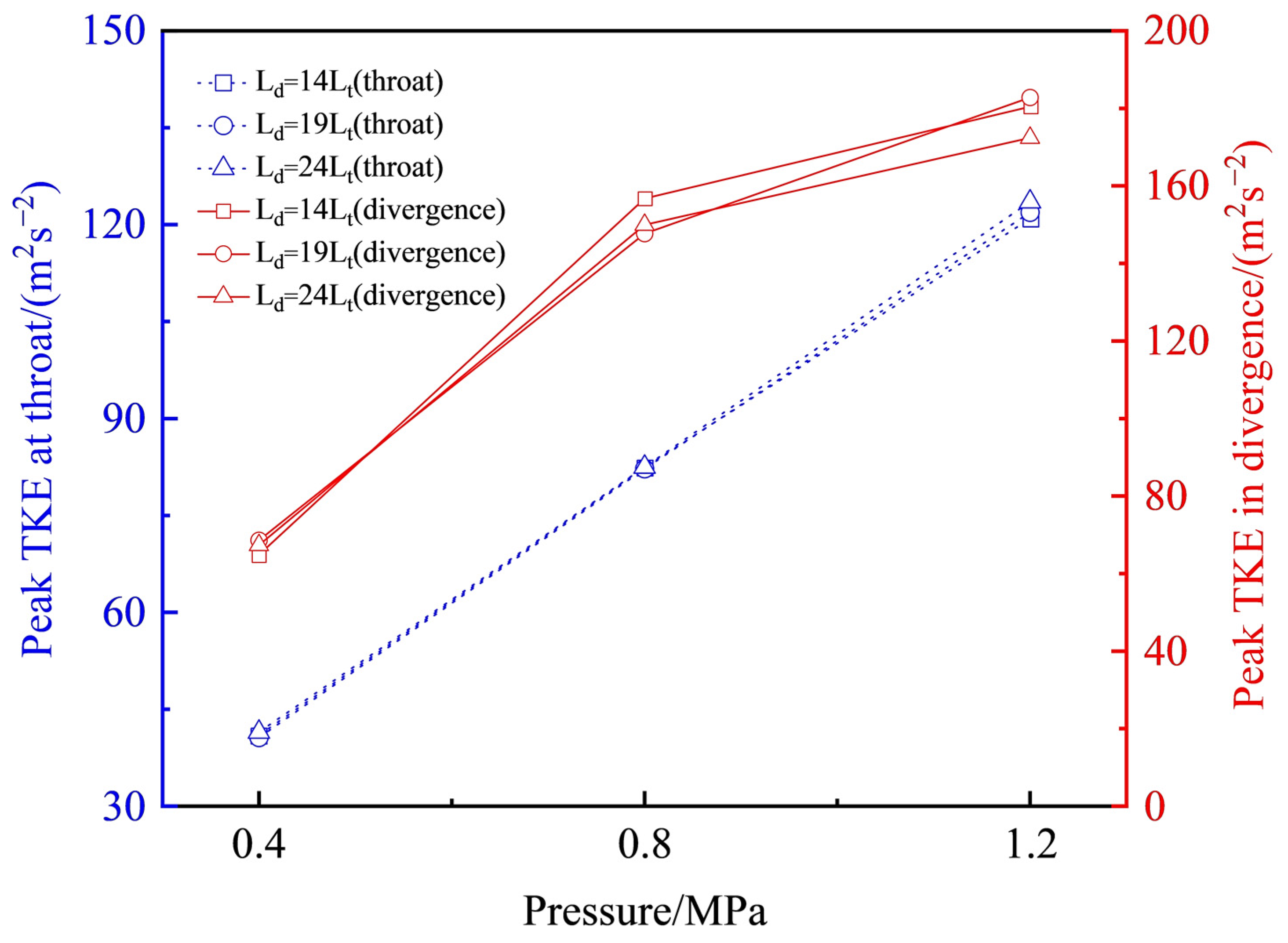
3.2.3. Analysis of Flow Field Parameters
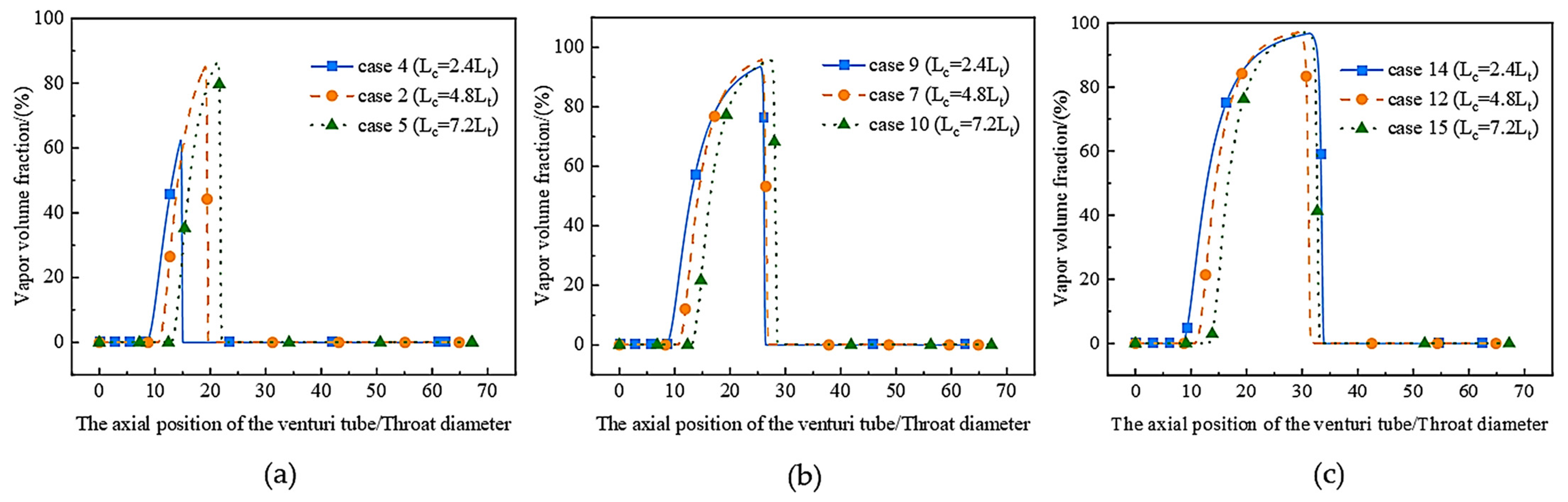
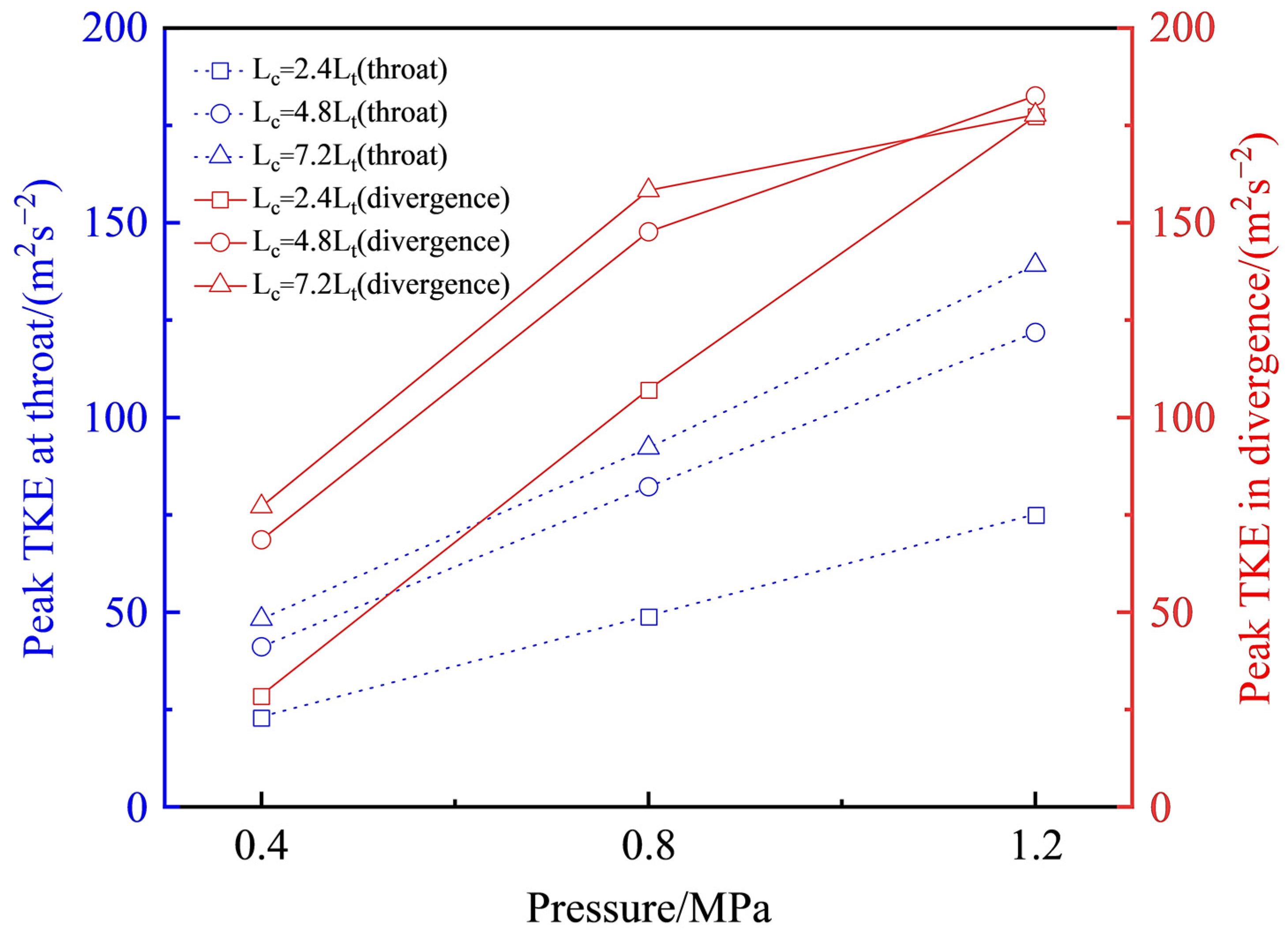
3.3. Effects of the Convergent Length on Cavitation Characteristics
3.3.1. Analysis of Pressure and Vapor Volume Fraction
3.3.2. Analysis of Cavitation Collapse Strength
3.3.3. Analysis of Flow Field Parameters
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carpenter, J.; Badve, M.; Rajoriya, S.; George, S.; Saharan, V.K.; Pandit, A.B. Hydrodynamic cavitation: An emerging technology for the intensification of various chemical and physical processes in a chemical process industry. Rev. Chem. Eng. 2017, 33, 433–468. [Google Scholar] [CrossRef]
- Sarvothaman, V.P.; Simpson, A.; Ranade, V.V. Comparison of Hydrodynamic Cavitation Devices based on Linear and Swirling Flows: Degradation of dichloroaniline in water. Ind. Eng. Chem. Res. 2020, 59, 13841–13847. [Google Scholar] [CrossRef]
- Sarvothaman, V.P.; Simpson, A.T.; Ranade, V.V. Modelling of vortex based hydrodynamic cavitation reactors. Chem. Eng. J. 2018, 377, 119639. [Google Scholar] [CrossRef] [Green Version]
- Gogate, P.R.; Pandit, A.B. Hydrodynamic Cavitation Reactors: A state of the art review. Rev. Chem. Eng. 2001, 17, 1–85. [Google Scholar] [CrossRef]
- Rajoriya, S.; Bargole, S.; George, S.; Saharan, V.K. Treatment of textile dyeing industry effluent using hydrodynamic cavitation in combination with advanced oxidation reagents. J. Hazard. Mater. 2018, 344, 1109–1115. [Google Scholar] [CrossRef]
- Wang, C.; Jin, R.; He, Z.; Qiao, Y.; Wang, Y.; Wang, K.; Lu, Y.; Wang, X.; Liu, D. A new water treatment technology for degradation of B[a]A by Hydrodynamic Cavitation and Chlorine Dioxide Oxidation. Ultrason. Sonochem. 2020, 61, 104834. [Google Scholar] [CrossRef] [PubMed]
- Abbas-Shiroodi, Z.; Sadeghi, M.T.; Baradaran, S. Design and optimization of a cavitating device for Congo red decolorization: Experimental investigation and CFD simulation. Ultrason. Sonochem. 2021, 71, 105386. [Google Scholar] [CrossRef]
- Innocenzi, V.; Prisciandaro, M.; Vegliò, F. Study of the effect of operative conditions on the decolourization of azo dye solutions by using hydrodynamic cavitation at the lab scale. Can. J. Chem. Eng. 2020, 98, 1980–1988. [Google Scholar] [CrossRef]
- Bagal, M.V.; Gogate, P.R. Degradation of diclofenac sodium using combined processes based on hydrodynamic cavitation and heterogeneous photocatalysis. Ultrason. Sonochem. 2014, 21, 1035–1043. [Google Scholar] [CrossRef]
- Mezule, L.; Tsyfansky, S.; Yakushevich, V.; Juhna, T. A simple technique for water disinfection with hydrodynamic cavitation: Effect on survival of Escherichia coli. Desalination. 2009, 248, 152–159. [Google Scholar] [CrossRef]
- Badve, M.; Gogate, P.; Pandit, A.; Csoka, L. Hydrodynamic cavitation as a novel approach for wastewater treatment in wood finishing industry. Sep. Purif. Technol. 2013, 106, 15–21. [Google Scholar] [CrossRef]
- Wang, B.; Su, H.; Zhang, B. Hydrodynamic cavitation as a promising route for wastewater treatment—A review. Chem. Eng. J. 2021, 412, 128685. [Google Scholar] [CrossRef]
- Wang, B.; Liu, Y.; Zhang, H.; Shi, W.; Xiong, M.; Gao, C.; Cui, M. Hydrodynamic cavitation and its application in water treatment combined with ozonation: A review. J. Ind. Eng. Chem. 2022, 114, 33–51. [Google Scholar] [CrossRef]
- Simpson, A.; Ranade, V.V. Modeling Hydrodynamic Cavitation in Venturi: Influence of Venturi Configuration on Inception and Extent of Cavitation. AIChE J. 2019, 65, 421–433. [Google Scholar] [CrossRef]
- Li, M.; Bussonnière, A.; Bronson, M.; Xu, Z.; Liu, Q. Study of Venturi tube geometry on the hydrodynamic cavitation for the generation of microbubbles. Miner. Eng. 2019, 132, 268–274. [Google Scholar] [CrossRef]
- Sato, K.; Hachino, K.; Saito, Y. Inception and Dynamics of Traveling-Bubble-Type Cavitation in a Venturi. Nippon. Kikai Gakkai Ronbunshu B Hen 2004, 70, 69–76. [Google Scholar] [CrossRef] [Green Version]
- Brunhart, M.; Soteriou, C.; Gavaises, M.; Karathanassis, I.; Koukouvinis, P.; Jahangir, S.; Poelma, C. Investigation of cavitation and vapor shedding mechanisms in a Venturi nozzle. Phys. Fluids. 2020, 32, 083306. [Google Scholar] [CrossRef]
- Fang, L.; Li, W.; Li, Q.; Wang, Z. Numerical investigation of the cavity shedding mechanism in a Venturi reactor. Int. J. Heat Mass Transf. 2020, 156, 119835. [Google Scholar] [CrossRef]
- Long, X.; Zhang, J.; Wang, J.; Xu, M.; Lyu, Q.; Ji, B. Experimental investigation of the global cavitation dynamic behavior in a Venturi tube with special emphasis on the cavity length variation. Int. J. Multiphase Flow. 2017, 89, 290–298. [Google Scholar] [CrossRef]
- Kuldeep; Saharan, V.K. Computational study of different Venturi and orifice type hydrodynamic cavitating devices. J. Hydrodyn. 2016, 28, 293–305. [Google Scholar] [CrossRef]
- Shi, H.; Li, M.; Nikrityuk, P.; Liu, Q. Experimental and numerical study of cavitation flows in Venturi tubes: From CFD to an empirical model. Chem. Eng. Sci. 2019, 207, 672–687. [Google Scholar] [CrossRef]
- Zhao, L.; Sun, L.C.; Mo, Z.Y.; Du, M.; Huang, J.; Bao, J.J.; Tang, J.G.; Xie, G. Effects of the divergent angle on bubble transportation in a rectangular Venturi channel and its performance in producing fine bubbles. Int. J. Multiphase Flow. 2019, 114, 192–206. [Google Scholar] [CrossRef]
- Kim, H.J.; Nguyen, D.X.; Bae, J.H. The performance of the sludge pretreatment system with Venturi tubes. Water Sci. Technol. 2008, 57, 131–137. [Google Scholar] [CrossRef]
- Ramisetty, K.A.; Pandit, A.B.; Gogate, P.R. Novel Approach of Producing Oil in Water Emulsion Using Hydrodynamic Cavitation Reactor. Ind. Eng. Chem. Res. 2014, 53, 16508–16515. [Google Scholar] [CrossRef]
- Maddikeri, G.L.; Gogate, P.R.; Pandit, A.B. Intensified synthesis of biodiesel using hydrodynamic cavitation reactors based on the interesterification of waste cooking oil. Fuel 2014, 237, 285–292. [Google Scholar] [CrossRef]
- Dastane, G.G.; Thakkar, H.; Shah, R.; Perala, S.; Raut, J.; Pandit, A.B. Single and multiphase CFD simulations for designing cavitating Venturi. Chem. Eng. Res. Des. 2019, 149, 1–12. [Google Scholar] [CrossRef]
- Chitsaz, H.R.; Omidkhah, M.R.; Ghobadian, B.; Ardjmand, M. Optimizing Different Angles of Venturi in Biodiesel Production Using CFD Analysis. Iran. J. Chem. Chem. Eng. 2019, 38, 285–295. [Google Scholar]
- Hwang, H.J.; Park, J.; Min, J.K. A numerical study on the flow control characteristic of a cavitating Venturi with one- and two-stage diffusers. J. Mech. Sci. Technol. 2021, 35, 1463–1472. [Google Scholar] [CrossRef]
- Ashrafizadeh, S.M.; Ghassemi, H. Experimental and numerical investigation on the performance of small-sized cavitating Venturis. Flow Meas. Instrum. 2015, 42, 6–15. [Google Scholar] [CrossRef]
- Long, X.P.; Wang, J.; Zuo, D.; Zhang, J.Q.; Ji, B. Experimental investigation of the instability of cavitation in veturi tube under different cavitation stage. J. Mech. Eng. 2018, 54, 209–215. [Google Scholar] [CrossRef] [Green Version]
- Bashir, T.A.; Soni, A.G.; Mahulkar, A.V.; Pandit, A.B. The CFD driven optimisation of a modified Venturi for cavitational activity. Can. J. Chem. Eng. 2011, 89, 1366–1375. [Google Scholar] [CrossRef]





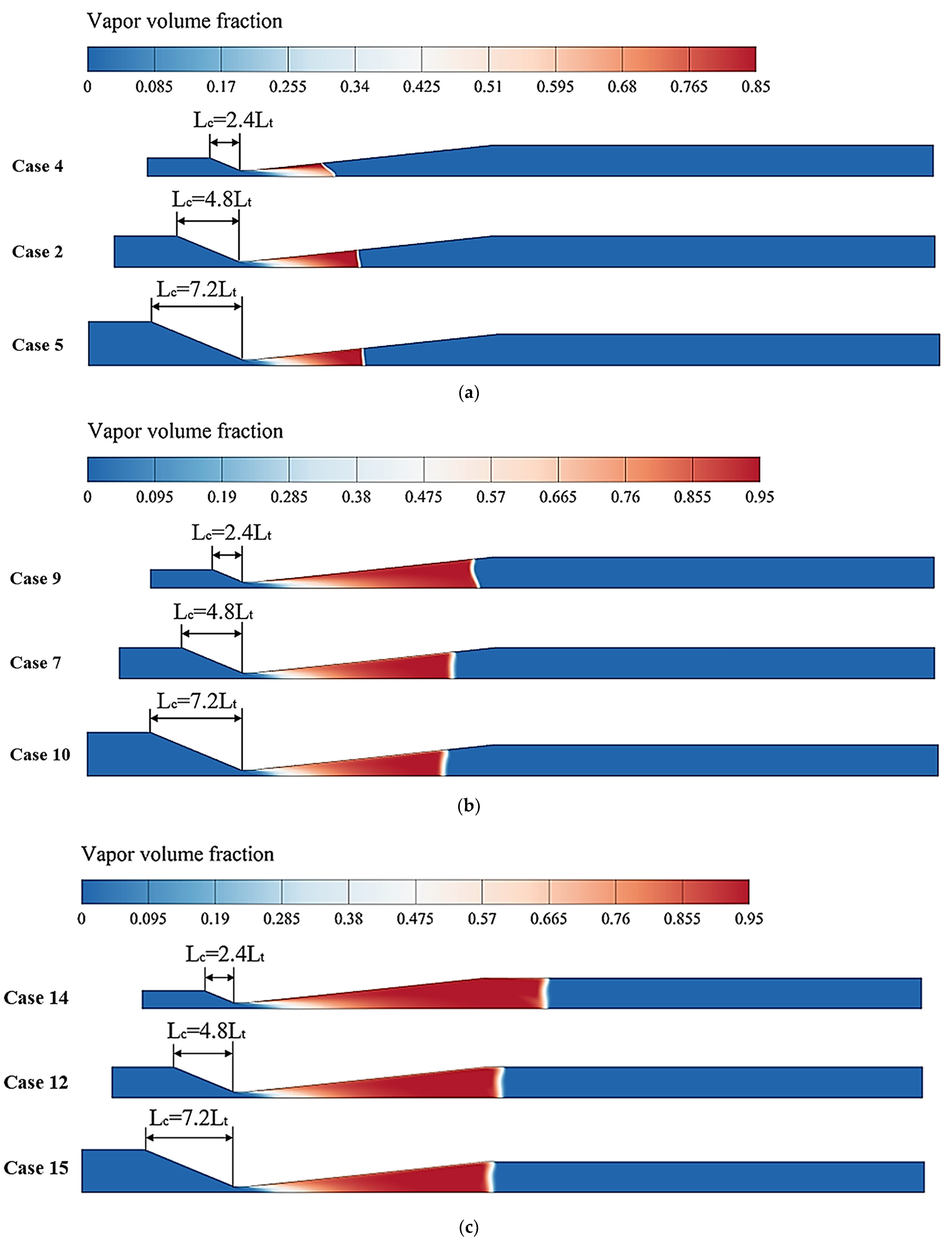
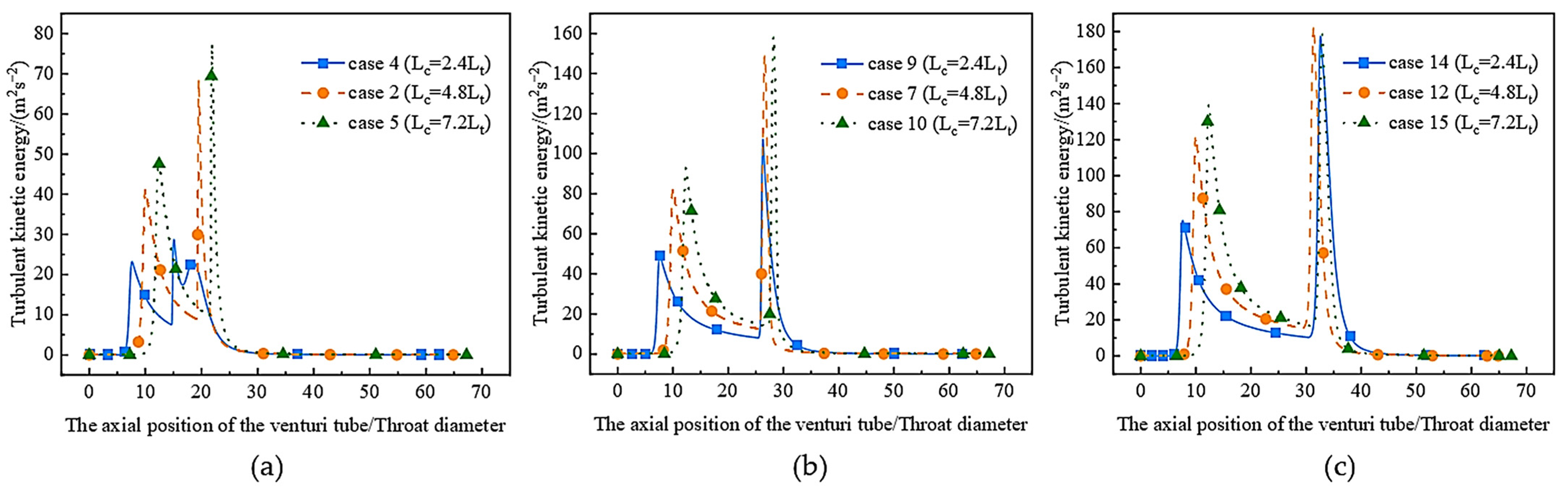
| Cases | Pin (MPa) | σ | LC (mm) | Din (mm) | LC/Din | Ld (mm) | Dout (mm) | Ld/Dout |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.4 | 0.2595 | 48 | 50.00 | 0.960 | 140 | 39.42 | 3.55 |
| 2 | 0.2603 | 48 | 50.00 | 0.960 | 190 | 50.00 | 3.80 | |
| 3 | 0.2608 | 48 | 50.00 | 0.960 | 240 | 60.46 | 3.97 | |
| 4 | 0.2480 | 24 | 29.88 | 0.803 | 190 | 50.00 | 3.80 | |
| 5 | 0.2678 | 72 | 69.64 | 1.030 | 190 | 50.00 | 3.80 | |
| 6 | 0.8 | 0.1294 | 48 | 50.00 | 0.960 | 140 | 39.42 | 3.55 |
| 7 | 0.1298 | 48 | 50.00 | 0.960 | 190 | 50.00 | 3.80 | |
| 8 | 0.1299 | 48 | 50.00 | 0.960 | 240 | 60.46 | 3.97 | |
| 9 | 0.1236 | 24 | 29.88 | 0.803 | 190 | 50.00 | 3.80 | |
| 10 | 0.1328 | 72 | 69.64 | 1.030 | 190 | 50.00 | 3.80 | |
| 11 | 1.2 | 0.0860 | 48 | 50.00 | 0.960 | 140 | 39.42 | 3.55 |
| 12 | 0.0863 | 48 | 50.00 | 0.960 | 190 | 50.00 | 3.80 | |
| 13 | 0.0865 | 48 | 50.00 | 0.960 | 240 | 60.46 | 3.97 | |
| 14 | 0.0823 | 24 | 29.88 | 0.803 | 190 | 50.00 | 3.80 | |
| 15 | 0.0881 | 72 | 69.64 | 1.030 | 190 | 50.00 | 3.80 |
| Section | Boundary Conditions | Remark |
|---|---|---|
| Working fluid | - | Primary phase: water Second phase: vapor |
| Inlet | Pressure inlet | Table 1 (0.4–1.2 MPa) |
| Outlet | Pressure outlet | 0.1 MPa |
| Wall | No slip condition | The wall treatment method: standard wall functions |
| Turbulence | Intensity and hydraulic diameter | Intensity: 3% Hydraulic diameter: 50 mm |
| Cases | Pin (MPa) | σ | Ld (mm) | Q (kg·s−1) | Vt (m·s−1) | Vol (mm3) | Vapm |
|---|---|---|---|---|---|---|---|
| 1 | 0.4 | 0.2595 | 140 | 1.88831842 | 27.29931 | 17,694.4 | 0.8916025 |
| 2 | 0.2603 | 190 | 1.88298337 | 27.26803 | 18,965.5 | 0.8933302 | |
| 3 | 0.2608 | 240 | 1.88450754 | 27.23960 | 18,932.1 | 0.8932120 | |
| 6 | 0.8 | 0.1294 | 140 | 2.67930270 | 38.68253 | 106,551 | 0.9799927 |
| 7 | 0.1298 | 190 | 2.67167545 | 38.62886 | 85,491.1 | 0.9747809 | |
| 8 | 0.1299 | 240 | 2.67394078 | 38.60078 | 85,072.4 | 0.9747983 | |
| 11 | 1.2 | 0.0860 | 140 | 3.29722403 | 47.45741 | 268,358.5 | 0.9915485 |
| 12 | 0.0863 | 190 | 3.28465412 | 47.39365 | 162,272.6 | 0.9926510 | |
| 13 | 0.0865 | 240 | 3.28479553 | 47.33728 | 149,088.7 | 0.9912778 |
| Cases | Pin (MPa) | σ | LC (mm) | Q (kg·s−1) | Vt (m·s−1) | Vol (mm3) | Vapm |
|---|---|---|---|---|---|---|---|
| 4 | 0.4 | 0.2480 | 24 | 1.92805647 | 28.05349 | 8058.9 | 0.9013388 |
| 2 | 0.2603 | 48 | 1.88341402 | 27.27604 | 19,173.1 | 0.8957157 | |
| 5 | 0.2678 | 72 | 1.86739731 | 26.88531 | 19,232.4 | 0.8973735 | |
| 9 | 0.8 | 0.1236 | 24 | 2.72222116 | 39.70596 | 110,433.2 | 0.9740466 |
| 7 | 0.1298 | 48 | 2.67167545 | 38.62886 | 85,491.1 | 0.9747809 | |
| 10 | 0.1328 | 72 | 2.65792438 | 38.19953 | 77,281.3 | 0.9731250 | |
| 14 | 1.2 | 0.0823 | 24 | 3.34104545 | 48.63226 | 253,014.8 | 0.9919481 |
| 12 | 0.0863 | 48 | 3.28465412 | 47.39365 | 162,272.6 | 0.9926510 | |
| 15 | 0.0881 | 72 | 3.26788526 | 46.89446 | 146,933.8 | 0.9918739 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, B. Numerical Investigation of the Cavitation Characteristics in Venturi Tubes: The Role of Converging and Diverging Sections. Appl. Sci. 2023, 13, 7476. https://doi.org/10.3390/app13137476
Liu Y, Li B. Numerical Investigation of the Cavitation Characteristics in Venturi Tubes: The Role of Converging and Diverging Sections. Applied Sciences. 2023; 13(13):7476. https://doi.org/10.3390/app13137476
Chicago/Turabian StyleLiu, Yi, and Bin Li. 2023. "Numerical Investigation of the Cavitation Characteristics in Venturi Tubes: The Role of Converging and Diverging Sections" Applied Sciences 13, no. 13: 7476. https://doi.org/10.3390/app13137476
APA StyleLiu, Y., & Li, B. (2023). Numerical Investigation of the Cavitation Characteristics in Venturi Tubes: The Role of Converging and Diverging Sections. Applied Sciences, 13(13), 7476. https://doi.org/10.3390/app13137476





