DABaCLT: A Data Augmentation Bias-Aware Contrastive Learning Framework for Time Series Representation

Abstract

Contrastive learning, as an unsupervised technique, has emerged as a prominent method in time series representation learning tasks, serving as a viable solution to the scarcity of annotated data. However, the application of data augmentation methods during training can distort the distribution of raw data. This discrepancy between the representations learned from augmented data in contrastive learning and those obtained from supervised learning results in an incomplete understanding of the information contained in the real data from the trained encoder. We refer to this as the data augmentation bias (DAB), representing the disparity between the two sets of learned representations. To mitigate the influence of DAB, we propose a DAB-aware contrastive learning framework for time series representation (DABaCLT). This framework leverages a raw features stream (RFS) to extract features from raw data, which are then combined with augmented data to create positive and negative pairs for DAB-aware contrastive learning. Additionally, we introduce a DAB-minimizing loss function (DABMinLoss) within the contrasting module to minimize the DAB of the extracted temporal and contextual features. Our proposed method is evaluated on three time series classification tasks, including sleep staging classification (SSC) and epilepsy seizure prediction (ESP) based on EEG and human activity recognition (HAR) based on sensors signals. The experimental results demonstrate that our DABaCLT achieves strong performance in self-supervised time series representation, 0.19% to 22.95% accuracy improvement for SSC, 2.96% to 5.05% for HAR, 1.00% to 2.46% for ESP, and achieves comparable performance to the supervised approach. The source code for our framework is open-source.

1. Introduction

Time series data, collected from diverse sources such as personal devices, clinical centers, and financial institutions, have a wide range of applications such as sleep stage classification, human activity recognition, and epilepsy seizure prediction [1,2,3,4,5]. Representation learning is crucial for reducing dimensionality and constructing effective representations of time series data, enabling tasks such as classification, forecasting, and clustering. Consequently, representation learning methods for time series have gained significant attention [6,7,8,9]. However, challenges arise in designing supervised representation methods due to labeling limitations and difficulties in capturing context. These challenges necessitate improved generalization ability and the availability of more labeled data. In this context, Ref. [10] compares heuristics and event detection algorithms to determine optimal window sizes for time representation, highlighting the reliable estimation provided by the false nearest neighbors method. Additionally, Ref. [11] refines feature representations for time series using instance-level augmentation, dropout, and iterative bilinear temporal–spectral fusion. Moreover, Ref. [12] proposes a novel framework for multivariate time series representation learning using the transformer encoder architecture and unsupervised pre-training.

Unlabeled time series data are frequently encountered in practical situations, leading to increased attention on unsupervised and self-supervised time series representation learning [11]. Contrastive learning, initially proposed for representation learning in computer vision and natural language processing, has also found applications in unsupervised time series representation learning [13,14,15]. For example, Ref. [16] presents a universal representation learning framework for time series using hierarchical contrasting to learn scale-invariant representations within augmented context views. Furthermore, Ref. [17] proposes a contrastive learning framework for learning domain-invariant semantics in multivariate time series through nearest-neighbor contrastive learning. This approach constructs positive and negative pairs via data augmentation and aims to maximize the similarity of positive pairs while minimizing the similarity of negative pairs. Additionally, Ref. [9] combines adversarial training with self-supervised learning for emotion recognition, optimizing classifiers using diverse simulated time series samples. Another contrasting approach introduced by [18] utilizes expert features to encourage desirable properties in learned representations.

Various augmentation methods are specifically designed to construct positive and negative pairs. For instance, Ref. [19] considers sampled subseries as augmentation pairs, while Ref. [11] adopts a dropout strategy to randomly mask parts of the original data. Ref. [20] transforms time series into the frequency domain, and Ref. [7] selects various transformations, such as scaling and permutation, to learn transformation-invariant representations. Contrastive learning methods typically employ two variants of the same augmentation [21], aiming to improve robustness and convergence efficiency.

However, most contrastive methods overlook the representation biases introduced by augmentation techniques. Most of the previous frameworks only train encoders using augmented views [22], leading to a misunderstanding of the underlying data distribution when real data are absent. This gap between the representations learned from augmented data in contrastive learning and those learned from supervised learning is referred to as the data augmentation bias (DAB). The DAB represents the disparity between representations learned from augmented data in contrastive learning and those obtained from supervised learning. Consequently, when fine-tuning the classifier for downstream tasks, the encoder fails to rectify the misconceptions embedded within its representations, and the learned representations may not capture the underlying features of the raw data. The existence and impact of the DAB problem are discussed in the fourth section.

To address the influence of the DAB, we propose the DAB-aware contrastive learning framework (DABaCLT) that aims to recognize and minimize the impact of DAB on downstream tasks. The framework consists of two streams: the DAB features stream (DABFS) and the raw features stream (RFS). The DABFS extracts augmented temporal and contextual features, while the RFS helps identify and mitigate the DAB issue present in the learned representations from DABFS. The DABFS incorporates a transformation inconsistency augmentation (TIA) module with a tempo-scale strategy for data augmentation. In the RFS, features from raw data are also extracted and used in the contrasting module alongside augmented data to create negative and positive pairs for DAB awareness. To minimize the DAB in the learned representations, we design DAB-minimizing temporal and contextual contrasting modules (DABa-TC and DABa-CC) that operate in higher dimensions and leverage the assistance of RFS to extract temporal and contextual features. This work is the first to address the DAB problem and propose a method to minimize it in learned representations.

In summary, the main contributions of this work are the following:

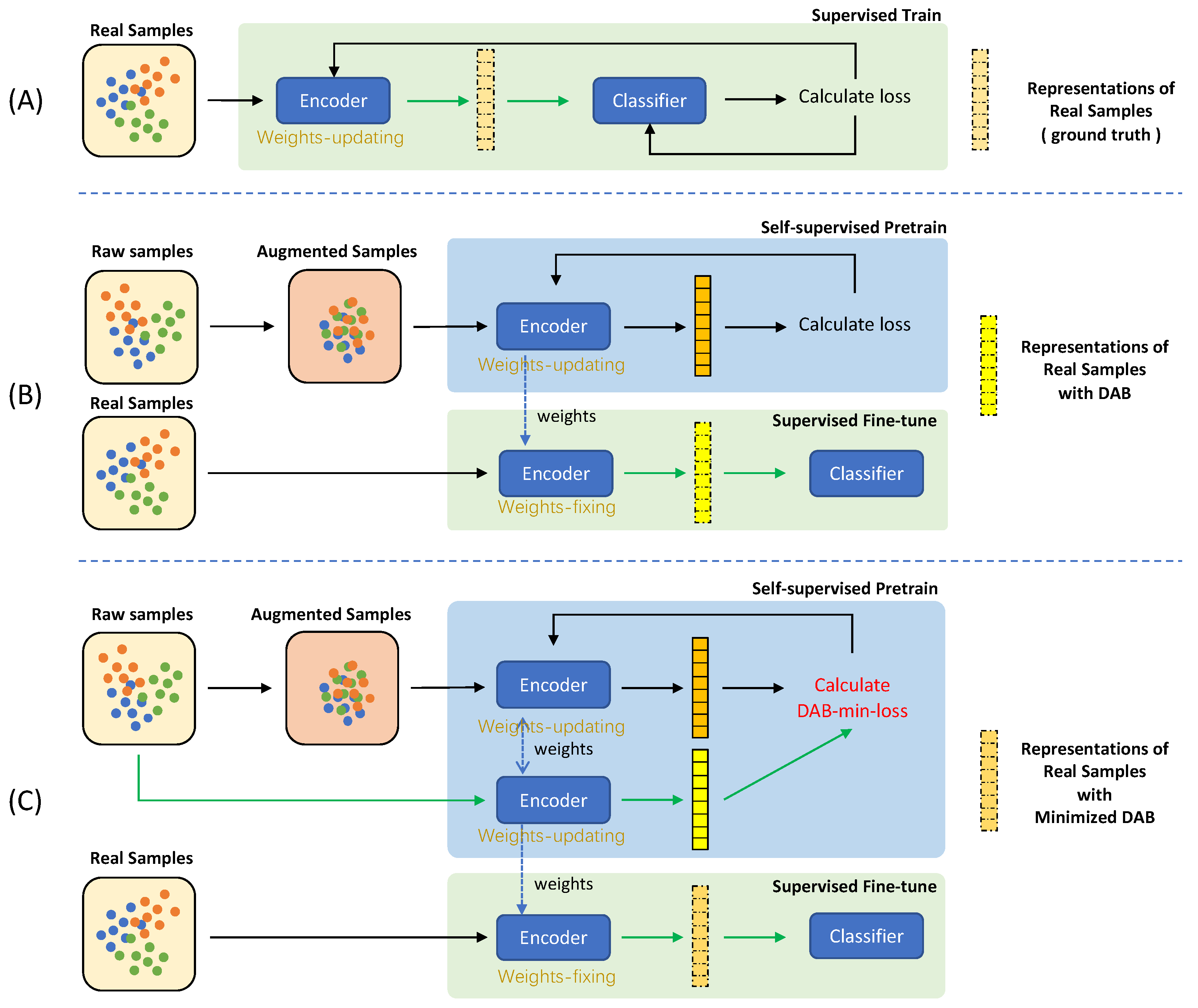
• We introduce the concept of the data augmentation bias problem (DAB) and present the DABaCLT framework to recognize and minimize DAB during the learning of time series representations. The RFS is developed as a criterion for perceiving DAB and is effectively combined with the DABFS.
• We propose DAB-minimizing contrastive loss (DABMinLoss) in the contrasting module to reduce the DAB in extracted temporal and contextual features. The complete DABMinLoss consists of five parts implemented in the DABa-TC and DABa-CC modules.
• Extensive experiments demonstrate the superiority of DABaCLT over previous works. Compared to self-supervised learning, DABaCLT achieves significant improvements ranging from 0.19% to 22.95% in sleep staging classification, 2.96% to 5.05% in human activity recognition, and 1.00% to 2.46% in epilepsy seizure prediction. The results also compete favorably with supervised methods.

2. Materials and Methods

2.1. Data Description

Three real-world time series tasks were utilized for method evaluation, including sleep stage classification (SSC), human activity recognition (HAR), and epilepsy seizure prediction (ESP). We compared our performances with state-of-the-art approaches on three publicly available datasets.

Table 1. Description of datasets used in our experiments. The train and valid data are randomly divided 10 times with 10-fold validation.

Dataset	#Train	#Valid	#Test	Length	#Channel	#Class
Sleep-EDF	31,952	3551	6805	3000	1	5
HAR	6616	736	2947	128	9	6
ESR	8280	920	2300	178	1	2

summarizes the details of each dataset, e.g., the number of training samples (Train), validation samples (Valid), and testing samples (Test), the length of the sample (Length), the number of sensor channels (Channel), and the number of classes (Class).

Sleep staging classification is a task that involves classifying EEG signals into one of five sleep stages: wake (W), non-rapid eye movement (N1, N2, N3), and rapid eye movement (REM). For this task, we utilized the Sleep-EDF dataset [23]. The Sleep-EDF dataset contains 42,308 epochs in 39 sleep cassette files collected from 20 subjects aged 25–34. Each subject in the Sleep-EDF database contains 2 day–night PSG recordings, except subjects 13, 36, and 52, whose 1 recording was lost due to device failure. The duration of each epoch is 30 s, and it has been labeled as wake, REM, N1, N2, N3, N4, MOVEMENT, UNKNOWN by experts according to the R&K standard. Specifically, we focused on a single EEG channel (Fpz-Cz) sampled at a rate of 100 Hz, following the methodology established in previous studies [21,24].

Human activity recognition is concerned with the classification of sensor readings into one of six activities: walking, walking upstairs, walking downstairs, standing, sitting, and lying down. To address this task, we utilized the UCI HAR dataset [25]. Human activity recognition contains 8828 epochs from 30 participants aged 19–48 years. It is concerned with the classification of sensor readings into one of six activities: walking, walking upstairs, walking downstairs, standing, sitting, and lying down. Each sample selects data in a fixed time window of 2.56 s, which is 128 sampling points.

Epilepsy seizure prediction involves predicting the occurrence of epileptic seizures using EEG recordings. For this task, we leveraged the Epileptic Seizure Recognition (ESR) dataset [26], which consists of EEG recordings obtained from 500 subjects. Each subject’s brain activity was recorded for a duration of 23.6 s. As the dataset originally included multiple seizure-related classes, we merged four out of the five classes into a single class as they did not include epileptic seizures. Consequently, the task was transformed into a binary classification problem.

2.2. The Proposed Method

2.2.1. Transformation Inconsistency Augmentation

For contrastive learning, the construction of positive and negative pairs is mainly based on the design of the augmentation method. The original time series is augmented by two random operations. Usually, the operations are selected from the same augmentation algorithm, such as dropout [11], timestamp masking, and cropping [16], to preserve the global temporal information and maintain the original properties for time series. Different augmentations can improve the robustness of the learned representations and reduce the training time for contrastive loss convergence. In this paper, the TIA module is designed in DABFS to learn invariant representations. To obtain more discriminating representations, a tempo-scale strategy is adopted. The scale augmentation lightly scales up the magnitude of the time series with random variations. For temporal augmentation, a permutation-and-jitter strategy is applied, which randomly splits the time series into a set of segments, randomly shuffles segments, and adds random variations. The max segment number $N_s$ is a hyper-parameter. The augmentation operations do not change the dimensions of the time series. The number of segments and parameters of random variations are selected based on previous research on augmentation.

Given an original time series $x\in {\mathbf{R}}^S$, the augmentation can be described as $x^{\mathrm{t}}={\mathcal{A}}_t\left(x\right)$ and $x^{\mathrm{s}}={\mathcal{A}}_s\left(x\right)\in {\mathbf{R}}^S$,where S represents the number of samples. The tempo-scale strategy results in different similarities between the transformed and the original time series. As shown in Figure 1, the transformed time series $x^{\mathrm{t}}$ and $x^{\mathrm{s}}$ are fed into a basic encoder module to extract their high-dimensional space representation, $z^{\mathrm{t}}$ and $z^{\mathrm{s}}$. The encoder adopts a 3-block convolutional architecture as in previous studies. The complexity of the encoder is controlled by hyper-parameters to ensure that representation and generalization capabilities are balanced. The encoding operation is defined as $\mathbf{Z}={\mathcal{F}}_{enc}\left(x\right)$, $\mathbf{Z}=\{z_i\in {\mathbf{R}}^d,i\le T\}$, where d is the feature length of each step and T is the time steps of each time series representation. Meanwhile, the original time series x is also encoded as $z^{\mathrm{u}}$ for following bias awareness. The $z^{\mathrm{s}}$, $z^{\mathrm{t}}$, and $z^{\mathrm{u}}$ are fed into DAB-aware Temporal Contrasting module.

2.2.2. DAB-minimize Contrasting Learning

The DAB-minimize contrasting module algorithm, presented in Algorithm 1, comprises two submodules: DABa-TC and DABa-CC. These modules aim to perceive and minimize the data augmentation bias (DAB) by optimizing the prediction performance and vector similarity with the assistance of the raw features stream (RFS). The loss functions are designed for both the min and max options.

Algorithm 1 DAB-aware Contrasting module algorithm.

Input: ${\left\{z_n^{\mathrm{t}}\right\}}_{n=1}^N$, ${\left\{z_n^{\mathrm{s}}\right\}}_{n=1}^N$, ${\left\{z_n^{\mathrm{u}}\right\}}_{n=1}^N$, K define: ${\mathcal{F}}_{trans}$: the transformer encoder ${\mathcal{T}}_k$: a set of linear layers $Projector$: a non-linear projection head T: the time steps of each time series representation B: the batch size $dis(y^{\prime },y)$: the difference between prediction output $y^{\prime }$ and ground truth y ${\mathrm{sim}}_{\mathrm{c}}(\mathrm{u},\mathrm{v})$: the cosine similarity between u and v ${\mathrm{sim}}_{\mathrm{d}}(\mathrm{u},\mathrm{v})$: the dot similarity between u and v Initialize: randomly select: t from 1 to $(T-K)$ $Z_{n,t}^{\mathrm{t}}=\{z_{n,i}^{\mathrm{t}},i\le t\}$, $Z_{n,t}^{\mathrm{s}}=\{z_{n,i}^{\mathrm{s}},i\le t\}$ for all $n\in \{1,\dots N\}$ do    $c_{n,t}^{\mathrm{t}}={\mathcal{F}}_{trans}\left(Z_{n,t}^{\mathrm{t}}\right),$ $c_{n,t}^{\mathrm{s}}={\mathcal{F}}_{trans}\left(Z_{n,t}^{\mathrm{s}}\right),$ $c_{n,t}^{\mathrm{u}}={\mathcal{F}}_{trans}\left(Z_{n,t}^{\mathrm{u}}\right)$    $p_n^{\mathrm{t}}=Projector\left(c_{n,t}^{\mathrm{t}}\right),$ $p_n^{\mathrm{s}}=Projector\left(c_{n,t}^{\mathrm{s}}\right),$ $p_n^{\mathrm{u}}=Projector\left(c_{n,t}^{\mathrm{u}}\right)$    for $1\le k\le K$ do      ${\alpha }_{n,k}^{\mathrm{t}}={\mathcal{T}}_k\left(c_{n,t}^{\mathrm{t}}\right),$ ${\alpha }_{n,k}^{\mathrm{s}}={\mathcal{T}}_k\left(c_{n,t}^{\mathrm{s}}\right)$      min $dis({\alpha }_{n,k}^{\mathrm{t}},z_{n,t+k}^{\mathrm{u}})+dis({\alpha }_{n,k}^{\mathrm{t}},z_{n,t+k}^{\mathrm{s}}),$ min $dis({\alpha }_{n,k}^{\mathrm{s}},z_{n,t+k}^{\mathrm{u}})+dis({\alpha }_{n,k}^{\mathrm{s}},z_{n,t+k}^{\mathrm{t}})$      max ${\sum }_{m\ne n}(dis({\alpha }_{n,k}^{\mathrm{t}},z_m^{\mathrm{u}})+dis({\alpha }_{n,k}^{\mathrm{t}},z_m^{\mathrm{s}})),$ max ${\sum }_{m\ne n}(dis({\alpha }_{n,k}^{\mathrm{s}},z_m^{\mathrm{u}})+dis({\alpha }_{n,k}^{\mathrm{s}},z_m^{\mathrm{t}}))$    end for    max $sim(p_n^{\mathrm{t}},p_n^{\mathrm{s}}),sim(p_n^{\mathrm{t}},p_n^{\mathrm{u}}),sim(p_n^{\mathrm{s}},p_n^{\mathrm{u}})$    min ${\sum }_{m\ne n}(si{m}_c(p_n^{\mathrm{t}},p_m^{\mathrm{s}})+si{m}_c(p_n^{\mathrm{s}},p_m^{\mathrm{t}})),$ min ${\sum }_{m\ne n}(si{m}_d(p_n^{\mathrm{t}},p_m^{\mathrm{u}})+si{m}_d(p_n^{\mathrm{s}},p_m^{\mathrm{u}}))$ end for

DAB-Aware Temporal Contrasting

In contrast to image and natural language data, temporal feature awareness is crucial for time series representation. To enhance the temporal aspect of the final representation, the DABa-TC module was designed as shown in the Figure 2. This module incorporates two attention blocks as a temporal encoding model, inspired by the transformer encoder ${\mathcal{F}}_{trans}$, known for its superior capability in extracting temporal features. The time steps ${\mathbf{Z}}_t^{\mathrm{s}}=z_i^{\mathrm{s}},i\le t$ and ${\mathbf{Z}}_t^{\mathrm{t}}=z_i^{\mathrm{t}},i\le t$ are temporally represented as $c_t^{\mathrm{s}}$ and $c_t^{\mathrm{t}}\in {\mathbf{R}}^m$, respectively, where m denotes the dimension of the hidden layers in the transformer.

The encoded $c_t$ is then used to predict the future time steps ${\mathbf{z}}_{t,K}=\{z_{t+k},1\le k\le K\}$, where t is randomly selected from 1 to $T-K$, and K is a hyper-parameter. Inspired by TS-TCC, the cross-view prediction is adopted. The temporal representation $c_t^{\mathrm{s}}$ is used to predict the scale future time steps ${\mathbf{z}}_{t,K}^{\mathrm{t}}$, and vice versa. Meanwhile, to minimize the DAB, both the $c_t^{\mathrm{s}}$ and $c_t^{\mathrm{t}}$ are used to predict raw future time steps ${\mathbf{z}}_{t,K}^{\mathrm{u}}$. Specifically, $c_t$ is mapped to have the same dimension as $z_t$ by a set of linear layers ${\mathcal{T}}_k$.

DABa-TC aims to optimize the prediction performance for the positive pairs, minimize the performance for negative pairs, and minimize the DAB of extracted temporal features. For the negative pairs, z generated by other samples within the same minibatch are defined as $z_n$. Thus, the loss functions $L_{TC}^{\mathrm{s}}$ and $L_{TC}^{\mathrm{t}}$ can be formed as follows:

$$L_{TC}^{\mathrm{s}}=\frac{-1}{K}\sum _{k=1}^{K}log\frac{exp({\mathcal{T}}_k{\left(c_t^{\mathrm{s}}\right)}^T{z}_{t+k}^{\mathrm{t}}+{\mathcal{T}}_k{\left(c_t^{\mathrm{s}}\right)}^T{z}_{t+k}^{\mathrm{u}})}{{\sum }_{n}exp({\mathcal{T}}_k{\left(c_t^{\mathrm{s}}\right)}^T{z}_n^{\mathrm{t}}+{\mathcal{T}}_k{\left(c_t^{\mathrm{s}}\right)}^T{z}_n^{\mathrm{u}})}$$

(1)

$$L_{TC}^{\mathrm{t}}=\frac{-1}{K}\sum _{k=1}^{K}log\frac{exp({\mathcal{T}}_k{\left(c_t^{\mathrm{t}}\right)}^T{z}_{t+k}^{\mathrm{s}}+{\mathcal{T}}_k{\left(c_t^{\mathrm{t}}\right)}^T{z}_{t+k}^{\mathrm{u}})}{{\sum }_{n}exp({\mathcal{T}}_k{\left(c_t^{\mathrm{t}}\right)}^T{z}_n^{\mathrm{s}}+{\mathcal{T}}_k{\left(c_t^{\mathrm{t}}\right)}^T{z}_n^{\mathrm{u}})}$$

(2)

DAB-Aware Contextual Contrasting

As shown in the Figure 2. To generate contextual information, a non-linear projection head [13] is applied to the temporal representations $c_t^{\mathrm{t}}$, contextual representations $c_t^{\mathrm{s}}$, and raw representations $c_t^{\mathrm{u}}$, resulting in projected representations $p_t=Proj\left(c_t\right)\in {\mathbf{R}}^{\frac{m}{4}}$. Figure 3 illustrates the formation of positive and negative pairs. Positive pairs consist of the representations obtained from the same sample, but are transformed using temporal and scale augmentation. Negative pairs, on the other hand, are formed by taking the representations transformed from different samples.

In the TIA module, $2N$ augmented samples are generated from N time series samples. Traditionally, contrastive learning methods only utilize the $2N$ augmented samples for encoding, resulting in one positive pair and $2(N-1)$ negative pairs for each sample. In contrast, DABaCLT takes into account the raw N samples and feeds them into the encoder concurrently with the augmented samples. Similarity-based techniques have been applied in various time series classification tasks and other applications [27,28].

In the contrasting module, assessing the similarity between the temporal- and scale-augmented samples is crucial for learning discriminative representations. To maximize the similarity of positive pairs and minimize the similarity of negative pairs, the loss function $L_{CC}^{sw}$ is defined as follows:

$$L_{CC}^{\mathrm{st}}=-\sum _{i=1}^{N_b}log\frac{exp(\mathrm{sim}((p_i^{\mathrm{s}},p_i^{\mathrm{t}})/\tau )}{{\sum }_{k\ne i,a\in \{\mathrm{s},\mathrm{t}\}}exp(\mathrm{sim}((p_i^{\mathrm{s}},p_k^a)/\tau )}$$

(3)

The $\mathrm{sim}(\mathrm{u},\mathrm{v})=u^{\mathrm{T}}v/\parallel u\parallel \parallel v\parallel$ denotes the dot product between $\mathcal{L}2$-normalized u and v (i.e., cosine similarity), $N_b$ is the sample size of a minibatch, and $\tau$ is the temperature parameter to help the model learn from hard negatives. Furthermore, evaluating the similarity between raw and augmented samples makes the representation closer to the original data distribution, thereby minimizing the DAB of extracted contextual features. This similarity is optimized by $L_{CC}^{\mathrm{t}}$ and $L_{CC}^{\mathrm{t}}$ as follows:

$$L_{CC}^{\mathrm{s}}=-\sum _{i=1}^{N_b}log\frac{exp(\mathrm{sim}((p_i^{\mathrm{s}},p_i^{\mathrm{u}})/\tau )}{{\sum }_{k\ne i}exp(\mathrm{sim}((p_i^{\mathrm{s}},p_k^{\mathrm{u}})/\tau )}$$

(4)

$$L_{CC}^{\mathrm{t}}=-\sum _{i=1}^{N_b}log\frac{exp(\mathrm{sim}((p_i^{\mathrm{t}},p_i^{\mathrm{u}})/\tau )}{{\sum }_{k\ne i}exp(\mathrm{sim}((p_i^{\mathrm{t}},p_k^{\mathrm{u}})/\tau )}$$

(5)

For Equations (4) and (5), $\mathrm{sim}(\mathrm{u},\mathrm{v})=u^{\mathrm{T}}v$ denotes the dot product (i.e., dot similarity). The DABMinLoss is the combination of the $L_{TC}$ and $L_{CC}$ as follows:

$$\mathcal{L}={\lambda }_1·L_{TC}^{\mathrm{s}}+{\lambda }_2·L_{TC}^{\mathrm{t}}+{\lambda }_3·L_{CC}^{\mathrm{st}}+{\lambda }_4·(L_{CC}^{\mathrm{t}}+L_{CC}^{\mathrm{s}})$$

(6)

where ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, and ${\lambda }_4$ are fixed scalar hyper-parameters denoting the relative weight of each loss. DABMinLoss minimizes the DAB of extracted temporal and contextual features. Therefore, the learned representation has lower DAB, which can achieve better performance in the downstream task.

3. Results

Comparison with Baseline Approaches

The performances of DABaCLT are compared with the baseline approaches: (1) Supervised: supervised training of both encoder and classifier models; (2) SimCLR [13]; (3) TS-TCC [21]; and (4) TS2Vec [16]. The publicly available or re-implemented codes were used for the baseline models. Brief descriptions of the models are as follows:

simCLR learns representations by maximizing the agreement between different augmented views of the same data example through contrastive loss in latent space. Two different data augmentation operators are sampled from the same augmentation family.

TS-TCC encourages the consistency of different data augmentations to learn trans-formation-invariant representations. It learns robust representations from time series data through a difficult cross-view prediction task.

TS2Vec uses the hierarchical contrast method to capture multi-scale context information in the instance time dimension. It can learn the context representations of any subsequence at different semantic levels.

For fair comparisons, we further trained a linear classifier on the learned representations. Two matrices were used to evaluate the performance of the sleep stage models, namely, the prediction accuracy (ACC) and the macro-averaged F1 score (MF1). We implemented the TS-TCC, SimCLR, and supervised methods through a common code with the same encoder architecture and parameters. The original encoder architecture of TS2Vec was used because the TS2Vec has a specially designed encoder architecture for contrastive learning. To evaluate the performance and robustness of the proposed DAB-aware contrastive learning framework (DABaCLT) for classification tasks, we adopted a rigorous evaluation strategy using 10-fold cross-validation. The available labeled time series data were divided into 10 equal-sized subsets. The training and validation procedure was then repeated 10 times, with each fold serving as the validation set once and the remaining nine folds used for training. The more detailed experimental setup is shown in Appendix A.

Table 2. Comparison between DABaCLT model against baselines using linear classifier evaluation experiments.

Method	SSC		HAR		ESP
	Avg. Acc	MF1	Avg. Acc	MF1	Avg. Acc	MF1
supervised	81.14 ± 0.36	74.07 ± 0.33	91.47 ± 0.75	91.09 ± 0.83	96.63 ± 0.31	94.56 ± 0.54
simCLR	56.58 ± 0.44	48.81 ± 0.13	86.99 ± 0.18	86.05 ± 0.20	96.00 ± 0.20	93.33 ± 0.35
TS-TCC	79.34 ± 0.33	72.92 ± 0.49	89.08 ± 0.19	88.45 ± 0.19	95.59 ± 0.13	92.62 ± 0.21
TS2Vec	73.50 ± 1.48	65.93 ± 0.25	87.91 ± 0.02	86.55 ± 0.22	97.05 ± 0.36	94.63 ± 0.21
DABaCLT (ours)	79.53 ± 0.11	73.25 ± 0.15	92.04 ± 0.24	91.52 ± 0.26	98.05 ± 0.10	96.93 ± 0.18

shows that with only a linear classifier, DABaCLT performs best on two of three datasets, while achieving comparable performance to the supervised approach on the third dataset. Compared with self-supervised learning, the average accuracy of DABaCLT achieves a 0.19% to 22.95% improvement for SSC, 2.96% to 5.05% for HAR, and 1% to 2.46% for ESP. The results demonstrate that DABaCLT adequately learns temporal and contextual information in time series, and further perceives and minimizes the DAB between the augmented and raw representations. As shown in Figure A1, the performance of DABaCLT can be observed in the confusion matrix for each category. More detailed results with precision, recall, sensitivity, and specificity are presented in the table in the Appendix B.

4. Discussion

4.1. Comparisons of Time Series Augmentation Methods

To further prove the effectiveness of our TIA (tempo-scale strategy) module, we compared our method with the other four augmentation strategies: slice, scaling, dropout, and permutation. The classification accuracy comparisons of different augmentations on the HAR dataset are illustrated in Figure 4A. The proposed tempo-scale strategy has the best performance in average accuracy, which demonstrates that the discriminating representations are learned using tempo-scale transformation augmentation. Further, considering the random transformation with the same augmentation method generates two similar views, our TIA generates views with more information entropy. Previous studies consider the dropout strategy to be the best augmentation. However, when the DAB is aware, more discriminative features are constructed, and the model can achieve better performance. Though the augmentation process introduces the DAB, it can be perceived and minimized by the DABa-TC and DABa-CC modules, which means the TIA is more stable for the DABaCLT framework.

4.2. Impact of Raw Features Stream

RFS is the essential part of DABaCLT, which includes the raw time series $x^{\mathrm{u}}$, encoded representation $z^{\mathrm{u}}$, and the loss functions $L_{TC}$ in the DABa-TC and $L_{CC}$ DABa-CC modules. We argue that the DAB exists in different levels of features and can be minimized by different raw features (UF). To evaluate whether the RFS does assist the DAB awareness in learned representations, we conducted ablation experiments on the HAR dataset. We compared four situations: (1) drop total RFS, (2) calculate $L_{TC}^{\mathrm{s}}$ and $L_{TC}^{\mathrm{t}}$ without $z^{\mathrm{u}}$ (drop UF in DABa-TC), (3) drop $L_{CC}^{\mathrm{s}}$ and $L_{CC}^{\mathrm{t}}$ (drop UF in DABa-CC), and (4) complete DABaCLT (no drops). Figure 4B shows the classification performance when dropping different raw features. When dropping the total RFS, the framework can still learn temporal and contextual information. However, the classification performance is not as good as using $z^{\mathrm{u}}$ or calculating $L_{CC}^{\mathrm{s}}$ and $L_{CC}^{\mathrm{s}}$. Moreover, the complete DABaCLT achieves the best average accuracy, which means the RFS is greatly meritorious in terms of DAB awareness and minimization.

4.3. Impact of Parameter Selection

The sensitivity analysis was performed on the HAR dataset to study the influence of parameters $\lambda 1$, $\lambda 2$, $\lambda 3$, and $\lambda 4$ on the contrasting learning process. Figure 5 shows the evaluation results. When evaluating ${\lambda }_i$, the others are fixed to 1. It is observed that the model is not sensitive to $\lambda 1$, and it is easier for $\lambda 2$, $\lambda 3$, and $\lambda 4$ to influence the representation. Commonly, the model achieves the best performance when $0.1<\lambda$s $<10$.

4.4. The Visualization of DAB Problem

The distribution of raw signals and augmented signals from the three datasets is shown in Figure 6. It can be observed that the HAR and ESR datasets exhibit a more chaotic distribution after applying data augmentation methods. However, there is no significant change in the distribution of the Sleep-EDF data. The spatial distribution of different categories in the Sleep-EDF dataset appears to be more uniform compared to the other two datasets. This can be mainly attributed to the sample length of the data. For the HAR and ESR datasets, the number of sampling points in their individual samples is 128 and 178, respectively, making the tempo-scale augmentation method significantly alter the data distribution. On the other hand, the Sleep-EDF dataset has a sample length of 3000, resulting in a less-pronounced disruption of its distribution by the tempo-scale augmentation method. The accuracy results further support this observation, as DABaCLT demonstrates improved prediction accuracy for the HAR and Epilepsy datasets compared to supervised methods, while showing no improvement for SSC.

5. Conclusions

This paper introduces the concept of the DAB and presents a DAB-aware contrastive learning framework for time series representations. It incorporates DABFS and RFS, and utilizes DAB-aware temporal and contextual contrasting modules to minimize DAB through DAB-aware contrastive loss. The experimental results demonstrate the effectiveness of the framework, with improved accuracy compared to self-supervised learning. The tempo-scale strategy and RFS play important roles in enhancing the discriminative power of the learned representations and addressing the data augmentation bias. The DAB problem proposed in this article is a common phenomenon in contrastive learning. The ideas of RFS and DABmin Loss proposed in this article provide a solution for more contrastive learning methods. However, the current research has not yet addressed the impact of data length on the model, and the complexity of the model needs further optimization. The influence of sample length and the quantification of DAB will be explored in future research.