The Low-Loss Spot Size Converter for Alignment with Cleaved Single Mode Fiber
Abstract
:1. Introduction
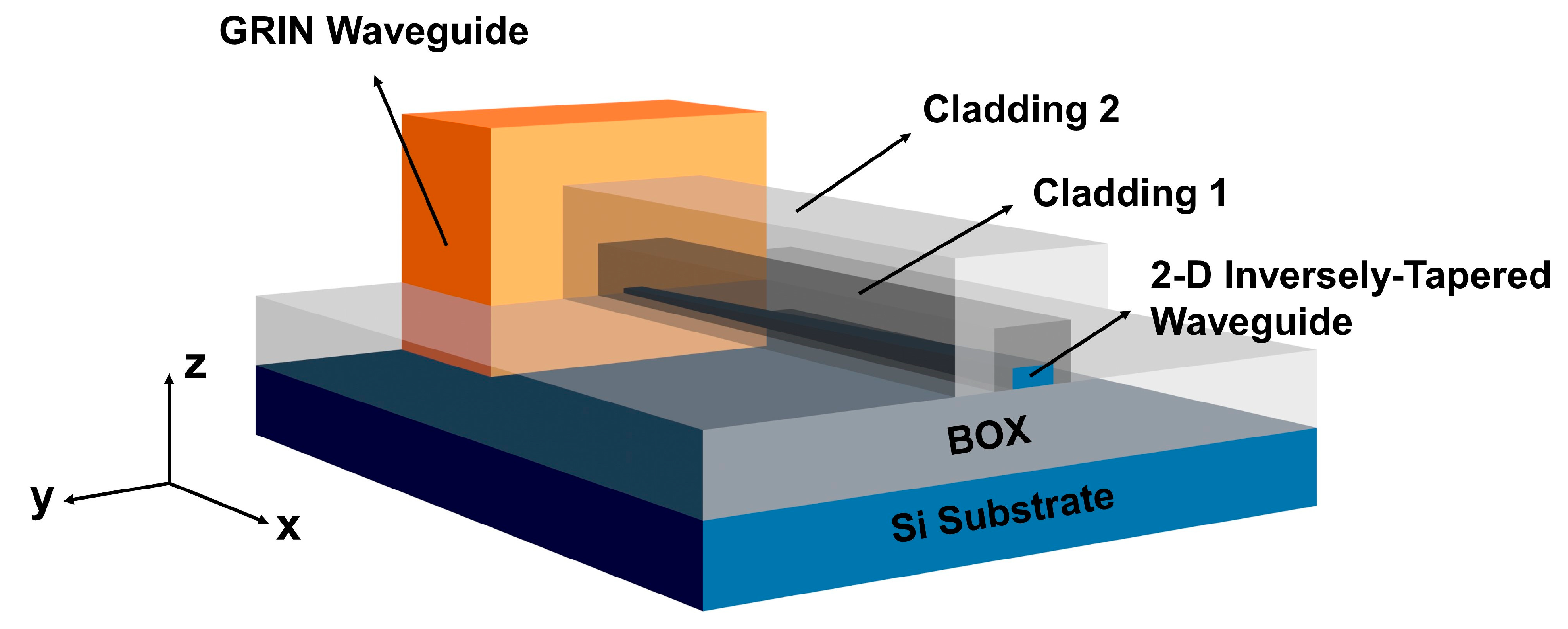
2. Design of Materials and Methods
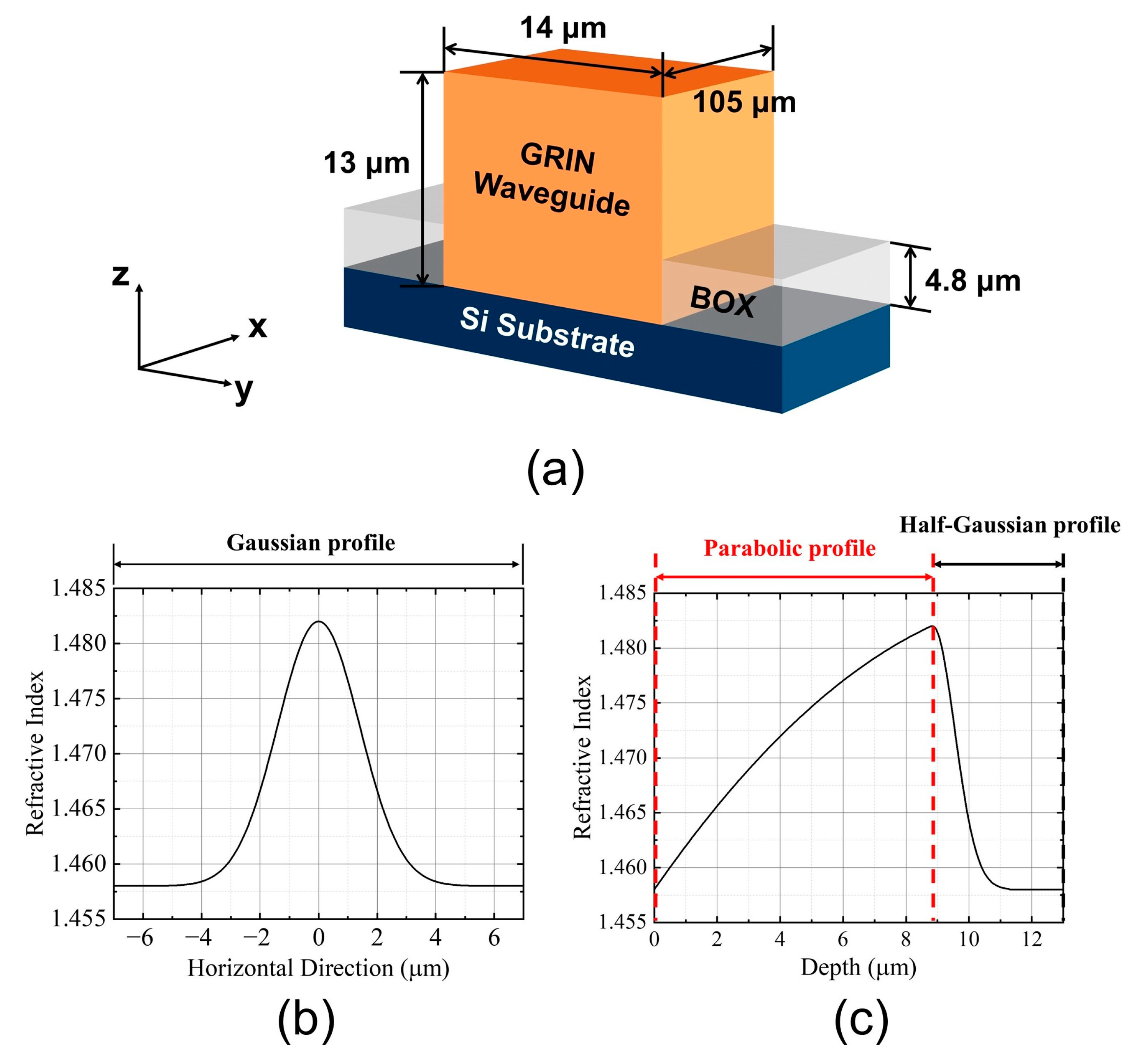
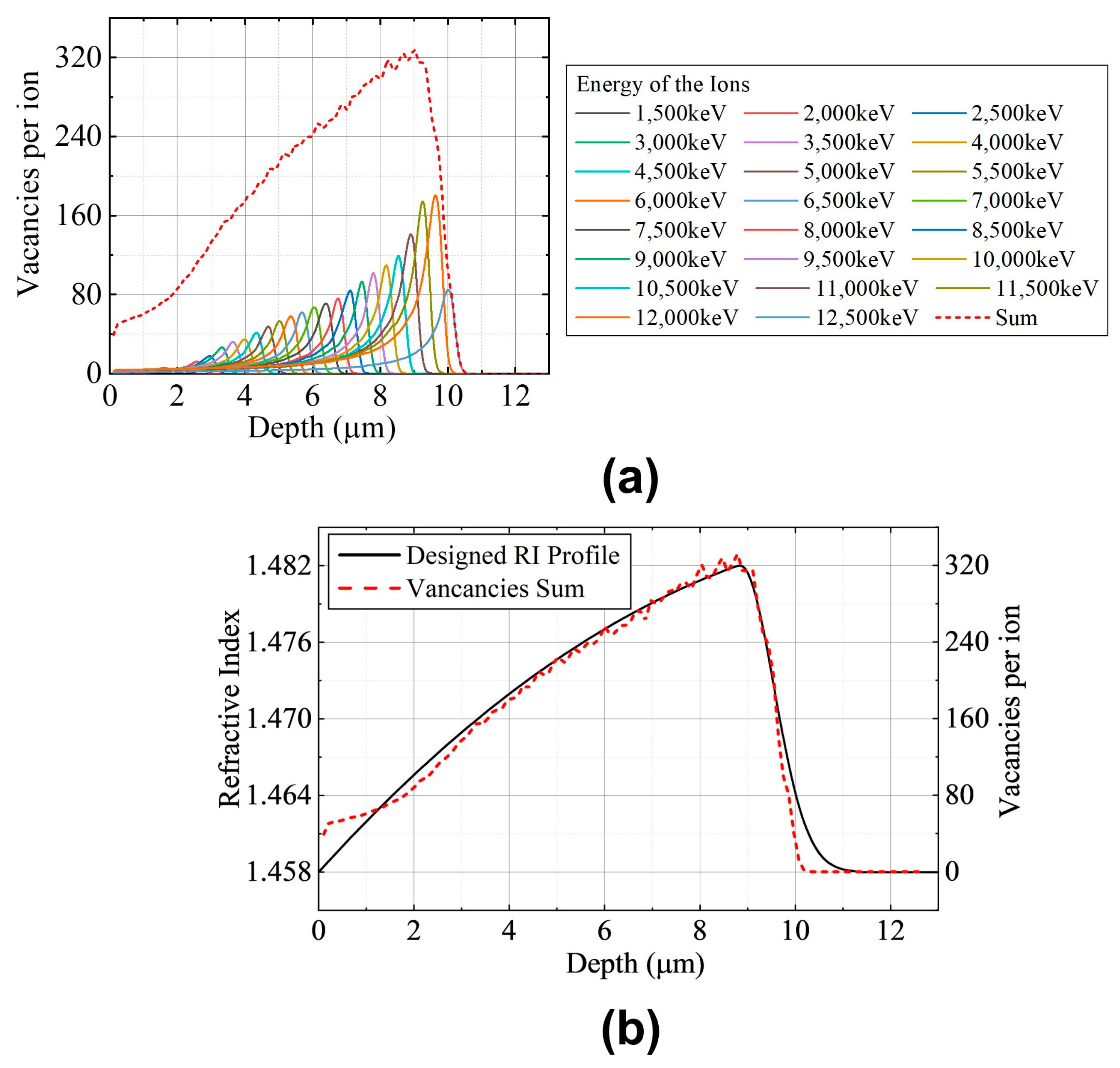
2.1. GRIN Waveguide
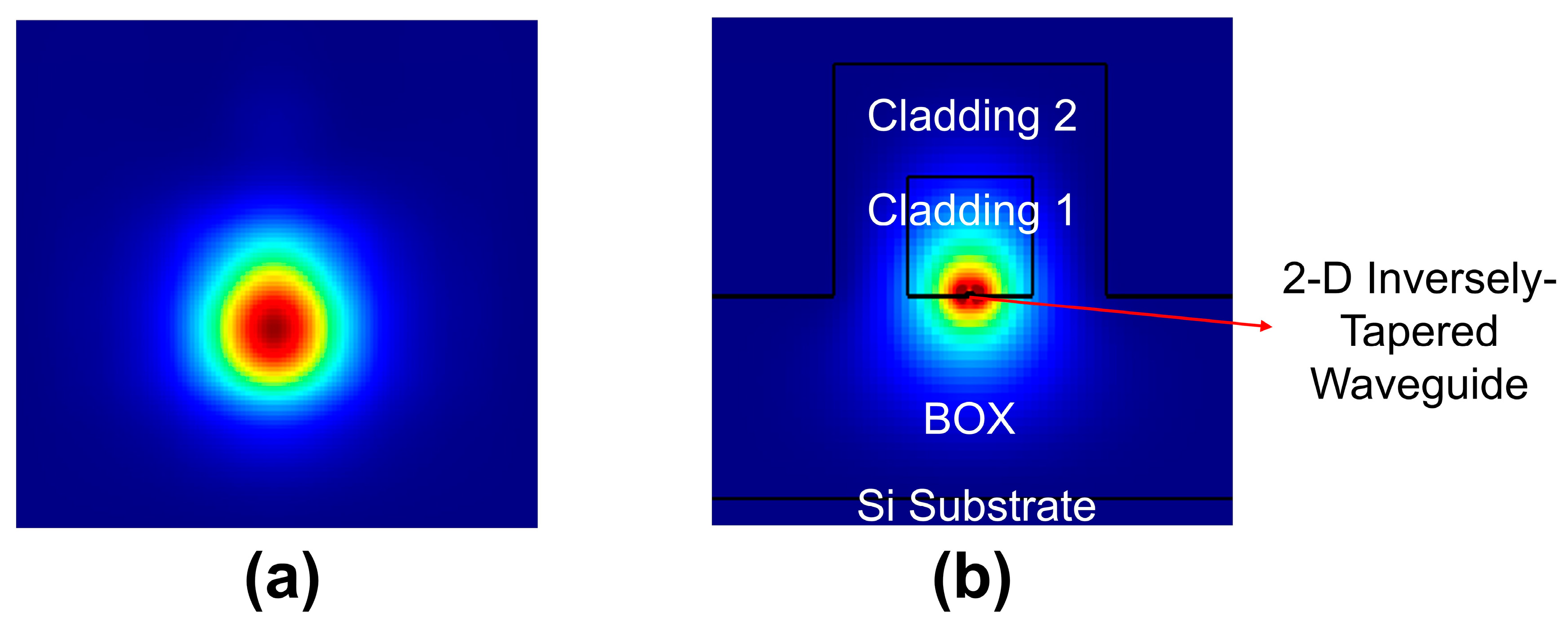
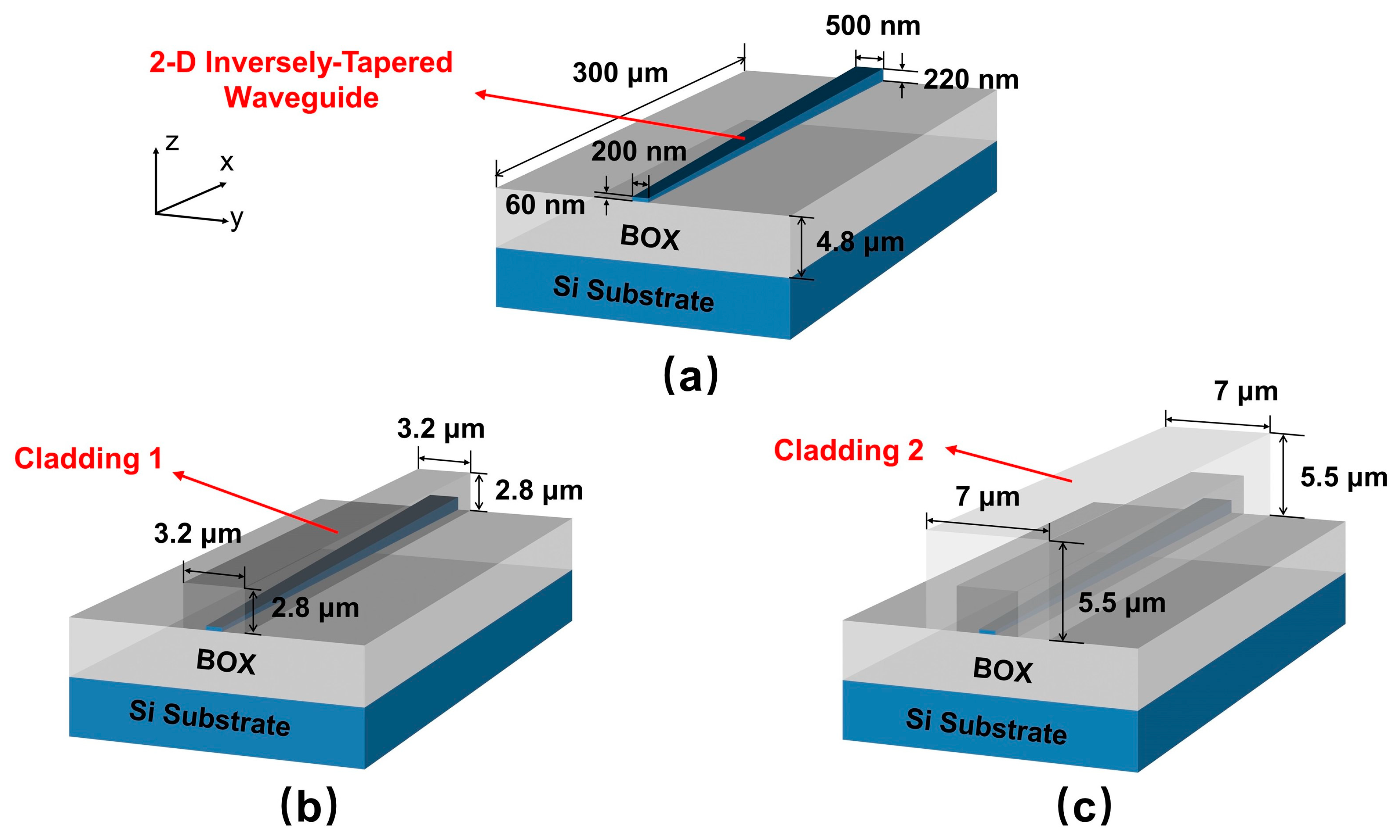
2.2. The 2-D Inversely-Tapered Waveguide
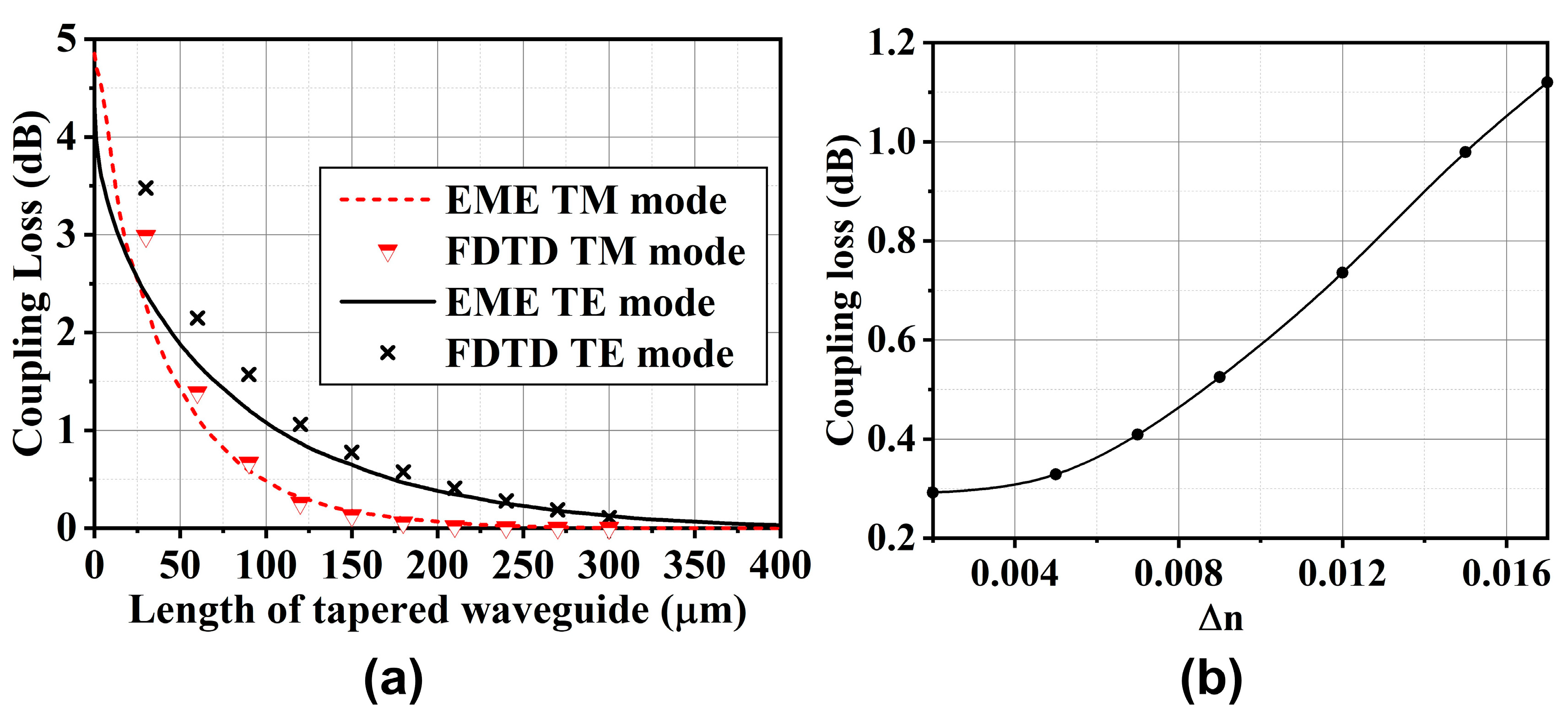
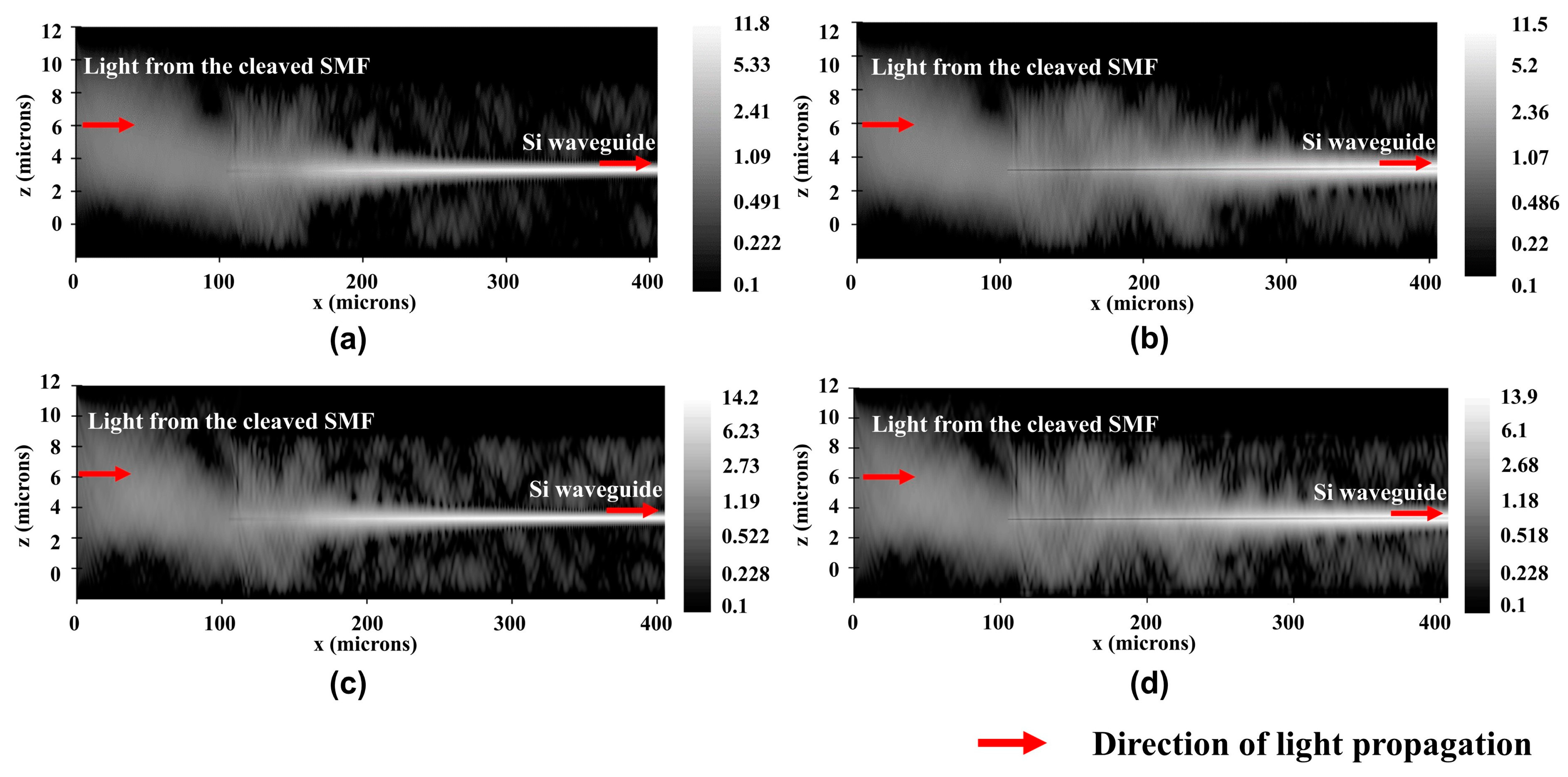
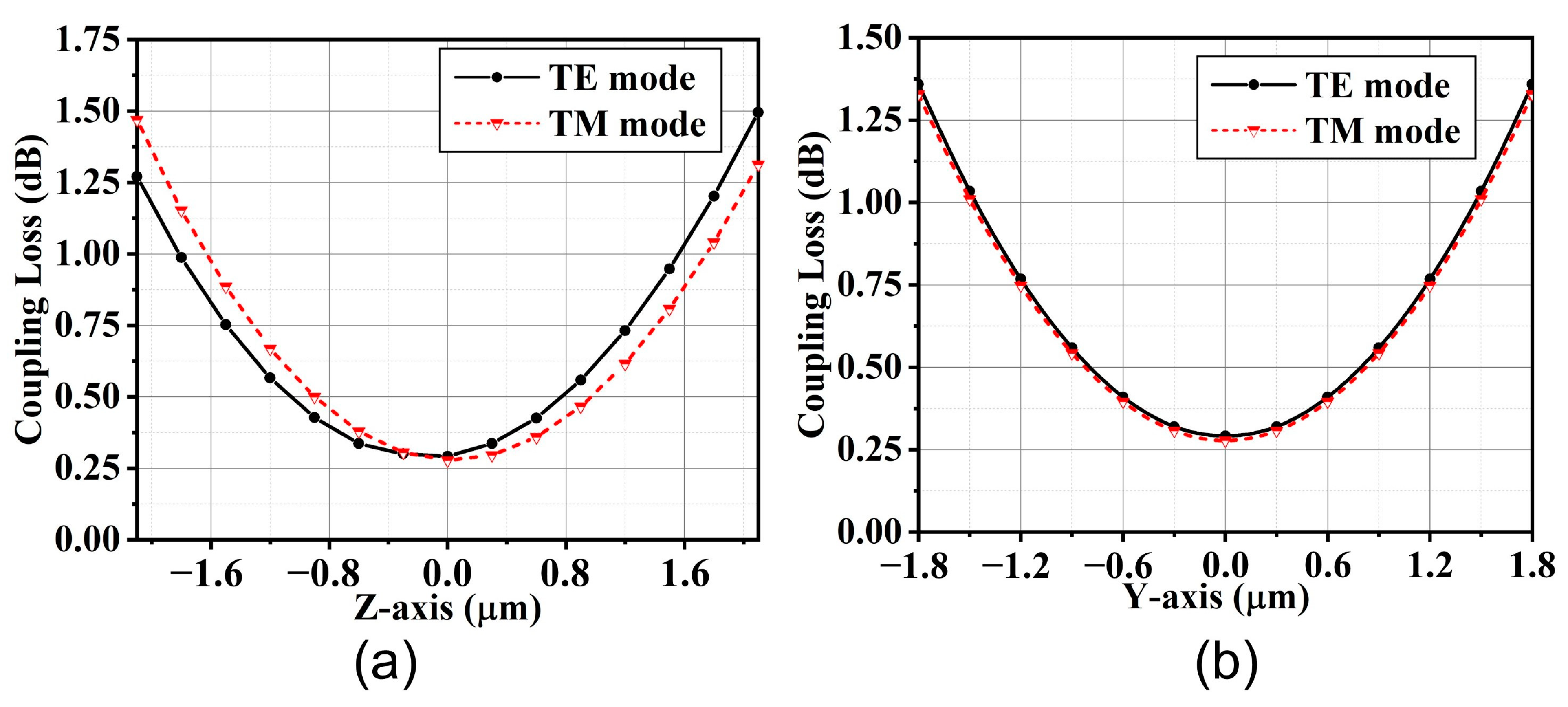
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marchetti, R.; Lacava, C.; Carroll, L.; Gradkowski, K.; Minzioni, P. Coupling strategies for silicon photonics integrated chips. Photon. Res. 2019, 7, 201–239. [Google Scholar] [CrossRef]
- Kasaya, K.; Mitomi, O.; Naganuma, M.; Kondo, Y.; Noguchi, Y. A simple laterally tapered waveguide for low-loss coupling to single-mode fibers. IEEE Photon. Technol. Lett. 1993, 5, 345–347. [Google Scholar] [CrossRef]
- Larrea, R.; Gutierrez, A.M.; Griol, A.; Brimont, A.; Sanchis, P. Fiber-to-Chip Spot-Size Converter for Coupling to Silicon Waveguides in the O-Band. IEEE Photon. Technol. Lett. 2019, 31, 31–34. [Google Scholar] [CrossRef]
- He, A.; Guo, X.; Wang, K.; Zhang, Y.; Su, Y. Low Loss, Large Bandwidth Fiber-Chip Edge Couplers Based on Silicon-on-Insulator Platform. J. Lightwave Technol. 2020, 38, 4780–4786. [Google Scholar] [CrossRef]
- Papes, M.; Cheben, P.; Benedikovic, D.; Schmid, J.H.; Pond, J.; Halir, R.; Ortega-Moñux, A.; Wangüemert-Pérez, G.; Ye, W.N.; Xu, D.; et al. Fiber-chip edge coupler with large mode size for silicon photonic wire waveguides. Opt. Express 2016, 24, 5026–5038. [Google Scholar] [CrossRef]
- Xiao, Y.; Xu, Y.; Dong, Y.; Zhang, B.; Ni, Y. A 60 μm-Long Fiber-to-Chip Edge Coupler Assisted by Subwavelength Grating Structure with Ultralow Loss and Large Bandwidth. Photonics 2022, 9, 413. [Google Scholar] [CrossRef]
- Almeida, V.R.; Panepucci, R.R.; Lipson, M. Nanotaper for compact mode conversion. Opt. Lett. 2003, 28, 1302–1304. [Google Scholar] [CrossRef]
- Galán, J.V.; Sanchis, P.; Sánchez, G.; Martí, J. Polarization insensitive low-loss coupling technique between SOI waveguides and high mode field diameter single-mode fibers. Opt. Express 2007, 15, 7058–7065. [Google Scholar] [CrossRef]
- Fang, Q.; Song, J.; Luo, X.; Tu, X.; Jia, L.; Yu, M.; Lo, G. Low Loss Fiber-to-Waveguide Converter With a 3-D Functional Taper for Silicon Photonics. IEEE Photon. Technol. Lett. 2016, 28, 2533–2536. [Google Scholar] [CrossRef]
- Loh, T.; Wang, Q.; Ng, K.; Lai, Y.; Ho, S. CMOS compatible integration of Si/SiO2 multilayer GRIN lens optical mode size converter to Si wire waveguide. Opt. Express 2012, 20, 14769–14778. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Sakaguchi, Y.; Yasuhara, K.; Ishigure, T. Mosquito method based polymer tapered waveguide as a spot size converter. Opt. Express 2021, 29, 9513–9531. [Google Scholar] [CrossRef]
- Delage, A.; Janz, S.; Xu, D.X.; Dalacu, D.; Lamontagne, B.; Bogdanov, A.L. Graded-index coupler for microphotonic SOI waveguides. In Proceedings of the Photonics North 2004: Optical Components and Devices, Ottawa, ON, Canada, 20 December 2004. [Google Scholar] [CrossRef]
- Chen, F.; Wang, X.; Wang, K. Development of ion-implanted optical waveguides in optical materials: A review. Opt. Mater. 2007, 29, 1523–1542. [Google Scholar] [CrossRef]
- Pezzagna, S.; Naydenov, B.; Jelezko, F.; Wrachtrup, J.; Meijer, J. Creation efficiency of nitrogen-vacancy centres in diamond. New J. Phys. 2010, 12, 065017. [Google Scholar] [CrossRef]
- Márquez, H.; Salazar, D.; Rangel-Rojo, R.; Angel, J.L.; Vázquez, G.V.; Flores-Romero, E.; Rodríguez-Fernández, L.; Oliver, A. Waveguides by multiple implantations of Ag ion on SiO2 substrates. In Proceedings of the 22nd Congress of the International Commission for Optics: Light for the Development of the World, Puebla, Mexico, 25 October 2011. [Google Scholar] [CrossRef]
- Matsumura, H.; Furukawa, S. Theoretical considerations in lateral damage distribution formed by ion-implantation. Jpn. J. Appl. Phys. 1975, 14, 1783–1790. [Google Scholar] [CrossRef]
- Faik, A.B.; Chandler, P.J.; Townsend, P.D.; Webb, R. Refractive index changes formed by N+ implants in silica. Radiat. Eff. Defects Solids. 1986, 98, 233–241. [Google Scholar] [CrossRef]
- Fu, Y.; Ye, T.; Tang, W.; Chu, T. Efficient adiabatic silicon-on-insulator waveguide taper. Photon. Res. 2014, 2, A41–A44. [Google Scholar] [CrossRef]
- Lee, K.K.; Lim, D.R.; Kimerling, L.C.; Shin, J.; Cerrina, F. Fabrication of ultralow-loss Si/SiO2 waveguides by roughness reduction. Opt. Lett. 2001, 26, 1888–1890. [Google Scholar] [CrossRef]
- Teng, M.; Wu, H.; Li, C.; Wang, F.; Du, Y.; Zheng, X. O-Band Fiber-to-Chip Edge Coupler for High NA Fiber Based on a CMOS Compatible SOI Platform. In Proceedings of the 2022 Optical Fiber Communication Conference (OFC), San Diego, CA, USA, 6–10 March 2022. [Google Scholar] [CrossRef]
- Shiraishi, K.; Yoda, H.; Tsai, C.S. A two-port polarization-insensitive coupler module between single-mode fiber and silicon-wire waveguide. Opt. Express 2012, 20, 24370–24375. [Google Scholar] [CrossRef]
- Morgan, B.; Waits, C.M.; Krizmanic, J.; Ghodssi, R. Development of a deep silicon phase Fresnel lens using Gray-scale lithography and deep reactive ion etching. J. Microelectromech. Syst. 2004, 13, 113–120. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Fan, Z.; Xing, B.; Yu, Y.; Yu, J. Fabrication and optical optimization of spot-size converters with strong cladding layers. J. Opt. A Pure Appl. Opt. 2009, 11, 085002. [Google Scholar] [CrossRef]
- Kim, Y.T.; Kim, D.S.; Yoon, D.H. PECVD SiO2 and SiON films dependant on the rf bias power for low-loss silica waveguide. Thin Solid Film. 2005, 475, 271–274. [Google Scholar] [CrossRef]

| References | MFD (µm) | Width of Taper Tip (nm) | Coupling Loss (dB) | Simulated or Experimental | |
|---|---|---|---|---|---|
| TE Mode | TM Mode | ||||
| [3] | 8 | 70 | 2 | 2 | Experimental |
| [5] | 6/10 | 150 | 0.42/0.75 | NA | Simulated |
| [8] | 8 | 200 | 3.5 | 3.7 | Simulated |
| [9] | 10.5 | 100 | 1.5 | 2.1 | Experimental |
| [10] | 9~10 | No Inversely Taper | 2.6 ± 0.3 | 2.6 ± 0.3 | Experimental |
| This Work | 8/10 | 200 | 0.29/0.58 | 0.27/0.56 | Simulated |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Wang, Z.; Ye, N.; Pang, F.; Song, Y. The Low-Loss Spot Size Converter for Alignment with Cleaved Single Mode Fiber. Appl. Sci. 2023, 13, 8157. https://doi.org/10.3390/app13148157
Zhao J, Wang Z, Ye N, Pang F, Song Y. The Low-Loss Spot Size Converter for Alignment with Cleaved Single Mode Fiber. Applied Sciences. 2023; 13(14):8157. https://doi.org/10.3390/app13148157
Chicago/Turabian StyleZhao, Jinyang, Zhutian Wang, Nan Ye, Fufei Pang, and Yingxiong Song. 2023. "The Low-Loss Spot Size Converter for Alignment with Cleaved Single Mode Fiber" Applied Sciences 13, no. 14: 8157. https://doi.org/10.3390/app13148157
APA StyleZhao, J., Wang, Z., Ye, N., Pang, F., & Song, Y. (2023). The Low-Loss Spot Size Converter for Alignment with Cleaved Single Mode Fiber. Applied Sciences, 13(14), 8157. https://doi.org/10.3390/app13148157









