Linear/Nonlinear Active Disturbance Rejection Switching Control for Near-Space Morphing Vehicles Based on Type-2 Fuzzy Logic System
Abstract
:1. Introduction
- The mismatched uncertainty model for NMVs was established considering the large range of parameter uncertainty and external disturbance. A cascade ADRC method was developed for a class of multi-input multioutput high-order coupled system.
- According to the model characteristics of NMV, both linear active disturbance rejection control (LADRC) and nonlinear active disturbance rejection control (NLADRC) were designed for velocity and altitude subsystems of NMVs. Furthermore, the stabilization of the cascade closed-loop and switching control systems were analyzed.
- A novel switching control strategy based on the interval type-2 fuzzy logic system was developed. Furthermore, both fuzzy rules and the corresponding results of the velocity and altitude subsystems were examined, and the defuzzification algorithm of each step was established.
- The change rules of aerodynamic parameters with Mach number and angle of attack under the condition of winglet stretch out and draw back were analyzed. The efficiency and robustness of the proposed control method were demonstrated by numerical simulations.
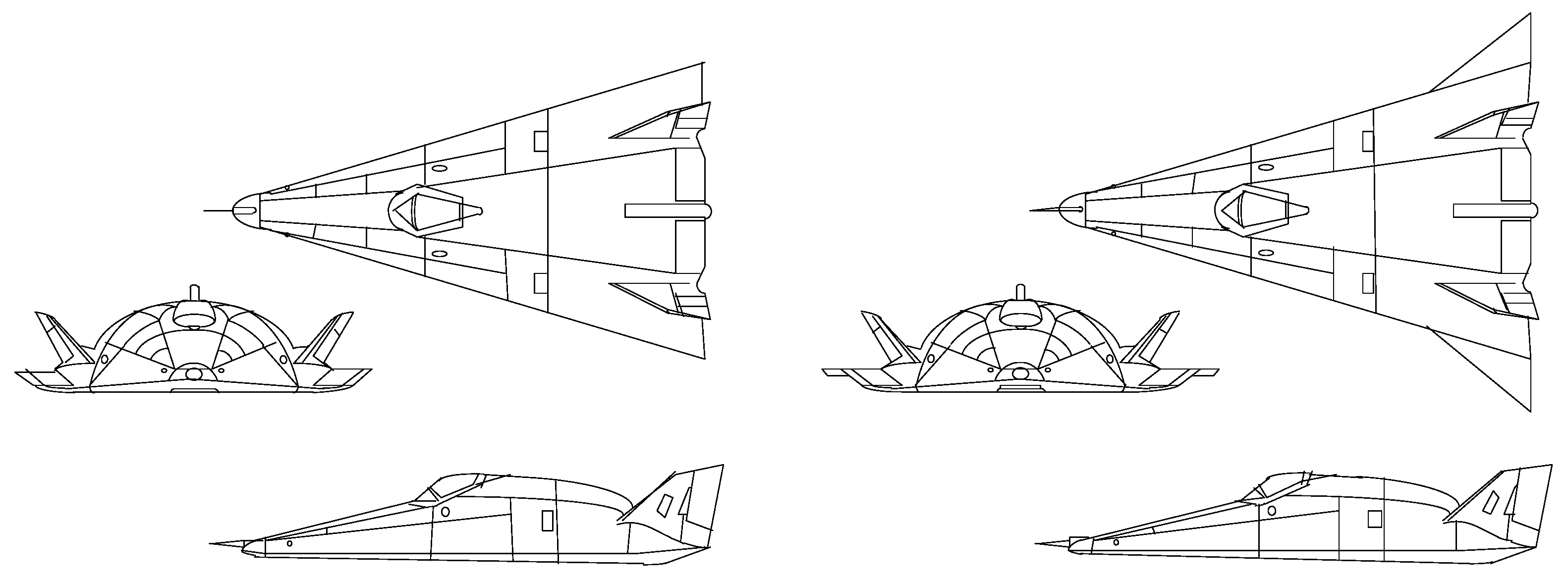
2. NMV Model Description
3. Controller Design
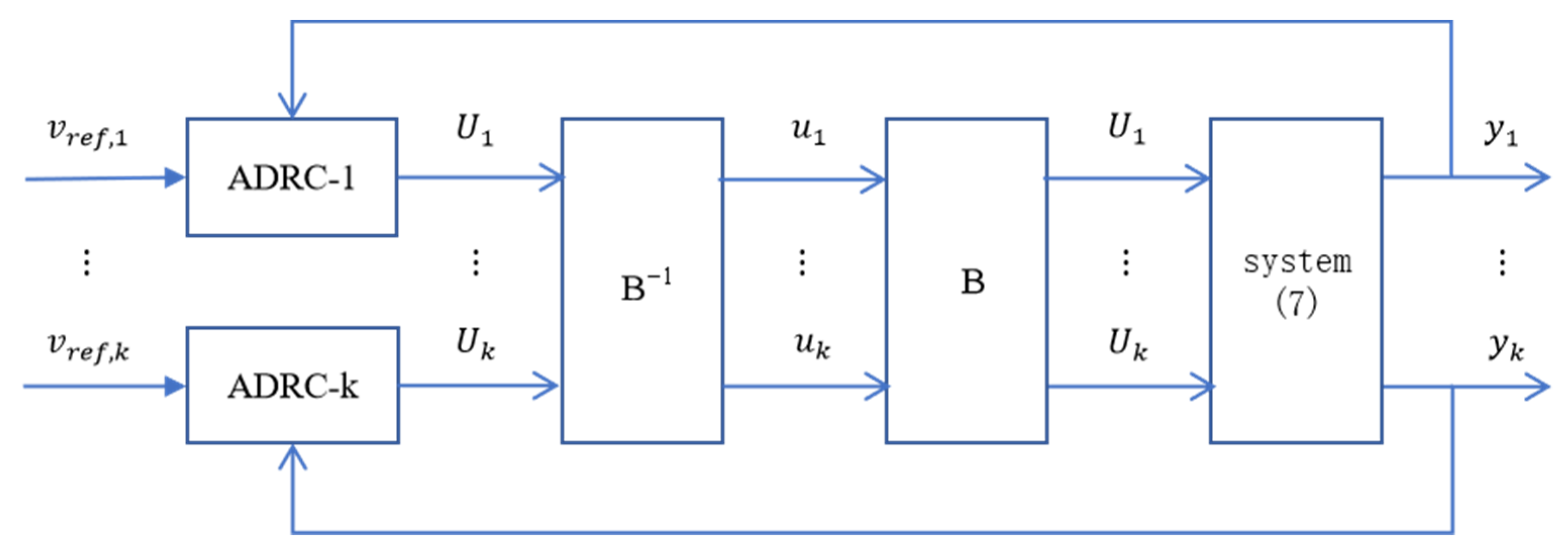
3.1. ADRC for Multivariate Coupled Systems
3.2. Linear/Nonlinear Extended State Observer Design
3.3. Cascade ADRC Design
3.4. Cascade ADRC Convergence Analysis
3.5. Stable Analysis of LADRC/NLADRC Switching
3.6. Switch Control Strategy Based on the Interval Type-2 Fuzzy Logic System
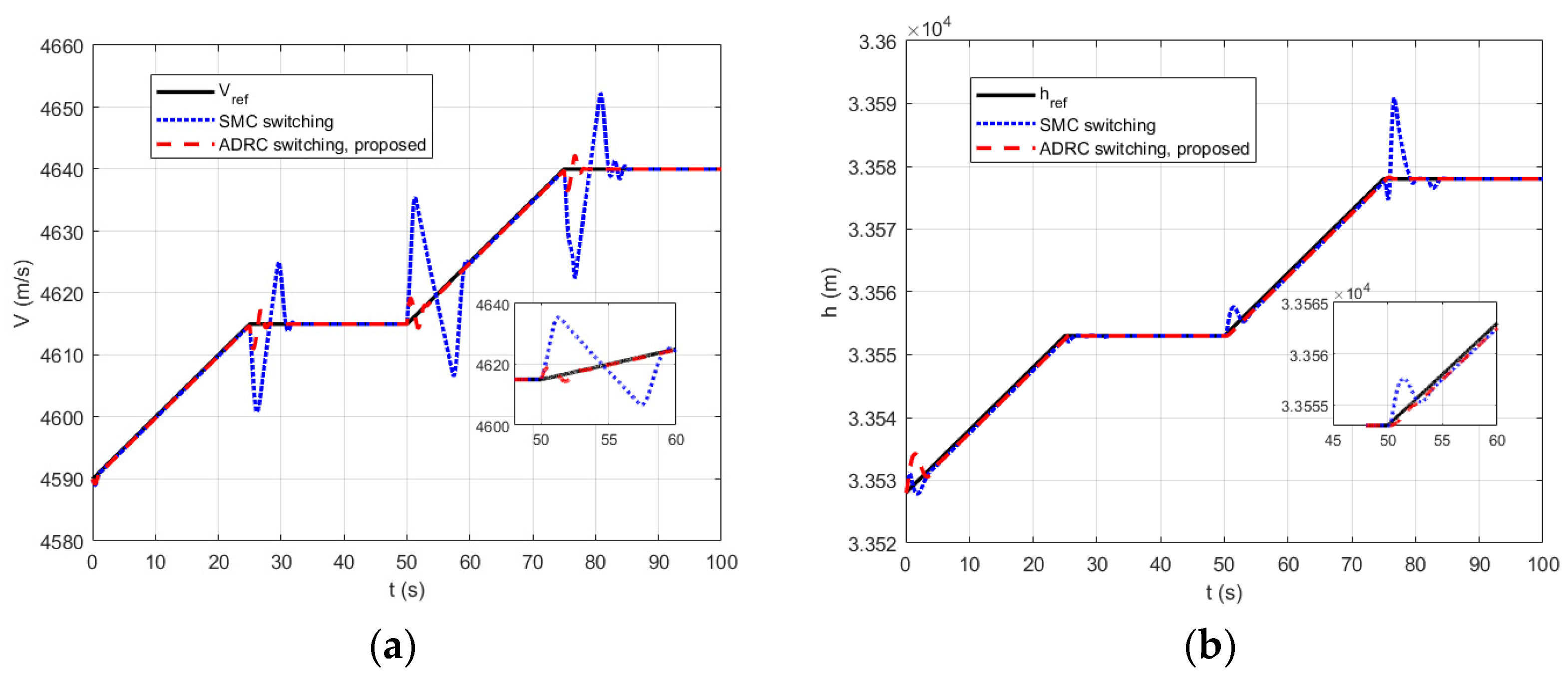
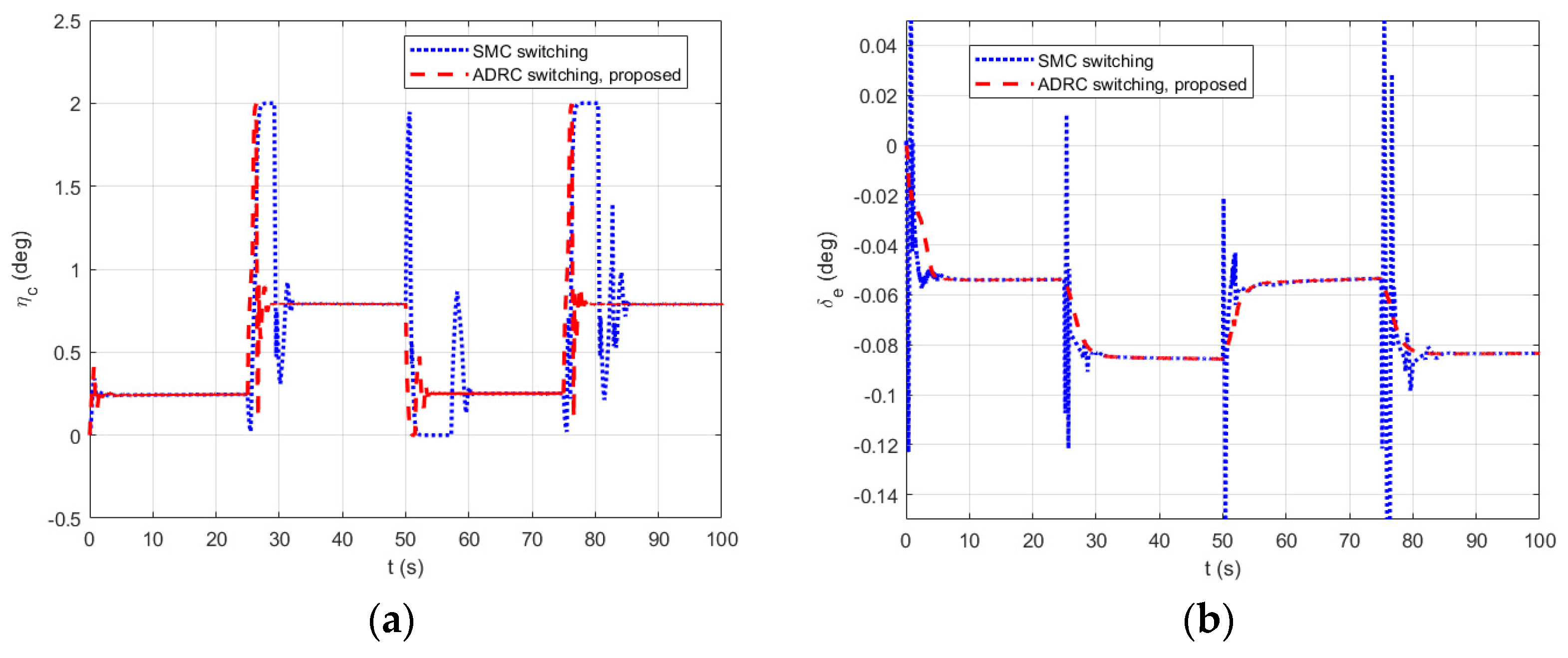
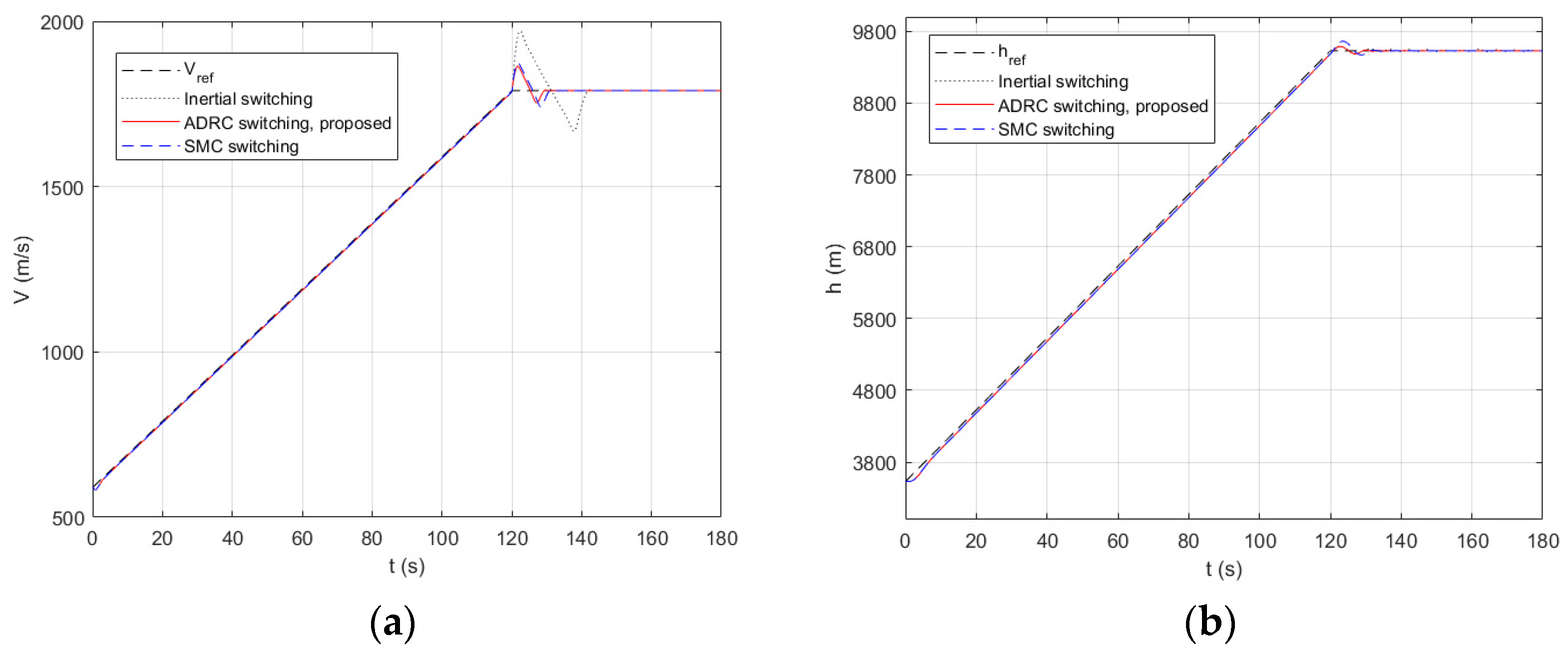
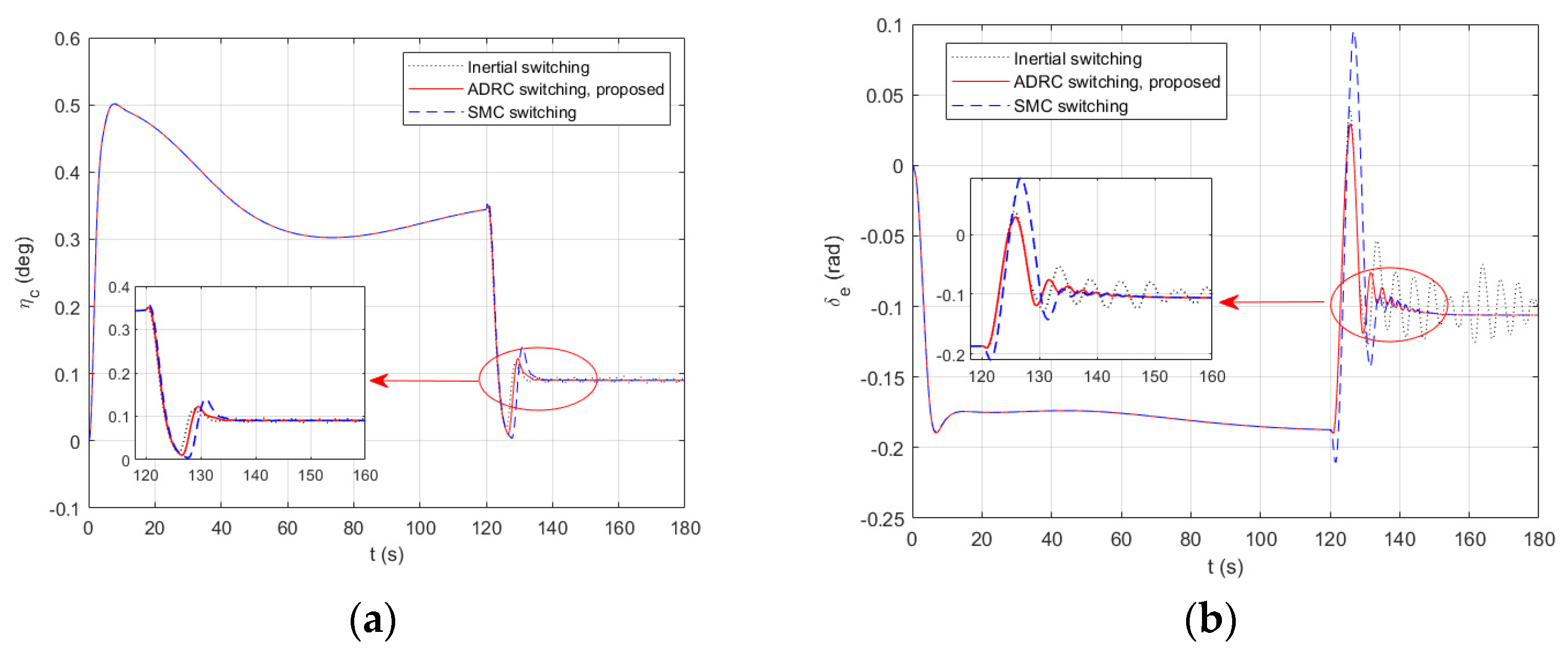
4. Simulation and Discussion
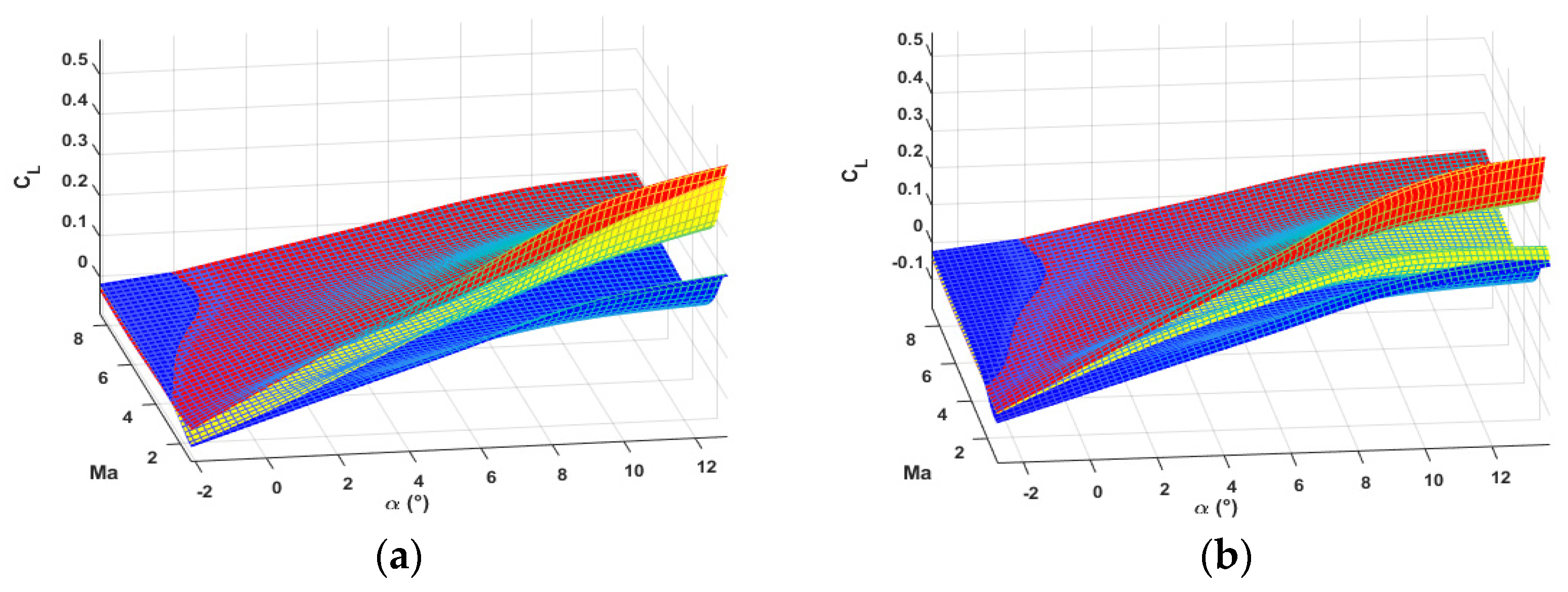
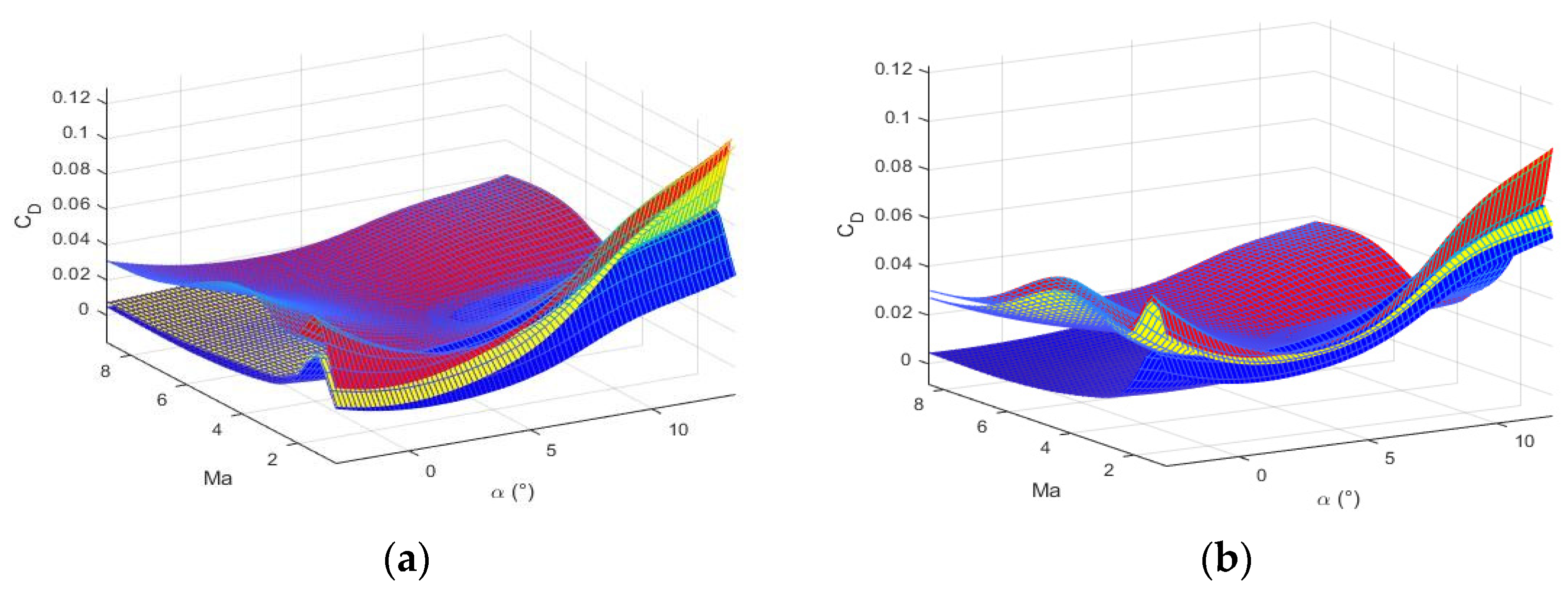
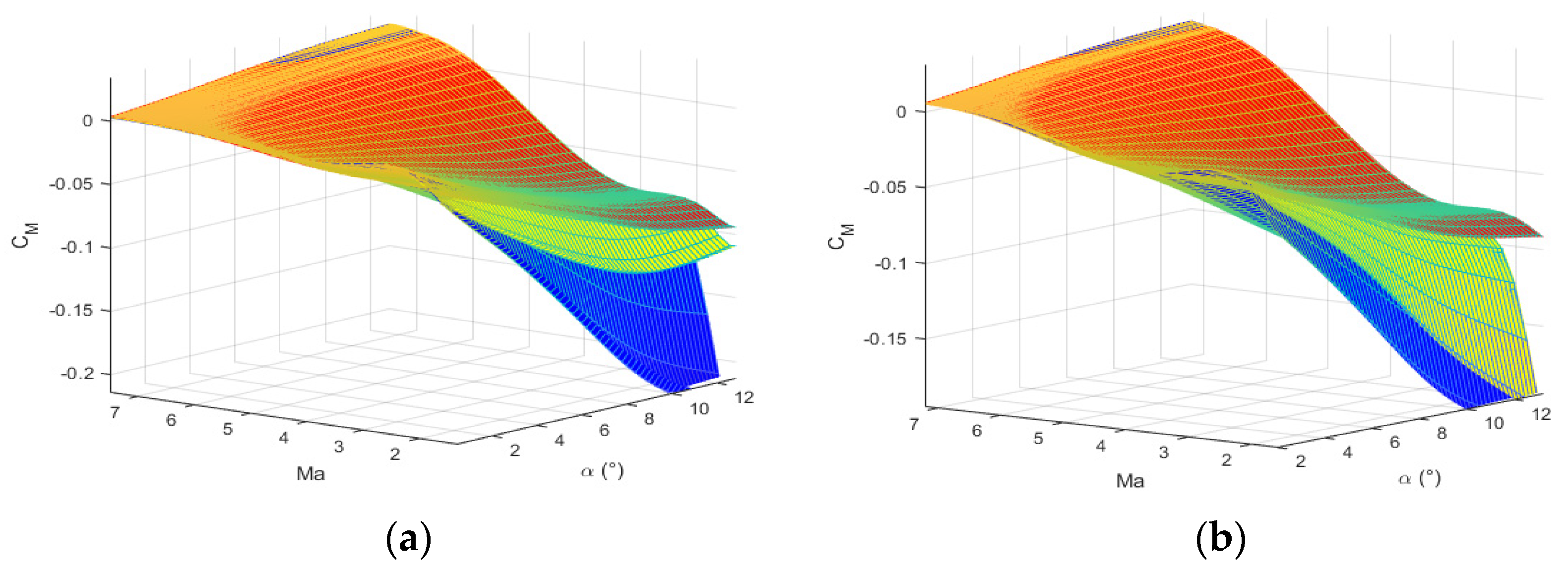
4.1. Aerodynamic Characteristics Analysis
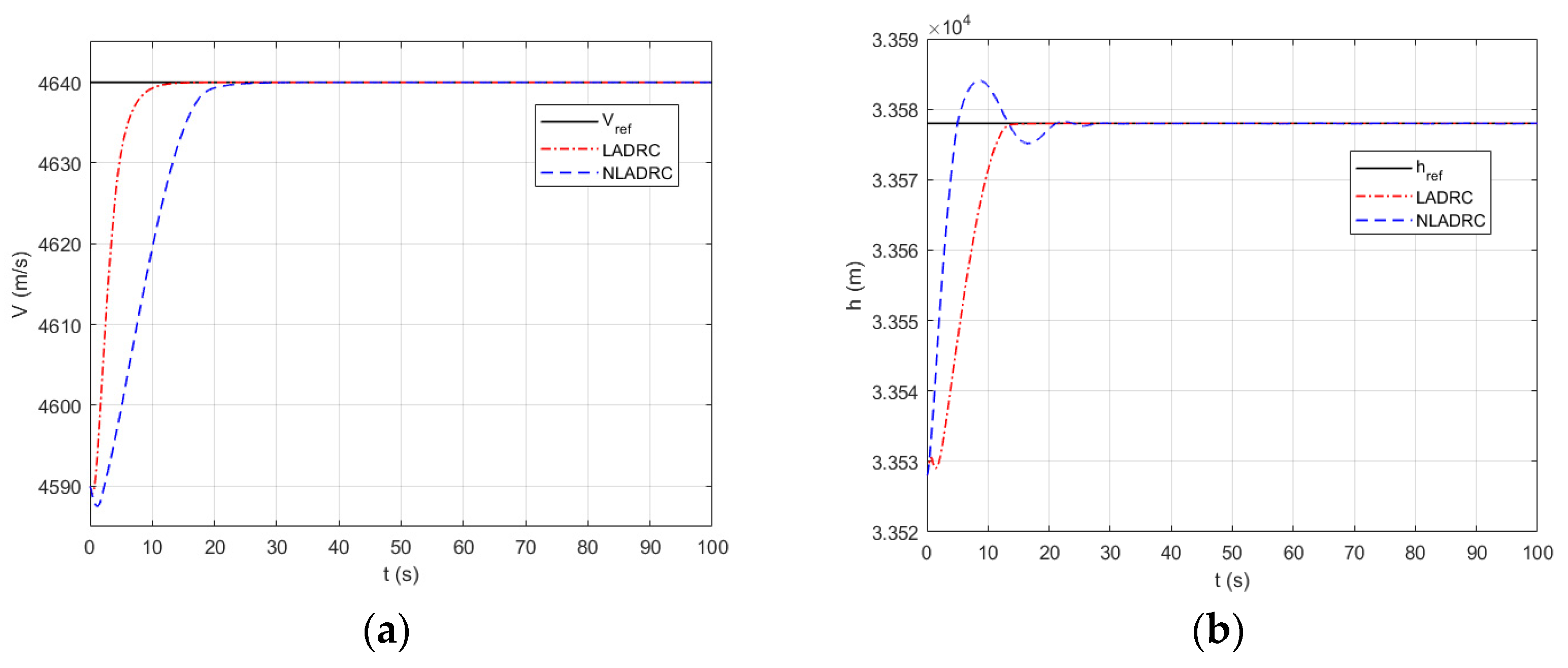
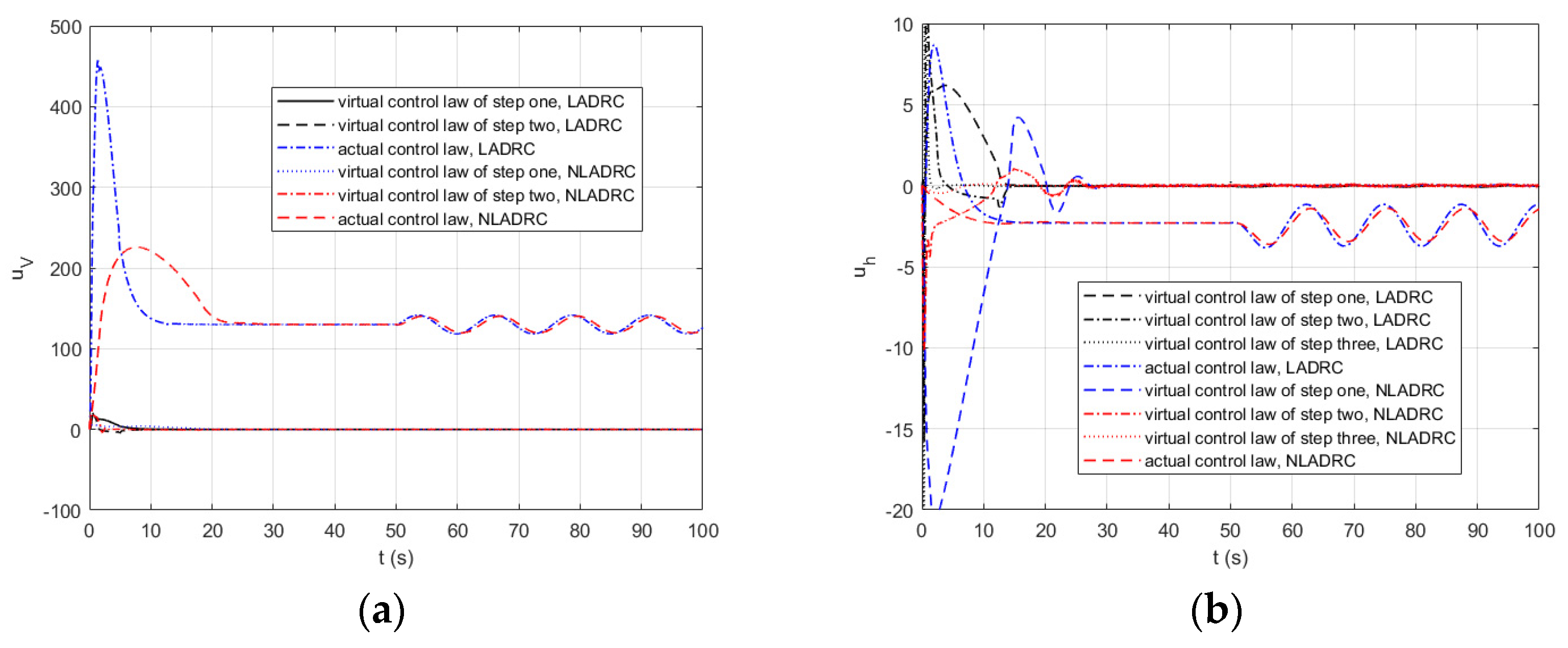
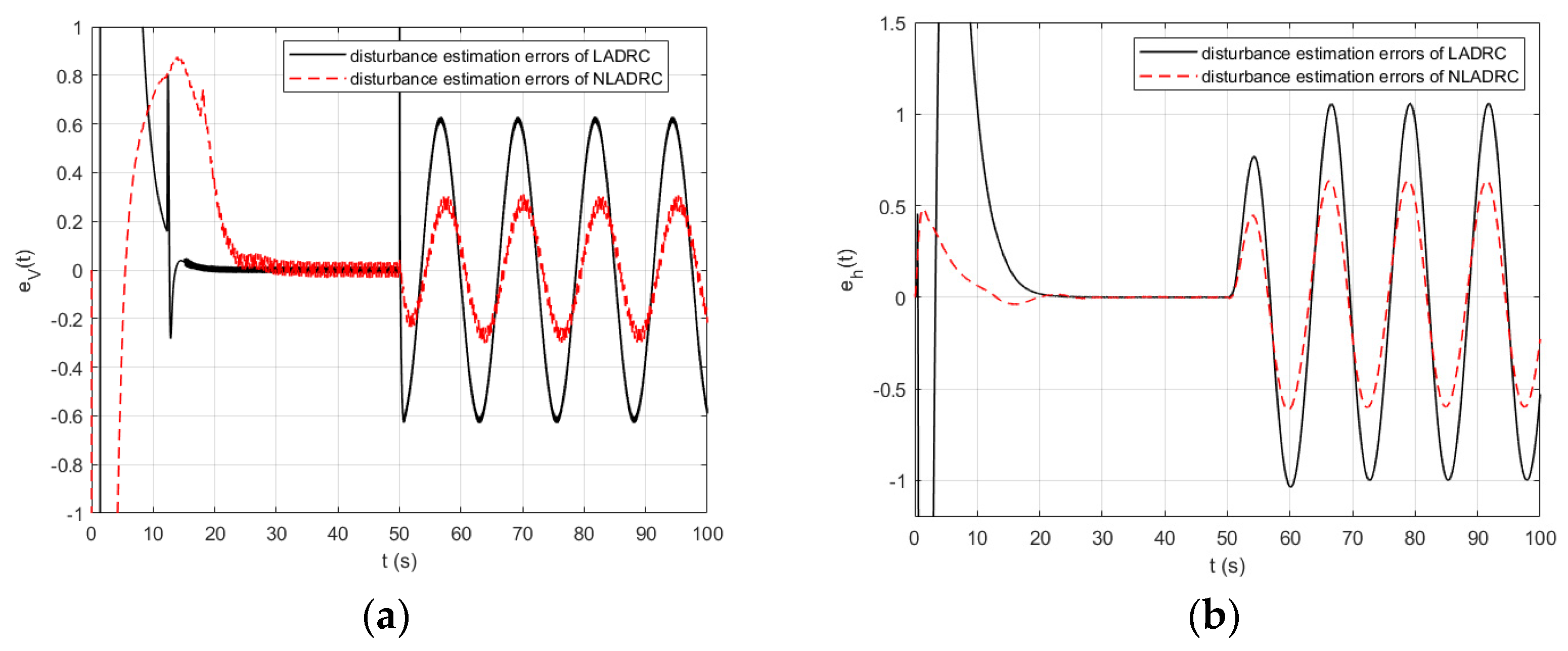
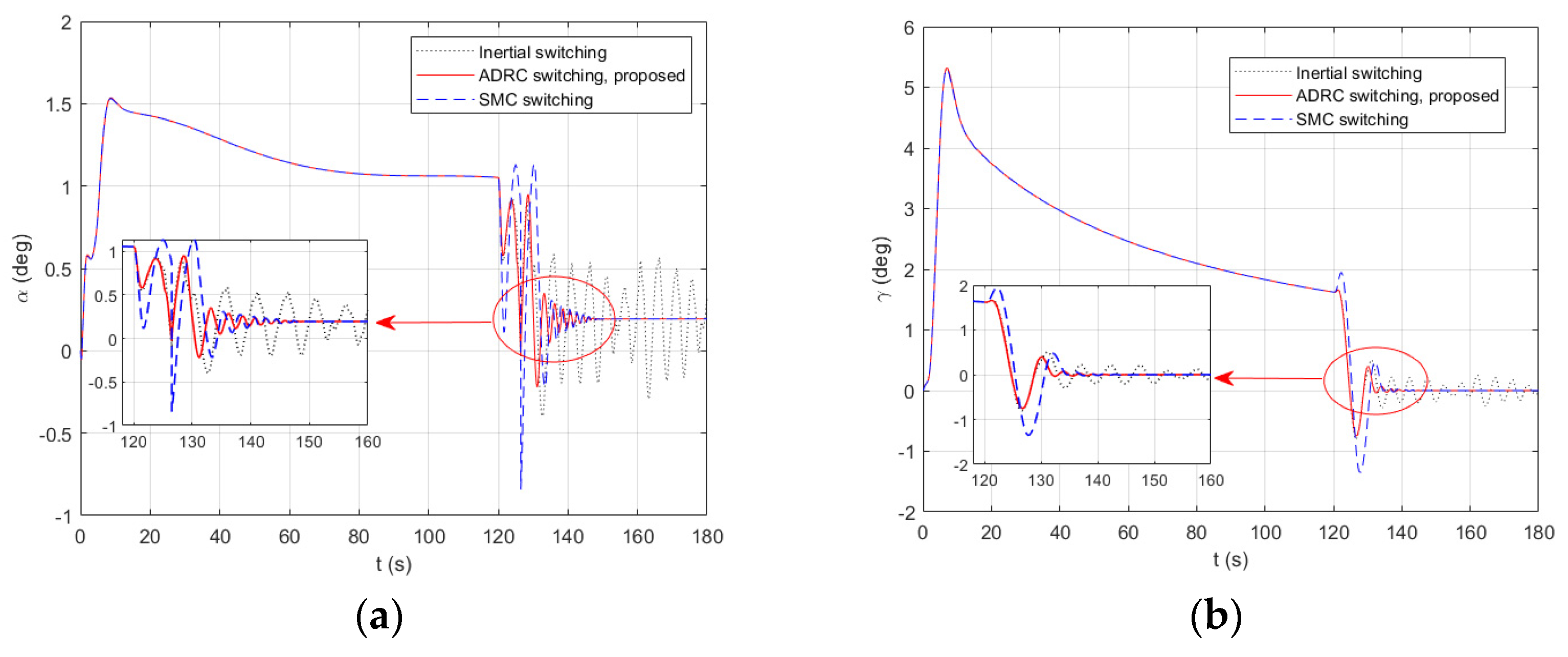
4.2. Multimodal Switching Simulation Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, J.; Li, S.; Sun, C.; Guo, L. Nonlinear Disturbance Observer Based Robust Flight Control for Airbreathing Hypersonic Vehicles. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1263–1275. [Google Scholar] [CrossRef]
- Sun, H.; Li, S.; Sun, C. Finite time integral sliding mode control of hypersonic vehicles. Nonlinear Dyn. 2013, 73, 229–244. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, Q.; Pan, Y. Neural network based dynamic surface control of hypersonic flight dynamics using small-gain theorem. Neurocomputing 2016, 173, 690–699. [Google Scholar] [CrossRef]
- Xu, B.; Wang, D.; Zhang, Y.; Shi, Z. DOB-Based Neural Control of Flexible Hypersonic Flight Vehicle Considering Wind Effects. IEEE Trans. Ind. Electron. 2017, 64, 8676–8685. [Google Scholar] [CrossRef]
- Bu, X.; He, G.; Ke, W. Tracking control of air-breathing hypersonic vehicles with non-affine dynamics via improved neural back-stepping design. ISA Trans. 2018, 75, 88–100. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z. Active disturbance rejection control: A paradigm shift in feedback control system design. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006. [Google Scholar] [CrossRef]
- Huang, Y.; Xue, W. Active disturbance rejection control: Methodology and theoretical analysis. ISA Trans. 2014, 53, 963–976. [Google Scholar] [CrossRef] [PubMed]
- Guo, B.; Liu, J. Sliding mode control and active disturbance rejection control to the stabilization of one-dimensional Schrdinger equation subject to boundary control matched disturbance. Int. J. Robust Nonlinear Control 2015, 24, 2194–2212. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Guo, B. On active disturbance rejection control for nonlinear systems using time-varying gain. Eur. J. Control 2015, 23, 62–70. [Google Scholar] [CrossRef]
- Aguilar, I.C.; Sira, R.H.; Acosta, J.A. Stability of active disturbance rejection control for uncertain systems: A Lyapunov perspective. Int. J. Robust Nonlinear Control 2017, 27, 4541–4553. [Google Scholar] [CrossRef]
- Du, H.; Fan, Y.; Yan, J. Active Disturbance Rejection Control for Airbreathing Hypersonic Vehicle. Comput. Mod. 2013, 16, 1612–1622. [Google Scholar]
- Tian, J.; Zhang, S.; Li, S. Active disturbance rejection control based robust output feedback autopilot design for airbreathing hypersonic vehicles. ISA Trans. 2018, 74, 45–59. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Sun, C.; Yang, M.; Liu, Q. Active disturbance rejection control for hydraulic systems with full-state constraints and input saturation. IET Control Theory Appl. 2022, 16, 1127–1136. [Google Scholar] [CrossRef]
- Yang, Z.; Yan, Z.; Lu, Y.; Wang, W.; Yu, L.; Geng, Y. Double DOF Strategy for Continuous-Wave Pulse Generator Based on Extended Kalman Filter and Adaptive Linear Active Disturbance Rejection Control. IEEE Trans. Power Electron. 2022, 37, 1382–1393. [Google Scholar] [CrossRef]
- Bu, X.; Qi, Q. Fuzzy optimal tracking control of hypersonic flight vehicles via single-network adaptive critic design. IEEE Trans. Fuzzy Syst. 2022, 30, 270–278. [Google Scholar] [CrossRef]
- Bu, X.; Qi, Q.; Jiang, B. A Simplified Finite-time Fuzzy Neural Controller with Prescribed Performance Applied to Waverider Aircraft. IEEE Trans. Fuzzy Syst. 2022, 30, 2529–2537. [Google Scholar] [CrossRef]
- Zeghlache, S.; Kara, K.; Saigaa, D. Fault tolerant control based on interval type-2 fuzzy sliding mode controller for coaxial trirotor aircraft. ISA Trans. 2015, 59, 215–231. [Google Scholar] [CrossRef]
- Erdal, K.; Reinaldo, M. Type-2 Fuzzy Logic Trajectory Tracking Control of Quadrotor VTOL Aircraft With Elliptic Membership Functions. IEEE/ASME Trans. Mechatron. 2017, 22, 339–348. [Google Scholar]
- Wang, J.; Hu, L.; Chen, F.; Wen, C. Multiple-step fault estimation for interval type-II T-S fuzzy system of hypersonic vehicle with time-varying elevator faults. Int. J. Adv. Robot. Syst. 2017, 14, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Jiao, X.; Fidan, B.; Jiang, J.; Kamel, M. Type-2 fuzzy adaptive sliding mode control of hypersonic flight. Proc. Inst. Mech. Eng. 2019, 233, 2731–2744. [Google Scholar] [CrossRef]
- Tao, X.; Yi, J.; Pu, Z.; Xiong, T. Robust Adaptive Tracking Control for Hypersonic Vehicle Based on Interval Type-2 Fuzzy Logic System and Small-Gain Approach. IEEE Trans. Cybern. 2021, 51, 2504–2517. [Google Scholar] [CrossRef]
- Chen, F.; Hu, L.; Wen, C. Improved adaptive fault-tolerant control design for hypersonic vehicle based on interval type-2 T-S model. Int. J. Robust Nonlinear Control 2018, 28, 1097–1115. [Google Scholar] [CrossRef]
- Yu, C.; Jiang, J.; Wang, S.; Han, B. Fixed-time adaptive general type-2 fuzzy logic control for air-breathing hypersonic vehicle. Trans. Inst. Meas. Control 2021, 43, 2143–2158. [Google Scholar] [CrossRef]
- Huang, Y.; Sun, C.; Qian, C.; Wang, L. Linear parameter varying switching attitude control for a near space hypersonic vehicle withparametric uncertainties. Int. J. Syst. Sci. 2014, 46, 3019–3031. [Google Scholar] [CrossRef]
- An, H.; Wu, Q.; Xia, H.; Wang, C.; Cao, X. Adaptive controller design for a switched model of air-breathing hypersonic vehicles. Nonlinear Dyn. 2018, 94, 1851–1866. [Google Scholar] [CrossRef]
- Dou, L.; Gao, J.; Zong, Q.; Ding, Z. Modeling and switching control of air-breathing hypersonic vehicle with variable geometry inlet. J. Frankl. Inst. 2018, 355, 6904–6926. [Google Scholar] [CrossRef] [Green Version]
- Ye, H.; Jiang, B. Adaptive Switching Control for Hypersonic Vehicle with Uncertain Control Direction. J. Frankl. Inst. 2020, 357, 8851–8869. [Google Scholar] [CrossRef]
- Jiao, X.; Baris, F.; Jang, J.; Mohamed, K. Adaptive mode switching of hypersonic morphing aircraft based on type-2 TSK fuzzy sliding mode control. Sci. China Inf. Sci. 2015, 58, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Bolender, J.M.; Doman, D. Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle. J. Spacecr. Rocket. 2007, 44, 374–387. [Google Scholar] [CrossRef]
- Xu, W.; Li, Y.; Lv, M.; Pei, B. Modeling and switching adaptive control for nonlinear morphing aircraft considering actuator dynamics. Aerosp. Sci. Technol. 2022, 122, 107349.1–107349.17. [Google Scholar] [CrossRef]
- Li, J.; Qi, X.; Xia, Y.; Gao, Z. On Linear/Nonlinear Active Disturbance Rejection Switching Control. Acta Autom. Sin. 2016, 42, 202–212. [Google Scholar]
- Wu, Z.; Deng, C.; Wen, H. Fuzzy Linear/Nonlinear Active Disturbance Rejection Switching Control and Its Application. Acta Aeronaut. Astronaut. Sin. 2021, 42, 473–480. [Google Scholar]





| S | M | B | ||
|---|---|---|---|---|
| S | ||||
| M | ||||
| B | ||||
| S | M | B | ||
|---|---|---|---|---|
| S | ||||
| M | ||||
| B | ||||
| Winglet States | Reference Area | Aerodynamic Chord | Aerodynamic Parameters |
|---|---|---|---|
| Stretch out state | 389 | 30 | |
| Draw back state | 369 | 27 | |
| Stretch out state to draw back state | |||
| Draw back state to stretch out state | |||
| States | Value | States | Value |
|---|---|---|---|
| 4590 | 50,200 | ||
| 33,528 | 8,466,900 | ||
| 0 | 369 | ||
| 0 | 28 | ||
| 0 | 0.0292 |
| Winglet Switching Time | Aerodynamic Parameters |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, O.; Deng, L.; Jiang, J.; Huang, S. Linear/Nonlinear Active Disturbance Rejection Switching Control for Near-Space Morphing Vehicles Based on Type-2 Fuzzy Logic System. Appl. Sci. 2023, 13, 8255. https://doi.org/10.3390/app13148255
Li O, Deng L, Jiang J, Huang S. Linear/Nonlinear Active Disturbance Rejection Switching Control for Near-Space Morphing Vehicles Based on Type-2 Fuzzy Logic System. Applied Sciences. 2023; 13(14):8255. https://doi.org/10.3390/app13148255
Chicago/Turabian StyleLi, Ouxun, Li Deng, Ju Jiang, and Shutong Huang. 2023. "Linear/Nonlinear Active Disturbance Rejection Switching Control for Near-Space Morphing Vehicles Based on Type-2 Fuzzy Logic System" Applied Sciences 13, no. 14: 8255. https://doi.org/10.3390/app13148255





